Adaptive Noise Suppression of Pediatric Lung Auscultations With Real Applications to Noisy Clinical Settings in Developing Countries

Abstract

Goal

Chest auscultation constitutes a portable low-cost tool widely used for respiratory disease detection. Though it offers a powerful means of pulmonary examination, it remains riddled with a number of issues that limit its diagnostic capability. Particularly, patient agitation (especially in children), background chatter, and other environmental noises often contaminate the auscultation, hence affecting the clarity of the lung sound itself. This paper proposes an automated multiband denoising scheme for improving the quality of auscultation signals against heavy background contaminations.

Methods

The algorithm works on a simple two-microphone setup, dynamically adapts to the background noise and suppresses contaminations while successfully preserving the lung sound content. The proposed scheme is refined to offset maximal noise suppression against maintaining the integrity of the lung signal, particularly its unknown adventitious components that provide the most informative diagnostic value during lung pathology.

Results

The algorithm is applied to digital recordings obtained in the field in a busy clinic in West Africa and evaluated using objective signal fidelity measures and perceptual listening tests performed by a panel of licensed physicians. A strong preference of the enhanced sounds is revealed.

Significance

The strengths and benefits of the proposed method lie in the simple automated setup and its adaptive nature, both fundamental conditions for everyday clinical applicability. It can be simply extended to a real-time implementation, and integrated with lung sound acquisition protocols.

I. Introduction

The use of chest auscultation to diagnose lung infections has been in practice since the invention of the stethoscope in the early 1800s. It is a diagnostic instrument widely used by clinicians to “listen” to lung sounds and flag abnormal patterns that emanate from pathological effects on the lungs. While often complemented by other clinical tools, such as chest radiography or other imaging techniques, as well as chest percussion and palpation, the stethoscope remains a key diagnostic device due to its portability, low cost, and its noninvasive nature. Chest auscultation with standard acoustic stethoscopes is not limited to resource-rich industrialized settings. In low-resource high-mortality countries with weak health care systems, there is limited access to diagnostic tools like chest radiographs or basic laboratories. As a result, health care providers with variable training and supervision rely upon low-cost clinical tools like standard acoustic stethoscopes to make critical patient management decisions. Despite its universal adoption, the use of the stethoscope is riddled by a number of issues including subjectivity in interpretation of chest sounds, interlistener variability and inconsistency, need for medical expertise, as well as vulnerability to ambient noise which can mask the presence of sound patterns of interest.

The issue of environmental noise contaminations is of particular interest, especially in busy clinics and rural health centers where a quiet examination environment is often not possible, background chatter and other environmental noises are common, and patient agitation (especially in children) contaminate the sound signal picked up by the stethoscope. This distortion affects the clarity of the lung sound, hence limiting its clinical value for the health care practitioner. It also impedes the use of electronic auscultation combined with computerized lung sound analysis which are gaining traction in an effort to remedy the inconsistency limitations of standard (acoustic) stethoscope devices and to provide an objective and standardized interpretation of lung sounds [1]–[3]. However, these automated approaches have mainly been validated in well-controlled or quiet clinical settings with adult subjects. The presence of background noise impedes the applicability of these algorithms or leads to unwanted false positives [4].

The current study investigates the use of multiband spectral subtraction to address noise contaminations in busy patient-care settings, where prominent subject-centric noise and room sounds corrupt the recorded signal and mask the lung sound of interest. The setup employs a simple digital stethoscope with a mounted external microphone capturing the concurrent environmental or room noise. The algorithm focuses on two parallel tasks: 1) suppress the surrounding noise; 2) preserve the valuable lung sound content. While spectral subtraction is a generic signal denoising approach, its applicability to the problem at hand is nontrivial in two ways: First, although the signal of interest (i.e., lung sounds) has relatively well-defined characteristics [5], [6], unknown anomalous sound patterns reflecting lung pathology complicate the analysis of the obtained signal. These adventitious patterns vary from quasi-stationary events, such as wheezes to highly transient sounds such as crackles [7], [8]. They are unpredictable irregular patterns whose signal characteristics are not well defined in the literature [9]–[11]. Yet, any processing needs to faithfully preserve these occurrences given their presumed clinical and diagnostic significance. Second, noise is highly nonstationary and its signal characteristics differ in the degree of overlap with the signal of interest. Noise contaminations can include environmental sounds picked up in the examination room (chatter, phones ringing, fans, etc.), patient-specific noises (child cry, vocalizations, agitation), or electronic/mechanical noise (stethoscope movement, mobile interference).

This paper tries to balance the suppression of the undesired noise contaminations while maintaining the integrity of the lung signal along with its adventitious components. The multiband spectral scheme presented here carefully tunes the critical parameters in spectral subtraction in order to maximize the improved quality of the processed signal. The performance of the proposed approach is validated by formal listening tests performed by a panel of licensed physicians as well as objective metrics assessing the quality of the processed signal. Sections II and III describe the theory and implementation details of the proposed algorithm. Section IV discusses the formal listening experiment setup. Evaluation results are described in Section V, including comparisons to existing methods. We finish with a general discussion of the proposed approach in Section VI.

II. Multiband Spectral Subtraction

Spectral subtraction algorithms have been widely used in fields of communication and speech enhancement to suppress noise contaminations in acoustic signals [12], [13]. The general framework behind these noise reduction schemes can be summarized as follows: let y(n) be a known measured acoustic signal of length N and assume that it comprises of two additive components x(n) and d(n), corresponding respectively to a clean unknown signal we wish to estimate and an inherent noise component which is typically not known. In many speech applications, the noise distortion is estimated from silent periods of the speech signal that are identified using a voice activity detector [13]. Alternatively, the noise distortion can be estimated using a dual or multimicrophone setup, where a secondary microphone picks up an approximate estimate of the noise contaminant. Here we employ the latter, a dual-microphone setup capturing both the internal signal coming from the stethoscope itself, and the external signal coming from a mounted microphone. The external signal is assumed to be closely related to the actual noise that contaminates the lung signal of interest, and shares its spectral magnitude characteristics with possibly different phase profiles due to their divergent traveling trajectories to the pickup microphones.

Here noise is assumed to have additive effects on the desired signal and originate through a wide-sense stationary process. Without loss of continuity, we alleviate the stationarity requirements for the noise process, and assume a smoothly varying process whose spectral characteristics change gradually over successive short-time periods. In this paper, such noise signal d(n, τ) represents the patient- or room-specific noise signal; x(n, τ) denotes the desired unknown clean lung sound information, free of noise contaminations; and y(n, τ) denotes the acoustic information captured by the digital stethoscope

$$y(n,\tau )=x(n,\tau )+d(n,\tau ).$$ (1)

τ is used to represent processing over short-time windows w(n). In other words, x(n, τ) = x(n)w(τ − n) and similarly for y(n, τ) and d(n, τ). For the corresponding frequency-domain formulation, let X(ω, τ) denote the discrete Fourier transform (DFT) of x(n, τ), implemented by sampling the discrete-time Fourier transform at uniformly spaced frequencies ω. Letting Y (ω, τ) and D(ω, τ) be defined in a similar way for y(n, τ) and d(n, τ), (1) becomes: |Y (ω, τ)|e^{j φ _y (ω, τ)} = |X(ω, τ)|e^{j φ _x (ω, τ)} + |D(ω, τ)|e^{j φ _d (ω, τ)}. Short-term magnitude spectrum |D(ω, τ)| can be approximated as $\mid \widehat{D}(\omega ,\tau )\mid$ using the signal recorded from the external microphone. Phase spectrum φ_d (ω, τ) can also be reasonably replaced by the phase of the noisy signal φ_y (ω, τ) considering that phase information has minimal effect on signal quality especially at reasonable signal-to-noise ratios (SNR) [14]. Therefore, the denoised signal can be formulated as

$$\widehat{X}(\omega ,\tau )=(\mid Y(\omega ,\tau )\mid -\mid \widehat{D}(\omega ,\tau )\mid )e^{j{\varphi }_y(\omega ,\tau )}.$$ (2)

The same formulation can be extended to the power spectral density domain by making the reasonable assumption that environmental noise d(n, τ) is a zero-mean process, uncorrelated with the lung signal of interest x(n, τ)

$${\mid \widehat{X}(\omega ,\tau )\mid }^2={\mid Y(\omega ,\tau )\mid }^2-{\mid \widehat{D}(\omega ,\tau )\mid }^2.$$ (3)

Building on this basic spectral subtraction formulation to synthesize the desired signal, we extend this design in a number of ways

• 1) Extending the subtraction scheme into multiple frequency bands $\left\{w_k\right\}\in [{\omega }_k^{\min },{\omega }_k^{\max }]$. This localized frequency treatment is especially crucial given the variable, unpredictable, and nonuniform nature of noise distortions that affect the lung recording (see [15] for a discussion of signal characteristics of noise contaminants). Looking back in (3), the subtraction term $\widehat{D}(\omega ,\tau )$ can be weighted differently across frequency bands by constructing appropriate weighting rules (δ_k) that highlight the most informative spectral bands for lung signals.

• 2) Altering the scheme to weight the subtraction operation across time windows and frequency bands by taking into account the current frame’s SNR.

• 3) Reducing the residual noise in the signal reconstruction by smoothing Y (ω, τ) estimate over adjacent frames.

Therefore, for frame τ and frequency band ω_k, the enhanced estimated signal spectral density is given by

$${\mid \widehat{X}({\omega }_k,\tau )\mid }^2={\mid \widehat{Y}({\omega }_k,\tau )\mid }^2-{\alpha }_{k,\tau }{\delta }_k{\mid \widehat{D}({\omega }_k,\tau )\mid }^2.$$ (4)

Bar notation $\stackrel{‒}{Y}({\omega }_k,\tau )$ signifies a smooth estimate of Y (ω_k, τ) over adjacent frames. α_k,τ is an oversubtraction factor adjusted by the current frame’s SNR, for each band ω_k and frame τ. δ_k is a spectral weighting factor that highlights lower frequencies typically occupied by lung signals [5, 16] and penalizes higher frequencies where noise interference can spread. Partial noise is then added back to the signal (5) using a weighing factor γ_τ ∈ (0, 1) to suppress musical noise effects [12], [17]. The final estimate $\tilde{x}\left(n\right)$ is resynthesized using the inverse DFT and overlap and add method across frames [13]

$${\mid \tilde{X}({\omega }_k,\tau )\mid }^2=(1-{\gamma }_{\tau }){\mid \widehat{X}({\omega }_k,\tau )\mid }^2+{\gamma }_{\tau }{\mid \stackrel{‒}{Y}({\omega }_k,\tau )\mid }^2.$$ (5)

III. Methods

Lung signals were acquired using a Thinklabs ds32a digital stethoscope at 44.1-kHz rate, by the Pneumonia Etiology Research for Child Health (PERCH) study group [18]. Thinklabs stethoscopes used for the study were mounted with an independent microphone fixed on the back of the stethoscope head, capturing simultaneous environmental contaminations without any hampering of the physician’s examination. Auscultation recordings were obtained from children enrolled into the PERCH study with either World Health Organization-defined severe and very severe clinical pneumonia (cases) or community controls without clinical pneumonia [19] in a busy clinical setting in Basse, Gambia in West Africa. A total of 22 infant recordings among hospitalized pneumonia cases with an average age of 12.2 months (2–37 months) were considered. Following the examination protocol, nine body locations were auscultated for a duration of 7 s each. The last body location corresponded to a cheek position and is not used in this study.

Noise contaminations were prominent throughout all recordings in the form of ambient noise, mobile buzzing, background chatter, intense subject’s crying, musical toys in the waiting room, power generators, vehicle sirens, or animal sounds. Patients were typically seated in their mothers’ lap and were quite agitated, adding to the distortion of auscultation signal.

A. Preprocessing

All acquired signals were low-pass filtered with a fourth-order Butterworth filter at 4 kHz cutoff, downsampled to 8 kHz, and centered to zero mean and unit variance. Resampling can be justified by guidelines of the CORSA project of the European Respiratory Society [16], as lung sounds are mostly concentrated at lower frequencies.

A clipping distortion algorithm was then applied to correct for truncated signal amplitude (occurring when the microphone reached maximum acoustic input). Although clipped regions were of the order of a few samples per instance, they produced very prominent signal distortions. The algorithm identifies regions of constant (clipped) amplitude, and replaces these regions using cubic spline interpolation [20].

B. Implementation

The proposed algorithm employs a wide range of parameters that can significantly affect the reconstructed sound quality. An initial evaluation phase using informal testing and visual inspection reduced the parameter space. The preliminary assessment of the algorithm suggests that 32 frequency bands were adequate, using frequency-domain windowing to reduce complexity. Since the algorithm operates independently among bands, their boundaries can affect the final sound output. Two ways of creating the subbands were explored: 1) logarithmic spacing along the frequency axis and 2) equienergy spacing. The latter spacing corresponds to splitting the frequency axis into band regions containing equal proportions of the total spectral energy. Other band splitting methods were excluded from analysis after the initial assessment phase.

An important factor related to the frequency binning of the spectrum is the weighing among frequency bands, regulated by factor δ_k in (4). Since interfering noise affects the spectrum in a nonuniform manner, we imposed this nonlinear frequency-dependent subtraction to account for different types of noise. It can be thought of as a signal-dependent regulator, taking into account the nature of the signal of interest. Lung sounds are complex signals comprised of various components [16], [21], [22]: normal respiratory sounds typically occupy 50–2500 Hz; tracheal sounds reach energy contents up to 4000 Hz, and heart beat sounds vary within 20–150 Hz. Finally, wheeze and crackles, the commonly studied adventitious (abnormal) events, typically have a range of 100–2500 and 100–500 Hz, respectively. Other abnormal sounds like stridor, squawk, low-pitched wheeze or cough, all exhibit a frequency profile below 4 kHz. The motivation for appropriately setting factor δ_k is to minimize distortion of lung sounds that typically occupy low frequencies and penalize noise occurrences with strong energy content at high frequencies [15]. Our analysis suggested two value sets for parameter δ_k in Table I. In logarithmic spacing, subbands F₁₇, F₂₅, F₂₆, and F₂₇ correspond to 80, 650, 850, and 1100 Hz, respectively. In equienergy spacing, F_m corresponds to the mth subband whose frequency ranges are signal dependent; F₁₇, F₂₅, and F₂₆ roughly correspond to 750, 2000, and 2300 Hz. Comparing the proposed sets, δ⁽¹⁾ resulted in stronger suppression of high-frequency content.

TABLE I.

Two Proposed Sets of Values for δ_k

fk band range	${\delta }_k^{\left(1\right)}$ value	${\delta }_k^{\left(2\right)}$ value
(0, F17 ]	0.01	0.01
(F17 , F25 ]	0.015	0.02
(F25 , F26 ]	0.04	0.05
(F26 ,F27]	0.2	0.7
else	0.7	0.7

This nonlinear subtraction scheme was further enforced by the frequency-dependent oversubtraction factor α_k,τ defined in (6) which regulates the amount of subtracted energy for each band, using the current frame’s SNR. Larger values were subtracted in bands with low a posteriori SNR levels, and the opposite was true for high SNR levels. This way, rapid SNR level changes among subsequent time frames could be accounted for. On the other hand, such rapid energy changes were not expected to occur within a frequency band, considering the natural environment where recordings took place; thus, the factor α_k,τ could be held constant within bands. Such frame-dependent SNR calculations could also remedy for a type of signal distortion known as musical noise, which can be produced during the enhancement process.

$${\alpha }_{k,\tau }=\{\begin{array}{cc}4.75\hfill & :{\mathrm{SNR}}_{k,\tau }<-25\hfill \\ 4-\frac{3{\mathrm{SNR}}_{k,\tau }}{20}\hfill & :-25\le {\mathrm{SNR}}_{k,\tau }\le 40\hfill \\ 1\hfill & :{\mathrm{SNR}}_{k,\tau }>40\hfill \end{array}\phantom{\}}$$

$${\mathrm{SNR}}_{k,\tau }=10{\log }_{10}\left(\sum _{\omega \in \omega k}{\mid \stackrel{‒}{Y}(\omega ,\tau )\mid }^2∕\sum _{\omega \in \omega k}{\mid \widehat{D}(\omega ,\tau )\mid }^2\right)$$ (6)

The window length for short-time analysis of the signal was another crucial parameter that can result in noticeable artifacts, since a long-time window might violate the stationarity assumptions made in Section II. Following the initial algorithm assessment phase, we proposed two ways of short-time processing: 1) 50-ms window (N = 400) and 90% overlap; and 2) 80-ms window (N = 640) with 80% overlap. Hamming windowing w(n) was applied in the time waveform to produce all frames. Negative values possibly arising by (4) were replaced by a 0.001% fraction of the original noisy signal energy, instead of using hard thresholding techniques like half-wave rectification.

Finally, the enhancement factor γ_τ for frame τ in (5) was an SNR-dependent factor and was set closer to 1 for high SNR_τ, and closer to 0 for low SNR_τ values. For the calculation of $\stackrel{‒}{Y}({\omega }_k,\tau )$, the smooth magnitude spectrum was obtained by weighting across ±2 time frames, given by $\mid \stackrel{‒}{Y}({\omega }_k,\tau )\mid ={\sum }_{j=-2}^{2}W\left(j\right)\mid Y_{\tau -j}\left({\omega }_k\right)\mid$ with coefficients W = [0.09, 0.25, 0.32, 0.25, 0.09].

C. Postprocessing

Typically, time intervals where the stethoscope is in poor contact with the subject’s body tended to exhibit insignificant or highly suppressed spectral energy. After the application of the enhancement algorithm, intervals with negligible energy below 50 Hz were deemed uninformative and removed. A moving average filter smoothed the transition edges.

IV. Human Listener Experiment

The listening experiment was designed with a two-fold purpose: 1) evaluate the effectiveness of the proposed enhancement procedure and 2) evaluate the effect of the proposed parameters including frequency band binning, window size, and customized band-subtraction factor δ_k,τ on the perceived sound quality. All methods were designed within the scope of the PERCH study and approved by the Johns Hopkins Bloomberg School of Public Health Institutional Board of Review (IRB).

A. Participants

Eligible study participants were licensed physicians with significant clinical experience auscultating and interpreting lung sounds from children. A total of 17 physicians (6 pediatric pulmonologists and 11 senior pediatric residents) were enrolled, all affiliated with Johns Hopkins Hospital in Baltimore, MD, USA, with informed consent, as approved by the IRB at the Johns Hopkins Bloomberg School of Public Health, and were compensated for participation.

B. Setup

The experiment took place in a quiet room at Johns Hopkins University and was designed to last for 30 min, including rest periods. Data recorded in the field in the Gambia clinic were played back on a computer to participants in the listening experiment. Participants were asked to wear a set of Sennheiser PXC 450 headphones and listen to 43 different lung sound excerpts of 3 s duration each. The excerpts originated from 22 distinct patients diagnosed with World Health Organization-defined severe or very severe pneumonia [19]. For each excerpt, the participant was presented with the original unprocessed recording, along with four enhanced versions A, B, C, D. These enhanced lung sounds were obtained by applying the proposed algorithm with different sets of parameter values, as shown in Table II. In order to increase robustness of result findings, the experiment was divided into two groups consisting of eight and nine listeners, respectively. Each group was presented with a different set of lung sound excerpts, making sure that at least one excerpt from all 22 distinct patients were contained within each set. In order to minimize selection bias, fatigue, and concentration effects, the sound excerpts were presented in randomized order for every participant. The list of presented choices was also randomized so that, on the test screen, choice A would not necessarily correspond to algorithmic version A for different sound excerpts, and similarly for choices B, C, and D.

TABLE II.

Implementation Details Behind Algorithms A, B, C, D Running on Different Short-Time Analysis Windows, Frequency Band Splitting and Selection of the Band-Subtraction Factor δ_k

	A	B	C	D
Window (ms)	50	50	50	80
Band Split	log	equilinear	log	log
Selection δk	${\delta }_k^{\left(1\right)}$	${\delta }_k^{\left(1\right)}$	${\delta }_k^{\left(2\right)}$	${\delta }_k^{\left(1\right)}$

Listeners were given a detailed instruction sheet and presented with one sound segment at a time. They were asked to listen to each original sound and the enhanced versions as many times as needed. Listeners indicated their preferred choice while considering the preservation or enhancement of lung sound content and breaths, and the perceived sound quality. Instructions clearly stated that this was a subjective listening task with no correct answer. If participants preferred more than one options, they were instructed to just choose one of them. If they preferred all of the enhanced versions the same, but better than the original, an extra choice, “Any,” (brief for “Any of A, B, C, D”) was added.

C. Dataset

Data included in the listening experiment was chosen “pseudo-randomly” from the entire dataset available. Although initial 3-s segments were chosen randomly from the entire data pool, the final dataset was slightly augmented in order to include: 1) abnormal occurrences comprising of wheeze, crackles or other; 2) healthy breaths; and 3) abnormal and normal breaths in both low- and high-noise environments. A final selection step ensured that recordings from different body locations were among the tested files.

V. Results

The validation of the proposed enhancement algorithm requires a balance of the audio signal quality along with a faithful conservation of the spectral profile of the lung signal. It is also important to consider that clinical diagnosis using stethoscopes is ideally done by a physician or health care professional whose ear has been trained accordingly, i.e., for listening to stethoscope-outputted sounds. Any signal processing to improve quality should not result in undesired signal alterations that stray too far from the “typical” stethoscope signal, since the human ear will be interpreting the lung sounds at this time. For instance, some aspects of filtering result in “tunnel hearing” effects, which would be undesirable even if the quality is maintained. In order to properly assess the performance of the proposed algorithm, we used three forms of evaluations: visual inspection, objective signal analyses, and formal listening tests, as detailed below. We also used the field recordings employed in the current study to compare the performance of existing enhancement algorithms from the literature.

A. Visual Inspection

Fig. 1 shows the time–frequency profile of four lung sound excerpts appearing per column. Typical energy components that emerge from such spectrograms are the breaths and heart beats, producing repetitive patterns that follow the child’s respiratory and heart rate—[see (a) and (b)]. Such energy components are well preserved in the enhanced signals (bottom). Middle rows depict concurrent noise distortions captured by the external microphone. Contamination examples include (a) mobile interference and (b)–(d) background chatting or crying, which have successfully been suppressed or eliminated, providing a clearer image of the lung sound energies.

Fig. 1.

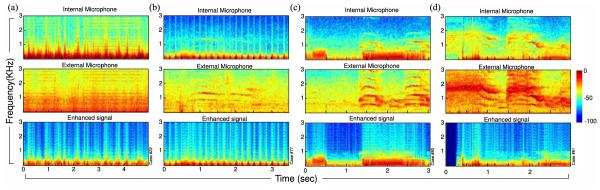
Spectrogram representation of four lung sound excerpts. Top panel: internal microphone; middle panel: external microphone recording; bottom panel: signal as outputted by spectral subtraction algorithm B. The quasi-periodic energy patterns, more pronounced in (a) and (b), correspond to the breathing and heart cycles and are well preserved in the enhanced signal. (a) Electronic interference contaminations and (b) soft background cry have successfully been removed. Panels (c) and (d) show cases heavily contaminated by room noise and loud background crying which have substantially been suppressed using the proposed algorithm. Notice how concurring adventitious events were kept intact in (c) at 1.5–3 s and in (d) at 0.6–0.8 s . The period at the beginning of (d) corresponded to an interval of no contact with the child’s body and was silenced after the postprocessing algorithm.

B. Objective Validation of Processed Signals

To further assess improvements on the processed signals, objective methods were used to compare the signals before and after processing. Choosing an evaluation metric for enhancement is a nontrivial issue; many performance or quality measures commonly proposed in the literature often require knowledge of the true clean signal or some estimate of its statistics [23]. This is not feasible in our current application: biosignals, such as lung sounds, have both general characteristics that can be estimated over a population, but also carry individual traits of each patient that should be carefully estimated. It is also important to maintain the adventitious events in the lung sound while mitigating noise contamination and other distortions. To provide an objective assessment of the proposed method, we employed a number of qualitative and quantitative measures coming from telecommunication and speech processing fields but adapted to the problem at hand. The metrics were chosen to assess how much shared information remains in the original and enhanced signals, relative to the background noise recording. While it is important to stress that these are not proper measures of signal quality improvement, they provide an informative assessment of shared signal characteristics before and after processing.

1) Segmental Signal-to-Noise Ratio (fSNRseg): Objective quality measure estimated over short-time windows accounting for signal dynamics and non-stationarity of noise [13]

$$\mathrm{fSNRseg}=\frac{10}{T}\sum _{\tau =1}^T\frac{\sum _{k=1}^K{w}_k{\mathrm{SNR}}^F}{\sum _{k=1}^K{w}_k}$$

with ${\mathrm{SNR}}^F={\log }_{10}\{\left({\mid X(k,\tau )\mid }^2\right)∕{(\mid X(k,\tau )\mid -\mid \widehat{X}(k,\tau )\mid )}^2\}$, where w_k represents the weight for frequency band k, $\widehat{X}$ represents the processed signal, and X typically represents the clean (desired) signal. As mentioned above, in this paper, X will represent the background noise, since the clean uncontaminated signal in not available. SNR^F is calculated over short-time windows of 30 ms to account for signal dynamics and non-stationarity of noise using a Hanning window. For each frame, the spectral representations X(k, τ) and $\widehat{X}(k,\tau )$ are computed by critical band filtering. The bandwidth and center frequencies of the 25 filters used and the perceptual (Articulation Index) weights w_k follow the ones proposed in [24] and [13]. Using the described method, fSNRseg value can reach a maximum of 35 when the signals under comparison are identical. Comparatively, a minimum value just below −8 can be achieved when one of the signals comes from a white Gaussian process.

2) Normalized-Covariance Measure (NCM): A metric used specifically for estimated speech intelligibility (SI) by accounting for audibility of the signal at various frequency bands. It is a speech-based speech transmission index measure capturing a weighted average of a signal to noise quantity SNR^N, where the latter is calculated from the covariance of the envelopes of the two signals over different frequency bands k [25] and normalized to [0,1]. The band-importance weights w_k followed ANSI-1997 standards [26]. Though this metric is speech-centric (as many quality measures in the literature), it is constructed to account for audibility characteristics of the human ear, hence reflecting a general account of improved quality of a signal as perceived by a human listener

$$\mathrm{NCM}=\left\{\sum _{k=1}^K{w}_{k}SN{R}^N\left(k\right)\right\}∕\sum _{k=1}^K{w}_k.$$

3) Three-Level Coherence Speech Intelligibility Index (CSII): The CSII metric is also a SI-based metric based on the ANSI standard for the speech intelligibility index (SII). Unlike NCM, CSII uses an estimate of SNR in the spectral domain, for each frame τ = 1,…,T : the signal-to-residual ${\mathrm{SNR}}_{\mathrm{ESi}}^N$; the latter is calculated using the roex filters and the magnitude-squared coherence followed by [0,1] normalization. A 30-ms Hanning window was used and the three-level CSII approach divided the signal into low-, mid-, and high-amplitude regions, using each frame’s root-mean-square level information [13], [27]

$$\mathrm{CSII}=\frac{1}{T}\sum _{\tau =1}^T\frac{\sum _{k=1}^K{w}_k{\mathrm{SNR}}_{\mathrm{ESI}}^N(k,\tau )}{\sum _{k=1}^K{w}_k}.$$

All metrics generally require knowledge of the ground truth undistorted lung signal, which is not available in our setup. In this paper, we apply them to contrast how much information is shared between the improved and the background (noise) signal, relative to the nonprocessed (original) auscultation signal. Specifically, each metric was computed between the time waveforms of the original y(n) and the background noise $\widehat{d}\left(n\right)$ signals, then contrasted for the enhanced $\tilde{x}\left(n\right)$ and the background $\widehat{d}\left(n\right)$ signals. The higher the achieved metric value, the “closer” the compared signals are, with respect to their sound contents. Fig. 2(a) shows histogram distribution results for each metric: fSNRseg yielded, on average, a value of 1.02 between the original and the noise signals, likely reflecting leak through the surrounding environment to the internal microphone. Such measure was reduced to −0.44 when contrasting the improved with the noise signal indicating reduced joint information. The two distributions were statistically significantly different (paired t-test: t-statistic = 15.99 and p-value p_t = 3E − 13; Wilcoxon: Z-statistic = 4.5 and p-value p_w = 8E − 6) providing evidence that the original signal was “closer”—statistically—to the surrounding noise, relative to the enhanced signal. Significant difference was also observed in all other metrics [see Fig. 2(a)] with NCM (p_t = 1E − 10; p_w = 2 E − 6) , CSII_med (p_t = 1E − 10; p_w = 3 E − 5), and CSII_high (p_t = 7E − 10; p_w = 7E − 6).

Fig. 2.

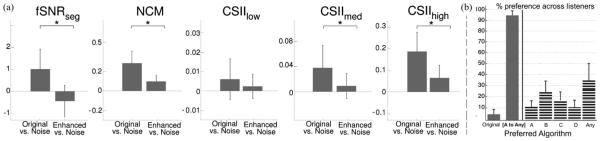
(a) Average results with error bars on the evaluation of objective, quality, and intelligibility measures for original noisy signal (left bar) and the enhanced signal (right bar), compared with noise as the ground truth. Enhanced signals were found to be more “distant” representations of the noise signals. Stars indicate statistically significant differences. (b) Average responses of the listening text where bars indicate the preference percentage per choice. Left: overall results, comparing average preference of the original sounds versus preference of any of the enhanced versions. Panel [A to Any] includes choices {A, B, C, D, Any}; Right: the breakdown among all choices. Choice Any of A,B,C,D has been abbreviated to Any.

C. Listening Experiment

While objective signal metrics hint to significant improvements in the original recording postprocessing, the way to effectively validate the denoising value of the proposed algorithm along with its clinical value for a health care professional is via perceptual listening tests by a panel of experts. Following the methods described in Section IV, the perceived quality of the processed signals was assessed with formal listening evaluations. Fig. 2(b) summarizes the opinions of the panel of experts. Considering all listeners and all tested sound excerpts, the bars indicate the percentage of preference among the available choices. Bar plots were produced by first forming a contingency table per listener, counting his/her choice preferences, and then averaging across listeners. The vertical lines depict the standard variation among all listeners. The listed choices on the x-axis correspond one by one to the ones presented during the listening test, where choice Any of A, B, C, D has been abbreviated to Any. An extra panel [A to Any] is added here illustrating preference percentages for any enhancement version of the algorithm, irrespective of choice of parameters. On average, listeners prefer mostly choice Any (34.06% of the time), followed by choices B and C. Overall, listeners prefer the enhanced signal relative to the original unprocessed signal 95.08% of the time. Considering responses across groups of listeners, results are consistent across Group 1 and Group 2. A statistical analysis across the two groups using a parametric t-test and a nonparametric Wilcoxon rank sum test shows no difference among the two populations except possibly for choice D. The corresponding p-values for the t-test and the Wilcoxon test (p_t, p_w) are: for choice Original: (0.28, 0.23); choice A: (0.37, 0.52); choice B: (0.74, 0.62); choice C: (0.33, 0.74); choice D: (0.08, 0.10); choice Any: (0.11, 0.05); and choice [A to Any]: (0.28, 0.23).

Analyzing the results, choice C is preferred over B when the test sound consists of a low or fade normal breath. To better understand this preference, it is important to note that algorithm C is relaxed for higher frequencies due to the δ_k parameter. Qualitatively, all low-breath excerpts retained the normal breath information after noise suppression, but with an added soft-wind sound effect. This wind distortion or hissing was at a lower frequency range for algorithm B and proved to be less pleasant than the one produced by algorithm C, which ranged in higher frequencies. This observation was consistent across different files and listeners. Looking further into algorithm C,a larger preference variation was noticed for Group 2 when compared to Group 1. This variation was found to be produced by two participants who preferred C over any other choice 35% of the time and both preferred the original only in two cases.

The original recording was preferred 4.9% of the time. While this percentage constitutes a minority on the tested cases, a detailed breakdown provides valuable insights on the operation of the enhancement algorithm. In most cases, it is determined that low-volume resulting periods affect the listeners’ judgments.

• 1) Clipping distortions make abnormal sound events even more prominent. Clipping tends to corrupt the signal content and produce false abnormal sounds for loud breaths. However, when such clipping occurs during crackle events, it results in more distinct abnormal sounds, which can be better perceived than a processed signal with muted clipping. For two such sound files in Group 1, 2/8 users prefer the original raw audio and for one such file in Group 2, 2/9 prefer the original.

• 2) Child vocalization are typically removed after enhancement. Since the algorithm operates with the internal recording as a metric, any sound captured weakly by the internal but strongly by the external microphone is flagged as noise. One such file in Group 2 leads 4/9 users to prefer the original sound: a faint child vocalization is highly suppressed in the enhanced signal. As users are not presented with the external recording information, it can be hard to tell the origin of some abnormal sounds that overlap with profiles of abnormal breaths. Nevertheless, a postanalysis on the external microphone shows that this is indeed a clear child vocalization.

• 3) Reduced normal breath sounds. The proposed algorithm has an explicit subtractive nature; the recovered signal is, thus, expected to have lower average energy compared to the original internal recording. Before the listening test, all recordings are amplified to the same level; however, isolated time periods of the enhanced signal are still expected to have lower amplitude values than the corresponding original segment, especially for noisy backgrounds. This normalization imbalance has perceivable effects in some test files. For auscultation recordings in lower site positions, breath sounds can be faintly heard, and the subtraction process reduces those sounds even further. Two such cases were included in the listening test, where suppression of a loud power generator noise resulted in a faded postprocessed breath sound. In this case, listeners preferred the original file where the breath sounds stronger than the processed version.

A finalized enhancement algorithm is proposed consisting of parametric choices that combine versions B and C. The smoother subtraction scheme enforced by factor δ⁽²⁾ is kept along with the equilinear model of frequency band splitting using a 50-ms frame size window. An informal validation by a few members of the original expert panel confirms that the combined algorithm parameters result in improved lung sound quality and preservation of low breaths.

D. Relation to Previous Work

A proper comparison to existing noise suppression methods for auscultation signals is largely limited due to the scarce literature on this topic, especially when dealing with busy real-life environments, particularly in pediatric patients. Published methods typically consider auscultations in soundproof chambers, highly controlled environments with low ambient or Gaussian noise [28]–[29]. Moreover, the term noise often refers to suppressing heart sounds in the context of healthy lung sound analysis [30], [31], or to separate normal airflow from abnormal explosive occurrences [32], [33]. Extending results from published studies to realistic settings is nontrivial, particularly in nonhealthy patients where abnormal lung events occur in an unpredictable manner and whose signal characteristics may overlap with those of environmental noise.

Here, we contrast our results with the performance of a published lung sound enhancement scheme [34], which mainly focuses on the postclassification of auscultation sounds, rather than the production of improved-quality auscultation signals to be used by health care professionals in lieu of the original recording. The authors adopted the speech-based spectral subtractive scheme of Boll [35], which has well documented shortcomings [36], [37]. For a fairer comparison, we used a more robust instantiation of speech-based spectral subtraction, proposed in [13] and [38], which we call here speechSP. We contrasted our proposed method with speechSP, maintaining the same window size, window overlap factor, and number of frequency bands of Section III-B; both algorithms were applied on the same preprocessed signals after downsampling, normalizing, and correcting for clipping distortions.

A visual inspection of the speechSP method is sufficient to observe the notable resulting artifacts. Fig. 3(a) illustrates an example comparing the two methods when applied on the same auscultation excerpt. SpeechSP algorithm highly suppressed the wheezing segment around 2 s in Fig. 3(a), along with the crackle occurrences around 0.5 and 3.5 s. In this example (and all cases in the current study—not shown), the speechSP method suffered from significant sound deterioration; and in the majority of cases, the speechSP-processed signal was corrupted by artifacts impeding the acoustic recognition of alarming adventitious events. Overall, the combination of visual inspection, signal analysis and informal listening tests, clearly indicates that speechSP maximizes the subtraction of background noise interference, at the expense of deterioration of the original lung signal as well as significant masking of adventitious lung events. Both effects are largely caused by its speech-centric view which considers specific statistical and signal characteristics for the fidelity of speech that do not match the nature of lung signals.

Fig. 3.

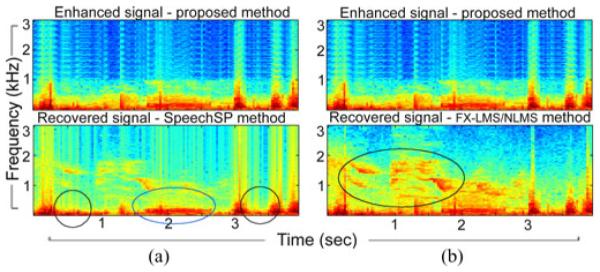
Spectrogram illustrations comparing the proposed method with (a) speechSP and (b) FX-LMS applied on the same sound excerpt. SpeechSP suppresses important lung sounds like crackle patterns (black circles) and wheeze pattern (blue circle). FX-LMS convergence is challenged by both the parametric setup and the complex, abrupt noise environment resulting in non-optimal lung sound recovery. Colormap is the same as Fig. 1.

Next, we compared the proposed method to active noise cancellation (ANC) schemes. Such algorithms typically focus on noise reduction using knowledge of a primary signal and at least one reference signal. Here, we consider the case of a single reference sensor and use a feed-forward Filtered-X Least Mean Squared algorithm (FX-LMS). FX-LMS has been previously used for denoising in auscultation signals recorded in a controlled acoustic chamber with simulated high-noise interference [39]. Here, we adopt an implementation of the normalized LMS (NLMS) as in [39] and [40]. Using all signals of the study, we tested the effectiveness of the NLMS in suppressing external noise interference. The filter coefficients were optimized in the MSE sense with filter tap-order N_LMS varying between [4,…, 120], step size η_LMS varying between [1E − 8, … , 2] and denominator term offset step size C_LMS in [1E − 8, … , 1E − 2]. A representative example is shown in Fig. 3(b); zero initial filter weights were assumed with the optimal solution occurring for (N_LMS, η_LMS, C_LMS) = (90, 5E − 7, 1E − 8). Our results indicate that NLMS fails to sufficiently reduce the effect of external noise, especially in low SNR instances or during abrupt transitions in background interferences.

As previously noted in [40], difficult acoustic environments typically pose a challenge to ANC methods for auscultation where ambient recordings are rendered ineffective as reference signals. This limitation is due to a number of reasons [41]. First, the presence of uncorrelated noise between the primary and reference channels largely affects the convergence of NLMS and the performance of the denoising filter. Nelson et al. [40] have indeed demonstrated that using an external microphone is suboptimal in case of auscultation recordings, proposing use of accelerometer-based reference mounted on the stethoscope in line with the transducer, a nonfeasible setup for our study. Furthermore, iterative filter updates in the NLMS are heavily dependent on the statistics of the observed signal and reference noise [42]. Abrupt changes in signal statistics pose real challenges in updating filter parameters fast enough to prevent divergence [43], [44]. This is particularly true in field auscultation recordings where brusque changes in the signal often occur due to poor body seal of the stethoscope—caused by child movement or change of auscultation site. Noise sources are also abruptly appearing and disappearing from the environment (e.g., sudden patient cry, phone ring); hence, posing additional challenges to the convergence of the algorithm without any prior constraints or knowledge about signal statistics or anticipated dynamics. Furthermore, unfavorable initial conditions of the algorithm can highly affect the recovered signal and lead to intractable solutions.

VI. Discussion

In this paper, the task of suppressing noise contaminations from lung sound recordings is addressed by proposing an adaptive subtraction scheme that operates in the spectral domain. The algorithm processes each frequency band in a nonuniform manner and uses prior knowledge of the signal of interest to adjust a penalty across the frequency spectrum. It operates in short-time windows and uses the current frame’s signal-to-noise information to dynamically relax or strengthen the noise suppression operation. As is the case with most spectral subtraction schemes, the current algorithm is formulated for additive noise and is unable to handle convolutive or nonlinear effects. A prominent example of such distortions are clipping effects which are processed separately in this paper and integrated with the proposed algorithm.

The efficiency and success of the proposed algorithm in suppressing environmental noise, while preserving the lung sound content, was validated by a formal listening test performed by a panel of expert physicians. A set of abnormal and normal lung sounds were used for validation, chosen to span the expected variability in auscultation signals, including the unexpected presence of adventitious lung events and low breath sounds. The expert panel judgments reveal a strong preference for the enhanced signal. Post hoc analysis and informal followup listening tests suggest that simple volume increase can help to balance few cases where the desired lung sound is perceived as weak.

Over the last years, an augmented literature has emerged on lung sound processing with the aid of computerized analysis. Most popular work has been on airflow estimation, feature extraction, and detection of abnormal sounds and classification, while recordings were acquired in quiet or soundproof rooms to overpass the inherent difficulty of noisy environments. In this context, noise cancellation typically refers to heart sound suppression and a wide range of techniques have successfully been used: high-pass filtering, adaptive filtering, higher-order statistics, independent component analysis, or multiresolution analysis [30], [32], [45]. On the other hand, very few studies address ambient noise in lung sound recordings and results are typically presented on a small number of sounds, using graphical methods or informal listening [33], [46]. This paper focuses on real-environment noise cancellation, applicable to both normal and abnormal respiratory sounds, and evaluated on a large scale by objective/quality measures and a panel of expert physicians.

The strengths and benefits of the proposed paper lie in the simple automated setup and its adaptive nature; both are fundamental conditions for applicability in everyday clinical environments, especially in crowded low-resource health centers, where the majority of childhood respiratory morbidity and mortality takes place. By design, the proposed approach can be simply extended to a real-time implementation and integrated with lung sound acquisition protocols. By improving the quality of auscultation signals picked-up by stethoscopes, the proposed study hopes to provide medical practitioners with an improved recording of lung signals that minimizes the effect of environmental distortions and improves and facilitates the interface between auscultation and automated methods for computerized analysis and recognition of auscultation signals.

Biographies

Dimitra Emmanouilidou received the M.Sc. and B.Sc. degrees from the Computer Science Department, University of Crete, Rethymno, Greece, in 2010 and 2007, respectively. During her B.Sc. and early M.Sc. years, she worked on cardiac arrhythmia detection, and concluded her M.Sc. working on magnetic resonance imaging analysis. She is currently working toward the Ph.D. degree in electrical and computer engineering at the Laboratory for Computational Audio Perception, Johns Hopkins University, Baltimore, MD, USA.

Her research interest includes medical signal processing with the aim of disease diagnosis/prognosis.

Daniel E. Park received the B.S. degree in biology from the University of Maryland, College Park, MD, USA, in 2009, and the M.S.P.H. degree in international health from Johns Hopkins University, Baltimore, MD, in 2011.

He is currently a Faculty Member at the Johns Hopkins Bloomberg School of Public Health, Baltimore, MD, serving as a Research Associate at the International Vaccine Access Center.

Eric McCollum is a Pediatric Pulmonologist with the Faculty at the Eudowood Division of Pediatric Respiratory Sciences, Johns Hopkins School of Medicine, Baltimore, MD, USA. He has nearly ten years experience in child respiratory diseases specific to low-resource settings in southern African and South Asia. As of 2015, he is the PI of a NIH K01 International Research Scientist Development Award, Dhaka, Bangladesh, examining the role of pulse oximetry in Bangladeshi children with clinical pneumonia. In addition to his collaborative digital auscultation work, he is also the PI of a clinical trial starting 2015 investigating bubble CPAP as an intervention to reduce pneumonia mortality in Malawi in HIV-affected or severely malnourished children.

He has received multiple early career research awards and is currently a Member of the WHO Scientific Advisory Committee for the revision of child pneumonia diagnostic and treatment failure criteria and the Bill and Melinda Gates Foundation advisory panel for the development of a target product profile for pulse oximetry in low-resource settings.

Mounya Elhilali (S’00–M’05) received the Ph.D. degree in electrical and computer engineering from the University of Maryland, College Park, MD, USA, in 2004.

She is currently an Associate Professor at the Department of Electrical and Computer Engineering, Johns Hopkins University, Baltimore, MD. She is affiliated with the Center for Speech and Language Processing and directs the Laboratory for Computational Audio Perception. Her research interests include the neural and computational bases of sound and speech perception in complex acoustic environments, with applications in medical signal processing, audio systems, and speech technologies.

Dr. Elhilali received the National Science Foundation CAREER Award and the Office of Naval Research Young Investigator Award.