Measures for the degree of overlap of gene signatures and applications to TCGA

Abstract

For cancer and many other complex diseases, a large number of gene signatures have been generated. In this study, we use cancer as an example and note that other diseases can be analyzed in a similar manner. For signatures generated in multiple independent studies on the same cancer type and outcome, and for signatures on different cancer types, it is of interest to evaluate their degree of overlap. Many of the existing studies simply count the number (or percentage) of overlapped genes shared by two signatures. Such an approach has serious limitations. In this study, as a demonstrating example, we consider cancer prognosis data under the Cox model. Lasso, which is representative of a large number of regularization methods, is adopted for generating gene signatures. We examine two families of measures for quantifying the degree of overlap. The first family is based on the Cox-Lasso estimates at the optimal tunings, and the second family is based on estimates across the whole solution paths. Within each family, multiple measures, which describe the overlap from different perspectives, are introduced. The analysis of TCGA (The Cancer Genome Atlas) data on five cancer types shows that the degree of overlap varies across measures, cancer types and types of (epi)genetic measurements. More investigations are needed to better describe and understand the overlaps among gene signatures.

Introduction

For cancer and many other complex diseases, profiling studies have been extensively conducted, measuring multiple layers of molecular activities. Available measurements include gene expression, miRNA, methylation, copy number alteration (CNA), phosphorylation, protein expression and others. In this article, we use cancer as an example because of its clinical importance and the huge amount of recently generated cancer profiling data. For multiple cancer types, a large number of gene signatures has been generated for various outcomes and phenotypes.

Different from many published studies, the focus of this study is not on generating more gene signatures but on measuring the degree of overlap of two (or more) signatures. Analyzing the degree of overlap is important in multiple scenarios. First, consider gene signatures generated on the same cancer type and outcome in multiple independent studies. The reproducibility of gene signatures, or equivalently their high degree of overlap across studies, is an essential requirement for potential clinical usage [1]. For major cancer types such as breast cancer [1], lung cancer [2] and non-Hodgkin lymphoma [3], there are multiple review articles discussing the overlap of gene signatures across studies. Second, consider gene signatures on different cancer types and outcomes. Multiple studies have examined whether the signatures of two or more cancers have overlap [4]. Such overlap has many important implications. For instance, the degree of overlap has been used to reclassify diseases [5]. Two diseases belong to the same class if their signatures have a high degree of overlap. In cancer studies, the overlapped genes have been suggested as representing the more essential features of cancer. Studies such as the human disease network (HDN) [6] define the pairwise ‘distance’ between diseases using their gene signatures. It has been conjectured that diseases ‘close’ to each other at the molecular level can be treated using similar strategies. From both practical and scientific perspectives, it is important to accurately quantify the degree of overlap of gene signatures.

Two types of analyses have been conducted to measure the degree of overlap. The first is more biological [7]. Studies of this kind examine the biological functionalities of gene signatures (for example, the enriched pathways or represented molecular functions) by interrogating KEGG, GO and other databases. This type of analysis is limited by our partial or even wrong knowledge regarding the biological functions of genes. In addition, it is difficult to develop a mathematically rigorous measure based on the biological functions. The second type of analysis is more statistical. In quite a few published studies [4, 8], the number and percentage of overlapped genes between two signatures are calculated. Such statistical analysis does not demand extensive knowledge of biological functions and is very easy to conduct. However, simply counting the number of overlapped genes has limitations. Different genes can have highly similar biological functions and strongly correlated measurements. Since they are different genes, they are not counted as overlapped in the signatures. However, from a biological or statistical perspective, they should be counted as ‘partially overlapped’. Another limitation shared by the existing statistical analyses is that the impact of tuning parameters—which are needed for many methods—on the degree of overlap has not been given attention [8].

In this article, we will introduce multiple measures for quantifying the degree of overlap of two gene signatures. Although the overlap of signatures has been discussed in published studies, there is still no mathematically rigorous definition of ‘overlap’. Thus, it is prudent to develop multiple measures, which have different statistical interpretations and cannot replace each other. In addition, they quantify overlap both at fixed tunings and for a sequence of tunings along the solution paths. The analysis of The Cancer Genome Atlas (TCGA) data demonstrates that they lead to results different from those using the simple method.

TCGA data

The overlap measures were applied to the TCGA (https://tcga-data.nci.nih.gov/tcga/) data. To clearly set up the analysis framework, we will first describe the data sets. TCGA is a combined effort by multiple research institutes organized by the National Cancer Institute (NCI). The tumor and normal samples from >6000 patients have been profiled, covering 37 types of (epi)genetic and clinical data for 33 cancer types. Comprehensive profiling data have been published on cancers of the breast, ovary, skin, head/neck, lung and other organs and will soon be available for many other cancer types. TCGA data were chosen for multiple reasons. With rigorous control by the NCI and individual institutes, the data are of high quality. And with almost unified data generation protocols, the comparability across cancers/data sets is much higher than that of other studies. In our previous study [8], we analyzed the Gene Expression Omnibus (GEO) data and found a low degree of overlap within and across cancers. However, as GEO data sets were generated independently under different protocols, their data quality varies significantly. It is hard to determine how much of the low overlap is attributable to the low data quality. This problem is much alleviated with TCGA. In addition, TCGA data are multidimensional, with gene expression, CNA, methylation, miRNA and other types of (epi)genetic measurements on the same subjects. They are more comprehensive than data with a single type of measurement. And they are being analyzed by multiple research groups, making them an ideal testbed.

With TCGA, it is possible to conduct analysis on multiple gene signatures of the same cancer type. However, TCGA is unique in that it provides an opportunity to study multiple cancer types. Specifically, as shown in Table 1, we analyzed prognosis data on five cancer types: breast cancer (BRCA), glioblastoma (GBM), leukemia (LAML), lung cancer (LUSC) and melanoma (SKCM). Such data have measurements on overall survival, clinical and environmental variables (details provided in the Supplementary Appendix), gene expressions, methylation and CNAs. miRNA data are also available. However, as the number of miRNAs measured for two or more cancer types is extremely small, miRNA data were not analyzed. The five cancer types were chosen because of their clinical importance and because their data have been analyzed multiple times in the literature.

Table 1.

Description of the five TCGA data sets

Data type	BRCA	GBM	LAML	LUSC	SKCM
Clinical variables
Number of patients	739	299	180	308	366
Overall survival (month)	(0.00, 196.97)	(0.13, 76.90)	(0, 95.37)	(0, 176.53)	(1, 362.5667)
Event rate	7.58%	88.96%	64.44%	35.39%	37.98%
Gene expression
Platform	Agilent 244K Custom Gene Expression G4502A_07	Agilent 244K Custom Gene Expression G4502A_07	Affymetrix Human Genome HG-U133_Plus_2	Agilent 244K Custom Gene Expression G4502A_07	Illumina HiSeq 2000 RNA Sequencing Version 2 analysis
Number of patients	526	500	173	154	371
Features before clean	15 639	16 407	18 131	15 521	19 425
Features after clean	2500	2500	2500	2500	2500
DNA methylation
Platform	Illumina DNA Methylation 27/450 (combined)	Illumina DNA Methylation 27/450 (combined)	Illumina DNA Methylation 450	Illumina DNA Methylation 27/450 (combined)	Illumina DNA Methylation 450
Number of patients	929	398	194	385	373
Features before clean	1662	1622	14 959	1578	193
Features after clean	193	193	193	193	193
Copy number alteration
Platform	Affymetrix Genome-Wide Human SNP Array 6.0	Affymetrix Genome-Wide Human SNP Array 6.0	Affymetrix Genome-Wide Human SNP Array 6.0	Affymetrix Genome-Wide Human SNP Array 6.0	Affymetrix Genome-Wide Human SNP Array 6.0
Number of patients	934	563	191	178	374
Features before clean	20 500	20 501	20 501	17 869	23 689
Features after clean	2500	2500	2500	2500	2500

Data processing

All data analyzed in this study are publicly available and downloaded from TCGA Provisional using the CGDS-R package. For (epi)genetic measurements, processed level 3 data were downloaded. The following processing was conducted before analysis. In the first step, we conducted the within-cancer processing of data on each cancer type separately using the same approach. Take the BRCA data as an example. As shown in Figure 1, for clinical data, we removed samples with missing overall survival times. For (epi)genetic data, the missing rates are low. We conducted imputation and filled in missing values with medians across samples. Then clinical and (epi)genetic data were merged using sample ID. In the second step, as the goal was to compare gene signatures across data sets (cancer types), we conducted across-cancer processing. The flowchart for processing gene expression data is shown in Figure 1. CNA and methylation data were processed similarly. We first identified the 13 835 gene expressions measured in all five data sets. In principle, we can analyze all these genes. However, as the number of genes associated with cancer prognosis was expected to be small, to improve stability, we conducted a marginal screening and selected the top 2500 gene expressions for downstream analysis [9].

Figure 1.

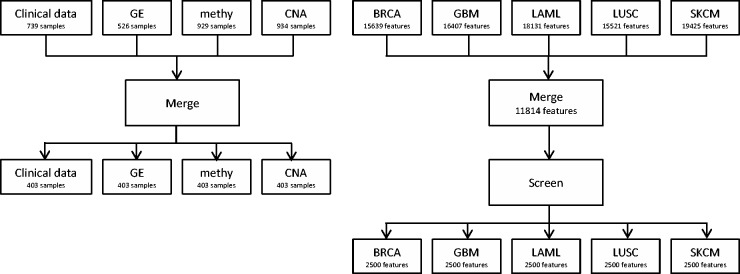
Flowchart of data processing.

Generating gene signatures

The processed data were analyzed to generate gene signatures. A large number of methods are applicable for such a purpose. We refer to published studies [10–12] for relevant discussions. Briefly, there are two families of methods. The first family analyzes one genetic unit (gene, methylation locus, etc.) at a time and selects the top-ranked ones using, for example, marginal P-values and the false discovery rate approach. The second family jointly analyzes a large number of genetic units in a single model. In the article, we used Lasso, which is a joint analysis method, to generate gene signatures [11]. Lasso is perhaps the most popular penalization method and has been used in a large number of cancer genetic data analyses [10], including a recent TCGA study [9]. A closer examination of the measures described in the next section reveals that they are directly applicable to gene signatures generated using other methods.

For a prognosis data set, denote $T$ as the survival time and $C$ as the random censoring time. Under right censoring, one observes $\{Y=\min \left(T,C\right),\delta =I(T\le C)\}$ where $I(.)$ is the indicator function. To avoid confusion of terminology, we used gene expression as an example in the description of methodology. Denote $X$ as the $d$ gene expressions, $Z$ as the $s$ clinical/environmental variables and $W={(X^T,Z^T)}^T$. In the Cox model, denote $\theta ={({\beta }^T,{\gamma }^T)}^T$ as the coefficients of $W$. Assume $n$ iid observations. For the TCGA data and data alike, $d\gg n\gg s$. Under the Cox model, the log-partial-likelihood function is $\ell (\theta )=\sum _{i=1}^n{\delta }_i\left\{W_i^T\theta -\log \left[\sum _{j=1}^{n}I\left(Y_j\ge Y_i\right)\exp \left(W_j^T\theta \right)\right]\right\}$. The Lasso estimate is defined as $\widehat{\theta }=argmax\left\{\ell \left(\theta \right)-\lambda \sum _{k=1}^d\left|{\beta }_k\right|\right\}$, where the subscript $k$ denotes the $k$th component. Note that only the coefficients of gene expressions are penalized, as the clinical variables are low-dimensional and usually ‘of interest’ (so there is no need for regularization or selection). In the literature, models with gene expressions only have also been fit. Compared with such models, the one that also includes clinical variables can better describe cancer biology and have more clinical implications.

Multiple software packages are available for computing the Cox-Lasso estimates. In our numerical study, we used the R package glmnet. With Lasso, many components of $\widehat{\beta }$ are exactly zero, and only a small number of genes with nonzero coefficients are included in the model. The identified set of genes depends on the tuning parameter $\lambda$. Specifically, a smaller value of $\lambda$ leads to more genes with nonzero estimated coefficients. The dependence of identified genes on tuning is also true for many other methods. For example, with the popular marginal analysis approach, the cutoff of P-value can be viewed as a tuning. For the boosting, thresholding and other joint analysis methods, there are also one or multiple tunings.

Prediction analysis

To further motivate examining the overlap of gene signatures across cancer types, we conducted prediction analysis. The flowchart is shown in Supplementary Figure A1.

Consider two cancer types, say A and B. The analysis consisted of the following steps: (a) randomly split cancer A data into a training set and a testing set with sizes 3:1; (b) conduct within-cancer prediction: (b.1) apply the Cox-Lasso method to the training set; (b.2) use the training set model to make a prediction for the testing set subjects. Compute the logrank statistic to quantify prediction performance [9]; (c) conduct across-cancer prediction: (c.1) apply the Cox-Lasso method to the data on cancer B; (c.2) using the cancer A training data and genes identified in (c.1), fit a Cox model; (c.3) using the model generated in (c.2), make a prediction for the cancer A testing data in the same manner as in (b.2); (d) repeat (a)-(c) 100 times. In each split, two logrank statistics are generated. The one generated in (b.2) measures prediction performance in an ‘ordinary’ way: the model and genes are identified using cancer A training data and used to make a prediction for cancer A testing data. The second logrank statistic, generated in (c.3), differs from the first one and those in published studies. Specifically, the genes are identified using cancer B data but used to make a prediction for cancer A subjects. If the two cancers have no similarity at the molecular level, then insignificant prediction should be expected in (c.3).

The prediction results are shown in Supplementary Table A1. Most of the across-cancer logrank statistics are not significant. (The logrank statistic has a chi-squared distribution with degree of freedom one. A logrank statistic >3.84 is significant at the 0.05 level.) However, there are a few significant or close-to-significant ones. For example, the across BRCA and SKCM logrank is 4.837. Although prediction and gene signature construction are different analysis goals, the across-cancer prediction may still suggest that the signatures of some cancers have overlap.

Measures of the degree of overlap between gene signatures

Different gene signatures contain a different amount of information. Some contain information on the set of identified important genes, their estimates and significance level. As shown in Table 1, different data sets can be generated using different platforms (for example, three different platforms have been used for gene expression), and the measurements are not directly comparable, leading to incomparable estimates. For joint analysis methods including Lasso, inference techniques are still being developed, and there is a lack of consensus. Thus, in what follows, we focus on evaluating the degree of overlap of the sets of identified genes. In principle, we can evaluate the overlap of multiple signatures. For description simplicity, we compared two gene signatures. To facilitate future applications, the analysis code is available at http://works.bepress.com/shuangge/48/.

Measures at fixed tuning

With Cox-Lasso, the tuning parameter is not specified a priori and needs to be chosen data-dependently. In the data analysis, we chose $\lambda$ using cross validation, which is the default in glmnet. For some other methods (for example, marginal analysis), the tuning parameters can be pre-fixed but can also vary.

Denote $X_A$ and $X_B$ as the matrices of gene expressions for cancers A and B, respectively. Consider the Cox-Lasso estimates at the optimal tuning parameter values. For cancer A (B), denote IA (IB) as the index set of identified genes with size $p$ ($q)$. Further, denote $X_A^{IA}$ as the sub-matrix of $X_A$ corresponding to IA. Assume $n$ iid samples for cancer A.

Index-based measure

This measure has been adopted in multiple published studies [8] and serves as a benchmark here. It starts with simply counting the number of genes identified in both signatures. Taking into account the sizes of IA and IB, it is defined as

The numerator and denominator are sizes of the intersection and union, respectively, similar to the Jaccard index [13].

This measure has the strictest definition of overlap. Despite its simplicity, it has limitations. Consider a scenario in which two different genes have highly correlated measurements, which is not uncommon in practice. This measure counts such genes as different (not overlapped). However, from a statistical modeling perspective, they should be counted as ‘similar’ or ‘partially overlapped’. The following measures are motivated by such a consideration.

Rank-based measure

With Cox-Lasso and many other methods, the covariate effects are linear combinations of selected genes. Mathematically, if any linear combination of variables in the first set can be written as a linear combination of variables in the second set, these two sets are linearly equivalent. Motivated by such a consideration, we developed the rank-based measure, which quantifies the degree of overlap based on the similarity of two variable sets in a linear sense. Specifically, with $X_A^{IA}$ and $X_A^{IB}$, which are sets IA and IB on $X_A$, the measure is defined as

$$m^2\left(IA,IB\right)=\frac{r\left(X_A^{IA}\right)+r\left(X_A^{IB}\right)-r\left(X_A^{IA\cup IB}\right)}{r\left(X_A^{IA\cup IB}\right)},$$

where $r(.)$ denotes the rank of a matrix. This measure has the following properties. When IA and IB are linearly equivalent, $m^2$ equals 1. When IA and IB are linearly orthogonal, $m^2$ equals 0. A value of $m^2$ between 0 and 1 indicates partial overlap, with a higher value corresponding to a higher degree of overlap.

Note that $m^2$ defined above is calculated using the observed gene expressions on cancer A. Using the cancer B data, another measure can be computed in the same manner and is not necessarily equal to the one computed above. This may be inconvenient in practice but is reasonable. The observed rank, computed on a finite sample, is a stochastic realization of the population rank. It is expected that, as the sample sizes grow, the two measures computed using cancers A and B data will converge to the same population value, and hence the discrepancy will disappear. In practical data analysis with finite sample sizes, we suggest computing two $m^2$ values, using data on cancers A and B separately. If desired, a simple average can be computed to remove discrepancy.

To calculate $m^2$, we must calculate the ranks of multiple matrices. This can be realized through singular value decomposition: the rank of a matrix is equal to its number of nonzero singular values. In data analysis, we found that some singular values are very close to zero, and counting such singular values may lead to unstable results. To tackle this problem, we calculated the rank of a matrix as $\sum _{j}I\left({\sigma }_j>\gamma \right),$ where ${\sigma }_j$’s are the singular values and $\gamma$ is the user-defined tolerance level (0.1 in our data analysis). For $X_A^{IA\cup IB}$, the tolerance level is calculated as $\text{min}\left\{{\sigma }_i{}^{A}I\left({\sigma }_i{}^A>\gamma \right)\right\}\wedge \text{min}\left\{{\sigma }_j{}^{B}I\left({\sigma }_j{}^B>\gamma \right)\right\}$. In data analysis, the rank-based measure is calculated with the assistance of R package svd.

Correlation-based measure

The rank-based measure quantifies overlap using the linear spaces spanned by two gene sets. It is not easy to identify which genes contribute to the overlap. The correlation-based measure, on the other hand, may better reflect contribution(s) (to overlap) from individual genes. This measure starts with computing the correlation coefficients between individual genes. Specifically, let ${\rho }_{ij}=cor\left(X_{A,i}^{IA}, X_{A,j}^{IB}\right)$ be the correlation between gene $i$ in IA and gene $j$ in IB, computed using the cancer A data. We proposed

$$m^3(IA,IB)=\frac{{\sum }_i{\sum }_{j}I\{|{\rho }_{ij}|>\rho \}}{pq}.$$

It calculates the percentage of correlations above a cutoff $\rho$ and counts how many pairwise correlations are strong enough.

The cutoff $\rho$ is determined based on the Fisher transformation. Specifically, let $z_{ij}=0.5\text{log}((1+{\rho }_{ij})/(1-{\rho }_{ij}))$. If the correlation between $X_{A,i}^{IA}$ and $X_{A,j}^{IB}$ is zero, $\sqrt{n-3}{z}_{ij}$ is approximately distributed as $N(0, 1)$ [14]. We can use this result to determine a threshold $\xi$ for $\sqrt{n-3}{z}_{ij}$. The corresponding threshold for ${\rho }_{ij}$ is $\rho =(\exp \left(\frac{2\xi }{\sqrt{n-3}}\right)-1)/(\exp \left(\frac{2\xi }{\sqrt{n-3}}\right)+1)$. A counterpart of $m^3$ can be computed using the cancer B data.

R-squared-based measure

The above measure is built on the correlation between two individual genes. Another scenario of correlation is that a gene in IA is correlated with a linear combination of multiple genes in IB, not necessarily a specific gene.

This R-squared-based measure starts with regressing a gene in IA onto genes in IB. The R-squared statistic of this regression is then calculated, with a higher value indicating a higher correlation. When $q$ is moderate to large compared to the sample size, the ordinary least squares estimation and calculation of R-squared cannot be straightforwardly conducted. To solve this problem, we resorted to penalized regression. Define the Lasso estimate for gene $i$ in IA a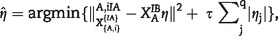s where $\eta$ is a$\text{ q}\times 1$ vector of regression coefficients. The R-squared statistic was then calculated using only variables corresponding to the nonzero components of $\widehat{\eta }$. With the regularized regression and R-squared statistics, the degree of overlap measure is defined as

The cutoff of 0.5 can be somewhat subjective. In practice, users may change this cutoff if warranted.

Remarks

Four measures have been described. They take different angles. The first, the index-based measure, is more ‘mechanistic’ and only accounts for the identity of genes but not their values. The rest are built on the values of genes and, with finite sample sizes, also depend on whether data on cancer A or B are used. The rank-based measure is on the overlap of linear spaces spanned by the two gene sets. The correlation-based measure is built on the pairwise similarity of genes. And the R-squared-based measure is built on the similarity between a gene and a set. There are multiple other ways of defining correlation [15]. The ones described above perhaps have the simplest definitions and are the most commonly adopted.

Measures that use the whole solution paths

Analyzing gene signatures at fixed tunings may face problems. First, multiple approaches can be used to choose the tuning parameter with Lasso as well as other estimation methods, and different approaches lead to different tunings. Thus, the gene signatures and their overlap depend on the tuning selection approach. Cross validation is the default in glmnet, but other approaches (such as Generalized Cross Validation (GCV) and Bayesian Information Criterion (BIC)) have also been extensively used. Second, the analysis may lack stability. A small deviation from the selected tuning may result in a significant change in the identified gene signature and, hence, overlap.

With Cox-Lasso, when we vary the tuning parameter, a sequence of estimates can be generated, which is referred to as the ‘solution path’ in the literature [16]. A sample plot of the solution path (GBM data, gene expression measurement) is shown in Supplementary Figure A2. Recent studies suggest that estimates corresponding to other tuning parameter values can provide information beyond what is selected using cross validation [17]. Let ${\lambda }_{max}$ be the smallest value of tuning under which all components of $\beta$ are estimated as zero. Let ${\lambda }_{min}$ be the minimum value of $\lambda$, set as $0.01{\lambda }_{max}$. Along the solution path, we select $K$ equally spaced tuning parameter values. In the numerical study, we set $K=500.$

Integrate the point-wise measures along the solution path

For each data set (cancer type) along the solution path, we now have $K$ sets of genes identified using Cox-Lasso. For cancers A and B, denote the $K$ index sets as $\{I{A}_1,\dots ,I{A}_K\}$ and $\{I{B}_1,\dots ,I{B}_K\}$. We proposed first evaluating the degree of overlap between $I{A}_k$ and $I{B}_k$ for each $k$ and then summarizing across the $K$ measures. We noted that the tuning parameter values corresponding to each $k$ for cancers A and B are different. However, since they occupy the same position between the smallest and largest tunings, they roughly represent the same degree of regularization. Hence, it is meaningful to compare $I{A}_k$ and $I{B}_k$. At each $k$, measures $m^l(l=1,\mathrm{..},4)$ can be computed as described in the last section.

It is not appropriate to simply sum up the $m^l$ values along the solution path. Estimates with tunings close to the optimal can be more informative than those with very small/large tunings (which select a large/small number of genes). Motivated by such a consideration, we proposed the weighted sum measure of the degree of overlap as

$$S^l\left(A,B\right)={\displaystyle \sum }_{k}w\left(k;c,n\right)m^l(I{A}_k,I{B}_k),$$

where $l=1,\dots ,4$ and $w\left(k;c,n\right)$ is the weight at the $k$th point and defined as

$$\left(k;c,n\right)=\{\begin{array}{c}\frac{2k}{nc}, 0<k\le c\\ \frac{2(n-k)}{n(n-c)}, c<k\le n \\ 0, k>n\end{array}.$$

Further, $c$ is the point of optimal tuning. This weight function has the following properties. The sum of all weights is equal to 1. The largest weight is assigned to the point of optimal tuning. The weights get smaller as the tunings get away from the optimal. A linear-decreasing function is used for simplicity.

Frequency-based measure

The above integrated measures are the weighted sums of $K$ measures. Loosely speaking, if a gene is included in more of the $K$ Cox-Lasso estimates, it has more contributions to the $K$ individual overlap measures and hence to the integrated measures. This observation shares a similar spirit with that of quantifying the relative importance of genes based on their reproducibility (stability) [18].

Motivated by the role reproducibility plays in gene signatures, we proposed the frequency-based measure, which is calculated as follows: (a) For cancer A and cancer B separately, compute the $K$ Cox-Lasso estimates as described in the above sections. (b) For gene $j(=1,\dots ,d)$, count the frequencies of it being selected, and denote as $f_j{}^A$ and $f_j{}^B$, respectively. These frequencies quantify its importance relative to other genes, with a higher frequency indicating more importance. (c) Let $f^A$ ($f^B$) be the sorted gene frequency lists in a decreasing order and $r_j{}^A$ ($r_j{}^B$) be the position of the $j$th gene. (d) Define the degree of overlap measure as

$$S^f\left(A, B\right)= {\displaystyle \sum }_{j=1}^d\frac{1}{r_j{}^A}\frac{1}{r_j{}^B}.$$

This measure has been partly motivated by published studies [19]. Its value gets larger if there are more genes with higher rankings for both cancers. It is not strongly related to the measures defined in the above sections and has different magnitudes and interpretations.

Remarks

The concept of gene signature overlap has been discussed multiple times in the literature. However, there is still no rigorous mathematical definition. Because of that, it is prudent to develop multiple measures to address overlap from different angles. The proposed measures have different definitions and, as to be shown below, lead to different numerical results. Choosing a proper measure in practice needs to be done on a case-by-case basis and heavily depends on the analysis goal. When there is high confidence in the selected tunings, the measures at fixed tunings should be adopted. Otherwise, those integrating over solution paths are preferred. When it is desirable to stress the contribution of individual genes to overlap, the correlation- and R-squared-based measures should be adopted. Otherwise, the rank-based measure is appropriate. In some studies, reproducibility is emphasized, which calls for the frequency-based measure. With these considerations, we do not expect a universally optimal measure for practical data sets. The differences in measures mostly stem from the different aspects they address. To facilitate application, we have developed the above measures with computational simplicity and intuitive interpretability in mind. We acknowledge that there can be other measures but likely with more complicated formulations.

The proposed measures provide point estimates of overlap. In statistics, downstream analysis would include inference (significance level). Our literature search suggests that no published study has examined the inference aspect of gene signature overlap. We conjecture that it is possible to apply a permutation approach and conduct inference. However, we note that statistical inference with high-dimensional data, even the ‘simple’ Lasso estimate, is still being debated. Thus in this study, we focus on estimation and do not pursue the inference aspect.

Analysis of TCGA data

We analyzed the TCGA prognosis data on five cancers. There are a small number of recent studies developing integrative gene signatures that are composed of multiple types of (epi)genetic measurements. Here, we took the more common approach and analyzed each type of measurement separately.

The results on the degree of overlap evaluated at the optimal tunings are shown in Table 2. We also ‘decomposed’ Table 2 and present the results on each measure separately in Supplementary Table A2a–d. Multiple observations have been made.

Table 2.

Degree of overlap between the signatures of different cancer types measured at the optimal tunings

	BRCA					GBM					LAML					LUSC					SKCM
	I	R	RR	C	R2	I	R	RR	C	R2	I	R	RR	C	R2	I	R	RR	C	R2	I	R	RR	C	R2
BRCA						0.000	0.037	1/27	0.490	0.000	0.000	0.049	2/41	0.359	0.000	0.000	0.100	1/10	0.286	0.000	0.000	0.023	1/44	0.360	0.000
						0.000	0.025	1/40	0.450	0.025	0.097	0.118	8/68	0.524	0.325	0.127	0.119	8/67	0.474	0.275	0.021	0.044	2/45	0.450	0.075
						0.000	0.029	1/34	0.450	0.000	0.000	0.100	1/10	0.455	0.000	0.000	0.125	1/8	0.636	0.000	0.000	0.045	1/22	0.600	0.000
GBM	0.000	0.037	1/27	0.396	0.000						0.000	0.033	2/61	0.365	0.250	0.000	0.107	3/28	0.440	0.000	0.000	0.032	2/63	0.392	0.333
	0.000	0.025	1/40	0.283	0.000						0.000	0.025	1/40	0.427	0.333	0.000	0.026	1/39	0.392	0.333	0.091	0.200	2/10	0.296	0.333
	0.000	0.034	1/29	0.225	0.000						0.000	0.028	1/36	0.352	0.150	0.020	0.057	2/35	0.248	0.150	0.016	0.067	3/45	0.243	0.250
LAML	0.000	0.024	1/42	0.154	0.000	0.000	0.068	4/59	0.186	0.077						0.000	0.022	1/45	0.293	0.000	0.000	0.053	4/76	0.215	0.179
	0.097	0.158	9/57	0.272	0.410	0.000	0.029	1/35	0.248	0.000						0.145	0.161	9/56	0.280	0.385	0.043	0.105	4/38	0.256	0.154
	0.000	0.200	1/5	0.182	0.000	0.000	0.120	3/25	0.536	0.727						0.000	0.125	1/8	0.421	0.000	0.000	0.059	1/17	0.553	0.364
LUSC	0.000	0.100	1/10	0.179	0.000	0.000	0.033	1/30	0.143	0.000	0.000	0.070	3/43	0.114	0.143						0.000	0.043	2/46	0.153	0.000
	0.127	0.167	10/60	0.283	0.425	0.000	0.054	2/37	0.375	0.050	0.145	0.197	12/61	0.321	0.450						0.043	0.071	3/42	0.281	0.075
	0.000	0.028	1/7	0.000	0.000	0.020	0.086	3/35	0.120	0.909	0.000	0.077	1/13	0.041	0.000						0.029	0.083	2/24	0.207	0.364
SKCM	0.000	0.023	1/44	0.293	0.000	0.000	0.066	4/61	0.298	0.024	0.000	0.013	1/79	0.268	0.073	0.000	0.043	2/46	0.373	0.000
	0.021	0.043	2/47	0.742	0.444	0.091	0.333	3/9	0.704	0.111	0.043	0.067	3/45	0.735	0.667	0.043	0.065	3/46	0.792	0.556
	0.000	0.048	1/21	0.520	0.080	0.016	0.040	2/50	0.427	0.480	0.000	0.069	2/29	0.309	0.000	0.029	0.077	2/26	0.469	0.280

Note. I, R, RR, C and R² correspond to the index-based, rank-based, rank ratio, correlation-based and R-squared based measures, respectively. In each cell, rows 1–3 correspond to gene expression, methylation and CNA.

The first is that different measures lead to different conclusions. Take gene expression data for BRCA and LAML as an example. The index-based measure is 0, indicating that there is no gene identified in both signatures. The rank-based measure is 0.049. The union of the two identified gene sets has a rank of 41, while the intersection has a rank of 2, suggesting a small but nonzero overlap of the two signatures. In all, 35.9% of the pairwise correlations are statistically significant. None of the R-squared statistics is >0.5. The proposed rank, correlation and R-squared measures identify small but nonzero overlap not observable with the index-based measure. The second observation is that different types of (epi)genetic measurements lead to different results. Again, take BRCA and LAML as an example. For gene expression, methylation and CNA, the rank-based measures are 0.049, 0.118 and 0.1, respectively. The dimension of methylation measurements is much lower than that of gene expression and CNA. However, we do not believe this causes the higher degree of overlap of the methylation signatures. For example, for GBM and LUSC, the methylation signatures actually have a lower rank-based measure. Different types of (epi)genetic measurements describe different molecular activities. Gene expression is regulated by CNA and methylation, as well as other known and unknown mechanisms. CNA and methylation affect prognosis by regulating gene expression. In addition, they can also modify molecular profiles by influencing DNA profiles, without ‘passing’ gene expression. With different types of (epi)genetic measurements containing different information on prognosis, it is reasonable that their signatures have different degrees of overlap. The third observation is that, in general, the degree of overlap is low. This is reasonable, as there is no strong evidence that the five cancers share highly related molecular mechanisms. The fourth observation is that the matrix in Table 2 is not symmetric, suggesting a need to compute the overlap measures in both directions.

The results on the degree of overlap evaluated along the solution paths are shown in Table 3 and Supplementary Table A3. Some observations are similar to those in Table 2. Specifically, different measures and different types of (epi)genetic measurements lead to different conclusions, and the matrix is asymmetric. To facilitate a more graphical comparison of the results in Tables 2 and 3, in Supplementary Figure A3 we pool the results across cancer types for each type of measure and plot the boxplots. For the correlation-based measure, the results at the optimal tunings and those integrating across the solution paths have similar distributions. However, for the other three measures, the distributions are significantly different. Namely, the measures that integrate along the solution paths tend to be higher. Along the solution paths, there are many other models beyond those at the optimal tunings. The higher degrees of overlap (of the integrated measures) observed in Supplementary Figure A3 suggest that the gene signatures at tunings other than the data-selected optimal have higher overlap.

Table 3.

Degree of overlap between the signatures of different cancer types measured along the whole solution paths

	BRCA				GBM				LAML				LUSC				SKCM
	I	R	C	R2	I	R	C	R2	I	R	C	R2	I	R	C	R2	I	R	C	R2
BRCA					0.032	0.091	0.413	0.172	0.073	0.076	0.372	0.153	0.012	0.152	0.355	0.013	0.10	0.09	0.40	0.26
					0.279	0.251	0.438	0.372	0.264	0.162	0.477	0.401	0.224	0.181	0.410	0.276	0.33	0.29	0.53	0.40
					0.019	0.082	0.397	0.254	0.039	0.076	0.427	0.315	0.029	0.104	0.433	0.125	0.06	0.08	0.40	0.52
GBM	0.020	0.107	0.387	0.265					0.052	0.188	0.370	0.370	0.025	0.131	0.406	0.133	0.06	0.33	0.37	0.48
	0.160	0.269	0.340	0.221					0.370	0.282	0.410	0.495	0.282	0.205	0.383	0.354	0.32	0.37	0.37	0.41
	0.017	0.125	0.243	0.294					0.002	0.085	0.263	0.220	0.056	0.176	0.247	0.387	0.03	0.14	0.26	0.45
LAML	0.050	0.113	0.243	0.121	0.047	0.319	0.198	0.207					0.016	0.131	0.296	0.080	0.06	0.41	0.23	0.26
	0.197	0.183	0.214	0.232	0.370	0.297	0.258	0.426					0.282	0.194	0.268	0.287	0.35	0.28	0.27	0.39
	0.033	0.197	0.401	0.206	0.002	0.176	0.419	0.216					0.003	0.117	0.321	0.182	0.03	0.18	0.31	0.23
LUSC	0.011	0.212	0.126	0.123	0.044	0.328	0.162	0.231	0.023	0.306	0.144	0.204					0.05	0.34	0.16	0.29
	0.175	0.314	0.207	0.305	0.297	0.343	0.375	0.449	0.290	0.270	0.324	0.526					0.31	0.34	0.23	0.46
	0.032	0.121	0.140	0.242	0.065	0.160	0.161	0.609	0.004	0.065	0.096	0.055					0.03	0.13	0.17	0.40
SKCM	0.054	0.115	0.372	0.053	0.061	0.126	0.327	0.143	0.063	0.092	0.268	0.122	0.032	0.082	0.341	0.027
	0.271	0.228	0.676	0.409	0.377	0.342	0.751	0.580	0.404	0.239	0.747	0.668	0.353	0.175	0.776	0.495
	0.027	0.121	0.405	0.343	0.033	0.127	0.506	0.389	0.028	0.104	0.273	0.070	0.027	0.129	0.385	0.282

Note. I, R, RR, C and R² correspond to the index-based, rank-based, correlation-based and R-squared based measures, respectively. In each cell, rows 1–3 correspond to gene expression, methylation and CNA.

The results on the frequency-based measure are shown in Table 4. Take BRCA and GBM as an example. We first compared the lists of genes (methylation loci, CNAs) identified across the whole paths. For gene expression, methylation and CNA, the numbers of overlapped indexes are 12, 94 and 91, respectively. When we used the Jaccard index to account for the sizes of signatures, the degree of overlap of methylation signatures was much higher. However, the result was reversed with the frequency-based measure, under which the CNA signatures have a higher degree of overlap. This observation suggests that, for this specific analysis, the Jaccard index-based result may lack stability, and the frequency-based measure can provide additional information beyond the other measures. In Supplementary Figure A4, for BRCA and GBM, we plotted the frequencies of genes identified along the solution paths. For gene expression, there are only a few genes with high frequencies for both BRCA and GBM. However, for methylation and CNA, there are quite a few genes with high frequencies for both cancers. As described above, the genes with high frequencies for both cancer types make the main contribution to the overlap. In viewing Supplementary Figure A4, we can identify which genes lead to the overlap of signatures for GBM and BRCA.

Table 4.

Evaluation of similarity/overlap between the signatures of different cancer types using the frequency-based measure

	GBM			LAML			LUSC			SKCM
	mRNA	methy	CNA	mRNA	methy	CNA	mRNA	methy	CNA	mRNA	methy	CNA
BRCA
Raw	12	94	91	12	67	144	4	36	26	22	93	78
Jaccard	0.032	0.490	0.094	0.047	0.396	0.129	0.022	0.277	0.060	0.057	0.492	0.113
Overlap score	3.097	23.596	28.362	5.373	14.584	44.605	0.746	9.269	8.459	6.347	26.028	23.814
GBM
Raw				31	141	412	10	72	103	49	187	237
Jaccard				0.074	0.731	0.286	0.028	0.375	0.109	0.090	0.969	0.211
Overlap score				8.878	38.684	97.607	3.878	18.402	30.281	13.421	46.849	61.942
LAML
Raw							5	49	135	27	139	275
Jaccard							0.021	0.297	0.122	0.061	0.728	0.215
Overlap score							1.362	13.939	38.494	8.137	34.630	79.060
LUSC
Raw										10	69	61
Jaccard										0.026	0.361	0.088
Overlap score										3.004	17.880	19.716

mRNA, methy and CNA correspond to gene expression, methylation and CNA, respectively.

Even though different measures quantify the overlap from different aspects, it is still of interest to quantify the consistency among measures. In Supplementary Table A3, we present the correlation coefficients between the overlap measures. It is observed that all correlation coefficients are positive, indicating overlap results in the same ‘direction’. Correlations tend to be higher within each type of measures (at optimal tuning, across path and frequency based) than across different types of measures. In general, the measures that take the whole path into consideration are more highly correlated than those at the optimal tuning. Overall, Supplementary Table A3 suggests reasonable consistency across different overlap measures.

Biological interpretations

We have also looked into possible biological interpretations of the overlap results. The five cancers occur at different organs. A literature search does not suggest any strong evidence of two or more of them being caused by the same molecular changes. Thus it is reasonable that the overlap measures are mostly small to moderate. On the other hand, there are also abundant evidences in the literature showing that the five cancer types can be connected at the molecular level. For example, it has been suggested that GBM is ‘correlated’ with breast cancer [20], and such correlation is partly attributable to genes regulating sex hormones. Cilia gene dysregulation has been associated with GBM, breast cancer, lung cancer and several other cancer types [21]. Gene NF1 has been suggested as important in the prognosis of GBM and melanoma. Gene ERBB2 plays an important role in GBM and breast cancer prognosis. Genes TP53 and PIK3R1 are important in the prognosis of multiple cancer types including those analyzed in this study. BRCA2, a hallmark gene of breast cancer, is also implicated in the progression of leukemia [22]. Family history of breast cancer is a risk factor for leukemia, suggesting their possible genetic connections [23]. Patients with breast cancer or melanoma have a significant higher risk of developing the other. Genetic factors are expected to play a role in such a correlation. Genes possibly shared by breast cancer and melanoma have also been identified by Wang and others [24]. A study conducted by Yanaihara and others [25] has looked into the correlation between lung cancer and leukemia and attributed that correlation partly to microRNAs. Genetic changes that can lead to the Li-Fraumeni syndrome may be associated with the progression of breast cancer, leukemia and several other cancer types. Genetic changes on chromosome 9p have been suggested as associated with melanoma, GBM, lung cancer and leukemia [26]. Genes in the RAS-BRAF pathway have been implicated in the progression of multiple cancer types, especially including lung cancer and melanoma [27]. The EGFR pathway has been implicated in the prognosis of multiple cancers including those analyzed. Studies reported in the aforementioned references and in the literature suggest that it is plausible to observe overlaps of gene signatures for the five analyzed cancers. However, the published studies have been mostly focused on a small number of genes, and it is not possible to infer the overall overlap of gene signatures from those studies.

Remarks

Published studies [6, 28, 29] have suggested that even a small overlap in gene signatures may have important implications. Thus, the presented results can still be valuable. In the literature, the existing studies on gene signature overlap have focused on the overlap of individual genes (i.e. the index-based measure). With a few overlapped genes, the study authors have been able to examine the downstream products of the overlapped genes to draw biological conclusions and conduct functional validation studies. This study has an analytic nature. We acknowledge the limitation of not being able to conduct biological validation, which should be the ultimate criterion for evaluating the analysis results. The proposed measures may face challenges not encountered by the simple index-based measure. Specifically, they are on the overlap of whole gene signatures. With the great heterogeneity across cancer types, we do not expect two cancers to have highly overlapped gene signatures. It is not entirely clear how to design functional studies to validate the partial overlap of gene signatures.

All of the proposed measures are sums of individual terms. Potentially, as a remedy to the aforementioned problem, we can examine each term, identify which terms contribute more to the overlap, and examine the corresponding genes. For example in Supplementary Figure A4, those genes with their names marked are potentially more interesting.

Discussion

For many complex diseases, a large number of gene signatures have been generated. Recent effort has been devoted to evaluating the degree of overlap of gene signatures. However, most of the existing analyses have focused on the index-based measure, which has multiple limitations. The main addition of this study to the literature is a set of new measures, which have very solid statistical basis and can overcome some of the limitations of the index-based measure. All of the proposed measures have intuitive interpretations and can be easily realized. To facilitate their applications, we have also made the computer code publicly available. The analysis of TCGA data demonstrates that the new measures can lead to conclusions different from using the simple index-based measure. This observation suggests that some conclusions on gene signature overlap, for example, those on GEO data [8] and in HDN studies, may need to be reexamined.

In this study, we used cancer prognosis data as an example. The proposed measures are directly applicable to other diseases and other types of data (etiology, continuous biomarker, etc.). We used Lasso as the tool for generating signatures. The proposed measures are also directly applicable to other analysis methods. In the data analysis, we observed different results for different cancer types, different types of (epi)genetic measurements, different measures and different approaches. There is a lack of a clear pattern. Such results are reasonable. Different measures quantify different aspects of gene signatures. Multiple measures will be needed to comprehensively describe the relationship between two signatures. We have not tried to match the overlap results with the prediction results in Supplementary Table A1. The proposed measures focus on the overlap of gene sets. Prediction depends on the set of genes as well as magnitudes and signs of their estimates. Thus, we do not expect the computed overlap measures to be able to fully explain the prediction results.

The research on overlap between gene signatures is still immature. Some studies—including the present one—are statistical, whereas others are biological. To really comprehensively measure the overlap of two signatures, both biological and statistical information is needed. The proposed measures focus on the sets of identified genes. Information on the estimates and significance level is not used. When the estimates are comparable across data sets, it is desirable to develop methods that can take the estimates and significance into account. More methodological development is needed, and more research is needed to comprehend and use the overlap information.

Supplementary data

Supplementary data are available online at http://bib.oxfordjournals.org/.

Key Points.

• It is important to evaluate the overlap of gene signatures on a single cancer type and outcome and on multiple different cancer types.

• Multiple measures for the degree of overlap, under fixed tunings and multiple tunings along the whole solution paths, have been examined.

• The analysis of TCGA data on the prognosis of five cancer types suggests that different measures generate different results, and the proposed measures can provide additional insights beyond the existing simple measure.

• More investigations are needed to evaluate and understand the overlap between gene signatures.

Biographies

Xingjie Shi is Assistant Professor in Department of Statistics, School of Economics at Nanjing University of Finance and Economics.

Huangdi Yi is a graduate student in Department of Statistics, School of Economics at Xiamen University.

Shuangge Ma is Associate Professor in Department of Biostatistics at Yale University.

Funding

This study was supported by awards from the National Institutes of Health (CA182984, CA152301, P50CA121974, P30CA16359).