Mixed Model with Correction for Case-Control Ascertainment Increases Association Power

Abstract

We introduce a liability-threshold mixed linear model (LTMLM) association statistic for case-control studies and show that it has a well-controlled false-positive rate and more power than existing mixed-model methods for diseases with low prevalence. Existing mixed-model methods suffer a loss in power under case-control ascertainment, but no solution has been proposed. Here, we solve this problem by using a χ² score statistic computed from posterior mean liabilities (PMLs) under the liability-threshold model. Each individual’s PML is conditional not only on that individual’s case-control status but also on every individual’s case-control status and the genetic relationship matrix (GRM) obtained from the data. The PMLs are estimated with a multivariate Gibbs sampler; the liability-scale phenotypic covariance matrix is based on the GRM, and a heritability parameter is estimated via Haseman-Elston regression on case-control phenotypes and then transformed to the liability scale. In simulations of unrelated individuals, the LTMLM statistic was correctly calibrated and achieved higher power than existing mixed-model methods for diseases with low prevalence, and the magnitude of the improvement depended on sample size and severity of case-control ascertainment. In a Wellcome Trust Case Control Consortium 2 multiple sclerosis dataset with >10,000 samples, LTMLM was correctly calibrated and attained a 4.3% improvement (p = 0.005) in χ² statistics over existing mixed-model methods at 75 known associated SNPs, consistent with simulations. Larger increases in power are expected at larger sample sizes. In conclusion, case-control studies of diseases with low prevalence can achieve power higher than that in existing mixed-model methods.

Introduction

Mixed-model association statistics are a widely used approach to correct for population structure and cryptic relatedness in genome-wide association studies (GWASs).^1–11 However, recent work shows that existing mixed-model association statistics have less power than standard logistic regression in studies of ascertained case and control subjects.¹¹ It is widely known that appropriate modeling of case-control ascertainment can produce substantial increases in power for case-control studies with fixed-effect covariates,^12–14 but such increases in power have not yet been achieved with models that include random effects.

We developed an association-score statistic based on a liability-threshold mixed linear model (LTMLM). The LTMLM statistic relies on the posterior mean liability (PML) of each individual; the PML is calculated with a multivariate Gibbs sampler.¹⁵ The PML of each individual is conditional on the genetic relationship matrix (GRM), the case-control status of every individual, and the disease prevalence. Existing methods use a univariate prospective model to compute association statistics, but here we use a multivariate retrospective model.

The LTMLM statistic provides an increase in power in simulations of case-control studies of diseases with low prevalence, as demonstrated in settings of either simulated or real genotypes. In a Wellcome Trust Case Control Consortium 2 (WTCCC2) multiple sclerosis (MS) dataset with >10,000 samples, LTMLM was correctly calibrated and attained a 4.3% improvement (p = 0.005) in χ² statistics over existing mixed-model methods at 75 known associated SNPs, consistent with simulations.

Material and Methods

Overview of Method

We improve upon standard mixed-model methods¹¹ by using a retrospective association-score statistic (LTMLM) computed from PMLs under the liability-threshold model. The improvement over previous approaches comes from appropriate modeling of case-control ascertainment. We consider all individuals simultaneously and incorporate prevalence information.

Our method consists of three steps. First, the GRM is calculated, and a corresponding heritability parameter is estimated, modeling the phenotype covariance of all individuals (see “Estimation of Heritability Parameter”). The heritability parameter is estimated with Haseman-Elston (H-E) regression on the observed scale and then transformed to the liability scale. Second, PMLs are estimated with a truncated multivariate normal Gibbs sampler (see “PMLs”). The PML of each individual is conditional on that individual’s case-control status, on every other individual’s case-control status, and on disease prevalence and liability-scale phenotypic covariance. Third, a χ² (1 degree of freedom) association-score statistic is computed on the basis of the association between the candidate SNP and the PML (see “LTMLM Association Statistic”).

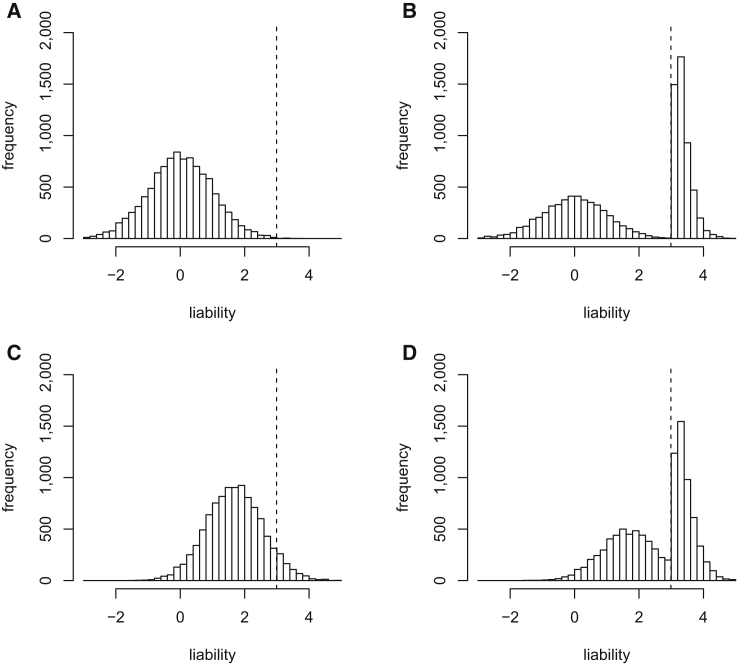
The toy example in Figure 1 illustrates how genetic relatedness to a disease-affected case subject can increase an individual’s PML. In Figures 1A and 1B, we plot the distribution of liabilities in 10,000 unrelated individuals who were randomly ascertained and ascertained according to case-control status (for a disease with a prevalence of 0.1%), respectively. In Figures 1C and 1D, we plot the same distributions but condition on an individual’s having a genetic relatedness of 0.5 with a disease-affected case subject while assuming a liability-scale heritability of 1.0. In each case, the posterior distribution of liabilities (and hence the PML) is shifted upward. (The magnitude and direction of this effect would be different for an individual with a genetic relatedness of 0.5 with a control subject). Our main focus below is on much lower levels of genetic relatedness (identity by state) among many unrelated samples, but the same principles apply.

Figure 1.

Genetic Relatedness to a Disease-Affected Case Subject Can Increase an Individual’s PML

In (A) and (B), we plot distributions of liabilities for a set of 10,000 individuals under (A) random ascertainment or (B) case-control ascertainment for a disease with a prevalence of 0.1% (see Figure 2 in Lee et al.¹⁶). In (C) and (D), we plot the same distributions but condition on an individual’s having a genetic relatedness of 0.5 with a disease-affected case subject while assuming a heritability of 1 on the liability scale.

Estimation of Heritability Parameter

Mixed-model association statistics rely on the estimation of a heritability parameter. We note that this heritability parameter, which Kang et al.⁴ refer to as “pseudo-heritability,” is generally lower than the total narrow-sense heritability (h²) in datasets not dominated by family relatedness but can be larger than the heritability explained by genotyped SNPs (h_g²)¹⁷ in datasets with population structure or family relatedness. However, for ease of notation, we use the symbol h² to represent this heritability parameter. A list of all notation used below is provided in Table S1.

The goal is to test for association between a candidate SNP and a phenotype. We first consider a quantitative trait:

$$\mathit{\phi }=\mathit{\beta x}+\mathit{u}+\mathit{e}.$$ (Equation 1)

The phenotypic data (transformed to have mean 0 and variance 1) can be represented as a vector (φ) with values for each individual (i). Genotype values of candidate SNPs are transformed to a vector (x) with mean 0, variance 1, and effect size β. The quantitative trait value depends on the fixed effect of the candidate SNP (βx), the genetic random effect excluding the candidate SNP (u), and the environmental component (e). We extend to case-control traits via the liability-threshold model, in which each individual has an underlying, unobserved, normally distributed trait called the liability. An individual is affected by a disease if the liability exceeds a specified threshold (t), corresponding to disease prevalence¹⁶ (Figure S1).

Standard mixed-model association methods generally estimate h² from a GRM and phenotypes by using restricted maximum likelihood (REML).^4,11 Genotypic data (excluding the candidate SNP¹¹) are used for building a GRM:

$$\hat{\mathit{\Theta }}=\frac{{\mathit{X}}^T\mathit{X}}{M},$$ (Equation 2)

where X is a matrix of non-candidate SNPs normalized to mean 0 and variance 1 and M is the number of SNPs. We estimate h² by using H-E regression followed by a transformation to the liability scale. We obtain the H-E regression estimate by regressing the product of the case-control phenotypes on the off-diagonal terms of the GRM:^18,19

$$\widehat{h_{\text{HE}}^2}=\frac{{\sum }_{i\ne k}{\mathit{\pi }}_i{\mathit{\pi }}_k{\hat{\mathit{\Theta }}}_{ik}}{{\sum }_{i\ne k}{\hat{\mathit{\Theta }}}_{ik}^2},$$ (Equation 3)

where π_i denotes the case-control status of individual i and $\hat{\mathit{\Theta }}$ _ik is the genetic relatedness of individuals i and k. This gives an estimate on the observed scale, and then the estimate is transformed to the liability scale:²⁰

$$\widehat{h_{\text{HE},\text{l}}^2}=\widehat{h_{\text{HE}}^2}\frac{{\left[K\left(1-K\right)\right]}^2}{z^2\left(P\left(1-P\right)\right)},$$ (Equation 4)

where z is the height of the standard normal density ($\left(1/2\pi \right)e^{-t^2/2}$) at the liability threshold t, K is disease prevalence, and P is the proportion of case subjects in the sample.²⁰

Then, the variance between the individuals is modeled as the phenotypic covariance,

$$\mathit{V}=h^2\hat{\mathit{\Theta }}+\left(\mathit{I}-h^2\right)\mathit{I},$$ (Equation 5)

where $\hat{\mathit{\Theta }}$ is the N × N GRM, V is the phenotypic covariance, h² is the heritability parameter, and I is the identity matrix.

Using the phenotypic covariance matrix V, the liability is modeled as a multivariate normal distribution:

$$L\left(\mathit{\phi }\right)={\left(2\pi \right)}^{\frac{-\mathit{n}}{2}}{\left|\left(\mathit{V}\right)\right|}^{-1/2}\text{exp}\left(\frac{-1}{2}{\left(\mathit{\phi }\right)}^T{\left(\mathit{V}\right)}^{-1}\left(\mathit{\phi }\right)\right).$$ (Equation 6)

We note that we observe the case-control phenotypes of the individuals and not the continuous liabilities.

PMLs

We first consider the univariate PML (PML_uni), constructed independently for each individual; we generalize to the multivariate setting below. As described in Equations 11 and 12 in Lee et al.,²⁰ these correspond to the expected value of the liability and are conditional on the case-control status:

$${\text{PML}}_{\text{uni},\text{case}}=E\left[\mathit{\phi }\text{|}{\mathit{\pi }}_i=1\right]=z/$$

$${\text{PML}}_{\text{uni},\text{control}}=E\left[\mathit{\phi }\text{|}{\mathit{\pi }}_i=0\right]=-z/\left(1-K\right).$$ (Equation 7)

These values are calculated analytically in the univariate setting, and depending on case or control status, they can be thought of as the mean of a truncated normal distribution above or below, respectively, the liability threshold t.²⁰

We next consider the multivariate PML (PML_multi), estimated jointly across individuals. The PML_multi for each individual is conditional on that individual’s case-control status, on every other individual’s case-control status, and on their phenotypic covariance. The PML_multi is estimated with a Gibbs sampler, as in previous work¹⁵ (which focused on family relatedness and did not consider association statistics). The Gibbs sampler is an iterative algorithm that generates random variables from conditional distributions in order to avoid the difficult task of explicitly calculating the marginal density for each random variable.

For each individual in turn, the conditional distribution of the liability is calculated on the basis of all of the other individuals, and a new value is generated. The algorithm is as follows:

Initialization: for each individual j,

$${\mathit{\phi }}_i=\text{PM}{\mathrm{L}}_{\text{uni},\text{case}}\text{if}{\mathit{\pi }}_i=1\text{or}{\mathit{\phi }}_i=\text{PM}{\mathrm{L}}_{\text{uni},\text{control}}\text{if}{\mathit{\pi }}_i=0$$ (Equation 8)

For each Markov Chain Monte Carlo (MCMC ) iteration n

• For each individual i

  • Sample φ_i from the constrained conditional univariate normal distribution
  • L(φ_i) ∼exp(–φ^TV⁻¹φ/2) and constraint φ_i ≥ t if π_i = 1, φ_i < t if π_i = 0
  • (where φ_≠i are fixed)

We use 100 burn-in iterations followed by 1,000 additional MCMC iterations. We estimate the PML_multi by averaging over MCMC iterations. We reduce the number of MCMC iterations needed via Rao-Blackwellization, which averages (across n iterations) the posterior means of the distributions from which each φ_i is sampled.

LTMLM Association Statistic

The LTMLM association statistic is calculated with the PML_multi. For simplicity, we first consider the case where the liability is known. We jointly model the liability and the genotypes by using a retrospective model, enabling appropriate treatment of sample ascertainment. We concatenate the two vectors (φ, x) and derive the joint likelihood for these combined terms. The covariance of φ and x between individuals i and k is

$$\text{Cov}\left({\mathit{\phi }}_i,{\mathit{x}}_k\right)=E\left[{\mathit{\phi }}_i,{\mathit{x}}_k\right]-E\left[{\mathit{\phi }}_i\right]E\left[{\mathit{x}}_{\mathit{k}}\right]=E\left[{\mathit{\phi }}_i,{\mathit{x}}_k\right]=E\left[\mathit{\beta }{\mathit{x}}_i,{\mathit{x}}_k\right]=\mathit{\beta }{\mathit{\Theta }}_{i,k},$$ (Equation 9)

where Θ is the true underlying GRM from which genotypes are sampled. (We note that Θ, which is unobserved, is different from the GRM $\hat{\mathit{\Theta }}$ estimated from the data). The variance of (φ, x) as a function of effect size $\mathit{\beta }$ is

$$\mathit{C}\left(\mathit{\beta }\right)=\left(\begin{array}{cc}\mathit{V}& \mathit{\beta \Theta }\\ \mathit{\beta }{\mathit{\Theta }}^T& \mathit{\Theta }\end{array}\right).$$ (Equation 10)

Thus,

$$\mathit{C}{\left(\mathit{\beta }\right)}^{-1}=\left(\begin{array}{cc}{\mathit{V}}^{-1}& -\mathit{\beta }{\mathit{V}}^{-1}\\ -\mathit{\beta }{\left({\mathit{V}}^{-1}\right)}^T& {\mathit{\Theta }}^{-1}\end{array}\right)+O\left({\mathit{\beta }}^2\right),$$ (Equation 11)

where both of these matrices are 2N × 2N. (We note that the product of the matrices in Equations 10 and 11 is $\left(\begin{array}{cc}\mathit{I}+O\left({\mathit{\beta }}^2\right)& 0\\ 0& \mathbf{I}+O\left({\mathit{\beta }}^2\right)\end{array}\right),$ whose difference from the identity contains only O(β²) terms.)

The joint likelihood of the liability and genotypes is distributed as a multivariate normal N(0,C(β)), and thus

$$L\left(\mathit{x},\mathit{\phi }|\mathit{\beta }\right)={\left(2\pi \right)}^{\frac{-n}{2}}{|\mathit{C}\left(\mathit{\beta }\right)|}^{-1/2}\text{exp}\left(\frac{-1}{2}{\left(\mathit{\phi },\mathit{x}\right)}^T\mathit{C}{\left(\mathit{\beta }\right)}^{-1}\left(\mathit{\phi },\mathit{x}\right)\right).$$ (Equation 12)

Taking the derivative of the log-likelihood results in the score equation. The determinant of the matrix V does not have any terms linear in β, so the terms with V alone drop out when we take the derivative:

$$S\left(\mathit{x},\mathit{\phi }|\mathit{\beta }\right)=\frac{d}{d\mathit{\beta }}\text{ln}L\left(\mathit{x},\mathit{\phi }|\mathit{\beta }\right)=\frac{d}{d\mathit{\beta }}\frac{-1}{2}{\left(\mathit{\phi },\mathit{x}\right)}^T\mathit{C}\left(\mathit{\beta }\right)\left(\mathit{\phi },\mathit{x}\right)$$

$$=\frac{d}{d\mathit{\beta }}{\left(\mathit{\phi },\mathit{x}\right)}^T\left(\begin{array}{cc}{\mathit{V}}^{-1}& -\mathit{\beta }{\mathit{V}}^{-1}\\ -\mathit{\beta }{\left({\mathit{V}}^{-1}\right)}^T& {\mathit{\Theta }}^{-1}\end{array}\right)\left(\mathit{\phi },\mathit{x}\right)={\mathit{V}}^{-1}\mathit{\phi x}.$$ (Equation 13)

The marginal score statistic tests the null hypothesis, which is that the fixed effect of the candidate SNP is 0 (H₀: β = 0), against the alternative hypothesis (H_A: β ≠ 0). The denominator of the score statistic is the variance of the score evaluated under the null:

$$\text{Var}\left(S\left(\mathit{x},\mathit{\phi }|\mathit{\beta }\right)\right)={\left({\mathit{V}}^{-1}\mathit{\phi }\right)}^T\mathit{\Theta }\left({\mathit{V}}^{-1}\mathit{\phi }\right).$$ (Equation 14)

This leads to the score statistic

$$\frac{{\left({\mathit{x}}^T{\mathit{V}}^{-1}\mathit{\phi }\right)}^2}{{\left({\mathit{V}}^{-1}\mathit{\phi }\right)}^T\mathit{\Theta }\left({\mathit{V}}^{-1}\mathit{\phi }\right)},$$ (Equation 15)

where Θ, the true underlying genetic relatedness of the individuals, can be approximated by the identity matrix in datasets of unrelated individuals.

In Equations 9, 10, 11, 12, 13, 14, and 15, the liability was assumed to be known for simplicity. We now consider a case-control trait, with unobserved liability, and derive the score function by using the observed case-control status, π, of each individual. When we return to the score function and conditioning on case-control status,

$$S{\left(\mathit{x},\mathit{\phi }|\mathit{\beta },\mathit{\pi }\right)}_{\mathit{\beta }=0}=\frac{d}{d\mathit{\beta }}\text{ln}L{\left(\mathit{x},\mathit{\phi }|\mathit{\beta },\mathit{\pi }\right)}_{\mathit{\beta }=0}=\frac{\frac{dL{\left(\mathit{x},\mathit{\phi }|\mathit{\beta },\pi \right)}_{\mathit{\beta }=0}}{d\mathit{\beta }}}{L{\left(\mathit{x},\mathit{\phi }|\mathit{\beta },\pi \right)}_{\mathit{\beta }=0}}.$$ (Equation 16)

When we introduce the unobserved quantitative liability, φ, the score function can be rewritten in terms of the probability density of the liability:

$$\frac{\frac{dL{\left(\mathit{x},\mathit{\phi }|\mathit{\beta }\right)}_{\mathit{\beta }=0}}{d\mathit{\beta }}}{L{\left(\mathit{x},\mathit{\phi }|\mathit{\beta }\right)}_{\mathit{\beta }=0}}=\frac{\int P\left(\mathit{\phi }\right)\frac{dL{\left(\mathit{x},\mathit{\phi }|\mathit{\beta }\right)}_{\mathit{\beta }=0}}{d\mathit{\beta }}d\mathit{\phi }}{L{\left(\mathit{x},\mathit{\phi }|\mathit{\beta }\right)}_{\mathit{\beta }=0}}$$

$$S\left(\mathit{x},\mathit{\phi }|\mathit{\beta },\pi \right)=\mathit{C}\int P\left(\mathit{\phi }\right)S\left(\mathit{x},\mathit{\phi }|\mathit{\beta },\mathit{\pi }\right)d\mathit{\phi }=S\left(\mathit{x},E\left[\mathit{\phi }|\pi \right]|\mathit{\beta }\right),$$ (Equation 17)

where P(φ) is the probability density of the liability and E[φ| π] is the PML. It follows that an appropriate LTMLM score statistic is

$$\frac{{\left({\mathit{x}}^T{\mathit{V}}^{-1}\mathbf{P}\mathbf{M}{\mathbf{L}}_{\mathbf{m}\mathbf{u}\mathbf{l}\mathbf{t}\mathbf{i}}\right)}^2}{{\left({\mathit{V}}^{-1}\mathbf{P}\mathbf{M}{\mathbf{L}}_{\mathbf{m}\mathbf{u}\mathbf{l}\mathbf{t}\mathbf{i}}\right)}^T\mathit{\Theta }\left({\mathit{V}}^{-1}\mathbf{P}\mathbf{M}{\mathbf{L}}_{\mathbf{m}\mathbf{u}\mathbf{l}\mathbf{t}\mathbf{i}}\right)}.$$ (Equation 18)

Again, Θ can be approximated by the identity matrix in datasets of unrelated individuals; we note that this choice affects only a constant calibration factor (because the denominator is the same for each candidate SNP) and that other calibration options are available (see below). As with other association statistics, the LTMLM score statistic generalizes to non-normally distributed genotypes.^21–23 The overall computational cost of computing the LTMLM statistic is O(MN²) when M > N > number of iterations (Table S2). We have fixed the number of iterations at 100 burn-in iterations followed by 1,000 additional iterations.

We calculate the GRM via leave one chromosome out (LOCO) analysis, i.e., for each candidate SNP on a given chromosome, we calculate GRM by using all of the other chromosomes. This prevents deflation due to double counting of the candidate SNP as both a fixed effect and a random effect in the mixed model.^4,6,11

Simulated Genotypes and Simulated Phenotypes

We performed simulations both by using simulated genotypes and simulated phenotypes and by using real genotypes and simulated phenotypes (see below). Quantitative liabilities for each individual were generated from SNP effects and an environmental component. All simulations included M candidate SNPs and an independent set of M SNPs used for calculating the GRM (so that candidate SNPs were not included in the GRM). For each scenario, a set of 100 simulations were run. We set ten candidate SNPs and ten GRM SNPs to be causal in simulations with N = 1,000 samples and set 50 candidate SNPs and 50 GRM SNPs to be causal in simulations with N = 5,000 samples to ensure that causal SNPs had similar average χ² statistics independent of M and N. We then dichotomized the resulting quantitative liabilities on the basis of the liability threshold to categorize each individual as a case or control subject. Case-control ascertainment was performed and simulated 50% case and 50% control subjects. We compared Armitage trend test (ATT), logistic regression (LogR), mixed linear model (MLM), and LTMLM statistics (see Table 1). MLM statistics were computed with the genome-wide complex trait analysis (GCTA)-LOCO statistic described in Yang et al.,¹¹ and the heritability parameters were estimated with the GCTA software.²⁴ We evaluated performance by using average χ² statistics at causal, null, and all markers, λ_GC at all markers (median χ² divided by 0.455),²⁵ and the proportion of causal and null markers that were significant at the p value thresholds of 0.05, 0.001, 1 × 10⁻⁶, and 5 × 10⁻⁸.

Table 1.

List of Association Statistics

	ATT	MLM	LTMLM
Quantitative or case-control trait	both	both	case-control
Estimates of heritability parameter	none	REML	H-E regression
Prospective or retrospective	prospective	prospective	retrospective
Equation	$\frac{{\left({\mathit{x}}^T{\pi }^{\ast }\right)}^2}{{\mathit{x}}^T\mathit{x}}$	$\frac{{\left({\mathit{x}}^T{\pi }^{\ast }{\mathit{V}}^{-1}\right)}^2}{{\mathit{x}}^T{\mathit{V}}^{-1}\mathit{x}}=\frac{{\left({\mathit{x}}^T{\mathit{V}}^{-1}{\mathbf{P}\mathbf{M}\mathbf{L}}_{\mathbf{uni}}\right)}^2}{{\mathit{x}}^T{\mathit{V}}^{-1}\mathit{x}}$	$\frac{{\left({\mathit{x}}^T{\mathit{V}}^{-1}\mathbf{P}\mathbf{M}{\mathbf{L}}_{\mathbf{m}\mathbf{u}\mathbf{l}\mathbf{t}\mathbf{i}}\right)}^2}{{\left({\mathit{V}}^{-1}\mathbf{P}\mathbf{M}{\mathbf{L}}_{\mathbf{m}\mathbf{u}\mathbf{l}\mathbf{t}\mathbf{i}}\right)}^T\mathit{I}\left({\mathit{V}}^{-1}\mathbf{P}\mathbf{M}{\mathbf{L}}_{\mathbf{m}\mathbf{u}\mathbf{l}\mathbf{t}\mathbf{i}}\right)}$
Corrects for confounding?	no	yes	yes
Models case-control ascertainment	no	no	yes

We list properties of the Armitage trend test (ATT), standard mixed-model association statistic (MLM), and proposed statistic (LTMLM). π^∗ is the normalized case-control status (mean 0 and variance 1), x is the normalized genotype, PML_uni is the univariate PML conditional on the case-control status of a single individual, PML_multi is the multivariate PML conditional of the case-control status of all individuals, I is the identity matrix, and V is the phenotypic covariance (on the observed scale for MLM and on the liability scale for LTMLM).

In the primary analyses, we simulated individuals without population structure or linkage disequilibrium (LD) with N = 1,000 or 5,000 samples; M = 1,000, 5,000, or 50,000 SNPs; and prevalence K = 50%, 10%, 1%, or 0.1%. Genotypes were sampled from independent binomials with allele frequencies sampled from a uniform distribution over the values [0.1, 0.9]. In secondary analyses, we simulated population structure by simulating two populations with F_ST = 0.01 and allele frequencies drawn from beta distributions with parameters p(1 – F_ST)/F_ST and (1 – p)(1 – F_ST)/F_ST, based on ancestral allele frequency p sampled from a uniform distribution over the values [0.1, 0.9].

To test the impact of the generative distribution, we simulated the underlying distribution by using a logit model instead of a liability-threshold model. The ten causal candidate SNPs were simulated with alternating fixed-effect sizes of β = 0.4 or β = −0.4. Then, case-control phenotypes were generated from a binomial distribution where the probability of being a case subject was $\left(\text{case}\right)=1/\left(1+\text{exp}\left(-\left[c+\mathit{\beta x}\right]\right)\right)$, shifted by the affine term (c) and based on the desired disease prevalence.

WTCCC2 Genotypes and Simulated Phenotypes

We also conducted simulations by using real genotypes from WTCCC2 to incorporate LD and realistic population structure. The WTCCC2 data contained 360,557 SNPs and 15,633 samples, as described previously.¹¹ Because the goal of the power study is to demonstrate a comparison of the statistics under case-control ascertainment, we used N = 1,000 samples (500 case and 500 control subjects) and simulated phenotypes with a prevalence of 50%, 25%, and 10%. The prevalence was restricted to a lower bound of 10% because of the limitation of having only 15,633 WTCCC2 samples for simulating case-control ascertainment. We computed ATT, LogR, MLM, and LTMLM statistics as described above.

WTCCC2 Genotypes and MS Phenotypes

Finally, we analyzed WTCCC2 individuals with ascertained case-control phenotypes for MS,¹¹ a disease with a prevalence of around 0.1%. As in previous work, we assume that the disease prevalence is known on the basis of external epidemiological literature.^20,26,27 For the WTCCC2 MS data, we used a threshold of 3.0, corresponding to a disease prevalence of 0.1%.²⁶ We computed ATT, LogR, MLM, and LTMLM statistics as described above. Although the underlying MS study was appropriately matched for ancestry,²⁸ the data made available to researchers included only pan-European case and UK control subjects. Thus, the WTCCC2 dataset shows a severe mismatch in ancestry of case and control subjects; this severe mismatch between case and control subjects is not representative of a typical GWAS. We thus restricted our primary analysis to 10,034 samples with only a moderate mismatch in ancestry, but we also performed analyses of unmatched and stringently matched datasets (Figure S2). The unmatched dataset contained 10,204 case and 5,429 control subjects. We performed matching by first calculating 20 principal components (PCs) in the full cohort and weighing the contribution of each PC on the basis of how much phenotype variance it explained in a multiple regression. A Euclidean distance over these 20 weighted dimensions was then computed for all pairs of individuals, and each case subject was greedily assigned the nearest unmatched control subject until no matched case-control pairs could be identified. Finally, any matched case-control pairs who were not within 6 SDs of the mean pairwise distance were removed as outliers, yielding the 5,017 case and 5,017 matched control subjects used in our primary analysis. We performed stringent matching by additionally removing any matched case-control pairs who were not within 2 SDs of the mean pairwise distance, yielding the 4,094 case and 4,094 matched control subjects used in our stringently matched analysis.

We compared association statistics at 75 published SNPs associated with MS.¹¹ We used a jackknife approach to assess the statistical significance of differences in association statistics by excluding each of the 75 published SNPs in turn.

Results

Simulations: Simulated Genotypes and Simulated Phenotypes

We first conducted simulations by using simulated genotypes and simulated ascertained case-control phenotypes (see Material and Methods). Our main simulations involved unrelated individuals with no population structure, but the impact of population structure is explored below. We evaluated the power of ATT, LogR, MLM, and LTMLM. We report average χ² statistics at causal, null, and all markers and λ_GC at all markers in Table 2, and we report the proportion of causal and null markers that were significant at various p value thresholds in Table S3. For diseases with low prevalence, the LTMLM statistic outperformed the ATT, LogR, and MLM statistics. Improvements in average χ² statistics at causal markers (which are naturally interpreted as the increase in effective sample size) were larger than improvements in power to detect an association at a given p value threshold, most likely as a result of the variable (normally distributed) effect sizes in this simulation (see below). For LTMLM and MLM at disease prevalences of 0.1%, 26%, and 5%, improvements in average χ² statistics at causal markers were observed in simulations with 5,000 SNPs and 50,000 SNPs, respectively. Smaller improvements were observed at higher disease prevalences. Test statistics were well calibrated at null markers. Simulations at other values of M and N indicated that the magnitude of the improvement depends on the value of N/M (Tables S3 and S4). Simulations with population structure demonstrated similar results but also showed inflation in the ATT statistic as expected (Tables S5 and S6).

Table 2.

Results for Simulated Genotypes and Simulated Phenotypes

Prevalence	Set	Statistic	ATT (SE)	LogR (SE)	MLM (SE)	LTMLM (SE)
N = 5,000 and M = 5,000
50%	causal	average	16.492 (0.325)	16.399 (0.321)	16.880 (0.332)	16.867 (0.332)
null	average	0.988 (0.002)	0.988 (0.002)	0.990 (0.002)	0.989 (0.002)
all	average	1.143 (0.004)	1.142 (0.004)	1.148 (0.004)	1.148 (0.004)
all	λGC	1.010 (0.003)	1.010 (0.003)	1.014 (0.003)	1.014 (0.003)
25%	causal	average	18.637 (0.388)	18.509 (0.383)	19.014 (0.396)	19.056 (0.398)
null	average	1.000 (0.002)	1.000 (0.002)	1.000 (0.002)	1.001 (0.002)
all	average	1.177 (0.005)	1.175 (0.005)	1.180 (0.005)	1.181 (0.005)
all	λGC	1.012 (0.004)	1.012 (0.004)	1.013 (0.004)	1.013 (0.004)
10%	causal	average	25.235 (0.501)	25.014 (0.492)	25.386 (0.506)	25.778 (0.514)
null	average	0.993 (0.002)	0.992 (0.002)	0.991 (0.002)	0.992 (0.002)
all	average	1.235 (0.006)	1.233 (0.006)	1.235 (0.006)	1.24 (0.007)
all	λGC	1.005 (0.003)	1.005 (0.003)	1.007 (0.003)	1.008 (0.003)
1%	causal	average	45.376 (0.878)	44.682 (0.852)	42.594 (0.825)	46.691 (0.913)a
null	average	1.000 (0.002)	0.999 (0.002)	0.990 (0.002)	1.000 (0.002)
all	average	1.444 (0.011)	1.436 (0.011)	1.406 (0.010)	1.457 (0.011)
all	λGC	1.020 (0.003)	1.020 (0.003)	1.011 (0.003)	1.019 (0.003)
0.1%	causal	average	68.648 (1.301)	67.099 (1.248)	56.303 (1.082)	70.810 (1.364)a
null	average	1.000 (0.002)	1.000 (0.002)	0.918 (0.002)	1.000 (0.002)
all	average	1.677 (0.016)	1.661 (0.016)	1.472 (0.013)	1.698 (0.017)
all	λGC	1.026 (0.003)	1.026 (0.003)	0.942 (0.005)	1.025 (0.003)
N = 5,000 and M = 50,000
50%	causal	average	16.624 (0.331)	16.529 (0.327)	16.673 (0.332)	16.69 (0.333)
null	average	1.000 (0.001)	0.999 (0.001)	1.000 (0.001)	1.000 (0.001)
all	average	1.015 (0.001)	1.015 (0.001)	1.016 (0.001)	1.015 (0.001)
all	λGC	1.003 (0.001)	1.002 (0.001)	0.999 (0.001)	0.999 (0.001)
25%	causal	average	18.965 (0.37)	18.843 (0.366)	19.030 (0.372)	19.040 (0.372)
null	average	1.003 (0.001)	1.003 (0.001)	1.003 (0.001)	1.003 (0.001)
all	average	1.021 (0.001)	1.020 (0.001)	1.021 (0.001)	1.021 (0.001)
all	λGC	1.006 (0.001)	1.006 (0.001)	1.003 (0.001)	1.003 (0.001)
10%	causal	average	23.710 (0.444)	23.528 (0.437)	23.868 (0.449)	23.910 (0.450)
null	average	1.001 (0.001)	1.000 (0.001)	1.001 (0.001)	1.001 (0.001)
all	average	1.023 (0.001)	1.023 (0.001)	1.024 (0.001)	1.024 (0.001)
all	λGC	1.007 (0.001)	1.007 (0.001)	1.005 (0.001)	1.004 (0.001)
1%	causal	average	46.683 (0.883)	45.969 (0.859)	46.44 (0.881)	47.368 (0.905)
null	average	0.999 (0.001)	0.999 (0.001)	0.999 (0.001)	0.999 (0.001)
all	average	1.045 (0.001)	1.044 (0.001)	1.045 (0.001)	1.045 (0.001)
all	λGC	1.004 (0.001)	1.004 (0.001)	1.001 (0.001)	1.000 (0.001)
0.1%	causal	average	67.059 (1.278)	65.561 (1.225)	65.232 (1.251)	68.618 (1.333)a
null	average	0.999 (0.001)	0.999 (0.001)	0.999 (0.001)	0.999 (0.001)
all	average	1.065 (0.002)	1.063 (0.002)	1.063 (0.002)	1.067 (0.002)
all	λGC	1.004 (0.001)	1.004 (0.001)	1.000 (0.001)	1.000 (0.001)

We report average χ² statistics across 100 simulations for each individual scenario. N is the number of individuals, and M is the number of SNPs. The set indicates all SNPs, the 1% causal SNPs, or the 99% null SNPs. The disease prevalence ranges from 50% (no case-control ascertainment) to 0.1%.

^aThe settings where LTMLM demonstrated at least a 5% improvement over MLM in χ² statistics at causal markers.

The MLM statistics were calculated with an h² parameter estimated via REML,⁴ but the LTMLM statistics were calculated with an h² parameter first estimated via H-E regression on case-control phenotypes and then transformed to the liability scale^18,20 (see Material and Methods). As case-control ascertainment became more severe, the H-E regression estimate of h² remained unbiased, whereas the variance-component estimate was severely downwardly biased even after transformation to the liability scale (Table 3 and Table S7), consistent with previous work (see Golan et al.²⁹ and Table S9 in Yang et al.¹¹). Population structure resulted in bias for both REML and H-E-regression estimates of h², although the bias for the REML estimates was higher (Table S8). These biases did not inflate LTMLM or MLM statistics under the null hypothesis (Tables S5 and S6). We note that previous work has shown that running MLM with the correct h² parameter does not ameliorate the loss in power for MLM.¹¹

Table 3.

Heritability-Parameter Estimates from Simulated Genotypes and Phenotypes

Prevalence	Liability Scale		Observed Scale
H-E (SE)	REML (SE)	H-E (SE)	REML (SE)
N = 5,000 and M = 5,000
50%	0.255 (0.006)	0.253 (0.006)	0.162 (0.004)	0.161 (0.004)
25%	0.24 (0.005)	0.236 (0.004)	0.172 (0.003)	0.17 (0.003)
10%	0.24 (0.004)	0.23 (0.004)	0.228 (0.004)	0.219 (0.004)
1%	0.25 (0.004)	0.21 (0.002)	0.453 (0.007)	0.381 (0.004)
0.1%	0.253 (0.003)	0.158 (0.000)	0.719 (0.009)	0.449 (0.001)
N = 5,000 and M = 50,000
50%	0.272 (0.009)	0.274 (0.009)	0.173 (0.006)	0.174 (0.006)
25%	0.246 (0.010)	0.252 (0.010)	0.177 (0.007)	0.181 (0.007)
10%	0.225 (0.004)	0.231 (0.004)	0.214 (0.004)	0.219 (0.004)
1%	0.246 (0.004)	0.241 (0.004)	0.445 (0.008)	0.437 (0.008)
0.1%	0.259 (0.004)	0.241 (0.004)	0.734 (0.012)	0.684 (0.01)

We report results, on both the liability and observed scales, averaged over 100 simulations. The true h², explained by the SNPs used for building the GRM, is 25% on the liability scale for all simulations. These results correspond to the same sets of simulations in Table 2.

We also evaluated performance in settings where the liability threshold (equivalently, the disease prevalence) was misspecified (Tables S9 and S10). The LTMLM statistic remained properly calibrated under the null and continued to outperform the MLM statistic given that the impact of misspecifying the liability threshold was small. Misspecifying the liability threshold led to bias in liability-scale heritability estimates as a result of the inaccurate conversion from the observed scale to the liability scale (Table S11).

Finally, we evaluated performance when phenotypes were generated with a logit model instead of a liability-threshold model; for simplicity, we used a fixed effect size for causal candidate SNPs (see Material and Methods). At low disease prevalence, we observed improvements for LTMLM both in average χ² statistics at causal markers (Table S12) and in power to detect an association at a given p value threshold (Table S13); improvements in power depend heavily on the distribution of causal effect sizes and are larger in simulations with fixed causal effect sizes than in simulations with variable causal effect sizes.

Simulations: WTCCC2 Genotypes and Simulated Phenotypes

We next conducted simulations by using real WTCCC2 genotypes and simulated phenotypes from ascertained case and control individuals (see Material and Methods).^11,28 For a given value of M (M SNPs for calculating the GRM plus M candidate SNPs for a total of 2M SNPs), we used the first M/2 SNPs from each of the first four chromosomes. The GRM was calculated with SNPs on chromosomes 3 and 4, and SNPs on chromosomes 1 and 2 were treated as the candidate SNPs. The simulated phenotypes were generated from chromosomes 1 and 3, where 1% of the SNPs were randomly selected as being causal. Results are reported for causal SNPs on chromosome 1 and for null SNPs on chromosome 2, the latter of which were not used for building the GRM.

Results for simulations including 1,000 and 10,000 SNPs (M) and sample sizes fixed at 500 case and 500 control subjects are displayed in Table 4 and Tables S14 and S15. Once again, the LTMLM statistic outperformed ATT and MLM as case-control ascertainment became more severe. (A limitation of these simulations is that performing case-control ascertainment on a fixed set of individuals limits case-control sample size; thus, these simulations were restricted to a disease prevalence of 10% or higher. It is reasonable to infer that for rarer diseases with more extreme case-control ascertainment the LTMLM statistic would achieve even higher power gains, as was demonstrated in simulations with simulated genotypes.)

Table 4.

Results on Real Genotypes and Simulated Phenotypes

Prevalence	Set	Statistic	ATT (SE)	ATT + PCs (SE)	LogR (SE)	LogR + PCs (SE)	MLM (SE)	LTMLM (SE)
M = 1,000
50%	causal	average	16.234 (0.723)	15.775 (0.705)	15.566 (0.674)	15.14 (0.658)	17.48 (0.780)	17.412 (0.775)
null	average	1.444 (0.011)	1.425 (0.010)	1.433 (0.010)	1.415 (0.010)	1.472 (0.011)	1.471 (0.011)
all	average	1.592 (0.014)	1.569 (0.013)	1.574 (0.013)	1.552 (0.013)	1.632 (0.015)	1.630 (0.015)
all	λGC	1.214 (0.017)	1.224 (0.017)	1.214 (0.017)	1.223 (0.017)	1.234 (0.017)	1.226 (0.016)
25%	causal	average	19.277 (0.771)	18.581 (0.754)	18.47 (0.721)	17.822 (0.706)	20.493 (0.820)	20.642 (0.831)
null	average	1.551 (0.012)	1.507 (0.011)	1.538 (0.012)	1.495 (0.011)	1.571 (0.012)	1.577 (0.013)
all	average	1.728 (0.015)	1.678 (0.014)	1.707 (0.015)	1.658 (0.014)	1.761 (0.016)	1.768 (0.016)
all	λGC	1.256 (0.016)	1.245 (0.017)	1.255 (0.016)	1.245 (0.017)	1.241 (0.015)	1.243 (0.015)
10%	causal	average	22.838 (0.961)	21.406 (0.878)	21.618 (0.881)	20.336 (0.808)	23.865 (1.022)	24.661 (1.064)
null	average	1.664 (0.014)	1.583 (0.012)	1.647 (0.014)	1.568 (0.012)	1.668 (0.014)	1.695 (0.015)
all	average	1.876 (0.018)	1.781 (0.016)	1.846 (0.017)	1.756 (0.015)	1.890 (0.019)	1.925 (0.019)
all	λGC	1.271 (0.016)	1.285 (0.015)	1.270 (0.016)	1.284 (0.015)	1.251 (0.017)	1.270 (0.016)
M = 10,000
50%	causal	average	16.898 (0.702)	16.815 (0.698)	16.229 (0.659)	16.156 (0.655)	17.279 (0.725)	17.26 (0.725)
null	average	1.078 (0.002)	1.083 (0.002)	1.074 (0.002)	1.078 (0.002)	1.078 (0.002)	1.076 (0.002)
all	average	1.094 (0.002)	1.099 (0.002)	1.089 (0.002)	1.094 (0.002)	1.095 (0.002)	1.092 (0.002)
all	λGC	1.039 (0.005)	1.047 (0.005)	1.039 (0.005)	1.046 (0.005)	1.039 (0.005)	1.035 (0.005)
25%	causal	average	17.573 (0.726)	17.293 (0.696)	16.856 (0.679)	16.61 (0.654)	17.976 (0.749)	18.077 (0.758)
null	average	1.076 (0.002)	1.078 (0.002)	1.071 (0.002)	1.073 (0.002)	1.074 (0.002)	1.073 (0.002)
all	average	1.092 (0.002)	1.094 (0.002)	1.087 (0.002)	1.089 (0.002)	1.091 (0.002)	1.090 (0.002)
all	λGC	1.040 (0.004)	1.045 (0.004)	1.040 (0.004)	1.044 (0.004)	1.040 (0.004)	1.039 (0.004)
10%	causal	average	24.379 (1.026)	24.116 (1.014)	23.127 (0.944)	22.894 (0.934)	24.987 (1.071)	25.399 (1.091)
null	average	1.112 (0.002)	1.115 (0.002)	1.107 (0.002)	1.110 (0.002)	1.108 (0.002)	1.111 (0.002)
all	average	1.136 (0.003)	1.138 (0.003)	1.129 (0.002)	1.132 (0.002)	1.131 (0.003)	1.135 (0.003)
all	λGC	1.051 (0.005)	1.059 (0.004)	1.050 (0.005)	1.058 (0.004)	1.044 (0.004)	1.047 (0.004)

We report average χ² statistics. M is the number of SNPs, and sample size is fixed at 500 case and 500 control subjects.

The h² parameter estimates for simulations with real genotypes are displayed in Table 5. The H-E regression estimates are unbiased, but the REML estimates are again downwardly biased at lower prevalence and large N/M.

Table 5.

Heritability-Parameter Estimates on Real Genotypes and Simulated Phenotypes

Prevalence	Liability Scale		Observed Scale
H-E (SE)	REML (SE)	H-E (SE)	REML (SE)
M = 10,000
50%	0.259 (0.013)	0.252 (0.010)	0.165 (0.008)	0.161 (0.006)
25%	0.241 (0.010)	0.238 (0.008)	0.173 (0.007)	0.171 (0.006)
10%	0.245 (0.011)	0.242 (0.007)	0.233 (0.010)	0.230 (0.007)
M = 10,000
50%	0.236 (0.014)	0.245 (0.013)	0.150 (0.009)	0.156 (0.008)
25%	0.250 (0.014)	0.264 (0.013)	0.180 (0.010)	0.190 (0.010)
10%	0.259 (0.012)	0.261 (0.009)	0.246 (0.011)	0.248 (0.009)

These results are from the same simulations used to generate Table 4 and Tables S14 and S15. We report results on both the liability and the observed scales. The true h² explained by the SNPs used for building the GRM is 25% on the liability scale for all simulations.

WTCCC2 MS Dataset

We analyzed the WTCCC2 genotypes together with MS case-control phenotypes: 5,172 MS case subjects and 5,172 control subjects were genotyped on Illumina chips^11,28(see Material and Methods). We compared ATT, ATT with five PCs (ATT + PCs),²² LogR, LogR with five PCs (LogR + PCs), MLM, and LTMLM. We evaluated calibration by using the average χ² and λ_GC over all SNPs; we note that the average χ² and λ_GC are expected to be greater than 1 as a result of polygenic effects.^11,30 We believe that LTMLM is effective in correcting for confounding and that a higher value of λ_GC for LTMLM than for MLM is most likely due to true polygenic signal and reflects the higher power of LTMLM.

We evaluated power by using the average χ² over the 75 published SNPs (Table 6) and the proportion of published SNPs that were significant at various p value thresholds (Table S16). The LTMLM method performed best: it had a 4.3% improvement in average χ² statistics scaled by λ_GC over MLM (jackknife p = 0.005; see Material and Methods) and an even larger improvement over ATT and ATT + PCs, consistent with simulations (Table 2 and Table S3). LTMLM also detected 56/75 known associations as nominally significant (p < 0.05) after λ_GC correction, whereas MLM detected only 53/75, although this difference is not statistically significant. Similar results were obtained when association statistics were calibrated via LD-score regression³¹ (Table S17). A perfectly matched dataset with 4,094 MS case subjects and 4,094 control subjects yielded a similar improvement for LTMLM over MLM (Table S18). We also applied LTMLM to the full unmatched dataset of 10,204 MS subjects and 5,429 control subjects, where a severe mismatch in ancestry between case and control subjects was not representative of a typical GWAS. The LOCO estimates of h² demonstrated inflation before we controlled for population structure (Table S19). In this analysis, the H-E regression estimate of h² produced an unrealistic value of 7.3 on the observed scale (corresponding to 2.8 on the liability scale), which is outside the plausible 0–1 range, suggesting severe population stratification or other severe problems with the data. We do not recommend the use of LTMLM on unmatched samples when such severe problems are detected. For completeness, we report the results of running LTMLM, which results in a loss of power (Table S18).

Table 6.

Results on WTCCC2 MS Dataset

Category	Metric	ATT (SE)	ATT + PCs (SE)	LogR (SE)	LogR + PCs (SE)	MLM (SE)	LTMLM (SE)
Published	mean	11.661 (1.169)	9.98 (0.984)	11.619 (1.161)	9.871 (0.965)	9.919 (0.974)	10.587 (1.017)
Genome-wide	mean	1.379 (0.003)	1.152 (0.003)	1.378 (0.003)	1.142 (0.003)	1.144 (0.003)	1.172 (0.003)
Genome-wide	λGC	1.343	1.125	1.343	1.115	1.115	1.141
Published	mean/λGC	8.695	8.880	8.663	8.860	8.905	9.292

We report, going down the rows, the average χ² over 75 published SNPs, the average χ² across the entire genome, including 360,557 SNPs, the genome-wide λ_GC, and then the average χ² across 75 published SNPs after normalization by the λ_GC. All results are based on analysis of 10,034 individuals (see main text).

Discussion

We have shown that controlling for case-control ascertainment by using the LTMLM statistic can lead to significant power improvements in case-control studies of diseases of low prevalence. This was demonstrated via simulations using both simulated and real genotypes and in WTCCC2 MS case-control data. We emphasize that the improvement applies to case-control studies of diseases with low prevalence. We note that logistic and linear regression generally produce similar results and that logistic mixed-model score tests that do not explicitly model case-control ascertainment are likely to produce results similar to those of standard linear mixed-model methods.

The LTMLM statistic should not be used if the inferred liability-scale h² parameter is outside the plausible 0–1 bound, given that this is indicative of severe population stratification or other severe problems with the data (this can also be assessed via PC analysis; see Figure S2). In such settings, either matching based on ancestry should first be performed or other statistics should be used.

Several limitations of LTMLM are directions for future study. First, previous work has shown that using the PMLs in conjunction with fixed effects such as body mass index, age, or known associated SNPs will further increase power.^12,20 The incorporation of fixed-effect covariates into the LTMLM statistic is not considered here and remains a future direction. Second, the calibration of our statistic in unrelated samples relies on an approximation that works well in the WTCCC2 data analyzed but that might not work well in all datasets. Here, calibration via LD-score regression offers an appealing alternative.³¹ Third, we did not consider case-control studies in family datasets, which also represents a future direction. The LTMLM score statistic in its current form is appropriate for association testing in population case-control samples with low levels of relatedness. In family datasets, other approaches to calibration, such as LD-score regression, could potentially be explored.³¹ Fourth, the method relies on the assumption of an underlying normally distributed liability. Although this assumption is widely accepted by many geneticists,^32,33 and the method also performs well under a different generative model (Tables S12 and S13), further work on whether case-control traits are accurately modeled by normally distributed liabilities is warranted. Fifth, the method does not estimate odds ratios; in this respect, the method is similar to other mixed-model association methods.^4,5,8,11 However, liability-scale effect sizes can be converted to odds ratios.¹³ Sixth, analogous to standard mixed-model association methods, LTMLM requires running time O(MN²) when M > N > number of MCMC iterations. This might be computationally intractable in very large datasets. We are developing much faster mixed-model methods,³⁴ but these methods do not consider case-control ascertainment and should not be applied to ascertained case-control data for diseases of low prevalence. The incorporation of the ideas we have described here into these methods is an open question. Seventh, potential application of the LTMLM statistic to rare-variant datasets is not considered here and remains a future direction. Finally, our methods could potentially be extended to multiple traits.^7,27,35

Published: April 16, 2015

Web Resources

The URLs for data presented herein are as follows:

• GCTA (Genome-wide Complex Trait Analysis), http://www.complextraitgenomics.com/software/gcta/

• Liability threshold mixed linear model (LTMLM) in LTSOFT, http://www.hsph.harvard.edu/alkes-price/software/