Testing in Microbiome-Profiling Studies with MiRKAT, the Microbiome Regression-Based Kernel Association Test

Abstract

High-throughput sequencing technology has enabled population-based studies of the role of the human microbiome in disease etiology and exposure response. Distance-based analysis is a popular strategy for evaluating the overall association between microbiome diversity and outcome, wherein the phylogenetic distance between individuals’ microbiome profiles is computed and tested for association via permutation. Despite their practical popularity, distance-based approaches suffer from important challenges, especially in selecting the best distance and extending the methods to alternative outcomes, such as survival outcomes. We propose the microbiome regression-based kernel association test (MiRKAT), which directly regresses the outcome on the microbiome profiles via the semi-parametric kernel machine regression framework. MiRKAT allows for easy covariate adjustment and extension to alternative outcomes while non-parametrically modeling the microbiome through a kernel that incorporates phylogenetic distance. It uses a variance-component score statistic to test for the association with analytical p value calculation. The model also allows simultaneous examination of multiple distances, alleviating the problem of choosing the best distance. Our simulations demonstrated that MiRKAT provides correctly controlled type I error and adequate power in detecting overall association. “Optimal” MiRKAT, which considers multiple candidate distances, is robust in that it suffers from little power loss in comparison to when the best distance is used and can achieve tremendous power gain in comparison to when a poor distance is chosen. Finally, we applied MiRKAT to real microbiome datasets to show that microbial communities are associated with smoking and with fecal protease levels after confounders are controlled for.

Introduction

The advent of massively parallel sequencing has enabled high-throughput profiling of the microbiota in a large number of samples via targeted sequencing of the 16S rDNA sequence,^1–4 which contains information about species identity. Knowledge on how microbial communities differ across individuals can provide key information on the role of communities in relation to variation in biological and clinical variables and is essential for gaining a broader understanding of biological mechanisms underlying disease and response to exposures.^5–9 Although considerable resources have been devoted to sequencing technologies and to quantifying individual taxa, successful application of microbial profiling to studying biomedical conditions requires novel statistical methods for efficiently testing for associations with microbial diversity.

A popular strategy for evaluating the association between overall microbiome composition and outcomes of interest utilizes distance- or dissimilarity-based analysis, referred to here as just distance-based analysis for simplicity. Via standard methods, the 16S sequence tags are clustered on the basis of their sequence similarity to form operational taxonomic units (OTUs), which can essentially be considered surrogates for biological taxa. Distance metrics are then constructed to measure the phylogenetic or taxonomic dissimilarity between each pair of samples by incorporating the phylogenetic relationship or the absolute and relative abundance of different taxa. Then, for assessing the association between the microbiome diversity and an outcome variable of interest, the pairwise distance between each pair of samples is compared to the distribution of the outcome variable. For categorical outcome variables, this is essentially comparing the pairwise distances within and between categories. Operationally, multivariate analysis¹⁰ or the top principal coordinates¹¹ of the matrix of pairwise distances are used for testing for associations via permutation.

Among the many possible distances, the UniFrac distances are the most popular in the literature and are constructed on the basis of a phylogenetic tree relating taxa to one another.^12,13 There are several different versions of UniFrac distances. The original, unweighted UniFrac distance between any pair of microbial communities is calculated as the proportion of the total branch length within the tree, which leads to un-shared taxa (i.e., taxa in one community but not the other). Thus, the UniFrac distance primarily considers only the species presence and absence information and is most efficient in detecting abundance change in rare lineages given that more prevalent species are likely to be present in all individuals. Weighted UniFrac distance uses species abundance information to weight the UniFrac distance and thus has more power to detect changes in common lineages. The generalized UniFrac distance¹⁴ was introduced as a compromise between weighted and unweighted UniFrac distances; it down-weights its emphasis on either abundant or rare lineages and therefore has more power to detect changes in OTU clusters with modest abundance. Generalized UniFrac distance involves an additional parameter (α), such that the generalized UniFrac distance with α = 1 is equivalent to the weighted UniFrac distance. A range of other distances that do not incorporate phylogeny are also available. For example, Bray-Curtis dissimilarity, which is also commonly used, quantifies the taxonomic dissimilarity between two different sites on the basis of counts at each site. Similarly, Euclidean distance can also be used and is frequently thought to be similar to weighted UniFrac distance because abundance information from common taxa tends to dominate.

Despite successes, distance-based analysis suffers from a number of limitations. First, as noted, many different distance metrics have been developed. Although there are similarities, they are designed to capture distance differently, leading to differential performance across different scenarios. This creates problems in which choosing a particular metric to use as the best metric for any particular dataset depends on the unknown true state of nature. A non-optimal distance metric will reduce power to discover true associations. Using multiple metrics and cherry picking the best result will result in inflated type I rates and lead to large numbers of spurious results. Beyond difficulties in choosing a particular distance metric, the need for permutation can be computationally expensive. Furthermore, the analysis framework is not easily interpretable and does not allow for easy covariate adjustment. Consequently, extending such approaches to accommodate more-sophisticated outcomes, such as survival or multivariate information, is challenging.

We propose in this paper the microbiome regression-based kernel association test (MiRKAT), a flexible regression approach for testing the association between microbial community profiles and a continuous or dichotomous variable of interest, such as an environmental exposure or disease. MiRKAT formalizes and extends the strategy of Chen and Li¹⁵ to use the kernel machine regression framework, previously developed for genotyping data,^16–18 to directly regress the variable of interest on the covariates (including potential confounders) and the microbiome compositional profiles. The kernel is a measure of similarity between samples’ microbiome compositions and characterizes the relationship between the microbiome and the variable of interest. We propose using kernels that incorporate phylogenetic relationships among taxa by transforming existing distance metrics into similarities. A variance-component score test can be used to rapidly obtain a p value for the association between microbial community profiles and the variable of interest.

In addition to providing fast computation, use of the kernel machine approach enables flexible modeling and testing, while still incorporating phylogenetic information and naturally accommodating covariates, under a well-studied, interpretable, and statistically rigorous framework. Beyond providing extensions to allow alternative types of outcomes, the framework allows for simultaneous examination of multiple distance metrics. This enables development of the “optimal” MiRKAT, which has high power in the omnibus. We have demonstrated through simulations and analysis of real data that MiRKAT and optimal MiRKAT can be easily applied and can be more robust than existing tests with well-controlled type I error across a range of models for both continuous and dichotomous variables. We also explicitly establish connections between MiRKAT and existing distance-based approaches.

The well-studied kernel machine framework forms the statistical underpinnings for our work, which is a strength because this allows leverage of existing machinery within a rigorous framework. However, MiRKAT differs from previous, related kernel methods in the need to accommodate unique features of microbiome data. In particular, we tailor the approach to accommodate microbiome data by adopting kernels on the basis of dissimilarity measures commonly used in microbiome compositional analysis. Furthermore, microbiome studies usually have more modest sample sizes, yet the kernels built on standard distance metrics are frequently of full rank and have poor eigenvalue behavior. Consequently, in contrast to previous analytic^17–19 and perturbation-based²⁰ p-value-calculation approaches, which do not control type I error well, our method uses alternative small-sample corrections²¹ (unpublished data) and permutation methods. The present study differs from that detailed in our earlier conference manuscript¹⁵ in that we formalize and fully flesh out the overall framework, explicitly relate the approach to existing distance methods, use alternative small-sample corrections to control type I error, and develop the optimal MiRKAT method for testing across choices of distance metrics.

Material and Methods

Notationally, we assume that n samples have been collected and that their microbial communities have been profiled. For the i^th subject, let y_i denote the outcome variable of interest, ${\mathbf{Z}}_i={\left(Z_{i1},Z_{i2},\dots ,Z_{ip}\right)}^{\text{′}}$ denote the abundances of all OTUs for individual i (p is the total number of OTUs), and ${\mathbf{X}}_i={\left(X_{i1},X_{i2},\dots ,X_{im}\right)}^{\text{′}}$ be the covariates—such as age, gender, and other clinical and environmental variables that are suspected to influence microbial community diversity and are related to outcomes—that we want to control for. The goal is to test for association between the outcome and microbial profiles while adjusting for covariates X. Note that we will refer to y as an “outcome” that depends on the microbiome composition, although in some situations it might be a variable that is thought to influence microbial diversity; however, because our goal is association testing rather than causal modeling, the distinction does not affect the validity of our method given the duality.²² We first consider the problem of testing under a single distance metric (kernel) and then extend the approach to optimally accommodate multiple distances simultaneously.

MiRKAT Based on a Single Kernel

The intuition behind the kernel machine framework is that it compares pairwise similarity in the outcome variable to pairwise similarity in the microbiome profiles, and high correspondence is suggestive of association. MiRKAT exploits the kernel machine regression framework to relate the covariates and the microbiota profiles to the outcomes. Specifically, for a continuous outcome variable, we use the linear kernel machine model

$$y_i={\beta }_0+{\mathit{\beta }}^{\text{′}}{\mathbf{X}}_i+f\left({\mathbf{Z}}_i\right)+{\epsilon }_i,$$ (Equation 1)

and for a dichotomous outcome variable (e.g., y = 1 or 0 for case or control samples, respectively), we use the logistic kernel machine model

$$\text{logit}\left(P\left(y_i=1\right)\right)={\beta }_0+{\mathit{\beta }}^{\text{′}}{\mathbf{X}}_i+f\left({\mathbf{Z}}_i\right),$$ (Equation 2)

where ${\beta }_0$ is the intercept, $\mathit{\beta }={\left[{\beta }_1,\dots ,{\beta }_m\right]}^{\text{′}}$ is the vector of regression coefficients for the m covariates, and ${\epsilon }_i$ is an error term with mean 0 and variance ${\sigma }^2$ for continuous phenotypes. This regression framework can be easily extended to other, more-complicated outcomes, such as survival or multivariate outcomes.

The relationship between the microbiome profile and the outcome variable is fully characterized by the function $f(\cdot )$ —testing that there is no association between microbiome composition and the outcome is equivalent to testing that $f\left(\mathbf{Z}\right)=0$. Under the kernel machine regression framework, $f\left({\mathbf{Z}}_i\right)$ is assumed to be from a reproducing kernel Hilbert space, ${\mathcal{H}}_k$, generated from a positive definite kernel function, $K\left(\cdot ,\cdot \right)$, such that $f\left({\mathbf{Z}}_i\right)={\sum }_{i^{\text{'}}=1}^n{\alpha }_{i^{\text{'}}}K\left({\mathbf{Z}}_i,{\mathbf{Z}}_{i^{\text{'}}}\right)$ for some ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n$.

The kernel measures the similarity between different individuals, and different choices of $K\left({\mathbf{Z}}_i,{\mathbf{Z}}_{i^{\text{'}}}\right)$ correspond to different underlying models. For example, setting $K\left({\mathbf{Z}}_i,{\mathbf{Z}}_{i^{\text{'}}}\right)={\sum }_{j=1}^p{Z}_{ij}{Z}_{i^{\text{′}}j}$ implies that $f\left({\mathbf{Z}}_i\right)={\sum }_{j=1}^p{Z}_{ij}{\beta }_j$, i.e., that the model is linear. Therefore, by changing the kernel function, one is implicitly changing the model being used. Using more-sophisticated kernels will result in more-complex models that can allow for OTU interactions, nonlinear OTU effects, or incorporation of phylogenetic relationships among OTUs. The matrix of pairwise similarities between pairs of individuals is defined as kernel matrix K, where the ${\left(i,i^{\text{'}}\right)}^{\text{th}}$ element of K is $K\left({\mathbf{Z}}_i,{\mathbf{Z}}_{i^{\text{'}}}\right)$.

For microbiome composition data, the OTUs are related by a phylogenetic tree. Kernels that exploit the degree of divergence between different sequences can be much more powerful than similarity measures that ignore the phylogenetic-tree information. We can construct the kernel matrix, which measures similarities between the microbiome composition among subjects, by exploiting the correspondence with the well-defined distance metrics, which measure dissimilarities between subjects. Specifically, we can construct the kernel matrix via the following transformation of the phylogenetic or taxonomic distance metrics:

$$\mathbf{K}=-\frac{1}{2}\left(\mathbf{I}-\frac{{\mathbf{11}}^{\prime }}{n}\right){\mathbf{D}}^2\left(\mathbf{I}-\frac{{\mathbf{11}}^{\prime }}{n}\right),$$ (Equation 3)

where $\mathbf{D}=\left[d_{ij}\right]$ is the pairwise distance matrix (e.g., weighted or unweighted UniFrac distance or the Bray-Curtis dissimilarity), I is the identity matrix, 1 in $\left({\mathbf{11}}^{\text{'}}/n\right)$ is a vector of ones, and D² is the element-wise square. For each distance metric, we can construct the corresponding kernel matrix, e.g., weighted or unweighted UniFrac kernels (K_w or K_u, respectively) can be constructed on the basis of weighted or unweighted distance metrics, respectively. This choice of kernel is in line with the relationship between kernel machine regression and distance-based regression²³ in that it can recover the original distances by using standard kernel operation: $d_{ij}^2=K_{ii}+K_{jj}-2K_{ij}$. Further, to ensure that K is a positive semi-definite matrix, we apply the same positive semi-definiteness correction procedure as in Chen and Li.¹⁵ We first perform an eigenvalue decomposition of eigenvalues $\mathbf{K}=\mathbf{U}\text{Λ}{\mathbf{U}}^{\text{′}}$, where $\text{Λ}=\text{diag}\left({\lambda }_1,\cdots ,{\lambda }_n\right)$, and then reconstruct with the absolute eigenvalues K∗ = $\mathbf{U}{\text{Λ}}^{\text{∗}}{\mathbf{U}}^{\text{′}}$, where ${\text{Λ}}^{\text{∗}}=\text{diag}\left(\left|{\lambda }_1\right|,\cdots ,\left|{\lambda }_n\right|\right)$.

When only a single kernel is considered, we estimate the coefficients β and $f\left(\mathbf{Z}\right)$ by maximizing the following penalized log-likelihood:

$$\begin{array}{c}pl\left(f,\mathit{\beta }\right)=\stackrel{n}{\sum _{i=1}}\text{log}L\left(f,\mathit{\beta };y_i,x_i,z_i\right)-\frac{1}{2}\lambda \Vert f{\Vert }_{{\mathcal{H}}_k}^2\\ =\stackrel{n}{\sum _{i=1}}\text{log}L\left(f,\mathit{\beta };y_i,x_i,z_i\right)-\frac{1}{2}\lambda {\mathit{\alpha }}^{\text{′}}K\mathit{\alpha }.\end{array}$$

Through an important relationship between kernel machine regression and mixed models,^24–26 $f\left(\mathbf{Z}\right)$ can be viewed as a subject-specific random effect that follows a distribution with mean 0 and variance $\tau \mathbf{K}$. Then, testing for an association between the microbiome composition and the outcome is equivalent to testing the null hypothesis that $H_0:\tau =0$. Under the mixed-model framework, this can be done with a standard variance-component score test.²⁷

In particular, the score statistic is computed as

$$Q=\frac{1}{2\varphi }{\left(\mathbf{y}-{\hat{\mathbf{y}}}_0\right)}^{\text{′}}\mathbf{K}\left(\mathbf{y}-{\hat{\mathbf{y}}}_0\right),$$ (Equation 4)

where ${\hat{\mathbf{y}}}_0$ is the predicted mean of y under $H_0$ (i.e., ${\hat{\mathbf{y}}}_0={\hat{\beta }}_0+{\hat{\mathit{\beta }}}^{\text{′}}\mathbf{X}$ for continuous traits, and ${\hat{\mathbf{y}}}_0={\text{logit}}^{-1}\left({\hat{\beta }}_0+{\hat{\mathit{\beta }}}^{\text{′}}\mathbf{X}\right)$ for dichotomous traits), ${\hat{\beta }}_0$ and $\hat{\mathit{\beta }}$ are estimated under the null model by regression of y on only the covariates X, and ϕ is the dispersion parameter. For the linear kernel machine regression, $\varphi ={\hat{\sigma }}_0^2$, where ${\hat{\sigma }}_0^2$ is the estimated residual variance under the null model. In the logistic kernel machine regression, ϕ = 1.

Under the null hypothesis, Q asymptotically follows a weighted mixture of χ² distributions, and the p value can be analytically obtained through higher-order moment matching²⁸ or exact methods^29,30 with possible small-sample adjustments via resampling.¹⁹ However, the comparatively small sample sizes for many microbiome studies and the complexity of the kernels considered here (often of full rank and with erratic eigenvalue behavior) lead to very conservative tests. Previously considered Satterthwaite methods¹⁵ lead to inflation of type I error. Thus, MiRKAT further considers the use of new, alternative small-sample adjustments for both continuous and dichotomous traits²¹ (unpublished data).

A key advantage of the score test is that it only requires fitting the null model $y_i={\beta }_0+{\mathit{\beta }}^{\text{′}}{\mathbf{X}}_i+{\epsilon }_i$ for continuous traits and $\text{logit}\left(P\left(y_i=1\right)\right)={\beta }_0+{\mathit{\beta }}^{\text{′}}{\mathbf{X}}_i$ for dichotomous traits. Consequently, MiRKAT allows for fast, supervised, distance-based association testing under a regression framework that permits controls for potential confounding.

Because the proposed test is a score test, all the parameters are estimated under the null model (linear regression or logistic regression), i.e., $f\left(\mathbf{Z}\right)$ does not need to be estimated. This means that even if a poor kernel is chosen, the test is still statistically valid. Better choices of kernels simply improve power. From the perspective of testing, a metric that better reflects the true relationship between the microbiome compositional profiles and the outcome will result in substantially higher power.

Optimal MiRKAT, Based on Multiple Kernels

As noted, although MiRKAT is valid even if a poor kernel is chosen, better kernel choices can lead to improved power. Unfortunately, the best kernel requires knowledge of how the microbiome influences the outcome. This is unknown a priori given that knowledge of this would preclude need for analysis. Therefore, in this section, we develop the optimal MiRKAT, which extends MiRKAT to simultaneously consider multiple possible kernels.

Suppose that we have a set of $\ell$ different candidate kernels, ${\mathbf{K}}_1,\dots ,{\mathbf{K}}_{\ell }$, such as unweighted UniFrac, weighted UniFrac, Bray-Curtis kernels, etc., which are constructed from corresponding distance matrices via Equation 3.

The intuition behind the optimal MiRKAT is that it will consider testing with each individual kernel, obtain the p value for each of the tests, select the minimum p value, and then adjust for having taken the minimum via a multiple-comparison technique. If sample sizes are large, this can be accomplished via the perturbation-based approach of Wu et al.,²⁰ but when the sample size is more modest, we can apply a residual permutation approach to obtain the empirical null distribution of the test statistic. Specifically, we use the following procedure:

• 1.Fit the null linear or logistic regression model by regressing y on X and obtain the residuals $\mathbf{r}=\mathbf{y}-{\hat{\mathbf{y}}}_0$, where ${\hat{\mathbf{y}}}_0$ is the estimated value of y based on the null model.
• 2.For each K_k, calculate $Q_k=\left(1/2\varphi \right){\mathbf{r}}^{\text{′}}{\mathbf{K}}_k\mathbf{r}$ and the corresponding p values, p_k, through the asymptotic distribution of Q_k. Then, the minimum p value across all the $\ell$ kernels is ${\text{p}}_o={\text{min}}_{k\in \left(1,\dots ,\ell \right)}{\mathbf{p}}_k$.
• 3.
  Use residual permutation to obtain the null distribution of p_o to accommodate the fact that we have considered multiple kernels.

  • a.
    For a continuous outcome, use the permutation approach of Freeman and Lane.³¹ Specifically, for each permutation j,

    • i.
      Reshuffle the residuals, r, to obtain the permuted residuals, r^j.
    • ii.
      Create new values of y^j as ${\mathbf{y}}^j={\hat{\mathbf{y}}}_0+{\mathbf{r}}^j$.
    • iii.
      Consider y^j as the new outcome. Refit the null linear regression model by regressing y^j on X to obtain the estimated residuals ${\hat{\mathbf{r}}}^j$ and ${\hat{\varphi }}^j$ for calculating the score statistic $Q_k^j=\left(1/2{\hat{\varphi }}^j\right){\hat{\mathbf{r}}}^{j^{\text{'}}}{\mathbf{K}}_k{\hat{\mathbf{r}}}^j$ with each kernel. Obtain the kernel-specific p value, ${\text{p}}_k^j$, by comparing $Q_k^j$ to the same asymptotic distribution as in step 2.
    • iv.
      Obtain ${\text{p}}_o^j={\text{min}}_{k\in \left(1,\dots ,\ell \right)}{\mathbf{p}}_k^j$.
  • b.
    For a dichotomous outcome, use the permutation approach of Epistein et al.,³² which uses Fisher’s non-central hypergeometric distribution to generate permuted 1/0 outcome values. Specifically,

    • i.
      Obtain the estimated odds of being a case for each individual sample, i.e., $\text{exp}\left({\hat{\beta }}_0+{\hat{\mathit{\beta }}}^{\text{′}}{\mathbf{X}}_i\right)$, where ${\hat{\beta }}_0$ and $\hat{\mathit{\beta }}$ are the estimated coefficients under the null logistic regression model in step 1.
    • ii.
      For each permutation j, generate new binary outcomes on the basis of the estimated odds by using the Fisher’s non-central hypergeometric distribution (modified version of the BiasedUrn package³³ in R).
    • iii.
      Use the permuted outcome to calculate the score statistic, $Q_k^j$, as in step 2 for each kernel and the kernel-specific p value, ${\text{p}}_k^j$, by comparing $Q_k^j$ to the same asymptotical mixture of χ² distribution.
    • iv.
      Obtain ${\text{p}}_o^j={\text{min}}_{k\in \left(1,\dots ,\ell \right)}{\mathbf{p}}_k^j$.
• 4.Repeat step 3 for a large number of times B to form an empirical null distribution for p_o.
• 5.Calculate the final p value as $\text{p}=\left(1/B\right){\sum }_{b=1}^{B}I\left({\text{p}}_o>{\text{p}}_o^b\right)$.

For each permutation j, ${\text{p}}_1^j,\cdots ,{\text{p}}_{\ell }^j$ are calculated with the same set of permuted outcomes and are thus correlated; taking the minimum p value across different kernels accounts for this correlation. Although the optimal MiRKAT requires permutation for the final p value calculation, it only estimates residuals under each permutated data by using the null model, which essentially equates to finding the QR residuals for continuous outcomes or logistic regression for binary outcomes and thus can be done very fast. Additionally, for each kernel, each $Q_k^j$ follows the same weighted mixture of the χ² distribution with the weights and degree of freedom needed to be estimated only once.

Simulation Study

We conducted simulation studies under a range of scenarios in order to verify that MiRKAT correctly controls type I error rate and to assess the relative power of MiRKAT by using different kernels and the power of optimal MiRKAT.

We first simulated microbiome datasets according to Chen and Li’s general approach,¹⁵ which has been shown to generate simulated data reflective of real OTU counts. In particular, we simulated datasets composed of n = 100, 200, or 500 individuals. Then, we generated the OTU information for each individual in a simulated dataset from a Dirichlet-multinomial distribution, which accommodates the over-dispersion of OTU counts. To employ realistic parameter values for the Dirichlet-multinomial distribution, we estimated the dispersion parameters and the proportion means from Charlson et al.’s real upper-respiratory-tract microbiome dataset,³⁴ which consists of 856 OTUs measured on each of 60 samples. Then, for each individual we generated OTU counts on the same 856 OTUs by using the estimated parameters and assumed 1,000 total counts per sample. For both continuous outcomes and dichotomous outcomes, we considered two simulation scenarios that differed in how the OTUs were related to the outcome.

Under simulation scenario 1, the outcome was related to a cluster of taxa that depend on a phylogenetic tree. Specifically, we partitioned all the OTUs into 20 clusters (lineages) by performing the partitioning-around-medoids algorithm on the basis of the OTU distance matrix. The abundance of these OTU clusters varied greatly, such that each OTU cluster corresponded to some possible bacterial lineage. We then used the model to choose a relatively abundant OTU cluster that constituted 19.4% of the total OTU reads to be related to the outcome. For continuous outcomes, we simulated under the model

$$y_i=0.5X_{1i}+0.5X_{2i}+\beta \text{scale}\left(\sum _{j\in \mathcal{A}}{Z}_{ij}\right)+{\epsilon }_i,$$ (Equation 5)

where ${\epsilon }_i\sim N\left(\mathrm{0,1}\right)$.

For dichotomous outcomes, we simulated under the model

$$\text{logit}\left(E\left(y_i|{\mathbf{X}}_i,{\mathbf{Z}}_i\right)\right)=0.5\text{scale}\left(X_{1i}+X_{2i}\right)+\beta \text{scale}\left(\sum _{j\in \mathcal{A}}{Z}_{ij}\right).$$ (Equation 6)

For both continuous and dichotomous outcomes, $X_{1i}$ and $X_{2i}$ are covariates to be adjusted for, and $\mathcal{A}$ denotes the indices of the OTUs in the selected cluster. The “scale” function standardizes the total OTU abundance in the associated cluster to have mean 0 and SD 1. $X_{1i}$ was simulated as a Bernoulli random variable with success probability 0.5. For $X_{2i}$, we considered situations in which $X_{2i}$ and microbiome profiles (${\mathbf{Z}}_i$) were correlated and in which $X_{2i}$ and ${\mathbf{Z}}_i$ were independent. In the simulation wherein $X_{2i}$ and ${\mathbf{Z}}_i$ were independent, $X_{2i}$ was simulated as $N\left(\mathrm{0,1}\right)$. For the case wherein $X_{2i}$ and ${\mathbf{Z}}_i$ were correlated, we let $X_{2i}=\text{scale }\left({\sum }_{j\in \mathcal{A}}{Z}_{ij}\right)+N\left(\mathrm{0,1}\right)$.

Under simulation scenario 2, the outcome was associated with the ten most abundant OTUs in all samples, without regard for the phylogeny. In particular, instead of clustering the OTUs on the basis of the phylogenetic relationship, we simply selected the ten OTUs with the largest average number of reads across all samples. Then, we simulated the continuous outcome as

$$y_i=0.5X_{1i}+0.5X_{2i}+\beta \text{scale}\left(\sum _{j\in \mathcal{A}}\frac{Z_{i\left(j\right)}}{{\overline{Z}}_{\left(j\right)}}\right)+{\epsilon }_i.$$ (Equation 7)

We simulated the dichotomous outcome as

$$\text{logit}\left(E\left(y_i|{\mathbf{X}}_i,{\mathbf{Z}}_i\right)\right)=0.5\text{scale}\left(X_{1i}+X_{2i}\right)+\beta \text{scale}\left(\sum _{j\in \mathcal{A}}\frac{Z_{i\left(j\right)}}{{\overline{Z}}_{\left(j\right)}}\right),$$ (Equation 8)

where ${\epsilon }_i\sim N\left(\mathrm{0,1}\right)$, $X_{1i}$ and $X_{2i}$ are defined as earlier, $\mathcal{A}$ denotes the set of the ten most abundant OTUs, and ${\overline{Z}}_{\left(j\right)}$ is the average number of reads for the j^th OTU across samples. We divided the OTU reads by their corresponding average to avoid a situation in which a single or a few OTUs could dominate the total effect.

We simulated the additional covariates (X) as before, and we again considered the scenario in which the covariates were associated with the microbiome and the scenario in which the covariates were independent of the microbiome.

For both simulation scenarios, we considered using the weighted and unweighted UniFrac kernels (K_w and K_u, respectively), the Bray-Curtis kernel (K_BC), and four generalized UniFrac Kernels with α values chosen as 0, 0.25, 0.5, and 0.75, which are denoted as K₀, K_0.25, K_0.5, and K_0.75, respectively. All of these kernels were computed from the corresponding distances. We considered these particular kernels (distances) because they represent a range of different classes of kernels: the UniFrac-based methods utilize phylogenetic relationships, whereas the Bray-Curtis kernel does not, and the weighted and generalized UniFrac kernels account for abundance information to differing degrees, whereas the unweighted UniFrac kernel does not.

We used each kernel to apply MiRKAT to the simulated datasets to test for associations between the simulated OTUs (Z) and the outcome (y). Additionally, we also applied optimal MiRKAT. We applied tests with and without adjustment for the potential confounders (X). For comparison, we further considered a naive Bonferroni-adjusted test, which selects the minimum p value across all the single-kernel testing and uses $\ell \times {\text{p}}_{\min }$, where p_min is the smallest p value across all single-kernel tests and $\ell$ is the total number of tests, as the final p value. For each choice of sample size n, simulation scenario, and correlation structure between the microbiome and covariates, we conducted 5,000 simulations with β = 0 to examine the type I error rate. To assess the statistical power of the tests across both simulation scenarios, we varied values of the coefficient β and conducted 2,000 simulations for each choice of sample size, simulation scenario, correlation structure, and value of β.

Results

In this section, we present the simulation results from performing our proposed MiRKAT and optimal MiRKAT methods, as well as the results from applying our methods to two real datasets. We also consider the relationship between MiRKAT and existing methods and demonstrate a close connection.

Simulation Results

The type I error rates of MiRKAT and optimal MiRKAT across different simulation scenarios for continuous outcomes are shown in Table 1. In simulation scenario 1, a single phylogenetic cluster of OTUs was associated with the outcome, and in simulation scenario 2, the ten most abundant OTUs were associated with the outcome. Note that when the covariates were independent of the microbiome, both simulation scenarios were equivalent because there was no association between y and Z. For both simulation scenarios, when the covariates (X) and the microbiome composition (Z) were independent, MiRKAT was valid with or without adjusting for X. However, when X and Z were correlated, adjusting for X was necessary: the type I error was seriously inflated if the confounder X was not accounted for.

Table 1.

Empirical Type I Errors for MiRKAT and Optimal MiRKAT with Continuous Outcome

Simulation Setup	n	Empirical Type I Errors
Kw	Ku	KBC	K0	K0.25	K0.5	K0.75	Koptimal	${\mathit{K}}_{{\mathbf{p}}_{\mathbf{min}}}$
Simulation Scenario 1: Clustered OTUs
$X\perp Z$, no adjustment for X	100	0.053	0.050	0.050	0.046	0.047	0.048	0.052	0.050	0.023
200	0.052	0.047	0.051	0.053	0.049	0.048	0.051	0.051	0.026
$X\perp Z$, adjustment for X	100	0.056	0.048	0.047	0.049	0.045	0.050	0.048	0.046	0.024
200	0.051	0.050	0.053	0.048	0.047	0.052	0.049	0.050	0.027
XZ, no adjustment for X	100	0.389∗	0.062∗	0.172∗	0.268∗	0.345∗	0.384∗	0.182∗	0.268∗	0.183∗
200	0.790∗	0.080∗	0.398∗	0.587∗	0.732∗	0.791∗	0.387∗	0.651∗	0.547∗
XZ, adjustment for X	100	0.055	0.047	0.047	0.049	0.046	0.049	0.046	0.049	0.024
200	0.052	0.049	0.051	0.047	0.047	0.052	0.050	0.049	0.026
Simulation Scenario 2: Top Ten OTUs
$X\perp Z$, no adjustment for X	100	0.053	0.050	0.050	0.045	0.048	0.049	0.053	0.050	0.025
200	0.051	0.047	0.050	0.053	0.050	0.047	0.051	0.050	0.026
$X\perp Z$, adjustment for X	100	0.056	0.048	0.047	0.050	0.046	0.051	0.047	0.049	0.021
200	0.051	0.049	0.053	0.047	0.047	0.052	0.050	0.051	0.023
XZ, no adjustment for X	100	0.153∗	0.048∗	0.669∗	0.105∗	0.124∗	0.147∗	0.157∗	0.516∗	0.067∗
200	0.307∗	0.048∗	0.976∗	0.194∗	0.239∗	0.293∗	0.320∗	0.932∗	0.151∗
XZ, adjustment for X	100	0.056	0.048	0.047	0.049	0.046	0.050	0.047	0.049	0.020
200	0.052	0.049	0.051	0.048	0.048	0.051	0.049	0.049	0.024

Type I error was evaluated for scenarios in which additional covariates were independent of the OTUs $\left(X\perp Z\right)$ or related to the OTUs (XZ) with the use of 5,000 simulated datasets. K_w, K_u, K_BC, K₀, K_0.25, K_0.5, and K_0.75 represent MiRKAT results for the weighted UniFrac kernel, unweighted UniFrac kernel, Bray-Curtis kernel, and generalized UniFrac kernels with α = 0, 0.25, 0.5, and 0.75, respectively. K_optimal represents the simulation results for optimal MiRKAT considering all seven kernels, and $K_{{\mathrm{p}}_{\min }}$ shows the results for a naive Bonferroni-adjusted test. The p values for optimal MiRKAT were obtained by 1,000 permutations. ^∗Inflated type I error.

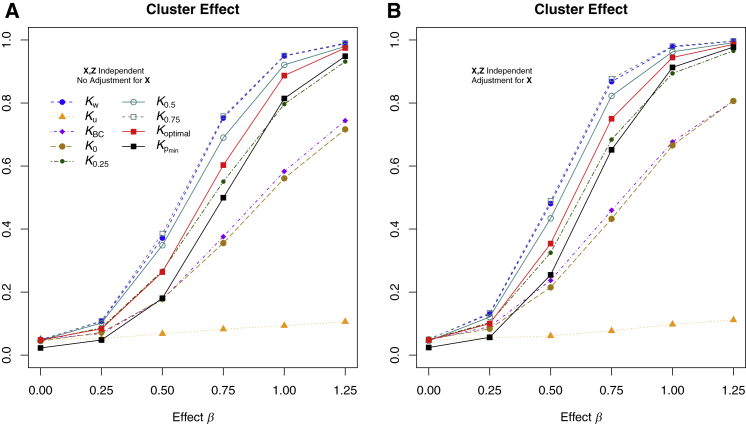
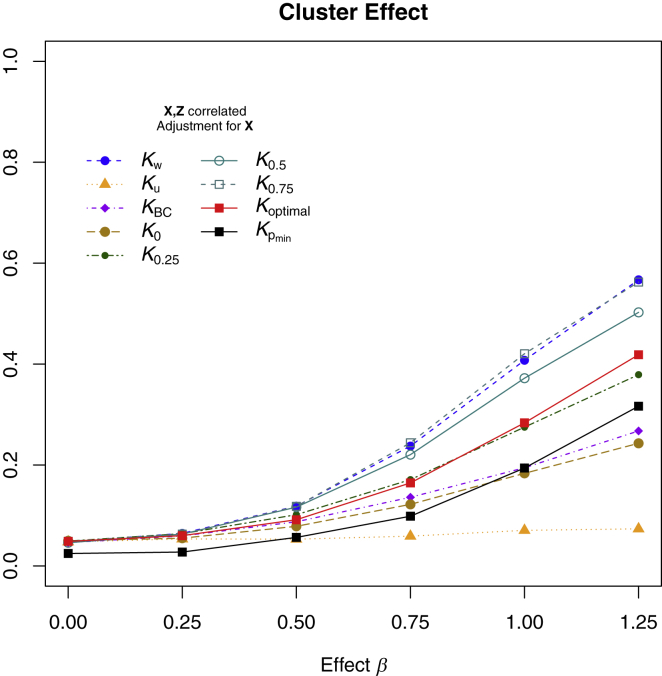
Figures 1 and 2 show the statistical power for the tests with continuous outcomes in simulation scenario 1, in which a phylogenetic cluster of OTUs was associated with the outcome. Specifically, Figure 1 shows the power when X and Z were independent, and Figure 2 shows the power when X and Z were correlated. Note that for Figure 2, we only considered statistical tests that adjusted for X because the tests without X adjustment had inflated type I error and were invalid in such situations.

Figure 1.

Type I Error and Power of MiRKAT Based on Different Kernels for Simulation Scenario 1 with Continuous Outcome when X and Z Are Independent

A selected phylogenetic cluster of the OTUs were associated with the outcome, and covariates (X) and the microbiome profiles (Z) were simulated independently. Results are shown for tests that did (A) or did not (B) adjust for X. K_w, K_u, K_BC, K₀, K_0.25, K_0.5, and K_0.75 represent MiRKAT results from the weighted UniFrac kernel, unweighted UniFrac kernel, Bray-Curtis kernel, and generalized UniFrac kernels with α = 0, 0.25, 0.5, and 0.75, respectively. K_optimal represents the simulation results for optimal MiRKAT considering all seven kernels, and $K_{{\mathrm{p}}_{\min }}$ shows the results for a naive Bonferroni-adjusted test. Sample size n = 100.

Figure 2.

Type I Error and Power of MiRKAT Based on Different Kernels for Simulation Scenario 1 with Continuous Outcome when X and Z Are Correlated

A selected phylogenetic cluster of the OTUs were associated with the outcome, and covariates (X) and microbiome composition (Z) were correlated such that $X_{2i}=\text{scale }\left({\sum }_{j\in \mathcal{A}}{Z}_{ij}\right)+N\left(\mathrm{0,1}\right)$, where $\mathcal{A}$ represents the selected cluster. Results are presented only for MiRKAT with X adjustment because unadjusted tests gave seriously inflated type I error. K_w, K_u, K_BC, K₀, K_0.25, K_0.5, and K_0.75 represent MiRKAT results for the weighted UniFrac kernel, unweighted UniFrac kernel, Bray-Curtis kernel, and generalized UniFrac kernels with α = 0, 0.25, 0.5, and 0.75, respectively. K_optimal represents the simulation results for optimal MiRKAT considering all seven kernels, and $K_{{\mathrm{p}}_{\min }}$ shows the results for a naive Bonferroni-adjusted test. Sample size n = 100.

The power is presented for MiRKAT with each individual kernel, the optimal MiRKAT (which incorporates multiple kernels), and the naive Bonferroni-adjusted test. For all the kernels that were considered, the power increased when the association strength increased. Good kernel choices can greatly improve the statistical power of detecting association, whereas improper kernel choice leads to little power to detect the association. For this simulation scenario, the weighted UniFrac kernel and the generalized UniFrac kernel with α = 0.75 produced the highest power, and the unweighted UniFrac kernel was the least powerful. Compared to the weighted UniFrac kernel, the optimal MiKRAT, which considers all metrics, lost some power but still maintained power considerably better than that of many other kernel choices. As expected, the optimal test was always more powerful than the naive Bonferroni-adjusted test.

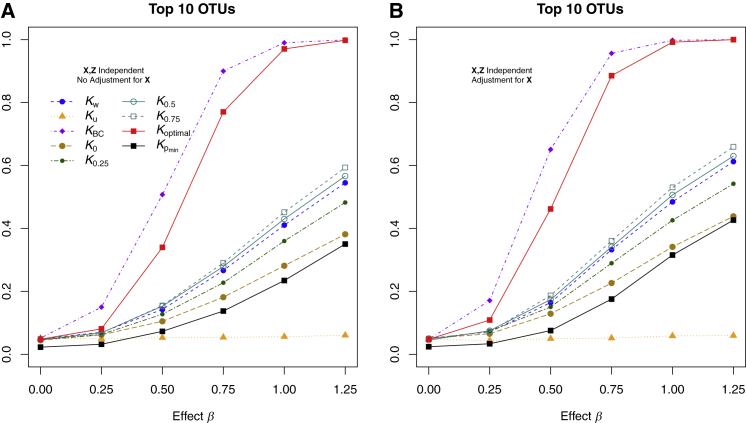
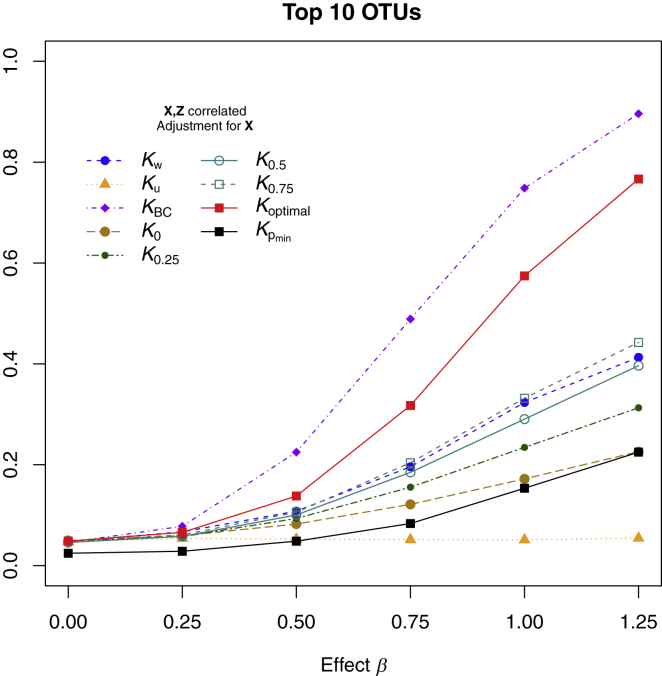
Figures 3 and 4 show the statistical power for simulation scenario 2, where the top ten most abundant OTUs were associated with the outcome without regard for phylogeny. We again show the power when X and Z were independent (Figure 3) and when X and Z were correlated (Figure 4). Results were similar to those of simulation scenario 1, except that the Bray-Curtis distance metric gave the highest power. Optimal MiRKAT, which considers all distance metrics, had power that was smaller but comparable to that of the Bray-Curtis distance but much higher than that of the naive Bonferroni-corrected test. The unweighted UniFrac kernel provided the least power.

Figure 3.

Type I Error and Power of MiRKAT Based on Different Kernels for Simulation Scenario 2 with Continuous Outcome when X and Z Are Independent

The ten most abundant OTUs were associated with the outcome. Additional covariates (X) and the microbiome profiles (Z) were simulated independently. Results are shown for tests that did (A) or did not (B) adjust for X. K_w, K_u, K_BC, K₀, K_0.25, K_0.5, and K_0.75 represent MiRKAT results for the weighted UniFrac kernel, unweighted UniFrac kernel, Bray-Curtis kernel, and generalized UniFrac kernels with α = 0, 0.25, 0.5, and 0.75, respectively. K_optimal represents the simulation results for optimal MiRKAT considering all seven kernels, and $K_{{\mathrm{p}}_{\min }}$ shows the results for a naive Bonferroni-adjusted test. Sample size n = 100.

Figure 4.

Type I Error and Power of MiRKAT Based on Different Kernels for Simulation Scenario 2 with Continuous Outcome when X and Z Are Correlated

The ten most abundant OTUs were associated with the outcome. Additional covariates (X) and the microbiome profiles (Z) were correlated such that $X_{2i}=\text{scale}\left({\sum }_{j\in \mathcal{A}}{Z}_{ij}\right)+N\left(\mathrm{0,1}\right)$, where $\mathcal{A}$ represents the top ten most abundant OTUs. Results are presented only for MiRKAT with X adjustment because unadjusted tests gave seriously inflated type I error. K_w, K_u, K_BC, K₀, K_0.25, K_0.5, and K_0.75 represent MiRKAT results for the weighted UniFrac kernel, unweighted UniFrac kernel, Bray-Curtis kernel, and generalized UniFrac kernels with α = 0, 0.25, 0.5, and 0.75, respectively. K_optimal represents the simulation results for optimal MiRKAT considering all seven kernels, and $K_{{\mathrm{p}}_{\min }}$ shows the results for a naive Bonferroni-adjusted test. Sample size n = 100.

In practice, the optimal kernel depends on the true state of nature and can vary from case to case. The two simulation scenarios show that proper kernel choice is essential for being well powered to discover associations between microbiome composition and outcomes and that poor kernel choice leads to tremendous power loss. Optimal MiRKAT, however, alleviates the problem by considering different kernels and is more robust than single-distance-based analysis given that it hedges against different scenarios and works well in the omnibus.

The simulation results for dichotomous outcomes are quantitatively similar to the results obtained from continuous outcomes. The type I error results are summarized in Table S1, and power results are shown in Figures S1–S4.

Relationship between MiRKAT and Existing Methods

A key advantage of MiRKAT is that it is already closely related to existing approaches for analyzing the association between microbiome composition and an outcome. In particular, with large sample size, the PERMANOVA method¹⁰ can be shown to be a special case of the kernel machine testing framework under the scenario in which there are no confounding variables.²³ Consequently, MiRKAT with a single kernel can be viewed as a PERMANOVA generalization that accommodates additional covariates. In numerical simulations, the correlation between p values obtained from single-kernel MiRKAT and the corresponding distance-based method is usually more than 0.99 in scenarios without covariates to be adjusted for. For example, Figure S5 shows the p values for MiRKAT and the distance-based approach for 2,000 simulated datasets when a single distance or kernel was used. However, because it uses the asymptotic distribution, MiRKAT is considerably faster than corresponding distance-based approaches, especially with large sample sizes (Figure S6).

Analysis of Smoking Data

Recently, a microbiome-profiling study was conducted to examine the communities within the upper respiratory tract³⁴ in order to explain the effect of cigarette smoking on the orpharyngeal and nospharyngeal microbiome. Although details can be found in the original manuscript and subsequent re-analyses,¹⁴ in brief, swab samples were collected from the right and left nasopharynx and oropharynx of 29 smoking and 33 non-smoking adults. The variable region 1–2 (V1–V2) of the bacterial gene 16S rRNA was PCR amplified and subjected to multiplexed pyrosequencing. OTUs were constructed with the QIIME pipeline. Samples with fewer than 500 reads and OTUs with only one read were removed, resulting in an OTU table with 60 samples (28 smokers and 32 nonsmokers) and 856 OTUs. Additional covariates in these data included gender and antibiotic use within the last 3 months.

Distance-based analysis of the oropharyngeal samples via permutation-based distance analysis (PERMANOVA) with both weighted and unweighted UniFrac distances identified significant association between microbiome profiles and smoking status. However, the analyses did not take into account potential confounders: within the collected study sample, 75% of smokers were male, yet only 56% of non-smokers were male. The odds ratio of smoking between males and females was 2.33 within the dataset. The imbalance in the proportion of male and female subjects indicates strong potential for confounding: it is unclear whether the differences in microbiome profiles between smokers and non-smokers is driven by smoking or by the gender imbalance. Additionally, the tests were conducted with either weighted or unweighted UniFrac distance; it is practically attractive to consider multiple possible distance measurements while controlling for possible confounding effects. MiRKAT represents a natural analysis approach.

Therefore, we re-analyzed the data from the oropharyngeal samples by using MiRKAT. Specifically, we applied MiKRAT to analyze the association between smoking and microbial community composition by using weighted and unweighted UniFrac distance matrices and the Bray-Curtis distance, except that here we transformed them to be similarity metrics to form the kernels and further adjusted for gender and antibiotic use. We also applied the optimal MiRKAT. Using MiRKAT under individual distance metrics, we found the p values from K_w, K_u, and K_BC to be 0.0048, 0.014, and 0.002, respectively. The optimal MiRKAT generated a p value of 0.0031. Thus, despite the potential for confounding, our results show that the association between microbiome profiles and smoking status remains significant after the potential confounders are controlled for, reaffirming and providing greater confidence in the earlier results. In addition to validating a previous analysis, this result also demonstrates the utility and importance of MiRKAT with regard to accommodating covariates and multiple kernels.

Analysis of Fecal Protease Data

Fecal proteases (FPs) are enteric enzymes that are elevated in subsets of individuals with irritable bowel syndrome (IBS) and inflammatory bowel disease (MIM: 266600). It was demonstrated that FPs from IBS-affected individuals have a profound impact on intestinal physiology, including visceral sensitivity and colonic permeability in mice.³⁵ Although there is evidence that elevated FP levels can alter intestinal physiology by activating proteinase-activated receptors, it remains unclear whether the FP levels are of human or microbial origin. Consequently, Carroll et al.³⁶ conducted a study to examine the relationship between FP levels and microbiota in human fecal samples from 30 individuals affected by IBS and 24 healthy adults. 454 pyrosequencing of the gene 16S rRNA was again used for profiling the microbiomes, and QIIME was again applied to quantify the composition and diversity of each community.

The original study identified a significant association between microbiome composition and FP levels. However, analyses were restricted to the subjects with the highest and lowest FP levels. Thus, we applied MiRKAT to the dataset (limiting to the 23 diarrhea-predominant IBS-affected subjects and 23 healthy control subjects) to test for an association between FP levels and microbiome composition, except that we treated FP levels as continuous (so as to use all subjects), and we further adjusted for additional potential confounders, including age, body mass index, gender, race, and functional bowel disorder. We considered MiRKAT by using the weighted UniFrac, unweighted UniFrac, and Bray-Curtis kernels, as well as the optimal MiRKAT.

Interestingly, the three distances gave discordant conclusions in that the unweighted UniFrac kernel and Bray-Curtis kernel yielded significant p values (p = 0.0046 and 0.039, respectively), whereas the weighted UniFrac kernel gave a non-significant result (p = 0.124). The unweighted UniFrac kernel is primarily based on the presence or absence of an OTU, whereas the weighted UniFrac kernel further incorporates abundance, which could account for the differences, but the difference in association results makes it difficult to draw a single conclusion. The optimal MiRKAT, which simultaneously considers the three candidate kernels, gave a single p value of 0.0116 after covariate adjustment. This further demonstrates the advantages of optimal MiRKAT to be able to consider multiple kernels given that using individual distance metrics yielded disparate results and is difficult to interpret.

Discussion

We propose MiRKAT to test for the association between microbial community composition and a continuous or dichotomous outcome of interest in which covariate effects are modeled parametrically and the microbiome effect is modeled non-parametrically. The kernel matrix, which defines the functional form of the microbiome effect, is constructed via the exploitation of its correspondence with the popular distance metric designed to convey phylogenetic or taxonomic information among different OTUs. Additionally, the proposed method allows the incorporation of multiple candidate kernels simultaneously, enabling development of the optimal MiRKAT. Simulations and real-data analyses indicate that the approach has reasonable power and that the optimal MiRKAT is robust to poor kernel choice. Close connections between MiRKAT and existing analysis frameworks ensure that the approach is a natural addition to the currently available methodology.

The optimal MiRKAT enables researchers to consider multiple distance and dissimilarity metrics simultaneously. Here, we focused primarily on the UniFrac, weighted UniFrac, generalized UniFrac, and Bray-Curtis metrics because our experiences have shown that these tend to work well in practice. In principle, one can include a wide range of other metrics with little penalty with regard to the false-positive rate, but the trade-off is that one might lose power if there are too many overly disparate kernels under consideration—use of highly correlated kernels will not affect power very much. In the most extreme cases, optimal MiRKAT from multiple perfectly correlated kernels will generate the same p value as will each of the individual kernel tests. Furthermore, we note that the tests using each of the individual kernels are constructed on the basis of the same datasets and are non-negatively correlated (i.e., not competitive). Thus, the optimal MiRKAT should always have higher power than the naive Bonferroni-adjusted test.

A reasonable alternative to the proposed omnibus test approach is to construct, as a kernel, a weighted combination of multiple kernels. In practice, the optimal “weight” is unknown and needs to be estimated from data or selected via other approaches, such as a grid search. From the mixed-model point of view, estimating the weights is equivalent to estimating a variance component that disappears when the null hypothesis is true; this violates the common regularity conditions in the standard asymptotic tests. Statistical methods for such problems, such as likelihood-ratio tests, recently have been the focus of considerable statistical research.^37,38 However, this is frequently much more computationally intensive than the score test, especially when many kernels are under consideration. Furthermore, very limited work has been conducted on the likelihood-ratio test for variance components when some parameters disappear under the null and when the null values are on the boundary of the parameter space. On the other hand, selecting the best “weight” through a grid search can be conducted similarly to the optimal MiRKAT, in which each of the weighted combination of candidate kernels is treated as a new kernel. However, when the number of kernels under consideration increases or when a finer grid is used, the computation burden increases quickly as a result of the large search space and rapidly becomes computationally prohibitive. Therefore, if prior evidence is available to suggest that a single kernel is the best kernel, then using that single kernel or using a smaller set of kernels will be more powerful. In the absence of prior knowledge, then we suggest using a modest range of kernels with differing characteristics, e.g., a combination of phylogeny-based and non-phylogeny-based kernels, as in our simulations.

Beyond assessing the association with overall composition, there is considerable interest in identifying the individual taxa that are driving the apparent associations. This approach for analyzing microbiome data is frequently complementary and parallel to methods for testing overall composition and diversity. One common approach for doing this is to assess the marginal association between each OTU and the outcome. However, in addition to difficulties in determining the scale of the analysis, i.e., whether to use composition percentages or raw OTU counts, a problem of considerable interest lies in using distance metrics to inform the identification of individual taxa related to the outcome. To this end, as a regression-based approach combined with relatively fast computation, MiRKAT could enable a stepwise variable selection approach with the Akaike information criterion or the Bayesian information criterion. Such an approach could be applied post hoc to identify the variables most strongly driving apparent associations. It might also be possible to use a penalized regression approach within the kernel framework,³⁹ but this remains a topic for future research.

Microbiome studies are now being included within epidemiological, population-based, and clinical studies. In contrast to early microbiome studies with modest sample sizes and relatively controlled experimental conditions, current microbiome studies consider issues such as confounding, covariate adjustment, and accommodation of more-sophisticated outcomes to be increasingly important. MiRKAT’s ability to control for confounders within a principled regression-based framework while maintaining type I error and adequate power make it an attractive alternative to currently available methods. Furthermore, although we focused on dichotomous and continuous variables of interest, the framework can be generalized to alternative types of outcomes, such as multivariate, longitudinal, and survival data. Thus, with growing interest in applying the microbiome to complex clinical and population-based studies, MiRKAT can be extended to open new avenues of research by enabling analysis of data from the emerging studies with more-sophisticated outcomes.

Published: May 7, 2015

Web Resources

The URLs for data presented herein are as follows:

• Implementation of MiRKAT in the R language, http://research.fhcrc.org/wu/en.html

• MiRKAT R package and manual, http://research.fhcrc.org/wu/en.html

• OMIM, http://www.omim.org