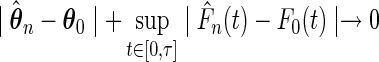Abstract
This paper proposes a new estimation procedure for the survival time distribution with left-truncated and right-censored data, where the distribution of the truncation time is known up to a finite-dimensional parameter vector. The paper expands on the Vardis multiplicative censoring model (Vardi, 1989. Multiplicative censoring, renewal processes, deconvolution and decreasing density: non-parametric estimation. Biometrika 76, 751–761), establishes the connection between the likelihood under a generalized multiplicative censoring model and that for left-truncated and right-censored survival time data, and derives an Expectation–Maximization algorithm for model estimation. A formal test for checking the truncation time distribution is constructed based on the semiparametric likelihood ratio test statistic. In particular, testing the stationarity assumption that the underlying truncation time is uniformly distributed is performed by embedding the null uniform truncation time distribution in a smooth alternative (Neyman, 1937. Smooth test for goodness of fit. Skandinavisk Aktuarietidskrift 20, 150–199). Asymptotic properties of the proposed estimator are established. Simulations are performed to evaluate the finite-sample performance of the proposed methods. The methods and theories are illustrated by analyzing the Canadian Study of Health and Aging and the Channing House data, where the stationarity assumption with respect to disease incidence holds for the former but not the latter.
Keywords: Biased sampling, Cross-sectional studies, Prevalent sampling, Profile likelihood, Smooth tests of goodness of fit
1. Introduction
Incident and prevalent cohort study designs are two primary approaches for collecting survival data in observational studies. When it is not feasible to conduct an incident cohort study because of limited resources or other constraints, a prevalent cohort study is a good alternative. Under a prevalent cohort study design, only individuals who have the disease of interest but have not yet experienced the failure event are enrolled, and the observed survival times are subject to left truncation in addition to the usual right censoring because those who have experienced the failure event before the recruitment time are not observable, and those who are recruited may not experience the failure event before the end of the study (Zelen and Feinleib, 1969; Lagakos and others, 1988). As a result, the observed survival times are a biased sample of the survival times that occur in the target population, as the sampling scheme favors subjects with slower disease progression. Statistical methods that fail to account for left truncation usually lead to substantial overestimation of the survival time.
Under the stationarity assumption that the incidence of disease onset is constant over time, the truncation time variable follows a uniform distribution, and, as shown in Vardi (1989), the likelihood for survival data that arise in a prevalent cohort study is proportional to the likelihood for data that are subject to multiplicative censoring. Hence, the Expectation–Maximization (EM) algorithm developed for the multiplicative censoring models, which has been shown to be fully efficient in Vardi and Zhang (1992) and Asgharian and others (2002), can be readily applied to analyze left-truncated and right-censored survival data when the stable disease condition holds. The stationarity assumption, however, can be easily violated in prevalent cohort studies. For example, in the event of an infectious disease outbreak, the number of people infected usually grows exponentially rather than linearly over time. Hence, the truncation time is unlikely to be uniformly distributed. The existing methods for non-parametric estimation of left-truncated and right-censored data have been based on the conditional likelihood, conditioning on the observed truncation time (Lynden-Bell, 1971; Wang, 1991; Tsai and others, 1987) so that information about the truncation time distribution is not required in the estimation procedure. Although knowing the censoring distribution does not provide additional information for estimating the survival time distribution using censored data, as pointed out in Wang (1991), the efficiency of the estimator can be improved substantially for truncated data if the truncation time distribution can be parameterized or fully specified. When the distribution of the truncation time is completely specified, Mandel (2007) generalized Vardi's EM algorithm to obtain the non-parametric maximum likelihood estimator for the survival time distribution. When the distribution of the truncation time variable is known up to a parameter, Shen (2007, 2009) applied the pseudo-profile likelihood procedure (Severini and Wong, 1992) to replace the nuisance parameters; that is, the distribution function of the survival times in the marginal likelihood of the truncation times with a consistent estimator that depends on the parameter of interest. As illustrated later, the resulting estimator is not the maximum likelihood estimator, and hence is not fully efficient. Moreover, the convergence of the iteration algorithm lacks rigorous justifications.
This paper is organized as follows. In Section 2, we study a generalized multiplicative censoring model and develop an EM algorithm to obtain the maximum likelihood estimator for the expanded model. In Section 3.1, we investigate a semiparametric truncation model where the distribution of truncation variable is parameterized up to an unknown parameter. We show in Section 3.2 that, with proper reparameterization, the semiparametric maximum likelihood estimator for the failure time distribution and the truncation time distribution can be easily obtained by employing the EM algorithm developed under a generalized multiplicative censoring model. Asymptotic properties of the proposed estimator are established. To assess whether the stationarity assumption of a constant incidence rate holds for the occurrence of the initiating event, in Section 3.3 we propose a semiparametric likelihood ratio test by embedding the null truncation time distribution in a smooth alternative (Neyman, 1937). In Section 4, simulation studies show that the proposed semiparametric maximum likelihood estimator and the semiparametric likelihood ratio test work well. We also apply the proposed methodology to two data sets: one from the Canadian Study of Health and Aging and the other is the Channing House data. We show that the stationarity assumption holds for the former but not the latter. A discussion concludes in Section 5.
2. The generalized multiplicative censoring model
In this section, we propose a generalized multiplicative censoring model. Consider non-negative random variable 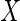 with density function
with density function 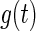 . Let
. Let 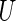 be a uniform
be a uniform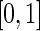 random variable independent of
random variable independent of 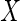 . Let
. Let 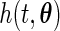 be a density function, where
be a density function, where 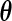 belongs to a compact set
belongs to a compact set 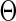 in
in 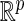 . Define the random variable
. Define the random variable 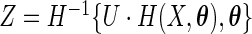 with
with 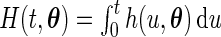 and
and 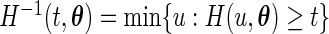 . Here
. Here  is referred to as subject to the generalized multiplicative censoring. Assume that
is referred to as subject to the generalized multiplicative censoring. Assume that 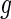 and
and 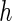 have support on
have support on 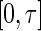 . In the special case where
. In the special case where 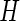 is the distribution function of the uniform
is the distribution function of the uniform 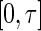 random variable, we have
random variable, we have 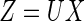 , hence the model reduces to the multiplicative censoring model considered by Vardi (1989). Moreover, given
, hence the model reduces to the multiplicative censoring model considered by Vardi (1989). Moreover, given 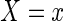 ,
, 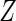 has a conditional density function
has a conditional density function 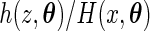 for
for 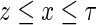 , hence the marginal density function of
, hence the marginal density function of 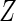 can be shown to be
can be shown to be 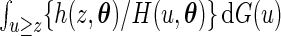 , where
, where 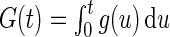 .
.
Define 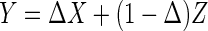 , where
, where 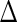 is a binary indicator independent of
is a binary indicator independent of 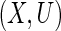 . Thus
. Thus 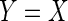 if
if 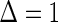 , and
, and 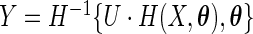 if
if 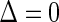 . Let
. Let 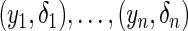 be
be 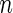 independently realizations of
independently realizations of 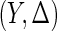 . The full likelihood function under the generalized multiplicative censoring model is proportional to
. The full likelihood function under the generalized multiplicative censoring model is proportional to
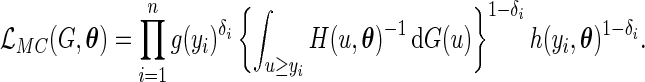 |
(2.1) |
Intuitively, one can estimate 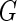 and
and 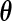 by applying the profile likelihood method.
by applying the profile likelihood method.
First, for a fixed 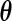 , we derive the EM algorithm to obtain the non-parametric maximum likelihood estimator for
, we derive the EM algorithm to obtain the non-parametric maximum likelihood estimator for 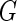 . Let
. Let 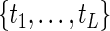 be the ordered and distinct values of
be the ordered and distinct values of 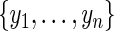 . Define
. Define 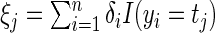 and
and 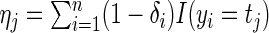 . Thus
. Thus 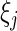 is the number of complete observations at
is the number of complete observations at 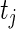 and
and 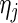 is the number of multiplicatively censored observations at
is the number of multiplicatively censored observations at 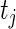 . Applying a similar argument as in Vardi (1989) and Mandel (2007), we can show that, for a fixed
. Applying a similar argument as in Vardi (1989) and Mandel (2007), we can show that, for a fixed 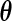 , the problem of maximizing (2.1) is equivalent to maximizing
, the problem of maximizing (2.1) is equivalent to maximizing
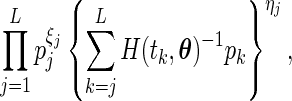 |
subject to the constraints 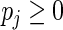 ,
, 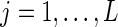 , and
, and 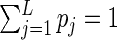 , where
, where 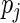 is the jump size of
is the jump size of 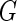 at
at 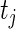 . Note that the log-likelihood for the complete data
. Note that the log-likelihood for the complete data 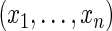 is given by
is given by 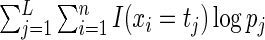 . It follows from the result that the conditional density function of
. It follows from the result that the conditional density function of 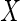 given
given 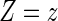 is
is
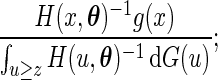 |
given the current estimated probabilities 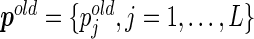 and the observed value
and the observed value 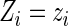 , the conditional expectation is given by
, the conditional expectation is given by
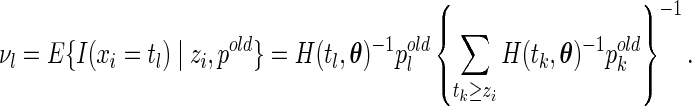 |
Replacing the missing indicator variable by its conditional expectation in the complete likelihood and maximizing the likelihood function yields the updated estimates
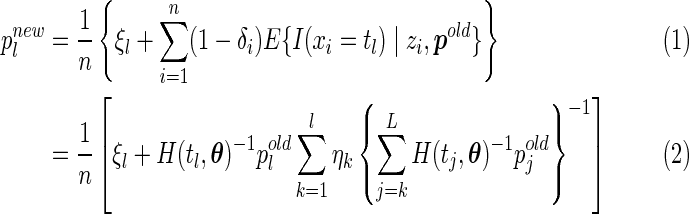 |
(2.2) |
for 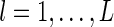 .
.
Let 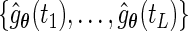 be the probabilities that the EM algorithm converges to. Thus, for fixed
be the probabilities that the EM algorithm converges to. Thus, for fixed 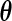 , the maximum likelihood estimator for
, the maximum likelihood estimator for 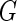 under the proposed generalized multiplicative censoring model is given by
under the proposed generalized multiplicative censoring model is given by  Then, by the profile likelihood approach, the parameter
Then, by the profile likelihood approach, the parameter  can be estimated by maximizing the full likelihood
can be estimated by maximizing the full likelihood  under generalized multiplicative censoring.
under generalized multiplicative censoring.
3. Application to left-truncated and right-censored data
3.1. Model setup
Next, we consider the estimation problem for data under cross-sectional sampling with follow-up. Let 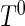 be the time from disease incidence to the failure event of interest in a target population. Let
be the time from disease incidence to the failure event of interest in a target population. Let 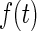 ,
, 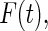 and
and 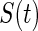 denote the density function, the cumulative density function, and the survival function of
denote the density function, the cumulative density function, and the survival function of 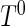 . Let
. Let 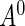 be the time from disease incidence to the (potential) study recruitment time, where the density function of
be the time from disease incidence to the (potential) study recruitment time, where the density function of 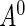 lies in a parametric family
lies in a parametric family 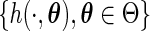 . In a cross-sectional study, the prevalent population consists of individuals with the disease who have not experienced the failure event at the recruitment time; that is, individuals whose time to failure satisfies
. In a cross-sectional study, the prevalent population consists of individuals with the disease who have not experienced the failure event at the recruitment time; that is, individuals whose time to failure satisfies 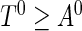 . Let
. Let 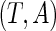 be the observed random variables in the prevalent population; then
be the observed random variables in the prevalent population; then 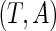 has the same distribution function as
has the same distribution function as 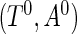 conditional on
conditional on 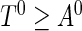 . The joint density function of
. The joint density function of 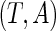 evaluated at
evaluated at 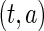 is
is
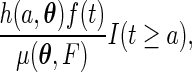 |
where 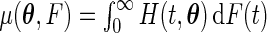 , with
, with 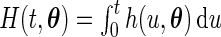 .
.
In practice, the observation of survival time can be terminated before an individual experiences an event. We assume that the residual life time  is subject to random censoring by an independent variable
is subject to random censoring by an independent variable 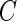 . Let
. Let 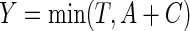 be the observed survival time, and
be the observed survival time, and 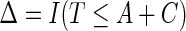 be the indicator of the failure event. Let the observed data
be the indicator of the failure event. Let the observed data 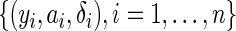 be independent and identically distributed copies of
be independent and identically distributed copies of 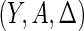 . Our goal is to estimate the survival time distribution as well as the truncation time distribution by maximizing the full likelihood function
. Our goal is to estimate the survival time distribution as well as the truncation time distribution by maximizing the full likelihood function
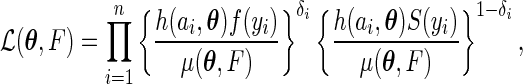 |
(3.1) |
which involves both the parametric component 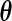 and the non-parametric component
and the non-parametric component 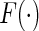 . In the absence of censoring, the semiparametric maximum likelihood estimator is given in Wang (1989). Her method, however, cannot be applied in the presence of censoring.
. In the absence of censoring, the semiparametric maximum likelihood estimator is given in Wang (1989). Her method, however, cannot be applied in the presence of censoring.
3.2. The semiparametric maximum likelihood estimator
We now derive the semiparametric maximum likelihood estimator 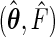 that maximizes the full likelihood (3.1) for left-truncated and right-censored data. Define the functions
that maximizes the full likelihood (3.1) for left-truncated and right-censored data. Define the functions 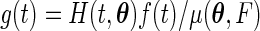 and
and 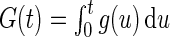 . Thus,
. Thus, 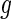 is a well-defined probability density function. The full likelihood (3.1) can be reparameterized as
is a well-defined probability density function. The full likelihood (3.1) can be reparameterized as
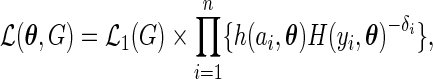 |
(3.2) |
where 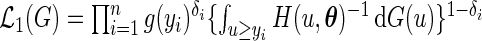 . Thus, for fixed
. Thus, for fixed 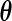 ,
, 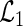 is proportional to the full likelihood function
is proportional to the full likelihood function 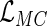 in (2.1) under the generalized multiplicative censoring model. Moreover, the second term on the right-hand side in (3.2) does not involve
in (2.1) under the generalized multiplicative censoring model. Moreover, the second term on the right-hand side in (3.2) does not involve 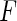 . Thus, holding
. Thus, holding 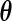 fixed, the full likelihood is maximized by the maximizer of
fixed, the full likelihood is maximized by the maximizer of 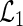 . Let
. Let 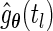 be the estimated jump size at time
be the estimated jump size at time 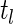 for fixed
for fixed 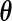 obtained by applying the EM algorithm (2.2), where
obtained by applying the EM algorithm (2.2), where 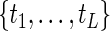 are the ordered and distinct values of
are the ordered and distinct values of 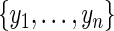 . Let
. Let 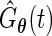 be the corresponding estimate of the cumulative distribution function. Replacing
be the corresponding estimate of the cumulative distribution function. Replacing 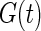 with
with 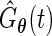 in
in 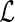 , we have the profile likelihood of
, we have the profile likelihood of 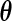
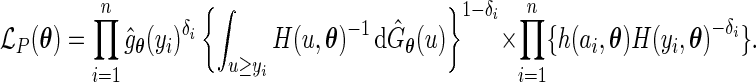 |
Let 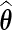 be the maximizer of the profile likelihood
be the maximizer of the profile likelihood 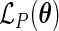 ; then the maximum likelihood estimator
; then the maximum likelihood estimator 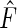 of
of 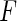 is given by
is given by
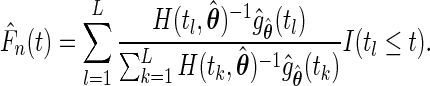 |
Note that 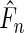 assigns positive probability mass at possibly all censored and uncensored event times
assigns positive probability mass at possibly all censored and uncensored event times 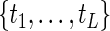 (Vardi, 1989; Qin and others, 2011) and the likelihood function is strictly concave in
(Vardi, 1989; Qin and others, 2011) and the likelihood function is strictly concave in 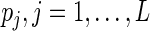 . Arguing as in Vardi (1989), we can show that, given the unique supporting points
. Arguing as in Vardi (1989), we can show that, given the unique supporting points 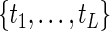 , the maximizer of (2.1) is unique for each given
, the maximizer of (2.1) is unique for each given 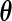 , and that the EM algorithm (2.2) converges to the unique maximizer since the set of the probability measure is convex.
, and that the EM algorithm (2.2) converges to the unique maximizer since the set of the probability measure is convex.
Another possible attempt to estimate 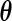 and
and 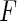 is to apply the iteration algorithm considered in Shen (2007, 2009). For any fixed
is to apply the iteration algorithm considered in Shen (2007, 2009). For any fixed 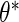 , the author applied the same EM algorithm described in Section 2 to obtain an estimator, denoted by
, the author applied the same EM algorithm described in Section 2 to obtain an estimator, denoted by 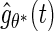 , for
, for 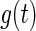 . Then the estimator
. Then the estimator
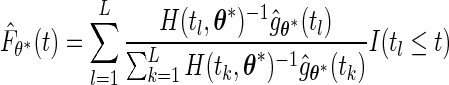 |
can be shown to be consistent for the true 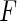 when
when 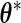 is the true parameter value. Replacing
is the true parameter value. Replacing 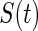 with
with 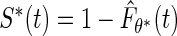 , the author proposed to maximize the marginal likelihood of
, the author proposed to maximize the marginal likelihood of 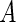
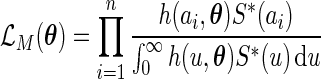 |
with respect to 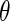 to obtain an updated estimate of
to obtain an updated estimate of 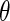 . The algorithm then iterates until convergence. Note that, in the absence of censoring, we have
. The algorithm then iterates until convergence. Note that, in the absence of censoring, we have
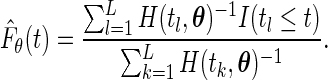 |
Thus, the estimator proposed by the author is equivalent to maximizing the marginal likelihood of the truncation times with 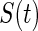 replaced with
replaced with 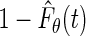 , that is, maximizing
, that is, maximizing
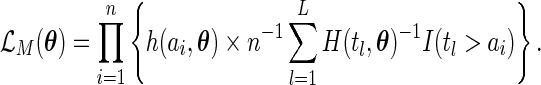 |
On the other hand, the maximum likelihood estimator proposed in our paper is obtained by maximizing the full likelihood with 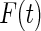 replaced with
replaced with 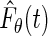 , that is,
, that is,
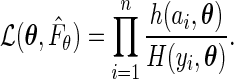 |
It is obvious that the estimator considered in Shen (2007, 2009) is not the maximum likelihood estimator, hence it is not expected to be fully efficient.
For the remainder of this paper, we assume that the support of 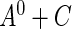 contains that of
contains that of 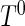 , so that
, so that 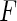 is estimable on the entire support of
is estimable on the entire support of 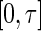 . This assumption is reasonable in many applications, for example, the disease incidence in a population could have occurred in the distant past. If the maximum support of
. This assumption is reasonable in many applications, for example, the disease incidence in a population could have occurred in the distant past. If the maximum support of 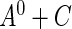 , say,
, say, 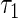 , is smaller than the maximum support of
, is smaller than the maximum support of 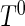 ,
, 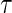 , then the proposed method estimates the conditional distribution function of
, then the proposed method estimates the conditional distribution function of 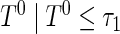 , that is,
, that is, 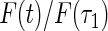 . In contrast, if the lower limit of the support for
. In contrast, if the lower limit of the support for 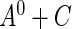 , say,
, say, 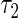 , is
, is 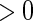 , then the proposed method estimates the conditional distribution function of
, then the proposed method estimates the conditional distribution function of 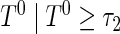 , that is,
, that is, 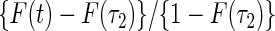 .
.
To establish the large-sample properties of the maximum likelihood estimator, we impose the following conditions:
(A1) The true parameters
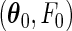 belong to the space
belong to the space 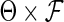 , where
, where 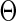 is a known compact set in
is a known compact set in 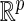 , and
, and 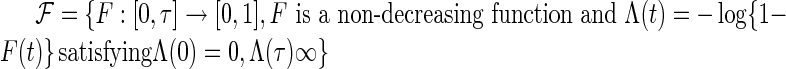 . Assume that the true cumulative hazard function
. Assume that the true cumulative hazard function 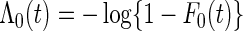 has a derivative
has a derivative 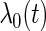 that is differentiable and satisfies
that is differentiable and satisfies 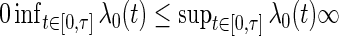 .
.(A2) The density function
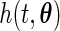 of the truncation time is positive on
of the truncation time is positive on 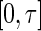 and is differentiable with respect to
and is differentiable with respect to 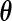 . Moreover, both
. Moreover, both 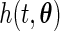 and its partial derivative
and its partial derivative 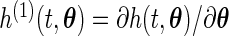 are bounded on
are bounded on 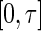 .
.(A3) The censoring time for the residual life time is not degenerate at
 , that is,
, that is, 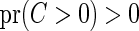 . The distribution function of
. The distribution function of 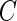 is absolutely continuous.
is absolutely continuous.(A4) The information matrix
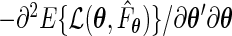 evaluated at the true value
evaluated at the true value 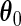 is positive definite.
is positive definite.
Denote by 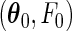 the true parameter values and by
the true parameter values and by 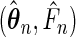 the maximum likelihood estimator that maximizes
the maximum likelihood estimator that maximizes 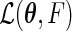 . The large-sample properties of
. The large-sample properties of 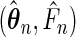 are summarized in Theorem 3.1, with proofs given in the supplementary material available at Biostatistics online.
are summarized in Theorem 3.1, with proofs given in the supplementary material available at Biostatistics online.
Theorem 3.1 —
Under regularity conditions (A1)–(A4), the maximum likelihood estimators
are consistent for the product of the Euclidean topology and the topology of uniform convergence on
, that is,
almost surely as
. Moreover,
converges weakly to a tight mean zero Gaussian process
as
, where definitions of
,
and
are given in the supplementary material available at Biostatistics online.
The strong consistency is proved by using the classical Kullback–Leibler information approach (Murphy, 1994; Parner, 1998). The asymptotic normality can be established by applying the general Z-estimator convergence theorem (van der Vaart and Wellner, 1996, Theorem 3.3.1). Although the variance–covariance matrix of 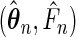 can be obtained by the empirical plug-in version of the asymptotic variance given in Theorem 3.1, it is computationally complicated. As an alternative, we may use the bootstrap resampling method to estimate the variance of the maximum likelihood estimators. By the weak convergence stated in Theorem 3.1 and arguing as in van der Vaart and Wellner (1996, Chapter 3.6), the bootstrap method is expected to produce valid estimates of the variance of
can be obtained by the empirical plug-in version of the asymptotic variance given in Theorem 3.1, it is computationally complicated. As an alternative, we may use the bootstrap resampling method to estimate the variance of the maximum likelihood estimators. By the weak convergence stated in Theorem 3.1 and arguing as in van der Vaart and Wellner (1996, Chapter 3.6), the bootstrap method is expected to produce valid estimates of the variance of 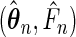 .
.
3.3. Test for stationarity of the incidence rate
In addition to the survival time distribution, the truncation time distribution may be of independent interest. In particular, researchers may want to know whether there is a temporal change in the disease incidence. If the incidence rate increases over time, the underlying truncation time random variable is likely to be right skewed. In contrast, if the incidence of disease is constant over time, the underlying truncation time is uniformly distributed.
To test the null hypothesis 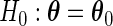 , we consider the semiparametric likelihood ratio test statistic
, we consider the semiparametric likelihood ratio test statistic
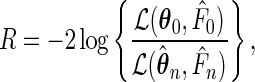 |
where 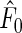 maximizes the likelihood function
maximizes the likelihood function 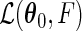 under the null. It follows from Theorem 3.1 and an extension of the general semiparametric likelihood ratio statistic theorem in Murphy and van der Vaart (1997) that
under the null. It follows from Theorem 3.1 and an extension of the general semiparametric likelihood ratio statistic theorem in Murphy and van der Vaart (1997) that 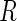 has a
has a 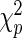 distribution as
distribution as 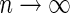 , where
, where 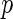 is the dimension of the vector parameter
is the dimension of the vector parameter 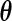 . This result can be used not only in hypothesis testing but also to construct approximate confidence sets for
. This result can be used not only in hypothesis testing but also to construct approximate confidence sets for 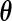 .
.
Next, we propose formal statistical tests for checking the stationarity assumption of the uniform truncation time distribution. Testing the stationarity assumption on disease incidence is an important yet understudied problem. To the best of our knowledge, only a few publications, including Asgharian and others (2006), Mandel and Betensky (2007), and Addona and Wolfson (2006), have focused on this problem. All three papers provided graphical examinations and formal tests of the stationarity condition based on the equality in the distribution of the observed truncation time 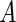 and that of the residual survival time
and that of the residual survival time  . In what follows, we propose a formal test based on the semiparametric likelihood ratio test statistic.
. In what follows, we propose a formal test based on the semiparametric likelihood ratio test statistic.
Following the spirit of Neyman's smooth tests of goodness of fit, we propose to embed the uniform density function to a parametric family of density functions that differ smoothly from the uniform density function. Neyman (1937) constructed a smooth alternative of order 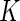 to the null density function
to the null density function 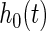 given by
given by
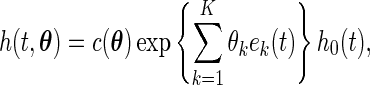 |
where 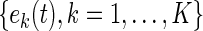 is a set of orthonormal functions which satisfies
is a set of orthonormal functions which satisfies
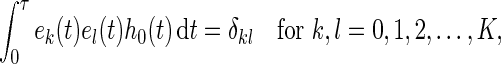 |
with 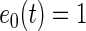 for
for 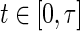 ,
, 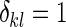 if
if 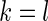 and
and 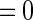 if
if 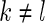 ,
, 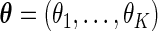 , and
, and 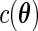 is a normalizing constant. When
is a normalizing constant. When 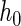 is the uniform density function, the orthonormal functions can be chosen to be the Legendre polynomials. In this way, an order
is the uniform density function, the orthonormal functions can be chosen to be the Legendre polynomials. In this way, an order 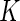 alternative is a polynomial of order
alternative is a polynomial of order 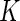 , while the null hypothesis is equivalent to a polynomial of degree
, while the null hypothesis is equivalent to a polynomial of degree  . In other words, the smooth alternatives are given by
. In other words, the smooth alternatives are given by
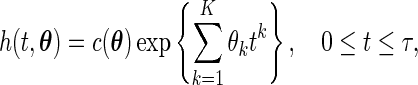 |
(3.3) |
with 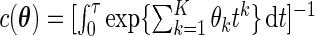 . Thus, testing for the uniform distribution is equivalent to testing
. Thus, testing for the uniform distribution is equivalent to testing 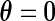 against
against 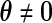 in (3.3).
in (3.3).
To test whether the underlying truncation distribution is uniform, we consider the semiparametric likelihood ratio test
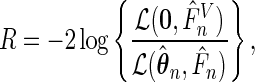 |
where 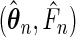 is the semiparametric maximum likelihood estimator that maximizes
is the semiparametric maximum likelihood estimator that maximizes 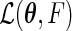 under Model (3.3), and
under Model (3.3), and 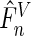 is Vardi's non-parametric maximum likelihood estimator under the null. It was recommended by Neyman (1937) and further investigated in Rayner and Rayner (2001) that a polynomial of degree
is Vardi's non-parametric maximum likelihood estimator under the null. It was recommended by Neyman (1937) and further investigated in Rayner and Rayner (2001) that a polynomial of degree 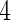 usually suffices to test for uniformity. In our experience, the smooth alternative with
usually suffices to test for uniformity. In our experience, the smooth alternative with 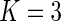 yields good power and is more numerically stable than tests with higher-order polynomials when applied to left-truncated and right-censored data. In the remainder of this paper, we set
yields good power and is more numerically stable than tests with higher-order polynomials when applied to left-truncated and right-censored data. In the remainder of this paper, we set 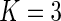 for the smooth alternative model (3.3).
for the smooth alternative model (3.3).
4. Simulations and data analysis
4.1. Monte Carlo simulations
To evaluate the finite-sample performance of the proposed methods, we conducted a series of Monte Carlo simulations. The first set of simulations compared the performance of the proposed semiparametric maximum likelihood estimator to existing methods. We generated survival time 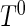 from a truncated Weibull random variable with shape and scale parameters of (0.7, 1). The underlying truncation time
from a truncated Weibull random variable with shape and scale parameters of (0.7, 1). The underlying truncation time 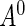 was independently generated from a truncated exponential distribution with survival function
was independently generated from a truncated exponential distribution with survival function 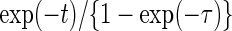 . To form a prevalent cohort, realizations of
. To form a prevalent cohort, realizations of 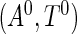 were generated repeatedly until there were
were generated repeatedly until there were 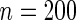 subjects satisfying the sampling constraint
subjects satisfying the sampling constraint 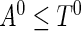 . The censoring time
. The censoring time 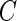 for the residual survival time
for the residual survival time  in the prevalent cohort was generated from a uniform distribution on the interval
in the prevalent cohort was generated from a uniform distribution on the interval 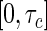 , where
, where 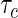 was chosen so that the overall censoring rate was approximately 0%, 25%, and 50%. We fit each generated data set by the proposed profile likelihood method, using the
was chosen so that the overall censoring rate was approximately 0%, 25%, and 50%. We fit each generated data set by the proposed profile likelihood method, using the  function with the option “Nelder-Mead” in R.
function with the option “Nelder-Mead” in R.
Five different methods were applied to estimate the failure time distribution: (I) the truncation product-limit estimator; (II) Vardi's non-parametric maximum likelihood estimator under uniform truncation time distribution (Vardi, 1989); (III) the estimator obtained by the iteration algorithm considered in Shen (2007, 2009) with the assumption of a Weibull truncation time distribution; (IV) the proposed estimator with the assumption of a Weibull truncation time distribution; and (V) the proposed estimator with the assumption that the truncation time has a smooth alternative density (3.3) with 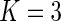 . Table 1 summarizes the Monte Carlo bias, standard deviation, and relative efficiency for each estimator at
. Table 1 summarizes the Monte Carlo bias, standard deviation, and relative efficiency for each estimator at 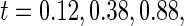 and
and 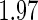 based on 1000 replications. The true cumulative distribution functions at the selected time points are 0.2, 0.4, 0.6, and 0.8, respectively. As expected, Vardi's estimator is biased, because the underlying truncation time is not uniformly distributed. Methods III, IV, and V outperform the truncation product-limit estimator by Method II in terms of Monte Carlo standard deviation. The proposed method with the assumption of a smooth alternative density (Method V) works very well and is most efficient when estimating the failure time distribution. Methods III and IV, which employ the Weibull density, also yield small biases. Interestingly, compared with Method IV, the estimator of the failure time distribution obtained using Method III can be slightly more efficient at early time points, but is equally efficient at later time points. For the parameters in the truncation distribution, Methods IV and V show clear superiority than Method III. Specifically, the biases in the estimated shape and scale parameters of the Weibull density by Method V are (0.011, 0.008), (0.010, 0.011), and
based on 1000 replications. The true cumulative distribution functions at the selected time points are 0.2, 0.4, 0.6, and 0.8, respectively. As expected, Vardi's estimator is biased, because the underlying truncation time is not uniformly distributed. Methods III, IV, and V outperform the truncation product-limit estimator by Method II in terms of Monte Carlo standard deviation. The proposed method with the assumption of a smooth alternative density (Method V) works very well and is most efficient when estimating the failure time distribution. Methods III and IV, which employ the Weibull density, also yield small biases. Interestingly, compared with Method IV, the estimator of the failure time distribution obtained using Method III can be slightly more efficient at early time points, but is equally efficient at later time points. For the parameters in the truncation distribution, Methods IV and V show clear superiority than Method III. Specifically, the biases in the estimated shape and scale parameters of the Weibull density by Method V are (0.011, 0.008), (0.010, 0.011), and 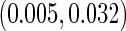 with standard deviations
with standard deviations 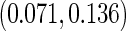 ,
, 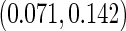 , and
, and 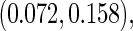 respectively, when the proportion of uncensored subjects is 100%, 75%, and 50%. When using Method III, the corresponding biases under three scenarios are respectively (
respectively, when the proportion of uncensored subjects is 100%, 75%, and 50%. When using Method III, the corresponding biases under three scenarios are respectively ( 0.027, 0.035), (
0.027, 0.035), ( 0.027, 0.043), and (
0.027, 0.043), and ( 0.034, 0.084) with standard deviations
0.034, 0.084) with standard deviations 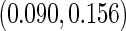 ,
, 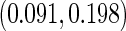 , and
, and 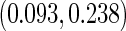 , which are larger than those by the proposed method (Method V).
, which are larger than those by the proposed method (Method V).
Table 1.
Simulation results for various estimators for the failure time distribution.
| Product-limit |
NPMLE |
Shen's method |
Weibull |
Smooth alternative |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
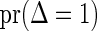 |
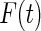 |
Bias | SE | Bias | SE | RE | Bias | SE | RE | Bias | SE | RE | Bias | SE | RE |
| 1 | 0.2 |
 1 1 |
14 | 5 | 13 | 1.10 |
 3 3 |
11 | 1.54 |
 2 2 |
12 | 1.48 |
 2 2 |
11 | 1.63 |
| 0.4 |
 1 1 |
11 | 11 | 10 | 1.42 |
 3 3 |
10 | 1.33 |
 1 1 |
10 | 1.38 |
 2 2 |
9 | 1.53 | |
| 0.6 | 0 | 8 | 14 | 5 | 2.32 |
 2 2 |
7 | 1.24 |
 1 1 |
7 | 1.33 |
 1 1 |
7 | 1.45 | |
| 0.8 | 0 | 4 | 11 | 2 | 5.10 |
 1 1 |
4 | 1.21 |
 1 1 |
4 | 1.27 |
 1 1 |
4 | 1.35 | |
| 0.75 | 0.2 |
 1 1 |
14 | 4 | 13 | 1.10 |
 3 3 |
11 | 1.52 |
 2 2 |
12 | 1.46 |
 2 2 |
11 | 1.63 |
| 0.4 |
 1 1 |
12 | 11 | 10 | 1.42 |
 3 3 |
10 | 1.33 |
 1 1 |
10 | 1.36 |
 2 2 |
9 | 1.52 | |
| 0.6 | 0 | 8 | 14 | 5 | 2.27 |
 2 2 |
7 | 1.23 |
 1 1 |
7 | 1.31 |
 1 1 |
7 | 1.43 | |
| 0.8 | 0 | 4 | 11 | 2 | 5.25 |
 1 1 |
4 | 1.19 | 0 | 4 | 1.24 |
 1 1 |
4 | 1.32 | |
| 0.5 | 0.2 |
 1 1 |
14 | 4 | 13 | 1.13 |
 3 3 |
11 | 1.53 |
 2 2 |
12 | 1.47 |
 2 2 |
11 | 1.57 |
| 0.4 |
 1 1 |
12 | 10 | 10 | 1.42 |
 3 3 |
10 | 1.34 |
 2 2 |
10 | 1.37 |
 2 2 |
10 | 1.46 | |
| 0.6 | 0 | 8 | 13 | 6 | 2.21 |
 2 2 |
7 | 1.24 |
 1 1 |
7 | 1.31 |
 1 1 |
7 | 1.37 | |
| 0.7 | 0 | 5 | 11 | 2 | 5.18 |
 1 1 |
4 | 1.18 | 0 | 4 | 1.21 | 0 | 4 | 1.25 | |
Product-limit, the truncation product-limit estimator; NPMLE, Vardi's non-parametric maximum likelihood estimator; Shen's method; Weibull, the proposed estimator with Weibull truncation time distribution; Smooth Alternative, the proposed estimator with smooth alternative truncation time distribution; Bias, the empirical bias 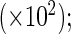 SE, the empirical standard deviation
SE, the empirical standard deviation 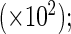 RE, the empirical variance of the truncation product-limit estimator divided by that of an estimator.
RE, the empirical variance of the truncation product-limit estimator divided by that of an estimator.
The second set of simulations evaluated the power of the proposed semiparametric likelihood ratio test under various scenarios. We simulated survival time 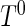 from a truncated exponential distribution with density function
from a truncated exponential distribution with density function 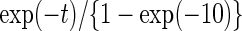 for
for 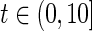 and
and 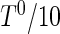 from a beta distribution with parameters 0.5 and 5. The underlying truncation times were generated so that
from a beta distribution with parameters 0.5 and 5. The underlying truncation times were generated so that 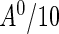 followed the uniform distribution on
followed the uniform distribution on 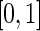 and a beta distribution with shape parameters
and a beta distribution with shape parameters 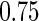 and
and 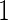 . The censoring times were generated from uniform distributions so that the proportions of uncensored subjects were
. The censoring times were generated from uniform distributions so that the proportions of uncensored subjects were 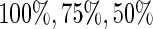 . For each set of simulations, we considered different sample sizes
. For each set of simulations, we considered different sample sizes 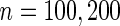 . The significance level of the semiparametric likelihood ratio test was set at
. The significance level of the semiparametric likelihood ratio test was set at 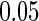 . Table S.1 in the supplementary material available at Biostatistics online summarizes the estimated size and power of the proposed semiparametric likelihood ratio test for testing
. Table S.1 in the supplementary material available at Biostatistics online summarizes the estimated size and power of the proposed semiparametric likelihood ratio test for testing 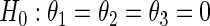 in the smooth alternative density (3.3).
in the smooth alternative density (3.3).
For comparison, we also applied the paired logrank test proposed by Mandel and Betensky (2007) that compares the truncation time distribution and the residual survival time distribution, and reported the size and power of the test in Table S.1 in the supplementary material available at Biostatistics online. When the underlying truncation time is uniformly distributed, the estimated sizes of both tests are close to the predetermined significance level 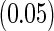 . As expected, when the truncation time distribution is not uniform, the power to reject the null hypothesis increases with the sample size but decreases with the proportion of censored subjects. The proposed test is more powerful than the paired logrank test when the proportion of censored subjects is low, and is as efficient as its competitor when the censoring proportion is high.
. As expected, when the truncation time distribution is not uniform, the power to reject the null hypothesis increases with the sample size but decreases with the proportion of censored subjects. The proposed test is more powerful than the paired logrank test when the proportion of censored subjects is low, and is as efficient as its competitor when the censoring proportion is high.
4.2. Analysis of Canadian study of health and aging
In this section, we report the results of data analysis for a cohort of prevalent cases in one of the largest epidemiologic studies of dementia, the Canadian Study of Health and Aging. From February 1991 to May 1992, an extensive survey was carried out and a total of 1132 persons aged 65 and older with dementia were identified in this first phase of the study. For each study subject, a diagnosis of possible Alzheimer's disease, probable Alzheimer's disease, or vascular dementia was assigned, and the date of dementia onset was determined by interviewing care-givers. Information on mortality was collected between January 1996 and May 1997.
We considered a subset of the study data by excluding those with missing date of onset or classification of dementia subtype. Moreover, as in Wolfson and others (2001), those with observed survival time of 20 or more years were excluded because these subjects are considered unlikely to have Alzheimer's disease or vascular dementia. As a result, a total of 807 dementia patients were included in our analysis. Among them, 388 had a diagnosis of probable Alzheimer's disease, 249 had possible Alzheimer's disease, and 170 had vascular dementia. In the second phase of the study a total of 627 deaths were recorded, among which 302 subjects has a diagnosis of probable Alzheimer's, 189 possible Alzheimer's, and 136 vascular dementia.
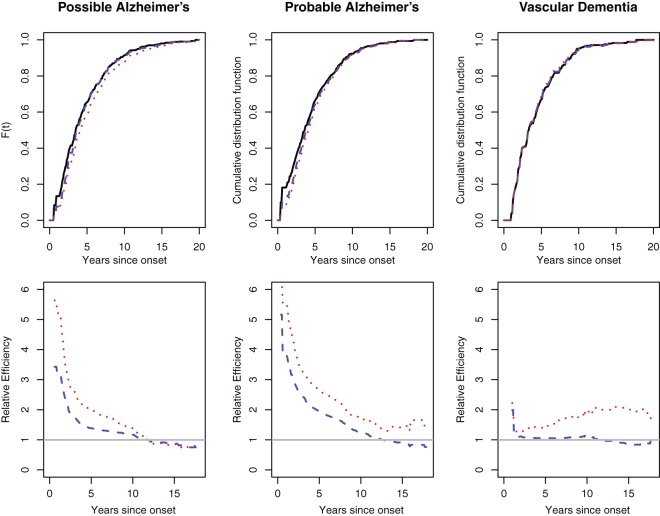
We first applied the proposed semiparametric likelihood ratio test to check the stationarity assumption that the incidence of dementia is constant over time within each subgroup. The 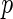 -values were 0.14, 0.17, and 0.28 for possible Alzheimer's, probable Alzheimer's and vascular dementia, respectively. Figure 1 shows the estimated cumulative distribution functions using the truncation product-limit estimator, Vardi's non-parametric maximum likelihood estimator, and the proposed estimator with the assumption that the truncation time has a smooth alternative density (3.3) with
-values were 0.14, 0.17, and 0.28 for possible Alzheimer's, probable Alzheimer's and vascular dementia, respectively. Figure 1 shows the estimated cumulative distribution functions using the truncation product-limit estimator, Vardi's non-parametric maximum likelihood estimator, and the proposed estimator with the assumption that the truncation time has a smooth alternative density (3.3) with 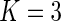 . In general, the three estimated survival curves are reasonably close to each other. Interestingly, the distribution function obtained by the proposed method is closer to the product-limit estimator than Vardi's non-parametric maximum likelihood estimator. In fact, as shown in Figure 5 of Asgharian and others (2002) and Figure 4 of Asgharian and others (2006), the truncation times appear to have a cyclic effect according to year. Figure 1 also shows the relative efficiency of the other two estimators compared with the truncation product-limit estimator at selected time points using these three estimators. To estimate the standard errors of the estimated survival probabilities, we adopted a non-parametric bootstrap method by sampling 807 subjects with replacement from the data set. The resampling procedure was repeated 2000 times, and the standard error was estimated by the standard deviation of the 2000 survival probability estimates at each time point. As expected, the proposed estimator is more efficient than the truncation product-limit estimator, but is less efficient than the non-parametric maximum likelihood estimator under uniform truncation time distribution.
. In general, the three estimated survival curves are reasonably close to each other. Interestingly, the distribution function obtained by the proposed method is closer to the product-limit estimator than Vardi's non-parametric maximum likelihood estimator. In fact, as shown in Figure 5 of Asgharian and others (2002) and Figure 4 of Asgharian and others (2006), the truncation times appear to have a cyclic effect according to year. Figure 1 also shows the relative efficiency of the other two estimators compared with the truncation product-limit estimator at selected time points using these three estimators. To estimate the standard errors of the estimated survival probabilities, we adopted a non-parametric bootstrap method by sampling 807 subjects with replacement from the data set. The resampling procedure was repeated 2000 times, and the standard error was estimated by the standard deviation of the 2000 survival probability estimates at each time point. As expected, the proposed estimator is more efficient than the truncation product-limit estimator, but is less efficient than the non-parametric maximum likelihood estimator under uniform truncation time distribution.
Fig. 1.
Upper panel: Estimated distribution functions using the truncation product-limit estimator (solid line), Vardi's non-parametric maximum likelihood estimator (dotted line), and the proposed estimator (dashed line) for different diagnosis subtypes. Lower panel: relative efficiency compared with the truncation product-limit estimator for Vardi's non-parametric maximum likelihood estimator (dotted line) and the proposed estimator (dashed line).
4.3. Analysis of nursing home data
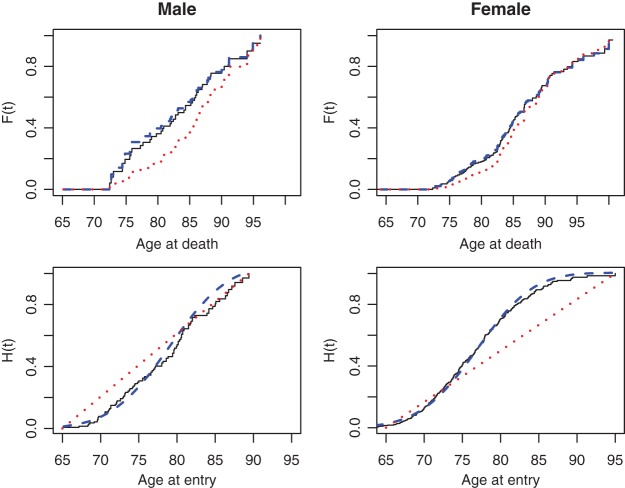
We next illustrate our methods by analyzing the well-known Channing House data (Hyde, 1977), which recorded age at entry and age at death for 462 residents of Channing House, a retirement center in Palo Alto, California, from its opening in 1964 to the data collection date July 1, 1975. The survival time is left-truncated by the age at entry and right-censored by end of study or loss to follow-up. As in Wang (1991), we considered a subset of 438 residents (94 male and 344 female) who survived longer than 866 months. The proposed semiparametric likelihood ratio test rejected the assumption that the entry age was uniformly distributed for both male and female residents (both with a 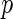 -value
-value 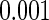 ). The upper panels of Figure 2 show the estimated distribution functions of the survival time for males and for females using the truncation product-limit estimator, Vardi's non-parametric likelihood estimator and the proposed semiparametric estimator with smooth alternative truncation distribution. Moreover, the lower panels of Figure 2 show the estimated distribution functions of the truncation time for different gender groups using the non-parametric estimator proposed in Wang (1991) and the smooth alternative density with
). The upper panels of Figure 2 show the estimated distribution functions of the survival time for males and for females using the truncation product-limit estimator, Vardi's non-parametric likelihood estimator and the proposed semiparametric estimator with smooth alternative truncation distribution. Moreover, the lower panels of Figure 2 show the estimated distribution functions of the truncation time for different gender groups using the non-parametric estimator proposed in Wang (1991) and the smooth alternative density with 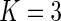 . Compared with males, the truncation time distribution for females further departs from the uniform distribution. The comparison of relative efficiency based on the bootstrap standard error estimates (data not shown), however, suggested that the product-limit estimator is preferred in this case, as the smooth alternative is as or less efficient than the truncation product-limit estimator.
. Compared with males, the truncation time distribution for females further departs from the uniform distribution. The comparison of relative efficiency based on the bootstrap standard error estimates (data not shown), however, suggested that the product-limit estimator is preferred in this case, as the smooth alternative is as or less efficient than the truncation product-limit estimator.
Fig. 2.
Estimates of 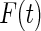 and
and 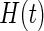 for Channing House data using Wang's non-parametric estimator (solid line), Vardi's non-parametric maximum likelihood estimator (dotted line), and the proposed estimator with the smooth alternative (dashed line).
for Channing House data using Wang's non-parametric estimator (solid line), Vardi's non-parametric maximum likelihood estimator (dotted line), and the proposed estimator with the smooth alternative (dashed line).
5. Remark
The purpose of this paper is 2-fold: first, to generalize Vardi's multiplicative censoring model with a unified EM algorithm for model estimation, and second, to establish the connection between the likelihood for data subject to the generalized multiplicative censoring (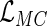 ) and that for left-truncated and right-censored data (
) and that for left-truncated and right-censored data (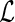 ), so that the EM algorithm developed for
), so that the EM algorithm developed for 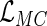 can be applied to obtain the maximum profile likelihood estimator for
can be applied to obtain the maximum profile likelihood estimator for 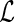 . Although the asymptotic properties of the maximum likelihood estimator for
. Although the asymptotic properties of the maximum likelihood estimator for 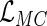 are not discussed in this paper, they can be established by applying a similar argument as that for the maximum profile likelihood estimator for
are not discussed in this paper, they can be established by applying a similar argument as that for the maximum profile likelihood estimator for 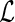 .
.
Left-truncated data can be viewed as selection-biased samples with sampling weights being proportional to the distribution functions of the truncation times. Many authors, including Vardi (1985) and Gill and others (1988), considered non-parametric estimation for selection bias models with known, non-negative weight functions, and Gilbert and others (1999) generalized Vardi's model to allow for the weighting functions to depend on an unknown parameter. However, these methods usually cannot be applied directly to the problem considered in this paper because the left-truncated survival times are further subject to right censoring. It is of interest to generalize the methods for selection bias models to deal with censoring. Future research is warranted.
6. Software
Software in the form of R code, together with a sample input data set and complete documentation is available on request from the corresponding author.
Supplementary material
Supplementary Material is available at http://biostatistics.oxfordjournals.org.
Funding
This work was supported in part by grants CA016672 and CA006973 from the National Institutes of Health. The core of the CSHA study was funded by the Seniors’ Independence Research Program through the National Health Research and Development Program of Health Canada (Project no.6606-3954-MC(S)). Additional funding was provided by Pfizer Canada Incorporated through the Medical Research Council/Pharmaceutical Manufacturers Association of Canada Health Activity Program, NHRDP Project 6603-1417-302(R), Bayer Incorporated, and the British Columbia Health Research Foundation Projects 38 (93-2) and 34 (96-1). The study was coordinated through the University of Ottawa and the Division of Aging and Seniors, Health Canada.
Supplementary Material
Acknowledgments
The authors are grateful to Professors Masoud Asgharian, Ian McDowell, and Christina Wolfson for sharing the Canadian Study of Health and Aging data. The data reported in the example were collected as part of the CSHA. Conflict of Interest: None declared.
References
- Addona V., Wolfson D. B. (2006). A formal test for the stationarity of the incidence rate using data from a prevalent cohort study with follow-up. Lifetime Data Analysis 12(3), 267–284. [DOI] [PubMed] [Google Scholar]
- Asgharian M., M’Lan C. E., Wolfson D. B. (2002). Length-biased sampling with right censoring: An unconditional approach. Journal of the American Statistical Association 97, 201–209. [Google Scholar]
- Asgharian M., Wolfson D. B., Zhang X. (2006). Checking stationarity of the incidence rate using prevalent cohort survival data. Statistics in Medicine 25(10), 1751–1767. [DOI] [PubMed] [Google Scholar]
- Gilbert P. B., Lele S. R., Vardi Y. (1999). Maximum likelihood estimation in semiparametric selection bias models with application to AIDS vaccine trials. Biometrika 86, 27–43. [Google Scholar]
- Gill R. D., Vardi Y., Wellner J. A. (1988). Large sample theory of empirical distributions in biased sampling models. The Annals of Statistics 16, 1069–1112. [Google Scholar]
- Hyde J. (1977). Testing survival under right censoring and left truncation. Biometrika 64, 225–230. [Google Scholar]
- Lagakos S., Barraj L. (1988). Nonparametric analysis of truncated survival data, with application to AIDS. Biometrika 75(3), 515–523. [Google Scholar]
- Lynden-Bell D. (1971). A method of allowing for known observational selection in small samples applied to 3CR quasars. Monograph National Royal Astronomical Society 155, 95–118. [Google Scholar]
- Mandel M. (2007). Nonparametric estimation of a distribution function under biased sampling and censoring. Complex Datasets and Inverse Problems: Tomography, Networks and Beyond. IMS Lecture Notes Onograph Series 54, 224–238. [Google Scholar]
- Mandel M., Betensky R. A. (2007). Testing goodness of fit of a uniform truncation model. Biometrics 63, 405–412. [DOI] [PubMed] [Google Scholar]
- Murphy S. A. (1994). Consistency in a proportional hazards model incorporating a random effect. The Annals of Statistics 22, 712–731. [Google Scholar]
- Murphy S. A. (1997). Semiparametric likelihood ratio inference. The Annals of Statistics 25, 1471–1509. [Google Scholar]
- Neyman J. (1937). Smooth test for goodness of fit. Skandinavisk Aktuarietidskrift 20, 150–199. [Google Scholar]
- Parner E. (1998). Asymptotic theory for the correlated gamma-frailty model. The Annals of Statistics 26, 183–214. [Google Scholar]
- Qin J., Ning J., Liu H., Shen Y. (2011). Maximum likelihood estimations and em algorithms with length-biased data. Journal of the American Statistical Association 106(496), 1434–1449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rayner G. D., Rayner J. C. W. (2001). Power of the Neyman smooth tests for the uniform distribution. Journal of Applied Mathematics and Decision Sciences 5(3), 181–191. [Google Scholar]
- Severini T. A., Wong W. H. (1992). Profile likelihood and conditionally parametric models. The Annals of Statistics 20, 1768–1802. [Google Scholar]
- Shen P.-S. (2007). A general semiparametric model for left-truncated and right-censored data. Journal of Nonparametric Statistics 19, 113–129. [Google Scholar]
- Shen P.-S. (2009). Semiparametric analysis of survival data with left truncation and right censoring. Computational Statistics and Data Analysis 53, 4417–4432. [Google Scholar]
- Tsai W.-Y., Jewell N. P., Wang M.-C. (1987). A note on the product-limit estimator under right censoring and left truncation. Biometrika 74, 883–886. [Google Scholar]
- van der Vaart A. W., Wellner J. A. (1996) Weak Convergence and Empirical Processes. New York: Springer. [Google Scholar]
- Vardi Y. (1985). Empirical distributions in selection bias models. The Annals of Statistics 13, 178–203. [Google Scholar]
- Vardi Y. (1989). Multiplicative censoring, renewal processes, deconvolution and decreasing density: nonparametric estimation. Biometrika 76, 751–761. [Google Scholar]
- Vardi Y., Zhang C. (1992). Large sample study of empirical distributions in a random-multiplicative censoring model. The Annals of Statistics 20(2), 1022–1039. [Google Scholar]
- Wang M.-C. (1989). A semiparametric model for randomly truncated data. Journal of the American Statistical Association 84, 742–748. [Google Scholar]
- Wang M.-C. (1991). Nonparametric estimation from cross-sectional survival data. Journal of the American Statistical Association 86, 130–143. [Google Scholar]
- Wolfson C., Wolfson D. B., Asgharian M. (2001). A reevaluation of the duration of survival after the onset of dementia. New England Journal of Medicine 344(15), 1111–1116. [DOI] [PubMed] [Google Scholar]
- Zelen M., Feinleib M. (1969). On the theory of screening for chronic diseases. Biometrika 56, 601–614. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.