Abstract
Technological advances have yielded a wealth of biomarkers that have the potential to detect chronic diseases such as cancer. However, most biomarkers considered for further validation turn out not to have strong enough performance to be used in clinical practice. Group sequential designs that allow early termination for futility may be cost-effective for biomarker studies based on biobanks of stored specimens. Previous studies proposed a group sequential design for the validation of a single biomarker. In this article, we adapt a 2-stage design to the setting where a panel of candidate biomarkers are under investigation. Conditional estimators of the clinical performance are proposed under an updated risk model that uses all accrued data, and can be computed through resampling procedures. Under a special case where a multivariate binormal distribution applies for biomarkers following a suitable transformation, these estimators have analytical forms, alleviating the computational burden while retaining statistical efficiency. Performance of the proposed 2-stage design and estimators are compared with a traditional fixed-sample design and an existing 2-stage design that allows early termination but does not update the risk model with accrued information. Our proposed design and estimators show an ability to reduce sample size when the biomarker panel is not promising, while controlling rejection rate and gaining efficiency when the panel is promising. We apply the proposed methods to a biomarker panel development for the detection of high-grade prostate cancer in a study conducted within the National Cancer Institute's Early Detection Research Network.
Keywords: Biomarker panel evaluation, Conditional estimate, Groupsequential methods, Two-stage design
1. Introduction
Technological advances have yielded a wealth of biomarkers that have the potential for early detection of chronic diseases such as cancer. The evaluation of diagnostic biomarkers often undergoes 5 phases (Pepe and others, 2001). Take a specific cancer as an example. A phase 1 study is usually a pre-clinical study to identify biomarkers that are differentially expressed in tumor and normal tissues; a phase 2 study retrospectively validates performance of biomarkers in subjects with known disease status; a phase 3 study is usually a retrospective longitudinal study to evaluate the ability of biomarkers to detect disease early; a phase 4 study involves a prospective screening test on relevant population to assess sensitivity and specificity; and a phase 5 study is usually a population-based screening study to estimate cancer mortality reduction. Rigorous and efficient study designs for the early phases are important but frequently overlooked, posing an obstacle for biomarker research.
In a phase 1 biomarker study, a large pool of biomarkers, for example based on genomic or proteomic studies, may be evaluated. False signals can be expected because of the large number of tests. When the candidate biomarkers are further evaluated in a phase 2 study, many of them will not meet performance criteria to continue to later phases. Different from clinical trials which may sequentially enroll patients, a phase 2 biomarker study is usually based on biobanks of stored biospecimens. An early termination option in a phase 2 study is desirable to conserve specimens and minimize assay cost. A 2-stage group sequential design for a phase 2 study has been proposed for this purpose (Pepe and others, 2009). The cases and controls are randomly divided into 2 stages. Samples assigned to stage 1 are assayed to test whether the biomarker performance passes a minimal acceptance criterion. If not, this biomarker is not considered further and samples assigned to stage 2 are saved for other purposes. Otherwise, stage 2 samples are assayed and analyzed. For biomarkers that complete both stages, one is interested in obtaining valid estimates of their clinical performance, such as sensitivities and specificities. These performance parameters can facilitate the design of a phase 3 study, for example in sample size determination. When such a sequential design is implemented, it is necessary to take the early termination possibility into account, to avoid overestimation of performance parameters. Pepe and others (2009) proposed conditional estimators under a 2-stage design for the sensitivity and specificity of a dichotomous biomarker. Koopmeiners and others (2012) extended this design and the conditional estimators to a continuous biomarker. Based on saving specimens and reducing cost when a biomarker is not useful and more efficient performance parameter estimates for a promising biomarker, this design and the corresponding conditional estimators have become standard in biomarker evaluation in the National Cancer Institute (NCI)'s Early Detection Research Network (EDRN).
For many diseases, such as prostate cancer, it has been recognized that a single biomarker usually does not have adequate performance to be used for population screening. When properly combined, a panel of biomarkers may have greater potential for adequate performance. However, validation of a biomarker panel is more challenging compared with that for a single biomarker. Overfitting can be expected if the same dataset is used for both developing a risk model and evaluating its performance. Recently, the Institute of Medicine Omics Committee proposed guidelines for a 2-phase marker panel development and validation process, which includes a discovery and test validation phase and an evaluation for clinical use phase. To avoid overfitting, the first phase consists of 2 stages: a discovery stage and a validation stage. A risk model is developed on training samples in the discovery stage, followed by a “lock-down” of all computational procedures. In the validation stage, the risk model is tested on independent blinded samples. For a pivotal trial, using a lock-down model is preferred to maintain simplicity, and there is typically no early termination option. However, for a biomarker panel discovery study with the goal of developing a robust and optimal biomarker panel, allowing early termination for futility and updating the risk model with complete data are desirable study features. Koopmeiners and Vogel (2013) proposed a 2-stage design for this purpose. They suggest a risk model be developed in stage 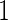 , and a Receiver Operating Characteristic (ROC) curve be constructed on the same set of data to provide the optimistic estimate of performance. If the performance achieves a pre-specified minimal criterion, the risk model is evaluated on stage
, and a Receiver Operating Characteristic (ROC) curve be constructed on the same set of data to provide the optimistic estimate of performance. If the performance achieves a pre-specified minimal criterion, the risk model is evaluated on stage 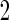 data to estimate its performance parameters. This study design allows model selection in stage
data to estimate its performance parameters. This study design allows model selection in stage 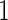 to accommodate a large number of candidate biomarkers, and could improve efficiency over fixed-sample design by allowing early stopping. However, since this design is proposed for a large number of biomarkers, the risk model is not updated with complete data to avoid complication of model selection in both stages. In situations where the number of candidate biomarkers is relatively small and model selection is not needed, the proposed design and estimators can be inefficient. In addition, since the termination decision is based on an over-fitted ROC curve, type I error may not be well controlled.
to accommodate a large number of candidate biomarkers, and could improve efficiency over fixed-sample design by allowing early stopping. However, since this design is proposed for a large number of biomarkers, the risk model is not updated with complete data to avoid complication of model selection in both stages. In situations where the number of candidate biomarkers is relatively small and model selection is not needed, the proposed design and estimators can be inefficient. In addition, since the termination decision is based on an over-fitted ROC curve, type I error may not be well controlled.
In this manuscript, we propose a sequential 2-stage design for a phase 2 biomarker panel development study that allows early termination for futility. Accompanying this design, we also provide estimators of both the risk model and the corresponding performance parameters that make full use of available data. In Section 2, we describe this study design and the conditional estimators. Resampling procedures are used to compute these estimates. We also discuss a simplification of computational procedures under a multivariate binormal distribution special case. In Section 3, we present simulation studies to compare our proposed approach with existing methods. In Section 4, we apply the proposed method to an EDRN prostate cancer biomarker study that aims to develop a biomarker panel for the detection of high-grade prostate cancer. We summarize our work with discussion in Section 5.
2. Methods
2.1. Two-stage design
We consider a panel of 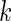 biomarkers
biomarkers 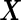 , where
, where 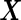 is a vector of length
is a vector of length 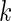 . The study aims to assess whether this panel can be used in clinical practice for the detection of a disease
. The study aims to assess whether this panel can be used in clinical practice for the detection of a disease 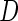 and to develop a risk model
and to develop a risk model 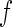 with parameter
with parameter 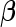 . Here, we restrict our discussion to a small set of candidate biomarkers, so no model selection is required. Extensions to allow model selection are mentioned in Section 5.
. Here, we restrict our discussion to a small set of candidate biomarkers, so no model selection is required. Extensions to allow model selection are mentioned in Section 5.
We assume an underlying logistic model:
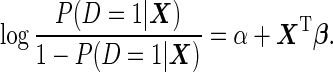 |
(2.1) |
According to McIntosh and Pepe (2002), the optimal risk score is  , and under the logistic model it can be written as
, and under the logistic model it can be written as
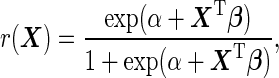 |
(2.2) |
which is a monotone function of 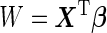 . Since ROC curve is invariant under monotone transformations, we will focus on the performance of
. Since ROC curve is invariant under monotone transformations, we will focus on the performance of 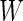 . In the following description and simulation, we use
. In the following description and simulation, we use 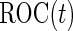 ,
, 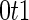 , which is the sensitivity at specificity
, which is the sensitivity at specificity  , as an example of a performance parameter of interest. Other performance parameters, such as the inverse of
, as an example of a performance parameter of interest. Other performance parameters, such as the inverse of 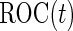 (
(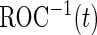 ), the area under the ROC curve (AUC), partial AUC, positive predictive value or negative predictive value can be considered similarly.
), the area under the ROC curve (AUC), partial AUC, positive predictive value or negative predictive value can be considered similarly.
A minimal desirable performance criterion needs to be specified beforehand. This criterion can reflect the performance of current standard practice, with a new test only acceptable if its performance is better than the current standard. For example, we may want the test to have sensitivity at least 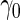 when the specificity is
when the specificity is  . That is,
. That is,
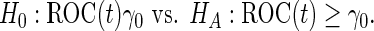 |
(2.3) |
For a fixed-sample phase 2 biomarker study, samples are randomly divided into a training and a validation dataset. A risk model with 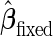 is built on the training dataset and evaluated on the validation dataset. We accept
is built on the training dataset and evaluated on the validation dataset. We accept 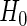 if the upper limit of the
if the upper limit of the 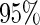 confidence interval for
confidence interval for 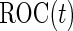 is smaller than
is smaller than 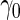 . In contrast, for a 2-stage design, one first randomly assigns
. In contrast, for a 2-stage design, one first randomly assigns 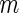 samples to stage
samples to stage 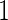 and the remaining
and the remaining 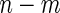 to stage
to stage 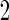 . Stage 1 samples are first assayed for their biomarker values
. Stage 1 samples are first assayed for their biomarker values 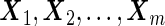 . There are several approaches to develop a risk model based on stage
. There are several approaches to develop a risk model based on stage 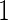 samples, such as
samples, such as 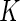 -fold cross-validation. Here, we propose a highly stable bootstrap approach, which is described in Section 2.2 as an inner bootstrap procedure. If the upper limit of the confidence interval of
-fold cross-validation. Here, we propose a highly stable bootstrap approach, which is described in Section 2.2 as an inner bootstrap procedure. If the upper limit of the confidence interval of 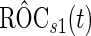 is less than
is less than 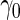 , we conclude there is not enough evidence to support this panel for further evaluation (
, we conclude there is not enough evidence to support this panel for further evaluation (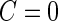 ). Otherwise, the study continues to stage 2 (
). Otherwise, the study continues to stage 2 (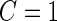 ), and the remaining
), and the remaining 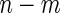 samples are assayed for their biomarker values
samples are assayed for their biomarker values 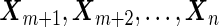 . The procedures for estimating
. The procedures for estimating 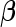 and
and 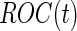 upon study completion are described in Section 2.3.
upon study completion are described in Section 2.3.
2.2. An inner bootstrap procedure for performance estimation
Consider stage 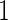 data
data 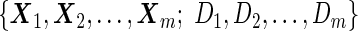 . Copas and Corbett (2002) discussed the magnitude of overestimation of
. Copas and Corbett (2002) discussed the magnitude of overestimation of 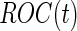 if a risk model is developed and evaluated on the same dataset, and pointed out that the overestimation is largest with the high specificities that are usually of the most interest. However, for most biomarker studies, especially for expensive biomarkers, sample size is usually not very large. Further dividing these subjects into a training and a validation dataset may result in efficiency loss and unstable estimates. Even if one starts with a relatively large study, e.g.
if a risk model is developed and evaluated on the same dataset, and pointed out that the overestimation is largest with the high specificities that are usually of the most interest. However, for most biomarker studies, especially for expensive biomarkers, sample size is usually not very large. Further dividing these subjects into a training and a validation dataset may result in efficiency loss and unstable estimates. Even if one starts with a relatively large study, e.g. 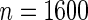 as will be discussed in Section 3, a random assignment of half patients to stage 1 will reduce the sample size to
as will be discussed in Section 3, a random assignment of half patients to stage 1 will reduce the sample size to  , and training and validation datasets will only have
, and training and validation datasets will only have 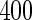 subjects, respectively. Also, it is known that maximum-likelihood estimates (MLEs) of logistic regression parameters can have non-trivial bias when sample size is small (Cordeiro and McCullagh, 1991), which can result in an underestimation of
subjects, respectively. Also, it is known that maximum-likelihood estimates (MLEs) of logistic regression parameters can have non-trivial bias when sample size is small (Cordeiro and McCullagh, 1991), which can result in an underestimation of 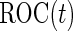 . Thus, methods that avoid sample size reduction are of interest.
. Thus, methods that avoid sample size reduction are of interest.
Here, we propose a bootstrap approach to develop a risk model and test its performance while making full use of available data. This approach will be used as the basis for the estimation procedure of the proposed 2-stage design, and we refer to it as an inner bootstrap procedure. We describe this procedure with an underlying logistic regression model, but it applies readily to other classes of models. For the  th bootstrap sample, we have the following steps:
th bootstrap sample, we have the following steps:
Step A: Sample
 subjects with replacement, and denote the data as
subjects with replacement, and denote the data as  .
.Step B: A logistic regression model is fitted to
 , to obtain
, to obtain  .
.Step C: Risk scores
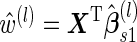 are computed for subjects who are not sampled in Step A, that is
are computed for subjects who are not sampled in Step A, that is 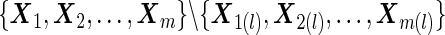 .
.Step D:
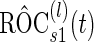 is estimated based on these risk scores and their corresponding disease status.
is estimated based on these risk scores and their corresponding disease status.
This procedure is repeated for a large number of times (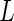 ). Then we estimate
). Then we estimate
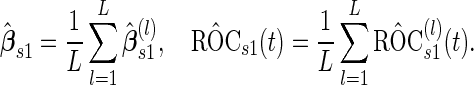 |
(2.4) |
A percentile bootstrap confidence interval can be formed to decide whether to continue to stage 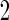 . This procedure is expected to provide an unbiased estimate, and it is computationally easy to implement. Also we expect this procedure to be efficient, since there is no sample size reduction in calculating
. This procedure is expected to provide an unbiased estimate, and it is computationally easy to implement. Also we expect this procedure to be efficient, since there is no sample size reduction in calculating 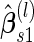 , and averaging over bootstrap replications allows us to use information of all
, and averaging over bootstrap replications allows us to use information of all  subjects. Although described based on stage
subjects. Although described based on stage 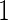 data, this inner bootstrap procedure can also be applied to stage
data, this inner bootstrap procedure can also be applied to stage 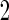 data, and to combined stage
data, and to combined stage 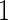 and
and 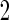 data, as will be amplified below.
data, as will be amplified below.
2.3. Estimation following completion of a 2-stage design
If after performing the inner bootstrap procedure on the 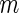 stage
stage 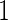 subjects, the biomarker panel showed sufficient promise, samples of the remaining
subjects, the biomarker panel showed sufficient promise, samples of the remaining 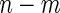 stage
stage 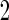 subjects are then assayed. We now consider how to estimate
subjects are then assayed. We now consider how to estimate 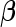 and
and 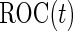 for a study that completes both stages. As discussed in Pepe and others (2009) and Koopmeiners and others (2012), for a single biomarker, there are several approaches, including an estimate based on all data, an estimate based on stage 2 data only, and a conditional estimate that takes the early termination possibility into account. All 3 estimates can be extended to the evaluation of a biomarker panel. Their implementation and corresponding properties are discussed below.
for a study that completes both stages. As discussed in Pepe and others (2009) and Koopmeiners and others (2012), for a single biomarker, there are several approaches, including an estimate based on all data, an estimate based on stage 2 data only, and a conditional estimate that takes the early termination possibility into account. All 3 estimates can be extended to the evaluation of a biomarker panel. Their implementation and corresponding properties are discussed below.
First, upon completion of a 2-stage study, we can estimate 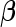 and
and 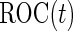 using the inner bootstrap procedure on all subjects
using the inner bootstrap procedure on all subjects 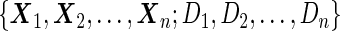 , and denote these estimates as
, and denote these estimates as 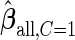 and
and 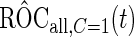 . Here, we treat the 2-stage study as a fixed-sample study, ignoring the fact that stage 1 data has to pass a minimal acceptable criterion for a study to continue to completion. These estimates are positively biased, because only studies that have high performances in stage 1 can continue to stage 2. To simplify the notation, we suppress the condition
. Here, we treat the 2-stage study as a fixed-sample study, ignoring the fact that stage 1 data has to pass a minimal acceptable criterion for a study to continue to completion. These estimates are positively biased, because only studies that have high performances in stage 1 can continue to stage 2. To simplify the notation, we suppress the condition 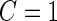 in the following discussion.
in the following discussion.
We may also estimate the ROC curve with stage 2 data 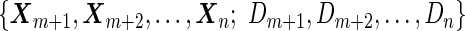 , again with the inner bootstrap procedure. We denote these estimates as
, again with the inner bootstrap procedure. We denote these estimates as 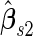 and
and 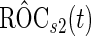 . These estimates are also conditional on
. These estimates are also conditional on  , but they are expected to be unbiased, since stage
, but they are expected to be unbiased, since stage 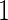 and
and 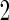 data are independent. However, they can be inefficient due to the lack of use of stage 1 data.
data are independent. However, they can be inefficient due to the lack of use of stage 1 data.
Unbiased conditional estimators, similar to those proposed by Pepe and others (2009) and Koopmeiners and others (2012) for a single biomarker study, can improve efficiency compared with estimators using solely stage 2 data. The conditional estimators are defined as
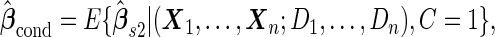 |
(2.5) |
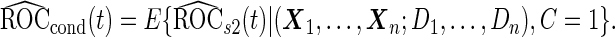 |
(2.6) |
It is straightforward to prove that 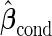 and
and 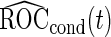 are unbiased for
are unbiased for 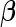 and
and 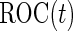 , and they have smaller variances than
, and they have smaller variances than 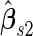 and
and 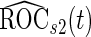 , respectively. For example, for a fixed
, respectively. For example, for a fixed 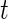 ,
,
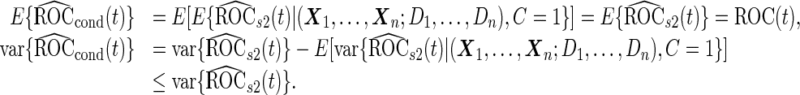 |
These estimators do not have closed forms for a general biomarker distribution. Hence, we propose the following resampling steps to estimate them: for the 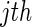 resampling,
resampling,
Step 1: From the
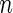 subjects, randomly sample
subjects, randomly sample 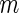 subjects to serve as the pseudo stage 1 data, and the remaining
subjects to serve as the pseudo stage 1 data, and the remaining 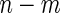 as the pseudo stage 2 data.
as the pseudo stage 2 data.Step 2: Use the inner bootstrap procedure on the pseudo stage 1 data to calculate
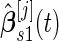 ,
, 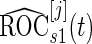 and the corresponding
and the corresponding 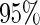 confidence interval. If the upper limit of the
confidence interval. If the upper limit of the 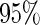 confidence interval of
confidence interval of 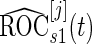 is lower than
is lower than 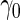 , we terminate with
, we terminate with 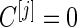 ; otherwise, we continue to stage 2 with
; otherwise, we continue to stage 2 with 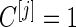 .
.Step 3: If
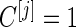 , the same inner bootstrap procedure is used on the pseudo stage 2 data to calculate
, the same inner bootstrap procedure is used on the pseudo stage 2 data to calculate 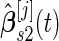 and
and 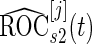 .
.
We repeat this procedure for a large number of times (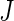 ). Then we estimate
). Then we estimate
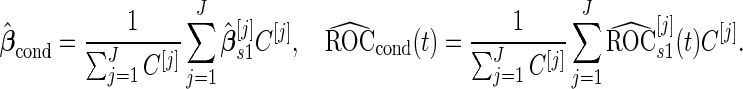 |
(2.7) |
We call this resampling procedure an outer bootstrap procedure. In order to provide percentile confidence intervals for 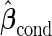 and
and 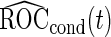 , another resampling layer is needed. This resampling procedure is similar to the non-parametric bootstrap approach in Pepe and others (2009), with extension to a biomarker panel by 3 nested bootstrap resampling procedures.
, another resampling layer is needed. This resampling procedure is similar to the non-parametric bootstrap approach in Pepe and others (2009), with extension to a biomarker panel by 3 nested bootstrap resampling procedures.
2.4. Special cases under multivariate binormal distributions
In the previous discussion, we described a 2-stage design and an inference procedure based on a widely used logistic regression model. The proposed conditional estimates at study completion can be calculated through the outer bootstrap procedure. Since each outer bootstrap replication involves the inner bootstrap, the computational burden can be heavy, especially for confidence interval calculation. Also, if the underlying model is not a logistic model, 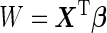 from the logistic model may be a suboptimal score, leading to an underestimation of the panel performance. In this section, we describe a simplification of the inner bootstrap procedure under a multivariate binormal distribution where the optimal risk score can be derived analytically. The proposed outer bootstrap procedure and the estimators at study completion follow only with minor changes.
from the logistic model may be a suboptimal score, leading to an underestimation of the panel performance. In this section, we describe a simplification of the inner bootstrap procedure under a multivariate binormal distribution where the optimal risk score can be derived analytically. The proposed outer bootstrap procedure and the estimators at study completion follow only with minor changes.
We assume the underlying distribution of biomarkers 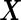 , or properly transformed
, or properly transformed 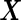 , is multivariate binormal:
, is multivariate binormal:
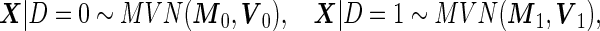 |
(2.8) |
where 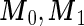 are mean vectors of length
are mean vectors of length 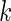 and
and 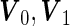 are
are 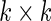 variance matrices. Under this model, the optimal risk score
variance matrices. Under this model, the optimal risk score 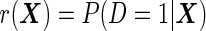 is a monotone function of
is a monotone function of
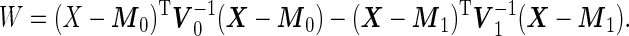 |
(2.9) |
Under the special case that 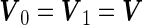 ,
, 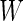 can be further simplified to
can be further simplified to 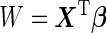 , where
, where 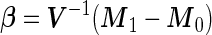 , which is also binormally distributed. Thus,
, which is also binormally distributed. Thus,  has an analytic form:
has an analytic form:
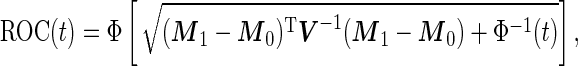 |
(2.10) |
where 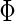 is a standard normal distribution function. This analytic form allows one to replace the inner bootstrap approach with a direct estimate of
is a standard normal distribution function. This analytic form allows one to replace the inner bootstrap approach with a direct estimate of 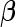 and
and 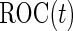 , by plugging in the corresponding estimates of
, by plugging in the corresponding estimates of 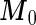 ,
, 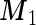 and
and 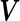 . To get
. To get 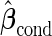 and
and 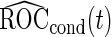 , the outer bootstrap procedure is slightly changed: in Step 2, we directly estimate
, the outer bootstrap procedure is slightly changed: in Step 2, we directly estimate 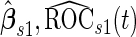 and
and 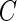 by plugging in
by plugging in 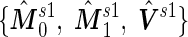 , which are group sample means and pooled sample variance from stage 1 data; in Step 3, we plug in
, which are group sample means and pooled sample variance from stage 1 data; in Step 3, we plug in 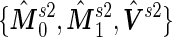 estimated from stage 2 data to obtain
estimated from stage 2 data to obtain 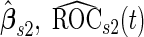 . Under this common variance special case, the optimal score
. Under this common variance special case, the optimal score 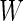 has the same linear form as arose from a logistic regression model. Hence replacing the inner bootstrap approach with direct estimates of
has the same linear form as arose from a logistic regression model. Hence replacing the inner bootstrap approach with direct estimates of  and
and 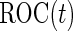 can be expected to result in small changes in point estimates, but also to improve efficiency of the estimates as well as the computational simplicity.
can be expected to result in small changes in point estimates, but also to improve efficiency of the estimates as well as the computational simplicity.
For a general case of 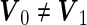 ,
, 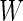 is a quadratic form of
is a quadratic form of 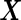 rather than a linear combination. This indicates that the logistic model is not correct under this distribution and using the quadratic combination
rather than a linear combination. This indicates that the logistic model is not correct under this distribution and using the quadratic combination 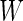 can lead to better accuracy under the binormal model. Once again, one can simplify the bootstrap procedure. First one can estimate
can lead to better accuracy under the binormal model. Once again, one can simplify the bootstrap procedure. First one can estimate 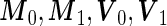 as sample means and variances from the corresponding disease group. Although one is not able to write the analytic form of
as sample means and variances from the corresponding disease group. Although one is not able to write the analytic form of  because
because 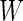 has a quadratic form of
has a quadratic form of 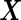 , we can simulate a large dataset of multivariate binormal random variables with
, we can simulate a large dataset of multivariate binormal random variables with 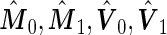 as the corresponding means and variances, and then calculate
as the corresponding means and variances, and then calculate 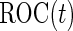 using an empirical estimator. Similar to the common variance special case, the outer bootstrap procedure is modified by replacing the inner bootstrap approach by this numerical approach. We note that, under this setting, mis-specification of a logistic model will provide a suboptimal risk model for the panel and underestimation of its performance. We expect this parametric bootstrap approach will tend to produce accurate risk models and efficient performance estimates in many application settings.
using an empirical estimator. Similar to the common variance special case, the outer bootstrap procedure is modified by replacing the inner bootstrap approach by this numerical approach. We note that, under this setting, mis-specification of a logistic model will provide a suboptimal risk model for the panel and underestimation of its performance. We expect this parametric bootstrap approach will tend to produce accurate risk models and efficient performance estimates in many application settings.
Furthermore, this parametric bootstrap approach is not restricted to the special case of binormal distribution. If the distribution of 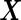 or transformed
or transformed 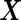 follows a known parametric distribution with parameters
follows a known parametric distribution with parameters 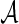 , we can use similar methods to estimate
, we can use similar methods to estimate 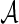 with appropriate data and simulate datasets to obtain empirical estimates of ROC curves. Although the simulation may have similar computational complexity as the inner bootstrap approach when the parametric distribution is complicated, this parametric bootstrap approach can be expected to provide more efficient estimates if the parametric model is well chosen.
with appropriate data and simulate datasets to obtain empirical estimates of ROC curves. Although the simulation may have similar computational complexity as the inner bootstrap approach when the parametric distribution is complicated, this parametric bootstrap approach can be expected to provide more efficient estimates if the parametric model is well chosen.
3. Simulation
We now examine the performance of the proposed 2-stage group sequential design and the conditional estimators with simulation studies.
We first simulated 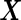 from a multivariate normal distribution with
from a multivariate normal distribution with 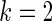 , means
, means  , variances
, variances 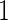 and correlation
and correlation 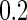 . Disease status
. Disease status 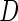 was simulated from a logistic model with
was simulated from a logistic model with 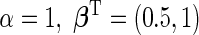 . We focus on
. We focus on 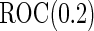 as an example, which has value
as an example, which has value 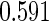 in this setting. We vary the sample size as
in this setting. We vary the sample size as 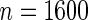 ,
,  ,
, 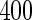 and
and  , and half of the subjects were assigned to stage
, and half of the subjects were assigned to stage 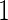 (i.e.
(i.e. 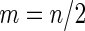 ). Minimal acceptance
). Minimal acceptance 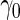 for
for 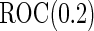 ranged from
ranged from 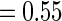 to
to 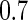 across simulation configurations. A similar simulation was repeated for
across simulation configurations. A similar simulation was repeated for  . Biomarker values
. Biomarker values 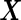 were simulated from a multivariate normal distribution with means
were simulated from a multivariate normal distribution with means  , variances
, variances 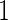 and correlations
and correlations 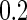 . Disease status
. Disease status 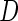 was simulated from a logistic model with
was simulated from a logistic model with 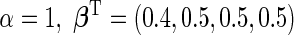 . The targeted
. The targeted 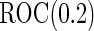 in this context is
in this context is 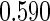 . All the simulations are repeated
. All the simulations are repeated 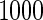 times. Simulation results for
times. Simulation results for 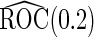 are summarized in Table 1, and those for
are summarized in Table 1, and those for 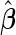 are provided in Table 1 of the supplementary material available at Biostatistics online.
are provided in Table 1 of the supplementary material available at Biostatistics online.
Table 1.
Simulation results on 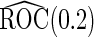 comparing performance between fixed-sample design, Koopmeiners and Vogel approach and the proposed 2-stage design with
comparing performance between fixed-sample design, Koopmeiners and Vogel approach and the proposed 2-stage design with 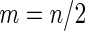 . True
. True 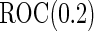 is
is 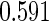 for
for 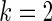 and
and 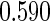 for
for 
| Fixed sample |
Koopmeiners and Vogel |
Two-stage design with 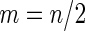 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
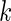 |
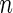 |
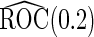 (se) (se) |
 Samples Samples |
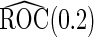 (se) (se) |
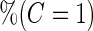 |
 Samples Samples |
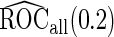 (se) (se) |
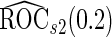 (se) (se) |
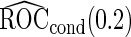 (se) (se) |
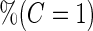 |
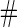 Samples Samples |
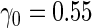 | |||||||||||
| 2 | 1600 | 0.590 (0.041) | 1600 | 0.590 (0.041) | 85.3 | 1482 | 0.589 (0.029) | 0.588 (0.039) | 0.589 (0.028) | 99.8 | 1598 |
| 800 | 0.589 (0.057) | 800 | 0.589 (0.058) | 78.2 | 713 | 0.589 (0.038) | 0.589 (0.051) | 0.588 (0.037) | 99.9 | 800 | |
| 400 | 0.586 (0.081) | 400 | 0.586 (0.081) | 73.0 | 346 | 0.589 (0.053) | 0.585 (0.072) | 0.587 (0.050) | 100.0 | 400 | |
| 200 | 0.582 (0.114) | 200 | 0.583 (0.114) | 70.6 | 171 | 0.588 (0.069) | 0.585 (0.097) | 0.583 (0.066) | 99.9 | 200 | |
| 4 | 1600 | 0.587 (0.040) | 1600 | 0.587 (0.040) | 87.3 | 1498 | 0.588 (0.027) | 0.586 (0.038) | 0.585 (0.026) | 100.0 | 1600 |
| 800 | 0.584 (0.058) | 800 | 0.584 (0.058) | 81.6 | 726 | 0.584 (0.038) | 0.579 (0.052) | 0.578 (0.036) | 99.9 | 800 | |
| 400 | 0.578 (0.081) | 400 | 0.578 (0.082) | 77.7 | 355 | 0.580 (0.052) | 0.570 (0.071) | 0.567 (0.050) | 99.8 | 400 | |
| 200 | 0.566 (0.117) | 200 | 0.568 (0.116) | 76.5 | 176 | 0.566 (0.074) | 0.545 (0.099) | 0.545 (0.070) | 99.9 | 200 | |
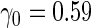 | |||||||||||
| 2 | 1600 | 0.590 (0.041) | 1600 | 0.590 (0.040) | 44.4 | 1154 | 0.591 (0.028) | 0.591 (0.039) | 0.590 (0.028) | 98.9 | 1591 |
| 800 | 0.589 (0.057) | 800 | 0.589 (0.058) | 46.9 | 587 | 0.590 (0.038) | 0.589 (0.051) | 0.588 (0.037) | 97.0 | 788 | |
| 400 | 0.586 (0.081) | 400 | 0.587 (0.081) | 51.0 | 302 | 0.590 (0.052) | 0.585 (0.072) | 0.587 (0.050) | 98.6 | 395 | |
| 200 | 0.582 (0.114) | 200 | 0.584 (0.114) | 54.3 | 154 | 0.588 (0.069) | 0.585 (0.097) | 0.583 (0.066) | 98.4 | 197 | |
| 4 | 1600 | 0.587 (0.040) | 1600 | 0.588 (0.041) | 46.9 | 1174 | 0.588 (0.027) | 0.586 (0.038) | 0.585 (0.027) | 97.1 | 1577 |
| 800 | 0.584 (0.058) | 800 | 0.584 (0.058) | 51.2 | 605 | 0.585 (0.037) | 0.579 (0.052) | 0.578 (0.037) | 97.4 | 786 | |
| 400 | 0.578 (0.081) | 400 | 0.579 (0.082) | 56.6 | 313 | 0.580 (0.052) | 0.570 (0.071) | 0.567 (0.051) | 98.3 | 395 | |
| 200 | 0.566 (0.117) | 200 | 0.567 (0.116) | 61.4 | 161 | 0.567 (0.073) | 0.545 (0.099) | 0.545 (0.071) | 98.3 | 197 | |
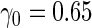 | |||||||||||
| 2 | 1600 | 0.590 (0.041) | 1600 | 0.590 (0.040) | 7.6 | 861 | 0.596 (0.026) | 0.591 (0.038) | 0.591 (0.029) | 83.2 | 1466 |
| 800 | 0.589 (0.057) | 800 | 0.592 (0.058) | 16.6 | 467 | 0.592 (0.036) | 0.589 (0.051) | 0.588 (0.038) | 93.8 | 775 | |
| 400 | 0.586 (0.081) | 400 | 0.587 (0.080) | 26.5 | 253 | 0.591 (0.052) | 0.585 (0.073) | 0.587 (0.051) | 97.3 | 395 | |
| 200 | 0.582 (0.114) | 200 | 0.584 (0.113) | 36.5 | 136 | 0.589 (0.069) | 0.584 (0.097) | 0.583 (0.067) | 98.1 | 198 | |
| 4 | 1600 | 0.587 (0.040) | 1600 | 0.587 (0.040) | 8.7 | 869 | 0.593 (0.025) | 0.587 (0.039) | 0.585 (0.029) | 84.1 | 1473 |
| 800 | 0.584 (0.058) | 800 | 0.584 (0.057) | 19.2 | 477 | 0.588 (0.036) | 0.579 (0.052) | 0.578 (0.038) | 91.4 | 766 | |
| 400 | 0.578 (0.081) | 400 | 0.580 (0.082) | 31.8 | 264 | 0.583 (0.050) | 0.570 (0.071) | 0.568 (0.052) | 95.5 | 391 | |
| 200 | 0.566 (0.117) | 200 | 0.570 (0.115) | 44.1 | 144 | 0.569 (0.073) | 0.544 (0.099) | 0.544 (0.072) | 97.6 | 198 | |
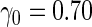 | |||||||||||
| 2 | 1600 | 0.590 (0.041) | 1600 | 0.585 (0.043) | 0.3 | 802 | 0.609 (0.025) | 0.594 (0.040) | 0.593 (0.033) | 38.4 | 1107 |
| 800 | 0.589 (0.057) | 800 | 0.593 (0.058) | 2.7 | 411 | 0.601 (0.034) | 0.589 (0.051) | 0.590 (0.039) | 70.7 | 683 | |
| 400 | 0.586 (0.081) | 400 | 0.585 (0.080) | 9.6 | 219 | 0.595 (0.050) | 0.585 (0.071) | 0.587 (0.053) | 90.3 | 381 | |
| 200 | 0.582 (0.114) | 200 | 0.582 (0.113) | 20.8 | 121 | 0.591 (0.068) | 0.584 (0.097) | 0.583 (0.068) | 95.5 | 196 | |
| 4 | 1600 | 0.587 (0.040) | 1600 | 0.585 (0.043) | 0.4 | 803 | 0.604 (0.023) | 0.585 (0.038) | 0.583 (0.031) | 34.5 | 1076 |
| 800 | 0.584 (0.058) | 800 | 0.586 (0.056) | 3.6 | 414 | 0.597 (0.033) | 0.579 (0.052) | 0.579 (0.040) | 65.1 | 660 | |
| 400 | 0.578 (0.081) | 400 | 0.583 (0.082) | 12.7 | 225 | 0.589 (0.048) | 0.571 (0.071) | 0.569 (0.054) | 84.2 | 368 | |
| 200 | 0.566 (0.117) | 200 | 0.571 (0.115) | 26.8 | 127 | 0.573 (0.071) | 0.544 (0.099) | 0.544 (0.075) | 92.5 | 193 | |
With a fixed-sample design, the estimate for 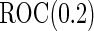 presents some bias with smaller sample sizes, due to bias in logistic regression parameter estimates. This bias becomes stronger as number of biomarkers increases. Comparing our 2-stage design with the design described in Koopmeiners and Vogel (2013) shows that our design has a higher continuation rate. When
presents some bias with smaller sample sizes, due to bias in logistic regression parameter estimates. This bias becomes stronger as number of biomarkers increases. Comparing our 2-stage design with the design described in Koopmeiners and Vogel (2013) shows that our design has a higher continuation rate. When 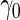 increases to
increases to 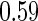 , which is the true
, which is the true 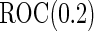 , the Koopmeiners and Vogel approach rejects about
, the Koopmeiners and Vogel approach rejects about 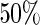 of simulated datasets, due to defining the rejection region in terms of point estimate. Our approach only rejects about
of simulated datasets, due to defining the rejection region in terms of point estimate. Our approach only rejects about 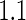 –
– of simulated studies, which is close to the expected
of simulated studies, which is close to the expected 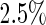 under
under 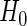 . This is a desirable property in the context of motivating research projects, and it derives from defining the continuation region in terms of the upper limit of
. This is a desirable property in the context of motivating research projects, and it derives from defining the continuation region in terms of the upper limit of 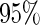 confidence interval. Although minimizing cost and saving samples is the main objective of a sequential design, it is also important that useful biomarker panels proceed for full evaluation. Our approach balances the reliability and cost of studies comparing to the other designs.
confidence interval. Although minimizing cost and saving samples is the main objective of a sequential design, it is also important that useful biomarker panels proceed for full evaluation. Our approach balances the reliability and cost of studies comparing to the other designs.
With our proposed 2-stage design, when 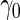 is higher than the true
is higher than the true 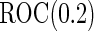 , the continuation rate increases as sample size decreases. This is because when sample size is large, our estimate based on stage 1 is less variable, and the confidence interval is less likely to cover
, the continuation rate increases as sample size decreases. This is because when sample size is large, our estimate based on stage 1 is less variable, and the confidence interval is less likely to cover 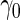 ; while with small sample size, we are less confident about stage 1 estimates and thus more likely to continue to stage
; while with small sample size, we are less confident about stage 1 estimates and thus more likely to continue to stage 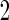 . Therefore, our proposed continuation rules takes the uncertainty in the initial evaluation into account. For the 3 estimators discussed before, i.e.
. Therefore, our proposed continuation rules takes the uncertainty in the initial evaluation into account. For the 3 estimators discussed before, i.e. 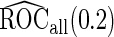 ,
, 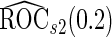 and
and 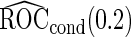 , their performances are as expected.
, their performances are as expected. 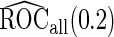 gives the highest estimates among the 3, while the standard error is low. The overestimation is obvious, especially for scenarios with large sample sizes (
gives the highest estimates among the 3, while the standard error is low. The overestimation is obvious, especially for scenarios with large sample sizes (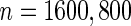 ) and high
) and high 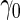 (
(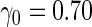 ). In these scenarios,
). In these scenarios, 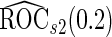 and
and 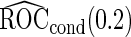 are both unbiased, and
are both unbiased, and 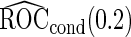 is always associated with a smaller standard error than
is always associated with a smaller standard error than 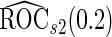 .
.
When sample size is small (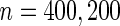 ), the underestimation due to bias in logistic parameter estimates offsets the overestimation due to ignoring the early stopping possibility, leading to a small bias in
), the underestimation due to bias in logistic parameter estimates offsets the overestimation due to ignoring the early stopping possibility, leading to a small bias in 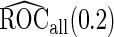 . On the other hand,
. On the other hand, 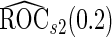 and
and 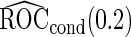 are lower than the true
are lower than the true 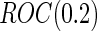 as expected, but
as expected, but 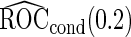 still has the smallest standard error. Although in these settings,
still has the smallest standard error. Although in these settings,  and
and 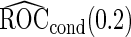 are biased for the true
are biased for the true 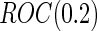 under optimal risk model with
under optimal risk model with 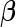 , they are unbiased estimates for the
, they are unbiased estimates for the 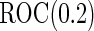 under suboptimal risk model with
under suboptimal risk model with 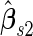 and
and 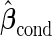 .
.
We also conducted a simulation study with 33% subjects assigned to stage 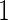 and remaining to stage
and remaining to stage 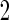 . Results based on
. Results based on 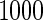 simulation replications are summarized in Table 2 of the supplementary material available at Biostatistics online. When stage
simulation replications are summarized in Table 2 of the supplementary material available at Biostatistics online. When stage 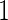 sample size is smaller, we are less likely to terminate a study for futility. For a study that continues to stage
sample size is smaller, we are less likely to terminate a study for futility. For a study that continues to stage 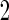 ,
, 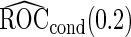 is still more accurate than
is still more accurate than 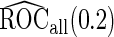 and more efficient than
and more efficient than 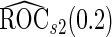 .
.
Table 2.
Simulation results on 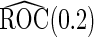 comparing logistic regression approach and parametric bootstrap approach, with equal variances. True
comparing logistic regression approach and parametric bootstrap approach, with equal variances. True 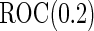 is
is 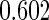
| Logistic regression approach |
Parametric bootstrap approach |
|||||
|---|---|---|---|---|---|---|
 |
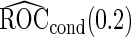 (se) (se) |
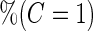 |
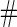 Samples Samples |
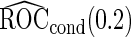 (se) (se) |
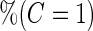 |
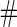 Samples Samples |
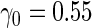 | ||||||
| 1600 | 0.596 (0.025) | 100.0 | 1600 | 0.603 (0.020) | 100.0 | 1600 |
| 800 | 0.590 (0.034) | 100.0 | 800 | 0.606 (0.029) | 100.0 | 800 |
| 400 | 0.579 (0.047) | 100.0 | 400 | 0.606 (0.042) | 100.0 | 400 |
| 200 | 0.556 (0.062) | 100.0 | 200 | 0.617 (0.056) | 99.9 | 199 |
 | ||||||
| 1600 | 0.597 (0.025) | 98.8 | 1590 | 0.603 (0.021) | 98.5 | 1588 |
| 800 | 0.589 (0.035) | 99.2 | 797 | 0.606 (0.029) | 98.7 | 795 |
| 400 | 0.579 (0.048) | 99.4 | 399 | 0.606 (0.043) | 99.3 | 399 |
| 200 | 0.557 (0.062) | 99.3 | 199 | 0.617 (0.057) | 99.3 | 199 |
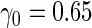 | ||||||
| 1600 | 0.597 (0.027) | 86.0 | 1488 | 0.603 (0.024) | 68.3 | 1346 |
| 800 | 0.589 (0.036) | 93.2 | 773 | 0.606 (0.033) | 82.0 | 728 |
| 400 | 0.579 (0.050) | 95.9 | 392 | 0.607 (0.045) | 89.0 | 378 |
| 200 | 0.556 (0.063) | 97.8 | 198 | 0.617 (0.058) | 95.1 | 195 |
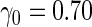 | ||||||
| 1600 | 0.597 (0.029) | 39.6 | 1117 | 0.601 (0.026) | 9.8 | 878 |
| 800 | 0.590 (0.038) | 68.0 | 672 | 0.602 (0.036) | 37.7 | 551 |
| 400 | 0.581 (0.051) | 83.0 | 366 | 0.610 (0.047) | 62.5 | 325 |
| 200 | 0.556 (0.065) | 92.5 | 193 | 0.618 (0.062) | 82.1 | 182 |
We now compare the performances of the proposed estimate with and without parametric distribution specification. We let  , and
, and
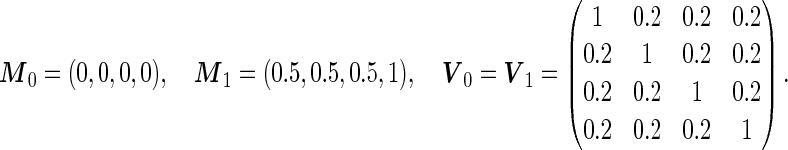 |
With this data structure, the optimal risk model has 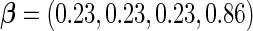 , and
, and 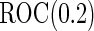 is 0.602. We applied both the logistic regression approach and the parametric bootstrap approach to the simulated datasets. Simulation results of
is 0.602. We applied both the logistic regression approach and the parametric bootstrap approach to the simulated datasets. Simulation results of 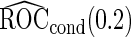 based on
based on 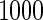 replications are summarized in Table 2. With both approaches,
replications are summarized in Table 2. With both approaches, 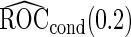 provides estimates that are close to the true value when sample size is large. As sample size decreases, both approaches are associated with some bias. However, this bias is larger with the logistic regression approach as expected, as
provides estimates that are close to the true value when sample size is large. As sample size decreases, both approaches are associated with some bias. However, this bias is larger with the logistic regression approach as expected, as 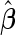 from logistic regression is more sensitive to small sample sizes. Standard errors are smaller with parametric approach in all scenarios. This leads to a lower continuation rate when
from logistic regression is more sensitive to small sample sizes. Standard errors are smaller with parametric approach in all scenarios. This leads to a lower continuation rate when 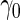 is high, which is desirable as more samples will be saved.
is high, which is desirable as more samples will be saved.
Simulation results with unequal variances based on 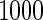 replications are summarized in Table 3. Here, we generated data similarly as in the equal variance scenario, but let
replications are summarized in Table 3. Here, we generated data similarly as in the equal variance scenario, but let
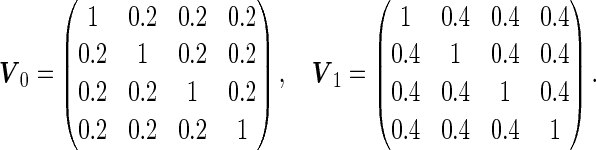 |
Table 3.
Simulation results on 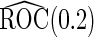 comparing logistic regression approach and parametric bootstrap approach, with unequal variances. True
comparing logistic regression approach and parametric bootstrap approach, with unequal variances. True 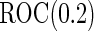 is
is 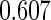
| Logistic regression approach |
Parametric bootstrap approach |
|||||
|---|---|---|---|---|---|---|
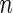 |
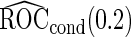 (se) (se) |
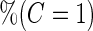 |
 Samples Samples |
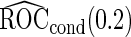 (se) (se) |
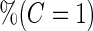 |
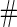 Samples Samples |
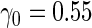 | ||||||
| 1600 | 0.583 (0.024) | 99.9 | 1599 | 0.610 (0.020) | 99.9 | 1599 |
| 800 | 0.577 (0.033) | 100.0 | 800 | 0.618 (0.028) | 99.7 | 799 |
| 400 | 0.565 (0.047) | 99.8 | 400 | 0.636 (0.037) | 98.8 | 398 |
| 200 | 0.540 (0.066) | 99.6 | 200 | 0.669 (0.047) | 98.9 | 199 |
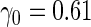 | ||||||
| 1600 | 0.583 (0.024) | 97.8 | 1582 | 0.610 (0.020) | 96.5 | 1572 |
| 800 | 0.577 (0.033) | 98.1 | 792 | 0.618 (0.028) | 95.2 | 781 |
| 400 | 0.565 (0.047) | 98.6 | 397 | 0.636 (0.038) | 94.7 | 389 |
| 200 | 0.540 (0.067) | 98.3 | 198 | 0.670 (0.048) | 95.6 | 196 |
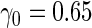 | ||||||
| 1600 | 0.584 (0.026) | 75.0 | 1400 | 0.610 (0.022) | 70.2 | 1362 |
| 800 | 0.577 (0.035) | 87.5 | 750 | 0.618 (0.029) | 75.5 | 702 |
| 400 | 0.565 (0.049) | 93.3 | 387 | 0.636 (0.040) | 79.9 | 360 |
| 200 | 0.540 (0.069) | 95.4 | 195 | 0.669 (0.050) | 86.8 | 187 |
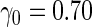 | ||||||
| 1600 | 0.582 (0.028) | 22.0 | 976 | 0.613 (0.023) | 23.7 | 990 |
| 800 | 0.576 (0.038) | 54.1 | 616 | 0.617 (0.032) | 35.6 | 542 |
| 400 | 0.565 (0.051) | 77.6 | 355 | 0.636 (0.043) | 49.0 | 298 |
| 200 | 0.541 (0.070) | 87.7 | 188 | 0.669 (0.053) | 67.8 | 168 |
Under this data structure, the true ROC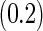 is 0.607. As expected,
is 0.607. As expected, 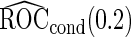 in logistic regression approach is biased even when sample size is large, while with the binormal parametric approach bias is negligible with large sample size. As sample size decreases, neither approach provides satisfactory estimates, as logistic regression approach suffers from both model mis-specification and parameter estimation bias with small sample size, and the parametric approach depends on the accuracy of binormal model parameter estimates. Standard errors are smaller with the parametric approach, which also leads to lower continuation rate with high
in logistic regression approach is biased even when sample size is large, while with the binormal parametric approach bias is negligible with large sample size. As sample size decreases, neither approach provides satisfactory estimates, as logistic regression approach suffers from both model mis-specification and parameter estimation bias with small sample size, and the parametric approach depends on the accuracy of binormal model parameter estimates. Standard errors are smaller with the parametric approach, which also leads to lower continuation rate with high 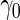 .
.
In summary, our proposed 2-stage design has the highest potential to save samples when the total planned sample size is large. In our various simulation settings, we can save up to 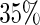 of available samples. When the total sample size is relatively small, the number of samples saved from this 2-stage design is limited regardless, and it might be preferable to use the fixed-sample design. Conditional estimators of the performance parameters are accurate and efficient.
of available samples. When the total sample size is relatively small, the number of samples saved from this 2-stage design is limited regardless, and it might be preferable to use the fixed-sample design. Conditional estimators of the performance parameters are accurate and efficient.
4. Prostate cancer biomarker application
In this section, we apply the proposed group sequential design and the estimators to a multi-center EDRN prostate cancer biomarker validation study. Prostate Specific Antigen (PSA) is widely used for prostate cancer screening, but has limited sensitivity and specificity. Prostate Cancer Antigen 3 (PCA3) is a urinary biomarker that is approved by the Food and Drug Administration as a risk assessment biomarker of prostate cancer. The objective of this study is to examine the performance improvement from adding PCA3 to the standard clinical PSA biomarker in detecting high-grade prostate cancer (i.e. Gleason score 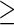 7). Since most low-grade prostate cancer are indolent, a reliable mean of distinguishing between low- and high-grade prostate cancers may allow some patients to avoid biopsies and other invasive treatments such as radical prostatectomy.
7). Since most low-grade prostate cancer are indolent, a reliable mean of distinguishing between low- and high-grade prostate cancers may allow some patients to avoid biopsies and other invasive treatments such as radical prostatectomy.
This study includes 859 men from 11 EDRN centers who are scheduled for a prostate biopsy due to some previous prostate cancer related indications. Among these patients, 562 patients were presenting for their initial biopsy, while the other 297 patients had a prior negative biopsy. PSA and PCA3 measures were taken prior to biopsy. Gleason scores were assessed by pathologists at each clinical center based on biopsy samples. We analyze the initial biopsy patients and the repeat biopsy patients separately. Since these patients were scheduled for biopsy for indications related to prostate cancer, we want the combined biomarker test to have high sensitivity to avoid missing high-grade prostate cancer, while improving specificity so that more low-grade patients can avoid biopsy and treatment. Hence we use 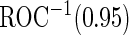 to evaluate the performance of combined test. Both PSA and PCA3 measures are log-transformed to achieve approximate normality in both the high-grade and low-grade groups.
to evaluate the performance of combined test. Both PSA and PCA3 measures are log-transformed to achieve approximate normality in both the high-grade and low-grade groups.
When we use PSA to distinguish high- and low-grade prostate cancer patients, 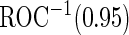 is 0.144 for the initial biopsy group and 0.149 for the repeat biopsy group. With PCA3 only, it is 0.235 and 0.406, respectively. PCA3 is a somewhat better marker to use in clinical practice, compared with PSA. To investigate if combining PSA and PCA3 will improve performance, we use the higher performance of the 2 biomarkers applied individually as the minimal acceptance criteria, that is
is 0.144 for the initial biopsy group and 0.149 for the repeat biopsy group. With PCA3 only, it is 0.235 and 0.406, respectively. PCA3 is a somewhat better marker to use in clinical practice, compared with PSA. To investigate if combining PSA and PCA3 will improve performance, we use the higher performance of the 2 biomarkers applied individually as the minimal acceptance criteria, that is 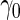 equals to 0.235 and 0.406 for the 2 patient groups. For each biopsy group, we randomly assign half of the patients to stage 1. Results are summarized in Table 4.
equals to 0.235 and 0.406 for the 2 patient groups. For each biopsy group, we randomly assign half of the patients to stage 1. Results are summarized in Table 4.
Table 4.
Estimates of 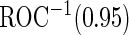 for the PSA, PCA3 and their combinations
for the PSA, PCA3 and their combinations
| Biomarkers | 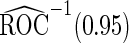 |
|
|---|---|---|
| Initial biopsy group | ||
| PSA | 0.144 (0.069, 0.201) | |
| PCA3 | 0.235 (0.129, 0.295) | |
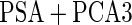 |
Logistic regression approach | Parametric bootstrap approach |
| Stage 1 | 0.353 (0.174, 0.580) | 0.362 (0.307, 0.441) |
| Stage 2 | 0.315 (0.154, 0.526) | 0.282 (0.238, 0.347) |
| Conditional | 0.324 (0.255, 0.418) | 0.319 (0.241, 0.370) |
| Repeat biopsy group | ||
| PSA | 0.149 (0.103, 0.322) | |
| PCA3 | 0.406 (0.284, 0.539) | |
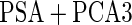 |
Logistic regression approach | Parametric bootstrap approach |
| Stage 1 | 0.639 (0.327, 0.746) | 0.582 (0.513, 0.632) |
| Stage 2 | 0.480 (0.122, 0.727) | 0.380 (0.295, 0.437) |
| Conditional | 0.509 (0.395, 0.692) | 0.494 (0.408, 0.672) |
For the initial biopsy group, we first use the logistic regression approach. Stage 1 data suggests an improved performance by combining PSA with PCA3, with estimated 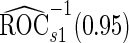 equal to 0.353 and confidence interval covering 0.235, and
equal to 0.353 and confidence interval covering 0.235, and 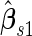 is
is 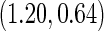 . Thus, the study continues to stage 2. Upon completion of stage 2, we estimate
. Thus, the study continues to stage 2. Upon completion of stage 2, we estimate 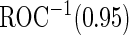 as 0.315 if only using stage 2 data, and 0.324 if using the conditional estimate. The corresponding
as 0.315 if only using stage 2 data, and 0.324 if using the conditional estimate. The corresponding 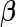 estimates are
estimates are 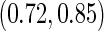 and
and 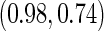 . Note that
. Note that 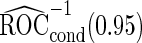 has a much narrower confidence interval than that of
has a much narrower confidence interval than that of 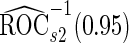 . In addition, note that
. In addition, note that 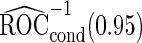 is between
is between 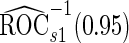 and
and 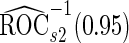 . Although in theory we would expect both
. Although in theory we would expect both 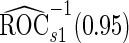 and
and 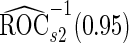 to be unbiased estimates of
to be unbiased estimates of 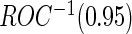 , they may not be accurate enough in practice with limited sample size. Under this situation, using
, they may not be accurate enough in practice with limited sample size. Under this situation, using 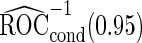 reduces bias due to the resampling stage
reduces bias due to the resampling stage 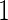 and
and 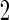 data in the outer bootstrap steps, and is expected to have more stable performance. We also investigated the parametric bootstrap approach. The sample covariance matrices are slightly different for the 2 outcome groups, so we allowed for unequal variances. The estimated
data in the outer bootstrap steps, and is expected to have more stable performance. We also investigated the parametric bootstrap approach. The sample covariance matrices are slightly different for the 2 outcome groups, so we allowed for unequal variances. The estimated 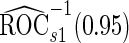 and
and 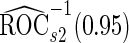 differ slightly from those from logistic regression approach, with narrower confidence intervals.
differ slightly from those from logistic regression approach, with narrower confidence intervals. 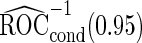 is quite similar to that with logistic regression approach, but again with a narrower confidence interval. This also suggests that a linear combination is likely to be suitable for these 2 biomarkers. Similar analysis were conducted for the repeat biopsy group. With randomly selected stage 1 data, both approaches suggests continuing to stage 2. Upon study completion, we estimate
is quite similar to that with logistic regression approach, but again with a narrower confidence interval. This also suggests that a linear combination is likely to be suitable for these 2 biomarkers. Similar analysis were conducted for the repeat biopsy group. With randomly selected stage 1 data, both approaches suggests continuing to stage 2. Upon study completion, we estimate 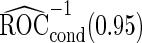 as 0.509 and
as 0.509 and 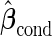 as
as 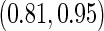 with the logistic regression approach and
with the logistic regression approach and 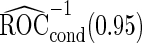 as 0.494 with the parametric bootstrap approach. Again, estimates from the parametric bootstrap approach is associated with a narrower confidence interval.
as 0.494 with the parametric bootstrap approach. Again, estimates from the parametric bootstrap approach is associated with a narrower confidence interval.
5. Discussion
Cost-effective designs are urgently needed for biomarker studies, as the number of biomarkers potentially useful in clinical practice has increased dramatically with technology developments. Group sequential methods have a natural place due to this early termination for futility possibility. Previous literature has discussed the use of a group sequential strategy for inference upon study completion with a single biomarker. In this manuscript, we extended existing methods to a phase 2 biomarker panel development study. We described a 2-stage study design, and proposed conditional estimators that take early termination into account. Although this 2-stage design has already been used in EDRN to conserve samples and minimize cost, its properties and the corresponding estimators following study completion have not been studied systematically. We compared this study design with fixed-sample design and a previously proposed 2-stage design that does not allow for updating the risk model. The proposed design has the ability to save samples when candidate biomarkers are not promising, while providing an efficient conditional estimate of performance when they are promising.
Resampling procedures are typically needed to calculate the proposed conditional estimates. In this manuscript, we provided an alternative approach if a multivariate binormal distribution can be assumed. As mentioned, our method also applies to other families of parametric distributions. Under parametric assumptions, one can expect the performance parameter estimates to be more efficient, and computational burden may be reduced.
Here, we restricted the application to a relatively small number of biomarkers. This is of practical importance for studies focusing on biomarkers that have strong evidence for use in clinical practice. Hence we defined the rejection criterion in terms of the 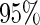 confidence interval, which is lenient in order not to miss potentially useful panels. In other situations where the potential utility of candidate markers not evident, we could use a stricter criterion, for example, by considering an approach similar to that of the Koopmeiners and Vogal approach, i.e. terminating the study when the point estimate is below a pre-specified threshold. Then we only need to modify how we define
confidence interval, which is lenient in order not to miss potentially useful panels. In other situations where the potential utility of candidate markers not evident, we could use a stricter criterion, for example, by considering an approach similar to that of the Koopmeiners and Vogal approach, i.e. terminating the study when the point estimate is below a pre-specified threshold. Then we only need to modify how we define 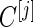 in the outer bootstrap procedure, and all the other steps will follow.
in the outer bootstrap procedure, and all the other steps will follow.
When the candidate panel is of high-dimensional, one needs to consider model selection procedures. Our proposed 2-stage design can be extended for use in conjunction with dimension reduction. For example, we can replace the logistic regression model with a LASSO model (Tibshirani, 1996) in both stages 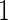 and
and 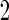 . For studies that continue to study completion, extra steps are needed to obtain conditional estimators of performance parameters. That is, when we perform the outer bootstrap procedure, different biomarkers can be selected each time. At the end of bootstrap replications, we may consider selecting the final model by restricting to those markers that appear enough number of times in the bootstrap replications. This selection needs to be taken into account in the conditional estimators. The methods for doing so are beyond the scope of this paper but well worth exploring. In the simulation, we compared our results with the Koopmeiners and Vogel approach. In the setting of validating a small number of markers with strong evidence, the Koopmeiners and Vogel approach suffers from high rejection rate and may not efficiently use all information. However, under a higher-dimensional panel setting of their original proposal, their approach is easy to use and performs well.
. For studies that continue to study completion, extra steps are needed to obtain conditional estimators of performance parameters. That is, when we perform the outer bootstrap procedure, different biomarkers can be selected each time. At the end of bootstrap replications, we may consider selecting the final model by restricting to those markers that appear enough number of times in the bootstrap replications. This selection needs to be taken into account in the conditional estimators. The methods for doing so are beyond the scope of this paper but well worth exploring. In the simulation, we compared our results with the Koopmeiners and Vogel approach. In the setting of validating a small number of markers with strong evidence, the Koopmeiners and Vogel approach suffers from high rejection rate and may not efficiently use all information. However, under a higher-dimensional panel setting of their original proposal, their approach is easy to use and performs well.
Our proposed 2-stage design and conditional estimators can be extended to assess the performance of a biomarker panel when outcome is a censored failure time. Instead of a disease indicator 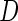 , the outcome is
, the outcome is 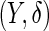 , where
, where  is the minimum of the actual event time
is the minimum of the actual event time 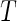 and the independent censoring time
and the independent censoring time 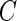 , and
, and 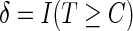 . At a specific time point
. At a specific time point 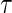 , we can define a binary outcome
, we can define a binary outcome 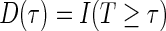 . With censoring present, a logistic regression with inverse probability weighting can be used as discussed in Zheng and others (2006): subjects censored before
. With censoring present, a logistic regression with inverse probability weighting can be used as discussed in Zheng and others (2006): subjects censored before 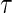 will have weight
will have weight  , subjects having events before
, subjects having events before 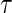 are weighted by
are weighted by 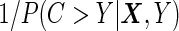 , and those still at risk at
, and those still at risk at 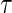 are weighted by
are weighted by 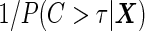 . With the 2-stage design, we can replace the standard logistic regression with this re-weighted logistic regression in Step B of the inner bootstrap procedure. The probability in the weighting can be estimated as described in Zheng and others (2006), with the data from current cohort under investigation. The conditional estimators can be applied with a valid
. With the 2-stage design, we can replace the standard logistic regression with this re-weighted logistic regression in Step B of the inner bootstrap procedure. The probability in the weighting can be estimated as described in Zheng and others (2006), with the data from current cohort under investigation. The conditional estimators can be applied with a valid 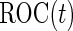 estimate in each stage.
estimate in each stage.
Supplementary material
Supplementary Material is available at http://biostatistics.oxfordjournals.org.
6. Funding
This work was supported by grants U01-CA86368, P01-CA053996, R01-GM085047 awarded by the National Institutes of Health.
Supplementary Material
Acknowledgement
Conflict of Interest: None declared.
References
- Copas J. B., Corbett P. (2002). Overestimation of the receiver operating characteristic curve for logistic regression. Biometrika 89, 315–331. [Google Scholar]
- Cordeiro G. M., McCullagh P. (1991). Bias correction in generalized linear models. Journal of the Royal Statistical Society B 53, 629–643. [Google Scholar]
- Koopmeiners J. S., Feng Z., Pepe M. S. (2012). Conditional estimation after a two-stage diagnostic biomarker study that allows early termination for futility. Statistics in Medicine 31, 420–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koopmeiners J. S., Vogel R. I. (2013). Early termination of a two-stage study to develop and validate a panel of biomarkers. Statistics in Medicine 32, 1027–1037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntosh M. W., Pepe M. S. (2002). Combining several screening tests: optimality of the risk score. Biometrics 58, 657–664. [DOI] [PubMed] [Google Scholar]
- Pepe M. S., Etzioni R., Feng Z., Potter J. D., Thompson M. L., Thornquist M., Winget M., Yasui Y. (2001). Phases of biomarker development for early detection of cancer. Journal of the National Cancer Institute 93, 1054–1061. [DOI] [PubMed] [Google Scholar]
- Pepe M. S., Feng Z., Longton G., Koopmeiners J. S. (2009). Conditional estimation of sensitivity and specificity from a phase 2 biomarker study allowing early termination for futility. Statistics in Medicine 28, 762–779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R. (1996). Regression shrinkage and selection via the LASSO. Journal of the Royal Statistical Society B 58, 267–288. [Google Scholar]
- Zheng Y., Cai T., Feng Z. (2006). Application of the time-dependent (ROC) curves for prognostic accuracy with multiple biomarkers. Biometrics 62, 279–287. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


