Thermodynamics of Long Supercoiled Molecules: Insights from Highly Efficient Monte Carlo Simulations

Abstract

Supercoiled DNA polymer models for which the torsional energy depends on the total twist of molecules (Tw) are a priori well suited for thermodynamic analysis of long molecules. So far, nevertheless, the exact determination of Tw in these models has been based on a computation of the writhe of the molecules (Wr) by exploiting the conservation of the linking number, $\text{Lk}=\text{Tw}+\text{Wr}$, which reflects topological constraints coming from the helical nature of DNA. Because Wr is equal to the number of times the main axis of a DNA molecule winds around itself, current Monte Carlo algorithms have a quadratic time complexity, $O\left(L^2\right)$, with respect to the contour length (L) of the molecules. Here, we present an efficient method to compute Tw exactly, leading in principle to algorithms with a linear complexity, which in practice is $O\left(L^{1.2}\right)$. Specifically, we use a discrete wormlike chain that includes the explicit double-helix structure of DNA and where the linking number is conserved by continuously preventing the generation of twist between any two consecutive cylinders of the discretized chain. As an application, we show that long (up to 21 kbp) linear molecules stretched by mechanical forces akin to magnetic tweezers contain, in the buckling regime, multiple and branched plectonemes that often coexist with curls and helices, and whose length and number are in good agreement with experiments. By attaching the ends of the molecules to a reservoir of twists with which these can exchange helix turns, we also show how to compute the torques in these models. As an example, we report values that are in good agreement with experiments and that concern the longest molecules that have been studied so far (16 kbp).

Introduction

The folding properties of DNA are strongly constrained by the physical intricacy of its strands. In a situation of torsional stress, this induces the polymer to curl up for complementary bases to properly face each other. As a result, when DNA molecules are underwound (negative supercoiling) or overwound (positive supercoiling), so-called plectonemes form (Fig. 1). Although these properties have important implications both for the physics of single molecules (1,2) and for our understanding of DNA biology (3), several aspects have remained elusive, especially for long molecules that exceed 10 kilobasepairs (kbp). A proper modeling of DNA that can handle multiple scales, from the kbp scale (gene scale) to a scale of hundreds of kbp, is nevertheless a strong requirement for improving our capacity to model biological systems (4), more particularly to rationalize the impact of chromosome structuring on the functioning of cells (5).

Figure 1.

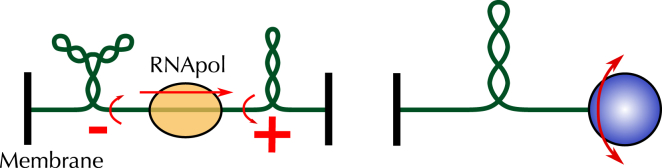
Torsionally induced super-structuring of DNA molecules. (Left) In vivo, plectonemes, which can be branched, occur because, e.g., of the activity of RNA polymerases and of the anchoring of DNA to the membrane (52). (Right) Topological constraints are exerted in vitro by keeping one end of a molecule fixed and adding helix turns at the other end, thanks to magnetic tweezers (9). To see this figure in color, go online.

The fact that local properties of double-stranded DNA can be accommodated only via a global folding of the molecule stems from the existence of a topological invariant, the linking number (Lk), which occurs both for circular molecules and for linear molecules whose ends cannot rotate (Fig. 1). Namely, the conservation of Lk imposes that the variation of the twist (Tw) be equal to the opposite variation of the writhe (Wr):

$$\text{Lk}=\text{Tw}+\text{Wr},$$ (1)

with Tw reflecting the torsional properties of the molecule and Wr its global geometry (see below) (6).

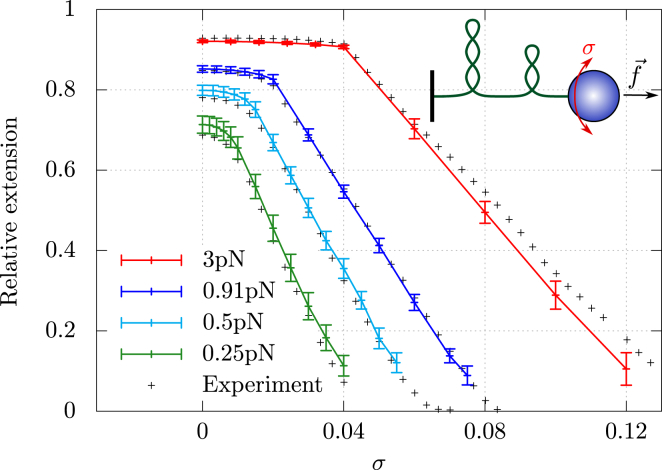
Direct information about the conformations of supercoiled molecules was first provided by numerical simulations of circular molecules (1). Deep insights have then been provided at the single-molecule level thanks to magnetic tweezers experiments (7–9). In these experiments, one end of the molecule is maintained fixed, whereas the other end is tethered to a superparamagnetic bead that can be rotated using small magnets (see Figs. 1 and 4). The end-to-end extension of the molecule is measured as a function of the stretching force, f, applied to the molecule and of the number of turns of the magnetic bead, that is, as a function of the supercoiling density, $\sigma =\left(\text{Lk}-{\text{Lk}}_0\right)/{\text{Lk}}_0$, where ${\text{Lk}}_0$ is the linking number of the molecule at rest. The formation of plectonemes is then monitored indirectly by a distinctive diminution of the extension as σ varies (10–12) (see Fig. 4).

Figure 4.

Simulating long supercoiled molecules. Relative extension of a simulated 16 kbp DNA molecule (533 cylinders) as a function of σ for different stretching forces, with $C=86$ nm, $l_{\text{p}}=50$ nm, and $r_{\text{e}}=2$ nm $\left(\left[\text{NaCl}\right]=100\text{mM}\right)$. Bars indicate the mean ± SD over four simulations of 10⁷ iterations. Black crosses represent experimental results (11), where one end of the molecule is kept fixed and the other end is manipulated by magnetic tweezers (upper right), allowing to add helix turns to the molecule and to stretch it. To see this figure in color, go online

Several theoretical models have been able to reproduce with good accuracy the mean extension of these molecules (2,13–15). Nevertheless, predictions differ in the numbers of plectonemes and in the types of structures that are able to form (14,15). Apparently incompatible reports have also raised important questions about the proper way to measure the torques these molecules can exert (15). Recently, structural predictions have been compared to experiments that combine magnetic tweezers with fluorescent staining of DNA, allowing direct visualization of the formation and dynamics of plectonemes (16). In these experiments, multiple plectonemes were observed to form in a wide range of forces and supercoiling densities, putting some important constraints on the outcomes of models.

Polymer simulations are expected to provide deep insights into the problem. In this regard, Monte Carlo (MC) methods are particularly well adapted to investigate thermodynamic properties of supercoiled molecules and, in particular, to rationalize single-molecule experiments (17–19). To this end, DNA is modeled as a wormlike chain (WLC) and the WLC is simulated by discretizing the chain into a succession of rigid segments that include bending and torsional energies (1). In the spirit of Brownian dynamics (20–22), a torsional energy can then be defined locally using Euler angles between local frames associated to the segments, with, in particular, the possibility of measuring the torques these molecules can exert (18,19). In this case, a local twist can be defined between any two consecutive segments as the sum of the local Euler angles, providing an approximation of the exact twist that is all the better when torsional angles are small (18,20,21).

The torsional energy can also be defined globally, as a function of the total twist of the molecule (17,23,24), with the advantage of leading to much smaller relaxation times (25) (see below). In this case, the exact twist can be computed by using the topological relationship $\text{Tw}=\text{Lk}-\text{Wr}$ (17,23,25); Lk is then constrained to remain constant during the simulation (topological constraint), and Wr, which is a geometrical property solely of the main axis of the molecule, is computed at every iteration. As Wr is a double integral over this main axis (26), the corresponding algorithms have nevertheless a quadratic time with respect to the contour length (L) of the polymer, making them poorly adapted for investigating thermodynamic properties of long (e.g., >10 kbp) molecules. Moreover, in contrast to models with local torsional energies (18,19), torque computation has remained an open issue in these models.

Here, we propose, to our knowledge, a novel treatment of the topological properties of WLC-based DNA models by including an explicit representation of the double-helix, which allows an easy exact computation of Tw. As a result, we obtain a highly efficient MC algorithm that both relies on a global torsional energy and features a theoretical linear time complexity, $O\left(L\right)$, which in practice is $O\left(L^{1.2}\right)$. Our approach also provides a basis for computing torques in models with global torsional energies. As an application, we study the thermodynamic properties of 16 kbp (11) and 21 kbp long molecules (16), which are the longest molecules that have been exhaustively investigated so far.

Materials and Methods

The self-avoiding supercoiled wormlike chain with a global torsional energy

Our model is based on the self-avoiding supercoiled wormlike chain (sWLC) introduced by Vologodskii and collaborators (23,27), which has been successfully used in the context of magnetic tweezers experiments to rationalize extension curves and to provide structural aspects of small molecules (17). In this model, self-avoidance of the chain simplifies the treatment of the short-range electrostatic repulsions of DNA at the cost, nevertheless, of introducing an effective radius that cannot be determined directly experimentally and that is related to the second virial coefficient of the sWLC (25). Here, in accord with recent Brownian dynamics studies (28), best results were obtained over a wide range of experimental conditions by considering an effective radius, $r_e$, that is given by $r_e=r_0+{\lambda }_D$; $r_0=1$ nm is the radius of the DNA double-helix (B-form) and $\lambda \simeq 10/\sqrt{\left[\text{NaCl}\right]}$, with $\left[\text{NaCl}\right]$ in mM, and λ in nm corresponding to the Debye screening length for an aqueous solution of NaCl at room temperature (29). In the sWLC model, the conformational energy of the chain reads

$$E=E_{\text{b}}+E_{\text{t}}+E_{\text{s}},$$ (2)

with $E_{\text{b}}$, $E_{\text{t}}$, and $E_{\text{s}}$ the energies of bending, torsion, and stretching, respectively. The bending energy is given by $E_{\text{b}}=K/2{\int }_0^L{\left({\partial }_{\text{s}}\overrightarrow{t}\right)}^{2}ds$, where $\overrightarrow{t}\left(s\right)$ is the vector tangent to the chain at the curvilinear abscissa s and K is the bending modulus that defines the persistence length: $l_{\text{p}}=K/k_{\text{B}}T$. The stretching energy is given by $E_{\text{s}}=-fz$, where z is the molecular extension along the direction of the stretching force, f.

Strictly speaking, the torsional energy should be given by $E_{\text{t}}=2{\pi }^2{k}_{\text{B}}TC{\int }_0^L{\left(\tau \left(s\right)-{\tau }_0\right)}^{2}ds$, with C the torsional modulus and $\tau \left(s\right)$ the local twist of the molecule, that is, the number of times per unit of contour length that the DNA helix turns around its main axis, ${\tau }_0$ being the corresponding value at rest (0.29 turns/nm for the B-form of DNA). Nevertheless, $E_{\text{t}}$ can be decomposed as the sum of two terms: $2{\pi }^2{k}_{\text{B}}TC{\left(\text{Tw}-{\text{Tw}}_0\right)}^2/L$, which reflects the cost of having a total twist, Tw, different from that at rest $\left({\text{Tw}}_0\right)$, plus a term accounting for the fluctuations around Tw. The latter term can then be dropped without affecting the folding properties of DNA, with the advantage of drastically reducing the sWLC equilibration time (17,24). As a result, we use a sWLC for which the torsional energy is a function of the total twist (Tw) only:

$$E_{\text{t}}=2{\pi }^2{k}_{\text{B}}TC{\left(\text{Tw}-{\text{Tw}}_0\right)}^2\text{/}L.$$ (3)

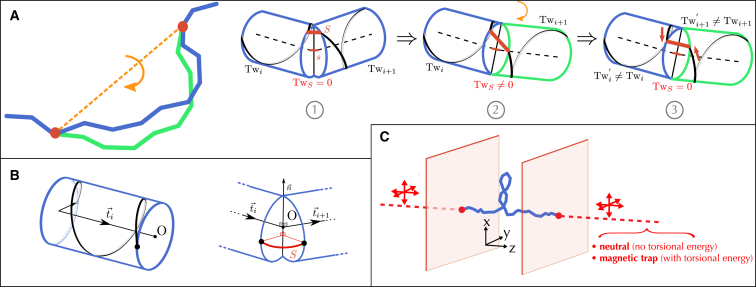
Provided a discretization of the polymer chain into a string of cylinders articulated by pivots (Fig. 2 A), the folding of the sWLC can then be simulated using an MC algorithm, with thermodynamic equilibrium being achieved through numerous block rotations of contiguous cylinders. In a typical algorithm (25), an elementary motion consists of 1) randomly drawing two pivots and 2) rotating the corresponding cylinders around the axis joining the pivots (crankshaft rotation; Fig. 2 A) or 1) drawing one pivot and 2) rotating the cylinders between the pivot and one end around a random axis, which modifies the extension of the molecule. Should the rotation not lead to an overlap (self-avoidance constraint), it is accepted with a probability that depends on the variation of the total energy, $\text{Δ}{E}_{\text{b}}+\text{Δ}{E}_{\text{t}}+\text{Δ}{E}_{\text{s}}$, and that verifies detailed balance conditions—for a linear molecule, the topological constraint akin to the action of magnetic tweezers is further imposed by forbidding the chain to go beyond the end points along the direction of the stretching force (Fig. 2 C) (17).

Figure 2.

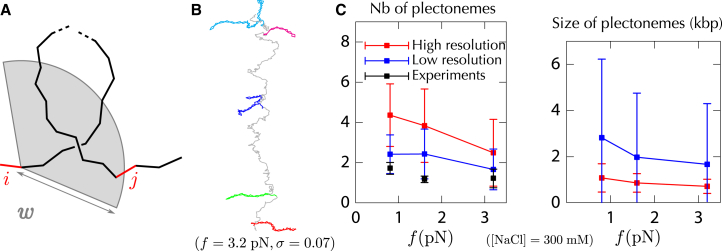
A local MC algorithm for simulating supercoiled molecules. (A) (Left) In the discrete version of the sWLC, a rotation of a block of cylinders (green) changes the relative direction of the pairs of cylinders that are on each side of the pivots (red). (Right) (1) In our algorithm, every cylinder, i, is allocated with a twist, ${\text{Tw}}_i$, that is equal to the helicoidal winding of the strands (one strand is indicated in black). Schematically, pivots correspond to infinitesimal segments (red s) that connect the main axis of the pivot cylinders (dashed lines). Strand continuity between contiguous cylinders is then ensured by using a junction segment (red S) that is kept parallel with s such that S does not contribute to the overall twist $\left({\text{Tw}}_S=0\right)$ (see B for further details). (2) A rotation misaligns S with respect to s, generating some twist, ${\text{Tw}}_S\ne 0$. (3) As indicated by the red arrows, ${\text{Tw}}_S=0$ is recovered by displacing the end and start positions of the strands around the pivot such that S remains parallel to s, which results in a variation of the length of the strands in each pivot cylinder. The corresponding twist variations within each cylinder and, hence, the corresponding variation of the writhe can thus be easily computed, leading to an algorithm with a theoretical linear time complexity (see main text). (B) In practice, a junction strand, S, corresponds to a piece of strand that connects the end and start points (black points) of the strands associated to two consecutive cylinders—to this end, we use additional coordinates to mark the entry and exit points of the helix of every cylinder. The junction strand is constrained to remain within a plane that is parallel to the plane defined by the main axis of the two cylinders, ${\overrightarrow{t}}_i$ and ${\overrightarrow{t}}_{i+1}$. To this end, the start point of the strand in $i+1$ is obtained by rotation of the end point in i around the axis $\left(\text{O},\overrightarrow{n}\right)$, with O the intersection of the main axis and $\overrightarrow{n}={\overrightarrow{t}}_i\wedge {\overrightarrow{t}}_{i+1}$. Junction strands, although ensuring the continuity of the molecule, do not thus generate any twist, because they remain parallel to the main axis of the molecule. (C) For linear open chains (blue), the conservation of the linking number is implemented by closing the chain at infinity. To this end, we consider at each end of the molecule an infinitely long cylinder (dashed red lines). These external cylinders cannot rotate; they can only translate, as indicated by the red arrows, to follow the motion of the end pivots (red spheres). As originally discussed by Vologodskii and Marko (17), this framework makes it possible to properly handle the conservation of the linking number by associating the well-defined linking number of the closed, infinitely long chain to that of the open chain, which is otherwise ill-defined. To ensure the conservation of this linking number, we further prevent the open chain from crossing the virtual cylinders. In practice, we prevent the open chain from going beyond the end points along the z-axis, as indicated here by the two red walls (the same hard-wall boundary condition was implemented as well in Vologodskii and Marko (17)). Very interestingly, the use of external cylinders further opens the possibility to compute, in a direct way, the torques that are exerted by the open chain. To this end, a torsional energy, characterized by a torsional stiffness, is associated to the excess twist that is transferred from the end cylinders of the open chain to the external cylinders. By losing their torsional neutrality, external cylinders thus behave as magnetic traps, which can be used to investigate the torsional response of the open chain (see Torque measurements for further details). To see this figure in color, go online.

Using this MC algorithm, one can first compare the capacity of different polymer models to reach equilibrium, depending on whether a global (Eq. 3) or a local $\left(2{\pi }^2{k}_{\text{B}}TC{\int }_0^L{\left(\tau \left(s\right)-{\tau }_0\right)}^{2}ds\right)$ torsional energy is used. In this regard, we observe that both types of models reach equilibrium within a similar number of iterations for small (2.2 kbp) molecules equivalent to those reported experimentally by Forth and colleagues (10,30) or to those reported numerically by Schöpflin and colleagues (18,19) (Fig. S1, left column, in the Supporting Material). By contrast, and in accord with previous results (25), for long (21 kbp) molecules similar to those investigated in van Loenhout et al. (16), compared to global torsional energy models, local torsional energy models converge much more slowly with, in particular, the presence of long-living metastable states that prevent the system from reaching equilibrium during simulation runs (Fig. S1, right column).

Although global torsional energy models are efficient to reach equilibrium, their time complexity, that is, the effective amount of time needed for MC algorithms to perform a given number of elementary motions, has been limited by the twist computation. Specifically, $\text{Δ}{E}_{\text{s}}$ is efficiently computed by measuring the extension of the molecule. Likewise, computing $\text{Δ}{E}_{\text{b}}$ is fast, since it involves only the cylinders located on each side of the pivots, referred to as pivot cylinders in the sequel. In contrast, computing $\text{Δ}{E}_{\text{t}}$ has remained costly, since for these models the exact total twist of the molecule has been determined as a function of Wr by taking advantage of the conservation of Lk, leading to a torsional energy that reads $E_{\text{t}}=2{\pi }^2{k}_{\text{B}}TC{\left(\text{Lk}-\text{Wr}\right)}^2\text{/}L$. Since Wr is equal to the number of times the main axis winds around itself, it is then computed as a double integral over this axis (26), hence leading to an algorithm with a quadratic time complexity, $O\left(L^2\right)$ (Fig. 2). Although simplifications have been proposed for folded proteins (31,32), they are not applicable to DNA plectonemes (33).

A local algorithm for the conservation of the linking number

Here, to compute the twist exactly without referring to the writhe, following upon previous studies (34–36), we consider an explicit helical structure along the chain. In contrast to these studies, though, we ensure that the linking number is conserved after each iteration by adjusting the twist in the pivot cylinders such that, for each elementary motion, the twist in the pivots remains equal to zero (Fig. 2). More precisely, we consider DNA strands as being composed of the strands that are associated to the cylinders plus junction strands that ensure continuity between any two consecutive cylinders (Fig. 2, A and B, red S). For each rotation, we then adapt the end and start positions of the strands of consecutive cylinders such that the corresponding junction strands remain parallel to the plane defined by the main axis of the cylinders (Fig. 2 B)—in that sense, our method is reminiscent of the concept of “parallel transport” that has been used to parametrize flexible and twistable rods within the field of discrete rigid-body physics (37). The junction strands do not thus introduce any twist to the molecule. They are used to update the positions of the strands at the ends of the pivot cylinders when they rotate around each other (Fig. 2 A), which in turn modifies the length of the strands in the pivot cylinders and, hence, their twist (Fig. 2 A).

To test that our method ensures that the variation of writhe caused by any rotation is indeed exactly compensated by the variation of twist in the pivot cylinders, we compared the writhe obtained by our direct measurement of Tw, using $\text{Wr}=\text{Lk}-\text{Tw}$, to the exact value obtained from the double integral (26). As a result, we obtained a maximal relative error that was always < ${10}^{-9}$ for both circular and linear molecules, and for all values of σ, f, and $r_{\text{e}}$.

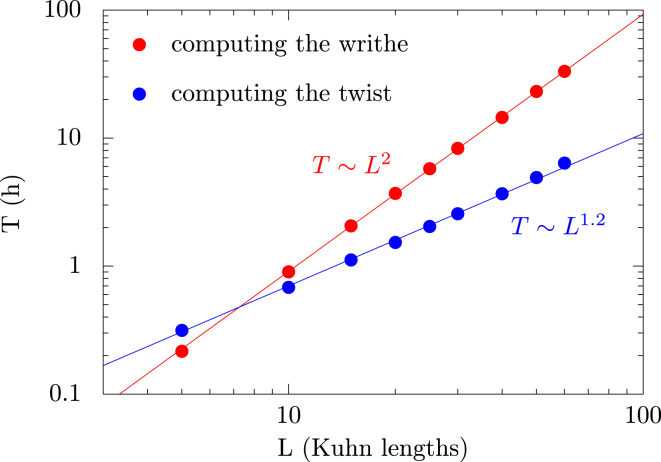
$\text{Δ}{E}_{\text{t}}$ can thus be computed by considering only the pivot cylinders, meaning that the theoretical computational complexity of our algorithm is linear. In practice, we must ensure that the molecule does not cross itself during a rotation. This leads to additional tests that make the execution time scale as $L^{1.2}$ (Fig. 3) but also efficiently prevent the formation of knots, whose detection is otherwise time-consuming, as it scales as $L^3$ (25). More precisely, due to the nature of the crankshaft motions, some cylinders may travel a long distance during an elementary motion (especially those in the middle of a large block) and hence may cross other cylinders along their way. To prevent these events, we determine the surface swept by the cylinders during their rotation and check whether this surface crosses any other cylinder. If this is the case, the rotation is rejected. Although only the cylinders in the vicinity of the surface are checked, as the length of the molecule increases, so does the average size of the blocks and the typical distance traveled by the cylinders. This results in a larger surface and a greater number of verifications, leading to the superlinear scaling of the time complexity of the algorithm (Fig. 3). We note, nevertheless, that for very large molecules, we could limit the maximal size of the blocks and, hence, expect a linear time complexity.

Figure 3.

Algorithm performances. Time T in hours (h) needed to perform 10⁷ block rotations, as a function of the length, L, of the chain, measured in Kuhn lengths $\left(l_{\text{Kuhn}}=2l_{\text{p}}\right)$. Blue dots indicate our algorithm, which consists of computing the twist. Red dots represent the classical algorithm (25), consisting of computing the writhe. Straight lines are the best fits to a power law. To see this figure in color, go online.

In practice, to get the best performances, the number of cylinders should be as small as possible while still yielding accurate results. In accord with previous studies (38), we find that five cylinders per $l_{\text{p}}$ is a good tradeoff for estimating the extension and the torque values; doubling this number has almost no effect on the results (Fig. S2), although the situation is different for computing the structural properties of the plectonemes (see below). Compared to existing softwares, the time required to simulate a 21 kbp molecule, as studied experimentally in the van Loenhout study (16), is then six times shorter. The simulation of a small bacterial chromosome such as that of Mycoplasma genitalium (580 kbp) would be 90 times shorter.

Results and Discussion

Thermodynamics of superstructuration

Numerical simulations have confirmed the ability of short (typically ≤3 kbp) sWLC chains to reproduce the relative extension of long supercoiled molecules (2,25). Here, we first use our MC algorithm to quantitatively confirm that the sWLC provides an excellent model of long supercoiled molecules. To this end, we simulate the folding properties of a 16-kbp-long molecule (533 cylinders in the case of 5 cylinders per $l_{\text{p}}$ ), as studied experimentally in Mosconi et al. (11). We use an effective electrostatic radius $\left(r_{\text{e}}\right)$ that reflects the salt dependence of the Debye screening length (see Methods). The persistence length, $l_{\text{p}}=50$ nm, is estimated from previous single-molecule experiments in the absence of torsion (39), where it was shown to be independent of the salt concentration, provided that $\left[\text{NaCl}\right]>10\text{mM}$. Values of the torsional modules are usually in the range of 80–110 nm (see Mosconi et al. (11) for a discussion); here, we consider $C=86\text{nm}$, which was previously considered to model an experimental salt condition where $\left[\text{NaCl}\right]=100\text{mM}$ (40) (see Fig. 7 for further details).

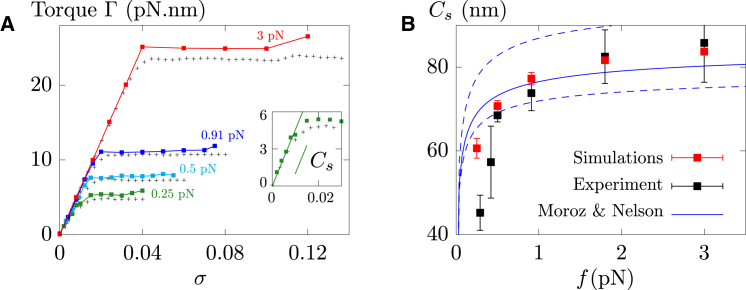
Figure 7.

(A) Direct numerical estimation of the torque, $\text{Γ}$, for different f and σ for a 16 kbp molecule. (Inset) At low forces ( $f=0.25$ pN), our estimation of $C_{\text{s}}$, which is proportional to the slope of $\text{Γ}\left(\sigma \right)$ (44), is consistent with the experimental torques of Mosconi et al. (11). Discrepancies in (B) between experiments and simulations for the estimation of $C_{\text{s}}$ at $f<0.5$ pN are thus likely to be due to a too small number of experimental points. (B) The effective torsional modulus, $C_{\text{s}}$, as a function of f. Simulations were run using $C=86$ nm. The solid blue line represents the large force expansion by Moroz and Nelson (44) using $C=86$ nm. Dashed blue lines show the same expansions but using $C=80$ nm (lower curve) and $C=100$ nm (upper curve), hence justifying the use of $C=86$ nm. The bars indicate the mean ± SE. To see this figure in color, go online.

Using these parameters, we obtain end-to-end extensions that are in excellent agreement with experimental values for most σ and f (Fig. 4). Note, here, that for every point in Fig. 4, we have considered four different simulations where we start from a fully stretched conformation. We next let the system relax for a long time (>10⁷ iterations) with respect to the typical relaxation timescale of the system (∼10⁶ iterations; see Fig. S3 A). We finally measure the properties over ${10}^7$ iterations. Using a simulated annealing procedure (Fig. S3 B), we have further checked that these extensions, together with other structural properties (see below), are not sensitive to the annealing rate (Fig. S4).

Small discrepancies can be observed, though, when σ <0.01 and f < 0.5 pN (also reported previously for small molecules (40)), as well as in the plectonemic (or buckling) regime for $\sigma \ge 0.1$ and $f\ge 3$ pN. Several factors can explain these differences. For high σ, one expects, for instance, a contribution from nonharmonical terms in the bending and torsional energies, and in their coupling. Heterogeneities in the DNA sequence, and hence in the microscopic parameters of the molecule, may also play a role (16), as may the hard-core approximation of the electrostatic repulsions (18), especially when the DNA molecule writhes in many different places (41). Note, finally, that the buckling transition for this molecule is rather smooth. In contrast, and in accord with previous results obtained from an sWLC model with local torsional energies (18,19), abrupt transitions are observed for small (2.2 kbp) molecules. In this case, extension jumps are all the larger when the salt concentration is high (Fig. S5), in agreement with experiment (10,18) and theoretical analysis (12,14,15).

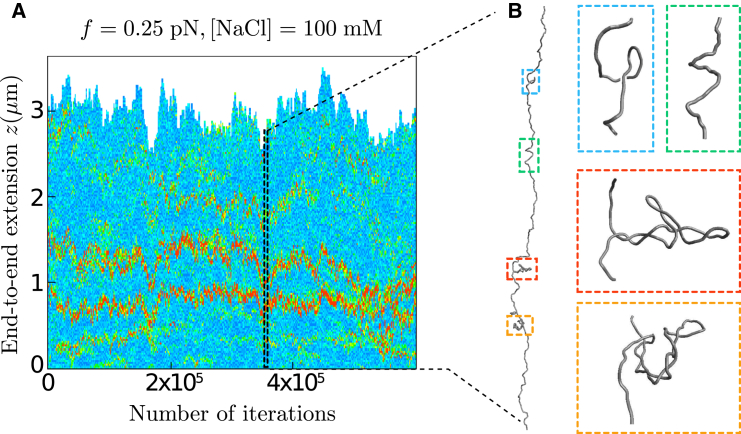
Concerning the structural properties of the plectonemic regime, in agreement also with recent experimental observations (16), we find that long (16 kbp and 21 kbp) molecules are mostly composed of several plectonemes (Fig. 5). This confirms the importance of multiple plectonemes for the folding properties of long molecules (14–16), even at high ($\ge 2$ pN) forces (15,16). Remarkably, we find a number of plectonemes that is consistent with experiments, provided we consider the same resolution as that associated with the fluorescent visualization of the plectonemes (500 nm) (Fig. 6 C). A close inspection of our results nevertheless reveals that the numbers of plectonemes in our simulations tend to be slightly larger than those reported in experiments (see, for instance, Figs. 6 C and S6). Sequence effects, which have been invoked to explain the slow diffusion of plectonemes (16), may contribute to this discrepancy. Along this line, we also note that in our simulations, the number of plectonemes is highly sensitive to the chain discretization, which can be interpreted as a sensitivity to the local properties of DNA. Specifically, contrary to the computation of the extension where 5 cylinders per $l_{\text{p}}$ are sufficient (see above), we find that 10 cylinders per $l_{\text{p}}$ (1400 cylinders in total) are necessary for having, in the buckling regime, a number of plectonemes that become insensitive to the discretization (Fig. S7). Let us mention here that the radius of the end-loop of the plectonemes is ∼ $\sqrt{K/f}$ (2), which is 14 nm at 1 pN and 8 nm at 3 pN (to be compared to the 10-nm-long cylinders in the case of 5 cylinders per $l_{\text{p}}$).

Figure 5.

Structural insights of long supercoiled molecules in the buckling regime. (A) Plectoneme tracking in a 21 kbp molecule using a color code that reflects the density of DNA on the axis along which the molecule is stretched (see the Supporting Material for details) (inspired by the work of van Loenhout and colleagues (16)). High densities (red) reveal plectonemic structures that can be more or less branched, as shown by extracting a particular conformation—the red and orange zooms indicate a branched and a straight plectoneme, respectively. (B) Plectonemes can coexist with curls (blue zoom) and helices (green zoom). To see this figure in color, go online.

Figure 6.

Plectoneme properties in the buckling regime. (A) In the spirit of the van Loenhout study (16), we developed a method to detect, count, and measure the plectonemes obtained in our simulations. Namely, for each cylinder i, we test whether i is the starting point of a plectoneme, that is, if there exist cylinders much farther away along the chain that are in the neighborhood of i. Denoting w as the expected width of plectonemes, we thus search whether there exists a cylinder at least 500 bp away from i that is located within a distance w of i (500 bp is the resolution reported by van Loenhout and colleagues (16)). If so, we consider as the end of the plectoneme (j in the figure) the cylinder with this property that is the most distant from i along the DNA. We then repeat the procedure from cylinder $j+1$, and so on. Here, we report results using an expected width $w=2\sqrt{K/f}$ (2), which lies between 16 and 32 nm in the experiments presented here—the exact value of w actually has a negligible effect (Fig. S7). (B) Application of the method on a 21 kbp molecule (1400 cylinders) using $f=3.2$ pN and $\sigma =0.07$, where five plectonemes are detected and painted with different colors (note that the blue ones are branched). (C) Using this automatic detection, compared to the results of van Loenhout and colleagues (16) (black), we obtain a significantly higher number of plectonemes (red). To be able to properly compare our results with experiments, we further consider the spatial resolution (∼500 nm (16)) that is intrinsic to the fluorescent staining of DNA due to light diffraction. To this end, we merge the plectonemes whenever their distance along z is <500 nm. In this case, we still find a larger number of plectonemes (blue) but that is nevertheless consistent with experimental results. Here, parameters of the simulations are such that 25% of DNA is plectonemic (16). The bars indicate the standard variation over 12 simulations. To see this figure in color, go online.

Fig. 5 further reveals that plectonemes are often branched, more particularly at low forces. This figure also reveals that curls, as theoretically predicted by Marko and Neukirch (14), are present both at the buckling transition (Fig. S8) and in the plectonemic regime (Fig. 5 B). In addition, we also find that curls and plectonemes can coexist, at low forces, together with helical structures (Fig. 5 B). The relative proportion of these helical structures is expected to be particularly sensitive to salt conditions, which have been shown to nontrivially affect the tendency, at small scales, for writhing (41). In particular, helical structures are expected to become ubiquitous for low (nonphysiological) salt concentration, as previously observed for small molecules (17) (see Fig. S9).

Finally, although MC methods are not well suited to address temporal properties (as they rely on artificial dynamics), our work offers insights into the dynamics of existing plectonemes. In our simulations (e.g., Figs. S6 and S8), this dynamics is mostly achieved through the disappearance of an existing plectoneme and the concomitant or posterior appearance of another one at a different place. Interestingly, such a destruction/creation mechanism was observed early on by Langowski and co-workers in Brownian dynamics simulations (21). It was proposed in particular to be the main mode of structural fluctuations in the plectonemic regime (21), which is in accord with the observation of plectoneme hopping in single-molecule experiments (16). Finally, we note that existing plectonemes diffuse little in our simulations (Figs. S6 and S8). Diffusion may, however, be accelerated by nonlocal elementary motions, resulting in faster convergence to equilibrium (Fig. S12).

Torque measurements

Supercoiled molecules exert a torque on the device that is used to impose the torsional stress. Its estimation can provide important information about the operational mode of proteins that are known to modify the topological properties of DNA (42). Experimentally, the equilibrium torque, $\text{Γ}$, has been estimated using two different methods.

• 1)Directly, as originally reported by Forth and colleagues (10,30) using a small (2.2 kbp) molecule, by measuring the small angular deviations of beads that are attached to the end of molecules and are manipulated either by optical tweezers (30) or by low-stiffness torsional traps (43).
• 2)Indirectly, as originally reported by Mosconi and colleagues (11) using a long (16 kbp) molecule, by integrating the change of molecular extension with respect to f as the molecule is coiled, and supposing a constant torque in the plectonemic regime.

Importantly, the two methods have led to significantly different values for the buckling torques, that is, for the torque values in the plectonemic regime. It has been proposed that this might come from the constant buckling torque approximation (15).

From a numerical viewpoint, direct measurements of torque have been reported so far in models with local torsional energies (18–21,28). Here, we extend our framework and develop a method to measure torques directly in global torsional energy models. To this end, we take advantage of the fact that the end cylinders of our sWLC can exchange helix turns with the external cylinders, which thus can act, just as in single-molecule experiments, as torsional traps (Fig. 2 C). The direct estimation of $\text{Γ}$ can indeed be realized by measuring the fluctuations, $\delta \theta$, of the angle between the direction of a marker that is covalently bound to the tip of the molecule and the direction of a magnet used to manipulate this marker and characterized by a torsional stiffness k (43). By definition, the torque is then given by $\text{Γ}=k\langle \delta \theta \rangle$ or, converting angles to twists, by $\text{Γ}=2\pi k\langle \delta \text{Tw}\rangle$. We thus implement this method with the external cylinders playing the role of the torsional trap (Fig. 2 C). Note, in this regard, that our external cylinders are used in a manner that is different from that implemented in models with local torsional energies. In these models, external cylinders are used to define the local twists at the extremities of the molecule, whose associated energy can then be used to compute torques (18,19); in global energy models, such local quantities cannot be defined.

Specifically, denoting $\delta \text{Tw}$ as the variation of the twist within the external cylinders, which thus act as a reservoir of twists, we mimic a torsional trap by allocating this reservoir with a torsional stiffness $k_{\text{R}}$, hence associating an energy cost to $\delta \text{Tw}$: $E_{\text{tt}}=2{\pi }^2{k}_{\text{B}}T{k}_{\text{R}}\delta {\text{Tw}}^2$. Just as in single-molecule experiments, the torque is then given by $\text{Γ}=2\pi k_{\text{R}}\langle \delta \text{Tw}\rangle$. The slope of the curve $\text{Γ}\left(\sigma \right)$ before the buckling transition (Fig. 7) leads in turn to the effective torsional modulus, $C_{\text{s}}$, which is the torsional modulus a straight rod should have to yield the same torque (44): $\text{Γ}=2\pi k_{\text{B}}T{C}_{\text{s}}\sigma /h$, where h is the pitch of the DNA double-helix ( $h=3.47$ nm).

Using this technique, we find a good agreement with experimental results for the 16 kbp molecule (Fig. 7 A), with different values of $k_{\text{R}}$ consistently leading to identical results (Fig. S10). In particular, we obtain an effective torsional modulus (C_s) that is consistent with both experiments and early theoretical predictions (44) (Fig. 7 B). In accord with the approximation of the constant torque used in Mosconi et al. (11), we also find a plectonemic regime that is characterized by a fairly constant buckling torque, showing that additional torsional stress in this regime is directly converted into writhe. Note, then, that the slightly larger values obtained in our simulations are likely to be due to the hard-core approximation of the electrostatic repulsion, since they noticeably depend on the effective radius, $r_{\text{e}}$ (Fig. S11).

Strikingly, and in accord with previous results obtained from an sWLC model with local torsional energies (18,19), for 2.2 kbp molecules we find buckling torques that significantly differ from experimental results (Fig. S5). In particular, for $\left[\text{NaCl}\right]=150\text{nm}$, we find a sharp decrease of the torque at the buckling transition, which is in accord as well with theoretical analysis (12,14). Just as in the case of the structural properties of long molecules (see above), sequence effects might be at the root of these discrepancies. This may suggest, in particular, that a more detailed model than the sWLC should be used, including, for instance, sequence effects and a proper consideration of the electrostatic interactions.

Conclusions

Our MC algorithm takes advantage, on the one hand, of the quick relaxation of sWLC models that rely on a global torsional energy and, on the other hand, of an explicit representation of the DNA helix that allows both an efficient computation of the exact total twist and a direct measurement of torques. In this regard, we note that preventing the generation of twist between any two consecutive cylinders, which is at the basis of the conservation of the linking number in our framework, is reminiscent of the principle of parallel transport that has been used for parametrizing flexible and twistable rods by using zero-torque transformations of Euler frames (37). Interestingly, this rigid-body type of framework has recently been implemented in novel, efficient types of Brownian dynamics simulations of supercoiled DNA (28,45), which have been used, for instance, to investigate thermodynamic properties of 3-kbp-long supercoiled molecules in the context of magnetic tweezer experiments (28). This suggests interesting connections between helix-based and Euler-frames-based frameworks, which need to be further explored.

Using our algorithm, we have been able to reproduce experimental results about the thermodynamic properties of molecules that are 16 kbp and 21 kbp long. We have provided, in particular, to our knowledge, novel insights into the structural properties of these molecules, such as the coexistence of both curls and helical structures together with plectonemes, or the number and length of these plectonemes. As far as the torques are concerned, we have confirmed that these remain constant in the buckling regime, meaning that additional torsional stress is systematically converted into plectonemes in this regime.

Altogether, our work opens the way for investigating the folding properties of very long molecules and, hence, for rationalizing the long-range properties of DNA loops in relation to gene regulation (46) and for investigating the multiscale folding of extended chromosome regions (47). Along this line, let us note that our local treatment of topological constraints offers the possibility of efficiently parallelizing the algorithm. A rough estimate considering 10 CPUs in parallel should allow us to obtain in typically one week folding trajectories that are similar to those of Figs. S6 and S8 but for molecules that are as long as that of the chromosome of M. genitalium (580 kbp).

Finally, including in the algorithm other types of elementary motions, such as reptation moves (48), and in the model the possibility of denaturation (49), sequence heterogeneities (16), and the presence of bridging protein complexes (50) and independent topological microdomains (51) are avenues for future investigation.

Author Contributions

F.K. and I.J. headed research; T.L. and I.J. designed simulation tools; T.L. performed research; T.L., F.K. and I.J. analyzed data; and T.L., F.K., and I.J. wrote the article.

Editor: Keir Neuman.