Relative Cosolute Size Influences the Kinetics of Protein-Protein Interactions

Abstract

Protein signaling occurs in crowded intracellular environments, and while high concentrations of macromolecules are postulated to modulate protein-protein interactions, analysis of their impact at each step of the reaction pathway has not been systematically addressed. Potential cosolute-induced alterations in target association are particularly important for a signaling molecule like calmodulin (CaM), where competition among >300 targets governs which pathways are selectively activated. To explore how high concentrations of cosolutes influence CaM-target affinity and kinetics, we methodically investigated each step of the CaM-target binding mechanism under crowded or osmolyte-rich environments mimicked by ficoll-70, dextran-10, and sucrose. All cosolutes stabilized compact conformers of CaM and modulated association kinetics by affecting diffusion and rates of conformational change; however, the results showed that differently sized molecules had variable effects to enhance or impede unique steps of the association pathway. On- and off-rates were modulated by all cosolutes in a compensatory fashion, producing little change in steady-state affinity. From this work insights were gained on how high concentrations of inert crowding agents and osmolytes fit into a kinetic framework to describe protein-protein interactions relevant for cellular signaling.

Introduction

Cellular functions are carried out through networks of signaling proteins, relaying information at different frequencies with precise timing in specific subcellular locations. Cells have evolved to organize molecules into various organelles as well as non-membrane-bound phases (1), each containing optimal compositions of molecules to enhance signaling efficiency for specific functions. Describing the kinetics of protein-protein interactions in these settings presents a nontrivial challenge, as we must begin to account for the effects of the surrounding environment. Although many variables could be considered, the physical constraints imposed by neighboring molecules are universal and have acknowledged impacts on protein-protein interactions (for reviews, see Ellis and Minton (2), Zhou et al. (3), and Schreiber et al. (4)). Two such constraints are the excluded-volume effect, where cosolutes limit the space any given molecule can occupy; and small-scale viscosity, which creates barriers to diffusion and protein dynamics (2–5). Excluded volume is generally thought to stabilize proteins through steric effects and soft interactions with the solvent (6–8), but how this influences protein-protein association and affinity remains incompletely understood. However, it is generally accepted that describing the cytosol in the so-called “bag of proteins” paradigm (9) fails to acknowledge that specialized intracellular compartmentalization may actually intensify the effects of crowding and confinement.

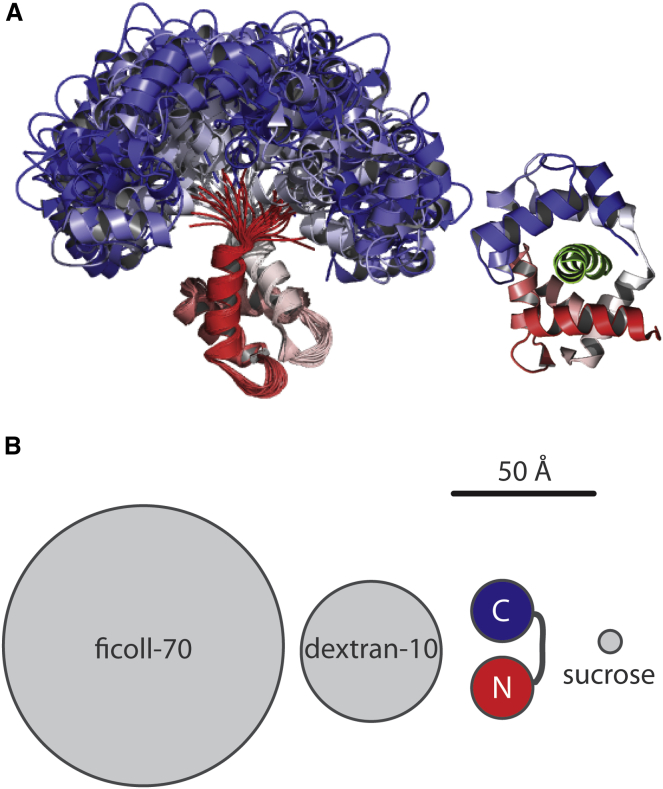
In this work, we investigated how these nonspecific effects influence the specific interaction of the ubiquitous signaling messenger calmodulin (CaM) with a target, focusing on how the size and concentration of surrounding molecules (cosolutes) influence each step of the target association mechanism. CaM is highly flexible and its conformational plasticity is essential for accommodating binding to >300 diverse targets (see Fig. 1 A) (10–12). Its two globular domains are connected by a flexible linker, each containing a pair of EF-hand motifs to accommodate the reversible binding of four total Ca²⁺ ions (13). CaM exists as an ensemble of conformers (14–16) fluctuating around a large flat energy minimum, where conformational sampling permits a continuum of structures with similar energies (17–20). CaM function depends on dynamics occurring on various spatial scales, where backbone dynamics have been shown to drive Ca²⁺ affinity (13) and accommodation of a target requires large rearrangements of its domains (21). Flexibility and disorder are particularly susceptible to the volume exclusion effect of crowded environments, making CaM an ideal choice as a model protein.

Figure 1.

CaM plasticity and experimental system. (A) The structural ensemble from NMR experiments (PDB:1DMO (15)) are aligned to the N-lobe (red) and overlaid to illustrate the flexibility and conformational sampling of CaM. In contrast, CaMKI peptide-bound Ca²⁺/CaM (green) adopts a compact conformation (PDB:1MXE (12)). (B) Reagents used in the experimental system are of varying sizes, with approximate radii of 51, 24, and 4 Å for ficoll-70, dextran-10, and sucrose, respectively. CaM, illustrated in cartoon form with C-lobes (blue circles) and N- lobes (red circles), connected by a flexible linker, is most similar in size to dextran-10. To see this figure in color, go online.

In addition to macromolecular crowders, the cellular interior also contains high concentrations of small hydrophilic molecules (osmolytes), which have a significant potential to influence protein-protein interactions. These highly abundant osmolytes make up ∼25% of solutes inside cells (3,22), play vital roles in maintaining protein function through stabilizing protein structure (23–25), and may exert frictional effects at smaller spatial scales than macromolecules. Unlike macromolecules, osmolytes are not traditionally considered to contribute to the excluded volume effect, but rather minimize protein surface area (26) to favor more compact states (27,28). We therefore utilized purified polymer systems to investigate volume exclusion (29,30) and sucrose to mimic osmolytes in our analysis of association.

We determined that crowders and osmolytes stabilize compact conformers of CaM, reduce translational and rotational diffusion, and modulate association and dissociation kinetics. Importantly, these effects are dependent on the size of the reagent used to create each environment and we show that differently sized molecules can selectively enhance or impede distinct steps of the association pathway. We show that diffusion limited models were insufficient to describe the results and that it was necessary to include contributions from conformational transitions. We additionally demonstrate that both on-rates and off-rates are reduced, resulting in little change in steady-state affinity. This indicates that steady-state measurements may not reveal important effects of crowed environments (2–4).

Materials and Methods

Protein and peptide preparation

Wild-type mammalian calmodulin (CaM) (31–33), T34C/T110C CaM (17), K75C CaM (34), D2C CaM (35,36), and ¹⁵N-isotope-labeled CaM (31,37,38) were expressed and purified as previously described in the cited works. The target peptide representing the CaM recognition motif for CaMKI (AKSKWKQAFNATAVVRHMRKLQ) was purchased from LifeTein (Somerset, NJ). The peptide was additionally purified with a Sep-Pak C18 resin (Waters, Milford, MA). The University of Texas Medical Branch Biomolecular Resource Facility (Galveston, TX) completed quantitative analysis of purified proteins and peptide.

Förster resonance energy transfer

Labeling and purification of CaM engineered with two cysteine substitutions at residues 34 and 110 with Alexa 488 (donor) and QSY9 (quencher; Invitrogen Molecular Probes, Carlsbad, CA) was accomplished exactly as described in Homouz et al. (17). Förster resonance energy transfer (FRET) experiments were accomplished in the presence or absence of 1 mM CaCl₂, and/or ficoll-70 (GE Healthcare, Piscataway, NJ), dextran-10 (GE Healthcare), or sucrose (Sigma-Aldrich, St. Louis, MO) in 25 mM MOPS, 150 mM KCl, 0.1 mg/mL BSA, 0.1 mM EGTA, pH 7.2. Fluorescent CaM was excited at 494 nm and emitted fluorescence was collected at 517 nm on a PTI fluorimeter. Intensities were recorded for 30 s at a sampling rate of 10 points/s and average intensities were determined for each condition. FRET efficiencies were calculated using E = 1−(F′_D/F_D), where E is the quantum yield of the energy transfer transition, F′_D is the fluorescence intensity of the Alexa488 donor in the presence of the QSY9 acceptor, and F_D is the fluorescence intensity of donor in the absence of acceptor. The interprobe distance was then calculated using E = 1/(1+(r/R₀)⁶), where r is the donor-acceptor distance and R₀ is the Förster distance of the Alexa488/QSY9 FRET pair (R₀ = 64 Å). Isotropic reorientation of fluorophores was assumed (κ² = 2/3).

Nuclear magnetic resonance

Nuclear magnetic resonance (NMR) experiments were carried out with a model No. DRX 600-MHz spectrometer (Bruker, Billerica, MA) equipped with a 5 mm triple-resonance cryoprobe or broadband probe at 298 K. The ¹H-heteronuclear single quantum coherence spectra for 0.5 mM ¹⁵N-isotope-labeled CaM were collected in buffer consisting of 10 mM imidazole pH 6.3, 100 mM KCl, and 5% D₂O in the presence or absence of 5 mM CaCl₂ or 5 mM EDTA and/or 20% w/v polymer or sucrose. All NMR spectra were processed and analyzed using the software TOPSPIN 3.2 (Bruker). ¹H chemical shifts were referenced to DSS (2,2-dimethyl-2-silapentane-5-sulfonate) and residue assignments for amide chemical shifts were made as described in Kleerekoper and Putkey (39). Changes in chemical shifts comparing conditions with and without volume exclusion were determined using the formula $\Delta \delta =\sqrt{{\left(\Delta \delta H\right)}^2+{\left(\Delta \delta N/5\right)}^2}/2$. Changes in peak intensities of individual residues in CaM were determined by dividing the intensities under conditions of volume exclusion by the intensities in the absence of volume exclusion, I/I₀.

Steady-state Ca²⁺ affinity measurements

Ca²⁺ binding to CaM was monitored at steady state under conditions that ensured significant populations of Ca²⁺-bound and Ca²⁺-free forms at each Ca²⁺ titration point. Experiments were carried out in a chelator system consisting of EGTA, NTA, and HEDTA so that the free Ca²⁺ concentration (i.e., Ca²⁺ available to bind CaM) was controlled by the buffering capacity of the chelators. Ca²⁺ titrations were carried out in a 1-mL reaction volume consisting of 50 mM MOPS, 100 mM KCl, 1 mM EGTA, 1 mM HEDTA, 1 mM NTA, and 5 μM CaM at pH 7.2 in the absence or presence of ficoll-70, dextran-10, or sucrose. For each tested concentration, a solution of the same reagents including 25 mM CaCl₂, was added to produce from 0 to 1000 μM free Ca²⁺. To maintain a 1 mL reaction volume throughout the experiment, a volume equivalent to the titrated volume was first removed from the reaction for each titration point. Values for [free Ca²⁺] were determined with the MAXCHELATOR program (Webmaxc extended version 2012; www.maxchelator.stanford.edu) assuming an ionic strength of 0.133 M and temperature of 24°C. Native Tyr fluorescence of CaM, shown to be sensitive to Ca²⁺ binding to the C-lobe, was monitored on a PTI fluorimeter (Photon Technology International, Edison, NJ) with 276 nm excitation and 304 nm emission wavelengths with 1 and 10 nm slit widths, respectively. Fluorescence was monitored for 30 s at 10 points/s after each addition and the average intensities at each point were plotted as a function of [free Ca²⁺]. Data was fit with the Hill equation $y=\text{START}+\left(\text{END}\text{-}\text{START}\right)\times x^n/\left(k^n+x^n\right)$, where y is the fluorescence intensity average, x is [free Ca²⁺], k is the rate constant, n is the Hill coefficient, and kⁿ is the dissociation constant, K_d. For interexperiment comparisons, data was normalized.

Isothermal titration calorimetry

Isothermal titration calorimetry (ITC) measurements were performed in a MICROCAL VP-ITC instrument (Malvern Instruments, Malvern, UK) in a buffer consisting of 25 mM MOPS, 150 mM KCl, and 2 mM CaCl₂ in the presence or absence of 20% w/v ficoll-70, dextran-10, or sucrose. All samples were degassed and brought to 25°C before starting experiments. Titrations were carried out by injecting 5 μL of 150 μM CaMKI peptide into the cell containing 5 μM CaM at 25°C with constant stirring. Each experiment consisted of 28 injections with a 20 s injection duration and 210 s spacing between injections. The raw data were baseline-corrected and integrated peak areas were calculated using the MICROCAL software (Malvern Instruments) then plotted as a function of mole ratio. Data were fit with single binding-site models to determine the binding stoichiometry, N; association constant, K_a; enthalpy, ΔH; and entropy, ΔS.

Fluorescence correlation spectroscopy

A D2C mutant CaM was labeled with Alexa 488 dye (Invitrogen Molecular Probes) and purified on a reverse-phase C18 Vydac column (W. R. Grace, Columbia, MD). Protein was lyophilized, resuspended, and stored as aliquots at −80°C. Spectroscopy was accomplished in buffer (1 mM CaCl₂, 25 mM MOPS, 150 mM KCl, 0.1 mg/mL BSA, and 0.1 mM EGTA at pH 7.2) at the indicated concentrations of ficoll-70, dextran-10, or sucrose. Diffusion coefficients were determined using multiphoton fluorescence correlation spectroscopy (FCS) in an instrumental setup previously described in Sanabria et al. (30) with a mode-locked Ti:S laser (Mira 900F; Coherent, Santa Clara, CA) pumped by a 5 W frequency-doubled Nd:YVO4 laser (Verdi-5; Coherent). A quantity of 50 nM samples, yielding ∼5 molecules in the observation volume on average, was prepared in a chambered No. 1 cover-glass dish (model No. 155411; Nalge Nunc, Rochester, NY). Changes in refractive index of the samples at increasing concentrations of crowders or sucrose were compensated for by adjustments in the objective lens correction collar (40). Samples were excited at 780 nm with ∼6 mW of power at the specimen plane and emission was detected with a photon-counting avalanche photodiode module (SPCM-AQR-W4; PerkinElmer, Wellesley, MA) by an optical fiber over a 60 s recording period. A commercial autocorrelator board (model No. Flex01-D; Correlator.com, Bridgewater, NJ) was used to compute the correlation curves from fluorescence intensity fluctuations recorded in real-time. Data was analyzed by a custom-written GUI (FCSSeriesGUI) in the software MATLAB (The MathWorks, Natick, MA). Diffusion coefficients, D, were determined for each recording from a single component-fitting algorithm and average diffusion coefficients were calculated from three consecutive recordings on the same experimental sample as previously described in Sanabria et al. (30). The D values are reported as the average of duplicate samples.

Rate determination

K75C CaM was labeled with acrylodan (Acr; Invitrogen, Grand Island, NY) to make CaM-Acr and purified as described previously in Putkey and Waxham (37). Association and dissociation rates were measured using a model No. SV7.1 stopped-flow fluorimeter (Applied Photophysics, Surrey, UK) with an instrument dead-time of ∼1.7 ms. For association rates, reactions were carried out by rapidly mixing solutions from two syringes in equal volumes at 4°C unless otherwise indicated. One syringe contained 200 nM CaM-Acr in a standard buffer (1 mM CaCl₂, 25 mM MOPS, 150 mM KCl, 0.1 mg/mL BSA, and 0.1 mM EGTA at pH 7.2) and the other contained increasing amounts of peptide in the standard buffer to achieve pseudo first-order reaction conditions. For on-rate determination, data were collected for six injections and the average was fit to a single exponential equation to determine $k_{\text{obs}},F=\left(F_{\text{initial}}\times e^{-k_{\text{obs}}t}\right)+F_{\text{final}}$, where F is the observed fluorescence intensity at time t and k_obs is the observed rate. On-rates were then calculated for each condition by plotting k_obs as a function of peptide concentration and determining the slope of the linear fit. For off-rates, CaM-Acr was preincubated with CaMKI peptide in standard buffer, then rapidly mixed with 50fold excess unlabeled CaM and fluorescence decay was monitored over time at 4°C. Five-to-six injections were made for each condition, the results averaged, and the fluorescence decay was fit with a double-exponential equation, $F=F_1{e}^{-k_{1}x}+F_2{e}^{-k_{2}x}+F_{\text{final}}$. The value k₁ accounts for ∼90% of the amplitude and was used to calculate an estimated dissociation constant at equilibrium from the relationship K_d = k₁/k_on.

Diffusion-limited and diffusion-influenced reactions

In a bimolecular reaction (41,42), we have

$$\begin{array}{c}A+B\underset{k_D^{\prime }}{\overset{k_D}{\rightleftharpoons }}AB\underset{k_R^{\prime }}{\overset{k_R}{\rightleftharpoons }}P,\\ A+B\underset{k_{\text{off}}}{\overset{k_{\text{on}}}{\rightleftharpoons }}P,\end{array}$$ (1)

where P is the formed complex and AB is the collisional complex with reaction rate constants k_D, k′_D, k_R, and k′_R. The on-rate (k_on) (or measured complex formation), and off-rate (k_off), can be obtained by relating a set of kinetic equations, given as

$$\frac{d\left[A\right]\left[B\right]}{dt},\frac{d\left[P\right]}{dt},\text{and}\frac{d\left[AB\right]}{dt},$$

to derive

$$k_{\text{on}}=\frac{k_R\times k_D}{k_R+k_D^{\prime }}\text{and}{k}_{\text{off}}=\frac{k_R^{\prime }\times k_D^{\prime }}{k_R+k_D^{\prime }},$$ (2)

where k_R and k′_R make up a distinct process that takes the collisional complex into the final product state. The value k_D is controlled by diffusion and can be written as

$$k_D=4\pi R_{AB}{N}_{A}D.$$ (3)

In this equation, N_A is Avogadro’s number, and R_AB is the reacting distance, which to first approximation is the sum of the hydrodynamic radii of A and B. The value D is the sum of the diffusion of the reactants, D = D_A +D_B.

When k′_D << k_R, the reaction is said to be a diffusion-limited one and Eq. 2 reaches the limit of

$$k_{\text{on}}\simeq k_D=4\pi R_{AB}{N}_{A}D.$$ (4)

However, when k_R is comparable to k′_D, it is possible to write k_on in Eq. 2 as

$$k_{\text{on}}\simeq \frac{K4\pi R_{AB}{N}_A{k}_{R}D}{4\pi R_{AB}{N}_A\left(\frac{K{k}_R}{4\pi R_{AB}{N}_A}+D\right)},$$ (5)

where $K=\left(k_D/k_D^{\prime }\right)$ is the equilibrium constant for the part of the reaction that reads as $A+B\underset{k{\prime }_D}{\overset{k_D}{\rightleftharpoons }}AB$. For simplicity, we can present Eq. 5 in terms of the variables $\alpha =K{k}_R$ and $\beta =\left(K{k}_R/4\pi R_{AB}{N}_A\right)$ to satisfy

$$k_{\text{on}}=\frac{\alpha \times D}{\beta +D}.$$ (6)

Finally, in a more general form, considering an offset on the diffusion, D₀, that accounts for the fact that the assumption D = D_A + D_B fails to include changes in the radii of gyration of the reactants upon binding, it is then possible to rewrite Eq. 6 as

$$k_{\text{on}}=\frac{\alpha \times \left(D-D_0\right)}{\beta +\left(D-D_0\right)}.$$ (7)

Results

Description of experimental system

Differences in CaM structure and target association were quantified under conditions of increasing concentrations of cosolutes. We found it necessary to use inert uncharged polymers rather than proteins to crowd the environment because the proteins bovine serum albumin and lysozyme stick nonspecifically to CaM at the high concentrations required, confounding interpretation of diffusion and reaction rates. This is likely due to weak nonspecific chemical interactions (43–45), which attenuate diffusion rates (46,47). We focused instead on ficoll-70 and dextran-10, which are uncharged, branched polysaccharides predicted to have generally spherical shapes, where ficoll-70 (70 kDa) is larger than the 17 kDa CaM molecule and dextran-10 (10 kDa) is of similar size (Fig. 1 B). Volume exclusion by these polymers creates barriers to CaM diffusion and confines the space in which conformational changes take place. We also evaluated CaM in the presence of the osmolyte sucrose (340 Da), which minimizes the solvent-exposed surface area of proteins (27,28,48) through an osmophobicity effect, where burial of the backbone is favored (49,50). Osmolytes are also preferentially excluded from protein surfaces and have the potential to create a caging effect where water molecules trapped on protein surfaces have decreased ability to exchange with the bulk solvent (22). Sucrose has been shown to stabilize compact conformers of protein ensembles, and has been suggested to reduce structural fluctuations significantly when proteins are in loose extended conformations with high internal hydration (26,51,52).

Polymers and sucrose decrease CaM interlobe distance and slow rotational diffusion

To investigate structural consequences, cysteine residues were engineered into sites 34 and 110 of the N- and C-lobes of CaM, respectively, and labeled with Alexa488 donor fluorophore and QSY9 quencher acceptor to produce the FRET pair. FRET efficiencies were determined from fluorescence intensities and used to calculate interprobe distances (Table 1) as done in Homouz et al. (17). In the absence of cosolutes, interprobe distances were reduced in the presence of Ca²⁺ (from 61 to 54 Å), and a further reduction was observed when bound to the CaMKI target peptide (to 41 Å). In the presence of cosolutes, the interprobe distances in apo CaM or Ca²⁺/CaM were decreased ∼10 Å (Table 1). Interestingly, in the presence of CaMKI target, inclusion of cosolutes does not greatly change interprobe distance, likely due to the already highly compact nature of the target-bound conformation. The absence of cosolute-induced FRET change of the Ca²⁺/CaM/CaMKI complex also serves as an important control showing that these agents, even at high concentrations, do not produce detectable effects on either the probe orientation or photophysics that could have influenced the reduced distances measured for apo-CaM and Ca²⁺/CaM. These trends are largely consistent for ficoll-70, dextran-10, and sucrose, with decreases in interlobe distances saturating at ∼10% because no further decrease was detected at 20% (Table 1). These results indicate that each reagent causes a compacting of apo CaM and Ca²⁺/CaM, increasing the probability of sampling conformations with decreased interlobe distances.

Table 1.

Average interprobe distances determined from FRET

Experimental Condition	Apo CaM	Ca2+/CaM	Ca2+/CaM/CaMKI
None	61.46 ± 0.93	53.81 ± 1.4	41.05 ± 0.02
10% ficoll-70	49.11 ± 0.02	46.00 ± 0.70	42.07 ± 0.45
20% ficoll-70	46.29 ± 0.21	47.95 ± 0.43	41.34 ± 0.60
10% dextran-10	48.88 ± 0.26	45.05 ± 0.23	41.96 ± 0.43
20% dextran-10	51.15 ± 0.23	47.53 ± 0.27	41.96 ± 0.47
10% sucrose	52.38 ± 0.01	46.02 ± 0.69	42.09 ± 0.21
20% sucrose	50.81 ± 0.05	48.18 ± 0.13	41.70 ± 0.30

Interprobe distances determined from fluorescence measurements are shown for apo CaM, Ca²⁺/CaM, and CaMKI peptide-bound CaM in the presence of sucrose, dextran-10, and ficoll-70. Average values and standard deviations calculated from two separate experiments are reported in Å.

We next assessed whether significant reorganization of secondary structural elements accompanied the interlobe decrease detected by FRET measurements. For residue-level assessments, ¹H-heteronuclear single quantum coherence experiments were carried out for ¹⁵N-labeled apo CaM and Ca²⁺/CaM in the presence and absence of 20% polymer or sucrose. Compared to the condition lacking these reagents, there were virtually no changes in amide chemical shifts, Δδ, in the presence of ficoll-70, dextran-10, or sucrose with almost all residues demonstrating significant peak overlap (see Fig. S1 in the Supporting Material). These experiments are interpreted assuming an experimental error value of ∼0.02 for Δδ, a quantity twice that of observed experimental values. The lack of significant chemical-shift changes indicates that reorientation of secondary structural elements does not occur for apo or Ca²⁺-saturated CaM under the conditions examined. Together, our results suggest that although the distance between CaM lobes decreases, secondary structural elements are not detectably changed. Additionally, evaluation of the change in amide peak intensities, I/I₀, revealed that intensities were significantly reduced overall, indicating a reduction in rotational correlation time for CaM in the presence of the reagents. The I/I₀ values averaged across all residues were determined to be 0.50, 0.26, and 0.76 for sucrose, dextran-10, and ficoll-70, respectively, indicating that dextran-10 causes the most significant reduction of rotational correlation time. Generally, loop regions were observed to have slightly higher I/I₀ values than α-helical regions, suggesting conformational exchange dynamics may also contribute to peak intensity, as described in Wang et al. (38). Taken together, our steady-state FRET and NMR analyses indicate that volume exclusion and osmolyte stabilization are largely perturbing the rotational tumbling and interlobe dynamics, while secondary structural elements within CaM lobes are not significantly affected. In terms of the spatial scale of impacts, our results demonstrate that the similarly sized dextran-10 had the largest consequence on CaM rotational tumbling. All reagents affected interlobe orientation to a comparable degree, but little evidence was detected for the reagents impacting the protein on the scale of secondary structure.

Volume exclusion conditions do not modulate Ca²⁺ affinity for CaM

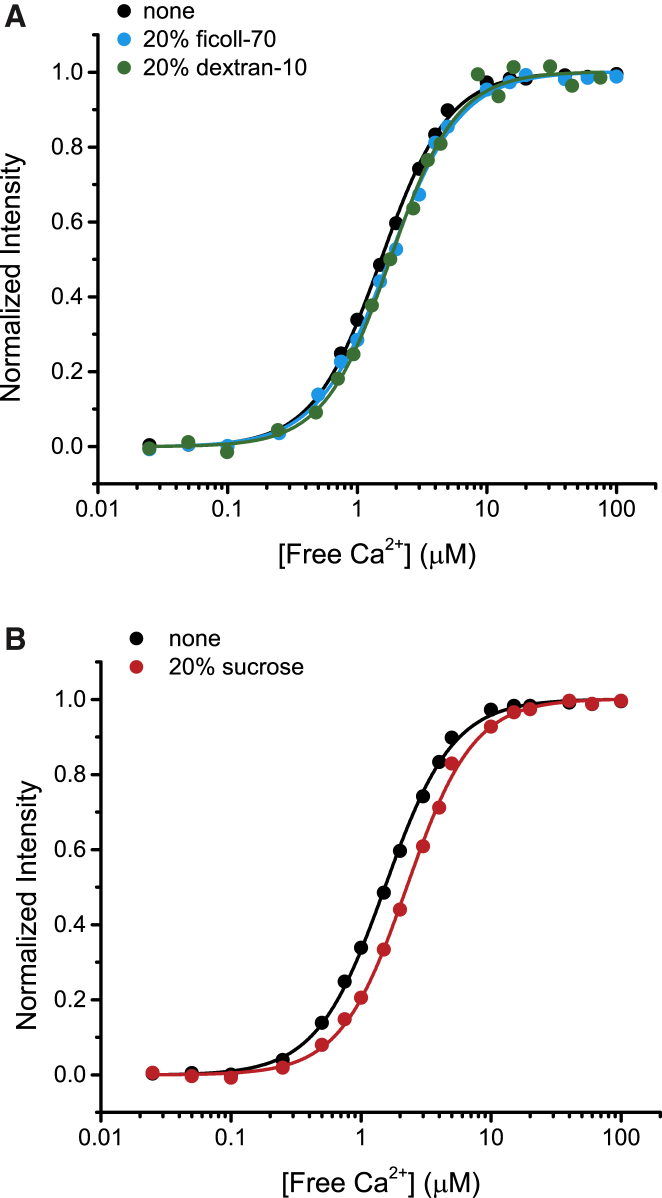
CaM’s Ca²⁺-binding affinity is dependent on electrostatic interactions as well as the conformational dynamics within each lobe (reviewed in Gifford et al. (13)). While fast backbone dynamics contribute principally to Ca²⁺ affinity, interactions also exist between lobes that influence Ca²⁺-binding properties (53–55). This raises the possibility that although ficoll-70, dextran-10, and sucrose are uncharged and produce no detectable effects on secondary structure, modulation of interlobe dynamics may influence Ca²⁺ affinity. Steady-state Ca²⁺ binding affinities were quantified in the presence of polymers or sucrose by monitoring native tyrosine fluorescence, a measure of Ca²⁺ binding specific to the C-lobe of CaM (56). Fluorescence intensity was measured as a function of free Ca²⁺ concentration and the data were fit with a Hill equation to determine K_d values (Fig. 2). Ficoll-70 and dextran-10 had little effect on Ca²⁺ affinity (Fig. 2 A). The K_d values were determined to be 2.2 μM in the absence of polymer and 2.6 μM in the presence of 20% ficoll-70 or dextran-10 (see Table S1 in the Supporting Material). There was also no significant difference apparent in the Hill coefficient (Table S1). In the case of sucrose, a K_d of 3.8 μM was determined, indicating a modest, but reproducible, decrease in affinity for Ca²⁺ with no significant change in the Hill coefficient (Fig. 2 B and Table S1). Osmolytes, like sucrose, are predicted to be preferentially excluded from protein surfaces as well as macromolecular interfaces (28). Because water is a better solvent for the peptide backbone than osmolytes, the burial of the backbone is favored through an apparent repulsion between protein and osmolyte via an osmophobicity effect (23,26,49,50). This is an entropic effect where osmolytes enhance water organization around proteins to promote reduction of protein surface area and burying of protein interfaces (23,49). Consequently, when a binding mechanism involves exposing an interface, the osmolyte will destabilize the binding reaction (49). Ca²⁺ binding to CaM exposes a new surface area to create interfaces for recognition of protein targets (57,58), and we speculate that sucrose destabilizes Ca²⁺ binding due to unfavorable exposure of protein surfaces. Additionally, it is possible that displacement of water molecules from the coordination sphere of the binding site by Ca²⁺ is inhibited in the presence of sucrose.

Figure 2.

Steady-state Ca²⁺ binding affinity for CaM. (A) Ca²⁺ affinities were determined by titrating Ca²⁺ into CaM in the absence of polymers (black) and in the presence of 20% ficoll-70 (blue) or 20% dextran-10 (green). (B) Ca²⁺ affinities were also determined in the presence (red) or absence (black) of 20% sucrose. Representative fluorescence intensities for each condition are plotted as a function of [free Ca²⁺], fit with a Hill function (solid lines), and normalized such that the fits spanned intensities from 0 to 1. To see this figure in color, go online.

Polymers and sucrose reduce CaM diffusion

In its simplest form, target association can be described in two steps: 1) the initial encounter and 2) subsequent conformational changes needed to arrive at the stable bound state. Potential effects of environmental factors on association rates will depend on which of these two processes is the rate-limiting step (59). If the association is a diffusion-limited one, i.e., it is principally dependent on encounter rates, rates will be slowed because of barriers to diffusion. If the rate is a transition-limited one, i.e., it is primarily dependent on overcoming conformational barriers after the initial encounter, crowding increases rates through stabilization of transition state intermediates (59). We showed previously that Ca²⁺/CaM association with CaMKI-peptide is considered to be in the diffusion-limited regime (19) (defined by Schreiber et al. (4) theoretically as 10⁵–10¹⁰ M⁻¹ s⁻¹), indicating that cosolute-mediated changes in diffusion will likely dominate any changes observed in association rates. However, structural information showed that large domain rearrangements in CaM are necessary to accommodate target binding (see Fig. 1 A) (12). This raises the possibility that the association rate may additionally be modulated through stabilization of transition-state intermediates. We therefore investigated how the polymers and sucrose modulate the diffusion and transition steps of CaM target association and determined their dependence on the relative size and concentration of each reagent.

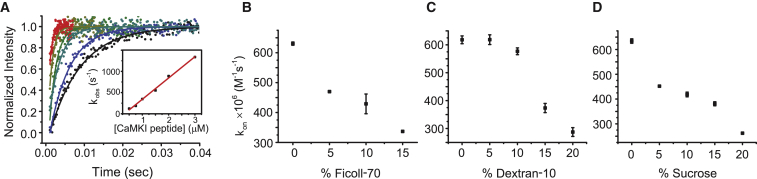
We employed FCS to extract diffusion coefficients for CaM labeled with Alexa 488 in varying concentrations of polymer or sucrose. All data was best fit with a single-component model to determine the diffusion coefficient, D (Fig. 3 A) indicating that D of the measured species was homogeneous through the illuminated volume under all experimental conditions evaluated here (30). All reagents decreased diffusion in a concentration-dependent manner to varying degrees, with the largest molecule, ficoll-70, having the most robust effect and the smallest, sucrose, having the least (Fig. 3, B–D). For comparison, D was reduced from 148 μm²/s in buffer to 34 and 59 μm²/s in 20% ficoll-70 and sucrose, respectively. Overall, diffusion coefficients were reduced in roughly linear fashions, consistent with an anticipated consequence of increased viscosities.

Figure 3.

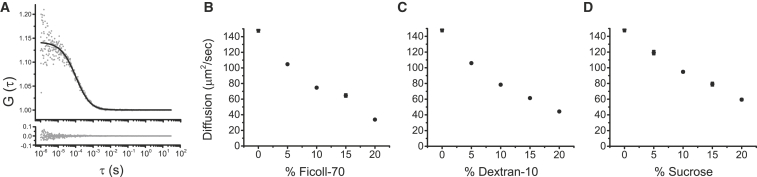
CaM diffusion coefficients. (A) Representative FCS data of CaM diffusion in buffer to illustrate data collection methodology. Autocorrelation functions were calculated in real-time from photon counts, then the averages of five experiments (shaded data points) were fit with single-component fits (solid trace) to determine diffusion coefficients. (Bottom inset) Residuals from the fit are shown. Diffusion coefficients were determined in various concentrations of ficoll-70 (B), dextran-10 (C), and sucrose (D). Experiments were completed in triplicate. Error bars represent mean ± SE.

Diffusion-limited models fail to describe association rates

In a diffusion-limited reaction, encounter probability dominates the association rate and association is proportional to reactant diffusion rates. Our results indicate CaM diffusion is decreased in the presence of polymers and sucrose, and we would expect a proportional decrease in association rate if reactions follow a diffusion-limited model. Deviation from this linear relationship would indicate that rates of conformational change are contributing significantly to the association rate. To measure association rates, target binding to CaM labeled with Acr was monitored in a stopped-flow fluorescence experiment as previously described in Waxham et al. (34). Acrylodan reports changes in local environment, and CaM-Acr is sensitive to conformational changes and binding of target. On-rates were determined by monitoring time-dependent changes in fluorescence as CaM was rapidly mixed with excess peptide under pseudo first-order binding conditions. Fig. 4 A depicts a representative experiment completed in the absence of polymers or sucrose. Binding reactions were carried out with varying concentrations of target (red through black scatter plots) and data were fit with a single-exponential model to determine the rate, k_obs. The value k_obs was plotted as a function of peptide concentration (inset) and a k_on value was determined from the fit of the slope. This procedure was then completed with varying concentrations of ficoll-70, dextran-10, and sucrose (Fig. 4, B–D). In general, on-rates were decreased as a function of polymer or sucrose concentration (data summarized in Table 2), with higher concentrations producing slower association rates. While all cosolutes influenced diffusion in roughly linear fashions, each reagent produced a unique trend in on-rates. For ficoll-70, on-rates decreased in a linear fashion (Fig. 4 B). However, on-rates in dextran-10 and sucrose were reduced in nonlinear ways and the trends require a more complicated description (Fig. 4, C and D). Dextran-10 produces, at most, a modest impact on the k_on at 5–10%; however, from 10 to 20% there is a major decrease in k_on that appears to follow a near-linear trend. In contrast, sucrose produces a significant slowing of k_on at 5% and then follows a complicated pattern of continuously slowed k_on at increasing concentrations. These distinct patterns suggest that each cosolute is impacting the process of association in unique ways. Importantly, cosolute-dependent changes in diffusion alone appear insufficient to describe changes in on-rates, and implies that cosolutes may also play a role in the transition between the initial encounter and bound complex.

Figure 4.

Measurement of CaM-CaMKI peptide association rates and determination of k_on. (A) A representative association experiment for CaMKI peptide is shown to illustrate data collection and fitting. CaM association rates were measured under pseudo first-order binding conditions and the data shown represent averages spanning a range of peptide concentrations (black to red scatter plots), with only every 20th data point plotted for clarity. Data was fit with single-exponential rates to determine observed rates, k_obs. Observed rates for each concentration were then plotted as a function of CaMKI peptide concentration (inset) and the k_on value was determined from the slope of the linear fit. This experimental procedure was repeated in varying concentrations of ficoll-70 (B), dextran-10 (C), and sucrose (D) to determine rates. Experiments were completed in duplicate. Error bars represent mean ± SE. To see this figure in color, go online.

Table 2.

Summary of association and dissociation rates for Ca²⁺/CaM-CaMKI peptide

Condition	kon (M−1 s−1)	koff (k1) (s−1)	koff (k2) (s−1)	Kd (M)a
None	6.3 × 108 ± 9.5 × 106	1.05 ± 0.13	0.11 ± 0.012	1.7 × 10−9
5% ficoll-70	4.7 × 108 ± 2.0 × 106	0.79 ± 0.10	0.09 ± 0.008	1.69 × 10−9
10% ficoll-70	4.3 × 108 ± 3.3 × 107	0.75 ± 0.05	0.08 ± 0.01	1.75 × 10−9
15% ficoll-70	3.4 × 108 ± 1.0 × 106	0.67 ± 0.07	0.08 ± 0.01	2.00 × 10−9
5% dextran-10	6.19 × 108 ± 1.8 × 107	0.72 ± 0.095	0.07 ± 0.02	1.16 × 10−9
10% dextran-10	5.77 × 108 ± 1.1 × 107	0.69 ± 0.078	0.06 ± 0.01	1.20 × 10−9
15% dextran-10	3.74 × 108 ± 1.7 × 107	0.62 ± 0.072	0.06 ± 0.01	1.65 × 10−9
20% dextran-10	2.87 × 108 ± 1.6 × 107	0.49 ± 0.067	0.02 ± 0.002	1.72 × 10−9
5% sucrose	4.52 × 108 ± 4.0 × 106	0.77 ± 0.11	0.10 ± 0.02	1.69 × 10−9
10% sucrose	4.19 × 108 ± 9.5 × 106	0.80 ± 0.10	0.12 ± 0.01	1.90 × 10−9
15% sucrose	3.81 × 108 ± 8.0 × 106	0.64 ± 0.07	0.08 ± 0.004	1.69 × 10−9
20% sucrose	2.63 × 108 ± 5.0 × 105	0.43 ± 0.03	0.05 ± 0.003	1.62 × 10−9

Averages of measured on-rates and off-rates are reported for volume exclusion (n = 2). Double-exponential equations were required to fit dissociation curves, where k₁ rates account for ∼90% of the change in amplitude and k₂ rates represent the remaining ∼10%.

^aEstimates of dissociation constants were calculated using the relationship K_d = k₁/k_on.

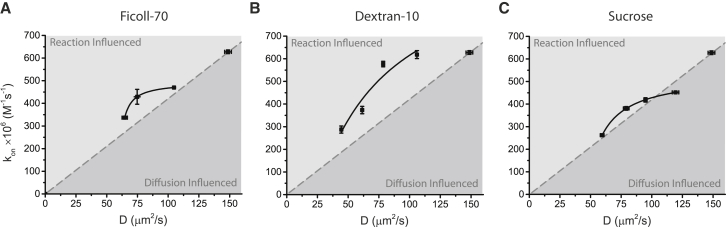
To begin to assess these trends, we produced a plot of k_on versus D for each reagent (Fig. 5). In a diffusion-limited model, the association rate is directly proportional to the diffusion-rate constant, k_D, and therefore proportional to the diffusion constant, D (see Eq. 4 in Materials and Methods). This relationship produces a linear trend (Fig. 5, gray dotted lines) that relates the zero data point collected in the absence of polymer or sucrose and the origin, where lack of diffusion results in no association. Plots of k_on versus D for the data collected in Ficoll-70 (Fig. 5 A), dextran-10 (Fig. 5 B), and sucrose (Fig. 5 C) all deviate, to a greater or lesser extent, from the simple diffusion-limited model. As a next step, we evaluated a model that includes a transition state to fit the data (Eq. 7; see Materials and Methods) (3). Interestingly, this model fit the relationship of k_on versus D for ficoll (Fig. 5 A) and sucrose (Fig. 5 C) reasonably well, consistent with the idea that these two cosolutes impose a significant effect on the rate of conformational transition during the association process. The fit of this model to the dextran-10 data was poor, indicating that the reaction-influenced model also failed to produce a trend line that falls within the error of the data. This finding highlights the complexities presented to diffusion and binding in crowded environments, and that across the concentration of dextran-10 evaluated, neither a diffusion-limited nor reaction-influenced model is sufficient to fully describe the reaction. It is of interest that the cosolute most similar in size to CaM (dextran-10) produces the most multipart reaction kinetics. Despite these complexities, in all cases, the association rates are decreased relative to buffer alone, indicating that while conformational transitions are stabilized to increase the rate of association, slowed diffusion still plays a significant factor in determining the overall rate.

Figure 5.

The fit of k_on versus D with diffusion-limited- or reaction-rate-influenced models. Association rates in the presence of (A) ficoll-70, (B) dextran-10, and (C) sucrose, i.e., k_on, were plotted, respectively, as a function of diffusion coefficient, D. To illustrate how data converge or deviate from the two models, hypothetical diffusion-limited relationships (dashed lines) and fits of data (solid lines) are given. Data were fit to the reaction-rate-influenced model k_on = (α(D−D₀))/(β+(D−D₀)) (Eq. 7; see Materials and Methods). The relationship for data collected in the presence of ficoll-70 was estimated with the following values: α = 494, β = 2.26, and D₀ = 59.8 μm²/s. Fits of dextran-10 data reveal that α = 1100, β = 59.5, and D₀ = 24.5 μm²/s, and fits for sucrose data are α = 531, β = 12.7, and D₀ = 47.1 μm²/s.

Polymers and sucrose modulate both association and dissociation rates, resulting in little change in steady-state binding constants

When CaM dissociates from the target, it transitions from a compact conformation to a more extended conformation (12,15). We predicted ficoll-70, dextran-10, and sucrose would favor the more-compact bound state and investigated if the Ca²⁺/CaM-target complex would be stabilized by these reagents and lead to slowed dissociation rates. We measured peptide off-rates using stopped-flow fluorescence as described in Materials and Methods. In these experiments, CaM-Acr dissociation from the peptide is quantified by rapid mixing with an excess of unlabeled CaM that competes with fluorescently labeled CaM for rebinding to the peptide after dissociation occurs. The resultant fluorescent decay represents the rate of dissociation of the peptide. We found that indeed off-rates (Table 2) were decreased in the presence of increasing concentrations of sucrose, dextran-10, or ficoll-70, indicating these reagents stabilize the Ca²⁺/CaM-CaMKI peptide complex likely due to its smaller volume occupancy. Our experiment cannot resolve the difference between a slow molecule dissociation event primarily dependent on conformational changes, and one where dissociation is limited because of quick rebinding of partners due to reduced diffusion. Changes to protein dynamics and diffusion can potentially contribute to reducing the dissociation rate and/or increasing the probability of CaM and target rebinding. For example, reduction in conformational dynamics of CaM lobes can inhibit the molecule from sampling the extended conformations required for forming the extended, unbound conformation. If molecules overcome this barrier and begin to dissociate, their rotational tumbling and translational diffusion is also inhibited. This presumably keeps reactive interfaces of binding partners in the right orientation and close proximity for a longer time, thereby decreasing the probability of completely separating in space and increasing the probability of quick rebinding. The experimental rate in this case is a concentration-independent one, indicating that total dissociation of partners and rebinding to different partners is not part of the measurement.

Having experimentally determined the association and dissociation rates under the various conditions, we were able to calculate an estimated dissociation constant from the relationship K_d = k_off/k_on. In all cases, these cosolutes decreased both on-rates and off-rates, resulting in little change in calculated dissociation constants (see K_d estimates in Table 2). This indicates that steady-state affinity does not seem to be substantially influenced by volume-exclusion or sucrose-mediated effects. To confirm these findings, we experimentally measured equilibrium constants of CaMKI peptide binding to Ca²⁺-saturated CaM using ITC in the presence or absence of 20% polymers or sucrose. Data was fit with a single binding-site model to determine K_a (Fig. S2 and Table S2). Consistent with the estimated K_d from k_off and k_on, no significant changes in measured affinity were observed in the presence of polymers or sucrose as compared to control.

Discussion

We discovered that ficoll-70, dextran-10, and sucrose each produce unique effects on the diffusion and association and dissociation rates of CaM with a target, processes that take place on distinct time- and spatial scales (for summary, see Table 3). Overall, these results show that differently sized molecules enhance or impede steps of the association process in distinctive ways. Our analysis of on-rates showing reduction of diffusional rate and increase in rate of conformational transition overall are consistent with the proposal that crowding will decrease rates when reactions are diffusion-limited and increase rates when they are reaction-limited (59). We further predict that in cases where conformational transitions are affected, rates are enhanced with formation of compactly bound structures and impeded when sampling of extended conformations is necessary or when molecules dissociate. Of the three differently sized cosolutes evaluated, we found that the smallest, sucrose, had the least impact on diffusion while the largest, ficoll-70, had the greatest. Interestingly, the reagent most similarly sized to CaM, dextran-10, had the most significant impact on rates of conformational change associated with on-rates. These size-dependent effects illustrate how the spatial scale of each step in a reaction pathway can be differentially influenced by environmental factors.

Table 3.

Summary of results

Property	Ficoll-70	Dextran-10	Sucrose
Structure
Interdomain distance	↓	↓	↓
Residue conformation	NC	NC	NC
Diffusion
Rotational tumbling	↓	↓	↓
Translational diffusion	↓	↓	↓
Steady-state affinity
Ca2+ affinity	NC	NC	↓
CaMKI peptide affinity	NC	NC	NC
Kinetic rates
CaMKI association	↓	↓	↓
Conformational rearrangements for binding	↑	↑	↑
CaMKI dissociation	↓	↓	↓

The effects of ficoll-70, dextran-10, and sucrose are summarized for each property of CaM investigated. (Arrows, increases and decreases; NC, no change.)

We discovered that reduction of both association and dissociation rates serve to counteract each other, resulting in little change in K_d in the presence of ficoll-70, dextran-10, and sucrose. We show that conformational dynamics are dampened as well as rotational tumbling and translational diffusion, the combination of which is likely responsible for this compensatory effect, complementary to the prediction proposed by Ellis (59). They propose that for association of molecules, crowding will reduce the diffusion component of the rate and increase the rate of conformational changes through the transition state. Correspondingly for molecule dissociation, the rate of conformational changes to dissociate is decreased and the rate of rebinding is increased due to favorable conformational transitions as well as reduction of molecule dissociation. Our steady-state measurements were insufficient to detect the impacts of crowders and osmolytes and instead nonequilibrium kinetic analyses were required. This finding may in part explain why crowding has shown variable impacts across different experimental systems (60,61). We assert that steady-state measurements are less informative to describe conditions in vivo where biochemical processes are at nonequilibrium (62). The modulation of kinetic reaction rates has potentially great consequences for controlling protein-protein interactions. In this case, the rate of association of proteins is functionally a more relevant kinetic parameter, where rapid association can enhance binding affinity. While slow dissociation also enhances binding affinity, long-lasting association is not ideal for temporal encoding by signaling molecules. Even with a fast off-rate, a protein can achieve short-lived high affinity at nonequilibrium because of rapid association. For a signaling molecule like CaM that has many potential intracellular targets, differences in association rates may be responsible for which target gets selected among the hundreds of potential possibilities. Because encounter of molecules is often the rate-limiting step of association, rapid binding may be more important than high steady-state affinity to determine how targets get chosen. With reaction rates occurring on several timescales, the composition of the cellular environment has the potential to differentially tune signaling processes occurring on different frequencies.

While cellular osmolyte concentration is dynamically regulated (49), the bulk concentration of macromolecules is believed to remain largely constant. However, the cytoplasm is organized in a nonrandom fashion, where organelles, non-membrane-bound phases, and large protein complexes serve to assemble variable and dynamic compositions of molecules (63–65). Interestingly, maintenance of bulk cellular concentration of molecules may be a necessary step to keep concentrations close to the threshold for liquid phase transitions (1). These phases can undergo dynamic reorganization where molecules selectively partition into or out of the phase, producing substantial kinetic consequences (66). Therefore, small changes in available volume within the phase, mediated by changes in cosolute concentration and composition, could potentially stimulate signaling responses that would otherwise not occur. This would seem to be an extremely efficient mechanism to tune localized signals without the need to alter the bulk-cellular concentration of cosolutes, and is particularly relevant for a molecule like CaM that depends on conformational plasticity for its function. This evolving appreciation for the dynamic organization of cell cytoplasm underscores the need to quantitatively assess the impacts of crowding and osmolytes in the regulation of protein function.

Author Contributions

L.H., M.S.C., and M.N.W. conceptualized the framework of the study. L.H. and M.N.W. designed and carried out experiments and interpreted data for FRET, steady-state affinity, kinetics, and FCS. X.W. and J.A.P. carried out and interpreted NMR experiments. H.S. carried out modeling of reaction pathways. L.H., H.S., and M.N.W. wrote the article.

Editor: Paul Wiseman.