fMRI-Based Inter-Subject Cortical Alignment Using Functional Connectivity

Abstract

The inter-subject alignment of functional MRI (fMRI) data is important for improving the statistical power of fMRI group analyses. In contrast to existing anatomically-based methods, we propose a novel multi-subject algorithm that derives a functional correspondence by aligning spatial patterns of functional connectivity across a set of subjects. We test our method on fMRI data collected during a movie viewing experiment. By cross-validating the results of our algorithm, we show that the correspondence successfully generalizes to a secondary movie dataset not used to derive the alignment.

1 Introduction

Functional MRI (fMRI) studies of human neuroanatomical organization commonly analyze fMRI data across a population of subjects. The effective use of this data requires deriving a spatial correspondence across the set of subjects, i.e., the data must be aligned, or registered, into a common coordinate space. Current inter-subject registration techniques derive this correspondence by aligning anatomically-defined features, e.g. major sulci and gyri, across subjects, either in the volume or on extracted cortical surfaces. Talairach normalization [1], for example, derives a piecewise affine transformation by matching a set of major anatomical landmarks in the brain volume. More advanced techniques match a denser set of anatomical features, such as cortical curvature [2], and derive nonlinear transformations between a reference space and each subject’s cortical surface.

It is known, however, that an accurate inter-subject functional correspondence cannot be derived using only anatomical features, since the size, shape and anatomical location of functional loci vary across subjects [3], [4]. Because of this deficiency in current alignment methods, it is common practice to spatially smooth each subject’s functional data prior to a population based analysis. However, this incurs the penalty of blurring the functional data within and across distinct cortical regions. Thus, the functional alignment of multi-subject fMRI data remains an important problem.

We propose to register functional loci directly by using anatomical and functional data to learn an inter-subject cortical correspondence. This approach was first explored in [5], where subject cortices were registered by maximizing the inter-subject correlation of the functional response elicited by a common stimulus (a movie viewing). In essence, the correspondence was selected to maximize the correlation of the fMRI time series between subjects. This relies on the functional response being time-locked with the experimental stimulus. Large regions of visual and auditory cortex stimulated by a movie viewing do indeed show consistent inter-subject synchrony [6]. However, other areas in the intrinsic [7] or default [8] system fail to exhibit significant correlations across repeated stimulus trials. The technique of [5] is hence not expected to improve alignment in these intrinsic regions.

In contrast to [5], we propose to achieve inter-subject alignment by aligning intra-subject patterns of cortical functional connectivity. By functional connectivity, we mean within-subject similarity of the temporal response of remote regions of cortex [9]. This can be estimated from fMRI data, for example, by correlating the functional time series between pairs of cortical nodes within a subject. This yields a dense set of functional features for each subject from which we learn an inter-subject correspondence. Unlike other functional connectivity work (see e.g. [10]), we define connectivity between pairs of cortical nodes rather than with respect to anatomical regions of interest. Our approach is inspired by studies showing that the patterns of functional connectivity in the intrinsic network are consistent across subjects [7], [11]. This suggests that our method has the potential to learn an inter-subject functional correspondence within both extrinsic and intrinsic cortical networks.

In summary, we formulate a multi-subject cortical alignment algorithm that minimizes the difference between functional connectivity vectors of corresponding cortical nodes across subjects. We do so by learning a dense-deformation field on the cortex of each subject, suitably regularized to preserve cortical topology [2]. Our key contributions are: a) the novel alignment objective, b) a principled algorithm for accomplishing the alignment, and c) experimental verification on fMRI data.

The paper is organized as follows. In §2 we formulate the multi-subject alignment problem, followed by a detailed exposition of the algorithm in §3 and§4. Finally, we exhibit results of the algorithm applied to multi-subject fMRI data in §5 and draw conclusions in§6.

2 Formulation of the Multi-Subject Alignment Problem

For each subject we are given volumetric anatomical MRI data and fMRI data. The anatomical data is used to extract a two-dimensional surface model of cortex. This greatly facilitates cortical based analysis and subsequent visualization [12], [13], [14]. Cortex is segmented, then each cortical hemisphere is inflated to obtain a smooth surface, which is projected to the sphere, S², represented by a discrete spherical mesh M_s = {p_k ∈ S²; 1 ≤ k ≤ N_v/2}. The two cortical hemispheres are hence modeled by the disjoint union S = S² ⊎ S², represented by the corresponding disjoint union of mesh points M = M_s ⊎ M_s. Anatomical cortical features, such as cortical curvature, are functions D_a : S → R^N_a sampled on M. Thus, our analysis is restricted to cortex only.

The fMRI volumeric data is first aligned with the anatomical scan, then mapped onto S. This assigns each mesh node p_k ∈ M a “volumetric cortical voxel” v_k ∈ ℝ³, with associated functional time series f_k ∈ ℝ^N_t. The functional time series data is then a function D_f: S → R^N_t sampled on M.

As indicated in the introduction, we do not directly register the fMRI time series but instead register the functional connectivity derived from the time series. Let σ(f₁, f₂) denote a similarity measure on pairs of time series f₁, f₂ ∈ R^N_t. A useful example is empirical correlation: σ(f₁, f₂) = corr(f₁, f₂); another possibility is an estimate of the mutual information between the pairwise entries of f₁, f₂. Define the functional connectivity of the fMRI data under σ as the map C(p_i, p_j) = σ(D_f(p_i), D_f(p_j)), i.e., the similarity of the functional times series at the pairs of cortical nodes. Functional connections both within and across cortical hemispheres are considered. Functional connectivity can be conceptualized as the adjacency matrix of an edge-weighted graph on all cortical nodes. The edge between nodes p_i, p_j is weighted by the pairwise similarity measure σ(f_i, f_j) codifying the functional similarity of p_i and p_j. In the case of correlation, C is the correlation matrix of the time series data. For typical values of N_v (≈ 72, 000), the functional connectivity data structure is huge. Hence we need efficient mechanisms for working with C.

We are given the data discussed above for N_s subjects. Subject k’s training data is specified by samples of the functions D_a,k : S_k → R^N_a, D_f,k : S_j → R^N_t, and the derived functional connectivity C_k, all sampled on the mesh M_k, k = 1, …, N_s. Our objective is to learn a relation consisting of N_s-tuples of corresponding points across the set of cortices. To do so, we could select a node from M₁ for subject 1 and learn the corresponding points on the cortices of the remaining N_s − 1 subjects through smooth and invertible mappings g_k : S₁ → S_k, k = 2, …, N_s. However, this arbitrarily and undesirably gives special status to one subject. Instead, we introduce a reference model S_ref = S² ⊎ S² with mesh M_ref. For each node p ∈ M_ref on S_ref, we seek to learn the N_s-tuple of corresponding points (g₁(p), g₂(p), …, g_Ns(p)), parameterized by g_k : S_ref → S_k, k = 1, …, N_s.

In general terms, we can now summarize our task as follows: use the functional connectivity data C_k, in conjunction with the anatomical data D_a,k, k = 1, …, N_s, to estimate warping functions {g_k : k = 1, …, N_s}, subject to specified regularity conditions, that bring some specified balance of anatomy and functional connectivity into alignment across subjects. That said, for the remainder of the paper we restrict attention to aligning only functional connectivity across subjects. There is no doubt that anatomy must be an integral part of a full solution; but that aspect is not new, and is already well understood. Restricting attention to the alignment of functional connectivity will allow us to concentrate on the most novel and important aspects of our approach.

To proceed, assume a reference connectivity C_ref, such that for each subject k = 1, …, N_s,

$$C_k(g_k(p_i),g_k(p_j))=C_{\text{ref}}(p_i,p_j)+{\epsilon }_k(p_i,p_j),p_i,p_j\in M_{\text{ref}}$$ (1)

where C_k(g_k(p_i), g_k(p_j)) = σ(D_f,k(g_k(p_i)), D_f,k(g_k(p_j))), and ε_k is zero-mean random noise. Since g_k(p) may not be a mesh point, computation of D_f,k(g_k(p)) requires interpolation of the time series using mesh nodes in a neighborhood of g_k(p). This will be important as we proceed.

Given (1), we estimate g by maximizing a regularized log likelihood:

$$\widehat{g}=arg\underset{g=(g_1,\cdots ,g_{N_s})}{max}logP(C_1,\dots ,C_{N_s}\mid g)-\lambda {\sum }_k\text{Reg}(g_k)$$ (2)

where Reg(g_k) constrains each warping function g_k to be smooth and invertible. Here, we will focus on the log likelihood term and delay the discussion of regularization to §3. Optimization of (2) is complicated by the fact that C_ref is a latent variable, so it must be estimated along with g. We use Expectation-Maximization to iteratively alternate between computing an expectation of C_ref (E-step), and a maximum likelihood estimate of g given both the observed and estimated unobserved data (M-step) [15]. In the E-step, the expectation of C_ref, C̄_ref, conditioned on the current estimate of g, ĝ, is computed by averaging the connectivity across subjects:

$${\overline{C}}_{\text{ref}}(p_i,p_j)=1/N_s{\sum }_{k=1}^{N_s}{C}_k({\widehat{g}}_k(p_i),{\widehat{g}}_k(p_j)),p_i,p_j\in S_{\text{ref}}$$ (3)

In the M-step, the estimate ḡ is refined to maximize the likelihood of the full data:

$$\widehat{g}=arg\underset{g=(g_1,\cdots ,g_{N_s})}{max}logP({\overline{C}}_{\text{ref}},C_1,C_2,\dots ,C_{N_s}\mid g)$$ (4a)

$$=arg\underset{g=(g_1,\cdots ,g_{N_s})}{min}{\sum }_{k=1}^{N_s}{\sum }_{p_i,p_j\in S_{\text{ref}}}{({\overline{C}}_{\text{ref}}(p_i,p_j)-C_k(g_k(p_i),g_k(p_j)))}^2$$ (4b)

where we have assumed that the noise in (1) is i.i.d. Gaussian. Because (4b) decouples, we can optimize over each subject’s warp separately, i.e., these optimizations can be done in parallel:

$${\widehat{g}}_k=arg\underset{g_k}{min}{\sum }_{p_i,p_j\in S_{\text{ref}}}{({\overline{C}}_{\text{ref}}(p_i,p_j)-C_k(g_k(p_i),g_k(p_j)))}^2$$ (5)

However, an interesting alternative is to perform these sequentially with an E-step after each that updates the reference estimate C̄_ref. This also allows some other interesting adaptations. We note:

$${({\overline{C}}_{\text{ref}}(p_i,p_j)-C_k(g_k(p_i),g_k(p_j)))}^2\propto {({\overline{C}}_k(p_i,p_j)-C_k(g_k(p_i),g_k(p_j)))}^2$$ (6a)

where

$${\overline{C}}_k(p_i,p_j)=\frac{1}{(N_s-1)}{\sum }_{n\ne k}{C}_n({\widehat{g}}_n(p_i),{\widehat{g}}_n(p_j)),p_i,p_j\in M_{\text{ref}},$$ (7)

is the leave-one-out template for subject k, which is indepedendent of g_k. Thus, we replace (5) by:

$${\widehat{g}}_k=arg\underset{g_k}{min}{\sum }_{p_i,p_j\in S_{\text{ref}}}{({\overline{C}}_k(p_i,p_j)-C_k(g_k(p_i),g_k(p_j)))}^2$$ (8)

From (5) and (8) we observe that the multi-subject alignment problem reduces to a sequence of pairwise registrations, each of which registers one subject to an average of connectivity matrices. If we use (5), each round of pairwise registrations can be done in parallel and the results used to update the average template. The difficulty is the computational update of C̄_ref. Alternatively, using (8) we do the pairwise registrations sequentially and compute a new leave-one-out template after each registration. This is the approach we pursue. An algorithm for solving the pairwise registration is derived in the next section and we examine the computation of leave-one-out templates in §4.

3 Pairwise Cortical Alignment

We now develop an algorithm for aligning one subject, with connectivity C_F, to a reference, with connectivity C_R, with C_F, C_R ∈ R^N_v×N_v. For concreteness, from this point forward we let σ(f₁, f₂) = corr(f₁, f₂) and assume that the time series have zero mean and unit norm.

A function g: M_R → S_F maps a reference mesh point p_i ∈ M_R to g(p_i) ∈ S_F. By interpolating the floating subject’s times series at the points g(p_i) ∈ S_F we obtain the associated warped functional connectivity: ${\stackrel{\sim }{C}}_F=[\sigma (f_{g(p_i)}^F,f_{g(p_j)}^F)]$. We seek ĝ that best matches C̃_F to C_R in the sense:

$$g=arg\underset{g}{min}{\left|\right|{\stackrel{\sim }{C}}_F-C_R\left|\right|}_f^2+\lambda \text{Reg}(g)$$ (9)

Here ||·||_f is the matrix Frobenius norm and the regularization term Reg(g) serves as a prior over the space of allowable mappings. In the following steps, we examine how to efficiently solve (9).

Step 1: Parameterizing the dependence of C̃_F on the warp

We first develop the dependence of the matrix C̃_F on the warping function g. This requires specifying how the time series at the warped points g(p_i) ∈ S_F is interpolated using the time series data { $f_i^F\in {ℝ}^{N_t}$, i = 1, …, N_v} at the mesh points { $p_i^F\in M_F$_, i = 1, …, N_v}. Here, we employ linear interpolation with a spherical kernel Φ: $f^F(p)={\sum }_{i=1}^{N_v}{f}_i^F\mathrm{\Phi }(p,p_i)$, p ∈ S_F. The kernel should be matched to the following specific objectives: (a) The kernel should be monomodal. Since the gradient of the registration objective depends on the derivative of the interpolation kernel, this will reduce the likelihood of the algorithm converging to a local minimum; (b) The support of the kernel should be finite. This will limit interpolation complexity. However, as the size of the support decreases, so will the capture range of the algorithm. At the initial stages of the algorithm, the kernel should have a broad extent, due to higher initial uncertainty, and become increasingly more localized as the algorithm converges. Thus, (c) The support of the kernel should be easily adjustable.

With these considerations in mind, we select Φ(p, p_i) to be a spherical radial basis function Φ_i : S² → ℝ centered at p_i ∈ S² and taking the form: Φ_i(p) = ϕ(d(p, p_i)), p ∈ S², where ϕ: [0, π] → ℝ and d(p, p_i) is the spherical geodesic distance between p and p_i [16]. Then Φ_i(p) is monomodal with a maximum at p_i, it depends only on the distance between p and p_i and is radially symmetric. In detail, we employ the particular spherical radial basis function:

$${\mathrm{\Phi }}_i(p)=\varphi (d(p,p_i))={(1-(2/r)sin(d(p,p_i)/2))}_{+}^4((8/r)sin(d(p,p_i)/2)+1)$$ (10)

where r is a fixed parameter, and (a)₊ = a1{a ≥ 0}. Φ_i(p) has two continuous derivatives and its support is {p ∈ S²: d(p, p_i) < 2sin⁻¹(r/2)}. Note that the support can be easily adjusted through the parameter r. So the kernel has all of our desired properties.

We can now make the dependence of C̃_F on g more explicit. Let $T_F=[f_1^F,f_2^F,\cdots ,f_{N_v}^F]$. Then ${\stackrel{\sim }{T}}_F=\left[\begin{array}{cccc}{f}^F(g(p_1))& f^F(g(p_2))& \cdots & f^F(g(p_{N_v}))\end{array}\right]=T_{F}A$ where A = [Φ_i(g(p_j))] is the N_v × N_v matrix of interpolation coefficients dependent on g and the interpolation kernel. Next, noting that $C_F=T_F^T{T}_F$, we use A to write the post-warp correlation matrix as:

$${\stackrel{\sim }{C}}_F=D{A}^T{C}_{F}AD$$ (11)

where D = diag(d₁, d_2, …, d_Nv) serves to normalize the updated data to unit norm: d_j = ||f^F(g(p_j))||⁻¹. Finally, we use à = AD to write:

$${\left|\right|{\stackrel{\sim }{C}}_F-C_R\left|\right|}_f^2={\left|\right|{\stackrel{\sim }{A}}^T{C}_F\stackrel{\sim }{A}-C_R\left|\right|}_f^2$$ (12)

Here, (12) encodes the dependence of the registration objective on g through the matrix Ã. It is also important to note that since the interpolation kernel is locally supported, Ã is a sparse matrix.

Step 2: Efficient Representation/Computation of the Registration Objective

We now consider the N_v × N_v matrices C_F and C_R. At a spatial resolution of 2 mm, the spherical model of human cortex can yield N_v ≈ 72, 000 total mesh points. In this situation, direct computation with C_F and C_R is prohibitive. Hence we need an efficient way to represent and compute the objective (12).

For fMRI data it is reasonable to assume that N_t ≪ N_v. Hence, since the data has been centered, the rank of $C_F=T_F^T{T}_F$ and of $C_R=T_R^T{T}_R$ is at most N_t − 1. For simplicity, we make the reasonable assumption that rank(T_F) = rank(T_R) = d. Then C_F and C_R can be efficiently represented by compact d-dimensional SVDs $C_F=V_F{\mathrm{\sum }}_F{V}_F^T$ and $C_R=V_R{\mathrm{\sum }}_R{V}_R^T$. Moveover, these can be computed directly from SVDs of the data matrices: $T_F=U_{T_F}{\mathrm{\sum }}_{T_F}{V}_{T_F}^T$ and $T_R=U_{T_R}{\mathrm{\sum }}_{T_R}{V}_{T_R}^T$. In detail:

V_F = V_TF, V_R = V_TR, ${\mathrm{\sum }}_F={\mathrm{\sum }}_{T_F}^T{\mathrm{\sum }}_{T_F}$, and ${\mathrm{\sum }}_R={\mathrm{\sum }}_{T_R}^T{\mathrm{\sum }}_{T_R}$.

The above representation avoids computing C_F and C_R, but we must also show that it enables efficient evaluation of (12). To this end, introduce the following linear transformation:

$$B=W_F^T\stackrel{\sim }{A}{W}_R$$ (13)

where $W_F=\left[\begin{array}{cc}{V}_F& V_F^{\perp }\end{array}\right],W_R=\left[\begin{array}{cc}{V}_R& V_R^{\perp }\end{array}\right]$, are orthogonal with the N_v − d columns of $V_F^{\perp }$ and $V_R^{\perp }$ forming orthonormal bases for range(V_F)^⊥ and range(V_R)^⊥, respectively. Write B as:

$$B=\left[\begin{array}{cc}{B}_1& B_2\\ B_3& B_4\end{array}\right]$$ (14)

with B₁ ∈ ℝ^d×d, B₂ ∈ ℝ^d×N_v, B₃ ∈ ℝ^(N_v−d)×d and B₄ ∈ ℝ^{(N_v−d)×(N_v−d)}. Substituting (13) and (14) into (12) and simplifying yields:

$${\left|\right|{\stackrel{\sim }{C}}_F-C_R\left|\right|}_f^2={\left|\right|B_1^T{\mathrm{\sum }}_F{B}_1-{\mathrm{\sum }}_R\left|\right|}_f^2+2{\left|\right|B_1^T{\mathrm{\sum }}_F{B}_2\left|\right|}_f^2+{\left|\right|B_2^T{\mathrm{\sum }}_F{B}_2\left|\right|}_f^2$$ (15)

with

$$B_1=V_F^T\stackrel{\sim }{A}{V}_R\text{and}{B}_2=V_F^T\stackrel{\sim }{A}{V}_R^{\perp }$$ (16)

The d × d matrix B₁ is readily computed since V_F, V_R are of manageable size. Computation of the d×N_v matrix B₂ depends on $V_R^{\perp }$. This has ON columns spanning the N_v − d dimensional subspace null(C_R). Since there is residual freedom in the choice of $V_R^{\perp }$ and B₂ is large, its selection merits closer examination. Now (16) can be viewed as a projection of the rows of $V_F^T\stackrel{\sim }{A}$ onto the columns of V_R and $V_R^{\perp }$. The columns of $\stackrel{\sim }{A}{V}_F-V_R{B}_1^T$ lie in null(C_R) and $B_2^T={(V_R^{\perp })}^T(\stackrel{\sim }{A}{V}_F-V_R{B}_1^T)$. Hence a QR-factorization $QR={\stackrel{\sim }{A}}^T{V}_F-V_R{B}_1^T$ yields d ON vectors in null(C_R). Choosing these as the first d columns of $V_R^{\perp }$, yields B2 = [R, 0], i.e., B₂ is very sparse.

In summary, we have derived the following efficient means of evaluating the objective. By onetime preprocessing of the time series data we obtain Σ_F, Σ_R and V_F, V_R. Then given a warp g, we compute: the interpolation matrix Ã, $B_1=V_F^T\stackrel{\sim }{A}{V}_R$, and finally B₂ via QR factorization of ${\stackrel{\sim }{A}}^T{V}_F-V_R{B}_1^T$. Then we evaluate (15).

Step 3: The Transformation Space and Regularization

We now examine the specification of g in greater detail. We allow each mesh point to move freely (locally) in two directions. The use of such nonlinear warp models for inter-subject cortical alignment has been validated over, for example, rigid-body transformations [17]. To specify g, we first need to set up a coordinate system on the sphere. Let U = {(φ, θ); 0 < φ < π, 0 < θ < 2π}. Then the sphere can be parameterized by x: U → ℝ³ with x(φ, θ) = (sin φ cos θ, sin φ sin θ, cos φ). Here, φ is a zenith angle measured against one of the principal axes, and θ is an azimuthal angle measured in one of the projective planes (i.e., xy-plane, xz-plane, or yz-plane). Note that x omits a semicircle of S²; so at least two such parameterizations are required to cover the entire sphere [18].

Consider p_i ∈ S² parameterized by x(φ, θ) such that p_i = x(φ_i, θ_i). Then the warp field at p_i is:

$$g(p_i)=x({\phi }_i+\mathrm{\Delta }{\phi }_i,{\theta }_i+\mathrm{\Delta }{\theta }_i)=x({\stackrel{\sim }{\phi }}_i,{\stackrel{\sim }{\theta }}_i)$$ (17)

for displacements Δφ_i and Δθ_i. The warp g is thus parameterized by: {φ̃_i, θ̃_i, i = 1, …, N_v}.

The warp g must be regularized to avoid undesired topological distortions (e.g. folding and excessive expansion) and to avoid over-fitting the data. This is achieved by adding a regularization term to the objective that penalizes such distortions. There are several ways this can be done. Here we follow [14] and regularize g by penalizing both metric and areal distortion. The metric distortion term penalizes warps that disrupt local distances between neighboring mesh nodes. This has the effect of limiting the expansion/contraction of cortex. The areal distortion term seeks to preserve a consistent orientation of the surface. Given a triangularization of the spherical mesh, each triangle is given an oriented normal vector that initially points radially outward from the sphere. Constraining the oriented area of all triangles to be positive prevents folds in the surface [14].

Step 4: Optimization of the objective

We optimize (3) over g by gradient descent. Denote the objective by S(g), let ã_ij = a_ijd_j be the (i, j)-th entry of à = AD and $a(p)={\left[\begin{array}{cccc}{\mathrm{\Phi }}_1(p)& {\mathrm{\Phi }}_2(p)& \cdots & {\mathrm{\Phi }}_{N_v}(p)\end{array}\right]}^T$. From the parameterization of the warp (17), we see that ã_ij = Φ_i(x(φ̃_j, θ̃_j))||T_F a(x(φ̃_j, θ̃_j))||⁻¹ depends only on the warp parameters of the j^th mesh node, φ̃_j and θ̃_j. Then, by the chain rule, the partial derivative of S(g) with respect to φ̃_j is given by:

$$\frac{\partial S(g)}{\partial {\stackrel{\sim }{\phi }}_j}={\sum }_{i=1}^{N_v}\frac{\partial {\left|\right|{\stackrel{\sim }{C}}_F-C_R\left|\right|}_f^2}{\partial {\stackrel{\sim }{a}}_{ij}}\frac{\partial {\stackrel{\sim }{a}}_{ij}}{\partial {\stackrel{\sim }{\phi }}_j}+\lambda \frac{\partial \text{Reg}(g)}{\partial {\stackrel{\sim }{\phi }}_j}$$ (18)

A similar expression is obtained for the partial derivative with respect to θ̃_j. Since the interpolation kernel is supported locally, the summation in (18) is taken over a small number of terms. A full expression for ∂S/∂φ̃_j is given in the supplemental, and that of ∂Reg(g)/∂φ̃_j in [14].

To help avoid local minima we take a multi-resolution optimization approach [19]. The registration is run on a sequence of spatial resolutions r₁ > r₂ > ··· > r_M, with r_M given by the original resolution of the data. The result at resolution r_m is used to initialize the alignment at resolution r_m+1. The alignment for r_m is performed by matching the kernel parameter r in (10) to r_m. Note that the reference dataset is also spatially smoothed at each r_m by the transformation in (11), with A = [a(p₁) a(p₂) ··· a(pN_v)]. The pairwise algorithm is summarized as Algorithm 1 in Figure 1.

Figure 1.

The registration algorithms.

4 Multi-Subject Alignment: Computing Leave-one-out Templates

We now return to the multi-subject alignment problem, which is summarized as Algorithm 2 in Figure 1. It only remains to discuss efficient computation of the leave-one-out-template (7). Since C̄_k is an average of N_s − 1 positive semi-definite matrices each of rank d, the rank d̄ of C̄_k is bounded as follows d ≤ d̄ ≤ (N_s − 1)d. Assume that C̃_n, the connectivity matrix of subject n after warp g_n (see (11)), has an efficient d ≪ N_v dimensional SVD representation ${\stackrel{\sim }{C}}_n={\stackrel{\sim }{V}}_n{\mathrm{\sum }^{\sim }}_n{\stackrel{\sim }{V}}_n^T$.

To compute the SVD for C̄_k, we exploit the sequential nature of the multi-subject alignment algorithm by refining the SVD of the leave-one-out template for subject k−1, ${\overline{C}}_{k-1}={\overline{V}}_{k-1}{\overline{\mathrm{\sum }}}_{k-1}{\overline{V}}_{k-1}^T$, computed in the previous iteration. This is achieved by expressing C̄_k in terms of C̄_k−1:

$${\overline{C}}_k={\overline{C}}_{k-1}+\frac{1}{N_s-1}({\stackrel{\sim }{C}}_{k-1}-{\stackrel{\sim }{C}}_k)$$ (19)

and computing matrix decompositions for the singular vectors of C̃_k−1 and C̃_k in terms of V̄_k−1:

$${\stackrel{\sim }{V}}_{k-1}={\overline{V}}_{k-1}{P}_{k-1}+Q_{k-1}{R}_{k-1}$$ (20a)

$${\stackrel{\sim }{V}}_k={\overline{V}}_{k-1}{P}_k$$ (20b)

where $P_j={\overline{V}}_{k-1}^T{\stackrel{\sim }{V}}_j\in {ℝ}^{\overline{d}\times d}$, for j = k − 1, k, projects the columns of Ṽ_j onto the columns of V̄_k−1. The second term of (20a), Q_k−1R_k−1, is the QR-decomposition of the residual components of Ṽ_k−1 after projection onto range(V̄_k−1). Since C̄_k−1 is an average of positive semi-definite matrices that includes C̃_k, we are sure that range(Ṽ_k) ⊆ range(V̄_k−1), (supplementary material).

Using the matrix decompositions (20a) and (20b), C̄_k in (19) above can be expressed as:

$${\overline{C}}_k=\left[\begin{array}{cc}{\overline{V}}_{k-1}& Q_{k-1}\end{array}\right]G{\left[\begin{array}{cc}{\overline{V}}_{k-1}& Q_{k-1}\end{array}\right]}^T$$ (21)

where G is the symmetric (d̄ + d) × (d̄ + d) matrix:

$$G=\left[\begin{array}{cc}{\overline{\mathrm{\sum }}}_{k-1}& 0\\ 0& 0\end{array}\right]+\frac{1}{N_s-1}(\left[\begin{array}{cc}{P}_{k-1}{\mathrm{\sum }^{\sim }}_{k-1}{P}_{k-1}^T& P_{k-1}{\mathrm{\sum }^{\sim }}_{k-1}{R}_{k-1}^T\\ R_{k-1}{\mathrm{\sum }^{\sim }}_{k-1}{P}_{k-1}^T& R_{k-1}{\mathrm{\sum }^{\sim }}_{k-1}{R}_{k-1}^T\end{array}\right]-\left[\begin{array}{cc}{P}_k{\mathrm{\sum }^{\sim }}_k{P}_k^T& 0\\ 0& 0\end{array}\right])$$ (22)

We now compute the SVD of $G=V_G{\mathrm{\sum }}_G{V}_G^T$. Then, using (21), we obtain the SVD for C̄_k as:

$${\overline{V}}_k=\left[\begin{array}{cc}{\overline{V}}_{k-1}& Q_{k-1}\end{array}\right]V_G\text{and}{\overline{\mathrm{\sum }}}_k={\mathrm{\sum }}_G$$ (23)

For a moderate number of subjects, (d̄ + d) ≤ N_sd ≪ N_v, this approach is more efficient than a brute-force $O(N_v^3)\text{SVD}$. Additionally, it works directly on the singular values Σ̃_k and vectors Ṽ_k of each warped connectivity matrix C̃_k, alleviating the need to store large N_v × N_v matrices.

5 Experimental Results

We tested the algorithm using fMRI data collected from 10 subjects viewing a movie split into 2 sessions separated by a short break. The data was preprocessed following [5]. For each subject, a structural scan was acquired before each session, from which the cortical surface model was derived (§2) and then anatomically aligned to a template using FreeSurfer (Fischl, http://surfer.nmr.mgh.harvard.edu). Similar to [5], we find that anatomical alignment based on cortical curvature serves as a superior starting point for functional alignment over Talairach alignment.

First, functional connectivity was found for each subject and session: C_k,i, k = 1, …, N_s, i = 1, 2. These were then aligned within subjects, C_k,₁ ↔ C_k,2, and across subjects, C_k,1 ↔ C_j,2, using Algorithm 1. Since the data starts in anatomical correspondence, we expect small warp displacements within subject and larger ones across subjects. The mean intra-subject warp displacement was 0.72 mm (σ = 0.48), with 77% of the mesh nodes warped less than 1 mm and fewer than 1.5% warped by more than the data spatial resolution (2 mm). In contrast, the mean inter-subject warp displacement was 1.46 mm (σ = 0.92 mm), with 22% of nodes warped more than 2 mm. See Figures 2(a)–(b).

Figure 2.

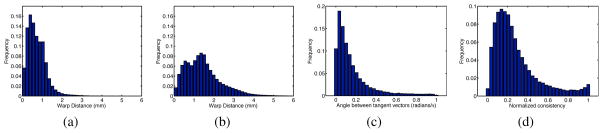
Consistency Histograms. (a) Intra-subject warp distances; (b) Inter-subject warp distances; (c) Angle between warp vectors across sessions; (d) Across-session normalized warp consistency measure WNC.

In a separate analysis, each subject was aligned to its leave-one-out template on each session using Algorithm 1, yielding a set of warps g_k,i(p_j), k = 1, …, N_s, i = 1, 2, j = 1, …, N_v. To evaluate the consistency of the correspondence derived from different sessions, we compared the warps g_k,1 to g_k,2 for each subject k. Here, we only consider nodes that are warped by at least the data resolution. This analysis provides a measure of the sensitivity to noise present in the fMRI data. At node p_j, we compute the angle 0 ≤ θ ≤ π between the warp tangent vectors of g_k,1(p_j) and g_k,2(p_j). This measures the consistency of the direction of the warp across sessions: smaller values of θ suggest a greater warp coherence across sessions. Figure 2(c) shows a histogram of θ averaged across the cortical nodes of all 10 subjects. The tight distribution centered near θ = 0 suggests significant consistency in the warp direction across sessions. In particular, 93% of the density for θ lies inside π/2, 81% inside π/4, and 58% inside π/8. As a secondary comparison, we compute a normalized consistency measure WNC(p_j) = d(g_k,1(p_j), g_k,2(p_j))/(d(g_k,1(p_j), p_j) + d(g_k,2(p_j), p_j)), where d(·, ·) is spherical geodesic distance. The measure takes variability in both warp angle and magnitude into account; it is bounded between 0 and 1, and WNC(p_j) = 0 only if g_k,1(p_j) = g_k,2(p_j). A histogram for WNC is given in 2(d); WNC exhibits a peak at 0.15, with a mean of 0.28 (σ = 0.22).

Finally, Algorithm 2 was applied to the first session fMRI data to learn a set of warps g = (g₁, …, gN_s) for 10 subjects. The alignment required approximately 10 hours on a Intel 3.8GHz Nehalem quad-core processor with 12GB RAM. To evaluate the alignment, we apply the warps to the held out second session fMRI data, where subjects viewed a different segment of the movie. This warping yields data { $f_{g_k(p_i)}^k$} for each subject k, with interpolation performed in the original volume to avoid artificial smoothing. The cross-validated inter-subject correlation ISC(p_i) is the mean correlation of each subject’s functional time series with the mean time series of the other subjects:

$$\text{ISC}(p_i)=(1/N_s){\sum }_{k=1}^{N_s}\text{corr}(f_{g_k(p_i)}^k,{\sum }_{n\ne k}{f}_{g_n(p_i)}^n),p_i\in M_{\text{ref}}$$ (24)

We also compute the mean inter-subject correlation, $\text{ISC}=(1/N_v){\sum }_{i=1}^{N_v}\text{ISC}(p_i)$.

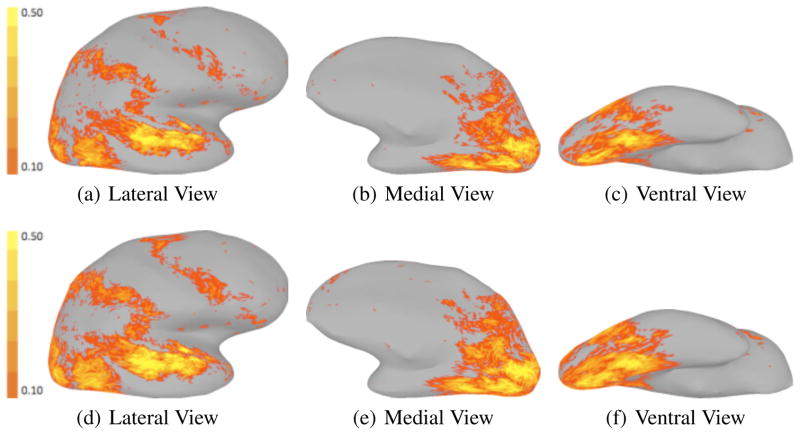
We compare the cross-validated ISC map with the ISC map of the second session movie viewing computed under anatomical correspondence. Mean ISC improved by 18%, from 0.072 to 0.085. In addition, the number of significant inter-subject correlations (ISC(p_i) > 0.1, P < 0.01) increased by 22.9%, from 19, 362 to 23, 789. Figure 3 shows the ISC maps computed under anatomical alignment and functional alignment on the inflated right cortical hemisphere. As expected, the areas of improvement in inter-subject correlation are consistent with the extrinsic regions of cortex [6].

Figure 3.

Map of ISC on right cortical hemisphere, alignment: anatomical (top), functional (bottom).

6 Conclusion

We have proposed a novel cortical registration algorithm that produces a functional correspondence across a set of subjects. The algorithm uses the fMRI data directly to align the spatial patterns of functional response elicited by a movie viewing. Despite the high-dimensionality of the data under consideration, the algorithm is efficient in both space and time complexity.

By comparing the inter-subject alignments derived from different fMRI experimental sessions, we show that the correspondence is consistent and robust to noise and variability in the fMRI temporal response. We also cross-validate the correspondence on independent test data that was not used to derive the alignment. On the test data, the algorithm produces a consistent increase in inter-subject correlation of fMRI time series, suggesting that functional alignment of extrinsic regions of cortex that are directly driven by the movie viewing experiment, such as visual and auditory areas, is improved considerably. Further testing is warranted to evaluate improvement in intrinsic areas of cortex whose response is not temporally synchronized with the experimental stimulus.