Incorporating Functional Information in Tests of Excess De Novo Mutational Load

Abstract

A number of recent studies have investigated the role of de novo mutations in various neurodevelopmental and neuropsychiatric disorders. These studies attempt to implicate causal genes by looking for an excess load of de novo mutations within those genes. Current statistical methods for assessing this excess are based on the implicit assumption that all qualifying mutations in a gene contribute equally to disease. However, it is well established that different mutations can have radically different effects on the ultimate protein product and, as a result, on disease risk. Here, we propose a method, fitDNM, that incorporates functional information in a test of excess de novo mutational load. Specifically, we derive score statistics from a retrospective likelihood that incorporates the probability of a mutation being damaging to gene function. We show that, under the null, the resulting test statistic is distributed as a weighted sum of Poisson random variables and we implement a saddlepoint approximation of this distribution to obtain accurate p values. Using simulation, we have shown that our method outperforms current methods in terms of statistical power while maintaining validity. We have applied this approach to four de novo mutation datasets of neurodevelopmental and neuropsychiatric disorders: autism spectrum disorder, epileptic encephalopathy, schizophrenia, and severe intellectual disability. Our approach also implicates genes that have been implicated by existing methods. Furthermore, our approach provides strong statistical evidence supporting two potentially causal genes: SUV420H1 in autism spectrum disorder and TRIO in a combined analysis of the four neurodevelopmental and neuropsychiatric disorders investigated here.

Introduction

Germline de novo mutations are genetic alterations that occur, for the first time, in the gametes that make up an individual and, as such, are not inherited from parents. De novo mutations generally occur at a rate of approximately 1.18 × 10⁻⁸ per locus per generation.^1,2 Because de novo mutations generally have not been pruned out of the population by purifying selection, they are often more likely to be considered associated with sporadic genetic-disease risk than are inherited variants.^3–5 Next-generation-sequencing technologies have made the detection of de novo mutations and the investigation of their role in human disease feasible. Indeed, de novo mutations have been reported to play an important role in several complex diseases, including severe intellectual disability (ID),⁶ epileptic encephalopathy (EE [MIM: 308350]),⁷ and autism spectrum disorder (ASD).^8,9

One goal of de novo mutation studies is to identify disease-associated genes by contrasting observed and expected patterns of de novo mutations in affected individuals, i.e., find genes with more de novo mutations among a cohort of similarly affected individuals than one would expect to see in a random sample of individuals from the general population. How one characterizes this expected distribution is critical, and the distribution obviously changes with the size and mutability of the gene. Because de novo mutations tend to originate independently of one another, recent work has characterized the expected distribution with a Poisson model, in which the sequence-context-informed mutation rate is summed over the “callable sequence real estate” of a gene to represent the gene-specific mutation rate.⁷ This approach, which we refer to as the “Poisson test,” has already been successfully applied to a number of de novo mutation studies, including studies of EE⁷ and ASD.¹⁰

The Poisson test, however, implicitly assumes that all de novo mutations found within the gene have the same influence on disease. It is well established that different mutations can have radically different impacts on the ultimate protein product, leading to vastly different effects on disease. Thus, when looking for shifts from expectation in the distribution of de novo mutations in an affected sample, considering the potential impact of those mutations could be important given that one might see a shift only in certain classes of mutations. There is some evidence that this is the case. For example, in the de novo mutation studies of ASD, although researchers could not establish a significant overall excess of de novo mutations given their cohort sizes, they did observe that the total number of non-synonymous de novo SNVs was significantly greater in probands than in their unaffected siblings.^9,11 Another study of ASD has reported finding an increased frequency of loss-of-function (LOF) mutations in probands relative to that in their unaffected siblings.⁸ Similar results have been observed in the study of severe ID; Rauch et al. found a higher proportion of individuals with LOF mutations among an affected group than they did among those in a control group.¹² These results suggest that a mutation’s predicted impact on gene function is an important factor in assessing the “burden” of de novo variants within a gene.

In this manuscript, we propose a de novo mutational load test that incorporates predictions of mutation functionality. In brief, the contribution of each de novo mutation is weighted by its predicted damage to the ultimate gene product with which it is affiliated. Weighting in this way is expected to add considerable power when damaging mutations in affected individuals are enriched over expectation based on the mutational process of the gene being considered.

There are multiple variant-annotation tools that can provide in silico predictions of the most likely functional impact of individual de novo mutations. For example, PolyPhen-2, SIFT, and others can be used to estimate the effect of missense mutations.^13,14 SIFT calculates the probability that an amino acid at a position is tolerated, whereas a PolyPhen-2 score is the naive Bayes posterior probability that a given mutation is damaging. Both methods quantitatively characterize the predicted functionality of these mutations. More recently, attempts have been made to assess variant functionality across the genome. For example, the recently developed C scores can be used to predict the effect of any possible human single-nucleotide variant or indel, even those found in introns or intergenic regions.¹⁵

One approach to incorporating variant functional impact in tests of de novo enrichment is to do so qualitatively by only considering certain classes of variation in the analysis. For example, in their TADA-denovo method, He et al.¹⁶ include only LOF mutations and missense mutations predicted to be probably damaging by PolyPhen-2. This approach is likely to work well if the truly damaging mutations are strongly clustered into the classes of variation incorporated in the statistic. However, in the absence of such strong clustering, this approach can ignore important mutations leading to a loss of power. Along these lines, we note that 21% of ClinVar pathogenic missense variants (i.e., missense mutations annotated as disease causal) would not be annotated as probably damaging.

In the next section, we develop a method that quantitatively incorporates functional information in a test of excess de novo mutational load (fitDNM) and show that, under the null, the test is distributed as a weighted sum of independent Poisson random variables. Interestingly, the cumulative distribution function of the resulting distribution is not available in closed form, and we show how p values can be accurately estimated with a saddlepoint approximation. In the Results section, we compare our test with the Poisson test and TADA-denovo method via simulations. Finally, we apply our method to analyze de novo mutations in 1,717 samples ascertained for an EE, ASD, severe ID, or schizophrenia (SZ) diagnosis.

Material and Methods

General Framework

The goal of a de novo load analysis is to identify disease genes by detecting an unexpected clustering of de novo mutations in the genes of affected individuals. In this section, we lay out a framework for an excess de novo load test that formally incorporates variant functionality. We begin by making three simplifying assumptions. First, we consider only loci that are non-polymorphic in the parents. Polymorphic loci represent a small fraction of the genome and are less likely to be functionally significant. Second, we assume that having two de novo mutations at the same site within an individual is rare enough to be negligible. Finally, we assume that the effect of a de novo mutation on offspring disease risk is the same regardless of whether the mutation is maternally or paternally derived; i.e., we ignore parent-of-origin effects. Under these three assumptions, the problem is greatly simplified, given that there are only four possible events that can occur in any given trio at any given site: there is either no mutation, so that the offspring retains two copies of the reference base, or there is a new mutation on one of the offspring’s haplotypes from the reference base to one of three alternative bases at that reference site. Because the reference base is potentially different at each locus $l$, we denote these four possible events as $x_{l0},x_{l1},x_{l2}$, and $x_{l3}$, where $x_{l0}$ represents the no-mutation event and $x_{l1},x_{l2}$, and $x_{l3}$ represent de novo mutations from the reference to the three alternative bases. For example, if, at locus $l$, the reference base was A, $x_{l0}$ would represent the null mutation from A $\to$ A, and $x_{l1},x_{l2},$ and $x_{l3}$ could represent de novo mutations A $\to$ C, A $\to$ G, and A $\to$ T, respectively. Let $X_{il}$ be the random variable denoting which of these events are observed at locus $l$ in trio $i$.

Characterizing the Distribution of De Novo Mutations at a Single Locus

We begin with two definitions that will help clarify the development below. First, we define a mutation to be “damaging” when it can destroy or severely impact gene function; i.e., it causes the gene to become “dysfunctional.” Second, we define a gene to be “pathogenic” when the presence of a dysfunctional gene product increases disease risk.

We characterize the distribution of de novo mutations in an affected individual at a single locus; i.e., $\mathrm{Pr}\left(X_{il}=x_{lk}\text{|}{A}_i=1\right)$, where $A_i=1$, denotes that the offspring in trio $i$ is affected. To simplify the notation, we define ${\lambda }_{lk}\equiv \mathrm{Pr}\left(X_{il}=x_{lk}\text{|}{A}_i=1\right)$. Using Bayes’ theorem and the total law of probability, we get

$${\lambda }_{lk}=\frac{{\pi }_{lk}\text{Pr}\left(A_i=1|X_{il}=x_{lk}\right)}{{\sum }_{k^{\ast }=0}^3{\pi }_{l{k}^{\ast }}\text{Pr}\left(A_i=1|X_{il}=x_{l{k}^{\ast }}\right)},$$ (Equation 1)

where ${\pi }_{lk}=\text{P}\text{r}\left(X_{il}=x_{lk}\right)$ and is the probability of mutation event $x_{lk}$ per individual in the general (unselected by disease) population.

The impact of mutations on disease is most likely mediated by protein function, i.e., by the effect of a mutation on protein structure or expression. Our approach attempts to leverage what is known about the functional impact of specific mutations on protein function into a test of association between mutation and disease. To do so, we expand the risk of a mutation, i.e., $\mathrm{Pr}\left(A_i=1\text{|}{X}_{il}=x_{lk}\right)$, to incorporate the probability that the mutation is damaging to protein function. Specifically, we write

$$\mathrm{Pr}\left(A_i=1\text{|}{X}_{il}=x_{lk}\right)=\sum _{d=0}^1\mathrm{Pr}\left(A_i=1\text{|}{X}_{il}=x_{lk},D=d\right)\mathrm{Pr}\left(D=d\text{|}{X}_{il}=x_{lk}\right),$$

where $D$ is an indicator of whether protein function is deleteriously impacted $\left(D=1\right)$ or not $\left(D=0\right)$. We assume that once we determine whether a protein is dysfunctional, the exact mutation no longer informs on disease risk, i.e., $\mathrm{Pr}\left(A_i=1\text{|}{X}_{il}=x_{lk},D=d\right)=\mathrm{Pr}\left(A_i=1\text{|}D=d\right)$. Let $\gamma$ denote the relative risk of an individual being affected with dysfunctional protein product in comparison to the likelihood of an individual having normal protein, i.e., $\text{γ}=\text{P}\text{r}\left(A_i=1\text{|}D=1\right)/\text{P}\text{r}\left(A_i=1\text{|}D=0\right)$. Thus, by factoring out $\text{P}\text{r}\left(A_i=1\text{|}D=0\right)$ and rearranging terms, we have that $\mathrm{Pr}\left(A_i=1\text{|}{X}_{il}=x_{lk}\right)=\text{P}\text{r}\left(A_i=1\text{|}D=0\right)\left[1+\left(\text{γ}-1\right){\rho }_{lk}\right],$

where ${\rho }_{lk}\equiv \text{P}\text{r}\left(D=1|X_{il}=x_{lk}\right)$. Plugging this back into Equation 1, we have

$${\lambda }_{lk}=\frac{\left[1+\left(\text{γ}-1\right){\rho }_{lk}\right]{\pi }_{lk}}{{\sum }_{k^{\ast }=0}^3\left[1+\left(\text{γ}-1\right){\rho }_{l{k}^{\ast }}\right]{\pi }_{l{k}^{\ast }}}.$$ (Equation 2)

Note that Equation 2 allows us to characterize the distribution of de novo mutations at locus $l$ in terms of the risk parameter $\gamma$; the probability that the mutation is damaging to protein function, ${\rho }_{lk}$; and the probability of observing such a mutation in an unselected sample, ${\pi }_{lk}$. The parameter of interest is $\gamma$, whereas ${\rho }_{lk}$ and ${\pi }_{lk}$ are estimated from external data and are assumed to be known. We will discuss how ${\rho }_{lk}$ and ${\pi }_{lk}$ are estimated below.

Assume we have a sample of $n_l$ trios at locus $l$, and let $N_{lk}={\sum }_{i=1}^{n_l}I\left(X_{il}=x_{lk}\right)$ and $k=0,1,2,\text{o}\text{r}3$ where $I$ is an indicator function. We let the number of trios be a function of $l$ to account for the fact that different sites might lead to a different subset of the total sample size being “callable,” i.e., to have adequate coverage and quality characteristics so that a de novo mutation would have a reasonable chance of being called if in fact it existed. Furthermore, when testing genes on the X chromosome, in order to account for differences in the number of chromosomes between males and females, we replace $n_l$ above with $n_l=\left(n_{lm}/2\right)+n_{lf}$, where $n_{lm}$ and $n_{lf}$ are the number of callable male offspring trios and callable female offspring trios, respectively, at locus $l$. It is not hard to see that the distribution of de novo mutations at locus $l$ is multinomial, i.e.,

$$\left(N_{l0},N_{l1},N_{l2},N_{l3}\right)\sim \text{Multinomial}\left(n_l,{\lambda }_{l0},{\lambda }_{l1},{\lambda }_{l2},{\lambda }_{l3}\right).$$ (Equation 3)

The de novo mutation rate, ${\pi }_{lk},$ where k = 1, 2, or 3, is often around 10⁻⁸ per locus per meiosis.¹ As a result, ${\lambda }_{l1},{\lambda }_{l2},$ and ${\lambda }_{l3}$ will be far smaller than ${\lambda }_{l0}$. In this situation, it can be shown that $\left(N_{l1},N_{l2},N_{l3}\right)$ can be accurately approximated by three independent Poisson random variables with means $n_l{\lambda }_{l1},n_l{\lambda }_{l2},$ and $n_l{\lambda }_{l3}$.¹⁷ We let $\left(n_{l0},n_{l1},n_{l2},n_{l3}\right)$ denote observed realizations of the random variables $\left(N_{l0},N_{l1},N_{l2},N_{l3}\right).$

Gene-Level Test of Excess De Novo Load

Equations 2 and 3 allow us to characterize the distribution of de novo mutations at a given locus among trios sampled on the basis of the offspring being affected. In order to derive a gene-level test, we characterize the distribution of de novo mutations throughout a gene. Note that “gene” here is being used rather generically and could include both coding-sequence sites as well as other sites thought to contribute to gene function (regulatory sites, splice sites, etc.), as well as collections of biologically grouped genes. Assume there are $p$ sites across the gene. Given that de novo mutations are thought to occur independently across loci,^7,18 by using the Poisson approximation highlighted above, we find that the likelihood can be written as

$$\prod _{l=1}^p\prod _{k=1}^3\frac{{\left({\lambda }_{lk}{n}_l\right)}^{n_{lk}}{e}^{-{\lambda }_{lk}{n}_l}}{n_{lk}!},$$ (Equation 4)

where ${\lambda }_{lk}$ is given by Equation 2. Taking the log of Equation 4, differentiating with respect to $\gamma$, and evaluating under the null hypothesis that the gene is not pathogenic, i.e., $\text{γ}=1$, leads to the score statistic

$$S_{\gamma }=\sum _{l=1}^p\sum _{k=1}^3{w}_{lk}{n}_{lk}-\sum _{l=1}^p\sum _{k=1}^3{w}_{lk}{\pi }_{lk}{n}_l,$$ (Equation 5)

where $w_{lk}={\rho }_{lk}-{\sum }_{k^{\ast }=0}^3{\rho }_{l{k}^{\ast }}{\pi }_{l{k}^{\ast }}$. Note that the second term of $S_{\gamma }$ is made up of known parameters and can be considered fixed. Under the null hypothesis, the first term of $S_{\gamma }$, i.e.,

$$T=\sum _{l=1}^p\sum _{k=1}^3{w}_{lk}{n}_{lk},$$ (Equation 6)

is a realization of a weighted (by the known weights $w_{lk}$, where k = 1, 2, or 3) sum of independent Poisson random variables, and a test (fitDNM) of excess de novo load can be constructed in terms of the quantiles of this distribution.

Saddlepoint Approximation for Null Distribution of Excess De Novo Load Test

Interestingly, we could not find an analytic method for computing cumulative probabilities for a weighted sum of independent Poisson random variables. Though a number of approximation methods have been proposed,¹⁹ they are based on moment matching and can be quite inaccurate in the extreme tails of the distribution. Because we are interested in genome-wide inference, in order to meet multiple testing thresholds, we are often interested in accurately estimating p values in the extreme tail (on the order of 10⁻⁶), making such approaches a poor choice. Because the cumulant generating function (CGF) is readily available for the weighted sum of independent Poisson random variables, both Edgeworth and saddlepoint approximations are possible. However, saddlepoint approximations have a decided advantage in our application given that Edgeworth approximations can only control the absolute error of the approximation, whereas saddlepoint approximations can control the relative error. This makes the saddlepoint approximation far more accurate in the tail. As a result, we have developed a saddlepoint approximation of the null distribution of our proposed statistic. Details can be found in Appendix A.

Mutation-Rate and Variant-Functionality Score Estimation

Both the mutation rates, i.e., the ${\pi }_{lk}$ values, and the probabilities of a mutation functionally impacting the gene, i.e., the ${\rho }_{lk}$ values, were estimated from external data and, thus, were assumed to be known and fixed. The locus-specific mutation rate per generation, ${\pi }_{lk}$,was computed on the basis of local sequence context² and the average de novo mutation rate (1.18 × 10⁻⁸).¹ Specifically, we began with a trinucleotide-based mutation matrix (provided by Drs. Shamil Sunyaey and Paz Polak) that characterizes the relative mutation rate of any base given its immediate flanking bases. We then derived locus-specific mutation rates by calibrating the relative rates so that, when integrated over the entire human reference genome, the average human de novo mutation rate (1.18 × 10⁻⁸) was obtained. In these analyses, we computed the de novo mutation rates for all possible non-null transitions. For example, in a locus with reference base A, we computed the mutation rate for alleles T, C, and G.

We used the following approach to estimating the ${\rho }_{lk}$ values. For loss-of-function single-nucleotide-substitution mutations predicted by SnpEff,²⁰ such as gain or loss of stop codon mutations, mutations in a canonical splice site, etc., we set ${\rho }_{lk}$ = 1. We set ${\rho }_{lk}$ = 0 for synonymous mutations. In all missense cases, ${\rho }_{lk}$ was set by PolyPhen-2 (HumDiv) to the probability that the mutation is damaging output.¹³ When multiple scores for different transcripts were available, the maximum score was used. When PolyPhen-2 predictions were not available, we removed that locus from our analysis. Note that the analyses presented here did not consider frameshift or codon indels because the mutation rates for these mutations are currently difficult to estimate reliably. However, when reliable estimates become available, our approach will be able to easily incorporate these classes of variation.

Simulation Studies

Simulation studies were performed to evaluate the accuracy of the saddlepoint approximation and to compare the power of our proposed de novo load test with that of the standard Poisson test.

Accuracy of Saddlepoint Approximation

In order to evaluate the performance of the saddlepoint approximation in a realistic setting, we based our simulations on a real, average-sized gene, GABRB3 (MIM: 137192). GABRB3 has 1,573 protein-coding loci according to the consensus coding sequence (CCDS) project (CCDS release 14; Genome Reference Consortium GRCh37), whereas the mean and median sizes of genes across the genome are approximately 1.7 kbp and 1.3 kbp, respectively. Both the ${\pi }_{lk}$ and the ${\rho }_{lk}$ values (and, hence, the $w_{lk}$ values) used in the simulation were defined by those observed in GABRB3. For each simulated dataset, we generated $N_{lk}$, i.e., the number of mutations of type $k$ at locus $l$, by sampling from a Poisson distribution with mean $n{\pi }_{lk}$ where $n$ is the total number of trios being simulated. Given the $N_{lk}$ values, we generated a weighted sum of Poisson random variables under the null by $Y={\sum }_{l=1}^m{\sum }_{k=1}^3{w}_{lk}{N}_{lk}$. Repeating this process 10⁸ times allowed us to reliably estimate the quantiles of the null distribution of $Y$ (down to quantiles on the order of 10⁻⁶). We compared our saddlepoint approximation to these empirical quantiles in order to evaluate the accuracy of the approximation. Specifically, we used the relative error defined as the ratio of the absolute difference between p values estimated by the saddlepoint approximation and those derived from the empirical distribution of $Y$ to the minimum of these two p values.

Power and Type I Error

Here, we compared the power and type I error of fitDNM to those of the Poisson test and TADA-denovo. To get a broader perspective on how incorporating functional information affects the performance of the test, we modeled our simulations on the basis of three genes (TSGA13, GABRB3, and KIRREL3 [MIM: 607761]) representing a spectrum of gene size. We also generated a hypothetical gene, which has an exact size of 1.5 kbp (corresponding to average gene size across the genome) and for which PolyPhen-2 scores and mutation rates were randomly sampled from the 222 genes observed to harbor de novo mutations in our data. We based our simulated sample sizes (ranging from 150 to 2,000 samples) on the number of trios used in the real data analysis described below. We simulated the data prospectively, simulating de novo mutations in the offspring of individuals from the general population, determining disease status on the basis of those mutations, and then sampling the given number of trios with affected offspring. Specifically, for each individual in the general population, de novo mutations (or the null mutation) at each of $p$ sites were generated from a multinomial distribution, i.e., $X_l\sim \text{Multinomial}\left(2;{\pi }_{l0},{\pi }_{l1},{\pi }_{l2},{\pi }_{l3}\right)$, where the ${\pi }_{lk}$ values were based upon the actual mutation rates of the gene being simulated. We then simulated whether each potential mutation was damaging, $D_{lk}$, via $D_{lk}\sim \text{Bernoulli}\left({\rho }_{lk}\right)$, where the ${\rho }_{lk}$ values are the PolyPhen-2 scores for the $k$^th-type mutation at site $l$ in the gene being simulated. The disease status of the offspring was then sampled from a Bernoulli distribution with mean $\text{expit}\left[\alpha +{\sum }_{l=1}^p{\sum }_{k=0}^3\beta D_{lk}I\left(X_l=x_{lk}\right)\right]$ where we took $\alpha =\log \left[\eta /(1-\eta \right)]$ so that the prevalence was approximately $\eta$. We repeated the above steps until we had the desired number of affected samples. Note that the above disease model reflects a dominant disease model so that the presence of a damaging mutation in a causal gene leads to a similar increase in disease risk. We chose $\beta$ from log(500) to log(2,000), i.e., almost fully penetrant, to reflect estimates derived from real data⁷ and modified disease prevalence, from 0.05% to 1%, so as to target the 50% power region of the power curve where relative power differences can be observed.

Misspecification of Variant Functional Impact

We used simulations to compare our method to the Poisson test and TADA-denovo when the estimated functional impact of a subset of mutations is misspecified. We considered two approaches to misspecifying the functional impact of mutations. First, we began by simulating damaging mutations by using PolyPhen-2 scores, as described above. However, we then introduced noise into the functional impact scores used in the actual test statistic. Specifically, we generated the scores from a normal distribution with the true PolyPhen-2 score as the mean. We considered different variances, from 0.3 to 3, for this normal distribution and truncated values at 0 and 1. For the second scenario, we considered a situation in which the true probability that a mutation is damaging is discrete, such that only LOF mutations and 50% of missense mutations with a PolyPhen-2 score ≥0.957 are simulated as damaging. However, when we analyzed the simulated data, we used the quantitative PolyPhen-2 score in the test.

Comparison with Other Methods

We compared our method, fitDNM, to the Possion test⁷ and TADA-denovo.¹⁶ Both methods require gene-specific mutation rates, i.e., the sum of the mutation rate of all possible mutations in the callable region of each gene. For TADA-denovo, in order to improve accuracy, the fraction of mutations in each category (LOF, probably damaging, etc.) is estimated for each gene separately. For all other parameters required by TADA-denovo, we adopted their default values. Null simulations of the Bayes factor were used to compute p values for TADA-denovo. When evaluating type I error, 10,000 simulation replicates were used. When evaluating power and in analyses of neurodevelopmental disease, 10⁸ replicates were used.

Results

Simulation Studies

Accuracy of the Saddlepoint Approximation

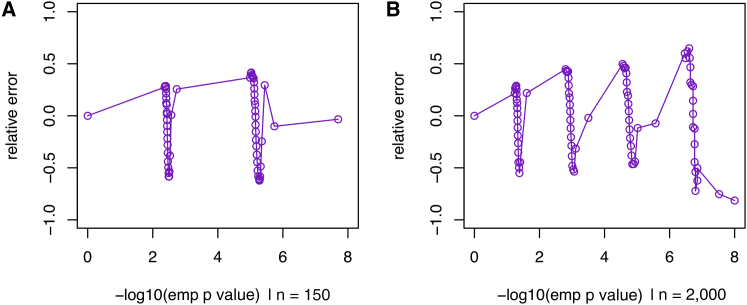
Figure 1 presents the relative error comparing p values computed via the saddlepoint approximation to empirical p values computed via simulation. The relative error is $\mathit{ϵ}=({\text{p}}_{\text{emp}}-{\text{p}}_{\text{est}})/\min \left({\text{p}}_{\text{emp}},{\text{p}}_{\text{est}}\right)$. When $\mathit{ϵ}$ is close to zero, the approximation is perfect. As can be seen in Figure 1,$\mathit{ϵ}$ is, in fact, close to zero and ranges from −1 to 1 for both small (n = 150) and large (n = 2,000) sample sizes. This confirms the high accuracy of the saddlepoint approximation and implies that the saddlepoint approximation yields p values of the same magnitude as those computed empirically, even in the extreme tail of the p value distribution (i.e., ≤10⁻⁶).

Figure 1.

Relative Errors of Saddlepoint Approximation

Relative error $=({\text{p}}_{\text{emp}}-{\text{p}}_{\text{est}})/\text{min}\left({\text{p}}_{\text{emp}},{\text{p}}_{\text{est}}\right)$, where ${\text{p}}_{\text{emp}}$ is the p value estimated from a simulation with 10⁸ replicates and ${\text{p}}_{\text{est}}$ is the p value estimated by saddlepoint approximation.

Power and Type I Error

Table 1 summarizes the results under the null hypothesis (i.e., the gene is not associated with disease) for the Poisson test, fitDNM, and TADA-denovo. All tests maintain the correct type I error rate. However, because these tests are highly discrete, it is impossible to guarantee a test with an exact $\alpha$-level; instead, we can only guarantee that a test’s type I error is at most $\alpha$. As a result, these tests appear to be somewhat conservative in most situations. Figure S1 gives a quantile-quantile (Q-Q) plot for fitDNM for a simulation (KIRREL13, n = 150) under the null hypothesis. We also include simulation-based 95% confidence intervals, constructed with 10,000 replicates. Note that even though the Q-Q plot does not follow the 45° line, due to the discreteness of the statistic, it falls well within the confidence interval, confirming that the null distribution for the statistics is correct. In Table 2, we compared power across different genes and sample sizes. We have found that incorporating variant functionality improves statistical power across most scenarios. For example, when using 150 trios and analyzing TSGA13, we found that our fitDNM yielded a >2-fold increase of power over the Poisson test and that it yielded similar results when compared to the TADA-denovo. In our simulation, neither TADA-denovo nor the Poisson test completely dominates the other. Note that, in our simulation, disease is quite rare (prevalence ≤ 1%) and damaging mutations are assumed to be almost fully penetrant, therefore the absolute power observed in our simulations will not be reflective of the power that would be obtained for a common, complex disease. Nevertheless, conclusions about the relative power of the approaches, which is our focus here, should remain valid.

Table 1.

Type I Error Rates from 10,000 Simulations

Method	Gene	Gene Size (bp)	α = 0.05				α = 0.005
n = 150	n = 500	n = 1,000	n = 1,500	n = 150	n = 500	n = 1,000	n = 1,500
Poisson	TSGA13	856	0.0039	0.0121	0.0250	0.0367	0.0039	0.0001	0.0007	0.0010
GABRB3	1,573	0.0074	0.0241	0.0021	0.0036	0.0003	0.0005	0.0021	0.0036
KIRREL3	2,440	0.0132	0.0469	0.0041	0.0097	0	0.0005	0.0041	0.0004
example	1,500	0.0071	0.0206	0.0441	0.0025	0.0001	0.0003	0.0014	0.0025
fitDNM	TSGA13	856	0.0030	0.0085	0.0177	0.0247	0.0030	0.0062	0.0039	0.0050
GABRB3	1,573	0.0050	0.0166	0.0328	0.0462	0.0043	0	0.0008	0.0013
KIRREL3	2,440	0.0091	0.0313	0.0449	0.0389	0.0033	0.0005	0.0017	0.0032
example	1,500	0.0048	0.0153	0.0325	0.0449	0.0046	0.0043	0.0006	0.0013
TADAa	TSGA13	856	0.0015	0.0035	0.0071	0.0094	0.0015	0.0005	0.0014	0.0023
GABRB3	1,573	0.0026	0.0097	0.0182	0.0291	0.0026	0.0024	0.0039	0.0005
KIRREL3	2,440	0.0064	0.0227	0.0454	0.0074	0.0007	0.0025	0.0010	0.0018
example	1,500	0.0027	0.0082	0.0197	0.0274	0.0027	0.0011	0.0037	0.0005

Because all of these three tests are constructed on the basis of discrete distribution, it is impossible to get the type I error rates exactly equal to the nominal level at most situations. Abbreviation is as follows: TADA, TADA-denovo.

^aParameters are gamma.mean.dn = (20, 4.7), beta.dn = (1, 1), and pi0 = (0.94).

Table 2.

Power Comparison

Gene	n = 150			n = 500			n = 1,000			n = 1,500
Poisson	fitDNM	TADA	Poisson	fitDNM	TADA	Poisson	fitDNM	TADA	Poisson	fitDNM	TADA
TSGA13a	0.131	0.352	0.143	0.442	0.465	0.137	0.326	0.328	0.098	0.180	0.332	0.053
GABRB3b	0.376	0.458	0.335	0.376	0.593	0.469	0.481	0.660	0.414	0.512	0.562	0.453
KIRREL3c	0.538	0.533	0.398	0.363	0.561	0.305	0.484	0.677	0.533	0.545	0.705	0.454
Exampled	0.455	0.517	0.352	0.596	0.588	0.407	0.343	0.545	0.261	0.490	0.533	0.367

Abbreviation is as follows: TADA, TADA-denovo.

^aParameters (sample size/prevalence/OR) used in each scenario for TSGA13: 150/0.0005/1,000; 500/0.0015/1,000; 1,000/0.005/1,000; 1,500/0.008/1,000.

^bParameters used in each scenario for KIRREL3: 150/0.001/500; 500/0.07/500; 1,000/0.01/500; 1,500/0.015/500.

^cParameters used in each scenario for GABRB3: 150/0.0005/800; 500/0.002/500; 1,000/0.005/500; 1,500/0.008/500.

^dParameters used in each scenario for the example: 150/0.001/2,000; 500/0.002/500; 1,000/0.008/1,500; 1,500/0.01/1,500.

Type I Error and Power when the Functional Impact of Variants Is Misspecified

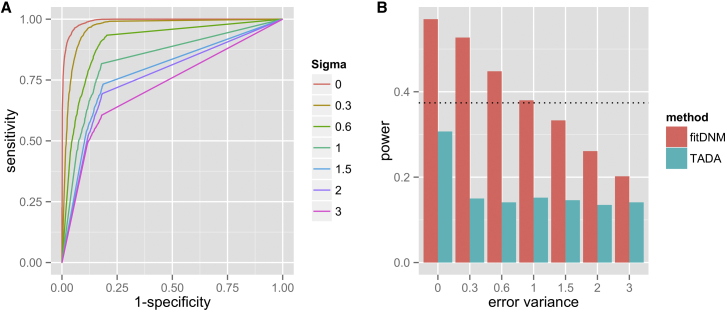
Figures S2 and S3 show the type I error rates of fitDNM when variant deleteriousness is misspecified. As can be seen, the type I error rates are well controlled. This is not unexpected. When the gene is not associated with the disease risk, i.e., $\gamma =1$ in Equation 2, ${\lambda }_{lk}={\pi }_{lk}$ and is not a function of ${\rho }_{lk}$. Thus, under the null hypothesis, the expected value of $n_{lk}$ in Equation 5 will be ${\pi }_{lk}{n}_l$, and we see that the score equation has mean zero regardless of the weights (i.e., the ${\rho }_{lk}$ values), implying that the test is robust, in terms of controlling type I error, to misspecification of the functional impact of variants. Figure 2 presents the power of fitDNM when the functional impact of variants is misspecified; KIRREL3 and a sample size of 500 is used as an example. Figure 2A is the receiver operator characteristic (ROC) curve for the classifier based on the simulated PolyPhen-2 scores. Both fitDNM and TADA-denovo are influenced by the misspecification of the impact of missense mutations. The power of fitDNM is positively associated with the area under the ROC curve: the more accurate the scores, the higher the power of fitDNM. We note that fitDNM has higher power than the Poisson test even when the correlation between the misspecified score and the probability of the mutation being damaging is around 0.6. The simulations based on other genes with different sample sizes are summarized in Figure S4. As can be seen, even in the worst scenario where the fitDNM has similar power to the Poisson test, we only see a modest loss of power when the correlation between the misspecified score and the probability of the mutation being damaging is less than 0.6.

Figure 2.

The Power of fitDNM when Variant Deleteriousness Is Misspecified

The left panel is the ROC curve for different deleterious predictions, and the right panel is the statistical power for corresponding misspecified deleteriousness. The dashed horizontal line indicates the power for the Poisson test.

Table 3 displays the power when the true probability that a mutation is damaging is discrete (i.e., LOF mutations and 50% of missense mutations with a PolyPhen-2 score ≥0.957 are simulated as damaging). In addition to fitDNM, which uses the quantitative PolyPhen-2 scores, we also, for comparison, present a test (fitDNM-true) in which the weights follow the true probability of being damaging, i.e., 0.5 if the PolyPhen-2 score is ≥0.957 and 0 if otherwise. All methods that utilize estimates of variant functionality have a higher power than the unweighted Poisson test. fitDNM and TADA-denovo show very similar statistical power, even though the simulation model mimics the weighting scheme used by TADA-denovo. Unsurprisingly, using the true weights (fitDNM-true) yielded the highest power.

Table 3.

Power Comparison under Categorical Deleteriousness

Gene	n = 150				n = 500
Poisson	fitDNM	TADA	fitDNM-true	Poisson	fitDNM	TADA	fitDNM-true
TSGA13a	0.153	0.400	0.399	0.365	0.071	0.205	0.216	0.236
GABRB3b	0.372	0.522	0.489	0.524	0.280	0.525	0.540	0.651
KIRREL3c	0.325	0.325	0.334	0.526	0.197	0.403	0.286	0.597

Abbreviation is as follows: TADA, TADA-denovo.

^aParameters (sample size/prevalence/OR) used in each scenario for TSGA13: 150/0.0003/10,000; 500/0.0015/8,000.

^bParameters used in each scenario for GABRB3: 150/0.0005/5,000; 500/0.002/5,000;

^cParameters used in each scenario for KIRREL3: 150/0.0015/3,000; 500/0.005/3,000.

Application to Four Neurodevelopmental De Novo Mutation Studies

Neurodevelopmental Disease Samples

We applied fitDNM, TADA-denovo, and the Poisson test to trios affected by four neurodevelopmental diseases: 264 by EE,⁷ 151 by severe ID,^12,21 354 by SZ,^22–24 and 948 by ASD.^8–10,25 These datasets have been previously analyzed in a number of ways. Many of the earlier studies simply reported genes that were recurrently hit with de novo mutations. For example, Rauch et al. highlighted STXBP1 (MIM: 602926), SCN2A (MIM: 182390), and SYNGAP1 (MIM: 603384) as being hit by de novo mutations more than once in their study of 45 severe-ID-affected trios;¹² Girard et al. did not find any recurrently hit genes in their study of 14 SZ-affected trios;²⁴ Gulsunner et al. identified one gene, CACNA1I (MIM: 608230), that was hit more than once across 105 SZ-affected trios.²³ This recurrently-hit-gene approach does not account for gene size, mutability, or even the size of the samples being investigated. To deal with this, Neale et al.²⁵ developed a simulation framework to characterize the null distribution of the number of de novo mutations found within a gene across a given set of trios and that explicitly accounts for gene size, mutability, and sample size. Their analysis failed to support any gene as a conclusive risk factor in their study of 175 ASD-affected trios. More recently, the Poisson test has been used to confidently implicate four genes (SCN1A [MIM: 182389], STXBP1, GABRB3, and CDKL5 [MIM: 300203]) as significantly enriched for de novo mutations in 264 EE-affected trios.⁷ The Poisson test was also used to implicate NTNG1 (MIM: 608818) as involved in ASD risk among 189 trios.¹⁰

In the analyses that follow, we define a gene as significantly associated with the disease if it has a p value less than 2.76 × 10⁻⁶, i.e., the Bonferroni significance threshold required when testing 18,116 genes with an overall family-wise error rate of 0.05. Table 4 lists genes designated as significantly associated by any test. Note that all genes identified by the Poisson test are also implicated by fitDNM and TADA-denovo. Furthermore, both fitDNM and TADA-denovo identified an additional, significantly associated gene: SUV420H1 (MIM: 610881) for ASD, which was underpowered to achieve genome-wide significance by the Poisson test.^26,27 The mutations are summarized in Table S2 and Figure S4.

Table 4.

De-Novo-Mutation-Enriched Genes among Neuropsychiatric and Neurodevelopmental Disease

Disease	No. of Females	No. of Males	Gene	Gene Sizea(bp)	Observed No. of De Novo Mutations			fitDNM	Poisson Test	TADAb
Total	LOF	Probably Damaging
ASD	184	764	SUV420H1	2,706	3	1	2	$1.6\times {10}^{-6}$	$5.59\times {10}^{-5}$	$1.79\times {10}^{-6}$
EE	108	156	CDKL5	3,173	3	1	2	$8.38\times {10}^{-9}$	$7.47\times {10}^{-7}$	$4\times {10}^{-8}$
SCN1A	6,134	7	3	4	$2.31\times {10}^{-17}$	$5.25\times {10}^{-14}$	$<1\times {10}^{-9}$
STXBP1	1,975	5	1	4	$9.46\times {10}^{-15}$	$1.35\times {10}^{-11}$	$<1\times {10}^{-9}$
GABRB3	1,573	4	0	4	$2.55\times {10}^{-11}$	$1.59\times {10}^{-9}$	$<1\times {10}^{-9}$
Combinedc	491	1,226	CDKL5	3,173	3	1	2	$2.18\times {10}^{-6}$	$1.47\times {10}^{-4}$	$3.58\times {10}^{-6}$
SCN2A	6,218	7	3	4	$2.45\times {10}^{-11}$	$1.98\times {10}^{-8}$	$<1\times {10}^{-9}$
SCN1A	6,134	8	3	5	$7.66\times {10}^{-13}$	$7.33\times {10}^{-10}$	$<1\times {10}^{-9}$
TRIO	9,522	5	0	5	$2.06\times {10}^{-6}$	$1.91\times {10}^{-4}$	$1.17\times {10}^{-5}$
STXBP1	1,975	8	1	6	$6.17\times {10}^{-16}$	$6.34\times {10}^{-13}$	$<1\times {10}^{-9}$
GABRB3	1,573	5	0	5	$2.62\times {10}^{-10}$	$4.87\times {10}^{-8}$	$1\times {10}^{-8}$

Listed are all genes that show a statistically significant (p value $<2.78\times {10}^{-6}$) enrichment of de novo mutations in the three tests. No gene in the analysis of SZ and severe ID was statistically significant in any of the three tests. Abbreviation is as follows: TADA, TADA-denovo.

^aSize of all exomes (plus canonical splice sites).

^bp values of TADA are estimated from ${10}^9$ null simulations, thus extremely small p values can only be bounded by $1\times {10}^{-9}$.

^cAnalysis combining the four neurodevelopmental diseases ASD, EE, SZ, and severe ID.

Neurodevelopmental and neuropsychiatric disorders co-occur far more often than can be explained by chance.²⁸ For example, familial studies show that children whose mother has SZ, bipolar disorder, or unipolar major depression have a significantly increased risk of ID.²⁹ Furthermore, individual copy-number variants have been implicated in multiple neurodevelopmental disorders.²⁸ These studies suggest that there are shared genetic components among different neurodevelopmental and neuropsychiatric disorders and motivate an analysis that combines samples across neurodevelopmental disorders. Hence, we also conducted an analysis that combined the EE-, ID-, SZ-, and ASD-affected trios into one dataset, resulting in 1,717 total trios. In 1,226 of these trios, the affected child was male, and in 491 of the trios, the affected child was female. Consistent with the individual disease-based analyses, in the combined neurodevelopmental cohort, all genes identified by the Poisson test and TADA-denovo were also implicated by the fitDNM test. The Poisson test implicated four genes, SCN1A, SCN2A, STXBP1, and GABRB3, whereas fitDNM implicated these and two others, CDKL5 and TRIO (MIM: 601893). Of particular note, SCN2A and TRIO were not implicated in any individual disease, but we found them to be significantly associated with neurodevelopmental and neuropsychiatric disorders as a collective set. Both SCN2A and TRIO had similar patterns of de novo mutations across the various disorders. For SCN2A, three de novo mutations were found in ASD-affected trios, two in severe ID-affected trios, and two in EE-affected trios. The role of the sodium-channel protein subunit SCN2A in neurodevelopment has long been established.^30–33 For TRIO, two de novo mutations were found in trios affected by ASD, two in trios affected by severe ID, and one among those affected by EE. De Rubeis et al.³⁴ report TRIO as a possible risk gene for ASD by combining information from de novo mutations and inherited variants in the TADA-denovo framework, assuming a false discovery rate of 10%. Here, we implicate the presence of de novo mutations within TRIO as an important risk factor across a number of neuropsychiatric disorders at the more stringent 5% family-wise error level. Though the more general relationship between TRIO and neurodevelopmental disease has not been previously established, the Deciphering Developmental Disorders Study³⁵ has reported TRIO as being one of twelve genes with “compelling evidence for pathogenicity” across a number of neurodevelopmental disorders even though a meta-analysis of 2,347 developmental disorder trios obtained a p value that did not appear to reach genome-wide significance. TRIO is a major regulator of neuronal development, and its function is conserved through evolution.³⁶ It has been shown that TRIO is an “essential” mouse gene; complete loss of TRIO in a mouse model results in abnormal neuronal migration (MP: 0006009) and perinatal lethality (MP: 0011089), the latter highlighting the gene’s importance in normal development.³⁷ Moreover, TRIO is among the FMRP-associated genes,³⁸ a set of genes that have been heavily linked and significantly enriched for de novo mutations among the neurodevelopmental disorders.^7,8,39

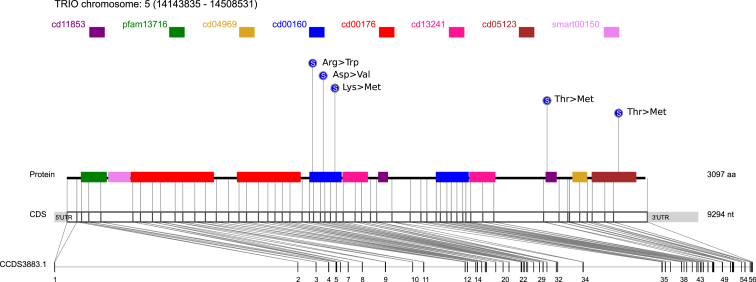
Both Petrovski et al.⁴⁰and Samocha et al.¹⁸ have highlighted SCN2A and TRIO as genes that are very intolerant to functional variation in the general population. Such genes have been shown to be increasingly associated with Mendelian disease. SCN2A achieves a RVIS (Residual Variation Intolerance Score) genic-intolerance percentile score of 1.77% and TRIO achieves a genic-intolerance score of 0.18%.⁴⁰ The mutations in TRIO and SCN2A are summarized in Table S1. The locations of mutations are displayed in Figure 3 and Figure S3.

Figure 3.

Schematic Representation of TRIO

Control Samples

We also analyzed 728 trios with healthy offspring (340 males, 368 females, and 20 unknown). Among these 728 samples, 18 genes were observed to be recurrently hit by de novo mutations. Note that none of the genes implicated in neurodevelopmental disorders (in Table 3) were observed to have non-synonymous de novo mutations among the 728 control trios. Analysis results for these 18 genes are summarized in Table S2. None of these genes show significant enrichment of de novo mutations, either by the Poisson test or fitDNM. Additionally, there was no pattern in the ordering of p values between the Poisson test and fitDNM.

Discussion

In this paper, we propose a statistical framework that incorporates mutation functionality when evaluating whether a gene is enriched for de novo mutations in individuals ascertained for a genetic disorder. In this framework, mutations are modeled as having different probabilities of disrupting a protein, leading to different weights for individual de novo mutations in the resulting test statistic. Severe disorders are often caused by increasingly damaging mutations instead of milder mutations. Unlike TADA-denovo, which only uses loss-of-function mutations and probably damaging missense mutations in analysis, our approach quantitatively evaluates all mutations across a gene. As a result, it avoids ignoring potentially damaging mutations while still leveraging information about their predicted impact, potentially leading to an increase in power. In this study, we observed such power increases both in simulation studies and real data analyses. We note, however, that the general TADA framework can also incorporate inherited variation, which could significantly improve its power for implicating causal genes when inherited variation plays an important role in the genetic architecture of the disorder.

In the analyses presented here, we use PolyPhen-2 scores to estimate the functional effect of missense de novo mutations. However, our framework is flexible in this respect and can easily accommodate other estimates of variant functionality. For example, the predictions of SIFT,¹⁴ conservation-based GERP++,⁴¹ and recently published C scores¹⁵ can also be used to estimate variant functionality. Furthermore, because these estimates are conditioned on external data, misclassifying the functional effect of a mutation will not affect the validity of the test. Of course, power will be maximized when in silico prediction of mutation deleteriousness is accurately estimated.

In this manuscript, we have excluded indels and copy-number variants from analyses because we do not believe that current population-level de novo mutation rates are well characterized for these classes of variation. Once good estimates are available, our approach can easily be adapted to incorporate these types of mutations. In fact, it is simply a matter of expanding the set of possible mutations that is summed over in the test statistic.

Our approach assumes that once a variant is damaging to the protein product, its effect on disease is the same regardless of the underlying mutation. However, this assumption might not always hold. For example, stop-gain mutations will always be damaging, but if the stop-gain occurs at the beginning of gene, it could completely knock out gene function, whereas a stop-gain that occurrs at the end of the gene might not. Though this will not affect the null behavior of our approach (i.e., impact type I error), it could affect power. A natural way to deal with this would be to have a mutation-specific risk parameter at each site and test the global null hypothesis that all these parameters are simultaneously equal to 1. This approach would lead to a separate score equation for each mutation type. These score equations could then be combined for a gene-level test with standard burden⁴² or kernel⁴³ approaches commonly used in rare-variant association methodology.

One interesting outcome of our study is that de novo mutations within the TRIO gene have been implicated as potential risk factors for developing neurodevelopmental disorders. TRIO is a member of the Rho-guanine nucleotide exchange factors (Rho-GEFs) and is named after its three domains with putative enzymatic activity. There are a total of 12 functional domains in TRIO, including two Dbl-homology (DH) domains, two Pleckstrin-homology (PH) domains, a divergent CRAL-TRIO domain, several spectrin-like repeats, two SH3 domains, an Ig-like domain, and a serine-threonine-kinase domain (Figure 3).⁴⁴ Among all the domains, the DH-PH domain is the key enzymatic unit for guanosine diphosphate (GDP) and guanosine triphosphate (GTP) exchange. The two DH domains in TRIO target different GTPases: the N-terminal DH domain (DH1) mediates the GDP-GTP exchange of Rac1 and RhoG, whereas the C-terminal DH domain (DH2) activates RhoA. Several isoforms of TRIO, including TRIO A, B, C, and D, have been identified. TRIO A, B, C, and D all contain the first DH-PH GEF domain. TRIO A, B, and D are strongly expressed in brain tissue, whereas TRIO C is exclusively expressed in the cerebellum during development.⁴⁵

The study of TRIO and its orthologs in C. elegans, Drosophila, and mice demonstrates that DH1 of TRIO plays a vital role in neurite outgrowth and axon guidance during the development of the neuronal system. C. elegans TRIO-like unc-73 is deeply involved in cell migration regulation,⁴⁶ whereas in Drosophila, dosage-sensitive interaction between TRIO and the tyrosine-protein kinase Abl determines the axon pathfinding.⁴⁷ TRIO knockout mice show strong deficits in neural organization.⁴⁸ Moreover, Estrach et al. show that human TRIO can induce the neurite outgrowth in PC12 cells through the DH1-dependent RhoG activation. They also reveal that TRIO regulates the nerve growth factor (NGF) differentiation pathway by upstream signaling of RhoG.⁴⁹

Defects in neuronal connectivity have been proposed to contribute to the pathogenesis of ASD, IDs, and SZ.^50,51 Indeed, neurite outgrowth and pathfinding of neuron cells during development establish the positioning and pattering of connections. Considering the role of TRIO, especially DH1 in regulating the neurite outgrowth and pathfinding, it suggests that TRIO could play an important role in pathogenesis of neurodevelopmental disorders.

In the combined analysis of individuals ascertained for a neurodevelopmental disorder, five de novo mutations were identified in TRIO among 1,717 samples. As can be seen from Figure 3, three of these mutations appear on DH1, two in children with ASD, and one in a child with severe ID. All of these mutations replace charged amino acids with hydrophobic amino acids, which has high potential to change the protein structure and deactivate DH1. This DH1 dysfunction results in impaired downstream neurite outgrowth and axon guidance functions.⁵²

In light of all the evidence, TRIO is highlighted here as a candidate risk gene for neurodevelopmental disorders and provides further support to the concept of shared genetic risk across neurodevelopmental disorders.

Published: July 30, 2015

Appendix A: Saddlepoint Approximation of the Distribution Function of a Weighted Sum of Independent Poisson Random Variables

Let $X_l,$ where $l=1,\dots ,p$, be $p$ independent Poisson random variables such that $E\left(X_l\right)={\lambda }_l,$ where $l=1,\dots ,p$. Let $Y={\sum }_{l=1}^p{c}_l{X}_l$, where the $c_l$ values are known constants and $Z={\sum }_{l=1}^p{X}_l$. Note that we can write the cumulative distribution function of $Y$ as

$$\text{P}\text{r}\left(Y\le y\right)={\sum }_z\text{P}\text{r}\left(Y\le y\text{|}Z=z\right)\text{P}\text{r}\left(Z=z\right).$$ (Equation A1)

Note that, whereas the support of $Y$ is infinite and not defined on a lattice, the conditional distribution of $Y$ given $Z$ is finite. In fact, it is easy to show that $Y$ given $Z$ is distributed as a linear combination of multinomial random variables. Therefore, $\text{P}\text{r}\left(Y\le y\text{|}Z=z\right)$ can be accurately approximated with the double saddlepoint approach of Skovagaard.⁵³ Before we are in a position to give Skovagaard’s approximation of $\text{P}\text{r}\left(Y\le y\text{|}Z=z\right)$, we need to define some of the involved quantities. The joint CGF of $\left(Y,Z\right)$ is given by

$$K_{Y,Z}\left(t,s\right)=\sum _{l=1}^p{\lambda }_l\left(e^{c_{l}t+s}-1\right).$$

The first and second derivatives of $K_{Y,Z}\left(t,s\right)$ are given by

$$K^{\prime }\left(t,s\right)=\left[\sum _{l=1}^p{\lambda }_l{c}_l{e}^{c_{l}t+s},\sum _{l=1}^p{\lambda }_l{e}^{c_{l}t+s}\right]$$

and

$$K^{″}\left(t,s\right)=\left[\begin{array}{cc}\sum _{l=1}^p{\lambda }_l{c}_l^2{e}^{c_{l}t+s}& \sum _{l=1}^p{\lambda }_l{c}_l{e}^{c_{l}t+s}\\ \sum _{l=1}^p{\lambda }_l{c}_l{e}^{c_{l}t+s}& \sum _{l=1}^p{\lambda }_l{e}^{c_{l}t+s}\end{array}\right],$$

respectively. Define the joint saddlepoint $\left(\hat{t},\hat{s}\right)$ as the root to $K^{\prime }\left(t,s\right)=\left(y,z\right)$.

Let $K_s^{\prime }$ denote the gradient of $K_{Y,Z}\left(t,s\right)$ with respect to $s$ only, and let $K_{ss}^{\prime \prime }$ denote its corresponding Hessian, i.e., $K_s^{\prime }\left(t,s\right)={\sum }_{l=1}^p{\lambda }_l{e}^{c_{l}t+s}$ and $K_{ss}^{\prime \prime }\left(t,s\right)={\sum }_{l=1}^p{\lambda }_l{e}^{c_{l}t+s}$. Define the marginal saddlepoint ${\hat{s}}_0$ (from the marginal CGF of $Z$) as the root of $K_s^{\prime }\left(0,s_0\right)=z$. Then Skovgaard’s approximation of $\text{P}\text{r}\left(Y\le y\text{|}Z=z\right)$ can be written as

$$\text{P}\text{r}\left(Y\le y\text{|}Z=z\right)=\text{Φ}\left(\hat{w}\right)+\varphi \left(\hat{w}\right)\left(\frac{1}{\hat{w}}-\frac{1}{\hat{u}}\right),\hat{t}\ne 0$$ (Equation A2)

where $\hat{w}=sgn\left(\hat{t}\right)\sqrt{2\left[\left[K\left({\hat{s}}_0,0\right)-{\hat{s}}_{0}z\right]-\left[K\left(\hat{s},\hat{t}\right)-\hat{s}z-\hat{t}y\right]\right]}$, $\hat{\mu }=\hat{t}\sqrt{\left|K^{″}\left(\hat{s},\hat{t}\right)\right|/K_{ss}^{″}\left({\hat{s}}_0,0\right)}$. $\text{Φ}$ and $\varphi$ are the standard normal distribution and density functions, respectively, and $sgn\left(\hat{t}\right)$ is the sign of $\hat{t}$.

When $\hat{t}=0$, $\hat{w}$ will equal $0$, so that Equation A2 is undefined. To address this case, we use the method proposed by Butler,⁵⁴ which averages two close, nonsingular points to approximate the distribution at the singularity.

We use Skovgaard’s approach to approximate $\text{Pr}\left(Y\le y\text{|}Z=z\right)$. To approximate $\text{P}\text{r}\left(Y\le y\right)$, we use Equation A1, where we truncate the summation when the terms become small. Specifically, if we define $f\left(y,z\right)\equiv \text{P}\text{r}\left(Y\ge y,Z=z\right)=\text{P}\text{r}\left(Y\ge y\text{|}Z=z\right)\text{P}\text{r}\left(Z=z\right)$ and $F\left(y,z\right)\equiv {\sum }_{j=0}^{z}f\left(y,j\right)$, then we truncate at $z^{\ast }$ such that $\left(f\left(y,z^{\ast }+1\right)/F\left(y,z^{\ast }\right)\right)<{10}^{-5}$ and approximate $\text{P}\text{r}\left(Y\le y\right)$ by $1-F\left(y,z^{\ast }\right)$.

Web Resources

The URLs for data presented herein are as follows:

• fitDNM, http://people.duke.edu/∼asallen/Software.html

• OMIM, http://www.omim.org/

• Residual Variation Intolerance Score, http://chgv.org/GenicIntolerance/