Instrument Assisted Regression for Errors in Variables Models with Binary Response

Abstract

We study errors-in-variables problems when the response is binary and instrumental variables are available. We construct consistent estimators through taking advantage of the prediction relation between the unobservable variables and the instruments. The asymptotic properties of the new estimator are established, and illustrated through simulation studies. We also demonstrate that the method can be readily generalized to generalized linear models and beyond. The usefulness of the method is illustrated through a real data example.

1 Introduction

Logistic and probit models are widely used in regression analysis with binary response. They belong to the family of generalized linear models. In real data analysis, particularly in the analysis of medical and clinical data, a ubiquitous problem is that some or all covariates cannot be directly or precisely measured and indirect or proxy measurements are used instead. For example, in studies of human immunodeficiency virus (HIV) and acquired immunodeficiency syndrome (AIDS), important variables such as CD4 lymphocyte count cannot be accurately measured due to instrument’s limitation or individual biological variation. Other well-known examples include blood pressure and cholesterol level in cardiovascular disease research. It is well-known that ignoring the measurement error and simply replacing the true covariates with their mismeasured proxies will lead to biased estimates and thus invalid conclusions (Stefanski & Buzas, 1995).

Although the problem of measurement error in general has been extensively studied in the literature, research focusing specifically on binary regression with instrumental variables is limited. Stefanski & Carroll (1985) and Stefanski & Buzas (1995) proposed approximate estimators for functional logistic models, while Stefanski & Carroll (1987) and Ma & Tsiatis (2006) studied consistent estimators for generalized linear models based on conditional score functions under the assumption of normal measurement errors or unknown measurement error distribution. Huang & Wang (2001) proposed alternative estimating function correction schemes to obtain consistent estimators for the cases where the measurement error distribution is known or the replicate data are available. These works did not use instrumental variable approach, although Huang & Wang (2001) discussed the possibility in their setup. Buzas & Stefanski (1996) considered instrumental variable approach to functional generalized linear models. However, their approach requires the normality assumption for both the measurement error and instrumental variables.

Since the true covariates and measurement errors are unobservable, it is difficult to verify their distributions in real applications. Therefore, an interesting question is whether it is possible to obtain consistent estimators without normality or any parametric assumption for either the unobserved covariates or measurement errors. In this paper, we demonstrate that this is possible in a wide range of models by using instrumental variables. In particular, we show that this can be achieved by employing a prediction relationship for the unobserved covariates using the instruments. Similar use of the instruments in some special models also appeared in Buzas (1997). This way of incorporating instrumental variables is different than most other methods mentioned above, and its applicability in the generality of the model has also not been achieved before. Thus, our work is the first in using instruments in the general regression models with measurement error and binary response, where the link between the response and the covariates does not need to belong to any special regression family.

Instrumental variable approach has been used by other authors to deal with errors-in-variables problem in general nonlinear models, e.g., Amemiya (1985), Amemiya (1990), Schennach (2007), Wang & Hsiao (2011), and Abarin & Wang (2012). In particular, Schennach (2007) and Wang & Hsiao (2011) show that the nonlinear measurement error models are generally identified when instrumental variables are available. In recent years, instrumental variable approach has drawn more and more attention in the literature, partly due to its methodological flexibility and practical applicability. In practice, any observable variables that are correlated with unobserved covariates but independent of measurement error can be used as instruments. In particular, the replicate measurements can be regarded as special instruments.

Instrumental variable method is commonly used in econometrics to treat the so-called endogeneity problem in regression models where some of the regressors are correlated with error terms for a variety of reasons. Theoretically this problem can be mitigated by incorporating instrumental variables because they are uncorrelated with the error terms. However, real application of this method was limited because instrumental data were rarely available in practice. In recent years, however, such data become widely available because large number of associated variables and their repeated measurements are collected in practical studies, such as panel data in economics and longitudinal data in medical and clinical research. In general, when many instruments are available, then there is a question of how to select optimal ones for a given problem. Intuitively, the variables strongly correlated with the unobserved or omitted covariates should be used. However, although theoretically an increasing number of instruments increases efficiency of the estimators asymptotically, too many instruments may lead to large finite sample bias or variance. Also, weak instruments may result in undesired finite sample properties of the estimators. This is usually referred as “the weak instruments problem”, See, e.g., Chao & Swanson (2005), Murray (2006), Donald et al. (2009) for elaboration on this issue.

The rest of paper is organized as the following. We present the model we study and our main methodology in Section 2. In this section, we also establish the asymptotic properties of our estimator. Numerical work including both simulations and real data analysis is given in Section 3. We conclude the paper with some discussions on the generalization and possible extension of the method in Section 4. All the technical details are given in the online supporting informaiton.

2 Main Results

2.1 The Model

The model we study can be explicitly written as

$$pr(Y=1\mid \mathbf{X}=\mathbf{x},\mathbf{Z}=\mathbf{z})=H({\mathbf{x}}^{\mathrm{T}}\mathit{\beta }+{\mathbf{z}}^{\mathrm{T}}\mathit{\gamma })$$ (1)

where H is a known inverse link function, for example, the inverse logit link function H(·) = 1−1={exp(·)+1} or the inverse probit link function H(·) = Φ(·). While the response variable Y and the covariate Z are observed, the covariate X is a latent variable. Instead of observing X, we observe an erroneous version of X, written as W and an instrumental variable S. The variables W and S are linked to X through

$$\mathbf{W}=\mathbf{X}+\mathbf{U}\text{and}\mathbf{X}=\mathbf{m}(\mathbf{S},\mathbf{Z},\mathit{\alpha })+\mathit{\epsilon },$$ (2)

where m is a known function up to an unknown parameter α. Here we assume the conditional mean of ε and the marginal mean of U to be zero, i.e. E(ε | S, Z) = 0, E(U) = 0. We further assume that (S, Z, X) is independent of U, U̇ is independent of ε, W is independent of (S, Z) given X, and Y is independent of (S, W) given (X, Z). The observed data are (Z_i, S_i, W_i, Y_i), i = 1, …, n. They are independent and identically distributed (iid) according to the model described in (1) and (2). Our main interest is in estimating θ = (β^T, γ^T)^T. The problem considered here can be viewed as a generalization of the one considered in Buzas & Stefanski (1996), in that we have much less stringent conditions. For example, we do not impose the normality assumption on X, S, ε, U, while this is required there. Note also that parametric assumption of the regression function m in (2) is not restrictive, because it can be easily checked using data on (W, S, Z) (see (3) below).

2.2 A Simplification

To proceed with estimation, we first recognize that from the relations described in (2), we have

$$\mathbf{W}=\mathbf{m}(\mathbf{S},\mathbf{Z},\mathit{\alpha })+\mathbf{U}+\mathit{\epsilon },$$ (3)

where E(U + ε | S, Z) = 0. It is easy to see that this is a familiar mean regression model, so we can use least squares method to get a consistent estimator of α. Specifically, we can solve the estimating equation

$$\sum _{i=1}^n{\mathcal{S}}_{\alpha }({\mathbf{S}}_i,{\mathbf{Z}}_i)=\sum _{i=1}^n\frac{\partial {\mathbf{m}}^{\mathrm{T}}({\mathbf{S}}_i,{\mathbf{Z}}_i,\mathit{\alpha })}{\partial \mathit{\alpha }}\mathbf{\Omega }({\mathbf{S}}_i,{\mathbf{Z}}_i)\{{\mathbf{W}}_i-\mathbf{m}({\mathbf{S}}_i,{\mathbf{Z}}_i,\mathit{\alpha })\}=\mathbf{0},$$ (4)

where Ω(S, Z) is any weight matrix, to obtain a consistent estimator α̂. Obviously, if we set Ω(S, Z) to be the identity matrix, we obtain the ordinary least squares (OLS) estimator of α, while if we set Ω(S, Z) to be the inverse of the error variance-covariance matrix conditional on (S, Z), we obtain the optimal weighted least squares estimator (WLS) of α. Once we have an estimate α̂, we can plug the relation between X and (S, Z) into model (1) to obtain the joint distribution of (Y, S, Z) as

$$\begin{array}{l}\text{pr}(Y=y,\mathbf{S}=\mathbf{s},\mathbf{Z}=\mathbf{z})\\ =f_{\mathbf{S},\mathbf{Z}}(\mathbf{s},\mathbf{z})\int [1-y+(2y-1)H\{\mathbf{m}{(\mathbf{S},\mathbf{Z},\widehat{\mathit{\alpha }})}^{\mathrm{T}}\mathit{\beta }+{\mathbf{z}}^{\mathrm{T}}\mathit{\gamma }+{\mathit{\epsilon }}^{\mathrm{T}}\mathit{\beta }\}]f_{\mathit{\epsilon }}(\mathit{\epsilon }\mid \mathbf{s},\mathbf{z})d\mu (\mathit{\epsilon }),\end{array}$$ (5)

where f_ε(ε | s, z) is a conditional probability density function (pdf) that satisfies ∫ εf_ε(ε | s, z)dμ(ε) = 0, and f_S,Z(s, z) is the joint pdf of (S, Z).

2.3 Semiparametric Derivation

We now derive the estimation procedure for β, γ from the above form. For simplicity, we write θ = (β^T, γ^T)^T and assume θ ∈ ℝ^p. Then the pdf in (5) involves the unknown parameter θ and unknown functions f_ε(·), f_S,Z(·), while we are only interested in θ. Thus, f_ε(·), f_S,Z(·) can be viewed as two infinite dimensional nuisance parameters. This allows us to view the model as a semiparametric model and use the existing semiparametric approaches (Bickel et al., 1993, Tsiatis, 2006). In the measurement error framework, semi-parametric methods were first introduced in Tsiatis & Ma (2004) in the context of a known error distribution. Following the semiparametric approach, our estimator will be based on the efficient score function. In general, the efficient score function can be obtained through projecting the score function S_θ(Y, S, Z) ≡ ∂logf_ε,S,Z{ε, s, z; θ, f_ε(·), f_S,Z(·)}/∂θ onto the orthogonal complement of the nuisance tangent space. The nuisance tangent space is defined as the mean square closure of the nuisance tangent spaces associated with all possible parametric submodels of a semiparametric model (See Tsiatis, 2006, Chapter 4), and is often hard to obtain. In the online supporting information, we derive the nuisance tangent space associated with model (5) as

$$\begin{array}{l}\mathrm{\Lambda }={\mathrm{\Lambda }}_1\oplus {\mathrm{\Lambda }}_2\\ =\{\mathbf{f}(\mathbf{S},\mathbf{Z}):\mathbf{f}\in {ℝ}^p,E(\mathbf{f})=\mathbf{0},E({\mathbf{f}}^{\mathrm{T}}\mathbf{f})<\infty ,\forall \mathbf{f}\}\oplus [E\{\mathbf{f}(\mathit{\epsilon },\mathbf{S},\mathbf{Z})\mid Y,\mathbf{S},\mathbf{Z}\}:\mathbf{f}\in {ℝ}^p,E(\mathbf{f}\mid \mathbf{S},\mathbf{Z})=\mathbf{0},E(\mathit{\epsilon }{\mathbf{f}}^{\mathrm{T}}\mid \mathbf{S},\mathbf{Z})=\mathbf{0},E({\mathbf{f}}^{\mathrm{T}}\mathbf{f})<\infty ,\forall \mathbf{f}].\end{array}$$

Here, we use the notation ⊕ to emphasize that an arbitrary function f₁(S, Z) in Λ₁ and an arbitrary function f₂(ε, S, Z) in Λ₂ satisfy $E\{{\mathbf{f}}_1(\mathbf{S},\mathbf{Z}){\mathbf{f}}_2^{\mathrm{T}}(\mathit{\epsilon },\mathbf{S},\mathbf{Z})\}=\mathbf{0}$. The orthogonal complement of Λ can then be derived as

$${\mathrm{\Lambda }}^{\perp }=\{\mathbf{f}(Y,\mathbf{S},\mathbf{Z}):\mathbf{f}\in {ℝ}^p,E(\mathbf{f}\mid \mathit{\epsilon },\mathbf{S},\mathbf{Z})=\mathbf{a}(\mathbf{S},\mathbf{Z})\mathit{\epsilon },E({\mathbf{a}}^{\mathrm{T}}\mathbf{a})<\infty \},$$

where a(S, Z) contains p rows and conforms with the dimension of ε. We also need to calculate the score function with respect to θ, which has the form

$${\mathcal{S}}_{\theta }(Y,\mathbf{S},\mathbf{Z})=(2Y-1)\frac{\int \left\{\begin{array}{c}\mathbf{m}(\mathbf{S},\mathbf{Z},\widehat{\mathit{\alpha }})+\mathit{\epsilon }\\ \mathbf{Z}\end{array}\right\}{H}^{\prime }\{\mathbf{m}{(\mathbf{S},\mathbf{Z},\widehat{\mathit{\alpha }})}^{\mathrm{T}}\mathit{\beta }+{\mathbf{Z}}^{\mathrm{T}}\mathit{\gamma }+{\mathit{\epsilon }}^{\mathrm{T}}\mathit{\beta }\}{f}_{\mathit{\epsilon }}(\mathit{\epsilon }\mid \mathbf{S},\mathbf{Z})d\mu (\mathit{\epsilon })}{\int [1-Y+(2Y-1)H^{\prime }\{\mathbf{m}{(\mathbf{S},\mathbf{Z},\widehat{\mathit{\alpha }})}^{\mathrm{T}}\mathit{\beta }+{\mathbf{Z}}^{\mathrm{T}}\mathit{\gamma }+{\mathit{\epsilon }}^{\mathrm{T}}\mathit{\beta }\}]f_{\mathit{\epsilon }}(\mathit{\epsilon }\mid \mathbf{S},\mathbf{Z})d\mu (\mathit{\epsilon })}.$$

The efficient score can now be obtained by projecting 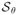to Λ^⊥, and can be verified as

$${\mathcal{S}}_{\text{eff}}(Y,\mathbf{S},\mathbf{Z})={\mathcal{S}}_{\theta }(Y,\mathbf{S},\mathbf{Z})-E\{\mathbf{b}(\mathit{\epsilon },\mathbf{S},\mathbf{Z})\mid Y,\mathbf{S},\mathbf{Z}\},$$

where b(ε, S, Z) satisfies

$$E[{\mathcal{S}}_{\theta }(Y,\mathbf{S},\mathbf{Z})-E\{\mathbf{b}(\mathit{\epsilon },\mathbf{S},\mathbf{Z})\mid Y,\mathbf{S},\mathbf{Z}\}\mid \mathit{\epsilon },\mathbf{S},\mathbf{Z}]=\mathbf{a}(\mathbf{S},\mathbf{Z})\mathit{\epsilon }$$ (6)

for some function a(S, Z). Unfortunately, a(S, Z) is unspecified in (6), hence we cannot directly solve for b(ε, S, Z) from (6). In order to determine the function a(S, Z), we multiply 3 on both sides of (6), take expectation conditional on (S, Z), and obtain

$$E[{\mathcal{S}}_{\theta }(Y,\mathbf{S},\mathbf{Z}){\mathit{\epsilon }}^{\mathrm{T}}-E\{\mathbf{b}(\mathit{\epsilon },\mathbf{S},\mathbf{Z})\mid Y,\mathbf{S},\mathbf{Z}\}{\mathit{\epsilon }}^{\mathrm{T}}\mid \mathbf{S},\mathbf{Z}]=\mathbf{a}(\mathbf{S},\mathbf{Z})E(\mathit{\epsilon }{\mathit{\epsilon }}^{\mathrm{T}}\mid \mathbf{S},\mathbf{Z}).$$

This implies

$$\mathbf{a}(\mathbf{S},\mathbf{Z})=E[{\mathcal{S}}_{\theta }(Y,\mathbf{S},\mathbf{Z}){\mathit{\epsilon }}^{\mathrm{T}}-E\{\mathbf{b}(\mathit{\epsilon },\mathbf{S},\mathbf{Z})\mid Y,\mathbf{S},\mathbf{Z}\}{\mathit{\epsilon }}^{\mathrm{T}}\mid \mathbf{S},\mathbf{Z}]{\{E(\mathit{\epsilon }{\mathit{\epsilon }}^{\mathrm{T}}\mid \mathbf{S},\mathbf{Z})\}}^{-1}.$$

We can now plug the form of a(S, Z) into (6) to obtain an explicit integral equation

$$\begin{array}{l}E[{\mathcal{S}}_{\theta }(Y,\mathbf{S},\mathbf{Z})-E\{\mathbf{b}(\mathit{\epsilon },\mathbf{S},\mathbf{Z})\mid Y,\mathbf{S},\mathbf{Z}\}\mid \mathit{\epsilon },\mathbf{S},\mathbf{Z}]\\ =E[{\mathcal{S}}_{\theta }(Y,\mathbf{S},\mathbf{Z}){\mathit{\epsilon }}^{\mathrm{T}}-E\{\mathbf{b}(\mathit{\epsilon },\mathbf{S},\mathbf{Z})\mid Y,\mathbf{S},\mathbf{Z}\}{\mathit{\epsilon }}^{\mathrm{T}}\mid \mathbf{S},\mathbf{Z}]{\{E(\mathit{\epsilon }{\mathit{\epsilon }}^{\mathrm{T}}\mid \mathbf{S},\mathbf{Z})\}}^{-1}\mathit{\epsilon }.\end{array}$$

This integral equation no longer contains unspecified component, and b(ε, S, Z) can be obtained as a solution to the equation.

2.4 Estimation Under Working Model

The above derivation is performed under a true density f_ε(ε | S, Z) which is usually unknown. In order to be able to compute or 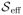, we propose to use a working model $f_{\mathit{\epsilon }}^{\ast }(\mathit{\epsilon }\mid \mathbf{S},\mathbf{Z})$, which may or may not be equal to f_ε(ε | S, Z), and perform all the calculations under this working model. The name “working model” means that $f_{\mathit{\epsilon }}^{\ast }(\mathit{\epsilon }\mid \mathbf{S},\mathbf{Z})$ is not a part of the model assumption. It is merely used for constructing our estimator. This is in contrast to f_ε(ε | S, Z), which is the true model that defines the data generation process. Using * to denote all the affected quantities by the substitution of f_ε(ε | S, Z) with $f_{\mathit{\epsilon }}^{\ast }(\mathit{\epsilon }\mid \mathbf{S},\mathbf{Z})$, our estimation procedure is the following.

1. Propose a working model $f_{\mathit{\epsilon }}^{\ast }(\mathit{\epsilon }\mid \mathbf{S},\mathbf{Z})$ that has mean zero. For example, we can propose $f_{\mathit{\epsilon }}^{\ast }(\mathit{\epsilon }\mid \mathbf{S},\mathbf{Z})$ to be a normal pdf with mean 0 and variance I.

2. Calculate the score function ${\mathcal{S}}_{\theta }^{\ast }(Y,\mathbf{S},\mathbf{Z})$ under the working model.

3. Obtain b(ε, S, Z) through solving the integral equation

   $$\begin{array}{l}E[{\mathcal{S}}_{\theta }^{\ast }(Y,\mathbf{S},\mathbf{Z})-E^{\ast }\{\mathbf{b}(\mathit{\epsilon },\mathbf{S},\mathbf{Z})\mid Y,\mathbf{S},\mathbf{Z}\}\mid \mathit{\epsilon },\mathbf{S},\mathbf{Z}]\\ =E^{\ast }[{\mathcal{S}}_{\theta }^{\ast }(Y,\mathbf{S},\mathbf{Z}){\mathit{\epsilon }}^{\mathrm{T}}-E^{\ast }\{\mathbf{b}(\mathit{\epsilon },\mathbf{S},\mathbf{Z})\mid Y,\mathbf{S},\mathbf{Z}\}{\mathit{\epsilon }}^{\mathrm{T}}\mid \mathbf{S},\mathbf{Z}]{\{E^{\ast }(\mathit{\epsilon }{\mathit{\epsilon }}^{\mathrm{T}}\mid \mathbf{S},\mathbf{Z})\}}^{-1}\mathit{\epsilon }.\end{array}$$ (7)
4. Form

   $${\mathcal{S}}_{\text{eff}}^{\ast }(Y,\mathbf{S},\mathbf{Z})={\mathcal{S}}_{\theta }^{\ast }(Y,\mathbf{S},\mathbf{Z})-E^{\ast }\{b(\mathit{\epsilon },\mathbf{S},\mathbf{Z})\mid Y,\mathbf{S},\mathbf{Z}\}$$
   and solve the estimating equation

   $$\sum _{i=1}^n{\mathcal{S}}_{\text{eff}}^{\ast }(Y_i,{\mathbf{S}}_i,{\mathbf{Z}}_i,\mathit{\theta })=\mathbf{0}$$

   to obtain the estimator θ̂.

In the above step 3, we solved the integration equation (7) via converting it to a linear algebra problem. Specifically, based on the working model, we first discretize the distribution of ε on m points ε₁, …, ε_m. A typical practice is to choose m equally spaced points on the support of the distribution. We then calculate the probability mass π_i(S, Z) at each of the m points and normalize the π_i(S, Z)’s so that ${\sum }_{i=1}^m{\pi }_i(\mathbf{S},\mathbf{Z})=1$. This allows us to approximate the calculation of E^* with Ê^*. For example, denoting

$${\widehat{f}}_{\mathit{\epsilon },Y}^{\ast }({\mathit{\epsilon }}_i,Y\mid \mathbf{S},\mathbf{Z})=[1-y+(2y-1)H\{\mathbf{m}{(\mathbf{S},\mathbf{Z},\widehat{\mathit{\alpha }})}^{\mathrm{T}}\mathit{\beta }+{\mathbf{z}}^{\mathrm{T}}\mathit{\gamma }+{\mathit{\epsilon }}_i^{\mathrm{T}}\mathit{\beta }\}]{\pi }_i(\mathbf{S},\mathbf{Z}),$$

we replace E^*{b(ε, S, Z) | Y, S, Z} with

$${\widehat{E}}^{\ast }\{\mathbf{b}(\mathit{\epsilon },\mathbf{S},\mathbf{Z})\mid Y,\mathbf{S},\mathbf{Z}\}=\frac{{\sum }_{i=1}^m\mathbf{b}({\mathit{\epsilon }}_i,\mathbf{S},\mathbf{Z}){\widehat{f}}_{\mathit{\epsilon },Y}^{\ast }({\mathit{\epsilon }}_i,Y\mid \mathbf{S},\mathbf{Z})}{{\sum }_{i=1}^m{\widehat{f}}_{\mathit{\epsilon },Y}^{\ast }({\mathit{\epsilon }}_i,Y\mid \mathbf{S},\mathbf{Z})}.$$

Let B(S, Z) = {b(ε₁, S, Z), …, b(ε_m, S, Z)}^T, C(S, Z) = {c(ε₁, S, Z), …, c(ε_m, S, Z)}^T, where

$$c({\mathit{\epsilon }}_i,\mathbf{S},\mathbf{Z})=E\{{\mathcal{S}}_{\theta }^{\ast }(Y,\mathbf{S},\mathbf{Z})\mid {\mathit{\epsilon }}_i,\mathbf{S},\mathbf{Z}\}-E\{{\mathcal{S}}_{\theta }^{\ast }(Y,\mathbf{S},\mathbf{Z}){\mathit{\epsilon }}^{\mathrm{T}}\mid \mathbf{S},\mathbf{Z}\}{\{E^{\ast }(\mathit{\epsilon }{\mathit{\epsilon }}^{\mathrm{T}}\mid \mathbf{S},\mathbf{Z})\}}^{-1}{\mathit{\epsilon }}_i.$$

Further, let A(S, Z) be an m × m matrix whose (i, j) block is

$$E\left\{\frac{{\widehat{f}}_{\mathit{\epsilon },Y}^{\ast }({\mathit{\epsilon }}_j,Y,\mathbf{S},\mathbf{Z})}{{\sum }_{i=1}^m{\widehat{f}}_{\mathit{\epsilon },Y}^{\ast }({\mathit{\epsilon }}_i,Y,\mathbf{S},\mathbf{Z})}\mid {\mathit{\epsilon }}_i,\mathbf{S},\mathbf{Z}\right\}-{\widehat{E}}^{\ast }\left\{\frac{{\widehat{f}}_{\mathit{\epsilon },Y}^{\ast }({\mathit{\epsilon }}_j,Y,\mathbf{S},\mathbf{Z})}{{\sum }_{i=1}^m{\widehat{f}}_{\mathit{\epsilon },Y}^{\ast }({\mathit{\epsilon }}_i,Y,\mathbf{S},\mathbf{Z})}{\mathit{\epsilon }}^T\mid \mathbf{S},\mathbf{Z}\right\}{\left\{{\widehat{E}}^{\ast }(\mathit{\epsilon }{\mathit{\epsilon }}^T\mid \mathbf{S},\mathbf{Z})\right\}}^{-1}{\mathit{\epsilon }}_i.$$

The integral equation (7) can then be converted into a linear algebra problem

$$\mathbf{A}(S,Z)\mathbf{B}(S,Z)=\mathbf{C}(S,Z),$$

and we can readily solve it for b(ε_i, S, Z)’s.

2.5 Asymptotic Properties

We now study the asymptotic properties of the estimators proposed in Section 2.4. We first list the regularity conditions required.

• C1The regression error ε under the working model $f_{\mathit{\epsilon }}^{\ast }(\mathit{\epsilon }\mid \mathbf{S},\mathbf{Z})$ has component-wise bounded positive-definite variance-covariance matrix.
• C2The efficient score function calculated under the working model $f_{\mathit{\epsilon }}^{\ast }(\mathit{\epsilon }\mid \mathbf{S},\mathbf{Z})$ is differentiable with respect to θ and the derivative matrix has component-wise bounded and invertable expectation.
• C3The efficient score function calculated under the working model $f_{\mathit{\epsilon }}^{\ast }(\mathit{\epsilon }\mid \mathbf{S},\mathbf{Z})$ has component-wise bounded positive-definite variance-covariance matrix.
• C4The matrix E{∂ 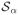/∂α^T} is invertable.

Although the working model $f_{\mathit{\epsilon }}^{\ast }(\mathit{\epsilon }\mid \mathbf{S},\mathbf{Z})$ does not necessarily equal to the true model f_ε(ε | S, Z), the above procedure still yields a consistent estimator θ̂. Let a^⊗2 = aa^T for all matrix or vector a throughout the text. Then we have the following result.

Theorem 1

Under regularity conditions C1–C3, if α is known, then θ̂ obtained from the procedure described above satisfies

$$\sqrt{n}(\widehat{\mathit{\theta }}-\mathit{\theta })\to N\{0,{\mathbf{A}}^{-1}\mathbf{B}{({\mathbf{A}}^{-1})}^{\mathrm{T}}\}$$

when n → ∞. Here

$$\mathbf{A}=E\left\{\frac{\partial {\mathcal{S}}_{\text{eff}}^{\ast }(Y,\mathbf{S},\mathbf{Z})}{\partial {\mathit{\theta }}^{\mathrm{T}}}\right\},\mathbf{B}=E\{{\mathcal{S}}_{\text{eff}}^{\ast }{(Y,\mathbf{S},\mathbf{Z})}^{\otimes 2}\}.$$

In addition, when $f_{\mathit{\epsilon }}^{\ast }(\mathit{\epsilon }\mid \mathbf{S},\mathbf{Z})=f_{\mathit{\epsilon }}(\mathit{\epsilon }\mid \mathbf{S},\mathbf{Z})$, the variance is [E{ 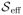(Y, S, Z)^⊗2}]⁻¹, which is the minimum semiparametric variance bound for estimating θ.

In practice, α is unknown and θ̂ is obtained from using α̂, an estimator obtained from solving (4). Hence additional variability associated with estimating α occurs and needs to be taken into account. In this case, we have the following result.

Theorem 2

When α is estimated from (4) and α̂ is used in the estimation procedure, then under the regularity conditions C1–C4, the resulting plug-in estimator θ̂(α̂) satisfies

$$\sqrt{n}\{\widehat{\mathit{\theta }}(\widehat{\mathit{\alpha }})-\mathit{\theta }\}\to N(\mathbf{0},\mathbf{V})$$

when n → ∞. Here V = A⁻¹B(A⁻¹)^T + V_α and

$${\mathbf{V}}_{\alpha }={\mathbf{A}}^{-1}\{{\mathbf{A}}_1{\mathbf{A}}_2^{-1}{\mathbf{B}}_2{({\mathbf{A}}_1{\mathbf{A}}_2^{-1})}^{\mathrm{T}}-{\mathbf{A}}_1{\mathbf{A}}_2^{-1}{\mathbf{B}}_1-{({\mathbf{A}}_1{\mathbf{A}}_2^{-1}{\mathbf{B}}_1)}^{\mathrm{T}}\}{({\mathbf{A}}^{-1})}^{\mathrm{T}},$$

where A, B are given in Theorem 1, ${\mathbf{A}}_1=E\{\partial {\mathcal{S}}_{\text{eff}}^{\ast }/\partial {\mathit{\alpha }}^{\mathrm{T}}\},{\mathbf{A}}_2=E\{\partial {\mathcal{S}}_{\alpha }/\partial {\mathit{\alpha }}^{\mathrm{T}}\},{\mathbf{B}}_1=E({\mathcal{S}}_{\alpha }{\mathcal{S}}_{\text{eff}}^{\ast \mathrm{T}}),{\mathbf{B}}_2=E({\mathcal{S}}_{\alpha }^{\otimes 2})$. In addition, when $f_{\mathit{\epsilon }}^{\ast }(\mathit{\epsilon }\mid \mathbf{S},\mathbf{Z})=f_{\mathit{\epsilon }}(\mathit{\epsilon }\mid \mathbf{S},\mathbf{Z})$, the resulting estimation variance is minimized among all the plug-in estimators.

The proofs of the above two theorems are given in the online supporting information.

3 Numerical Examples

We now demonstrate our method numerically through both simulated and real data examples. In all simulated examples, 1000 data sets were generated with sample size n = 1000.

3.1 Simulated Example One

In our first simulation, we generated the observations (Z_i, S_i, W_i, Y_i) from the model

$$\begin{array}{l}Pr(Y_i=1\mid X_i=x_i,Z_i=z_i)=H(\beta x_i+\gamma z_i),\\ W_i=X_i+U_i,\\ X_i={\alpha }_1+{\alpha }_2{S}_i+{\epsilon }_i.\end{array}$$

Here, H(·) is respectively set to be the inverse logit and the inverse probit link function, and α₁ = 1, α₂ = 1, β = 0.3, γ = 0.5. The observable covariate Z_i and the instrument variable S_i are generated from the standard normal distribution. We generated U_i from a normal distribution with mean zero and variance 0.6. We further generated ε_i respectively from a normal distribution with mean 0 and variance $S_i^2/2$ , and a t₅ distribution multiplied by (|S_i|/3)^1/2. Those two cases correspond to a normal and a non-normal regression model W_i = α₁S_i + α₂Z_i + U_i + ε_i with heteroscedastic error. finally, we proposed a normal working model on ε_i. Thus, the estimation in the two cases corresponds to a correct and a misspecified working model.

The combination of the logit and probit link functions with the normal and non-normal regression errors yields four different cases, and the performances of our method in all four scenarios are summarized in Table 1. Because the OLS and WLS are the most popular methods of estimating (α₁, α₂)^T, we calculated both of them in our simulation and compared the performance with the estimation under the known α.

Table 1.

Simulation One: Estimation and inference results on α̂₁, α̂₂, β̂, γ̂. The estimation mean, median, empirical standard error, estimated standard error and coverage rate of the 95% confidence intervals are reported. α₀ means the true α’s are used. “as” stands the adjusted score method, implemented in the logit model only.

	truth	α1 1.0	α2 1.0	β (logit) 0.3	γ (logit) 0.5	β (probit) 0.3	γ (probit) 0.5	β (as) 0.3	γ (as) 0.5
ε: Normal distribution
α0	mean	NA	NA	0.2994	0.4984	0.3006	0.4999	0.2992	0.4981
	median			0.3005	0.4948	0.3001	0.5002	0.2997	0.4945
	emp se			0.0526	0.0712	0.0366	0.0498	0.0521	0.0706
	est se			0.0509	0.0708	0.0355	0.0478	0.0501	0.0709
	95% cov			94.7%	95.3%	95.3%	93.0%	93.9%	95.6%
OLS	mean	0.9999	1.0013	0.2992	0.4981	0.3006	0.4997	0.2992	0.4980
	median	1.0015	1.0025	0.2990	0.4941	0.2994	0.4998	0.2998	0.4947
	emp se	0.0334	0.0443	0.0530	0.0707	0.0372	0.0496	0.0521	0.0707
	est se	0.0331	0.0456	0.0509	0.0708	0.0355	0.0478	0.0500	0.0709
	95% cov	94.3%	95.3%	94.0%	95.4%	93.9%	93.3%	93.9%	95.6%
WLS	mean	0.9999	0.9999	0.2994	0.4981	0.3008	0.4997	0.2992	0.4980
	median	1.0001	1.0007	0.2997	0.4943	0.2997	0.5000	0.2998	0.4946
	emp se	0.0299	0.0393	0.0531	0.0707	0.0371	0.0496	0.0521	0.0707
	est se	0.0297	0.0398	0.0510	0.0708	0.0356	0.0478	0.0500	0.0709
	95% cov	95.0%	96.1%	94.2%	95.4%	94.2%	93.3%	93.9%	95.6%
ε: Student t distribution t5
α0	mean	NA	NA	0.2994	0.4984	0.3004	0.4992	0.2986	0.4983
	median			0.2993	0.4960	0.2986	0.4974	0.2996	0.4972
	emp se			0.0528	0.0718	0.0370	0.0487	0.0515	0.0713
	est se			0.0507	0.0707	0.0349	0.0476	0.0498	0.0709
	95% cov			93.7%	95.9%	93.8%	94.4%	94.3%	95.7%
OLS	mean	0.9984	0.9993	0.2998	0.4984	0.3007	0.4989	0.2985	0.4983
	median	0.9969	0.9998	0.2996	0.4959	0.2988	0.4975	0.2994	0.4972
	emp se	0.0316	0.0378	0.0528	0.0718	0.0371	0.0487	0.0516	0.0713
	est se	0.0303	0.0384	0.0508	0.0707	0.0350	0.0476	0.0498	0.0709
	95% cov	95.3%	95.8%	94.0%	95.8%	94.0%	94.3%	94.2%	95.6%
WLS	mean	0.9989	0.9989	0.2997	0.4984	0.3007	0.4989	0.2985	0.4983
	median	0.9977	0.9996	0.2995	0.4961	0.2985	0.4976	0.2991	0.4972
	emp se	0.0303	0.0370	0.0529	0.0718	0.0372	0.0487	0.0516	0.0713
	est se	0.0308	0.0373	0.0508	0.0707	0.0350	0.0476	0.0498	0.0709
	95% cov	95.4%	95.8%	94.1%	95.8%	94.0%	94.3%	94.2%	95.6%

Based on Table 1, it is obvious that the estimators for (β, γ) have very small bias in all cases. In addition, the empirical and average estimated standard errors match closely, and the empirical coverage of the 95% confidence intervals are very close to the nominal level. All these indicate satisfactory accuracy of our inference results in the finite sample situations.

In the logistic model context, Buzas (1997) developed an adjusted score method. For comparison, we included the adjusted score results in our simulation, see Table 1. Its performance in terms of means, estimation variability and coverage probabilities are similar to our method. The drawback of the adjusted score method is its limited applicability. For example, it can only be used for the logistic link function.

One can observe an interesting phenomenon regarding the relative efficiency of the estimators for β and γ under different α estimators in comparison with the known α case. On the one hand, it is clear that for estimating α, the WLS is much more efficient than the OLS estimator. On the other hand, the difference in the estimation variability for α̂ does not seem to influence much the estimation variability for β̂ and γ̂. In fact, even when the estimation is conducted under the known α, the variability of β̂ and γ̂ does not seem to improve much in this simulation example. However, we point out that this is not always the case. For example, when we generate U_i from a centered normal distribution with variance 8, the estimation variability of β̂ and γ̂ decreased visibly when α is known, see Table 2 for details. In fact, how does the variability of α̂ affect that of β̂ and γ̂ is difficult to quantify, despite the analytic result in Theorem 2.

Table 2.

Simulation One: Estimation and inference results on α̂₁, α̂₂, β̂, γ̂ based on logit function and normal regression error. Measurement error variance is 8. The mean, median, empirical standard error, estimated standard error and coverage rate of the 95% confidence intervals are reported.

	Initial values	α1 1.0	α2 1.0	β (logit) 0.3	γ (logit) 0.5
α known	mean	NA	NA	0.3002	0.4993
	median			0.2990	0.4995
	emp se			0.0766	0.0938
	est se			0.0754	0.0950
	95% cov			94.8%	96.3%
OLS	mean	0.9983	1.0018	0.3023	0.4978
	median	1.0000	1.0006	0.2980	0.5004
	emp se	0.0930	0.0950	0.0813	0.0999
	est se	0.0923	0.0973	0.0811	0.1028
	95% cov	94.9%	95.6%	94.8%	96.8%
WLS	mean	0.9984	1.0009	0.3026	0.4975
	median	1.0000	1.0005	0.2979	0.5005
	emp se	0.0929	0.0950	0.0815	0.1001
	est se	0.0920	0.0968	0.0812	0.1030
	95% cov	95.0%	95.8%	94.7%	96.8%

3.2 Simulated Example Two

Our second simulation is designed to reflect the structure of the AIDS data which will be analyzed next. We generated the observations (Z_i, S_i, W_i, Y_i) from the model

$$Pr(Y_i=1\mid X_i=x_i,Z_i=z_i)=H\{x_i({\beta }_4+{\beta }_1{z}_{1i}+{\beta }_2{z}_{2i}+{\beta }_3{z}_{3i})+{\beta }_{c4}+{\beta }_{c1}{z}_{1i}+{\beta }_{c2}{z}_{2i}+{\beta }_{c3}{z}_{3i}\},$$ (8)

$$W_i=X_i+U_i,$$ (9)

$$X_i={\alpha }_1+{\alpha }_2{S}_i+{\epsilon }_i.$$ (10)

Here, H(·) is chosen to be the inverse logit link function. We set (α₁, α₂) = (1.0, 1.0) and (β₁, β₂, β₃, β₄, β_c1, β_c2, β_c3, β_c4) = (−0.5, 0.6, −0.4, 0.3, 1.0, −1.0, 0.5, −0.5). The observable covariates z_1i, z_2i and z_3i are all dichotomous variables, where z_1i = z_2i = z_3i = 0 indicates that the ith individual receives the reference treatment (treatment 1) and z_ki = 1 (k = 1, 2, 3) means that the ith individual receives treatment k +1. For the ith observation, at most one of the three Z_ki(k = 1, 2, 3) is 1, and the chances of receiving each of the four treatments are equal. The instrumental variable S_i is generated from the standard normal distribution, and we generated ε_i from the normal distribution with mean 0 and variance $S_i^2/8$, and U_i from a normal distribution with mean 0 and variance 0.4.

The simulation results are summarized in Table 3. It is evident that all the estimators show little bias. Although there are 10 unknown parameters in the problem, which is a relatively large number, the inference performance of our method is still satisfactory. In particular, the empirical and average estimated standard errors are close to each other, and the coverage rate of the 95% confidence intervals are all around the nominal level. We further conducted the simulation by replacing the logit link with a probit link, and observed very similar results, which are omitted here. Since this simulation is designed to have similar structure as the AIDS data, it provides certain confidence in our real data analysis result in the next subsection.

Table 3.

Simulation Two: Model structure similar to the AIDS data; Estimation and inference results on α̂₁, α̂₂, β̂₁, β̂₂, β̂₃, β̂₄, β̂_c1, β̂_c2, β̂_c3, β̂_c4. The median, empirical standard error, estimated standard error and coverage rate of the 95% confidence intervals are reported.

Initial value	α1 1	α2 1	β1 −0.5	β2 0.6	β3 −0.4
median	1.0011	1.0006	−0.5028	0.6029	−0.4064
emp se	0.0227	0.0270	0.1976	0.2319	0.1918
est se	0.0222	0.0264	0.1923	0.2339	0.1889
95% cov	94.1%	94.2%	94.1%	95.1%	95.6%

Initial value	β4 0.3	βc1 1.0	βc2 −1.0	βc3 0.5	βc4 −0.5
median	0.3006	1.0247	−0.9934	0.5068	−0.4973
emp se	0.1366	0.2752	0.3325	0.2559	0.1829
est se	0.1368	0.2705	0.3263	0.2645	0.1919
95% cov	95.9%	94.7%	95.7%	96.2%	96.7%

3.3 Real Data Analysis

We applied our method on the data set from an AIDS Clinical Trials Group (ACTG) study. This study evaluated four different treatments on HIV infected adults whose CD4 cell counts were from 200 to 500 per cubic millimeter. These four treatments are “ZDV”, “ZDV+ddI”, “ZDV+ddC” and “ddC”, labeled as treatment 1 to 4 in this order. Treatment 1 is a standard treatment hence is considered as the reference treatment; see Hammer et al. (1996), Huang & Wang (2000) and Huang & Wang (2001) for more detailed descriptions of the data set. We included 1036 patients who had no antiretroviral therapy at enrollment in our analysis.

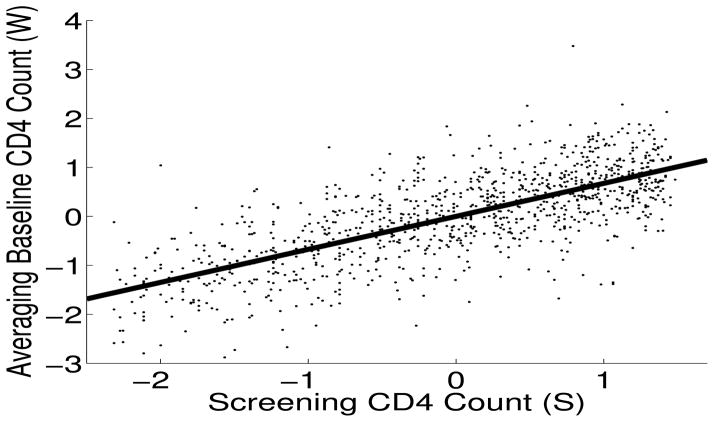
We are interested in studying the treatment difference in terms of whether a patient has his CD4 count drop below 50%, a clinically important indicator for the HIV infected patients, develops AIDS or dies from HIV related disease (Y = 1). Thus, our main model is given in (8), where Z_ik has the same meaning as in the second simulation study. Here, X is the baseline log(CD4 count) prior to the start of treatment and within 3 weeks of randomization. Of course X is not measured precisely, and we use the average of two available measurements as W. From the two repeated measurements, the measurement error variance is estimated as 0.3. In addition, a screening log(CD4 count) is available and is used as the instrumental variable S. The relationship between W and S is depicted in Figure 1. Apparently, a linear model will fit the data well. Therefore we assume the relation between W, X and S, Z can be described using (9) and (10).

Figure 1.

Plot of the covariate averaged baseline CD4 count versus the instrument variable screening CD4 count. Unit is ‘Cells per cubic millimeter’.

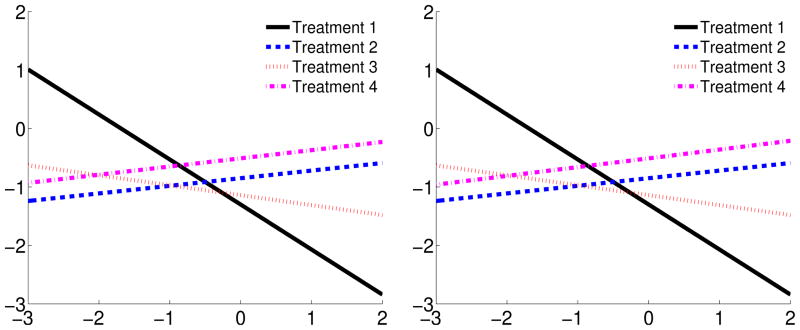
We conducted the analysis under both the logit and probit models, but report only the results in the logit model because the probit model yields very similar results. The estimate for (α₁, α₂) is (0.0001, 0.67) with the standard error (0.02, 0.02) using the OLS method. The result from the WLS is very similar. The subsequent estimate of β is given in Table 4. We further plotted the corresponding relations between the baseline log CD4 counts (X) and the estimated linear function of X under the four treatments in Figure 2. Different methods of estimating the α parameter make little difference in the β estimation since the estimations from OLS and WLS are themselves very similar. This is reflected in the information in both Table 4 and Figure 2. As manifested in the plots in Figure 2, treatment 1 shows a negative slope, indicating that the standard treatment seems to be more effective for patients with larger baseline CD4, or patients whose situation is less severe. On the contrary, the treatments 2 and 4 show positive slopes, indicating that these treatments are more effective for patients with smaller baseline CD4 counts, or patients with more grave situation.

Table 4.

Analysis of the ACTG 175 data: Estimates, two-sided and one-sided 95% confidence intervals for the model are reported. Results are based on logit model in combination with the OLS and the WLS method respectively for α estimation.

		β1	β2	β3	β4
OLS	Estimate	0.13	−0.17	0.14	−0.77
	two-sided	(−0.60, 0.86)	(−0.95, 0.61)	(−0.52, 0.81)	(−1.22, −0.31)
	one-sided	(−0.48, ∞)	(−∞, 0.49)	(−0.41, ∞)	(−∞, −0.39)
IWLS	Estimate	0.13	−0.17	0.15	−0.77
	two-sided	(−0.60, 0.86)	(−0.96, 0.62)	(−0.52, 0.81)	(−1.23, −0.31)
	one-sided	(−0.49, ∞)	(−∞, 0.49)	(−0.41, ∞)	(−∞, −0.39)

		βc1	βc2	βc3	βc4
OLS	Estimate	−0.85	−1.14	−0.51	−1.30
	two-sided	(−1.37, −0.32)	(−1.72, −0.56)	(−1.00, −0.03)	(−1.61, −0.98)
	one-sided	(−∞, −0.41)	(−∞, −0.65)	(−∞, −0.10)	(−∞, −1.03)
IWLS	Estimate	−0.85	−1.14	−0.51	−1.30
	two-sided	(−1.37, −0.32)	(−1.72, −0.56)	(−1.00, −0.03)	(−1.61, −0.98)
	one-sided	(−∞, −0.41)	(−∞, −0.65)	(−∞, −0.10)	(−∞, −1.03)

Figure 2.

Plots of the linear function of x inside the link H in four treatments, where x is the baseline CD4 count in the logarithm scale. The OLS (left) and the WLS (right) methods are used to estimate α.

In both the OLS (left plot in Figure 2) and the WLS (right plot in Figure 2) estimation, the lines from treatment 1 and the other three treatments intercept around x = −0.5, corresponding to the baseline CD4 level of 288. Thus, for patients with a baseline CD4 count larger than 288, treatment 1 is probably a good treatment since the corresponding probability of having a ≥ 50% drop of CD4 count is quite small compared to other treatments. On the other hand, if a patient’s baseline CD4 count is smaller than 288, there is probably good reason to use the new treatments.

To further confirm our intuitive conclusion from observing the plots, we perform statistical inference regarding the four treatments. Our first attempt is to test the treatment differences between treatment k, (k = 2, 3, 4) and treatment 1. From the second row of Table 4, it is clear that at 95% confidence level, all of the three new treatments (k = 2, 3, 4), are significantly different from the standard treatment.

Considering that our original goal of the study is to discover better new treatments (k = 2, 3, 4) than the standard one, we further constructed one-sided confidence intervals. The third row in Table 4 summarizes the one-sided confidence intervals. The fact that under both OLS and WLS, β_c1, β_c2 and β_c3 are significantly smaller than zero suggests that at 95% confidence level, treatments 2, 3 and 4 are better than treatment 1 for severe patients, in that these three treatments decrease the probability of severe CD4 count declination for patients with low baseline CD4 counts. On the other hand, with high baseline CD4 counts, no certain variation in the treatment effect can be declared since the intervals regarding β₁, β₂ and β₃ include zero. In other words, the improvement of the new treatments only applies to patients with low CD4 counts and is more significant if the patients’ situation are more grave in terms of their baseline CD4 counts. For patients whose baseline CD4 counts are sufficiently high, the standard treatment could be a preferred choice.

4 Discussion

The problem of measurement error arises in real data analysis in many scientific disciplines. Generally speaking, there are two approaches to dealing with this problem. The first approach assumes the distribution of the unobserved covariates or of the measurement error to be known, or can be estimated using replicate data. Therefore this approach has limited applicability in practice. Another approach uses the instrumental variables which are easier to obtain than replicate data. Hence this approach has wider applicability in practice.

Although the instrumental variable approach has been widely used in nonlinear models, its applicability in binary response models is unclear. In this paper we demonstrate that this is possible without making any parametric assumption for the distribution of the unobserved variables in the model. In particular, the proposed estimator is fairly efficient under semiparametric setup. The simulation studies show satisfactory performance of the proposed estimator in finite sample situation.

Through combining the relations of the unobservable variable X with the observed W and with the instruments S, we establish a direct relation between W and S, and estimate the parameter α before performing the estimation for the parameter of interest β. Although Theorem 2 clearly indicates that this estimated α alters the final estimation variability of β̂, it is still unclear if such alteration is detrimental or beneficial. The only clear message is that if a true error distribution f_ε(ε | S, Z) is implemented, then the estimation of α causes estimation variance inflation for β. Overall, how to best handle the estimation of α so that under a same working model $f_{\mathit{\epsilon }}^{\ast }(\mathit{\epsilon }\mid \mathbf{S},\mathbf{Z})$, the estimation variability of β is minimized is still unknown. Further study is certainly needed.

Although we present our main estimator in the context of logistic or probit models, the method is certainly not restricted only to these contexts. In fact, any regression model of Y conditional on X, Z can be handled by our method via a suitable H function. This indicates that Y is also not restricted to binary variables. Thus, for example, the method can readily be extended to generalized linear models.