Viscoelastic deformation of lipid bilayer vesicles

Abstract

Lipid bilayers form the boundaries of the cell and its organelles. Many physiological processes, such as cell movement and division, involve bending and folding of the bilayer at high curvatures. Currently, bending of the bilayer is treated as an elastic deformation, such that its stress-strain response is independent of the rate at which bending strain is applied. We present here the first direct measurement of viscoelastic response in a lipid bilayer vesicle. We used a dual-beam optical trap (DBOT) to stretch 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) giant unilamellar vesicles (GUVs). Upon application of a step optical force, the vesicle membrane deforms in two regimes: a fast, instantaneous area increase, followed by a much slower stretching to an eventual plateau deformation. From measurements of dozens of GUVs, the average time constant of the slower stretching response was 0.225 ± 0.033 s (standard deviation, SD). Increasing the fluid viscosity did not affect the observed time constant. We performed a set of experiments to rule out heating by laser absorption as a cause of the transient behavior. Thus, we demonstrate here that the bending deformation of lipid bilayer membranes should be treated as viscoelastic.

Introduction

Eukaryotic cells are compartmentalized into organelles for organizing and utilizing biomolecules to facilitate cellular survival and interaction with the environment. These organelles, as well as the plasma membrane itself, are defined by lipid bilayers. Lipid bilayers are essential for cellular function: they form durable barriers for compartmentalization while maintaining the fluidity and flexibility required for processes such as membrane protein assembly and activity, ¹ budding and fusion at the endoplasmic reticulum for cytoplasmic volume exchanges, ² and cell remodeling. ³ The phospholipid bilayer is the platform for a multitude of cellular events, so its mechanical properties are a subject of significant physiological interest and have been studied extensively. Membrane morphological transitions such as those involved in intra-and intercellular vesicular transport, cell division, and cell movement require generation of high curvatures in the lipid bilayer. ^3–6 To understand the energetics of such deformations, membrane bending rigidity has been experimentally characterized through a wide range of methods including the analysis of membrane thermal fluctuations using optical microscopy ^7–10 and scattering techniques, ^11,12 as well as through deformation of the membrane using hydrodynamic, ^13,14 electric, ¹⁵ magnetic, ¹⁶ and optical ^17–19 forces.

The classic description originated by Helfrich ²⁰ considers lipid bilayer bending to be purely elastic; in other words, the elastic modulus of bending (κ) is independent of the rate at which the membrane bends. There have been, however, suggestions from previous work that bilayers may exhibit viscoelastic deformation; in other words, that their stress-strain response depends on the rate at which the strain is applied. Viscoelastic behavior has been observed in lipid monolayers ²¹ and has been predicted in bilayers by simulation approaches. ²² In 2009, Bruckner et al. ²³ argued that cholesterol transport across the lipid bilayer on a 10 ms timescale corresponds to a viscous mechanical relaxation that follows the immediate elastic deformation of osmotically shocked liposomes. Earlier, Melzak et al. ²⁴ used an acoustic platform to mechanically excite a layer of surface-bound liposomes. They showed that when the liposomes contained cholesterol, they did not behave as a purely elastic material; rather, they viscously dissipated the acoustic energy, responding out-of-phase with the excitation signal. Foo et al. showed that trapped vesicles in a flow can exhibit a creeping shape recovery behavior, depending on the temperature of the system. ²⁵ Recently, Salipante and Vlahovska ²⁶ reported that the electrodeformation technique of stretching the bilayer membrane of a giant unilamellar vesicle (GUV) under an AC field yield transient behavior arising from viscous diffusion of charges on the surface of the membrane. These results are indirect and subtle, and contemporary treatments of membrane mechanics continue to treat the lipid bilayer as purely elastic. ^27,28 Here, we present the first direct measurements of viscoelastic response in a lipid bilayer vesicle, using a dual-beam optical trap device to characterize viscoelastic creep in a GUV subjected to a step stress function.

GUVs are lipid vesicles with diameters in the range of tens of microns. They offer the advantage of observation by optical microscopy, especially when used in combination with an optical gradient between the inner and outer media, ¹⁰ so they are a commonly utilized model membrane for bending modulus measurements. GUVs allow for measurement of κ through fluctuation analysis, ^7–10 which requires optically resolvable thermal undulations of liquid-phase membranes; ²⁹ the description of the membrane deformation is derived from the Helfrich free energy expression. Another technique for measuring membrane mechanics in a GUV format is micropipette aspiration. ^13,14 Here, the GUV is contacted to a tapered glass capillary, through which suction pressure is applied to induce membrane deformation as an aspirated tubule. Micropipette aspiration experiments are interpreted in the context of a purely elastic membrane with fully reversible membrane deformation upon the decrease of applied tension. ^13,30 The bending modulus may also be measured through tether stretching induced by manipulating a membrane-attached magnetic bead with magnetic field ¹⁶ or optical tweezers ¹⁷ while the vesicle is held by a micropipette at the opposite end. The electrodeformation technique described earlier is a non-contacting method, and GUVs elongated into prolate shapes are selected for analysis. ¹⁵ It requires homogeneous distribution of stress on the membrane so its application is limited to membranes with zwitterionic lipid species. ²⁹

In this report, we use a dual-beam optical trap (DBOT) to deform GUVs in a manner such that the application of stress can be rigorously synchronized with the observed strain response, allowing for the observation of short time-scale transient responses. The optical forces applied by a DBOT provide uniaxial stretching tension with light applied through optical fibers positioned at opposite ends of a GUV that is optically denser than its surrounding environment. The near-instantaneous response of the lasers to a control signal and the transmission of force to the membrane at the speed of light make this technique especially appropriate for transient measurements. We have previously used DBOT stretching to characterize the steady-state elasticity of GUVs. ^18,19

Here, we demonstrate and characterize a transient response of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) GUVs to a step stress function generated using a DBOT apparatus. Video microscopy of the strain response of POPC GUVs to this stress function reveals a transient response with a characteristic time scale on the order of 100s of ms, consistent with viscoelastic creep. This result implies that at physiologically relevant time scales, the bending mechanics of the membrane cannot be treated as purely elastic.

Experimental

Materials

POPC was purchased from Avanti Polar Lipids. Sucrose, glucose, HEPES, and glycerol were from Sigma-Aldrich. Heavy water, or deuterium oxide, was from Cambridge Isotope Laboratories, Inc. Rhodamine B was purchased from Alfa Aesar.

GUV Preparation

The giant unilamellar vesicles (GUVs) used in this study are composed of POPC and formed using the electroformation method adapted from Angelova. ³¹ The lipid dissolved in chloroform (10 μ L of 5 mg/mL solution) was deposited using a 10 μ L-volume syringe (Gastight with point style 3 needle, Hamilton) as approximately 1 μ L spots onto the conducting side of an indium tin oxide (ITO)-coated glass slide (Delta Technologies) inside the perimeter enclosed by a silicone o-ring (13/16″ ID, 1″ OD, Sterling Seal & Supply) adhered by silicone vacuum grease (Dow Corning). The lipid film was allowed to dry under vacuum overnight prior to hydration with a 487 mM sucrose solution in deuterium oxide solvent buffered with 20 mM HEPES to pH 7.0 (η = 1.43 mPa·s, RI = 1.3528). Viscosity (η) was measured using an Ubbelohde viscometer (Cannon Instrument Company), and refractive index (RI) was measured with the PAL-RI refractometer (Atago). For high-viscosity experiments, the solvent contains 20 % v/v glycerol (sucrose solution: η = 3.00 mPa·s, RI = 1.3807). Another piece of ITO-coated slide was attached to the o-ring with the conducting side facing towards the lipid film, and the AC field was applied at 10 Hz, 1.3 V by a function generator (Hewlett-Packard/Agilent Technologies) for 2 h, with the slides on a hot plate at 50°C (Electrothermal).

The medium exterior to the GUVs was replaced with an isoosmotic glucose solution (530 mM in the same buffer solution, η = 1.24 mPa·s, RI = 1.3452 without glycerol and η = 2.48 mPa·s, RI = 1.3718 with glycerol; osmolarity measured by the Gonotec Osmomat 030 freezing point osmometer) by first combining 880 μ L of the GUV solution in sucrose with 500 μ L of the glucose solution in a microcentrifuge tube (VWR International). After allowing 30 min for GUV sedimentation, 500 μ L was removed from the supernatant of the solution and replaced with 500 μ L of the glucose solution, and another round of sedimentation and solution replacement was carried out. Finally, 500 μ L was removed again from the supernatant of the solution and replaced with 500 μ L of the glucose solution. In preparation for GUVs in the high-viscosity media, 1 h was allowed for each sedimentation period, but this step was later replaced by centrifugation (Eppendorf) of the solution at 14,000 × g for 10 min. Note that this change in protocol was implemented to improve vesicle population density for the GUV stretching experiments and did not affect the reported temporal response behavior.

GUV Stretching with the Dual-beam Optical Trap (DBOT)

The DBOT apparatus consists of light emitting from two identical laser diodes (LU0808M200, Lumics GmbH) with end-coupled optical fiber creating a stable trap along the beam axis at the center of the channel. Due to the refractive index contrast between the interior and exterior of the GUV, the momentum exchange resulting from reflection and refraction produces the surface stress used to deform the GUV. GUVs in an aqueous solution were flowed through the microfluidic channel constructed using a square glass capillary (100 μ m inner diameter and 100 μ m wall thickness, Vitrocom) connected with microfluidic adapters (Upchurch) to flexible fluorinated ethylene-propylene (FEP) tubing (254 μ m inner diameter and 1526 μ m outer diameter, IDEX). The capillary tube and the two optical fibers were aligned on a custom-made silicon holder fabricated by photolithography and reactive ion etching. The fiber-capillary unit was coated with index-matching gel.

The channel flow was controlled by a peristaltic pump (P720/10 K, Instech). The flow speed was gradually decreased as a GUV approached the optical trap. The flow in the capillary tube was completely stopped and isolated by a shut-off valve (Upchurch) when a GUV arrived at the trap. The GUV was then visually inspected through the microscope, and only vesicles with clearly resolvable boundaries were selected for stretching. The dual-beam laser power was modulated by two laser diode controllers (ITC 4005, Thorlabs). A GUV was initially trapped by using 50 mW power from each diode laser (100 mW combined), and was then stretched five times at 250 mW (500 mW combined). Each stretching event consisted of a step increase of each diode laser from 50 mW to 250 mW (held for 5 s), and a step decrease back to 50 mW (held for another 5 s). The laser response time was characterized by a photodetector (918D-SL-OD3, Newport Corp).

DBOT Data Analysis

To characterize the temporal deformation of GUVs, a high speed camera (61 fps) equipped with CCD image sensor was used to record the experiments via a 50× objective as time-lapse series of micrographs. A MATLAB program was built to process each video image frame: the GUV edge contour was detected and used for calculating surface area. Expanding the spheroid contour from each frame in terms of spherical harmonics and assuming constant vesicle volume, the surface area strain can be obtained as a function of time for quantifying structural deformation. Note that the temporal resolution in our measurement was limited to 0.016 s due to the camera frame rate.

For time constant extraction, five measurements were averaged for each GUV to minimize the signal-to-noise ratio in extracted area strain. The resulting fluctuations in area strain have the frequency of ~29 Hz. A single exponential decay function was used to fit to the experimental data for extraction of the delay time constants. To address the slower stretching response, the preceding instantaneous response was first defined and removed from the data set for fitting. The instantaneous response occurred at a rate greater than the sampling limit for the system, so we excluded the first two points corresponding to those samples from both rising and falling edges for fitting. Some GUVs did not have apparent and consistent deformational behaviors leading to higher noise level in surface area strain, thus the poorly fitted results (adjusted R-square < 0.75) were excluded from the statistical analyses.

Results and discussions

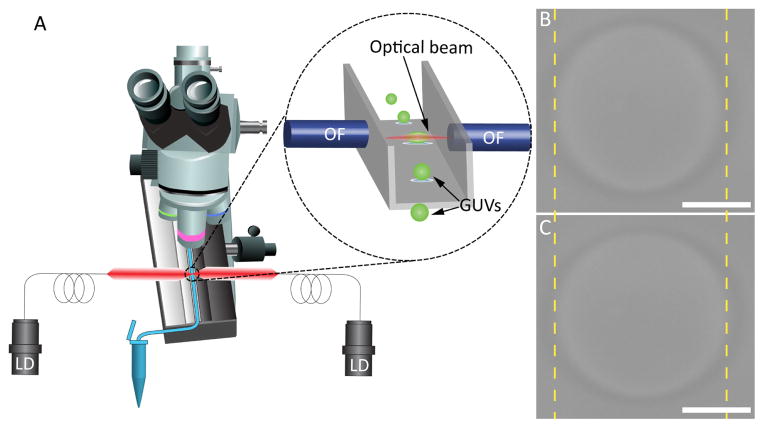
As in our previous work measuring steady-state elastic deformation of lipid bilayers, ^18,19 GUVs in an aqueous solution were flowed through a square glass capillary tube to a position between two laser diode-coupled optical fibers, where each vesicle was trapped and stretched via optical forces. Fig. 1A is the schematic of our DBOT apparatus. The microfluidic channel for trapping and stretching experiments was mounted on the stage of an upright optical microscope, where it was observed in transmitted light mode. The inset of Fig. 1A is the magnified image of the trapping site in the microfluidic channel (grey), where a GUV (green) is held in place by optical beams from two optical fibers (blue). A laser power of 100 mW (50 mW from each laser diode) was applied to trap a GUV, stretching it slightly into a spheroid shape. Upon increasing power, the stretch of the GUV was more pronounced. Images of a GUV trapped at 100 mW and 500 mW laser powers are shown in Fig. 1B and Fig. 1C, respectively. Here, the length of the major axis of the GUV increased from 22.94 ± 0.047 μ m (standard deviation, SD) to 24.88 ± 0.065 μ m (SD).

Fig. 1.

Schematic illustration of the DBOT apparatus and its trapping mechanism. (A) A schematic of a microscope integrated with a microfluidic channel and two fiber-coupled laser diodes. The inset is the magnified image of the trapping site, where the optical fibers are positioned towards a square glass capillary tube. Optical images of a trapped GUV (B) with 100 mW laser power and (C) with 500 mW laser power. The scale bars are 10 μ m.

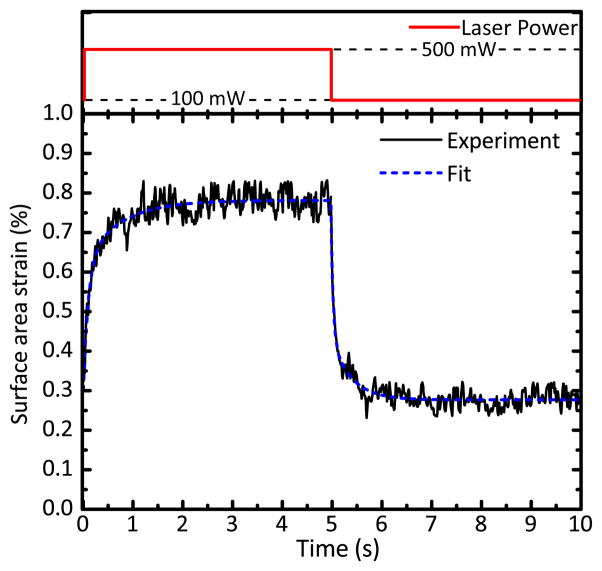
To characterize the temporal response of GUVs, we performed video microscopy at 61 frames per second. Videos were synchronized with a step ramp in laser power. In the course of a single measurement, a GUV was initially trapped in position using 100 mW laser power and was then stretched 5 times. Each stretching event consists of a step increase of laser power to 500 mW and a step decrease back to 100 mW, with the laser power was maintained for 5 s at each step, as shown in Fig. 2 (red). We consistently observed that vesicles responded to this power step at two timescales. There is a very fast, instantaneous stretching followed by a much slower stretching to an eventual constant plateau deformation. This apparently viscoelastic behavior led us to perform a detailed analysis of the vesicle shape change with time.

Fig. 2.

(Top) The step increase and step decrease in laser power (red). (Bottom) Time-dependent response and fit to Eq. 1. A single DBOT measurement of one GUV, averaged from 5 stretching events. The fit to this data set for time constants (blue, dashed) yields extracted rise and fall time constants of 0.284 ± 0.011 s (SEM) and 0.163 ± 0.006 s (SEM), respectively.

In each video frame, the contour formed by the vesicle boundary was traced, fitted to a second-order spherical harmonic term, and rotated to yield a surface with a known surface area. The deformation of the GUV is calculated as surface area strain (in percentage) of a spheroid by assuming constant volume. To characterize the time scale of the response, we treated the deformation of the membrane as a single-exponential decay process:

$$\frac{\mathrm{\Delta }A}{A_0}=C_0+C_1{e}^{-t/\tau }$$ (1)

where ΔA/A₀ is the time-dependent surface area strain, C₀ is the surface area strain at trapping power, compared to the surface area of an equivalent-volume sphere, C₁ is a fitting parameter, and τ is the time constant associated with the delay.

We characterized the time-dependent deformation of the membrane both upon a step increase in laser power (rise) and a step decrease in laser power (fall). A typical time-strain curve is shown in Fig. 2 (black, solid), together with the best-fit exponential decay model (blue, dashed). To analyze the timescale of the slower stretching response, the instantaneous response preceding it was defined and excluded from the fit. To minimize noise in the data, values from 5 stretching events were averaged. The instantaneous response occurred at a rate greater than the sampling limit for the system, so we rejected the first two points corresponding to those samples from both rising and falling edges for fitting. The remaining points were fitted to Eq. 1 for determination of the rise and fall delay time constants. For the particular data set shown in Fig. 2, the extracted rise and fall time constants are 0.284 ± 0.011 s (standard error of the measurement, SEM) and 0.163 ± 0.006 s (SEM), respectively.

To show that the observed time dependence is a function of membrane deformation rather than the result of a time dependence in applied power, we measured the effective laser response time (see Supporting Information; Fig. S1). The laser response time is on the order of 3–4 ms; orders of magnitude faster than the observed membrane deformation. The applied optical power is therefore effectively instantaneous in comparison to the observed time-dependent vesicle deformation response.

To identify the bilayer deformational mode associated with this transient behavior, we performed a simple stress-strain experiment as described in our previous work. ^18,19 This experiment covered the same range of applied laser powers as used in the previously described step power experiment. In the regime where bilayer deformation is dominated by bending modes, there is a log-linear relationship between applied tension and area strain. ¹⁴ We used a ray-optics technique ³² to calculate the total stress applied on the membrane surface and translated the stress to lateral tension. For a typical GUV at the powers applied here, we found that the bilayer is in fact in the bending-dominated deformational regime with a bending modulus of 11.47 ± 1.36 k_BT (SEM) (see Supporting Information; Fig. S2). This indicates that that the transient response reported here is a property of bilayer bending.

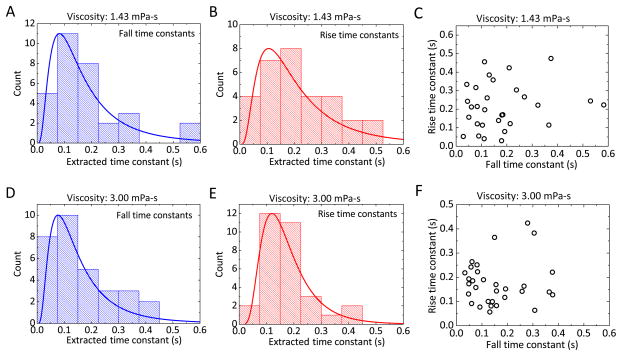
We repeated the step power DBOT experiment for dozens of GUVs (Fig. 3A and Fig. 3B). The distributions of rise and fall time constants were confirmed to be log-normal by a Kolmogorov-Smirnov test. Fitting to a log-normal distribution, we found the mean rise time constant to be 0.225 ± 0.033 s (SD) and the mean fall time constant to be 0.183 ± 0.024 s (SD). The difference between rise and fall time constants is not significant as verified by a Mann-Whitney test (p > 0.05). Further, rise and fall time constants are not correlated in individual vesicles (Fig. 3C). The linear Pearson’s correlation coefficient between the rise and fall time constants is 0.1488. This indicates that the breadths of the distributions in Fig. 3A and Fig. 3B reflect experimental error rather than an underlying distribution in bilayer material properties. The primary source of error in the experiment is related to clearly identifying and tracing the vesicle boundary; the square shape and relatively thick walls of the capillary channel introduce imaging effects that make bright field illumination challenging.

Fig. 3.

Ensemble statistics of vesicle deformation time constants in various media. (A) and (B) give rise and fall time constants for GUV populations in low-viscosity medium. (C) Rise time constant vs. fall time constant for each individual vesicle in low-viscosity medium. (D) and (E) give rise and fall time constants for GUV populations in high-viscosity medium. (F) Rise time constant vs. fall time constant for each individual vesicle in high-viscosity medium. The solid curves in (A), (B), (D), and (E) are the log-normal distribution functions fitted to the data, and the mean and standard deviation of each are (A) 0.225 ± 0.033 s, (B) 0.183 ± 0.024 s, (D) 0.176 ± 0.009 s, and (E) 0.162 ± 0.016 s.

While these experiments seem to clearly show that there is a time-dependent mechanical response to a step stress being placed on the vesicle, they provide no information on whether this response is an intrinsic property of the bilayer or a result of mechanical coupling between the bilayer and the aqueous medium in which the experiments are performed. The interactions between a vesicle and the surrounding fluid can be calculated as the hydrodynamic force acting on an object. The hydrodynamic force, including the influences of fluid velocity fields on an object, has strongly object-shape-dependent parameters, object-size-dependent parameters, and fluid-property-dependent parameters. ^33–35 Moreover, the deformational behavior of vesicles is shown to have crucial dependence on both the mechanical properties (i.e. bending modulus) of the membrane and the dissipative coupling to the surrounding fluids. ^36–38

To investigate the influence of the surrounding fluid on the transient behavior, we repeated the step stress experiment at a different medium viscosity. We increased the viscosity of the media both inside and outside the GUVs by approximately twofold. The measured viscosity of sucrose buffer (inside the vesicle) was increased from 1.43 mPa·s to 3.00 mPa·s. The viscosity of glucose buffer (outside the vesicle) was increased from 1.24 mPa·s to 2.48 mPa·s. Fig. 3D and Fig. 3E show the measured rise and fall time constants in high-viscosity medium. By log-normal fitting, the rise time is 0.176 ± 0.009 s (SD) and the fall time is 0.162 ± 0.016 s (SD). As with the time constants in low-viscosity medium, rise and fall constants are not significantly different and they are uncorrelated in individual vesicles (Fig. 3F). Comparing the time constants in low-viscosity and high-viscosity media, the differences between each rising or falling pair is not significant as verified by a Mann-Whitney test (p > 0.05). This suggests that the transient deformation of GUV does not come from the viscous dissipation in the surrounding medium.

If the transient deformational behavior can be attributed to viscous coupling with the medium, it would be expected that the magnitude of this coupling would vary with vesicle size. ³⁹ Fig. 4 is a pair of scatter plots comparing time constant and GUV diameter in low- and high-viscosity media. These parameters are uncorrelated, again suggesting that the transient mechanical response is a property of the bilayer rather than a result of coupling to the viscous medium.

Fig. 4.

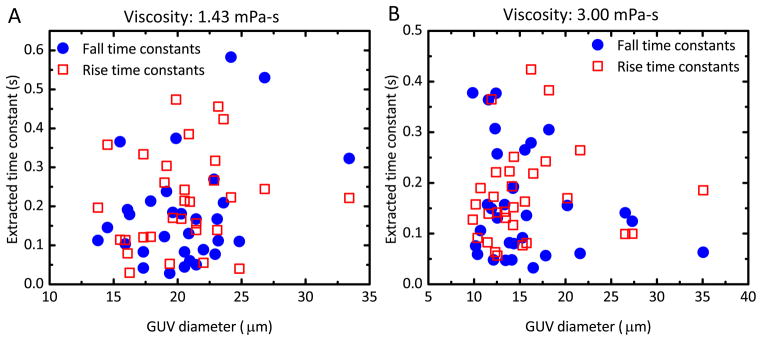
Scatter plot of time constant as a function of GUV diameter. (A) The rise (red, squares) and fall (blue, circles) time constants in low-viscosity medium. The linear Pearson’s correlation coefficient is 0.1613 for the rise time and 0.377 for the fall time. (B) The rise (red squares) and fall (blue circles) time constants in high-viscosity medium. Correlation coefficients are 0.0799 for rise time and −0.2177 for fall time.

Finally, we performed a set of experiments to rule out heating by laser light absorption as a cause of the transient behavior. Not only does the surface area strain depend on temperature ¹⁴ but so does the bending modulus of the lipid bilayer membrane. ^11,40 An increase in temperature in the DBOT channel could result in a corresponding change in membrane area if it relaxes the bending modulus, allowing the membrane strain to increase at a constant tension. If this is the case, the relaxation from 0–2 s in Fig. 2 would be the result of gradual heating of the membrane resulting in decreased bending modulus as the laser power is held constant. Heating in laser traps via water absorption is a phenomenon that has been noted in other biological trapping systems. ^41,42 To minimize this effect, we worked at the wavelength of 808 nm and used heavy water (D₂O) rather than water. Heavy water has an absorption coefficient of 2.5×10⁻⁴ cm⁻¹ at 808 nm, in contrast with 4.5×10⁻³ cm⁻¹ for water. ^43–45 Note that heavy water was used in all experiments described in this report.

We attempted to directly measure the temperature change in the channel using the temperature-dependent fluorescence of rhodamine B. ⁴⁶ We observed no change in rhodamine B fluorescence intensity during application of the standard DBOT step power protocol (see Supporting Information; Fig. S3). We calibrated this system using an infrared heat lamp to induce more drastic temperature changes and to directly measure these temperature changes with a thermocouple placed adjacent to the channel; the observed fluorescence intensity change during the course of heating is shown in the supporting information (Fig. S3). The minimum observable temperature change probed by rhodamine B intensity is approximately 0.3 K; this puts an upper limit on the possible temperature increase in the channel during a DBOT experiment. The temperature dependence of the bending modulus of lipid bilayer membrane can be written as

$$ln\kappa =\frac{{\epsilon }_{\kappa }}{k_{B}T}+\mathit{const}$$ (2)

where ε_κ is the internal energy, k_B is Boltzmann’s constant, and T is temperature. ^11,40 The ε_κ parameter for POPC is not available in the literature, so the value for 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) of 7×10⁻²¹ J was used. ¹¹ The relation between the bending modulus and the surface area strain ¹⁴ is

$$\frac{\mathrm{\Delta }A}{A_0}=\frac{k_{B}T}{8\pi \kappa }ln\left(\frac{{\sigma }_h}{{\sigma }_0}\right)$$ (3)

where σ_h/σ₀ is applied tension as a fraction of resting tension. Using the estimated upper limit on temperature change (0.3 K) from the experiment with rhodamine B, we estimated that thermal effects with this temperature change contributed to less than 0.18% of the total strain increase from ~0.3% to 0.75% (Fig. 2) observed as a transient response in our experiments (see Supporting Information for detailed calculations).

Conclusions

By using lasers with a ms response time to apply optical force to GUVs, we were able to observe the time course of the mechanical response of lipid bilayers to applied tension. Our data show apparent viscoelastic deformation of lipid bilayer vesicles. That is, upon application of a step increase in applied membrane tension, the vesicles strain in a transient manner. The time constant for this transient behavior is ~0.2 s. This behavior is not feasibly the result of absorptive heating and it is independent of medium viscosity, suggesting that it is an inherent property of the lipid bilayer.

The mechanical behavior of the bilayer membrane is a widely studied subject, and the particular curiosity towards characterizing the bending energy is largely motivated by drastic membrane deformation in curvatures accompanying routine cellular processes that include budding and fusion of endocytotic vesicles, ciliary movements, and cell reorganization and division. ^3–6 Various physiological processes occur at widely varying timescales; for instance, synaptic vesicle fusion occurs at a ~20 ms timescale ⁴⁷ while mechanosensing by membrane proteins occurs over minutes. ⁴⁸ Characterizing the membrane as a viscoelastic material is necessary to understand the dependence of membrane stress-strain behaviors on the rate of deformation at these varying timescales.

Though the time constants measured in this work are particular to a specific lipid composition, the general approach can be applied to different membrane compositions so long as an appropriate refractive index difference is maintained between the interior and exterior of the vesicles. It therefore has the potential to be used to ultimately understand relationships between lipid bilayer composition and viscoelastic properties. By further integrating these results with modeling of hydrodynamic coupling between the extracellular medium, the cytoplasm, and the membrane, a full picture of the time-dependent mechanical response of the membrane can be developed.