Bayesian Hierarchical Regression on Clearance Rates in the Presence of “Lag” and “Tail” Phases with an Application to Malaria Parasites

Summary

We present a principled technique for estimating the effect of covariates on malaria parasite clearance rates in the presence of “lag” and “tail” phases through the use of a Bayesian hierarchical linear model. The hierarchical approach enables us to appropriately incorporate the uncertainty in both estimating clearance rates in patients and assessing the potential impact of covariates on these rates into the posterior intervals generated for the parameters associated with each covariate. Furthermore, it permits us to incorporate information about individuals for whom there exists only one observation time before censoring, which alleviates a systematic bias affecting inference when these individuals are excluded. We use a changepoint model to account for both lag and tail phases, and hence base our estimation of the parasite clearance rate only on observations within the decay phase. The Bayesian approach allows us to treat the delineation between lag, decay, and tail phases within an individual’s clearance profile as themselves being random variables, thus taking into account the additional uncertainty of boundaries between phases. We compare our method to existing methodology used in the antimalarial research community through a simulation study and show that it possesses desirable frequentist properties for conducting inference. We use our methodology to measure the impact of several covariates on Plasmodium falciparum clearance rate data collected in 2009 and 2010. Though our method was developed with this application in mind, it can be easily applied to any biological system exhibiting these hindrances to estimation.

1. Introduction

Resistance to antimalarial medication has been, and continues to be, a grave global health concern. Over the past 400 years, numerous drugs have initially shown promise as effective treatments against Plasmodium falciparum (the most lethal of the malaria parasites). Unfortunately, these malaria parasites have successively developed resistance to each drug, with time intervals between drug deployment and first reported resistance (that is adequately detected) ranging from 278 years (quinine) to less than 1 year (sulfadoxine-pyrimethamine). For a detailed history of the struggle to find an effective treatment regimen for P. falciparum malaria, see Wongsrichanalai et al. (2002).

Artemisinin, first established as an antimalarial drug in 1978, has proven extremely effective against malaria both individually and as part of “Artemisinin Combination Therapy” in which fast acting artemisinin is combined with a slower acting antimalarial partner drug (e.g., mefloquine, lumefantrine, or piperaquine); however, recent evidence suggests that P. falciparum resistance to artemisinin is developing in Southeast Asia (see Dondorp et al., 2009; White, 2010; Amaratunga et al., 2012; Ashley et al., 2014). To accurately monitor the spread, independent emergence, or worsening of artemisinin resistance over time, researchers are interested in whether and to what extent patient level covariates are associated with resistance. Before one can answer these questions, a quantitative measure of antimalarial efficacy is required.

The parasite clearance rate is largely considered to be the most robust measure of artemisinin effect (Flegg et al., 2011; White, 2011). To calculate this rate, one first administers an artemisinin to an individual patient, and then counts the parasite density in the patient’s blood at a sequence of measurement times. The parasite clearance rate is then defined to be the negative of the slope of the log-parasitemia over the time in which the antimalarial is taking effect. Unfortunately, many factors make the calculation of this rate more complicated than it would appear to be.

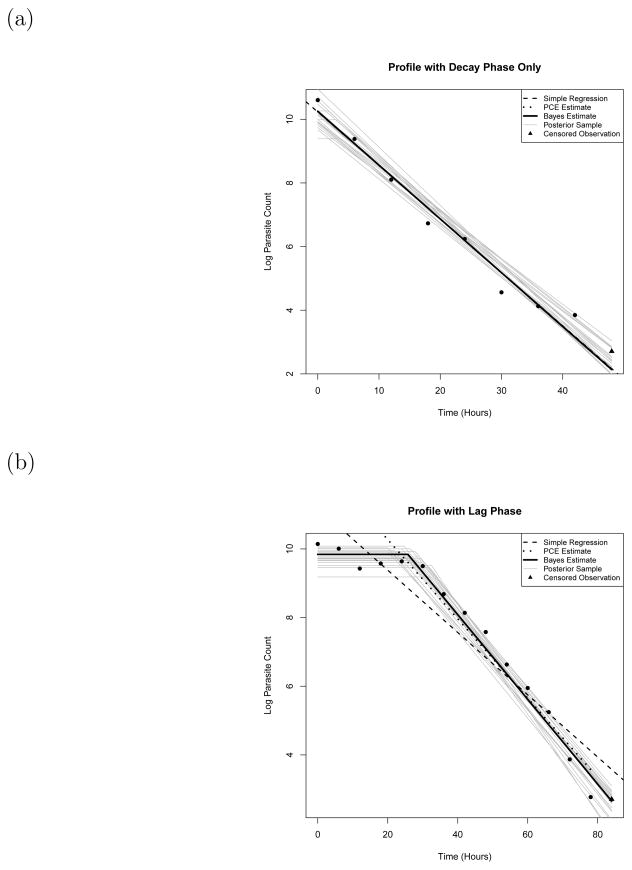
Some individuals exhibit an initial period after artemisinin administration in which their parasite densities remain roughly constant, or even increase, rather than decrease as would be expected (Doolan et al., 2002; Koning, 2007). These “lag” phases are thought to be caused by a combination of different factors, including the absorption time of drugs; the cyclical nature of malarial pathology; schizogony, which would result in a rapid increase in parasitemia; and the relatively synchronous development of sequestered parasites in microvessels, where they may be incidentally in the process of liberating new parasites into circulation at the same time artemisinin is administered (for example, see Dondorp et al., 2005). Flegg et al. (2011) and Nkhoma et al. (2013) estimated that 30% and 25.7% of clearance profiles in their respective data sets appeared to have lag phases. At present, it is accepted that only the linear part of the log-parasitemia curve is a good measure of antimalarial susceptibility (Nkhoma et al., 2013), and hence this lag phase should not factor into the calculation of the clearance rate. Failure to account for lag phases can result in a downwardly biased estimates of clearance rates, as is demonstrated in Figure 1 (b) of Section 4.1.

Figure 1.

Examples of posterior log parasitemia profiles. The first profile (a) is identified as only having a decay phase, whereas the second (b) is identified as having a lag phase before the decay occurs. The gray lines are various posterior samples. The solid black line represents the posterior mean clearance rate from our Bayesian procedure. The dotted black line is the fit given by the PCE. The dashed black line is the fit given by a simple to bit regression without lag and tail phases. The triangles are censored observations due to the detection limit

Beyond the existence of lag phases, there are other aspects of parasite clearance profiles that are potentially inimical to estimation. Due to the data collection process there is a detection limit, which means that we cannot actually observe a parasite density below a certain value. Hence, there are observations over time which are left censored (i.e., we know that the patient had a parasite density that was lower than the detection limit, but do not know its actual value). Additionally, some profiles exhibit a bottoming out in which the observed parasite densities hover around the detection limit. These “tail” phases also are not typically factored into the calculation of the clearance rate, as they are not within the time frame where the parasite load is steadily decaying. Finally, there is the potential for measurement errors, caused primarily by the imprecise nature of the technique used to calculate parasite densities. See Dowling and Shute (1966) and O’Meara et al. (2005) for more on variability caused by the data collection process. Further, if we interpret the circulating parasite density as a measure of (i.e., as proportional to) the full parasite load within the body, then differences in the fraction of parasites sequestered in microvessels may lead to measurement error.

White (2011) motivates the need for a principled methodology for estimating clearance rates while accounting for lag and tail phases, stating that “it remains to be decided what should be the criteria for defining the top of the slope (i.e. maximum value, or intersection of linear fit to the initial plateau, or modelled fit), and for the lowest densities that should be included at the tail of the curve.” Towards this end, Flegg et al. (2011) developed the Parasite Clearance Estimator (PCE), a method for estimating the parasite clearance rate while accounting for lag phases, tail phases, and measurement errors. This method is the current standard for measuring clearance rates and represents an improvement over previous methodologies that simply fit a line to the log parasitemia over time for each individual and ignored data points which fell below the detection limit. To assess how often the PCE is used, we searched PubMed to find papers that reported parasite clearance for P. falciparum malaria infections between November, 2011 and May, 2014. 48 papers were found and 25 of them had frequent parasite data, suitable for the PCE tool; of these 25 papers, 17 (68%) used the PCE to estimate parasite clearance, showing that PCE is widely used in practice. For the PCE method, Flegg et al. (2011) provide a step-by-step algorithm for identifying tail phases, and lag phases. Tail phases are defined in terms of a series of thresholds, whereas lag phases are determined by comparing linear, quadratic, and cubic fits when possible and assessing certain characteristics of these fits. To account for the detection limit, tobit regression is used whenever possible.

The PCE was developed with the sole objective of attaining clearance rate estimates for each patient, and has improved the estimation of clearance rates when this represents the primary end point of a study; however, the impact of patient level covariates on these clearance rates can be an important primary end point in other studies. A common approach taken in the antimalarial literature for conducting this latter analysis is the following two-stage procedure:

1. Estimate the clearance rate using the PCE

2. Estimate the effect of covariates on estimated clearance rate (or, equivalently, the half-life) through regression.

This approach has many shortcomings. Firstly, in using this two-stage approach the estimated clearance rates are treated as known in the second level, which drops all information about the variability in estimation. This variability differs in degree from individual to individual depending on the number of time points available. Hence, the standard approach uses homoskedastic errors when they are actually heteroskedastic, a problem which is known to potentially result in biased inference due to improper standard error estimates (White, 1980). Secondly, PCE handles profiles with a small number of measurement times in a way that can introduce substantial bias when conducting a second level regression. For individuals who had only one time recording before the detection limit was reached, the PCE cannot compute a clearance rate estimate and hence that individual is omitted from the analysis. Furthermore, for individuals with only two time measurements before censoring, the PCE replaces the censored observation with the censoring point, resulting in a clearance rate estimate that is biased downwards. The ramifications of these biases are discussed in Section 3.1. In addition, the methods for lag and tail detection used by PCE are quite complicated and are not derived from an underlying statistical model, which may bias both the estimates of the clearance rates and the estimates of covariate effects on these clearance rates. These factors are shown in Section 3.2 to result in confidence intervals that fail to meet their prescribed coverage guarantees and in estimators demonstrating substantial bias. For these reasons, a principled approach to address these issues in a way that produces statistically sound results is desired.

We model parasite clearance rates under the assumption that each observed time of an individual’s parasite density takes place in one of three phases: a lag phase, a decay phase, or a tail phase. Though we assume all profiles contain a decay phase, we allow for the possibility that certain individuals lack a lag phase, a tail phase, or both – consistent with what antimalarial researchers have observed. We also enforce continuity between the functions describing adjacent phases. To accomplish this analytical approach, we embed a changepoint model within a Bayesian hierarchical linear model. The hierarchical structure enables us to incorporate information about all patients, regardless of how many time points are available for their parasite clearance profile, and address the hindrances to estimation discussed earlier. The changepoint model determines whether or not a certain phase existed within an individual’s parasite clearance profile and isolates the time of transition between the phases if multiple phases occur. After giving a proper exposition of our model, we then show in a series of simulations the improvements our model provides relative to the standard two-stage approach in terms of desirable statistical properties. These included reduced mean squared error of estimated clearance rates and the creation of intervals that have better frequentist properties. We then present the results of using this method to investigate the relationship between covariates and parasite clearance half-lives in Cambodian patients treated with artesunate (a type of artemisinin) for P. falciparum malaria in 2009 and 2010.

2. The Bayesian Clearance Estimator

We propose a Bayesian model for parasite densities over time that accounts for lag phases, tail phases, and censored observations.

2.1 Data Likelihood

Let y_ij denote the malarial parasite density for the i^th individual at time t_ij, where 1 ≤ i ≤ N and 1 ≤ j ≤ n_i, and let t_i1, …, t_ini be the time points for the i^th individual. Let ${\delta }_i^{\ell }$ be the time of the changepoint between the lag and decay phase for the i^th individual, and let ${\delta }_i^{\tau }$ be the time of the changepoint between the decay phase and the tail phase. Our model for the data is:

$$log(y_{ij})={\alpha }_i-{\beta }_i({\delta }_i^{\ell }𝟙\{t_{ij}<{\delta }_i^{\ell }\}+t_{ij}𝟙\{{\delta }_i^{\ell }\le t_{ij}\le {\delta }_i^{\tau }\}+{\delta }_i^{\tau }𝟙\{t_{ij}>{\delta }_i^{\tau }\})+{\epsilon }_{ij}$$

where α_i and β_i are individual level parameters, and ε_ij are the individual level errors. Hence, {β_i} represent the clearance rates of interest.

We assume that the error terms represent biological variability and may possibly include measurement error of some type: ${\epsilon }_{ij}\stackrel{\mathit{iid}}{\sim }\mathcal{N}(0,{\sigma }_{\epsilon }^2)$. Note here that we assume independence between the errors at time t_ij and t_ik for all individuals i and all measurement numbers j ≠ k. We assess the validity of this assumption in Web Appendix A by looking at residuals from our data analysis.

A major concern among malarial researchers in fitting these profiles is the existence of “outlying” counts being recorded for individual that are biologically implausible and do not reflect the individual’s true parasite density. Such outliers often result from transcription errors (Flegg et al., 2011). These outlying observations have the potential to substantially impact the resultant fit. Flegg et al. (2011) developed an automated methodology for assessing whether or not each observed parasite count was scientifically feasible, and for removing them from the analysis before any profile fitting is done on these grounds, based on thresholds determined by scientists with subject matter experience (see the methodology supplement of Flegg et al. (2011) for details). We recommend that practitioners either examine each profile for outliers or use the automated methodology of Flegg et al. (2011) in determining whether an observed count is an outlier. We have built the Flegg et al. (2011) outlier detection schema into our methodology as an optional step to be undertaken before data analysis is conducted.

Due to the detection limit within the data collection process, we do not always observe the full set of parasite densities {y_ij}. Let ζ denote the detection threshold (two typical values of ζ are 40 parasites per microliter and 16 parasites per microliter, as described in Flegg et al. (2011)). Then, the actually observed counts, $y_{ij}^{\ast }$, are:

$$y_{ij}^{\ast }=\{\begin{array}{ll}{y}_{ij}& y_{ij}>\zeta \\ 0& y_{ij}\le \zeta \end{array}$$

2.2 Prior Distributions and Hierarchical Structure

We now specify prior distributions for our regression parameters and the outlier indicators. As part of the hierarchy for the {β_i}, we note that in many cases we are interested in the relationship between {β_i} and a host of covariates. We let X denote this N × p matrix of covariates. The case in which we do not have covariates is captured in this representation by simply letting X be an N × 1 vector of ones. Our priors are:

$$\begin{array}{rr}log({\beta }_i)\stackrel{\mathit{indep}}{\sim }\mathcal{N}(\mathit{\gamma }{\mathbf{X}}_i,{\sigma }_{\beta }^2)\hfill & \hfill p(\mathit{\gamma },{\sigma }_{\beta }^2)\propto 1/{\sigma }_{\beta }\\ log({\alpha }_i)\stackrel{\mathit{indep}}{\sim }\mathcal{N}(\mathit{\eta }{\mathbf{X}}_i,{\sigma }_{\alpha }^2)\hfill & \hfill p(\mathit{\eta },{\sigma }_{\alpha }^2)\propto 1/{\sigma }_{\alpha }\\ \hfill & \hfill p({\sigma }_{\epsilon }^2)\propto 1/{\sigma }_{\epsilon }^2\end{array}$$

where p(·) represents a prior density function. Our specification of lognormal priors on the clearance rates is in line with the standard analyses performed by antimalarial researchers and result in an analysis that is highly reminiscent of a random effects model. Our priors on {γ, ${\sigma }_{\beta }^2$} and {η, ${\sigma }_{\alpha }^2$} are specified so that we have proper posterior distributions, avoiding the trap described in Hobert and Casella (1996) and following the recommendations of Gelman (2006). We place the Jeffrey’s prior on ${\sigma }_{\epsilon }^2$. All told, this specification results in shrinkage estimation for the {β_i}, with the degree and direction of the shrinkage aided and influenced by the individual level covariates. The posterior distribution of γ is the primary focus of posterior inference, as γ represents the effect of the covariates of interest on the clearance rates.

We introduce two probabilities, π^ℓ and π^τ, which represent the a priori probabilities of there being a lag phase and a tail phase respectively. If there is not a lag phase for individual i, then the changepoint between lag and decay phase, ${\delta }_i^{\ell }$, occurs at time 0 with probability 1. If there is a lag phase, then we specify a prior distribution over the observed time domain for the i^th individual. The specification of priors on the tail phase is similar. If there is no tail phase, then the changepoint between the decay and tail phases occurs at the maximal time point for that individual, t_ini, with probability 1. Otherwise, we specify a prior for ${\delta }_i^{\tau }$ over its feasible range given the constraint that ${\delta }_i^{\ell }\le {\delta }_i^{\tau }$.

Traditionally, Bayesian changepoint models have used uniform priors for the location of changepoints; see Bacon and Watts (1971); Smith and Cook (1980); Carlin et al. (1992) among many. A uniform prior would have the unrealistic characteristic in our application of putting equal prior probability on changepoints near and far from the boundary, making it unappealing. In our application changepoints can be thought of as time-to-event quantities, which are commonly modeled by exponential distributions (resulting in a constant hazard rate over time). We note that the exponential distribution has a mode at 0 for any value of the rate parameter. This type of model would be appropriate if it was believed that all individuals had lag phases, just to varying degrees; however, antimalarial researchers believe that some individuals truly do not have lag phases, and that those with lag phases have modal changepoint values strictly away from zero.

We instead place hierarchical log-normal priors on ${\delta }_i^{\ell }$ and on $t_{{in}_i}-{\delta }_i^{\tau }$ (as tail phases tend to happen at the end of the trajectory, information should be pooled relative to distance from the last measurement time). This is a slight modification of Lange et al. (1992) and Slate and Turnbull (2000), wherein the use of hierarchical normal priors for changepoints is advocated. Hierarchical log-normal priors allow for different hazard rates at different time values and sharing of information between the observed clearance profiles while restricting the changepoints to take on positive values. The log-normal distribution also has its mode away from the boundary and can accommodate a long right tail, which is often found in studying time-to-event quantities. Our priors are:

$$\begin{array}{l}{\delta }_i^{\ell }\mid {\pi }^{\ell },{\pi }^{\tau }~{\pi }^{\ell }\mathcal{L}\mathcal{N}(a,c^2)𝟙\{{\delta }_i^{\ell }<t_{{in}_i}\}+(1-{\pi }^{\ell })𝟙\{{\delta }_i^{\ell }=0\}\\ (t_{{in}_i}-{\delta }_i^{\tau })\mid {\delta }_i^{\ell },{\pi }^{\ell },{\pi }^{\tau }~{\pi }^{\tau }\mathcal{L}\mathcal{N}(b,d^2)𝟙\{{\delta }_i^{\tau }>{\delta }_i^{\ell }\}+(1-{\pi }^{\tau })𝟙\{{\delta }_i^{\tau }=t_{{in}_i}\}\end{array}$$

For the hyperparameters a, b, c², d², we place proper yet diffuse priors to allow for posterior propriety. Past research suggests that lag and tail phases most commonly persist for around 6 hours (Flegg et al., 2011). We incorporate this information, and say that a, b = 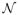(log(6), 0.5²), resulting in a 95% prior range of [2.2, 16] for the value of the median. We place Inverse Gamma(1, 1) priors on c² and d², allowing for substantial variability about the prior fit. Our priors on π^ℓ and π^τ; are π^ℓ, π^τ~Beta(1, 1). In Web Appendix B, we prove the propriety of the posterior distribution that results from our choice of prior distributions. In Web Appendix C, we describe a Gibbs sampling algorithm for attaining samples from the resulting posterior distribution. The simulation studies of Section 3 assess the robustness of our priors on lag and tail phases against misspecification of the lag and tail phase generative distribution when estimating the impact of the covariates of interest on clearance rates. In Web Appendix E, we perform a comparison of estimators produced by the log-normal and uniform both in simulation studies and in the data set analyzed in Section 4.

3. Comparison of Bayesian Methodology to the Standard Analysis

We now turn our attention to a detailed comparison of the Bayesian estimator to the standard two-stage analysis combining PCE with linear regression when the goal is the analysis of the effect of covariates via regression. We present a series of simulation studies that compare performance of the two methodologies under various data generative models. In these simulation studies, we simulate parasite clearance profiles that closely resemble those observed in real data by choosing parameter values based on those in the data set that we will be analyzing. The reason for this is that the PCE is specifically catered towards P. falciparum data, and incorporates “sanity” checks into its estimation procedure. Even though our method is generalizable to any scenario in which lag and tail phases are observed, we simulated as such to make the comparison as fair as possible. We focus herein on coverage of the resultant intervals from the two methods, as here valid frequentist inference is the primary objective.

3.1 Bias Due to Sparse Number of Measurement Times

As was discussed in Section 1, a two-stage approach is typically used when analyzing the effect of covariates on clearance rates. One drawback of the two-stage analysis is that information is dropped on subjects for whom the PCE could not estimate a clearance rate. These subjects would include those whose parasite count is zero at the first observed time point after drug administration. Additionally, if the individual only has two time points before censoring the PCE replaces that censored observation with the detection limit. This results in a loss of information and can create a substantial bias. We present an example of the bias. Consider the following model:

$$\begin{array}{l}log(y_{ij})={\alpha }_i-{\beta }_i{t}_{ij}+{\epsilon }_{ij}\\ log({\alpha }_i)=log(9.5)+x_i+u_i\\ log({\beta }_i)=log(0.25)+v_i\end{array}$$

We let ${\epsilon }_{ij}\stackrel{\mathit{iid}}{\sim }\mathcal{N}(0,{0.68}^2),x_i\stackrel{\mathit{iid}}{\sim }\mathcal{N}(0,{0.1}^2),u_i\stackrel{\mathit{iid}}{\sim }\mathcal{N}(0,{0.1}^2)$ and $v_i\stackrel{\mathit{iid}}{\sim }\mathcal{N}(0,{0.2}^2)$. The values for the variances of x_i, u_i, and v_i were chosen based on real data. For each individual, we “sampled” every 12 hours until a zero parasitema was recorded. We used a density of 40 parasites per microliter of blood as the detection limit for this simulation.

In this simulation, the covariate x_i is observed for each individual, but the u_i and v_i are unobserved errors. By construction, the covariate x_i has no effect on the clearance rate, meaning the true coefficient for its slope should be zero; however, it is positively correlated with the initial parasite density. The lower an individual’s initial parasite density, the lower one’s clearance rate needs to be such that we do not have a zero parasite count in the first measurement time after treatment (i.e, such that the individual is not omitted from the analysis). This induces a spurious positive correlation between the clearance rates and the covariate x_i if we use the conventional two-stage analysis. For individuals where PCE would replace censored observations by the detection limit, the same spuriously positive correlation exists. Replacing the censored observation by the detection limit would result in a negatively biased estimate of the clearance rate, and this replacement is more likely for lower values of x_i. The Bayesian methodology suffers less from this bias, as we are able to estimate clearance rates by borrowing information from the other profiles, rather than being forced to drop individuals or to replace censored observations by the detection limit.

To show this bias, we simulated from the above model 1000 times, having 60 individuals present within each simulation. The results are shown in Table1. As can be seen, the two-stage procedure is substantially biased, and results in 95% confidence intervals that fail to meet their coverage guarantees. The Bayesian estimator is able to overcome these issues, producing an unbiased estimate of the slope on x_i and credible intervals that have good frequentist coverage. The Bayesian estimator had an estimated mean squared error of 0.163, which represents a reduction by roughly 75% over the mean squared error of the two-stage estimator (0.638). This also demonstrates that the additional flexibility our model provides by allowing for lag and tail phases does not corrupt the properties of our estimator when lag and tail phases are not present.

Table 1.

Results from the simulation studies of Section 3.1. The true value of γ_x, the slope coefficient on x_i for predicting the clearance rates, is 0. From left the right, the columns represent the average value and standard deviation of the two-stage estimator across simulations; the average value and standard deviation of the Bayesian estimator across simulations; the percentage reduction in average loss (under squared error loss) attained by using the Bayesian estimator; the proportion of 95% intervals from the two-stage method that capture the true difference in means and length of those intervals; and the proportion of 95% intervals from the Bayesian method that capture the true difference in means and the length of those intervals

$\widehat{\mathbb{E}}[{\widehat{\gamma }}_x^{TS}]$(SD)	$\widehat{\mathbb{E}}[{\widehat{\gamma }}_x^B]$ (SD)	% Red. in Avg. Loss	$\widehat{\mathbb{P}}[{\gamma }_x\in C{I}_{95\%}^{TS}]$ (Length)	$\widehat{\mathbb{P}}[{\gamma }_x\in C{I}_{95\%}^B]$ (Length)
0.755 (0.261)	−0.05 (0.40)	74.5%	24.6% (1.04)	94.6% (1.57)

Our data generative model in this simulation study resulted in 5% of profiles being omitted entirely and in 49% of profiles having their censored observation replaced by the detection limit when clearance rates were estimated using the PCE as part of the two-stage method. The sparsity of measurement times in this simulation is quite extreme relative to what is found in typical data sets, and hence it is likely that the extent of biases in typical data sets are not as extreme as those found here. In fact, a data set exhibiting such sparsity would likely be discarded as useless. This simulation helps to elucidate an important pitfall of the standard two-stage analysis. Furthermore, it shows that even in a sparse situation, the Bayesian estimator can result in valid inference.

3.2 Behavior of Estimators with a Sufficient Number of Measurement Times

As was previously shown, the omission of profiles with too few measurement times can lead to a bias in the estimation of the effect of covariates on clearance rates. We would also like to assess the coverage properties of intervals created in the absence of this issue. To do this, we simulated from a model with two populations where each population shares a common average initial parasite density but has a distinct average clearance rate. We sample 30 people from each population in each simulation, for a total sample size of 60. In each simulation, we assess how well the respective methods are able to estimate the true difference on the log scale (i.e, the log of the ratio) between the true clearance rates for the two populations in terms of unbiasedness, and furthermore test the coverage of intervals created by both methods. We conducted three different simulation studies within this framework, with each study having different rates of lag and tail phase occurrence. We simulated 1000 data sets per set of lag and tail phase occurrences. Our data generative model is:

$$\begin{array}{l}log(y_{ij})={\alpha }_i-{\beta }_i({\delta }_i^{\ell }𝟙\{{\mathbf{t}}_{ij}<{\delta }_i^{\ell }\}+t_{ij}𝟙\{{\delta }_i^{\ell }\le t_{ij}\le {\delta }_i^{\tau }\}+{\delta }_i^{\tau }𝟙\{t_{ij}>{\delta }_i^{\tau }\})+{\epsilon }_{ij}\\ log({\alpha }_i)=2.3+u_i\\ log({\beta }_i)={\mathbf{X}}_i\mathit{\gamma }+v_i\\ {\delta }_i^{\ell }\stackrel{\mathit{iid}}{\sim }{\pi }^{\ell }\times \mathcal{N}(15,3^2)+(1-{\pi }^{\ell })\times \{{\delta }_i^{\ell }=0\}\\ {\delta }_i^{\tau }\stackrel{\mathit{indep}}{\sim }{\pi }^{\tau }\times \mathcal{N}(35,4^2)+(1-{\pi }^{\tau })\times \{{\delta }_i^{\tau }=t_{{in}_i}\}\end{array}$$

We let ${\epsilon }_{ij}\stackrel{\mathit{iid}}{\sim }\mathcal{N}(0,{0.68}^2),u_i\stackrel{\mathit{iid}}{\sim }\mathcal{N}(0,{0.1}^2)$ and $v_i\stackrel{\mathit{iid}}{\sim }\mathcal{N}(0,{0.07}^2)$. X_i is either [1, 0] or [1, 1] depending on which population individual i is from. We set γ= [log(0.15), log(0.25/0.15)]^T, resulting in population average log clearance rates log(0.15) and log(0.25) respectively. In the simulation, we sampled every 6 hours until a parasite density is observed below the censoring limit (again, this is how the data are collected in practice). We made the sampling at every 6 hours to ensure ourselves that profiles would have more than three time points apiece such that we avoid the biases mentioned in Section 3.1. We used a detection limit of 16 parasites per microliter of blood. In all three simulation set-ups, all of the profiles simulated had more than three time points, thus indicating that we were successful in removing the main cause of the bias discussed in Section 3.1

Table 2 presents the results of our simulation studies. We found that in all three scenarios, the Bayesian estimator outperformed the standard two-stage estimator in terms of mean squared error, coverage of intervals, and length of intervals. These gains were negligible in the model without lag and tail phases (Simulation 1), but were substantial once lag and tail phases were added to the data generative model (Simulations 2 and 3). The percent reductions in mean squared error for estimation via the Bayesian method versus the two-stage method were 6.5%, 48.5%, and 80.1% respectively for the simulation studies. These results further show the robustness of our procedure against misspecification of the lag and tail phase generative process. Simulation 1 does not have any lag and tail phases, while Simulations 2 and 3 not only generate changepoints from a normal versus our specified log-normal distribution, but also center the tail phase change points at a common mean regardless of distance from the last measurement time (which is how we have modeled them).

Table 2.

Results from the simulation studies of Section 3.2. In all three simulation studies, the true value of γ₂, the average log difference in clearance rates between the two simulated populations, was log(0.25/0.15) ≈ 0.511. See the caption of Table 1 for a description of the column headings.

	$\widehat{\mathbb{E}}[{\widehat{\gamma }}_2^{TS}]$ (SD)	$\widehat{\mathbb{E}}[{\widehat{\gamma }}_2^B]$ (SD)	% Red. in Avg. Loss	$\widehat{\mathbb{P}}[{\gamma }_2\in C{I}_{95\%}^{TS}]$ (Length)	$\widehat{\mathbb{P}}[{\gamma }_2\in C{I}_{95\%}^B]$ (Length)
Simulation 1 πℓ = πτ = 0	0.521 (0.039)	0.523 (0.037)	6.24%	94.4% (0.159)	95.2% (0.145)
Simulation 2 πℓ= 0.5, πτ= 0	0.490 (0.049)	0.515 (0.038)	48.5%	92.1% (0.188)	94.0% (0.152)
Simulation 3 πℓ = πτ = 0.25	0.562 (0.081)	0.523 (0.041)	80.1%	92.6% (0.350)	94.1% (0.167)

3.3 Small Sample Simulations

The simulations of Sections 3.1 and 3.2 are conducted with a moderate sample size. One may be concerned that with smaller sample sizes, our prior specifications may substantially bias the resulting estimators and corrupt the coverage properties of the resulting intervals. In Web Appendix D, we show that this is not the case with n = 20 individuals. Our estimators continue to outperform those of the two-stage analysis, resulting in marked reduction in mean squared errors and in interval lengths.

4. Analysis of Plasmodium falciparum Clearance Data

We now use data previously analyzed in Amaratunga et al. (2012) as a demonstration of our methodology. These data consist of P. falciparum clearance profiles measured in 2009 and 2010 in Western Cambodia, an area where artemisinin resistance is well established, along with individual level covariates. Among other research objectives, the relationship between these covariates and half-life values (calculated as log(2)/(Clearance Rate)) was of interest. See Amaratunga et al. (2012) for an in depth description of the data set and its collection process. Data on 110 patients were available for this analysis, and parasite densities were measured every 6 hours. The censoring limit for this data collection was 15 parasites per microliter. All 110 individuals were recorded until no parasites were found in the collected blood smear (i.e., until left censoring occurred). Initial parasite counts also varied substantially across individuals, with a geometric mean of 58,130 parasites per microliter of blood, a mean of 89,225 parasites per microliter and a standard deviation of 99,413. The minimal initial parasite count was 10,240 parasites per microliter of blood, and the maximal initial parasite count was 546,460 parasites per microliter. As such, the total number of observation times varied substantially from individual to individual. On average, we had 13.25 time measurments per individual with a standard deviation of 3.25. The minimal number of time measurements for an individual was 5, and the maximal number of time measurements was 22.

One point of interest was whether or not there is evidence of resistance to artemisinins developing over time. As such, indicator variables for the year of data collection were included. The coefficients on these indicators thus facilitate inference on whether the median clearance rate is decreasing over time. Researchers also wanted to investigate whether certain aspects of host genetics impact the resulting half-lives. As discussed in Amaratunga et al. (2012), it has been theorized that red blood cell polymorphisms – including hemoglobin E (HbE), α-thalassaemia, and G6PD deficiency - may act to strengthen the pro-oxidant activity of parasite defenses against artemisinins, hence resulting in lower clearance rates. To investigate this hypothesis, indicators were included for the existence of these three genetic factors. Additionally, parasites were broken into two genetically different groups (labeled group 1 and group 2), and group membership was included as a variable to see whether or not one particular group seemed more or less resistant to the antimalarial regimen; see Amaratunga et al. (2012) for details on how the groups were determined. Finally, the study wanted to assess the extent to which acquired immunity to the effects of P. falciparum may impact half-lives. As proxies for immunity, three covariates were included that are thought to correspond to increased likelihood of previous exposure to these malarial parasites. These were gender, whether an individual was 21 years of age or older versus younger than 21, and whether an individual was from the Kravanh or Veal Veng districts or not from those districts, as those two districts are heavily forested areas where malaria is transmitted (Amaratunga et al., 2012).

We first used the outlier detection methodology suggested in Flegg et al. (2011), and found that no observed counts were identified as outliers. We then ran our Gibbs sampling algorithm on this data set from six different starting locations, for 50,500 iterations per starting location. We show traceplots and autocorrelation function plots for a few of our parameters in Web Appendix F. Looking at the traceplots and autocorrelations, it is evident that our posterior samples take some time to reach stationarity and are correlated initially. As such, we discarded the first 500 iterations as burnin for each chain, and then thinned each chain by only keeping one out of every 100 iterations. The traceplots and autocorrelations after doing this are also included in Web Appendix E, and indicate that stationarity has been attained. In total, these six chains provided 3000 roughly independent posterior samples. The Gibbs Sampler was written in R (R Core Team, 2015), and is computationally intense. Sampling each of these six chains took 32 hours on a desktop computer with a 3.40 GHz processor and 16.0 GB RAM.

With our posterior samples now attained, we can conduct our posterior inference. Our analysis will focus on two aspects of the resultant posterior distributions. We will first investigate the ability of our method to fit individual level parasite profiles, including the detection of lag and tail phases. We will then provide intervals for the impact of our covariates of interest on the individual level P. falciparum half-lives after the administration of an antimalarial regimen.

4.1 Posterior Analysis of Individual Level Fits

Our methodology allows us to appropriately account for randomness in all aspects of the individual level parasite profiles. We can, for each individual, provide credible intervals for that individual’s clearance rate, pointwise credible bands for that individual’s true underlying parasite trajectory, and posterior predictive bands for the expected parasite counts at unobserved time points. We can also assess the frequency with which our model identified that an individual’s profile had lag phases and/or tail phases present.

Our posterior distribution indicates that lag phases are more prevalent in our data set than substantial tail phases. 28.2% of individuals were identified as having median lag phases of longer than 3 hours, and 12.7% of individuals had lag phases longer than 6 hours (the first measurement time after drug administration). Conversely, only 2 of the 110 individuals were identified as having a tail phase (based on their median changepoint between decay phase and tail phase).

Figure 1 (a) shows an individual whose profile seems to exhibit only a decay phase, whereas Figure 1 (b) shows an individual that is identified as having a lag phase before the decay occurs. To illustrate the type of individual level analysis possible through our method, we will now describe various attributes of the posterior distribution for these two individuals’ parasite profiles.

For the individual in Figure 1 (a), the posterior mean clearance rate was 0.169, with a 95% credible interval of [0.1432, 0.1969]. Only 7.6% of the posterior samples identified this individual as having a lag phase of more than 3 hours, and only 1% identified a lag phase of greater than 6 hours. 1.9% identified that a tail phase existed.

The posterior mean clearance rate for the individual in Figure 1 (b) was 0.123, with a 95% credible interval of [0.1019, 0.1455]. 99.3% of the posterior samples identified that this individual had a lag phase exceeding 6 hours, but only 1% identified that this individual had a tail phase. The posterior mean of the changepoint between lag phase and decay phase for this individual was at time 25.2, with a 95% credible interval of [14.55, 32.94].

Figure 1 also includes the clearance estimate that would have been attained using a tobit regression if lag phases and tail phases were not accounted for (the dashed lines). For the individual in Figure 1 (a), the estimates are similar as this individual’s profile doesn’t seem to exhibit lag or tail phases; however, the clearance rate estimate attained for the individual in Figure 1 (b) is substantially lower (0.0907, with a 95% confidence interval of [0.073, 0.108]). This provides further evidence that analyses not taking lag and tail phases into account could potentially be misleading.

4.2 Posterior Analysis of Covariate Impact

Table 3 displays our estimates for the impact of the covariates of interest on the log half-lives, along with the 95% posterior intervals. Note that although our method originally regressed log clearance rates rather than log half-lives on the covariates of interest, we can attain the slopes for a regression on the log half-lives since log(Half-Life) = log(log(2)) – log(Clearance Rate). The exponential of these coefficients have the interpretation of, all else equal, the factor increase in the median half-life caused by increasing the value of the covariate by 1 unit. For example, the slope of 0.191 on the indicator variable for male means that males have a median half life larger than that of females by a factor of e^0.191 = 1.21. We also report the standard 95% confidence intervals that a researcher would attain via the standard methodology (using the PCE to estimate the clearance rates) in Table 3. Though in general credible intervals and confidence intervals need not coincide, we deem it appropriate to use credible intervals to assess significance in the frequentist sense, just as a researcher would do with confidence intervals. We support this by noting the non-informative nature of our priors and the results of the simulations in Section 3, which showed time and time again that our 95% Bayesian intervals achieved coverage very close to 95%, even as we varied the number of measurement times per individual and the true rates of lag and tail phases. An alternative approach would be to use the standard Bayesian paradigm for hypothesis testing, by placing prior probabilities on hypotheses and assessing Bayes factors.

Table 3.

Estimates and Intervals for the Effect of Covariates on Log Half-Lives

	Bayesian Analysis			Standard Two-Stage Analysis
	Estimate	2.5%	97.5%	Estimate	2.5%	97.5%
Intercept	1.58	0.823	2.33	1.418	0.605	2.231
Sex (1 if Male)	0.191	0.01	0.370	0.204	0.021	0.387
Age Group (1 if < 21)	−0.015	−0.145	0.116	−0.035	−0.164	0.094
Kravanh or Veal Veng (1 if Yes)	−0.007	−0.134	0.127	−0.021	−0.153	0.112
Hemoglobin E (1 if Yes)	0.108	−0.004	0.219	0.095	−0.015	0.206
α-thalassaemia (1 if Yes)	−0.066	−0.200	0.063	−0.078	−0.212	0.057
G6PD Deficient (1 if Yes)	−0.001	−0.090	0.087	0.007	−0.082	0.097
Log Initial Parasite Density	0.021	−0.054	0.091	0.008	−0.067	0.082
Year (1 if 2010)	0.044	−0.086	0.172	0.095	−0.037	0.226
Parasite Group (1 if Group 1)	0.150	0.028	0.280	0.160	0.029	0.29

We have evidence to suggest that sex and parasite group membership has a significant impact on parasite half lives at significance level α = 0.05, with Parasite Group 1 and males appearing to have a longer half-life. We note that if we take multiple comparisons into account and run these tests using a Bonferroni corrected significance level of α = 0.05/9 (the number of covariates), the results becomes insignificant, with an interval of [−0.075, 0.447] for gender and [−0.024, 0.332] for parasite group. We have no evidence to suggest that any of the other included covariates have a significant impact the Log Half-Lives; however, for the indicator variables for hemoglobin E our credible interval comes very close to not covering 0. The results of the two-stage analysis provided in Table 3 are slightly different from those given in Amaratunga et al. (2012) [Supplementary Web Appendix, Appendix 3] based on the two-stage method, as there the regression was done on the half-lives rather than their logarithms. We notice that at least with this data set, the estimates and confidence intervals attained via the two-stage method tend to resemble those attained via the Bayesian methodology, although nontrivial discrepancies between the two do exist. Nonetheless, our simulations in Section 3 show that there are times in which the discrepancy between the two methodologies could be quite substantial, and that the Bayesian methodology presented herein results in estimators with better behavior in terms of bias, variance, and length of parameter interval.

4.3 Model Diagnostics

In Web Appendix A, we include two model checks based on our posteriorpredictive distribution. In the first, we check the coverage of pointwise 95% posterior predictive ranges for the log parasite profiles for each individual. In the second, we check whether or not our assumption of independence between errors within a parasite profile is reasonable given the data at hand. As is discussed in Web Appendix A, neither of these posterior predictive checks raised cause for concern, lending credence to the model based inference presented in this work.

5. Discussion

Our method is quite general, in that it does not try to capture the occurrences of lag and tail phases mechanistically. Different drugs may target different malarial life cycle stages and this could affect the existence and magnitude of lag and tail phases. A model derived with one particular antimalarial in mind may not be useful for other antimalarial regimens, a trap which our model avoids. It also allows for extensions of our methods to other biological systems exhibiting lag and tail phases. Our model can also readily facilitate hypothesis testing for the existence of lag and tail phases within certain populations through a comparison of Bayes factors for models that allow for lag and tail phases with those that do not. A model without lag and tail phases can be attained by deterministically setting π^ℓ = 0 and π^τ = 0.

We believe that this methodology may prove useful to researchers interested in clearance rate analysis of malarial parasites, as well as other parasites, viruses, and bacteria. As we have shown, our methodology provides a framework for investigating which factors affect clearance rates, and effectively uses shrinkage estimation and changepoint models to result in valid statistical inference.