Bayesian Nonlinear Model Selection for Gene Regulatory Networks

Summary

Gene regulatory networks represent the regulatory relationships between genes and their products and are important for exploring and defining the underlying biological processes of cellular systems. We develop a novel framework to recover the structure of nonlinear gene regulatory networks using semiparametric spline-based directed acyclic graphical models. Our use of splines allows the model to have both flexibility in capturing nonlinear dependencies as well as control of overfitting via shrinkage, using mixed model representations of penalized splines. We propose a novel discrete mixture prior on the smoothing parameter of the splines that allows for simultaneous selection of both linear and nonlinear functional relationships as well as inducing sparsity in the edge selection. Using simulation studies, we demonstrate the superior performance of our methods in comparison with several existing approaches in terms of network reconstruction and functional selection. We apply our methods to a gene expression dataset in glioblastoma multiforme, which reveals several interesting and biologically relevant nonlinear relationships.

1 Introduction

A gene regulatory network (GRN) consists of a group of DNA segments, such as genes and their products, and defines their regulatory relationships at the cellular level. GRNs are instructive for understanding complex biological processes and the regulatory mechanisms underlying cellular systems. In the context of cancer, GRN reconstruction amongst key genes in the signaling pathways helps to identify driver genes that direct carcinogenesis (Edelman et al., 2008), which then informs the diagnosis and prognosis of the disease.

Our work is motivated by a study in glioblastoma multiforme (GBM), which is the most common and aggressive form of primary brain cancer in human adults. Due to its lethalness, GBM was the first cancer profiled by The Cancer Genome Atlas (TCGA) research network (http://cancergenome.nih.gov/). Intensive molecular studies have identified three critical signaling pathways in human glioblastomas (Furnari et al., 2007): (1) activation of the receptor tyrosine kinase (RTK) and the phosphatidylinositol-3-OH kinase (PI3K) pathways; (2) inactivation of the p53 pathway; and (3) inactivation of the retinoblastoma (Rb) tumor suppressor pathway. The fact that most of the GBM tumors possess abnormalities in all three of these core pathways suggests they play a central role in the tumorigenesis of GBM (Verhaak et al., 2010). In this work, we focus on modeling GRNs in GBM using expression data assayed on genes mapped to these core pathways. Our aims are not only to reconstruct the underlying structure of the GRN, but also to discover the functional nature of the dependencies between the genes. A detailed description of the data is provided in Section 6.

Reverse engineering a GRN in a genomic context is known to be challenging. This is partly due to high dimensionality since the graph space grows super-exponentially with the number of variables, making it computationally prohibitive to use exhaustive search algorithms over the entire graph space. More importantly, the interactions between genes may include nonlinear dependencies due to the complex biochemistry behind them (Kitano, 2002); therefore, models that rely on linear assumptions may be inefficient in recovering the GRNs. In this paper, we work with directed acyclic graphs (DAGs), which are powerful tools for recovering GRNs (Friedman et al., 2000). DAGs, also known as Bayesian networks, are graphs that consist of nodes representing random variables (genes in our case study) and directed edges representing conditional dependencies. DAGs are useful tools to apply when we construct networks from microarray expression data because they are capable of detecting directed relationships and provide a compact representation of the joint distribution, which leads to convenient modeling, computation and inference.

Multiple methods based on DAGs have been proposed in the literature in a variety of contexts. Friedman et al. (2000) developed DAGs from gene expression data using a bootstrap-based approach. Li, Yang, and Xing (2006) also constructed GRNs from expression microarray data wherein they estimated a linear Gaussian DAG model and computed the precision matrix of the resulting joint distribution that defines an undirected graph. Stingo et al. (2010) proposed a DAG-based model to infer microRNA regulatory networks. Recently, Shojaie and Michailidis (2010) developed a penalized likelihood approach for estimating high-dimensional sparse networks. Altomare et al. (2013) proposed an objective Bayesian method for searching the DAG space with non-local priors. Fu and Zhou (2013) developed a penalized likelihood method to recover causal DAGs from experimental data. Some recent work includes the use of undirected graphical models to build biological networks (Peterson et al., 2013, 2014). A common thread underlying all these methods is that they allow for only linear dependencies between the nodes in the graph and do not explicitly incorporate nonlinear representations that may be present in the data. In the GRN context, nonlinear dependencies may suggest some dynamic patterns of interactions between genes, which could be the subject of further experimental validations. This is a gap in the literature that our work aims to fill. We develop a novel Bayesian framework for reconstructing GRNs based on the semiparametric estimation of DAGs. Our framework has four major innovations:

1. Allows for the detection of interpretable nonlinear functional relationships between nodes using semiparametric spline-based regressions.

2. Enables explicit model selection and sparsity using Bayesian model selection techniques that resolve the issue of the number of parameters being larger than the sample size, while obtaining parsimonious representations.

3. Uses a hierarchical two-level model selection approach. The first level is the edge selection, conditional on which we adopt the second level, functional selection, to classify the degree of nonlinearity of the functional relationship.

4. Is computationally efficient since the regression setup allows for parallelizable estimations and the incorporation of prior biological knowledge through reference networks to determine a priori the ordering of the genes. This greatly reduces the complexity of the model and the computational burden.

We evaluate the performance of our methods against those of alternative methods using simulations studies. Our methods are very competitive in network structure recovery, reconstruction of functional relationships and prediction. We subsequently apply our methods to the GBM data mentioned previously. While some of our results are consistent with previous findings in the literature, we find new nonlinear interactions that are potential targets for future experimentation and validation. Although motivated by this specific gene expression dataset, our approach is general and can be applied to other scientific settings where such network-based inference is desirable.

2 Model

Let Y be an n×G matrix, where n is the number of samples and G is the number of genes. Let $y_g^{(l)}$ denote the expression level of sample l and gene g, for g = 1, …, G and l = 1, …, n. A directed graph, also called a Bayesian network, 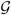= { 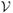, 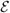} consists of a set 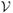= {1, 2, …, G} of nodes, representing random variables {Y₁, Y₂, …, Y_G}, and a set 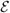⊆ {(i, j) : i, j ∈ 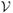} of directed edges, representing the dependencies between the nodes. Denote a directed edge from i to j by i → j where i is a parent of j. The set of all the parents of j is denoted by pa(j). The absence of edges represents conditional independence assumptions. We restrict this work to DAGs, since there is no suitable well-defined joint distribution on cyclic graphs (Whittaker, 2009). The joint distribution of a DAG can be conveniently expressed as the product of the conditional distributions of each node given its parents:

$$P(Y_1,\dots ,Y_G)=\prod _{g=1}^{G}P(Y_g|Y_{pa(g)}),$$ (1)

where Y_pa(g) = {Y_j: j ∈ pa(g)}. Without loss of generality, the ordering is defined as {1, 2, …, G}, which can be obtained through prior biological knowledge such as known reference pathways. Within our DAG framework, biological knowledge is then used to define the edge orientation such that gene i can affect gene j for i < j, but not vice versa. Define [g−] to be the set {1, 2, …, g − 1} and $y_{[g-]}^{(l)}$ to be $\{y_i^{(l)}:i\in [g-]\}$. Each conditional distribution in the product term of equation (1) can be expressed by the following regressions:

$$y_g^{(l)}=f_g(y_{[-1]}^{(l)})+{\epsilon }_g^{(l)},g=1,2,\dots ,G,l=1,2,\dots n,$$ (2)

where $f_g\left(y_{[g-]}^{(l)}\right)$ is the predictor function and ${\epsilon }_g^{(l)}$ is the error, which is independently and normally distributed, ${\epsilon }_g^{(l)}~N(0,{\lambda }_g^{-1})$.

Semiparametric modeling using penalized splines

In principle, f_g(·) can be characterized using any nonlinear functional representation, depending on the context of the application. For example, if the relationship between genes follows a periodic or circadian pattern, one could choose f_g(·) to be the Fourier basis; similarly if the relationship follows a very localized (“spiky”) behavior, wavelets could potentially be employed. However, in the absence of such information a priori, we model f_g(·) semiparametrically using a set of penalized spline basis functions. Splines yield several advantages that include flexibility as well as interpretability via representations that use a compact set of basis functions and coefficients. More importantly, the inherent construction of penalized splines as mixed models with structured Gaussian priors on the coefficients allows for analytical integration of the parameters (as we show in Sections 4 and Web Appendix C), and thus allows for computational tractability. In particular, the predictor $f_g\left(y_{[g-]}^{(l)}\right)$ is modeled as the sum of the spline functions:

$$f_g(y_{[g-]}^{(l)})={\mu }_g+f_{g,1}(y_1^{(l)})+f_{g,2}(y_2^{(l)})+\cdots +f_{g,g-1}(y_{g-1}^{(l)}),g=1,\dots ,G,$$ (3)

where μ_g is the intercept for gene g and $f_{g,i}(\cdot )={\sum }_{k=1}^M{\beta }_{gi}^{(k)}{B}_{ik}(\cdot )$, with B_ik(·) being the kth cubic B-spline basis. Let column vector ${\mathit{\beta }}_{gj}={({\beta }_{gj}^{(1)},{\beta }_{gj}^{(2)},\dots ,{\beta }_{gj}^{(M)})}^{\prime }$, column vector ${\mathit{\beta }}_{\mathit{g}}={({\mathit{\beta }}_{\mathit{g}\mathbf{1}}^{\prime },{\mathit{\beta }}_{\mathit{g}\mathbf{2}}^{\prime },\dots ,{\mathit{\beta }}_{\mathit{g},\mathit{g}-\mathbf{1}}^{\prime })}^{\prime }$, row vector ${\mathit{X}}_{\mathit{l}\mathit{g}}=(B_{g1}(y_g^{(l)}),B_{g2}(y_g^{(l)}),\dots ,B_{gM}(y_g^{(l)}))$ and block matrix X = [X_lg] with the (l, g)th block X_lg. Then model (3) can be written as

$${\mathit{y}}_{\mathit{g}}={\mathit{\mu }}_{\mathit{g}}+{\mathit{X}}_{\mathit{g}}{\mathit{\beta }}_{\mathit{g}}+{\epsilon }_{\mathit{g}},g=1,2,\dots G,$$ (4)

where ${\mathit{y}}_{\mathit{g}}={(y_g^{(1)},y_g^{(2)},\dots ,y_g^{(n)})}^{\prime },{\mathit{\mu }}_{\mathit{g}}={\mu }_g{\mathbf{1}}_n$, and ${\mathit{\epsilon }}_g={({\epsilon }_g^{(1)},{\epsilon }_g^{(2)},\dots ,{\epsilon }_g^{(n)})}^{\prime }$. X_g is the submatrix of X with the first g − 1 column blocks. Combining equations (1), (2), and (4) yields the following likelihood function:

$$L=\prod _{\mathit{g}=1}^G{\left(\frac{{\lambda }_{\mathit{g}}}{2\pi }\right)}^{\frac{n}{2}}exp\{-\frac{{\lambda }_{\mathit{g}}}{2}{({\mathit{y}}_{\mathit{g}}-{\mu }_{\mathit{g}}-{\mathit{X}}_{\mathit{g}}{\mathit{\beta }}_{\mathit{g}})}^{\prime }({\mathit{y}}_{\mathit{g}}-{\mathit{\mu }}_g-{\mathit{X}}_g{\mathit{\beta }}_g)\}.$$

A key component in fitting splines is the choice of the number and the placement of knots (M). We address this issue by using penalized splines (P-splines, (Eilers and Marx, 1996); (Ruppert, Wand, and Carroll, 2003)); wherein we choose a large enough number of knots that are sufficient to capture the local nonlinear features present in the data and control for overfitting by using a penalty matrix on the basis coefficients. Under the Bayesian framework, the penalties can be represented using Gaussian random walk priors (Lang and Brezger, 2004; Baladandayuthapani, Mallick, and Carroll, 2005) on the spline coefficients, ${\mathit{\beta }}_{gj}|{\tau }_{gj},{\lambda }_g~N(0,{({\tau }_{gj}{\lambda }_g\mathit{K})}^{-1})$, where τ_gj is the smoothing parameter and K is the penalty matrix. We construct K from the second order differences of the adjacent spline coefficients, namely, ${\beta }_{gj}^{(k+1)}-2{\beta }_{gj}^{(k)}+{\beta }_{gj}^{(k-1)}$ (Lang and Brezger, 2004), which can be construed as a “roughness penalty”. Note that in the above construction, the degree of smoothness of the fitted curve is controlled by the smoothing parameters, τ_gj. A large value of τ_gj, i.e., a strong roughness penalty, leads to a smoother fit, while a small value of τ_gj (close to zero) leads to an irregular fit and essentially interpolation of the data.

3 Model Selection

In this section, we introduce our hierarchical two-level selection on the edges as well as the functional form of the selected edges.

First-level Selection: “Edge selection”

Our goal is to infer the structure of the GRN; inference on the predictor functions, defined in equation (3), will automatically lead to the selection of the relevant connections. An important aspect of our methodology is sparsity, i.e., we believe that most of the gene-gene associations are almost negligible. To this end, we take a Bayesian model selection approach that allows for the selection of edges supported by the data. More importantly, model selection is desirable when the number of parameters to be estimated, $2G+\frac{G(G-1)}{2}M$ in our case, is much larger than the sample size, even for a moderate number of genes. For example, in our real data analysis, the number of parameters is more than 12,000 while the sample size is about 250.

Here, model selection is achieved through a mixture prior on the spline coefficients, where the first component is the second-order Gaussian random walk described in Section 2 and the second component is the point mass at 0, which is expressed as ${\mathit{\beta }}_{\mathit{g}\mathit{j}}|{\tau }_{gj},{\lambda }_g,{\gamma }_{gj}~{\gamma }_{gj}N(0,{({\tau }_{gj}{\lambda }_g\mathit{K})}^{-1}+(1-{\gamma }_{gj}){\delta }_0({\mathit{\beta }}_{\mathit{g}\mathit{j}}))$, where δ₀ is the Dirac delta function. The binary indicators,γ_gj, are latent variables that encode the structure of the network. If γ_gj = 1, the arrow from gene j to gene g (j → g) is included in the network, and γ_gj = 0 otherwise.

The smoothing parameter τ_gj controls the smoothness of the fitted curve, and small values of τ_gj lead to an undesirable irregular fit. The conjugate Gamma prior is right-skewed, which puts a lot of mass around zero; therefore, this standard prior (Lang and Brezger, 2004) is considered inappropriate in this setting where regularized fits are required for multiple regressions. Instead, we assume an inverted Pareto prior Ip(a_τ, b_τ) for the smoothing parameter (Morrissey et al., 2011), which takes the form $\pi (\tau |a,b)=\frac{a}{b}{\left(\frac{\tau }{b}\right)}^{a-1}$, for a > 0, 0 < τ < b. Contrary to that of Gamma distributions, the skewness of inverted Pareto distributions is easily adjusted through parameter a. This prior concentrates on large values when a > 1, and then encourages smooth fits of the data, which are desired in our scenario. See further detailed discussions in Web Appendix A. We refer to this model that has an absolutely continuous inverted Pareto prior on the smoothing parameter as the nonlinear DAG (nDAG).

Second-level Selection: “Functional selection”

In addition to edge selection (i.e. presence/absence of an edge), we are also interested in the functional nature of the interactions (i.e., linear or nonlinear) and let the data dictate this choice. We propose a hierarchical second-level selection technique, wherein conditional on γ_gj, the functional form of the relationship between genes is defined through τ_gj, as these parameters control the smoothness of the curve fitting. We enforce a discrete mixture of the inverted Pareto distribution and Gamma distribution: τ_gj|ϕ_gj ∼ ϕ_gjGamma(k_τ, θ_τ) + (1 − ϕ_gj)Ip(a_τ, b_τ), where ϕ_gj is the indicator of the mixture component. The Gamma distribution is concentrated at small values of τ, thus inducing nonlinear smoothing; whereas the inverted Pareto distribution places its mass on large values (i.e., setting a_τ > 1), thus leading to a more linear fit. Unlike a unimodal prior (such as the Gamma and inverted Pareto distributions), which is concentrated at either small values or large values (but not both), this mixture prior provides a sharper separation between “linear” and “nonlinear” relationships among genes because of its bimodal nature. One example of such a mixture prior is shown in Web Figure 3. In essence, ϕ_gj = 1 implies a nonlinear interaction between gene g and gene j; whereas ϕ_gj = 0 implies a linear interaction. The elicitation of this mixture prior is detailed in Web Appendix B. We call this the nonlinear mixture DAG (nMixDAG) so as to distinguish it from the nDAG.

4 Hyper-Prior Specifications

In this section, we complete the hierarchical formulation of our model by specifying the hyper-prior on the precision of error term λ_g, constant term μ_g, network parameter γ_gj and its hyperparameter ρ, and the mixture component indicator ϕ_gj and its hyperparameter ω.

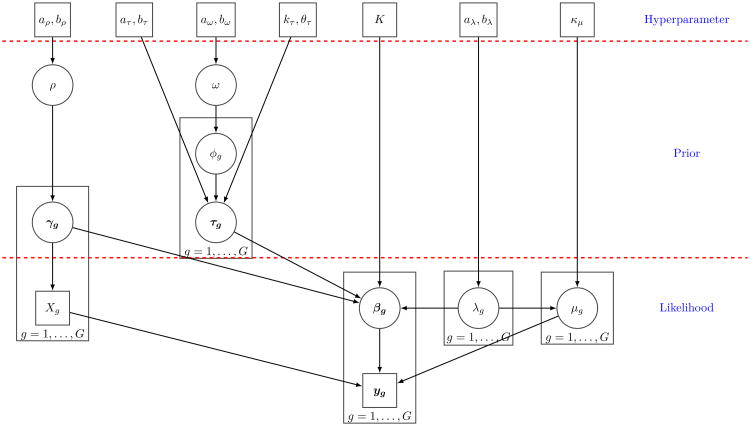
We assume conjugate priors for the error precision λ∼Gamma(a_λ, b_λ) and the constant term μ_g∼N(0, (λ_gk_μ)⁻¹). For the network parameter γ_gj, we use a Bernoulli prior with success probability ρ, γ_gj|ρ ∼ Bernoulli(ρ). The prior probability of inclusion ρ follows a Beta distribution, ρ ∼ Beta(a_ρ, b_ρ), which yields an automatic multiplicity penalty since the posterior distribution of ρ will become more concentrated at small values near 0 as the total number of variables increases (Scott and Berger, 2010). Similar to the prior for γ_gj, a Bernoulli distribution is assumed for ϕ_gj, with the success probability following a Beta hyper-prior, ϕ_gj|ω ∼ Bernoulli(ω), ω ∼ Beta(a_ω, b_ω). A schematic representation of the complete hierarchical formulation is shown in Figure 1. In Web Appendix C, we present the details of the posterior inference and MCMC sampling scheme.

Figure 1.

Schema of the nonlinear mixture directed acyclic graphical model. Model parameters/random variables are in circles and model constants/data are in boxes.

5 Simulated Examples

In this section, we illustrate our proposed methods with simulated examples. We design five scenarios with 150 samples, 50 genes and 100 connections, and run 50 simulations for each scenario. Although the number of genes is less than the sample size, using the spline basis expansions, the number of effective estimable parameters is 12,350 for the saturated model, which greatly exceeds the sample size. The five scenarios differ in the percentage of linearity in the data (0%, 20%, 48%, 72%, and 100%), corresponding to the proportion of the linear functions that generate the data. The structure of the network is assumed to be constant across all simulations. Error terms are distributed as N(0, 4²).

We use a cubic B-spline with 6 interior knots, i.e., 10 bases. For the nDAG, the prior parameters are specified as k_μ = 1/4, (a_λ, b_λ) = (2, 1), (a_ρ, b_ρ) = (2, 2), and (a_τ, b_τ) = (1.5, 400). For the additional parameter in the nMixDAG, we let (a_ω, b_ω) = (2, 2), and (k_τ, _τ) = (3, 2). The choice of these hyperparameters aims to be mainly non-informative. We provide a sensitivity analysis on the prior specifications at the end of this section. The results show a very low sensitivity to these choices. We run an MCMC algorithm with 20, 000 iterations, in which the first 2, 000 iterations are considered as a “burn-in” period for both methods.

Since the true simulated network is known, we can compute the operating characteristics of the methods using the true positive rate (TPR), the false discovery rate (FDR) and the area under the receiver operating characteristic (ROC) curve (AUC). We also compute the TPR separately for the linear and nonlinear relationships, which we refer to as TPR linear and TPR nonlinear, respectively. In addition, while the full AUC indicates the overall performance of the underlying method, researchers may be particularly interested in the performance with a controlled false positive rate (FPR), say, less than 5%; hence, we also report the partial AUC truncated at FPR< 5%, denoted by AUC5%. All the statistics mentioned above are summarized in Table 1. A separate simulation study on variable selection under the generalized additive model setting with varying sample sizes and signal-to-noise ratios is provided in Web Appendix D.

Table 1.

Simulated examples. The average operating characteristics over 50 simulations for each scenario are calculated for comparison. The bold numbers indicate the best performance and the underlined numbers indicate the second best. The standard error for each statistic is given in parentheses

		Percentage of linearity
Method		0%	20%	48%	72%	100%
SSVS
	AUC5%	0.235(0.024)	0.341(0.018)	0.541(0.024)	0.722(0.021)	0.913(0.022)
	AUC	0.652(0.031)	0.705(0.021)	0.800(0.024)	0.886(0.017)	0.987(0.007)
	TPR	0.293(0.032)	0.378(0.020)	0.561(0.023)	0.714(0.026)	0.889(0.028)
	TPR_linear	NA	0.775(0.062)	0.833(0.036)	0.884(0.031)	0.889(0.028)
	TPR_nonlinear	0.293(0.032)	0.278(0.021)	0.309(0.029)	0.275(0.036)	NA
	FDR	0.591(0.039)	0.463(0.044)	0.259(0.037)	0.146(0.038)	0.102(0.029)
nDAG
	AUC5%	0.481(0.045)	0.573(0.034)	0.677(0.036)	0.788(0.023)	0.865(0.028)
	AUC	0.777(0.028)	0.819(0.018)	0.862(0.020)	0.914(0.013)	0.958(0.013)
	TPR	0.389(0.036)	0.455(0.024)	0.581(0.031)	0.674(0.022)	0.740(0.019)
	TPR_linear	NA	0.674(0.044)	0.719(0.030)	0.740(0.025)	0.740(0.019)
	TPR_nonlinear	0.389(0.036)	0.400(0.029)	0.453(0.043)	0.502(0.040)	NA
	FDR	0.056(0.036)	0.037(0.027)	0.025(0.021)	0.005(0.009)	0.004(0.007)
nMixDAG
	AUC5%	0.536(0.052)	0.642(0.034)	0.718(0.036)	0.809(0.025)	0.873(0.028)
	AUC	0.798(0.028)	0.848(0.019)	0.879(0.019)	0.925(0.012)	0.964(0.013)
	TPR	0.439(0.037)	0.520(0.030)	0.618(0.027)	0.697(0.022)	0.746(0.019)
	TPR_linear	NA	0.687(0.043)	0.730(0.029)	0.748(0.027)	0.746(0.019)
	TPR_nonlinear	0.439(0.037)	0.479(0.035)	0.514(0.040)	0.565(0.043)	NA
	FDR	0.050(0.033)	0.031(0.022)	0.023(0.021)	0.004(0.010)	0.005(0.007)
WBN
	AUC5%	0.172(0.024)	0.277(0.037)	0.465(0.031)	0.599(0.030)	0.751(0.037)
	AUC	0.615(0.027)	0.676(0.029)	0.790(0.020)	0.862(0.022)	0.901(0.023)
	TPR	0.160(0.028)	0.254(0.035)	0.423(0.038)	0.561(0.031)	0.695(0.033)
	TPR_linear	NA	0.541(0.098)	0.661(0.054)	0.713(0.037)	0.695(0.033)
	TPR_nonlinear	0.160(0.028)	0.182(0.036)	0.204(0.043)	0.171(0.050)	NA
	FDR	0.810(0.035)	0.713(0.042)	0.554(0.048)	0.441(0.046)	0.356(0.037)
spikeSlabGAM
	AUC5%	0.596(0.059)	0.738(0.026)	0.789(0.030)	0.861(0.025)	0.883(0.026)
	AUC	0.858(0.032)	0.889(0.015)	0.915(0.021)	0.961(0.010)	0.977(0.008)
	TPR	0.537(0.057)	0.689(0.028)	0.742(0.029)	0.818(0.025)	0.835(0.027)
	TPR_linear	NA	0.792(0.059)	0.828(0.034)	0.843(0.028)	0.835(0.027)
	TPR_nonlinear	0.537(0.057)	0.664(0.031)	0.662(0.048)	0.754(0.043)	NA
	FDR	0.138(0.054)	0.096(0.029)	0.066(0.030)	0.061(0.029)	0.060(0.036)
SpAM
	AUC5%	0.391(0.081)	0.528(0.025)	0.549(0.049)	0.628(0.042)	0.635(0.036)
	AUC	0.792(0.045)	0.842(0.015)	0.867(0.021)	0.909(0.013)	0.907(0.013)
	TPR	0.834(0.070)	0.826(0.044)	0.870(0.036)	0.887(0.026)	0.887(0.029)
	TPR_linear	NA	0.835(0.071)	0.892(0.045)	0.894(0.032)	0.887(0.029)
	TPR_nonlinear	0.834(0.070)	0.824(0.046)	0.850(0.042)	0.871(0.046)	NA
	FDR	0.798(0.015)	0.767(0.018)	0.783(0.014)	0.774(0.015)	0.776(0.013)

Comparison with linear methods

We consider two linear methods for comparison: (1) the linear model selection method (George and McCulloch, 1993; Marin and Robert, 2007), referred to as SSVS; and (2) the ordering-free Bayesian network (WBN) approach that follows the implementation of Werhli, Grzegorczyk, and Husmeier (2006), which has been shown by Allen et al. (2012) to outperform competing ordering-free Bayesian network methods. In each of the five scenarios, our methods outperform both SSVS and WBN. For example, when the true model is completely nonlinear, the AUC of the SSVS is as low as 0.652, while the AUC of the nMixDAG is 0.798. The TPRs of WBN are always lower than those of the other three methods, while the FDRs are always higher. As expected, the performance of the SSVS is closer to those of our methods when the linearity increases, and SSVS slightly outperforms our methods when the data are completely linear. In addition, the average misclassification rate of the functional relationship (i.e., ϕ) for nMixDAG is between 0.07 and 0.24 across the scenarios, indicating a reasonable performance of the second-level selection. Given the model flexibility, nonlinear approaches are expected to include more spurious variables than linear methods; however, our approach retains very good specificity: the FDR is low for our methods, even though the TPR drops as the scenario becomes more challenging. And generally, nMixDAG works slightly better than nDAG in terms of AUC5%, AUC, TPR, TPR nonlinear and FDR across the scenarios.

Comparison with nonlinear methods

Several new variable selection approaches under the generalized additive model framework have been proposed in the literature, including both frequentist methods (Meier et al., 2009; Ravikumar et al., 2009) and Bayesian methods (Reich, Storlie, and Bondell, 2009; Scheipl, Fahrmeir, and Kneib, 2012). Although independently developed for nonlinear regression settings, the Bayesian method spikeSlabGAM by Scheipl et al. (2012) is similar in spirit to our proposed nMixDAG. However, there are substantial differences in terms of model and prior constructions. Specifically, Scheipl et al. (2012) decomposed the spline design matrix into unpenalized and penalized parts through spectral decomposition, which yields an orthogonal basis representation; whereas we directly work with spline basis functions. For model/variable selection, they imposed a spike-and-slab prior on the hyper-variance of the regression coefficients; whereas our approach introduces spike-and-slab priors with a point mass at zero directly on the regression coefficients. Together, these changes induce different shrinkage and selection properties for nonlinear regression in general and DAG models in particular, as we demonstrate via simulations and real data analysis. Here, we compare nMixDAG with spikeSlabGAM and the frequentist method SpAM (Ravikumar et al., 2009) in the context of nonlinear DAGs. Although Ravikumar et al. (2009) recommended choosing the tuning parameter of SpAM via generalized cross-validation, we picked the tuning parameter via 10-fold cross-validation as this approach resulted in better performances in our simulation studies.

Our methods show very competitive performance. The frequentist approach SpAM always has higher TPR than our methods and spikeSlabGAM, however it is achieved at the cost of unacceptably high FDR and hence it has the lowest AUC and AUC5%. For the Bayesian methods, we do not observe a statistically significant difference in all characteristics. For example, in scenario 3, the difference in AUC for nMixDAG and spikeSlabGAM is only 0.036, while their standard errors are 0.019 and 0.021. The AUCs are within two standard deviations of each other; hence, the difference is not significant. In Web Figure 7, we plot the ROC curves of the three nonlinear methods for one randomly selected simulation from scenario 3. There is a trade-off between TPR and FDR for the two competing methods. For instance, in scenario 1, the TPRs are 0.439 and 0.537 and the FDRs are 0.050 and 0.138 for nMixDAG and spikeSlabGAM, respectively. The low FDRs are particularly useful in a genomic context as the selected genes are typically targets of further validation via biological experiments. Hence, a parsimonious approach will probably save on research expenses and time.

Sensitivity analysis of ordering misspecification

The major assumption of our methods is the known prior ordering of the variables. When such ordering is available, this assumption is advantageous, as we have seen that our methods outperform the ordering-free WBN in all scenarios (Table 1). However, in some applications, the ordering may be partially known or not known at all. Under such circumstances, we would like to investigate the robustness of our methods compared to WBN. We follow the ideas of Shojaie and Michailidis (2010) and Altomare et al. (2013) and perform a sensitivity analysis of nMixDAG to different ordering misspecifications. The performance of our method depends on the distance between the true ordering and the assumed ordering, and the number of v-structures (i.e., i → j ← k) for both the true ordering and the assumed ordering. To quantify this distance, we use the normalized Kendall's tau distance, which is defined as the ratio of the number of discordant pairs over the total number of pairs. The normalized Kendall's tau distance lies between 0 and 1, with 0 indicating a perfect agreement of the two orderings and 1 indicating a perfect disagreement. Since our method is not able to learn the ordering, we evaluate the performance of our method based on only the skeleton of the true graph (i.e., the directions of the edges are ignored). We pick scenario 3 and shuffle the data according to the orderings with different normalized Kendall's tau distances. In Table 2, we list normalized Kendall's tau distances, the number of v-structures of the assumed ordering, the number of shared v-structures between the true and the assumed orderings, TPR, TPR linear, TPR nonlinear and FDR for both nMixDAG and WBN. When there is moderate misspecification (Kendall's tau=0.25), nMixDAG outperforms WBN in terms of AUC (0.838 vs 0.809) and remarkably FDR (0.102 vs 0.420). When Kendall's tau is 0.51 or even 1.00, nMixDAG still has a surprisingly reasonable AUC (0.785 and 0.765, respectively) that is just slightly lower than that of WBN (0.809), and a very good control of FDR (0.240 and 0.242, respectively), which is much lower than that of WBN (0.420).

Table 2.

Simulated examples. Sensitivity of nMixDAG to misspecified ordering. Directions of the edges are ignored. The standard error for each statistic is given in parentheses

Method	nMixDAG				WBN
Kendall's tau	0.00	0.25	0.51	1.00
V-structures (assumed)	124	146	138	159
V-structures (shared)	124	87	23	0
AUC5%	0.718(0.036)	0.603(0.031)	0.468(0.023)	0.424(0.023)	0.537(0.022)
AUC	0.879(0.019)	0.838(0.019)	0.785 (0.016)	0.765(0.018)	0.809(0.018)
TPR	0.618(0.027)	0.534(0.031)	0.456 (0.026)	0.374(0.022)	0.551(0.027)
TPR_linear	0.730(0.029)	0.651(0.040)	0.595 (0.045)	0.506(0.047)	0.806(0.041)
TPR_nonlinear	0.514(0.040)	0.425(0.039)	0.328 (0.023)	0.252(0.024)	0.316(0.035)
FDR	0.023(0.021)	0.102(0.033)	0.240 (0.034)	0.242(0.044)	0.420(0.033)

Performance in high-dimensional settings

We investigate the scalability of nMixDAG, setting the number of genes at G = 100, 150, 200 while keeping the number of connections fixed. With G = 200 and M = 10 bases, we have approximately 200, 000 parameters to estimate already given the nonlinear and network construction. We again pick scenario 3 (results shown in Web Table 2). The performance of nMixDAG is almost invariant with respect to the dimensions. As the dimension increases, TPR and AUC slightly decrease, but FDR also decreases. Computationally, the running time increases very slowly with the dimension. On a single AMD 6174 processor, the average computation times are 1.4, 1,8, 2.2, and 2.7 hours for G = 50, 100, 150, 200, respectively.

Sensitivity analysis of hyperparameter settings

We conduct a series of analyses to test the sensitivity of our method to different prior specifications. We pick scenario 3 as a representative case since it has about 50% linear functions, and show our results for nMixDAG. In Web Table 3 and Web Table 4, we report the performance under different hyper-prior specifications for ρ and τ, all of which demonstrate that the performance of our method is quite stable.

6 Data Analysis: GBM Data

We apply our methods to analyze TCGA-based GBM gene expression data, as introduced in Section 1. TCGA provides microarray-based gene expression data for a large cohort of GBM tumor specimens (241 in our case study) (TCGA, 2008). Among more than 10, 000 genes in the raw data, we focus our analysis on 49 genes that overlap with the three critical signaling pathways (Furnari et al., 2007), the RTK/PI3K signaling pathway, p53 signaling pathway, and Rb signaling pathway. A better understanding of the GRN will provide new insights into the tumorigenesis of GBM (Verhaak et al., 2010).

We assume the same prior specifications as in Section 5. Our reference network is the induced subgraph of the signaling pathways in glioblastoma from TCGA (2008), as shown in Figure 2(a), from which we obtain our prior ordering. We run two separate MCMC chains with different starting values, each with 20,000 iterations. For convergence diagnostics, we examine all the parameters that we sample from the MCMC algorithm. In particular, we calculate the Gelman-Rubin potential scale reduction factor (PSRF, Gelman and Rubin (1992)) for the continuous parameters τ_gj (ranging from 1.000 to 1.026) and ρ (1.000 and 1.001 for nMixDAG and nDAG, respectively). For the discrete parameter γ, the correlation between the posterior probabilities of the two chains is 0.994 for nMixDAG and 0.995 for nDAG. For the additional parameters of nMixDAG, ϕ and ω, the correlation and PSRF are 0.988 and 1.000, respectively. All the PSRFs and correlations are very close to 1, which is indicative of good mixing of the MCMC chain, as well as its convergence to the stationary region. The computation time is 1.9 hours on a 3.5 GHz Intel Core i7 processor. We combine the two chains and discard the first 10% of the iterations of each chain as a burn-in.

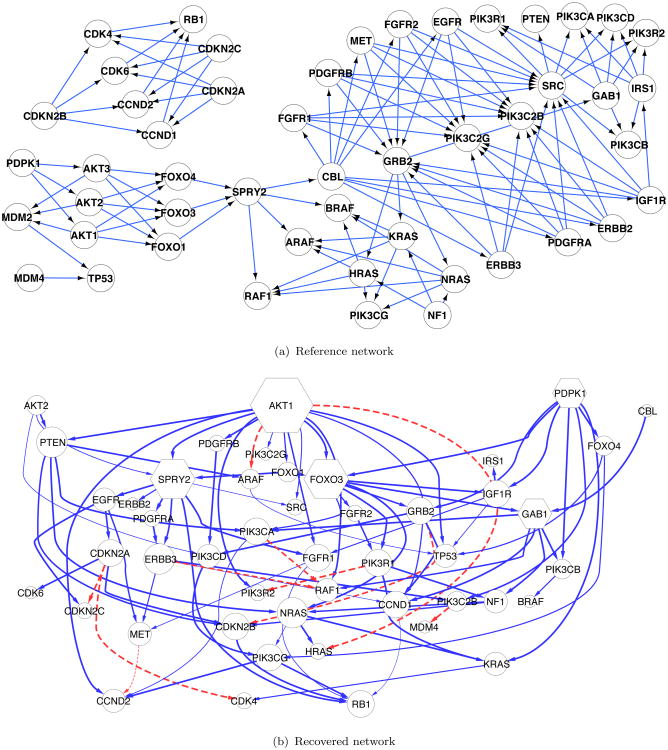
Figure 2.

GBM network. Panel (a): the reference signaling pathways in glioblastoma— the RTK/PI3K, p53, and Rb signaling pathways. The prior ordering is obtained from this network. Panel (b): the recovered network from GBM data with nMixDAG. The solid lines indicate linear interactions; the dashed lines indicate nonlinear interactions; the line width is proportional to its posterior probability; and the node size is proportional to its degree, except for the hub genes (in the hexagons), whose node sizes are further enlarged for clarity.

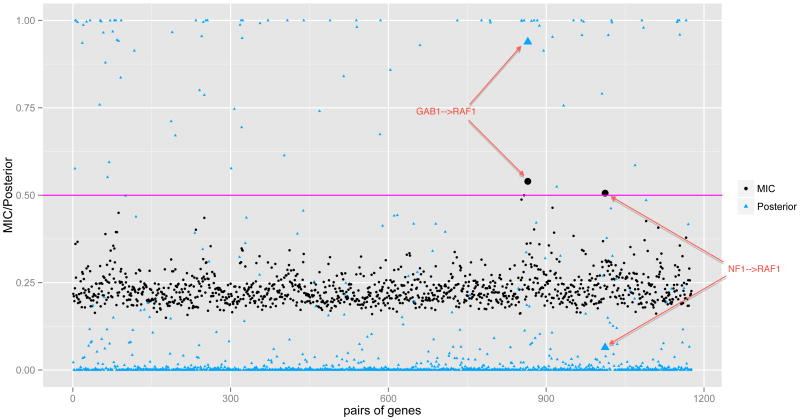
Figure 2(b) shows the network recovered by nMixDAG. The solid lines indicate linear interactions and the dashed lines indicate nonlinear interactions. The line width is proportional to the posterior probability, with thicker lines indicating a higher probability of the edge, and the node size is proportional to its degree, i.e., the number of edges connected to the node. A heat map of the marginal posterior inclusion probability of each edge is provided in Web Figure 5 (Web Appendix E). In total, we find 95 connections, of which 85 are linear and 10 are nonlinear. While we find several novel connections, some of our findings are consistent with known interactions reported in the biological literature. For instance, our study confirms that in the cytoplasm, the NF1 protein inhibits RAS function (Malumbres and Barbacid, 2003) and RAS proteins activate PI3K complexes (Blume-Jensen and Hunter, 2001). We also calculate the maximal information coefficient (MIC) (Reshef et al., 2011), as this approach has been widely used in the analysis of genomic data. The MIC measures the pairwise linear or nonlinear association by mutual information on continuous random variables for the 49 genes of interest (totaling 1176 pairs). The MICs are represented by dots in Figure 3. We find only two pairs of genes with MICs larger than 0.5: GAB1→RAF1 and NF1→RAF1, of which GAB1→RAF1 is also detected by our methods. The triangles are the posterior probabilities of the inclusion of gene pairs by nMixDAG, and the horizontal line is the 0.5 threshold. The enlarged markers are the pairs of genes for which the MICs are higher than the 0.5 threshold. This indicates that methods that estimate marginal nonlinear correlations, such as the MIC approach, may miss some relevant connections that are provided by the nonlinear graphical models. In addition, the MIC approach does not explicitly identify the formal relationships; whereas our approach does this from a functional reconstruction.

Figure 3.

GBM data. The maximal information coefficients (MICs) and posterior probabilities of all pairs of genes from the GBM data. The dots are MICs; triangles are posterior probabilities. The horizontal line indicates the 0.5 threshold. Only two pairs of genes have MICs above the threshold. The marker sizes of the two pairs are enlarged for both the MIC and posterior probability.

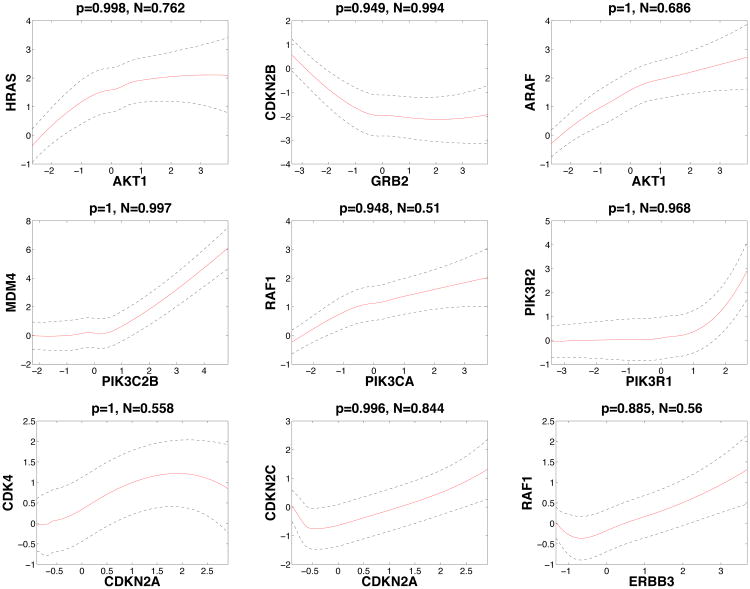
Based on the recovered network in Figure 2(b), several hub genes are identified: AKT1, FOXO3, SPRY2, GAB1 and PDPK1, with degrees of 15, 10, 10, 7, and 7, respectively. Hub genes are of particular interest as potential major drivers of disease etiology because they are often more involved in multiple regulatory activities than non-hub genes. All the five hub genes we find have been previously identified as driver genes (Cerami et al., 2010), and are significantly altered in GBM, e.g., the AKT family is often amplified, while the FOXO family is frequently mutated (TCGA, 2008) in GBM. We also plot the nonlinear functional reconstructions of nine edges, together with their 95% credible bands in Figure 4. Marginal posterior inclusion probabilities are shown on the top of each plot. We can see that the expression level of RAF1 decreases with that of ERBB3 when ERBB3 is low in expression, but starts to increase with ERBB3 after a cut-point around −0.7. It is even more interesting that CDKN2A manifests a sinusoidal trend with CDK4. These relationships have not been reported previously to the best of our knowledge and may deserve further validation via biological experiments.

Figure 4.

GBM data. Nine functional reconstructions with 95% credible bands for selected genes with nonlinear relationships. The marginal posterior inclusion probability (p) and nonlinearity measure (N) are shown at the top of each plot.

We define the nonlinearity measure ( 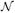) as 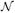_gj = p(ϕ_gj = 1|Y, γ_gj = 1), the probability that a given connection (γ_gj = 1) is nonlinear (ϕ_gj=1) a posteriori, which can be easily computed from MCMC samples of ${\varphi }_{gj},{\gamma }_{gj}:{\mathcal{N}}_{gj}\approx {\sum }_{i=1}^{N}I({\varphi }_{gj}^{(i)}=1,{\gamma }^{(i)}={\gamma }^{\mathit{\text{select}}},{\gamma }_{gj}^{(i)}=1)/{\sum }_{i=1}^{N}I({\gamma }^{(i)}={\gamma }^{\mathit{\text{select}}},{\gamma }_{gj}^{(i)}=1)$ where the superscript (i) labels the ith MCMC sample, N is the number of MCMC samples and γ^select indicates the selected γ from the highest posterior model. This measure quantifies the evidence for the nonlinearity of each curve reconstructed in Figure 4 (shown on the top of each plot). For example, the evidence for nonlinearity between PIK3C2B and MDM4 is strong (0.997), while the evidence between PIK3CA and RAF1 is much weaker (0.510), which is consistent with our observations.

For comparison, we apply spikeSlabGAM to the GBM data and evaluate the performance via the widely applicable information criterion (WAIC) of Watanabe (2010), which is a fully Bayesian predictive information criterion based on the point-wise posterior predictive density and is asymptotically equal to Bayesian leave-one-out cross-validation. Our methods, nDAG and nMixDAG, have lower WAICs than spikeSlabGAM (27378 and 27413 vs 32579), which is indicative of better prediction performance by our methods. The difference between nDAG and nMixDAG is almost negligible. We include more genes in our real data analysis for comparison purposes. We focus on the full RTK/PI3K signaling pathway (http://www.genome.jp/kegg/), which consists of 195 genes instead of the frequently mutated genes from the three core pathways. The difference in WAIC between nMixDAG and spikeSlabGAM is substantial (103559 vs 211571), which again indicates that nMixDAG has higher prediction power. The detailed analysis can be found in Web Appendix E.

7 Discussion

In this paper, we propose two methods, nDAG and nMixDAG, to reconstruct the structure of a gene regulatory network. We use penalized splines to capture the nonlinear interactions between genes as well as to prevent overfitting. We apply two-level model selection to select and distinguish linear and nonlinear interactions. Simulation studies show that our methods outperform methods that assume linearity and are highly competitive compared to the state-of-the-art nonlinear approaches. Furthermore, nMixDAG is able to distinguish linear and nonlinear relationships between genes and therefore provides a more detailed and flexible description of the gene network. Moreover, it is noteworthy that both nDAG and nMixDAG result in very low FDRs, even with highly nonlinear data. In general, we suggest nMixDAG since it works better than nDAG based on the simulations and real data analyses. When there is strong prior belief that all the edges are highly nonlinear, we suggest using nDAG rather than nMixDAG. High nonlinearity of the edges is rare in the context of gene regulatory networks, however, as confirmed by our analysis of the GBM dataset (85 linear and 10 nonlinear connections). A key assumption of our work is the prior ordering of the nodes. Without node ordering, we cannot distinguish between two DAGs within the same Markov equivalence class, where all DAGs encode the same conditional independence structure. Moreover, as we see in the simulation study (Section 5), the performance of WBN is far from satisfactory, partly due to the lack of a prespecified ordering of the variables. Although it can be argued that this assumption restricts the flexibility of our methods, given the sparsity of the gene regulatory network, our sensitivity analysis showed that we do not lose much by imposing a fixed ordering (Section 5). In the case where the prior ordering is completely unknown, a common approach is to decompose the problem into two sub-problems: (1) learn the ordering; and (2) given the ordering, learn the network structure. The first sub-problem can be solved by using an ordering-learning algorithm, for example, that by Friedman and Koller (2003). A more detailed discussion about the Markov equivalence class is given in Web Appendix F.