Summary
Perfusion computed tomography (CTp) is an emerging functional imaging modality that uses physiological models to quantify characteristics pertaining to the passage of fluid through blood vessels. Perfusion characteristics provide physiological correlates for neovascularization induced by tumor angiogenesis. Thus CTp offers promise as a non-invasive quantitative functional imaging tool for cancer detection, prognostication, and treatment monitoring. In this paper, we develop a Bayesian probabilistic framework for simultaneous supervised classification of multivariate correlated objects using separable covariance. The classification approach is applied to discriminate between regions of liver that contain pathologically verified metastases from normal liver tissue using five perfusion characteristics. The hepatic regions tend to be highly correlated due to common vasculature. We demonstrate that simultaneous Bayesian classification yields dramatic improvements in performance in the presence of strong correlation among intra-subject units, yet remains competitive with classical methods in the presence of weak or no correlation.
Keywords: Bayesian decision analysis, cancer detection, metastatic liver cancer, perfusion imaging, spatial correlation
1. Introduction
Perfusion computed tomography (CTp) is an emerging functional imaging technology that enables non-invasive observation and quantification of characteristics pertaining to the passage of fluid through blood vessels. Physiological models have been developed to quantify a variety of perfusion characteristics (such as relative blood volume, and capillary permeability) that derive from measuring temporal changes in contrast enhancement acquired under continuous CT scanning during intravenous administration of contrast medium (Lee, 2002). Consequently, CTp provides a quantitative basis for distinguishing between biologically distinct tissue types through evaluation of vasculature heterogeneity. The functional imaging technology has been utilized in a number of organs and tumors, including prostate, colorectal, head and neck, lung, liver, and normal tissue.
Tissue perfusion plays a critical role in oncology. Cancerous cell growth and migration requires the proliferation of networks of new blood vessels through the process of angiogenesis, triggering modifications to the vasculature of surrounding host tissue. Measurements from CTp provide physiological correlates for neovascularization induced by tumor angiogenesis (Miles, 2002). The potential remains for statisticians to develop and apply statistical models that enable utilization of biomarkers acquired from CTp for the purpose of discriminating malignant from healthy tissue to assist in diagnosis, treatment monitoring, and disease prognostication.
Several frequentist classification methods, including linear discriminant analysis and quadratic discriminant analysis, are used widely in practice (Ripley, 1996). A Bayesian implementation of quadratic discriminant analysis was first discussed by Geisser (1964), and thereafter extended to regularized classification when estimation of covariance is ill-posed due to limited sample size, see Srivastava et al. (2007) and references therein. Recently, a few classification methods have been proposed to handle correlated data. Brown et al. (2001) initially proposed a Bayesian discrimination approach for longitudinal data. Cruz-Mesía et al. (2007) generalize it to accommodate semiparametric hierarchical models using a mixture prior for the distribution of inter-cohort random effects. Marshall et al. (2009) further extended the approach to handle missing data. Classification approaches (including those aforementioned) predominantly evaluate possible class assignments for each classification target independently of neighboring targets, with Zhu et al. (2011) as a notable exception. For most biomedical applications this assumption is limiting. For example, perfusion observables acquired from functional CT tend to be highly interdependent across multiple liver regions within the same patient, due to shared features of the common hepatic vascular systems.
In this paper, we develop a Bayesian probabilistic framework for simultaneous supervised classification of multivariate correlated objects using separable covariance. The proposed approach broadens existing classification methods to accommodate prediction of interdependent collections of correlated objects, nested within multiple intra-subject units. The proposed classification approach is applied to discriminate between regions of liver that contain pathologically verified metastases from normal liver tissue using five CT perfusion characteristics. Our investigation reveals that simultaneous classification may yield dramatic gains in predictive accuracy when compared to conventional approaches to discriminant analysis, which treat the targeted units as independent. Additionally, the Bayesian classifier offers seamless incorporation of differential misclassification loss. A feature that is necessary in oncologic diagnostic radiology in general, and requisite to detection of metastatic disease. However, the general method offers the potential to improve classification performance in settings wherein multiple classification targets are evaluated within each subject, and thus appropriate for any biomedical application that utilizes biomarkers to identify features intrinsic to a particular disease at multiple interdependent sites within an organ.
The ideas in this paper are presented in the following sequence. In Section 2 we discuss the motivating CTp data. In Section 3 we present the Bayesian model. The resultant predictive density and simultaneous classification method is presented in Section 4. In Section 5 we use the method to discriminate between hepatic metastases from neuroendocrine tumors and normal liver tissue using the actual CTp data. Simulation and discussion of the method’s properties is presented in Section 6.
2. CT Perfusion Data
The study focused on patients with neuroendocrine liver metastases who underwent CT perfusion for a target lesion in the liver with the malignancy determined clinically or radiologically. The study collected data between April 2007 and September 2009 on 16 patients, 6 men and 10 women, with median age 54 and 59, respectively. More detailed description can be found in Ng et al. (2013). CT perfusion images (Figure 1 left) were obtained from a dual phase protocol spanning a duration of 590 seconds (s). Using a deconvolution analysis with the distributed parameter physiological model (Miles et al., 2000, Lee, 2002, and Stewart et al., 2008), five perfusion characteristics were acquired: blood flow (BF), blood volume (BV), mean transit time (MTT), permeability-surface area product (PS), and hepatic arterial fraction (HAF). Figure 1 (right) illustrates the five CTp characteristics obtained for a single patient at four acquisition durations. The resultant CTp datasets consisted of fifty-nine 8-slice cine images temporally sampled at 0.5s from the phase 1 acquisition, together with eight anatomically matched 8-slice images from the phase 2 acquisition. Our analysis used the average BF, BV, MTT, PS and HAF values obtained at around acquisition time 590s, a duration that was shown to yield stable acquisition in the liver (Ng et al., 2013). The values of the CTp characteristics were averaged over all 8 slices. As a result, a 5 × 1 vector is observed for each ROI. There were 25 separate tumor ROIs: 9 patients had two ROIs in the right and left lobes respectively, and 7 patients had one each. There were 30 separate normal liver tissue ROIs: twelve patients had one ROI each in the right and left lobes; 3 patients had two ROIs in the right lobe (which were averaged); and one patient did not have delineable normal tissue. The latter resulted in 27 lobe specific normal liver ROIs.
Figure 1.
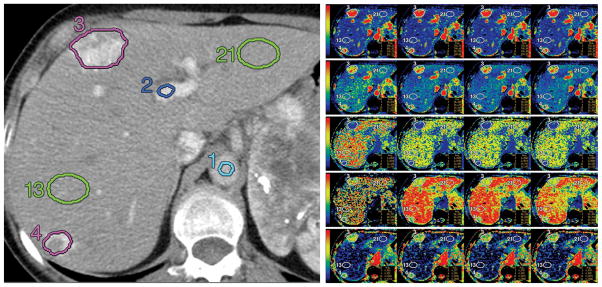
Left: Reference CT image in a patient with neuroendocrine metastases to liver with corresponding ROIs: aorta (1, light blue), portal vein (2, dark blue), tumors (3 and 4, purple), and normal liver tissues (13 and 21, green); Right: Maps for blood flow (first row), blood volume (second row), MTT (third row), PS (fourth row), and HAF (fifth row) at acquisition durations of 30, 160, 220, and 590 seconds (left to right columns, respectively). Blood flow is expressed in mL/min per 100 g; blood volume, in mL/100 g; MTT, in seconds; and PS, in mL/min per 100 g. The color scales are identical for each row. Figures are reproduced with permission from Ng et al. (2013) Figures 2b and 2c.
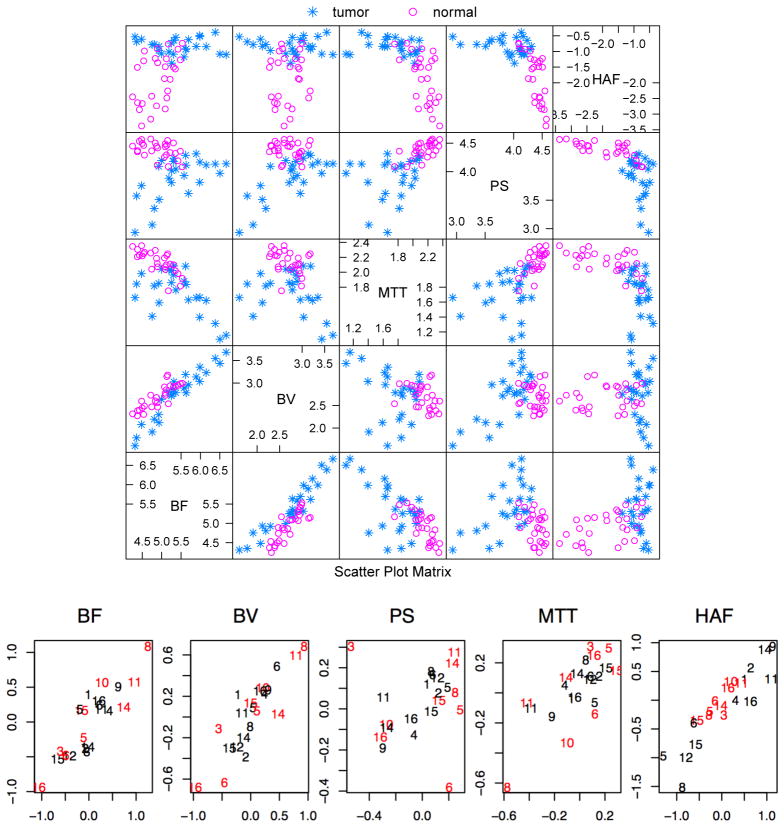
Scatterplots of the log scaled CTp measurements are provided in Figure 2 (top). In diagnostic radiology, CTp characteristics are often considered in isolation using univariate models that neglect to exploit the fact that independencies among the five perfusion features vary substantially in magnitude and direction between vasculatures surrounding malignant and healthy tissues. For example, BF is shown to increase with PS in the tumor tissues but decrease in normal liver. Table 1 (a) summarizes Pearson sample correlations among CTp characteristics from the same ROI for each tissue type. Correlations for normal liver (tumor) are provided in the lower (upper) triangle matrix. Correlations between BF and PS, BF and HAF, BV and PS, BV and HAF, present different signs for tumor and normal ROIs, reflecting systematic modification of the underlying hepatic vasculature surrounding tumor. Moreover, the strength of intra-region correlation differs among pairs of CTp measurements across tissue types.
Figure 2.
Top: Scatterplots of the log scaled CTp measurements: “*” represents tumor ROI and “○” represents ROI in normal liver. The variables names and values displayed in each subplot are given by the diagonal line. For example, the northwest subplot displays BF (x-axis) versus HAF (y-axis). Bottom: Graphical illustrations of intra-patient inter-region correlation for each CTp characteristic. The horizontal axes represents CTp values obtained in the left lobe, while the vertical axes represent right lobes. The label for each point reflects an anonymized patient identifier, with tissue type indicated by color: black for normal regions and red for tumor.
Table 1.
(a): Sample correlations among intra-region CTp measurements in normal (lower triangle) and tumor (upper triangle) ROIs. (b): Sample correlations among identical CTp measurements across neighboring ROIs with common tissue type.
| BF | BV | MTT | PS | HAF | |
|---|---|---|---|---|---|
| BF | 0.95 | −0.57 | 0.60 | −0.09 | |
| BV | 0.85 | −0.32 | 0.76 | −0.13 | |
| MTT | −0.74 | −0.34 | 0.19 | −0.21 | |
| PS | −0.41 | −0.10 | 0.62 | −0.29 | |
| HAF | 0.48 | 0.11 | −0.57 | −0.73 | |
| (a) Intra-region correlation | |||||
| BF | BV | MTT | PS | HAF |
|---|---|---|---|---|
| 0.88 | 0.86 | 0.72 | 0.16 | 0.90 |
|
| ||||
| (b) Inter-region correlation | ||||
Scatterplots for each of five characteristics from neighboring regions of the same tissue type are shown in Figure 2 (bottom), where the x-axis corresponds to ROIs in the left lobe and the y-axis for the right lobe. Notice that only patients with two normal ROIs or two tumor ROIs are shown. Figure 2 (bottom) suggests that neighboring ROIs of the same tissue type are highly correlated, which is expected because of common vasculature. Moreover, neighboring ROIs from the same patient but of different tissue types exhibit spread, which suggests no correlation across classes. Sample correlations between neighboring regions of common tissue type were calculated by computing deviations from the mean within each tissue group, then computing Pearson correlation to pairs of measurements obtained in neighboring intra-patient regions, as provided in Table 1 (b). Note that the sample correlation is calculated with pooled measurements from both tissue types because the inter-region correlation behaves similarly for tumor and normal tissues. Four characteristics presented high intra-patient correlations (> 0.7). By way of contrast, PS exhibited relatively weak interdependence (< 0.2) across ROI. However, the scatterplot in Figure 2 (bottom) illustrates that strong linear dependence is evident with the exception of two outliers contributed by patients 3 and 6. In the absence of the outliers, correlation for PS increases to 0.71.
Recall that our objective is to discriminate malignant lesions from normal ROIs using the CTp characteristics. Classification approaches predominantly evaluate possible class assignments for each classification target (in our case each ROI) independently of neighboring targets. However, as we have shown above, the CTp characteristics from neighboring ROIs within the same patient are highly correlated due to common vasculature. Next, we will develop a Bayesian probabilistic framework for simultaneous supervised classification to incorporate the interdependence among ROIs.
3. Multivariate Model
Let N denote the total number of patients in the study. For i = 1, …, N, let ni denote the total number of ROIs and the number of ROIs of type z contributed by the ith patient. Let represent the m × 1 observable vector corresponding to the jth ROI of type z, and denote the CT characteristics (observables) from ROIs of type z for the ith patient. We use z = 0 to denote normal ROIs and z = 1 for tumor ROIs in the CTp binary setting. The general case can be extended without loss of generality to accommodate multiple class labels z ∈ {0, 1, …, k − 1}. For patient i, we assume that
| (1) |
where denotes a vector of ones of length , μz a m × 1 vector of mean parameters, and Σz: m × m positive definite matrices, and ⊗ the Kronecker product. We further assume that measurements from different class are independent. Assuming independence across class facilitates sensitivity to inter-class heterogeneities in mean and covariance, which for CTp provide the vascular morphologic signatures that differentiate tissue types.
Covariance matrix Σz pertains to observables within the same ROI, and controls inter-ROI correlation, thereby facilitating separable correlation structure. The Kronecker product of the covariance matrix is unidentifiable since for any non-zero value a. Thus, we restrict the first diagonal element of to be 1. The assumption of separability reduces the degrees of freedom in the covariance from to . Thus, separable covariance models are parsimonious. Yet, by imposing structure on , the model may accommodate various types of inter-region correlation. Below we consider several options for specifying , that are relevant to classification problems. Brown et al. (2001) considered a more flexible model by relaxing the structure of the parameters and only requiring that the hyper-parameter in the prior distribution has the Kronecker product structure. However, this model requires balance (fixed number of ROIs) which will be violated for the CTp data because the dimension of , varies in relation to the number of ROIs contributed by each patient.
3.1 Compound Symmetry
For multivariate data, intra-class compound symmetric correlation may be imposed through the Kronecker product by assuming
| (2) |
where denotes the identity matrix. The diagonal vector of is , inducing common marginal covariance among observables from the same class and region. Correlations between any two units within the same subject are scaled by parameter ρz.
In our CTp example, (2) assumes that the extent of interdependence among CTp characteristics acquired in neighboring regions is equivalent for all regions of the same tissue type. Hereafter, when referring to compound symmetry we assume a common inter-region correlation multiplier, ρz = ρ, thereby enhancing efficiency. This assumption was assessed through preliminary analysis of sample correlation and model criticism using deviance information criterion (DIC) (Spiegelhalter et al., 2002).
3.2 Spatial Dependence
For many biomedical imaging applications, the extent of correlation among measures of biological function may depend on their spatial proximity or relative location to a landmark within an organ, thereby violating the assumption of compound symmetry. Spatial-temporal processes are often assumed separable as the product of a spatial covariance and temporal covariance (Ma, 2003). In this section we extend the model to accommodate multivariate prediction of targets that exhibit spatial dependence.
Let djj′ denote the distance between two regions j and j′. Inter-class spatial correlation with separable covariance assumes
| (3) |
where c(djj′; ρ) is the correlation function such that c(0; ρ) = 1 and ρ denotes the correlation parameter. We’ll abuse our notation slightly and allow the dimension and parameter space of ρ to vary by spatial model. Several correlation functions have been studied in the spatial literature (see e.g. Stein, 1999). In this article, we consider two commonly used models. Denoting the distance between two regions by d ∈ [0, ∞), the power family assumes that correlation between ROIs decays monotonically with increasing distance,
| (4) |
where the scale parameter ϕ controls the rate of decay. The well known exponential and Gaussian covariance functions follow as special cases of the power family with p = 1 and p = 2, respectively. The more flexible spherical correlation function is defined as
| (5) |
where ϕ has the interpretation as a scale parameter and controls the range of dependence. Two regions with distance exceeding ϕ are assumed independent.
Regardless of which correlation function used, the element in the jth column and j′th row of the inter-region correlation matrix (1) is defined as . Notice that the compound symmetric model is a special case where c(d) ≡ ρ for any d > 0. Heretofore, we have considered correlation functions that are isotropic, or homogenous as a function of distance. Notice that the model may be easily extended to accommodate anisotropic models using the correlation function c(sj − sj′; ρ) (Haskard et al., 2007), where sj and sj′ are spatial locations for region j and j′, respectively.
The choice of covariance should be informed by the application and data. However, conventional Bayesian model selection techniques, such as DIC, log-marginal pseudo-likelihood(LMPL) (see Geisser and Eddy, 1979; Gelfand and Dey, 1994), and so forth can be used to augment the choice of in the presence of the data. In the case study in liver perfusion presented in Section 5, we compare DIC among three choices of covariance. Before presenting the classification method, hereafter we provide expressions for the likelihood and marginal likelihood functions. Notice that the derivations presented in Sections 3 and 4 apply to a general and thus pertain to any spatial correlation structure.
3.3 Likelihood and posterior distribution
The processes for conducting posterior inference and predictive classification are universal under the varied inter-region correlation structures. In this section, we describe the likelihood and derive the posterior under the assumption of compound symmetry, where it is tractable.
Let
 denote the set of observables with known classes, and θ = {μz, Σz, ρ} the collection of model parameters. Let the inverse, trace and determinant of a matrix be denoted by (·)−1, tr(·) and | · |, respectively. Under model (1), the likelihood function is
denote the set of observables with known classes, and θ = {μz, Σz, ρ} the collection of model parameters. Let the inverse, trace and determinant of a matrix be denoted by (·)−1, tr(·) and | · |, respectively. Under model (1), the likelihood function is
| (6) |
where and etr{A} represents the exponential of the trace of the matrix A. Define ỹz, S̃z to be functions of unknown inter-region correlation parameter ρ, where is the summation of the jth column of ,
| (7) |
| (8) |
The likelihood function is equivalently expressed as
| (9) |
The details of this derivation are provided in Section A.1 of the supplemental material.
We assume the widely used prior for the mean and covariance parameters μz and Σz
| (10) |
where Ωz is the m × m matrix scale hyperparameter of the inverse Wishart distribution, δ the shape hyperparameter, and h(δ, Ωz) is a normalization constant, such that
| (11) |
This prior is flat for μz and inverse Wishart distribution for Σz. The shape hyperparameter δ is fixed to be δ = m − 1 in order to provide maximum entropy. Specification of the scale hyperparameter Ωz, which is class dependent, will be addressed in Section 4. The prior distribution for the correlation parameter ρ will be case specific.
The posterior distribution for our model parameter θ is derived as follows. Using the quadratic form of the likelihood function in (9), it is straightforward to show that the marginal likelihood of
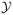 conditional on ρ is
conditional on ρ is
| (12) |
Notice that for the compound symmetric correlation, . For the spatial correlation structures, the value of depends on the distance between regions and assumed spatial structure.
The posterior distribution for ρ, π(ρ|
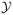 ), is proportional to the product of the marginal likelihood (12) and prior for ρ, that is, π(ρ|
), is proportional to the product of the marginal likelihood (12) and prior for ρ, that is, π(ρ|
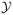 ) ∝ p(
) ∝ p(
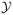 |ρ)π(ρ). Moreover, given the prior distribution (10), the posterior distribution of μz and Σz conditional on ρ is
|ρ)π(ρ). Moreover, given the prior distribution (10), the posterior distribution of μz and Σz conditional on ρ is
| (13) |
which are Gaussian and inverse Wishart, respectively. Integrating over the posterior for ρ therefore yields the posterior distribution for μz and Ωz,
4. Predictive Density and Classification
The objective of this paper is to develop a probabilistic classification framework that leverages intra-patient, inter-region interdependence to facilitate simultaneous classification of multiple ROIs contributed by a new patient. Denote the observables provided by the new patient by YN+1 = [yN+1,1, …, yN+1,nN+1] and let zN+1 = (zN+1,1, …, zN+1,nN+1) denote the unknown class indicator for each ROI. Thus, the goal is to predict the class index vector zN+1. In this section, we describe the predictive density for the model presented in Section 3 and corresponding method for classification.
4.1 Predictive Density
The conditional predictive density of the observed collection of random variables for the new patient conditional on a fixed value of the inter-ROI correlation parameter ρ is
| (14) |
where denotes the number of ROIs of type z for the new patient, and is the weighted sample covariance (8) with summation upper bound replaced by N +1. Derivation of this result is provided in Section A.2 of the supplemental material.
We may conduct full Bayesian inference by specifying a prior distribution for ρ, π(ρ). The predictive density under full Bayesian implementation is
| (15) |
eluding analytical tractability. When ρ is unit dimensional, implementation of numerical approximation using Riemann Sum is possible to avoid sampling-based computation of the predictive density. This approximate, unconditional predictive density may be expressed as the following weighted sum
| (16) |
where ρ1, …, ρK is a sequence of equally spaced points in the domain of ρ.
Remark 1
When there is no correlation among intra-patient regions, the predictive density reduces to
| (17) |
where is the sample covariance for regions of tissue type z.
Alternatively, one may circumvent this computation by adopting an empirical Bayesian (EB) approach that proceeds with inference using the conditional predictive density (14) with ρ fixed at its marginal maximum likelihood estimate (MMLE). The marginal likelihood (12) is maximized at
| (18) |
Derivation of this result is provided in Section A.3 of the supplemental material. Thus, the MMLE for ρ satisfies
| (19) |
EB inference typically “underestimates” variability in θ, since posterior uncertainty in ρ̂ is ignored. However, our case and simulation studies yield comparable results with the full Bayesian approach.
4.2 Classification
When classifying nN+1 ROIs simultaneously, the total number of possible class configurations is 2nN+1. Let
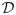 = {d1, …, d2nN+1} denote the set of all the possible class configurations. The posterior classification probability for a class configuration is
= {d1, …, d2nN+1} denote the set of all the possible class configurations. The posterior classification probability for a class configuration is
| (20) |
where Pr(zN+1 = dk) denotes the prior probability for class configuration dk. Generally, we use the binomial prior class probabilities Pr(zN+1 = dk) = pl(1 − p)nN+1−l, where l is the number of tumor ROIs given by dk. Hyperparameter p is fixed at the estimated rate of tumor incidence in the presence of the training data. The predictive density p(YN+1|
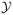 , zN+1 = dk) is given by (16) for the full Bayesian inference and (14) for empirical Bayesian with the value of ρ fixed at (19).
, zN+1 = dk) is given by (16) for the full Bayesian inference and (14) for empirical Bayesian with the value of ρ fixed at (19).
We select as the simultaneous Bayesian classifier, the class configuration that minimizes the Bayesian risk, R(z), over z ∈
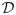 ,
,
| (21) |
where L(dk, z) is the loss function specifying the penalty attributed to decision z when the true class set is dk. Our application uses weighted 0–1 loss
| (22) |
where I{·} denotes the indicator function, and weight α characterizes the relative cost of false negative versus false positive errors. When α = 0.5, Lα(dk, z) corresponds to the total number of misclassifications, inducing equal cost. When α > 0.5, higher cost is assigned to false negative. The choice of α is always driven by the application. We present classification results with α = 0.2, 0.5, and 0.8 in the case study for conceptual illustration. However, in the context of diagnosing metastatic cancer, false negative classification would usually incite a higher penalty. Thus, the scenario with α = 0.8 is best suited to the motivating application.
Remark 2(a)
While conventional Bayesian classification requires a prior probability for each class label, our simultaneous classification necessitates prior specification for each possible class configuration.
Remark 2(b)
For single region classification at equal cost (α = 0.5), the Bayesian classifier is also the maximum a posteriori (MAP) classifier. This is not necessarily true in our simultaneous classification. Consider the case with 2 regions and 4 possible class configurations {d1 = (0, 0), d2 = (0, 1), d3 = (1, 0), d4 = (1, 1)}, and posterior probability q1, …, q4, respectively. Assume that z = d3 is the MAP classifier. When q1 + q2 > q3 + q4, simple calculation yields R(z = d1) < R(z = d3), thereby d3 is not the Bayesian classifier.
5. Case Study
In this section we discuss application of the proposed simultaneous classification method to the CT perfusion dataset presented in Section 2. Specifically, we consider classification based on minimizing Bayesian risk (MBR) and maximizing a posteriori (MAP) probability. Three structures are implemented to accommodate the inter-region correlation: compound symmetric, exponential (power correlation with p = 1), and spherical. The centroid distance were extracted from the CTp images in order to model the spatial dependence. For all the three structures, the correlation parameter assumed a uniform prior over a reasonable range of values given the extent of observed distances between ROIs. Specifically, for compound symmetry we assumed a uniform prior with ρ ∈ [0, 1), while ρ ∈ (0, 12) was used for power spatial correlation, and ρ ∈ (0, 20) for spherical spatial correlation. The range of ρ was chosen such that inter-region correlation fully spanned the parameter domain [0, 1) for the domain of inter-ROI distances presented in the liver perfusion data. For the compound symmetric structure, the posterior mean of inter-correlation was 0.735, while for exponential and spherical, the correlations between regions with the average distance (50mm) were 0.782 and 0.787, respectively. More results of the posterior inference are provided in Section B of the supplemental materials. Non-uniform priors for ρ were also considered, the results for which are provided in Section C of the supplemental materials. Generally, classification performance was robust to the choice of prior for ρ. Results are compared to linear discriminant analysis (LDA, implemented using R function lda provided in the package “MASS”), quadratic discriminant analysis (QDA, implemented using R function qda in “MASS”), and Bayesian quadratic discriminant analysis (BDA). Implementation of the BDA method follows Brown et al. (2001), with prior given in (10) and the scale hyperparameter Ωz fixed to maximize the marginal likelihood function, which yields Ωz = δSz, where Sz denotes the sample covariance of tissue type z and δ is the shape hyperparameter in (10). This value of Ωz is also used in the full Bayesian approach of the MBR method. For the empirical Bayesian approach, Ωz is estimated jointly with ρ, which is given in (18).
Three different values of the weight α were used to evaluate simultaneous Bayesian risk for the MBR method. Recall that larger value of weight α assigns higher penalty to false negative errors, thus preferring sensitivity over specificity. Therefore, the MBR classifier under α = 0.8 yields higher true positive and false positive rates when compared to α = 0.2. We also evaluated the extent to which performance was impacted by excluding CTp characteristics, and found that it was not necessary to use all five. Rather, arguably the best trade-off was obtained using four (excluding BV). However, generally leveraging an additional perfusion characteristic improved classification performance up to four. In what follows, we present results based on all five characteristics. Section D of the supplemental materials presents additional results for various combinations of CTp characteristics.
The true positive rate (TPR) and the false positive rate (FPR) are used in this paper to summarize the classification results. The TPR is defined as the number of tumor ROIs classified as tumor divided by the total number of tumor ROIs, and the FPR is the number of normal ROIs classified as tumor divided by the total number of normal ROIs. The results are summarized in Table 2. We considered leave-one-patient-out cross-validation (LOOCV) using the following implementation. At each step, the observables from a single patient are omitted from the training set, while posterior inference is implemented using data from the remaining 15 patients. Thereafter, ROIs contributed by the omitted patient are classified using each method, and the results are compared with each region’s true status.
Table 2.
Classification results using leave-one-patient-out cross-validation (LOOCV) for the CT perfusion dataset with 52 regions contributed by 16 patients. Results are shown for the following methods: maximizing a posteriori (MAP), minimizing Bayesian risk (MBR), Bayesian quadratic discriminant analysis (BDA), linear discriminant analysis (LDA), quadratic discriminant analysis (QDA). The first row indicates the correlation structure being used. For the MAP and MBR methods, the top rows provides the empirical Bayesian result (EB), and second rows the full Bayesian result (FB).
| CS | Exponential | Spherical | ||||||
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| method | TPR | FPR | TPR | FPR | TPR | FPR | ||
| MAP | (EB) | 0.96 | 0.07 | 0.96 | 0.04 | 0.96 | 0.04 | |
| (FB) | 0.96 | 0.07 | 0.96 | 0.04 | 0.96 | 0.04 | ||
|
| ||||||||
| MBR | α = 0.2 | (EB) | 0.92 | 0.04 | 0.92 | 0.00 | 0.92 | 0.00 |
| (FB) | 0.88 | 0.04 | 0.88 | 0.00 | 0.88 | 0.00 | ||
|
| ||||||||
| α = 0.5 | (EB) | 0.96 | 0.07 | 0.96 | 0.04 | 0.96 | 0.04 | |
| (FB) | 0.96 | 0.07 | 0.96 | 0.04 | 0.96 | 0.04 | ||
|
| ||||||||
| α = 0.8 | (EB) | 0.96 | 0.15 | 0.96 | 0.15 | 0.96 | 0.15 | |
| (FB) | 0.96 | 0.11 | 1.00 | 0.19 | 1.00 | 0.19 | ||
|
| ||||||||
| BDA | 0.76 | 0.18 | ||||||
| LDA | 0.88 | 0.15 | ||||||
| QDA | 0.84 | 0.22 | ||||||
| Logit | 0.80 | 0.15 | ||||||
Results in Table 2 demonstrate that our simultaneous methods outperform the existing methods that fail to leverage correlation between ROIs. Moreover, the simultaneous methods with spatial dependence structure mostly outperform the compound symmetric structure with slightly lower FPR. The gain in specificity is primarily attributed to classification for one patient presenting only 2 ROIs, 1 tumor and 1 normal, with distance 0.39cm. Inference using the compound symmetric structure, which yields an estimated inter-region correlation of 0.76 regardless distance, designates both regions as tumor. By way of contrast, the spatially dependent classifiers weigh inter-region correlation in relation to ROI proximity which imparts additional sensitivity for discriminating between nearby regions. Specifically, both spatial models estimate that regions of a common tissue type at a distance of 0.39cm should exhibit correlation of approximately 0.85, which is much higher than the extent of interdependence evident for the ROIs in question. Therefore, through incorporation spatial dependence, the approach resulted in proper classification of these two regions, thereby improving performance overall.
Differences between the two spatial models were not evident. This is likely due to the fact that each patient contributes a relatively small number of ROIs. Increasing the weight α yields a corresponding increase in FPR and TPR. Among the three correlation structures we have considered, compound symmetry yielded the smallest DIC, with the spherical model the highest, and the exponential model slightly smaller than spherical. Generally, results for the empirical Bayesian approach are quite comparable with full Bayesian implementation. Note that the computation time for one patient is less than 1 second for the empirical Bayesian approach while about 84s for the full Bayesian approach when the predictive density (16) is approximated by 500 samples.
6. Simulation Study
Simulation was used to further investigate the performance of the proposed simultaneous classification methods. The first simulation uses resampled data from the actual CT perfusion dataset. For each replication, a subsample of 10 patients is selected randomly and used for LOOCV classification. The average true positive rate (TPR), false positive rate (FPR), and misclassification rate (MCR) over 200 replicates are provided in Table 3. The proposed simultaneous classification methods outperform the conventional methods, yielding both higher sensitivity and specificity. The TPR increased as much as 17%, and the FPR and MCR dropped as much as 15% and 12%, respectively. Note that large values of α deliver higher sensitivity at the cost of diminished specificity for the minimizing Bayesian risk method.
Table 3.
Simulation with resampling from the CT perfusion dataset using maximizing a posteriori (MAP), minimizing Bayesian risk (MBR), linear discriminant analysis (LDA), quadratic discriminant analysis (QDA), and quadratic Bayesian discriminant analysis (BDA). For the MAP and MBR methods, both the empirical Bayesian approach (EB) and the full Bayesian approach (FB) are presented.
| method | TPR | FPR | MCR | ||
|---|---|---|---|---|---|
| MAP | (EB) | 0.92 | 0.13 | 0.11 | |
| (FB) | 0.91 | 0.12 | 0.11 | ||
|
| |||||
| MBR | α = 0.2 | (EB) | 0.86 | 0.08 | 0.11 |
| (FB) | 0.84 | 0.08 | 0.12 | ||
|
| |||||
| α = 0.5 | (EB) | 0.92 | 0.12 | 0.10 | |
| (FB) | 0.91 | 0.12 | 0.11 | ||
|
| |||||
| α = 0.8 | (EB) | 0.95 | 0.18 | 0.12 | |
| (FB) | 0.94 | 0.19 | 0.13 | ||
|
| |||||
| BDA | 0.78 | 0.20 | 0.21 | ||
| LDA | 0.80 | 0.16 | 0.18 | ||
| QDA | 0.79 | 0.23 | 0.22 | ||
Our second simulation augments the first, by investigating the impact of the difference between group means and the extent of correlation cross regions. For all the scenarios, data are randomly generated from model (1), with parameter values varying by scenario. We mimic the real CT perfusion data by fixing the covariance matrices for each group to be their posterior mean estimates. The mean for normal group is also fixed at its posterior mean μ̂0 under the compound symmetric structure. The mean for tumor group are specified to reflect a Δ% shift from normal: μ̂0(Δ + 1). Three values of Δ are considered: 0, 0.5, and 1. Higher values of Δ yield more separated classes. When Δ = 0, the two classes have identical means. When Δ = 1, the group mean vectors match closely with the posterior means for the actual CT perfusion data. We also considered three values of the cross-region correlation ρ, reflecting no correlation (ρ = 0), weak correlation (ρ = 0.4), and strong correlation (ρ = 0.8).
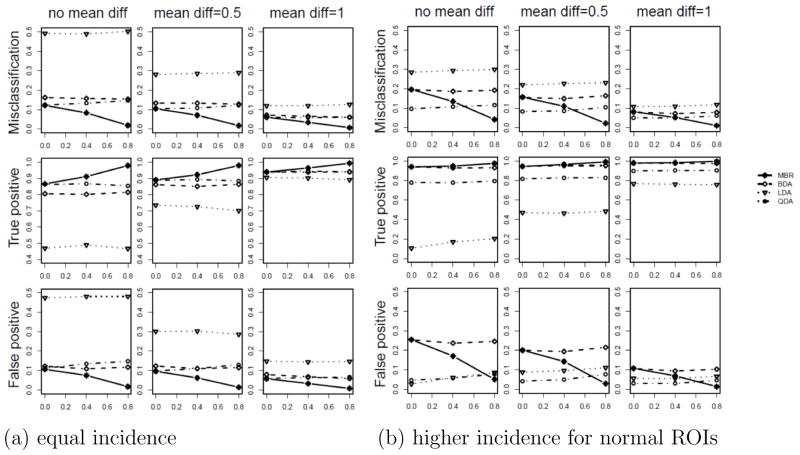
In the first scenario, the number of ROIs for each patient is randomly sampled from integers {1, 2, 3, 4} with equal probability for both tumor and normal groups. Figure 3 (a) plots the misclassification, true positive, and false positive rates averaged over 200 replicates. Empirical Bayesian implementation of MBR and MAP yields similar results to full Bayesian, and thus is omitted. LDA fails to discriminate in the absence of mean difference due to the assumption of common covariance structure across classes (shown to yield MCR= 50% in the first column of Figure 3 (a)). BDA and QDA generally perform better than LDA in the presence of the heterogeneous covariance structure across classes. Line segments (solid for simultaneous MBR and dotted for LDA, QDA, and BDA) illustrate trends for increasing interdependence among intra-patient ROIs. In the absence of correlation among ROIs (ρ = 0), simultaneous MBR yields similar performance with QDA and BDA. As correlation increases, BDA and QDA yield static true and false positive rate at 0.80 and 0.10, respectively, due to their inability to utilize interdependence among regions when evaluating class assignments. On the other hand, improvements for all classification properties are evident for the simultaneous methods. Moreover, when ρ = 0.8, the simultaneous MBR yields true positive rates as high as 0.98 and false positive rates as low as 0.03. As the mean difference between classes increases (shown in the second and third columns in Figure 3), the groups become more separable, thus yielding improved performance for all considered methods.
Figure 3.
Misclassification rate (top row), true positive rate (middle row) and false positive rate (bottom row) when (a) number of ROIs is randomly selected among {1, 2, 3, 4} for both tumor and normal groups; (b) number of normal ROIs is chosen randomly either 3 or 4 and the number of tumor ROIs is either 1 or 2. Results for the simultaneous classification by minimizing Bayesian risk (MBR with α = 0.5, shown by “*”, solid line), and conventional classification using quadratic Bayesian discriminant analysis (BDA, shown by “◇”, dashed line), quadratic discriminant analysis (QDA, shown by “○”, dotted dash line), and linear discriminant analysis (LDA, shown by “▽”, dotted line) are provided. As the correlation between ROIs increases, simultaneous MBR yields increasing true positive rate and decreasing false positive rate, while the conventional methods are static.
In the second scenario, the number of normal ROIs is selected randomly to be either 3 or 4 while the number of tumor ROIs is chosen randomly to be either 1 or 2. Thus, on average 70% of measurements are derived from normal ROIs. Results for this scenario are presented in Figure 3 (b). Generally, results follow the same trend across mean differences and correlations, which demonstrates that our proposed simultaneous MBR method consistently performs well even in the presence of imbalanced numbers of classes and/or regions. In addition, implementation of the simulations using N = 50 patients yielded similar results.
We also used simulation to investigate sensitivity to misspecification of inter-region correlation. Specifically, we evaluated the extent to which classification performance is diminished for simultaneous classification using compound symmetry, when the true underlying correlation structure exhibits spatial dependence with exponential decay. Classifiers were simulated under three true values of ϕ reflecting weak, moderate, and strong average spatial dependence. The results are presented in Section E of the supplemental materials. In the absence of strong spatial dependence, performance for simultaneous classification using compound symmetry is robust to the misspecification (with average difference less than 0.5%). When both nearby regions are strongly interdependent and distant regions are weakly interdependent, the assumption of compound symmetry for the MBR classifier with α = 0.5 resulted in a 1.8% decease in the true positive rate, 1.6% increase in the false positive rate, and 1.8% increase in the misclassification rate when compared to exponential. However, generally results for the simultaneous approaches outperform conventional methods in the presence of increasing inter-region correlation regardless of the assumed inter-region correlation.
7. Discussion
In this paper, we described a Bayesian probabilistic framework for simultaneous supervised classification of multivariate correlated objects with separable covariance. The extent to which classification performance may be improved by the proposed simultaneous approach depends on the extent of interdependence among classification targets. We demonstrated that in the presence of strong correlation, simultaneous classification may yield dramatic gains in predictive accuracy when compared to conventional approaches to discriminant analysis, which treat the targeted units as independent.
The approach was motivated within the realm of biomedical functional imaging wherein classification performance may be improved by leveraging intra-class interdependence among collections of correlated measurements of biological function. In the considered liver CTp setting, our Bayesian approach facilitates classification via multivariate synthesis of correlated perfusion characteristics (biomarkers for tumor angiogenesis) across neighboring interdependent hepatic regions, yielding a probabilistic basis for detecting the presence of malignant tissues using all of the available information. In addition, the method accommodates unequal misclassification costs and offers seamless incorporation of subjective prior class probabilities that could be adjusted in relation to reader discretion regarding the extent to which morphological features associated with malignancies are conspicuous. The assumption of separability provides interpretability and dramatically reduces the degrees of freedom of the covariance, thereby avoiding high dimensional matrix inversion. However, separable covariance may be inappropriate for data that exhibits region by variate heteroscedasticity, and thus should be assessed (Mitchell et al., 2006). Moreover, the proposed empirical Bayesian implementation was shown to reduce computation time by a factor of 84, with minimal impact to classification performance, facilitating scalability in the presence of a large set of classification targets.
Supplementary Material
Acknowledgments
This research was partially supported by National Cancer Institute grants P50-CA140388, R01-CA157458, R01-CA158113 and P30-CA016672.
Footnotes
Web Appendices, Tables, and Figures referenced in Sections 3–6 as well as software are available with this paper at the Biometrics website on Wiley Online Library.
References
- Brown PJ, Kenward MG, Bassett EE. Bayesian discrimination with longitudinal data. Biostatistics. 2001;2:417–432. doi: 10.1093/biostatistics/2.4.417. [DOI] [PubMed] [Google Scholar]
- Cruz-Mesía R, Quintana FA, Müller P. Semiparametric bayesian classification with longitudinal markers. Journal of the Royal Statistical Society: Series C. 2007;56:119–137. doi: 10.1111/j.1467-9876.2007.00569.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geisser S. Posterior odds for multivariate normal distributions. Journal of the Royal Society Series B Methodological. 1964;26:69–76. [Google Scholar]
- Geisser S, Eddy W. A predictive approach to model selection. Journal of the American Statistical Association. 1979;74:153–160. [Google Scholar]
- Gelfand AE, Dey DK. Bayesian model choice: asymptotics and exact calculations. Journal of the Royal Statistical Society, Series B. 1994;56:501–514. [Google Scholar]
- Haskard KA, Cullis BR, Verbyla AP. Anisotropic matern correlation and spatial anisotropic matern correlation and spatial prediction using reml. Journal of Agricultural, Biological, and Environmental Statistics. 2007;12:147–160. [Google Scholar]
- Lee TY. Functional CT: physiological models. Trends Biotechnol. 2002;20:S3–S10. [Google Scholar]
- Ma C. Spatio-temporal stationary covariance models. Journal of Multivariate Analysis. 2003;86:97–107. [Google Scholar]
- Marshall G, la Cruz-Mesía RD, Quintana FA, Barón AE. Discriminant analysis for longitudinal data with multiple continuous responses and possibly missing data. Biometrics. 2009;65:69–80. doi: 10.1111/j.1541-0420.2008.01016.x. [DOI] [PubMed] [Google Scholar]
- Miles K. Functional CT in Oncology. Eur J Cancer. 2002;38:2079–2084. doi: 10.1016/s0959-8049(02)00386-6. [DOI] [PubMed] [Google Scholar]
- Miles K, Charnsangavej C, Lee F, Horton K, Lee TY. Application of CT in the investigation of angiogenesis in oncology. Acad Radiol. 2000;7:840–850. doi: 10.1016/s1076-6332(00)80632-7. [DOI] [PubMed] [Google Scholar]
- Mitchell MW, Genton MG, Gumpertz ML. A likelihood ratio test for separability of covariances. Journal of Multivariate Analysis. 2006;97:1025–1043. [Google Scholar]
- Ng C, Hobbs B, Chandler A, Anderson E, Herron D, Charnsangavej C, Yao J. Metastases to the liver from neuroendocrine tumors: Effect of duration of scan acquisition on CT perfusion values. Radiology. 2013;269:758–767. doi: 10.1148/radiol.13122708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ripley BD. Pattern Recognition and Neural Networks. Cambridge University Press; 1996. [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, Linde AVD. Bayesian measures of model complexity and fit (with discussion) Journal of the Royal Statistical Society, Series B. 2002;64:583–639. [Google Scholar]
- Srivastava S, Gupta MR, Frigyik BA. Bayesian quadratic discriminant analysis. Journal of Machine Learning Research. 2007;8:1277–1305. [Google Scholar]
- Stein ML. Interpolation of Spatial Data. Springer; New York: 1999. [Google Scholar]
- Stewart EE, Chen X, Hadway J, Lee T. Hepatic perfusion in a tumor model using DCE-CT: an accuracy and precision study. Phys Med Biol. 2008;53:4249–4267. doi: 10.1088/0031-9155/53/16/003. [DOI] [PubMed] [Google Scholar]
- Zhu H, Brown PJ, Morris JS. Robust classification of functional and quantitative image data using functional mixed models. Biometrics. 2011;68:1260–1268. doi: 10.1111/j.1541-0420.2012.01765.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.