Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 1993 Feb 1;90(3):833–837. doi: 10.1073/pnas.90.3.833

Twist and writhe of a DNA loop containing intrinsic bends.

W R Bauer 1, R A Lund 1, J H White 1
PMCID: PMC45764  PMID: 8430093

Abstract

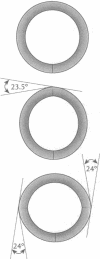
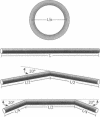
The finite-element method of solid mechanics is applied to calculation of the three-dimensional structure of closed circular DNA, modeled as an elastic rod subject to large motions. The results predict the minimum elastic energy conformation of a closed loop of DNA as a function of relaxed equilibrium configuration and linking number (Lk). We apply the method to four different starting states: a straight rod, two rods containing either one or two 20 degrees bends, and a circular O-ring. The results, here at low superhelix density, show the changes in writhe (Wr) and in twist (Tw) as Lk is progressively lowered. The presence of even a single intrinsic bend reduces significantly the linking number change at which Wr first appears, compared to an initially straight, bend-free rod. The presence of two in-phase bends, situated at opposite ends of a diameter, leads to the formation of at least two distinct regions of different but relatively uniform Tw increment. The O-ring begins to writhe immediately upon reduction of Lk, and the Tw increment distribution is sinusoidal along the rod. The mechanics calculations, unlike other theoretical approaches, permit us to calculate Tw and Wr independent of the constraint of constant Lk.

Full text

PDF

Images in this article

834Image
on p.834
834Image
on p.834

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Benham C. J. Geometry and mechanics of DNA superhelicity. Biopolymers. 1983 Nov;22(11):2477–2495. doi: 10.1002/bip.360221112. [DOI] [PubMed] [Google Scholar]
  2. Benham CJ. Onset of writhing in circular elastic polymers. Phys Rev A Gen Phys. 1989 Mar 1;39(5):2582–2586. doi: 10.1103/physreva.39.2582. [DOI] [PubMed] [Google Scholar]
  3. Hao M. H., Olson W. K. Molecular modeling and energy refinement of supercoiled DNA. J Biomol Struct Dyn. 1989 Dec;7(3):661–692. doi: 10.1080/07391102.1989.10508513. [DOI] [PubMed] [Google Scholar]
  4. Horowitz D. S., Wang J. C. Torsional rigidity of DNA and length dependence of the free energy of DNA supercoiling. J Mol Biol. 1984 Feb 15;173(1):75–91. doi: 10.1016/0022-2836(84)90404-2. [DOI] [PubMed] [Google Scholar]
  5. Klenin K. V., Vologodskii A. V., Anshelevich V. V., Klishko VYu, Dykhne A. M., Frank-Kamenetskii M. D. Variance of writhe for wormlike DNA rings with excluded volume. J Biomol Struct Dyn. 1989 Feb;6(4):707–714. doi: 10.1080/07391102.1989.10507731. [DOI] [PubMed] [Google Scholar]
  6. Le Bret M. Catastrophic variation of twist and writhing of circular DNAs with constraint? Biopolymers. 1979 Jul;18(7):1709–1725. doi: 10.1002/bip.1979.360180710. [DOI] [PubMed] [Google Scholar]
  7. Lobell R. B., Schleif R. F. AraC-DNA looping: orientation and distance-dependent loop breaking by the cyclic AMP receptor protein. J Mol Biol. 1991 Mar 5;218(1):45–54. doi: 10.1016/0022-2836(91)90872-4. [DOI] [PubMed] [Google Scholar]
  8. Lobell R. B., Schleif R. F. DNA looping and unlooping by AraC protein. Science. 1990 Oct 26;250(4980):528–532. doi: 10.1126/science.2237403. [DOI] [PubMed] [Google Scholar]
  9. Manning G. S. Three persistence lengths for a stiff polymer with an application to DNA B-Z junctions. Biopolymers. 1988 Oct;27(10):1529–1542. doi: 10.1002/bip.360271002. [DOI] [PubMed] [Google Scholar]
  10. Marini J. C., Levene S. D., Crothers D. M., Englund P. T. Bent helical structure in kinetoplast DNA. Proc Natl Acad Sci U S A. 1982 Dec;79(24):7664–7668. doi: 10.1073/pnas.79.24.7664. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Schleif R. DNA looping. Science. 1988 Apr 8;240(4849):127–128. doi: 10.1126/science.3353710. [DOI] [PubMed] [Google Scholar]
  12. Schlick T., Olson W. K. Supercoiled DNA energetics and dynamics by computer simulation. J Mol Biol. 1992 Feb 20;223(4):1089–1119. doi: 10.1016/0022-2836(92)90263-j. [DOI] [PubMed] [Google Scholar]
  13. Shimada J., Yamakawa H. Moments for DNA topoisomers: the helical wormlike chain. Biopolymers. 1988 Apr;27(4):657–673. doi: 10.1002/bip.360270409. [DOI] [PubMed] [Google Scholar]
  14. Shimada J., Yamakawa H. Statistical mechanics of DNA topoisomers. The helical worm-like chain. J Mol Biol. 1985 Jul 20;184(2):319–329. doi: 10.1016/0022-2836(85)90383-3. [DOI] [PubMed] [Google Scholar]
  15. Shore D., Baldwin R. L. Energetics of DNA twisting. I. Relation between twist and cyclization probability. J Mol Biol. 1983 Nov 15;170(4):957–981. doi: 10.1016/s0022-2836(83)80198-3. [DOI] [PubMed] [Google Scholar]
  16. Tan R. K., Harvey S. C. Molecular mechanics model of supercoiled DNA. J Mol Biol. 1989 Feb 5;205(3):573–591. doi: 10.1016/0022-2836(89)90227-1. [DOI] [PubMed] [Google Scholar]
  17. Travers A. A. DNA conformation and protein binding. Annu Rev Biochem. 1989;58:427–452. doi: 10.1146/annurev.bi.58.070189.002235. [DOI] [PubMed] [Google Scholar]
  18. Ulanovsky L., Bodner M., Trifonov E. N., Choder M. Curved DNA: design, synthesis, and circularization. Proc Natl Acad Sci U S A. 1986 Feb;83(4):862–866. doi: 10.1073/pnas.83.4.862. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. White J. H., Bauer W. R. Applications of the twist difference to DNA structural analysis. Proc Natl Acad Sci U S A. 1988 Feb;85(3):772–776. doi: 10.1073/pnas.85.3.772. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. White J. H., Bauer W. R. Calculation of the twist and the writhe for representative models of DNA. J Mol Biol. 1986 May 20;189(2):329–341. doi: 10.1016/0022-2836(86)90513-9. [DOI] [PubMed] [Google Scholar]
  21. Wu H. M., Crothers D. M. The locus of sequence-directed and protein-induced DNA bending. Nature. 1984 Apr 5;308(5959):509–513. doi: 10.1038/308509a0. [DOI] [PubMed] [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES