Skip to main content
PMC home page
Immunology logoLink to Immunology
. 2015 Aug 2;146(2):271–280. doi: 10.1111/imm.12500

Mathematical model reveals how regulating the three phases of T-cell response could counteract immune evasion

Tommaso Lorenzi 1,†,✉, Rebecca H Chisholm 2,†, Matteo Melensi 3, Alexander Lorz 4,5,6, Marcello Delitala 7
PMCID: PMC4582968  PMID: 26119966

Abstract

T cells are key players in immune action against the invasion of target cells expressing non-self antigens. During an immune response, antigen-specific T cells dynamically sculpt the antigenic distribution of target cells, and target cells concurrently shape the host’s repertoire of antigen-specific T cells. The succession of these reciprocal selective sweeps can result in ‘chase-and-escape’ dynamics and lead to immune evasion. It has been proposed that immune evasion can be countered by immunotherapy strategies aimed at regulating the three phases of the immune response orchestrated by antigen-specific T cells: expansion, contraction and memory. Here, we test this hypothesis with a mathematical model that considers the immune response as a selection contest between T cells and target cells. The outcomes of our model suggest that shortening the duration of the contraction phase and stabilizing as many T cells as possible inside the long-lived memory reservoir, using dual immunotherapies based on the cytokines interleukin-7 and/or interleukin-15 in combination with molecular factors that can keep the immunomodulatory action of these interleukins under control, should be an important focus of future immunotherapy research.

Keywords: mathematical modelling, memory, T cells, theoretical immunology, vaccination

Introduction

Antigen-specific T cells and target cells (i.e. cells expressing non-self antigens) can be viewed as predator and prey populations that are engaged in a continuous tussle.1–5 To catch target cells, T cells need to be efficient hunters. On the other hand, target cells must be able to escape predation by antigen-specific T cells, if enough of them are to survive and colonize host tissues.

Three main phases encompass the immune response that is orchestrated by antigen-specific T cells: expansion, contraction and memory (see Fig.1a). During the first phase, the presence of cells expressing a non-self antigen triggers the clonal expansion of antigen-specific T cells. Ideally, this expansion will continue until the T-cell population has reached the critical mass required to curb the target cell invasion. Thereupon homeostatic regulation mechanisms will induce a contraction in T-cell numbers.6 In this way, the immune response is kept under tight control, and the chance of developing immunopathologies is reduced.7 Following the contraction phase, the number of T cells targeted to the non-self antigen is maintained at a certain level, which can last for a long period of time.8 This reservoir of T cells acts as a safeguard against possible re-exposure to the same non-self antigen. In other words, the immune system has learnt from its past experience and immune memory is established.

Figure 1.

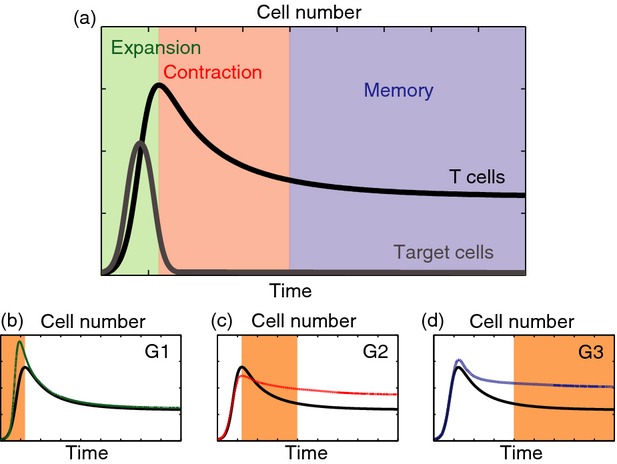
Figure 1

Open in a new tab

Three phases of T-cell responses and their possible therapeutically induced modulations. (a) Schematic illustration of the immune response mediated by antigen-specific T cells. Expansion, contraction and memory phases are highlighted. (b–d) Ad hoc alterations of the three phases of the immune response proposed in ref. 7 as possible strategies to counteract immune evasion. Here, (G1) refers to increasing the number of antigen-specific T cells by acting on the expansion phase, (G2) refers to shortening the duration of the contraction phase to limit T-cell death, and (G3) refers to stabilizing as many T cells as possible inside the long-lived memory reservoir.

Nevertheless, at any given time, the immune system can only support a finite number of antigen-specific T cells. Hence, maintaining a memory reservoir also limits the co-presence of T cells targeted to other non-self antigens.9 This, in turn, provides ecological opportunities for target cells that are able to escape T-cell recognition. Therefore, antigen-specific T cells dynamically sculpt the antigenic distribution of target cells, and target cells concurrently shape the host’s repertoire of antigen-specific T cells.6 Furthermore, the succession of these reciprocal selective sweeps can result in ‘chase-and-escape’ dynamics and lead to immune evasion.10,11

Kaech et al.7 propose that immune evasion can be countered by inducing ad hoc alterations in the three phases of immune response, which are schematized in Fig.1(b–d). In particular, they speculate that therapeutic interventions should achieve the following three goals, if they are to reduce the likelihood of immune evasion:

  1. G1 increase the number of antigen-specific T cells by acting on the expansion phase;

  2. G2 shorten the duration of the contraction phase to limit T-cell death;

  3. G3 stabilize as many T cells as possible inside the long-lived memory reservoir.

To explore these ideas, here we introduce a mathematical model of selection dynamics in a well-mixed system of antigen-specific T cells and target cells during a post-exposure prophylaxis. The treatment starts immediately after exposure of T cells to target cells, and relies on three hypothetical classes of immunotherapeutic agents designed to: stimulate antigen-driven expansion (E-agents); enhance antigen-independent T-cell proliferation (P-agents); interfere with homeostasis to promote self-renewal of antigen-specific T cells (M-agents).

T-cell and target-cell populations are structured by their respective target-antigenic and antigenic expression. Analogous models have previously been used to study, for instance, the co-evolution between pathogens and the host immune system,12,13 cancer immunoediting,14 trade offs associated with ageing in the adaptive immune system,15 and the T-cell mediated autoimmune response.16 In the absence of immunotherapy, the model proves to have validity for providing a consistent qualitative description of the predator–prey dynamics involving antigen-specific T cells and target cells. Therefore, we use the model with immunotherapy to address two fundamental questions that stem from the ideas presented in by Kaech et al.:7 can the hypothetical classes of therapeutic agents under consideration lead to the achievement of goals G1, G2 and G3? Is one therapeutic agent, or a combination of agents, more effective than the others against immune evasion?

Using a mathematical model as an in silico laboratory allows us to quickly and cheaply explore a variety of immunotherapy protocols to predict those that would be the most effective, and that should then be chosen for experimental testing. In particular, our model predicts that the three hypothetical classes of immunotherapies under study (i.e. E-agents, P-agents and M-agents) can lead to the achievement of goals G1 to G3. Moreover, the results of in silico experiments (i.e. numerical simulations) suggest that therapeutic protocols relying on the simultaneous delivery of sufficiently high concentrations of P-agents and M-agents are the most effective of the therapeutic protocols considered here. This implies that the success of an immunotherapy protocol correlates strongly with its ability to shorten the duration of the contraction phase and stabilize as many T cells as possible inside the long-lived memory reservoir.

Materials and methods

We focus on a well-mixed system of antigen-specific T cells and target cells, where: (i) target cells proliferate and die due to competition for limited space and resources; (ii) T cells undergo antigen-independent proliferation; and (iii) T-cell numbers are kept under control through homeostatic regulation mechanisms. In the reference system, interactions between antigen-specific T cells and their targets result in antigen-driven T-cell expansion as well as selective action against target cells. Furthermore, up to three hypothetical classes of immunotherapies can be present, that are respectively designed to stimulate antigen-driven expansion (E-agents), enhance antigen-independent proliferation (P-agents), and interfere with homeostasis to promote self-renewal of antigen-specific T cells (M-agents).

We characterize the state of each T cell by its target-antigenic expression, whereas the state of each target cell is identified by its antigenic expression. The target-antigenic expressions of T cells and the antigenic expressions of target cells are modelled, respectively, by the continuous, real variables v ∈ [0;1] and u ∈ [0;1] (see Fig.2a,b). The population density of T cells at the time instant t > 0 is identified by the function nT(t,v) ≥ 0, whereas the function nC(t,u) ≥ 0 stands for the population density of target cells. The values of nT and nC are in units of per μl. The respective global population densities of T cells and target cells are described by the functions ρT(t) and ρC(t). The infusion rates of E-agents, P-agents and M-agents at time t are modelled by the functions cE(t) ≥ 0, cP(t) ≥ 0 and cM(t) ≥ 0, respectively. The values of cE, cP and cM are in units of pg/μl.

Figure 2.

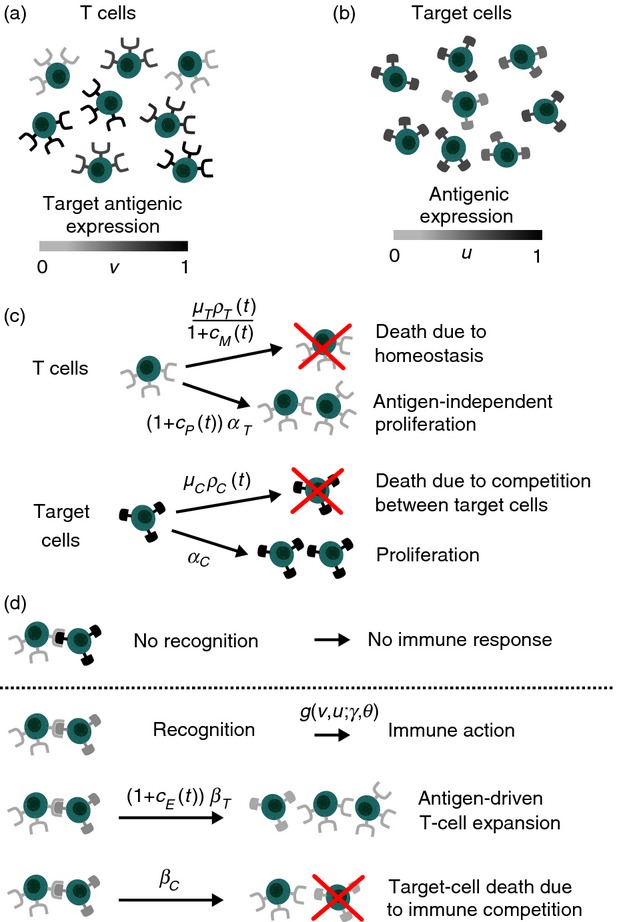
Figure 2

Open in a new tab

Structure of the mathematical model. (a) The target antigenic expression that characterizes each T cell (v) is represented by the colour of the receptors on its surface. (b) Likewise, the antigenic expression that characterizes each target cell (u) is represented by the colour of the antigens on its surface. (c) T cells undergo antigen-independent proliferation at a rate αT and die due to homeostatic pressure at a rate μT ρT(t), while target cells proliferate at a rate αC and die due to competition with other target cells at a rate μC ρC(t). (d) T cells recognize a target cell at rate g if their target antigenic expression is similar enough to the antigenic expression of the target cell (i.e. when the colours of receptors and the colour of antigens match). When this occurs, an immune response is initiated: T-cell expansion occurs at a rate βT and the immune system attacks target cells so that they are killed at a rate βC. The factors [1+cE(t)], [1+cP(t)] and 1/[1+cM(t)] mimic, respectively, the stimulation of antigen-driven expansion by E-agents, the enhancement of antigen-independent proliferation mediated by P-agents, and the promotion of self-renewal due to M-agents.

The functions κE(tf), κP(tf) and κM(tf) stand, respectively, for the total doses of E-agents, P-agents and M-agents that are delivered on the time interval [0;tf], and their sum defines the total delivered dose κ(tf).

We employ the assumptions and the mathematical modelling strategies described below, which are schematized in Fig.2(c,d). These strategies translate into the system of equations provided in the Supporting Information, to which we refer the mathematically inclined reader.

Proliferation and death of target cells

Target cells proliferate at an average rate αC > 0. We assume that a higher number of cells corresponds to less available space and resources; therefore, we let target cells die at rate μC ρC(t), where the parameter μC > 0 models the average rate of death due to competition between target cells.17

Antigen-driven expansion

T cells targeted to the antigenic expression v are able to recognize target cells characterized by an antigenic expression u on the condition that u is sufficiently close to v. Moreover, we assume that recognition can lead to T-cell replication at an average rate βT > 0. Accordingly, we let the rate of clonal expansion ηT(v, u) satisfy the following relations

graphic file with name imm0146-0271-m1.jpg 1

where the parameter θ > 0 stands for the average affinity range of T-cell receptors, and the parameter γ > 0 identifies the maximum affinity.15

Antigen-independent proliferation and homeostatic regulation

T cells undergo antigen-independent proliferation at an average rate αT > 0. Furthermore, we assume that regulation mechanisms induce T-cell death at a rate μT ρT(t), where the parameter μT > 0 identifies the average rate of homeostatic competition.18

Selective action of T cells against their targets

When target cells with the non-self antigenic expression u are recognized by T cells targeted to an antigenic expression v, immune competition takes place. We define the rate of target-cell death due to immune competition as

graphic file with name imm0146-0271-m2.jpg 2

where βC > 0 is the average killing rate of target cells, and, as noted previously, the parameter θ > 0 stands for the average affinity range of T-cell receptors, and the parameter γ > 0 identifies the maximum affinity.15

Therapeutic interventions based on E-agents, P-agents and M-agents

We let the rate of stimulation of antigen-driven expansion mediated by E-agents be proportional to the infusion rate cE(t). Moreover, we assume that P-agents enhance antigen-independent proliferation at a rate proportional to the infusion rate cP(t). Finally, we model the promotion of self-renewal due to M-agents by reducing the rate of T-cell death at a rate proportional to the infusion rate cM(t).

Results

We consider an initial system composed of uniformly distributed T cells together with target cells that are mainly characterized by the antigenic expression corresponding to u = 0. The values assigned to the parameters of the model are derived from experimental literature and are listed in Table1. Under this choice of the initial conditions and of the model’s parameters, the early dynamics of the global population densities resemble those that are usually observed during acute infection, with exponential growth of target cells and consequent expansion of T cells until target cells begin to decay. For each in silico experiment presented below, further technical details are provided in the Supporting Information.

Table 1.

Values and sources of the parameters in the mathematical model

Parameter Biological meaning Value Source
αC Rate of target-cell proliferation 3/day 12,13,19
αT Rate of antigen-independent T-cell proliferation 5 × 10−2/day 20,21
μC Rate of death due to competition between target cells 1·5 × 10−6 μl/day ad hoc
μT Rate of T-cell death due to homeostatic regulation 2·5 × 10−6 μl/day ad hoc
βC Killing rate of target cells by T cells 1 × 10−5 μl/day 12,13,19
βT Rate of T-cell replication following recognition 3 × 10−5 μl/day 12
θ Average affinity range of T-cell receptors 1 × 10−3 ÷ 1 × 10−1  12,22
γ Maximum affinity 1 × 10−2 ÷ 3 15,19
Open in a new tab

The values of the parameters αC, αT, βC and βT are consistent with previous measurement and estimation studies on the immune response mediated by T cells.12,13,19–21 The values of the parameters μC and μT are selected to guarantee that the carrying capacities of the two cell populations are biologically consistent. The range of values of the parameter θ is consistent with experimental estimations of the precursor frequency of T cells,22 and it is computed through a strategy analogous to that presented in ref. 12. The values of the parameter γ are consistent with those used in refs 15,19.

The model reproduces a range of observed behaviours of the adaptive immune response

We explore the dynamics of T cells and target cells across a range of virtual scenarios corresponding to different biologically reasonable values of the parameters γ (i.e. the maximum affinity) and θ (i.e. the average affinity range of T-cell receptors). Varying these parameters changes the extent to which T cells can recognize target cells, which affects both the rate of clonal expansion and the rate of target cell death due to T cells. To this end, we perform numerical simulations while holding all parameters constant except for γ and θ, and we record the resulting dynamics of the population densities nT and nC, and of the global population densities ρT and ρC.

When both γ and θ are large (i.e. high maximum affinity and broad affinity range), in response to an exponential growth of target cells, the population of antigen-specific T cells embarks on a proliferative expansion in number that continues until the T cells have reached the critical mass required to push the population of target cells towards extinction. Proliferation is followed by the transition to a contraction phase, which is characterized by a decline of the concentration of antigen-specific T cells to a level corresponding to the maintenance of immunological memory, see Fig.3(a). Overall, numerical simulations in this parameter regime display the succession of the expansion, contraction and memory phases that follow the exposure of T cells to target cells. The transition from the contraction to the memory phase is marked by the fact that the slope of the curve corresponding to the global population density of T cells approaches zero. The duration of each phase is consistent with average kinetics of CD8 T-cell response to acute viral infections23,24 in general, and with existing data on the dynamics of CD8 T-cell response to lymphocytic choriomeningitis virus (LCMV)25 in particular.

Figure 3.

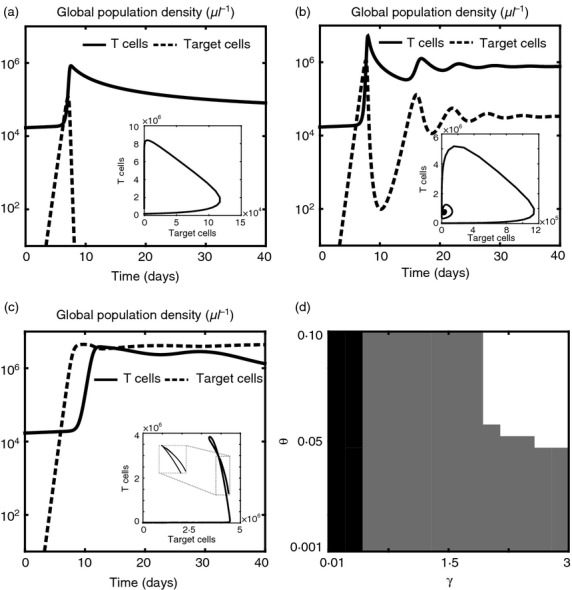
Figure 3

Open in a new tab

The model reproduces a range of observed behaviours of the adaptive immune response. (a–c) Sample dynamics of the global population densities of T cells (solid lines) and target cells (dashed lines), in the absence of therapeutic agents, for different values of the maximum affinity γ and the average affinity range of T-cell receptors θ. In all cases, the early dynamics of the global population densities resemble those that are usually observed during acute infection, with exponential growth of target cells and consequent expansion of T cells until target cells begin to decay. When both γ and θ are large (a), early clearance occurs. For intermediate values of γ and θ (b), the global population densities of T cells and target cells oscillate until they converge to a state of chronic infection, with a smaller number of target cells being kept under control by a larger number of T cells. When both γ and θ are low (c), early immune escape takes place, and the population of target cells keeps expanding until saturation. Insets of (a–c): corresponding trajectories in the (ρC,ρT) plane. (d) Phase diagram showing the regions of the (γ,θ) plane corresponding to early clearance (white), chronic infection (grey) and early escape (black). Although the specific boundaries of these regions can vary according to the values of the other parameters of the model, the trends of the global population densities of T cells and target cells in the case of early clearance, chronic infection and early escape remain qualitatively similar to those shown in (a–c).

For intermediate values of γ and θ, the global population densities of T cells and target cells oscillate over time – T cells undergo a succession of expansion and contraction phases that result in an alternate decay and growth of target cells – and converge to a state of chronic infection, with a smaller number of target cells being kept under control by a larger number of T cells, see Fig.3(b). In this parameter regime, the two cell populations undergo reciprocal selective sweeps that result in the emergence of ‘chase-and-escape’ dynamics. This is highlighted by the results presented in Fig.4, which track the time-evolution of the two population densities. More specifically, clonal expansion leads to a rapid proliferation of T cells that are targeted to the antigens mostly expressed by target cells, whereas homeostatic regulation induces formerly stimulated T cells to decay; in turn, the selective pressure exerted by T cells causes the selection of those target cells that are able to evade immune predation. Immune competition pushes the initially monomorphic target cell population to become, in succession, dimorphic (lower sub-panel), trimorphic (central sub-panel) and then tetramorphic (upper sub-panel). The dynamics of T cells follows a similar pattern, but with a shift corresponding to the time required for the T cells to adapt to the antigenic distribution of target cells. The time scale of the co-evolutionary dynamics between target cells and T cells is consistent with the results of in silico experiments reported elsewhere.12 Moreover, the decay of formerly stimulated T cells during chronic infection is consistent with experimental findings suggesting that, to maintain flexibility to respond against new non-self antigens, antigen-independent memory T cells do not develop during chronic infection.26

Figure 4.

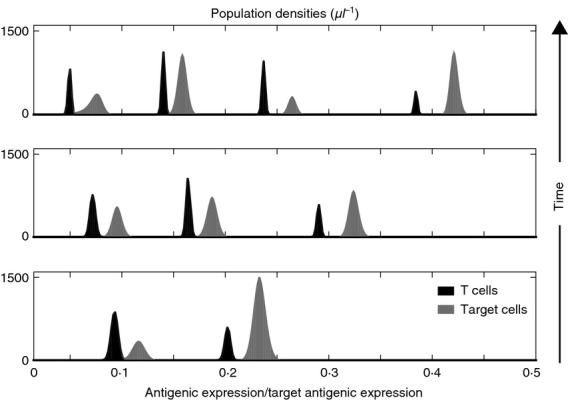
Figure 4

Open in a new tab

‘Chase-and-escape’ dynamics of antigen-specific T cells and target cells during chronic infection. Population densities of T cells (black) and target cells (grey) at t = 130 days (bottom panel), t = 400 days (central panel) and t = 1000 days (top panel), in the absence of therapeutic agents, for a choice of the maximum affinity γ and the average affinity range of T-cell receptors θ corresponding to chronic infection.

Finally, when both γ and θ are low (i.e. low maximum affinity and narrow affinity ranges), it takes too long for the population density of T cells to adapt to the antigenic distribution of target cells, and early immune escape occurs. Figure3(c) tracks the time-evolution of the two population densities for a choice of γ and θ in this parameter regime, and shows that, in the early stages of infection, the global population density of target cells overtakes the global population density of T cells, and keeps expanding until saturation.

The regions of the (γ,θ) plane corresponding to early clearance, chronic infection and early escape coincide, respectively, with the white, grey and black areas in the phase diagram of Fig.3(d). Sample dynamics of the global population densities of target cells and T cells in these three parameter ranges are presented in Fig.3(a–c). Although the specific boundaries of these areas can vary according to the values of the other parameters of the model, the trends of the global population densities of T cells and target cells in the case of early clearance, chronic infection and early escape remain qualitatively similar to those shown in Fig.3(a–c).

E-agents, P-agents and M-agents can accomplish goals G1 to G3

Taken together, the results that we have presented in the previous section suggest that the model has validity for providing a consistent qualitative description of the predator–prey dynamics involving antigen-specific T cells and target cells. Therefore, we use this model to systematically determine how each of the three types of therapeutic agents (in isolation) affects the immune response. We re-ran the previous simulations – for a choice of the maximum affinity γ and the average affinity range of T-cell receptors θ corresponding to early clearance – under constant infusion of either E-agents, P-agents or M-agents. Figure5 displays: sample kinetics of the concentration of target cells with antigenic expressions close to the antigenic expression that is most common at the beginning of the in silico experiments; the concentration of T cells targeted to those antigenic expressions. These results demonstrate that, compared with the case without treatment: E-agents lead to higher numbers of T cells at the acme of the expansion phase (see Fig.5b); P-agents reduce the duration of the contraction phase and favour the formation of a more populous memory reservoir (see Fig.5c); M-agents allow a larger number of T cells to stabilize during the memory phase (see Fig.5d). The shortening of the contraction phase due to P-agents is justified by noting that the enhancement of antigen-independent proliferation can promote an acceleration of the T-cell dynamics when the number of T cells is sufficiently high, that is, right after the expansion phase. Based on these results we can deduce that E-agents are capable of achieving goal G1 (compare the results in Fig.5b with the curves in Fig.1b), P-agents can achieve goal G2 (compare the results in Fig.5c with the curves in Fig.1c), and M-agents contribute to realizing goal G3 (compare the results in Fig.5d with the curves in Fig.1d).

Figure 5.

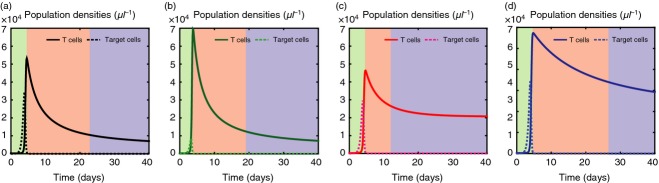
Figure 5

Open in a new tab

E-agents, P-agents and M-agents can accomplish goals G1 to G3. Sample kinetics of: the concentration of target cells with antigenic expressions close to the antigenic expression that is most common at the beginning of the in silico experiments (dashed lines); the concentration of T cells targeted to those antigenic expressions (solid lines). Black lines in (a), green lines in (b), red lines in (c) and blue lines in (d) refer, respectively, to the case without immunotherapy and under constant infusion of either E-agents, P-agents or M-agents. All curves refer to the same choice of the maximum affinity γ and the average affinity range of T-cell receptors θ, which corresponds to early clearance. The green, red and blue areas highlight, respectively, the expansion, contraction and memory phases. Compared with the case without treatment: E-agents lead to higher numbers of T cells at the acme of the expansion phase; P-agents reduce the duration of the contraction phase and favour the formation of a more populous memory reservoir; M-agents allow a larger number of T cells to stabilize during the memory phase.

The most effective immunotherapy protocols rely on the simultaneous infusion of P-agents and M-agents

Finally, we used the model to test the efficacy of different therapeutic protocols that rely on the infusion of E-agents, P-agents and M-agents separately and in combination.

The results are presented in Fig.6 and show the time-average of the global population density of T cells (see Fig.6a) and target cells (see Fig.6b) for several different doses of therapeutic agents κ (see Fig.6c). These results have been obtained under constant infusion of therapeutic agents; analogous results hold for periodic infusion (see Supporting Information, Fig. S1). Figure6 and Fig. S1 refer to some values of the maximum affinity γ and the average affinity range of T-cell receptors θ corresponding to chronic infection; we verified that the same qualitative dynamics hold for values of γ and θ that correspond to early clearance and early escape.

Figure 6.

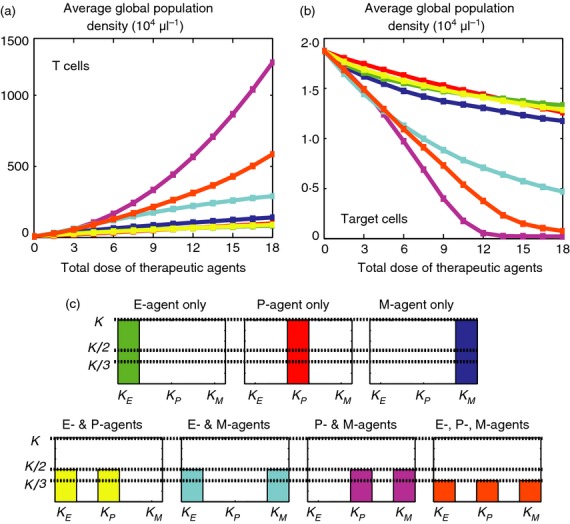
Figure 6

Open in a new tab

The most effective immunotherapy protocols rely on the simultaneous infusion of P-agents and M-agents. (a) Time-average of the global population density of T cells for increasing total doses of therapeutic agents κ (in units of 103 pg/μl). (b) Time-average of the global population density of target cells for increasing total doses of therapeutic agents κ (in units of 103 pg/μl). (a, b) Different colours correspond to different therapeutic protocols that rely on the constant infusion of E-agents, P-agents and M-agents separately and in combination (i.e. different values of κE, κP and κM). These results refer to some values of the maximum affinity γ and the average affinity range of T-cell receptors θ that correspond to chronic infection. The same qualitative dynamics can be observed for values of γ and θ corresponding to early clearance and early escape. (c) Illustration of the protocols in use during the in silico experiments of (a, b). Colours correspond to the plots shown in (a, b). All therapeutic protocols under consideration lead to an increase in the time-average of the total number of T cells and a reduction in the time-average of the total number of target cells. However, when the infusion rates of therapeutic agents are sufficiently high, the protocols relying on the simultaneous infusion of P-agents and M-agents lead to a larger population of T cells and to a significantly smaller population of target cells.

All therapeutic protocols under consideration lead to an increase in the time-average of the total number of T cells and a reduction in the time-average of the total number of target cells. In all cases, higher doses of therapeutic agents correspond to higher numbers of T cells and lower numbers of target cells. However, when the infusion rates of therapeutic agents are sufficiently high, the protocols relying on the simultaneous infusion of P-agents and M-agents are more effective than the others, because they lead to a larger population of T cells and to a significantly smaller population of target cells.

To verify the robustness of these conclusions with respect to the choice of the parameters, we perform a mathematical study of the global population density of T cells under the therapeutic protocols presented in Fig.6(c). The results established by Theorem 1.2 in the Supporting Information show that, if the infusion rates and the exposure time are larger than some threshold values, the aforementioned conclusions about the kinetics of T cells hold for any values of the model’s parameters.

It is then natural to wonder what could be possible candidates for P-agents and M-agents in the clinical setting. Although we discuss this point in more detail in the next section, we mention here that key homeostatic cytokines such as interleukin-7 (IL-7) and IL-15 could play the roles of P-agents and M-agents. In fact, although not much is known about the ability of exogenously administered cytokines to affect the formation of memory T cells, clues to the potential utility of IL-7 and IL-15 to control this process can be taken from experimental evidence. For instance, synergistic signalling from both IL-7 and IL-15 promote the formation of memory CD8 T cells,27 whereas increased levels of these interleukins can effectively enhance antigen-independent proliferation and self-renewal of CD4 and CD8 T cells in vivo.28–33

In this regard, we note that, for the initial population densities and the parameter values corresponding to Fig.6, the threshold for the infusion rate falls within the range of infusion rates used by Alves et al.34 to study the in vitro response of CD4 and CD8 T cells to IL-15. The corresponding threshold for the exposure time is compatible, for instance, with the duration of the average response of CD8 T cells to LCMV.25

Discussion and conclusions

To counteract immune evasion, it has been proposed that future immunotherapy protocols will need to achieve three goals (see G1 to G3),7 each relating to T-cell dynamics during a different phase of the immune response. Here, our aim was to test this hypothesis using a mathematical model, with parameters derived from experimental literature, that considers the immune response as a selection contest between T cells and target cells.

In our model, we have considered antigen-specific T cells as the primary tool of the immune system, and as one population structured by target antigenic expression. We chose not to split the T-cell population into different stages of differentiation, including naive, effector and memory T cells, to avoid having to specify the lineage of T-cell development, which is still not fully understood. However, if future experiments shed light on T-cell lineage, then it would be straightforward to extend the model to include additional sub-populations of T cells. Nevertheless, the outcomes of our mathematical model reproduce a range of observed behaviours of the adaptive immune response to viral infections, and are consistent with average expectations of the phenotypic co-evolution between T cells and target cells. Importantly, the model incorporates the actions of three classes of theoretical therapeutic agents (E-agents, P-agents and M-agents) which, we showed, are able to achieve goals G1 to G3. More specifically, stimulating clonal expansion through E-agents can achieve goal G1. Goal G2 can be accomplished by enhancing antigen-independent proliferation through P-agents which, together with M-agents (that promote self-renewal of antigen-specific T cells), also contribute to the achievement of goal G3.

Our model is not intended to provide a quantitative recommendation for the timing and duration of immunotherapy. Rather, its intention is to quickly predict which immunotherapy protocols are more likely to succeed (and should then be chosen for experimental testing); this is a key advantage of an in silico approach. In this regard, the main prediction of our model is that, ceteris paribus, therapeutic protocols relying on the simultaneous delivery of sufficiently high concentrations of P-agents and M-agents are the most effective, out of those considered here, at pushing the target-cell population towards extinction. Moreover, as P-agents and M-agents both act to increase the size of the long-lived memory T-cell reservoir, this result highlights the important role played by immune memory in thwarting immune evasion.

Therefore, we conclude that the simultaneous achievement of goals G2 and G3 – shortening the duration of the contraction phase and stabilizing as many T cells as possible inside the long-lived memory reservoir – should be an important focus of future research into immunotherapy protocols aimed at curbing infections, preventing disease and fighting carcinogenesis. In this respect, we propose that key homeostatic cytokines such as IL-7 and IL-15 could play the roles of P-agents and M-agents.

Several studies have reported that treatment with exogenous IL-7 and IL-15 can augment the generation of memory T cells by limiting the contraction of CD8 effector T cells.25 For example, it has been demonstrated that continuous infusion of IL-7 and/or IL-15 throughout the effector and contraction phases increases the generation of CD8 memory T cells.35–38 Furthermore, in a separate study on the effects of IL-7 treatment on the immune response to LCMV in mice, it was shown that infusion of this interleukin during the contraction phase of the T-cell response could augment the accumulation of functional viral-specific CD8 memory T cells.39 Finally, IL-15 administered in cynomolgus macaques to treat acute simian immunodeficiency virus infection was found to increase the number of effector memory CD8 T cells.40

Although mice and primates generally tolerate IL-7 and IL-15 therapy with no detectable side effects, a single-agent therapy relying on the administration of IL-7 and/or IL-15 may suffer from dysregulated immune reactions associated with cytokine storm,41 and may increase the chance of developing immunopathologies. Therefore, we propose a dual immunotherapy approach by employing IL-7 and IL-15 in combination with molecular factors, such as CTLA4Ig42 and OX40 inhibitors,43 which indirectly keep the immunomodulatory action of these interleukins under control by inhibiting the proliferation of memory T cells without affecting their viability. For instance, it has been shown that CTLA4Ig can alleviate ongoing autoimmunity in animal models,44 and it has proven to be clinically effective in treating diseases that are recognized to be driven by memory T cells45 such as rheumatoid arthritis46 and psoriasis.47 On the other hand, it has been demonstrated that blocking OX40 signalling decreases the memory T-cell pool,48 and the inhibition of OX40 ligand significantly reduces atherosclerotic lesions in mice.49,50

Authors’ Contributions

TL performed mathematical study of the model, and was involved in interpretation of results and drafting of the manuscript. RC carried out data processing, and was involved in interpretation of results and drafting of the manuscript. MM made substantial contributions to interpretation of data and critical revision of the manuscript. AL performed mathematical study of the model, made substantial contributions to the critical revision of the manuscript, and coordinated the project. MD made substantial contributions to critical revision of the manuscript, and coordinated the project. All authors gave final approval for publication.

Grant Support

This work was supported by the French National Research Agency through the ‘ANR blanche’ project Kibord [ANR-13-BS01-0004]. TL was also supported by the Fondation Sciences Mathematiques de Paris through a grant overseen by the French National Re-search Agency [ANR-10-LABX-0098], and by the Hadamard Mathematics Labex, backed by the Fondation Mathematique Jacques Hadamard, through a grant overseen by the French National Research Agency [ANR-11-LABX-0056-LMH].

Disclosures

The authors disclose no potential conflicts of interest.

Supporting Information

Figure S1. The most effective immunotherapy protocols rely on the simultaneous infusion of P-agents and M-agents.

imm0146-0271-sd1.eps (425.4KB, eps)

Figure S2. Graphical representation of the result established by Theorem 1.2.

imm0146-0271-sd2.eps (1.7MB, eps)

Appendix S1. Mathematical model, details of the numerical results and analysis of the model.

imm0146-0271-sd3.pdf (311.3KB, pdf)

References

  1. Komarova NL, Barnes E, Klenerman P, Wodarz D. Boosting immunity by antiviral drug therapy: a simple relationship among timing, efficacy, and success. Proc Natl Acad Sci USA. 2003;100:1855–60. doi: 10.1073/pnas.0337483100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Iwasa Y, Michor F, Nowak M. Some basic properties of immune selection. J Theor Biol. 2004;229:179–88. doi: 10.1016/j.jtbi.2004.03.013. [DOI] [PubMed] [Google Scholar]
  3. Wodarz D. Ecological and evolutionary principles in immunology. Ecol Lett. 2006;9:694–705. doi: 10.1111/j.1461-0248.2006.00921.x. [DOI] [PubMed] [Google Scholar]
  4. Lever M, Maini PK, van der Merwe PA, Dushek O. Phenotypic models of T cell activation. Nat Rev Immunol. 2014;14:619–29. doi: 10.1038/nri3728. [DOI] [PubMed] [Google Scholar]
  5. Frascoli F, Kim PS, Hughes BD, Landman KA. A dynamical model of tumour immunotherapy. Math Biosci. 2014;253:50–62. doi: 10.1016/j.mbs.2014.04.003. [DOI] [PubMed] [Google Scholar]
  6. Garrod KR, Moreau HD, Garcia Z, Lemaître F, Bouvier I, Albert ML, Bousso P. Dissecting T cell contraction in vivo using a genetically encoded reporter of apoptosis. Cell Rep. 2012;2:1438–47. doi: 10.1016/j.celrep.2012.10.015. [DOI] [PubMed] [Google Scholar]
  7. Kaech SM, Wherry EJ, Ahmed R. Effector and memory T-cell differentiation: implications for vaccine development. Nat Rev Immunol. 2002;2:251–62. doi: 10.1038/nri778. [DOI] [PubMed] [Google Scholar]
  8. Zinkernagel RM, Bachmann MF, Kündig TM, Oehen S, Pirchet H, Hengartner H. On immunological memory. Annu Rev Immunol. 1996;14:333–67. doi: 10.1146/annurev.immunol.14.1.333. [DOI] [PubMed] [Google Scholar]
  9. Franceschi C, Bonafe M, Valensin S. Human immunosenescence: the prevailing of innate immunity, the failing of clonotypic immunity, and the filling of immunological space. Vaccine. 2000;18:1717–20. doi: 10.1016/s0264-410x(99)00513-7. [DOI] [PubMed] [Google Scholar]
  10. Phillips RE. Immunology taught by Darwin. Nat Immunol. 2002;3:987–9. doi: 10.1038/ni1102-987. [DOI] [PubMed] [Google Scholar]
  11. Restif O, Grenfell BT. Vaccination and the dynamics of immune evasion. J R Soc Interface. 2007;4:143–53. doi: 10.1098/rsif.2006.0167. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Schlesinger KJ, Stromberg SP, Carlson JM. Coevolutionary immune system dynamics driving pathogen speciation. PLoS ONE. 2014;9:e102821. doi: 10.1371/journal.pone.0102821. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Stromberg SP, Antia R. On the role of CD8 T cells in the control of persistent infections. Biophys J. 2012;103:1802–10. doi: 10.1016/j.bpj.2012.07.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Delitala M, Lorenzi T. Recognition and learning in a mathematical model for immune response against cancer. Discrete Contin Dyn Syst Ser B. 2013;18:891–914. [Google Scholar]
  15. Stromberg SP, Carlson J. Robustness and fragility in immunosenescence. PLoS Comput Biol. 2006;2:e160. doi: 10.1371/journal.pcbi.0020160. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Delitala M, Dianzani U, Lorenzi T, Melensi M. A mathematical model for immune and autoimmune response mediated by T cells. Comput Math Appl. 2013;66:1010–23. [Google Scholar]
  17. Williams PD. Darwinian interventions: taming pathogens through evolutionary ecology. Trends Parasitol. 2010;26:83–92. doi: 10.1016/j.pt.2009.11.009. [DOI] [PubMed] [Google Scholar]
  18. Surh CD, Sprent J. Homeostasis of naive and memory T cells. Immunity. 2008;29:848–62. doi: 10.1016/j.immuni.2008.11.002. [DOI] [PubMed] [Google Scholar]
  19. Stromberg SP, Carlson JM. Diversity of T-cell responses. Phys Biol. 2013;10:025002. doi: 10.1088/1478-3975/10/2/025002. [DOI] [PubMed] [Google Scholar]
  20. de Pillis L, Fister KR, Gu W, Collins C, Daub M, Gross D, Moore J, Preskill B. Mathematical model creation for cancer chemo-immunotherapy. Comput Math Methods Med. 2009;10:165–84. [Google Scholar]
  21. Hellerstein L, Hanley MB, Cesar D, et al. Directly measured kinetics of circulating T lymphocytes in normal and HIV-1-infected humans. Nat Med. 1999;5:83–9. doi: 10.1038/4772. [DOI] [PubMed] [Google Scholar]
  22. Blattman JN, Antia R, Sourdive DJD, Wang X, Kaech SM, Murali-Krishna K, Altman JD, Ahmed R. Estimating the precursor frequency of naive antigen-specific CD8 T cells. J Exp Med. 2002;195:657–64. doi: 10.1084/jem.20001021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kaech SM, Cui W. Transcriptional control of effector and memory CD8+ T cell differentiation. Nat Rev Immunol. 2012;12:749–61. doi: 10.1038/nri3307. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kurtulus S, Tripathi P, Hildeman DA. Protecting and rescuing the effectors: roles of differentiation and survival in the control of memory T cell development. Front Immunol. 2013;3:404. doi: 10.3389/fimmu.2012.00404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Purton JF, Martin CE, Surh CD. Enhancing T cell memory: IL-7 as an adjuvant to boost memory T-cell generation. Immunol Cell Biol. 2008;86:385–6. doi: 10.1038/icb.2008.30. [DOI] [PubMed] [Google Scholar]
  26. Wherry EJ, Barber DL, Kaech SM, Blattman JN, Ahmed R. Antigen-independent CD8 T cells do not develop during chronic viral infection. Proc Natl Acad Sci USA. 2008;101:16004–9. doi: 10.1073/pnas.0407192101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Buentke E, Mathiot A, Tolaini M, Di Santo J, Zamoyska R, Seddon B. Do CD8 effector cells need IL-7R expression to become resting memory cells? Blood. 2006;108:1949–56. doi: 10.1182/blood-2006-04-016857. [DOI] [PubMed] [Google Scholar]
  28. Vella AT, Dow S, Potter TA, Kappler J, Marrack P. Cytokine-induced survival of activated T cells in vitro and in vivo. Proc Natl Acad Sci USA. 1998;95:3810–5. doi: 10.1073/pnas.95.7.3810. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Yajima T, Nishimura H, Ishimitsu R, Watase T, Busch DH, Pamer EG, Kuwano H, Yoshikai Y. Overexpression of IL-15 in vivo increases antigen-driven memory CD8+ T cells following a microbe exposure. J Immunol. 2002;168:1198–203. doi: 10.4049/jimmunol.168.3.1198. [DOI] [PubMed] [Google Scholar]
  30. Khan IA, Casciotti L. IL-15 prolongs the duration of CD8+ T cell-mediated immunity in mice infected with a vaccine strain of Toxoplasma gondii. J Immunol. 1999;163:4503–9. [PubMed] [Google Scholar]
  31. Maeurer MJ, Trinder P, Hommel G, Walter W, Freitag K, Atkins D, Störkel S. Interleukin-7 or interleukin-15 enhances survival of Mycobacterium tuberculosis-infected mice. Infect Immun. 2000;68:2962–70. doi: 10.1128/iai.68.5.2962-2970.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Kraynyak KA, Kutzler MA, Cisper NJ, Laddy DJ, Morrow MP, Waldmann TA, Weiner DB. Plasmid-encoded interleukin-15 receptor enhances specific immune responses induced by a DNA vaccine in vivo. Hum Gene Ther. 2009;20:1143–56. doi: 10.1089/hum.2009.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. O’Connor AM, Crawley AM, Angel JB. Interleukin-7 enhances memory CD8+ T-cell recall responses in health but its activity is impaired in human immunodeficiency virus infection. Immunology. 2010;131:525–36. doi: 10.1111/j.1365-2567.2010.03325.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Alves NL, Hooibrink B, Arosa FA, van Lier RA. IL-15 induces antigen-independent expansion and differentiation of human naive CD8+ T cells in vitro. Blood. 2003;102:2541–6. doi: 10.1182/blood-2003-01-0183. [DOI] [PubMed] [Google Scholar]
  35. Kutzler MA, Robinson TM, Chattergoon MA, et al. Coimmunization with an optimized IL-15 plasmid results in enhanced function and longevity of CD8 T cells that are partially independent of CD4 T cell help. J Immunol. 2005;175:112–23. doi: 10.4049/jimmunol.175.1.112. [DOI] [PubMed] [Google Scholar]
  36. Melchionda F, Fry TJ, Milliron MJ, McKirdy MA, Tagaya Y, Mackall CL. Adjuvant IL-7 or IL-15 overcomes immunodominance and improves survival of the CD8+ memory cell pool. J Clin Invest. 2005;115:1177–87. doi: 10.1172/JCI23134. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Oh S, Berzofsky JA, Burke DS, Waldmann TA, Perera LP. Coadministration of HIV vaccine vectors with vaccinia viruses expressing IL-15 but not IL-2 induces long-lasting cellular immunity. Proc Natl Acad Sci USA. 2003;100:3392–7. doi: 10.1073/pnas.0630592100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Villinger F, Miller R, Mori K, Mayne AE, Bostik P, Sundstrom JB, Sugimoto C, Ansari AA. IL-15 is superior to IL-2 in the generation of long-lived antigen specific memory CD4 and CD8 T cells in rhesus macaques. Vaccine. 2004;22:3510–21. doi: 10.1016/j.vaccine.2003.07.022. [DOI] [PubMed] [Google Scholar]
  39. Nanjappa SG, Walent JH, Morre M, Suresh M. Effects of IL-7 on memory CD8 T cell homeostasis are influenced by the timing of therapy in mice. J Clin Invest. 2008;118:1027–39. doi: 10.1172/JCI32020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Mueller YM, Petrovas C, Bojczuk PM, et al. Interleukin-15 increases effector memory CD8+ T cells and NK cells in simian immunodeficiency virus-infected macaques. J Virol. 2005;79:4877–85. doi: 10.1128/JVI.79.8.4877-4885.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Tisoncik JR, Korth MJ, Simmons CP, Farrar J, Martin TR, Katze MG. Into the eye of the cytokine storm. Microbiol Mol Biol Rev. 2012;76:16–32. doi: 10.1128/MMBR.05015-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Ndejembi MP, Teijaro JR, Patke DS, Bingaman AW, Chandok MR, Azimzadeh A, Nadler SG, Farber DL. Control of memory CD4 T cell recall by the CD28/B7 costimulatory pathway. J Immunol. 2006;177:7698–706. doi: 10.4049/jimmunol.177.11.7698. [DOI] [PubMed] [Google Scholar]
  43. Gramaglia I, Jember A, Pippig SD, Weinberg AD, Killeen N, Croft M. The OX40 costimulatory receptor determines the development of CD4 memory by regulating primary clonal expansion. J Immunol. 2000;165:3043–50. doi: 10.4049/jimmunol.165.6.3043. [DOI] [PubMed] [Google Scholar]
  44. Khoury SJ, Akalin E, Chandraker A, Turka LA, Linsley PS, Sayegh MH, Hancock WW. CD28-B7 costimulatory blockade by CTLA4Ig prevents actively induced experimental autoimmune encephalomyelitis and inhibits Th1 but spares Th2 cytokines in the central nervous system. J Immunol. 2006;155:4521–4. [PubMed] [Google Scholar]
  45. Bluestone JA, St. Clair EW, Turka LA. CTLA4Ig: bridging the basic immunology with clinical application. Immunity. 2006;24:233–8. doi: 10.1016/j.immuni.2006.03.001. [DOI] [PubMed] [Google Scholar]
  46. Kremer JM, Westhovens R, Leon M, et al. Treatment of rheumatoid arthritis by selective inhibition of T-cell activation with fusion protein CTLA4Ig. N Engl J Med. 2003;349:1907–15. doi: 10.1056/NEJMoa035075. [DOI] [PubMed] [Google Scholar]
  47. Abrams JR, Lebwohl MG, Guzzo CA, et al. CTLA4Ig-mediated blockade of T-cell costimulation in patients with psoriasis vulgaris. J Clin Invest. 1999;103:1243–52. doi: 10.1172/JCI5857. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Weinberg AD. The role of OX40 (CD134) in T-cell memory generation. Adv Exp Med Biol. 2010;684:57–68. doi: 10.1007/978-1-4419-6451-9_5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Wang X, Ria M, Kelmenson PM, et al. Positional identification of TNFSF4, encoding OX40 ligand, as a gene that influences atherosclerosis susceptibility. Nat Genet. 2005;37:365–72. doi: 10.1038/ng1524. [DOI] [PubMed] [Google Scholar]
  50. van Wanrooij EJ, van Puijvelde GH, de Vos P, Yagita H, van Berkel TJ, Kuiper J. Interruption of the Tnfrsf4/Tnfsf4 (OX40/OX40L) pathway attenuates atherogenesis in low-density lipoprotein receptor-deficient mice. Arterioscler Thromb Vasc Biol. 2007;27:204–10. doi: 10.1161/01.ATV.0000251007.07648.81. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Figure S1. The most effective immunotherapy protocols rely on the simultaneous infusion of P-agents and M-agents.

imm0146-0271-sd1.eps (425.4KB, eps)

Figure S2. Graphical representation of the result established by Theorem 1.2.

imm0146-0271-sd2.eps (1.7MB, eps)

Appendix S1. Mathematical model, details of the numerical results and analysis of the model.

imm0146-0271-sd3.pdf (311.3KB, pdf)

Articles from Immunology are provided here courtesy of British Society for Immunology

RESOURCES