Visual recovery in cortical blindness is limited by high internal noise

Abstract

Damage to the primary visual cortex typically causes cortical blindness (CB) in the hemifield contralateral to the damaged hemisphere. Recent evidence indicates that visual training can partially reverse CB at trained locations. Whereas training induces near-complete recovery of coarse direction and orientation discriminations, deficits in fine motion processing remain. Here, we systematically disentangle components of the perceptual inefficiencies present in CB fields before and after coarse direction discrimination training. In seven human CB subjects, we measured threshold versus noise functions before and after coarse direction discrimination training in the blind field and at corresponding intact field locations. Threshold versus noise functions were analyzed within the framework of the linear amplifier model and the perceptual template model. Linear amplifier model analysis identified internal noise as a key factor differentiating motion processing across the tested areas, with visual training reducing internal noise in the blind field. Differences in internal noise also explained residual perceptual deficits at retrained locations. These findings were confirmed with perceptual template model analysis, which further revealed that the major residual deficits between retrained and intact field locations could be explained by differences in internal additive noise. There were no significant differences in multiplicative noise or the ability to process external noise. Together, these results highlight the critical role of altered internal noise processing in mediating training-induced visual recovery in CB fields, and may explain residual perceptual deficits relative to intact regions of the visual field.

Introduction

Patients with damage to the primary visual cortex (V1) suffer from cortical blindness (CB)—a lack of conscious vision in the hemifield contralateral to the damaged hemisphere. Despite V1 damage, individuals with CB retain largely unconscious visual processing in their blind field—a phenomenon called blindsight (Weiskrantz, Warrington, Sanders, & Marshall, 1974). Visual training can improve residual performance for both static and moving stimuli in CB. For example, practice on detection tasks (Kasten, Wüst, Behrens-Baumann, & Sabel, 1998; Sabel, Kenkel, & Kasten, 2004; Bergsma & van der Wildt, 2009) can improve color and shape processing, letter discrimination, and reading speed (Bergsma, Elshout, van der Wildt, & van den Berg, 2012), whereas detection training with flickering sinusoidal gratings can improve detection of lower contrast gratings in the blind field, sometimes with awareness (Sahraie et al., 2006; Sahraie, Hibbard, Trevethan, Ritchie, & Weiskrantz, 2010). Training such patients to discriminate coarse (i.e., leftward vs. rightward) motion directions in their blind field allows them to recover normal direction range and coherence thresholds for left–right direction discriminations at the trained locations (Huxlin et al., 2009; Das, Tadin, & Huxlin, 2014). Contrast sensitivity and direction difference thresholds also improve at these locations, but they remain significantly impaired relative to performance at corresponding locations in the intact hemifield (Das et al., 2014). These residual deficits were seen every time CB subjects underwent coarse discrimination training, regardless of whether this involved motion direction or orientation, and regardless of whether they trained at a single or multiple blind field locations (Das et al., 2014). Overall, these findings suggest that recovered vision in CB subjects is not completely normal.

What limits full recovery? The fact that posttraining residual impairments involved deficits in contrast sensitivity as well as fine discrimination abilities suggest that they could arise from low signal-to-noise ratio and/or a general deficit in suppressing irrelevant signals at retrained blind field locations. Indeed, perceptual deficits have been shown to result solely or jointly from a failure to differentiate signal from both external and internal noise as well as from low information sampling efficiency (Pelli, 1981; Legge, Kersten, & Burgess, 1987; Dosher & Lu, 1999; Pelli & Farell, 1999; Simpson, Falkenberg, & Manahilov, 2003; Dakin, Mareschal, & Bex, 2005; Lu, Chu, Dosher, & Lee, 2005; Lu, Chu, & Dosher, 2006; Lu & Dosher, 2008). Visual deficits in normal aging (Bennett, Sekuler, & Ozin, 1999; Bower & Anderson, 2012), following visual cortex damage (Hayes & Merigan, 2006), and in amblyopia (Pelli, Levi, & Chung, 2004; Xu, Lu, Qiu, & Zhou, 2006; Huang, Lu, & Zhou, 2009) are all associated with at least one of these processing limitations. The present experiments tested the hypothesis that improved noise reduction underlies training-induced enhancements in CB fields, and that failure to filter noise efficiently is responsible for the residual visual deficits at trained blind field locations.

To test this hypothesis, we employed two theoretical frameworks: the linear amplifier model (LAM; Burgess, Wagner, Jennings, & Barlow, 1981; Pelli, 1981; Legge et al., 1987) and the perceptual template model (PTM; Dosher & Lu, 1999), which have been shown to account for performance changes induced by various manipulations, including attention (Lu & Dosher, 1998; Dosher & Lu, 2000; Lu, Lesmes, & Dosher, 2002; Ling, Liu, & Carrasco, 2009), perceptual training (Dosher & Lu, 1999; Gold, Bennett, & Sekuler, 1999), adaptation (Dao, Lu, & Dosher, 2006), and critical band masking (Solomon & Pelli, 1994; Talgar, Pelli, & Carrasco, 2004). Although other theoretical frameworks exist that could be used here, LAM and PTM are the two frameworks most often used in previous studies (Lu & Dosher, 2008). The LAM is a simple, elegant model, capable of differentiating the contributions of internal noise processing and sampling efficiency on behavioral performance, but it has some limitations. It does not discriminate signal-dependent from signal-independent internal noise (Lu & Dosher, 2008). For example, decreasing the quality of optical input to the visual system with a frosted glass lens placed in front of the eyes would generate a behavioral signature that the LAM would interpret as a change in equivalent internal noise. The PTM, however, theoretically differentiates two forms of internal noise (signal-dependent, multiplicative noise and signal-independent, additive noise), and it can separate them from the ability of the system to reduce external noise. In the present study, we used both models to systematically examine perceptual deficits in CB fields before and after left–right direction discrimination training. This allowed us to more precisely assess both the overall change in noise processing as a result of training, and the nature of the visual deficits that remained.

Methods

Subjects

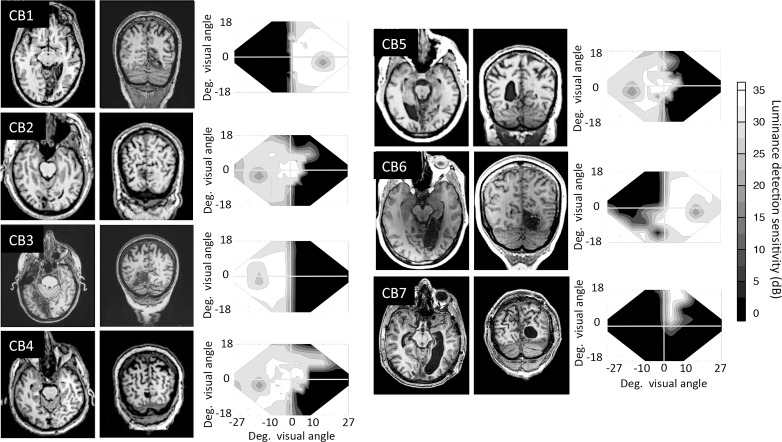
In this study, we used data from seven CB subjects and four visually intact, age-matched controls (see Table 1 for subject demographics). The CB subjects were recruited at least 6 months after a stroke resulting in damage to V1 and homonymous visual field defects (Figure 1). We excluded subjects with ocular diseases, such as macular degeneration, glaucoma, or cataracts, which would further interfere with vision. None of the subjects used psychoactive drugs, such as antidepressants, which may have altered the impact of training, during the study, and all had their visual acuity corrected to normal (with glasses or contact lenses) for training and testing.

Table 1.

Subject demographics and training/testing locations.

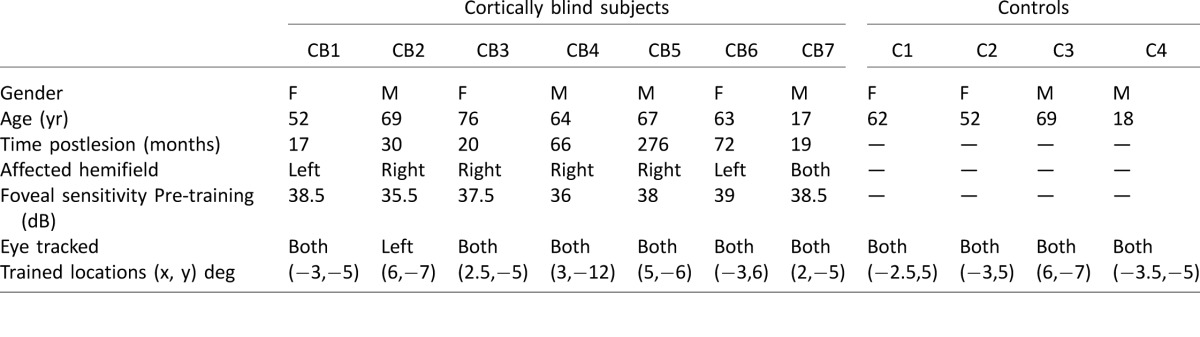
Figure 1.

Structural MRIs of the seven cortically blind participants (CB1–CB7), illustrating the location of their V1 damage and visual field defects. Images are T1-weighed structurals in both horizontal and coronal planes. Left is left and right is right on each MRI picture. Next to each patient's brain scans are composite visual field maps, illustrating visual loss induced by their stroke, averaged across the two eyes. Composites were created by plotting luminance detection values obtained from four 24-2 and 10-2 Humphrey visual field tests into a matrix. If these locations coincided, the values were averaged together. Interpolating between tested data points then filled the empty spaces between values. All values are measured in dB (grayscale legend at far right).

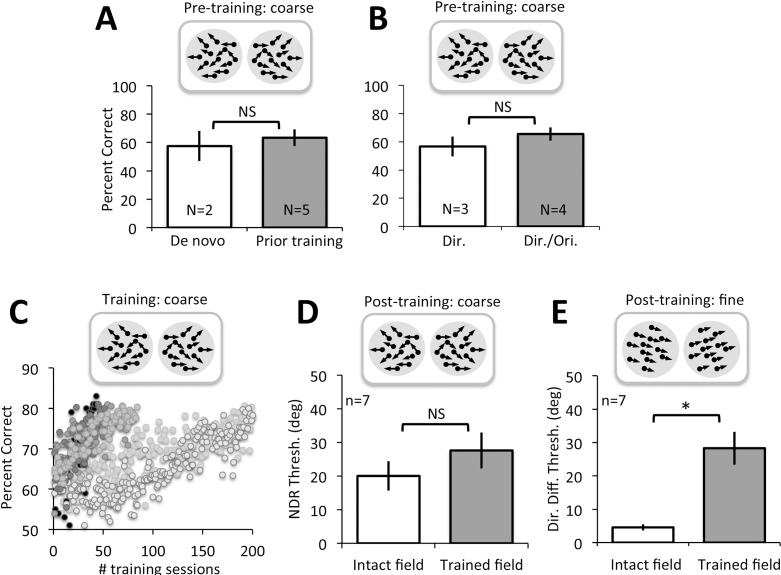
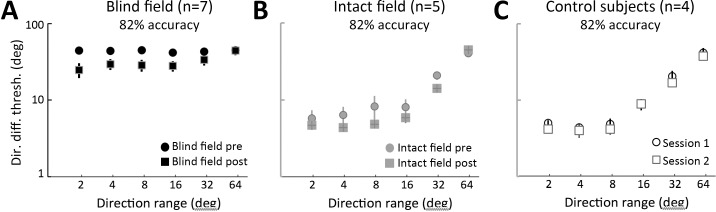
Most of the CB subjects whose data are presented here (CB1, CB2, CB4, CB5, CB6) took part in a prior visual training study (Das et al., 2014). CB2, CB4, CB5, and CB6 were trained on both orientation and direction discrimination by Das et al. (2014), but only their direction-trained locations were used for evaluations made in the present report. CB1 underwent orientation discrimination training by Das et al. (2014), followed by training on global direction discrimination in her lower blind field quadrant, as part of the present study. CB3 and CB7 were recruited de novo for the present study and trained only on the left–right global direction discrimination task (see below for details). For the present experiments, all CB subjects were trained at a previously untrained blind field location. Baseline performance at these untrained blind field locations was equally impaired (at chance levels) in all subjects prior to the onset of training (Figure 5A, B); all subjects demonstrated the ability to improve coarse discrimination abilities in the blind field with training (Figure 5C, D), and they all exhibited deficits in fine discrimination performance at these locations posttraining (Figure 5E). Given this behavioral consistency for the particular phenomena of interest, CB subjects were grouped together for the analyses performed in the present paper, irrespective of their prior training experience.

Figure 5.

Coarse and fine direction discrimination performance in CB subjects. (A) Pretraining performance for coarse, left–right global direction discrimination in subjects recruited de novo or who had undergone training as part of a previous study (Das et al., 2014). There were no significant differences between these two subject subgroups. (B) Pretraining performance for coarse, left–right global direction discrimination in subjects who received either direction discrimination training only or direction and orientation discrimination training. All subjects were equally impaired prior to the onset of training administered for the present study. (C) Example of training data for CB subjects, showing percent-correct performance on individual training sessions for the global left–right direction discrimination task. All subjects started around or just above chance, but eventually rose to ∼80% correct. (D) Following training, direction range thresholds across all subjects recovered to near-intact field levels. (E) Direction difference thresholds also improved following coarse discrimination training, but they remained significantly higher compared to direction difference thresholds measured at corresponding locations in the intact field of vision (*p = 0.003).

The average age (±SD) of CB subjects in the present study was 58 ± 20 years, ranging from 17 to 79 years of age. All procedures were approved by the Institutional Review Board of the University of Rochester Medical Center and were conducted only after obtaining written, informed consent from each participant. Four visually intact, age-matched control subjects were also recruited, with an average age of 50 ± 23 years, ranging from 18 to 69 years old (Table 1). Control subjects were recruited, consented, and tested at a separate laboratory at New York University using identical procedures and equipment. The Institutional Review Board of New York University approved testing procedures for control subjects.

Visual stimuli

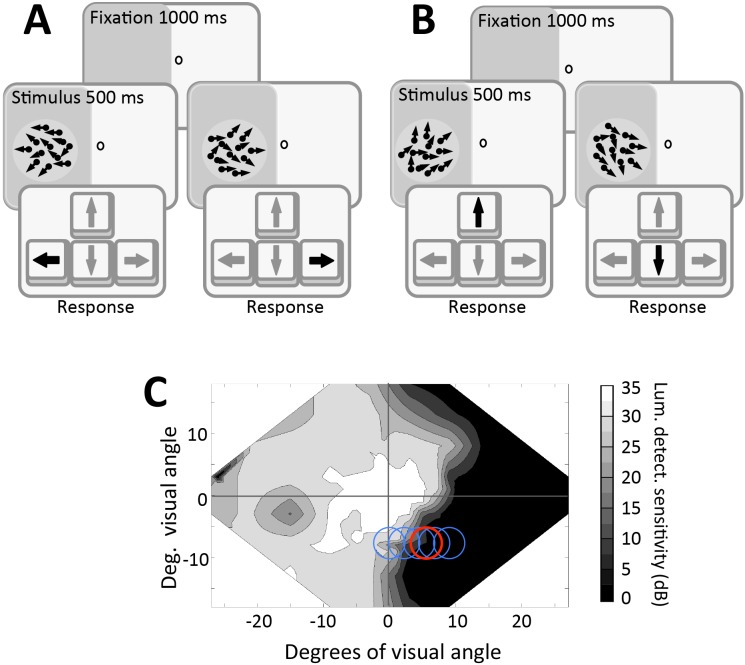
Moving random dot stimuli were used to assess global direction discrimination abilities. They were presented in a 2.5° radius, circular aperture, in a two-alternative forced choice task configuration. Dot speed was 10°/s and dot density was 3 dots/°². Individual dots were black on a midgray background, and had a lifetime of 250 ms. Stimuli were presented for 500 ms and accompanied by a tone to indicate their appearance (especially important when presenting stimuli in cortically blind regions of the visual field).

For coarse direction discrimination, the stimulus moved leftward or rightward and contained a variable range of dot directions, uniformly distributed around the left- or rightward vectors (Figure 2A). Direction range was increased from 0° to 360° in 40° steps according to performance, using a 3:1 staircase. The appearance of a fixation point signaled the start of each trial and an auditory signal informed subjects that the stimulus was being presented for 500 ms. The subjects were asked to respond by pressing one of two mouse keys to indicate whether they perceived movement to the left or to the right. Auditory feedback was then provided as to whether the response was correct or incorrect. After completing 300 trials, the program automatically closed and created a log file.

Figure 2.

Behavioral paradigms. (A) Coarse, left–right, global direction discrimination task used to train subjects and measure direction range thresholds. (B) Fine direction difference thresholds were collected at different levels of direction range by presenting a random dot stimulus within the blind field, which moved slightly above or below the horizontal meridian. (C) Sample visual field of a subject in the present study. Blue circles indicate locations where performance was mapped in order to select a training location (red circle).

In the fine direction discrimination tasks, random dot stimuli moved almost coherently (2° of direction range) towards the middle of the screen, at an angle above or below the horizontal meridian of the stimulus (Figure 2B). The size of the angle was adjusted down from 45° based on performance, using a QUEST staircase, which converged on 82% correct performance (Watson & Pelli, 1983).

In the external noise task (for LAM and PTM analysis), we used the fine direction discrimination task described above, but stimuli contained six possible noise levels (direction ranges of 2°, 4°, 8°, 16°, 32°, or 64°). In addition, the range of dot directions were distributed with a Gaussian profile around the global direction axis of the stimulus, as in Ling et al.'s (2009) prior study. Subjects were asked to discriminate whether the global motion of the stimulus was in a direction above (press up arrow key) or below (press down arrow key) the horizontal meridian (Figure 2B). Different auditory feedback was provided for correct and incorrect trials. Correct trials would lessen the angle difference between the direction of motion and the horizontal meridian from 45°, whereas incorrect trials would increase it. This was first done using QUEST staircases that converged on 82% correct performance (Watson & Pelli, 1983). Each test session consisted of six staircases, each containing 20 trials at each of the six noise levels, for a total of 720 trials. The entire procedure was then repeated in the CB subjects' intact field of vision, or in the other hemifield in visually intact controls. Finally, to analyze the data with the PTM, visual field locations of interest had to be tested at two different difficulty levels: one in which the QUEST staircases converged on a threshold set at 82% correct (described above) and a second, less difficult condition, in which the QUEST staircases converged on a threshold set at 75% correct. In all cases, subjects' performance was plotted in the form of threshold versus noise (TvN) curves (Ling et al., 2009).

Apparatus and eye tracking

During in-lab testing, visual stimuli were presented on a CRT monitor (HP 7217A, 48.5 × 31.5 cm, 1024 × 640 resolution, 120-Hz frame rate), whose luminance was calibrated with a ColorCalII automatic calibration system (Cambridge Research Systems, Rochester, Kent, UK). Viewing distance was 42 cm, enforced by a chin/forehead rest. Experiments were conducted on a Mac Pro computer using MATLAB (The MathWorks, Natick, MA) and Psychtoolbox (Pelli, 1997). Eye position was tracked using an Eyelink 1000 eye tracker (SR Research, Mississauga, Ontario, Canada) either monocularly or binocularly (refer to Table 1). During each trial, subjects were asked to view a fixation target at the center of the screen. Stimuli were presented in a gaze-contingent manner in either intact or blind regions of the visual field. Moving eye position more than 1° from the fixation target caused the trial to be aborted and repeated.

The Eyelink 1000 eye tracker that was used to enforce fixation is accurate to within 0.25°, with a sampling frequency of 1000 Hz. We allowed our subjects a fixation window of only 2° × 2°, meaning that at most they would be allowed to move their eyes 1.4° towards the visual target. More importantly, as we have previously reported (Huxlin et al., 2009), many subjects have improvements at distances greater than 10° from the intact visual field—almost an order of magnitude larger than the allowed fixation movement toward the target. Finally, the improvements exhibited by our subjects on psychophysical tasks were supported by improvements measured on a Humphrey Automated Perimeter (Carl Zeiss Meditec, Jena, Germany), with its own validated eye tracking system. It is also worth noting that our subjects were highly motivated to fixate accurately; we emphasized to subjects that accurate fixation on every trial was essential to recover vision and to attain usable data.

Two subjects (CB2 and CB3) underwent all visual training in the laboratory with eye tracking. The other five CB subjects trained at home using a lab-issued chin/forehead rest and software customized to their own computer and monitor's specifications (dimensions, resolution, and refresh rate). Viewing distance from the chin rest to the monitor was 42 cm. Home-trained subjects were told that poor fixation would reduce the effect of training and that their home-training results would be verified in-lab with eye tracking. Only subjects whose home-training data could be replicated under conditions of fixation control in the lab were included in the present study, and there were no qualitative differences between the training effects and visual performance of subjects trained in the lab versus those who trained at home. The four visually intact, age-matched control subjects were tested in the laboratory with eye tracking. They did not undergo any training.

Experimental design

Baseline measurements

For each CB subject, 24-2 and 10-2 Humphrey visual fields collected with controlled fixation were used to establish the rough location and extent of visual field loss (Figure 1). Based on the Humphrey fields, CB subjects underwent psychophysical mapping (Figure 2) to establish a blind field border by performing 50 trials of a two-alternative, forced-choice left–right global direction discrimination task (Figure 2A) at a number of laterally separated locations, starting at the vertical meridian and moving progressively across the blind field border (blue circles in Figure 2C). Training locations were then selected (e.g., red circle in Figure 2C; see Table 1 for [x, y] center coordinates of locations trained) as the sites at which left–right direction discrimination performance dropped from above chance to chance performance (∼50% correct) over a 1° lateral movement towards the blind field. Training locations always fell just inside the border of the subject's blind field. Because these locations were near spared regions of the visual field, fixation control with eye-tracking during pre- and posttraining tests were necessary to ensure that subjects' improvements in visual performance could not be simply explained by eye movements towards the stimuli (Huxlin et al., 2009; Martin, Das, & Huxlin, 2012; Das et al., 2014).

Once a training location in the blind field was selected for each CB subject, we collected baseline performance on both a left–right coarse direction discrimination task (Figure 2A), and a fine direction discrimination task measured with different levels of external noise (i.e., with a progressively increasing range of dot directions; Figure 2B), which was then modeled with the LAM and PTM.

Testing in control subjects

Each of the four control subjects was assigned to one of the visual field locations picked for training in four of the CB subjects, selected at random (see Table 1). Baseline direction difference thresholds were measured using the above external noise task, in order to capture TvN curves at two difficulty levels with controlled fixation as in CB subjects. After about 1 month, this performance was remeasured to assess the impact of repeat testing on TvN curves.

Visual training in cortically blind fields

The training regimen applied to cortically blind regions of the visual field in CB subjects consisted of 300 trials per day of the coarse (left–right), global direction discrimination task, performed at each training location, for a minimum of 5 days per week. If training at home, performance data contained in a log file automatically generated during each training session were sent weekly to the laboratory for analysis.

Each training session was run using a 3:1 staircase procedure, as previously reported (Huxlin et al., 2009; Das et al., 2014). Training performance for each session was fit using a Weibull function with a threshold criterion of 75% correct used to calculate a direction range threshold. This threshold was then normalized to the maximum range of dot directions (360°), generating a normalized direction range (NDR) threshold, defined as:

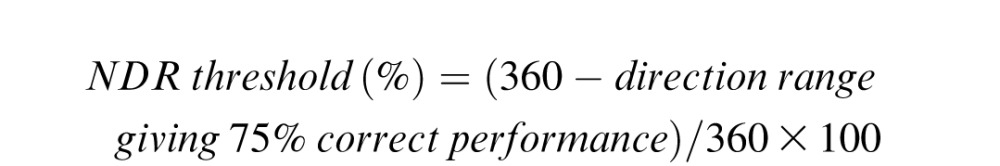Once NDR thresholds at a given blind field location reached the normal range (as defined by each subject's measured performance at equivalent locations in their intact field of vision prior to the onset of training), and stayed within the normal range for at least five consecutive training sessions, the training location was moved deeper into the blind field by 1° along the x-axis (in Cartesian coordinate space). This process was repeated until the individual patients trained for at least 6 months, and until they had recovered normal NDR thresholds at a minimum of one blind field location. At that point, if training at home, subjects were brought back to the lab for verification of their home training performance with fixation control and to complete posttraining tests.

Posttraining measurements

For all subjects who trained at home, improvements were verified with eye tracking in the laboratory. Once training-induced improvements in direction range thresholds were confirmed with controlled fixation, CB subjects underwent a repeat of baseline tests, including measurement of fine direction difference thresholds at different noise levels. These measurements were collected both at retrained blind field locations and at corresponding locations in each subject's intact visual hemifield. For fine direction difference performance, all seven subjects were tested at 82% correct, allowing data to be fit using the LAM. Due to the large number of trials needed to cover all conditions, and time constraints on the part of some of the CB subjects, only five of them also completed testing at 75% correct, allowing their data to be fit with the PTM.

Linear amplifier model and perceptual template model analyses

Theoretical background

The LAM assumes that the spatiotemporal signal stimulus energy required for an observer to achieve a given performance level is linearly amplified by external noise energy (Pelli, 1981; Legge et al., 1987). In the LAM, participant performance is usually compared to a hypothesized observer, in which an external stimulus is encoded, warped by internal Gaussian noise, passed through a template in the visual system, which then generates an internal response distribution. The accuracy of this template is determined by the sampling efficiency of the observer. The subject compares two population responses patterns generated by two possible stimulus inputs (left/right) to perform the discrimination task. Thus, two components contribute to the observer performance: (a) equivalent internal noise in which internal noise is expressed in the same units as external noise added to the stimuli, and (b) sampling efficiency, which measures how effectively the observer extracts the available information. Generally, signal thresholds c can be computed by:

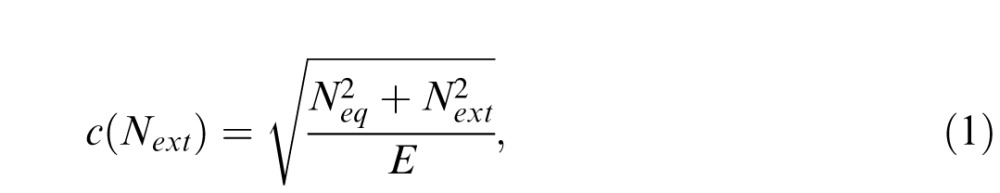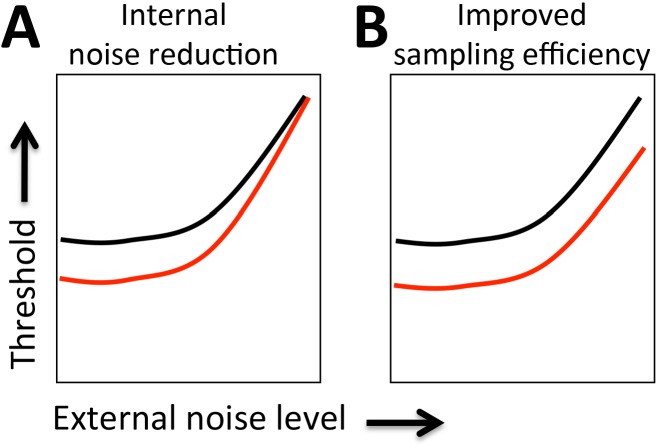
where N_eq is the amount of equivalent internal noise, N_ext is the amount of external noise power, whereas E is the visual sampling efficiency at this performance level. The effects of equivalent internal noise and sampling efficiency can be assessed by manipulating external noise, and then inferred by changes in TvN functions, which plot threshold performance level as a function of external noise. A reduction in equivalent internal noise predicts robustly improved performance at low external noise levels (Figure 3A). On the other hand, improved sampling efficiency predicts improved performance across all noise levels (Figure 3B).

Figure 3.

LAM predictions. TvN comparison between two test conditions may present two possible signatures when fit with the LAM: (A) Improved thresholds only at low-noise levels indicate a reduction of equivalent internal noise in the better performing condition relative to the impaired condition. (B) Improved thresholds at all noise levels indicate an improvement in sampling efficiency in the better performing condition relative to the impaired condition.

In addition to the LAM, we also implemented the PTM, which can accommodate additional perceptual limitations (such as external noise processing and multiplicative and additive internal noise; Dosher & Lu, 1999; Lu & Dosher, 2004; Chung, Levi, & Tjan, 2005). Unlike the LAM, which can only differentiate the effects of sampling efficiency and equivalent internal noise, the PTM theoretically separates signal-dependent internal noise (multiplicative noise) and signal-independent internal noise (additive noise), allowing for the identification of distinct behavioral signatures. Briefly, the PTM proposes that an observed stimulus is first filtered by a perceptual template, of which outputs are then passed through nonlinear transducer functions and subjected to varying levels of internal additive or multiplicative noise (Dosher & Lu, 1999). For any given performance level indexed by d′, we can express it as:

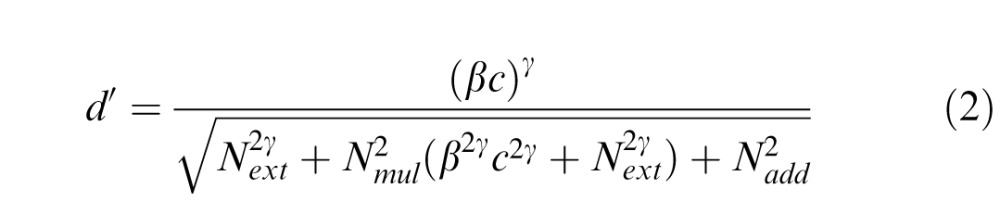Based on this, we can further express stimulus intensity at threshold (c_τ) as:

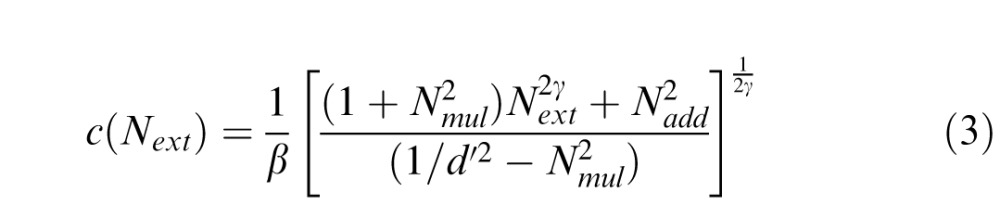where signal processing is modulated by five components. The visual system first multiplies input signal by a signal gain (template matching) factor β. The “tuned” signal then passes through a nonlinear transducer function, which amplifies such inputs to the γ^th power. Besides amplification of signal, three types of noise (internal additive noise N_add, internal multiplicative noise N_mul and external noise N_ext) also modulate signal processing. Internal additive noise is drawn from a Gaussian distribution with a mean of zero and standard deviation, independent of input signal strength. Internal multiplicative noise is also drawn from a Gaussian distribution with a standard deviation proportional to amplified signal strength. External noise is noise that we can directly observe and/or manipulate in the input signal (i.e., the stimulus). Eventually, a decision process determines performance level d′.

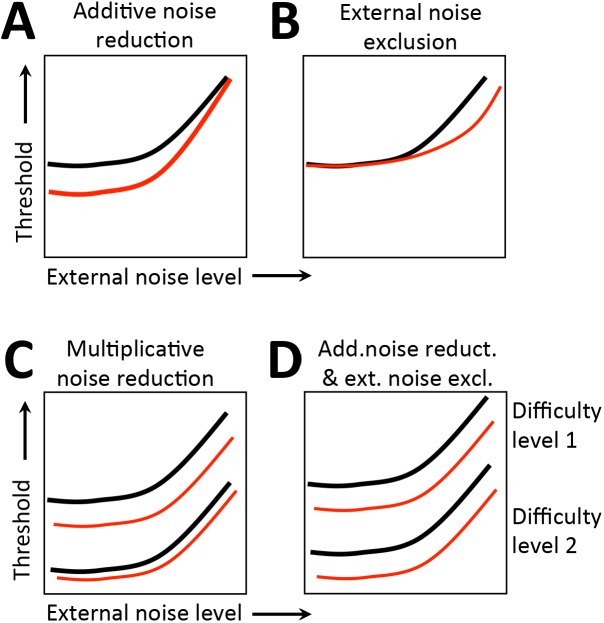
Thus, in the PTM, perceptual improvements can occur via several mechanisms. The first is stimulus enhancement, in which input signal is amplified by a factor >1. Mathematically, such enhancement is equal to a reduction in internal additive noise and predicts improved performance strongest at low external noise levels, but largely unchanged thresholds at high external noise levels (Figure 4A). If perceptual improvements occur via better external noise filtering, in which the noise directly embedded in the input signal is systematically reduced, there should be improved performance at high external noise levels, but relatively unchanged thresholds at low noise levels (Figure 4B). Perceptual improvements can also occur via internal multiplicative noise reduction, in which there is attenuation of noise proportional to the input signal energy. The predicted behavioral signature for this mechanism is significantly improved performance across all external noise levels, with higher improvements as difficulty increases (Figure 4C). Notably, a combination of internal additive noise reduction and external noise filtering can also lead to improved performance across all noise levels, but results in similar amounts of improvements at different performance levels (Figure 4D). To differentiate these two mechanisms, PTM requires measuring TvN functions across two distinct performance levels, which was impossible to obtain during pretraining because blind field thresholds were close to, or at ceiling, prior to the onset of training. Thus, we fit both the LAM and the PTM to better characterize the limits of visual training.

Figure 4.

PTM predictions. TvN comparisons between test conditions may present four possible signatures when fit with the PTM: (A) Lower thresholds at low-noise than high-noise conditions, indicating a reduction of additive internal noise in the better performing conditions compared to the impaired condition, suggestive of stimulus enhancement; (B) Improved performance only in high-noise conditions, suggesting an improved ability to exclude external noise when encoding the stimulus in the better performing condition compared to the impaired condition; (C) Improved performance at all noise conditions, but only at one difficulty level, indicating a reduction of multiplicative internal noise in the better performing condition compared to the impaired condition; (D) Lower thresholds at all noise levels and both difficulty levels, indicating a combined effect of reduced additive internal noise and improved external noise exclusion in the improved condition compared to the impaired condition.

Specification of model parameters

The overall model fitting and selection process used here was identical to those described by Lu and Dosher (2004). For the LAM, we introduced two deficit coefficient indices A_eq and A_e, to scale two components of the LAM: equivalent internal noise (eq) and sampling efficiency (e). We denoted pre, post, and i as three conditions: blind field pretraining, blind field posttraining, and matched intact field, respectively. Thus, six parameters A_eq(pre), A_eq(post), A_eq(i), A_e(pre), A_e(post), and A_e(i) can be viewed as coefficient indices of equivalent internal noise N_eq and sampling efficiency E in these three conditions. Fine direction discrimination thresholds in the blind field pre/posttraining and in the intact field were described as follows:

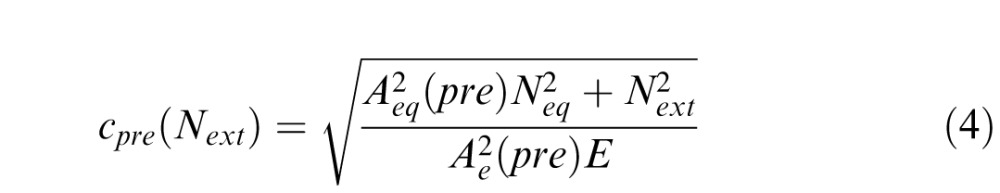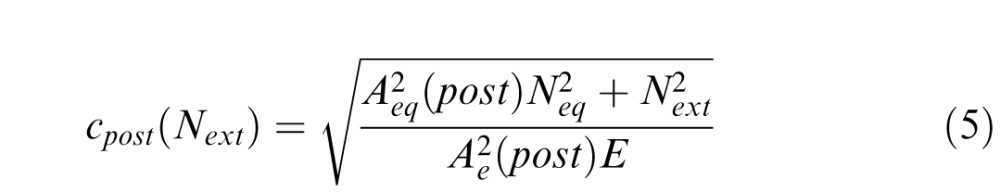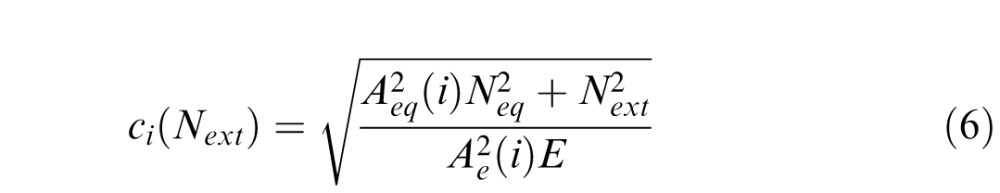where N_ext represents the amount of external noise in the stimulus (direction ranges of 2°, 4°, 8°, 16°, 32°, or 64°). To directly normalize equivalent internal noise and sampling efficiency between the blind field and the intact field to the same scale, we set coefficient indices of the intact field to 1 (A_eq[i] = A_e[i] = 1). As such, the full version of the LAM allowed for six free parameters to explain differences across conditions: A_eq(pre), A_eq(post), A_e(pre), A_e(post), N_eq, and E. The logic is that fitted coefficient indices A_eq(pre), A_eq(post) > 1, and/or A_eq(pre), A_eq(post) < 1, would suggest elevated equivalent internal noise and worse sampling efficiency, respectively.

Similarly, for the PTM, we introduced three deficit coefficient indices: A_a, A_m, and A_e, and multiplied them by internal additive noise N_add, internal multiplicative noise N_mul, and external noise N_ext respectively. The PTM requires thresholds to be measured at two performance levels (75% and 82%); because CB subjects had great difficulties performing the fine discrimination task in their blind field pretraining at both of these two levels, their performance was identical in the two conditions. Thus, the only comparisons we could reliably make with the PTM were between posttraining blind field performance (post) and performance in the intact field of vision (i). For these two conditions and the two accuracy levels (75% and 82%), thresholds were expressed as:

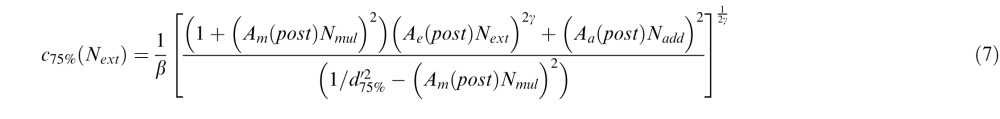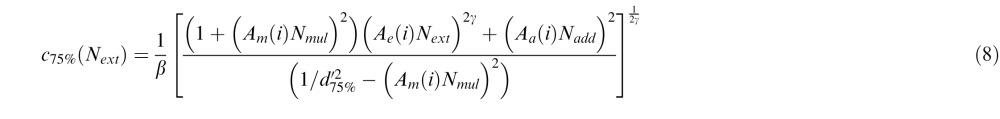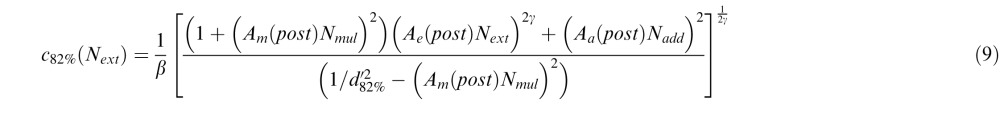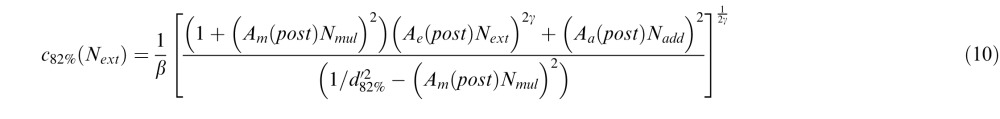where d_75% = 1.349, d_82% = 1.831. Again, we set coefficient indices for the three types of noise in the intact field A_a(i) = A_m(i) = A_e(i) = 1. To capture differences between trained blind field and intact field locations, we varied A_a(post), A_m(post), and A_e(post) as potential free parameters. Thus, together with two of the undetermined noise types, N_add and N_mul, the signal gain factor β and the nonlinear power factor γ, the full version of the PTM had seven free parameters.

Model-fitting procedure

To find the best-fitting models for the empirical data, the method of model lattice was adopted, whereby we compared all possible candidate models, each with different free parameter settings. Eight candidate models were considered in PTM fitting. As mentioned above, the full PTM assumed significant differences in all three types of noise between posttraining blind and intact fields, and thus had seven free parameters. The no-difference model assumed identical amounts of all three types of noise in the trained blind field locations and in corresponding locations in intact regions of the visual field. Thus, A_a(post) = A_e(post) = A_m(post) = 1. This results in four free parameters: two types of noise N_add and N_mul, the signal gain factor β, and the nonlinear power factor γ. Other than the full model and the no-difference versions of the PTM, there are six possible candidate models, which assume different combinations of the three types of noise, with the number of free parameters varying between four and seven.

For the LAM, 25 candidate models were compared, which ranged from assuming significant differences between pretraining blind field, posttraining blind field, and intact field in both equivalent internal noise and sampling efficiency, to assuming no differences in either factor across all three conditions. These models ranged from two to six free parameters.

In both LAM and PTM fitting, the goodness of fit of each candidate model to the data was gauged by r²:

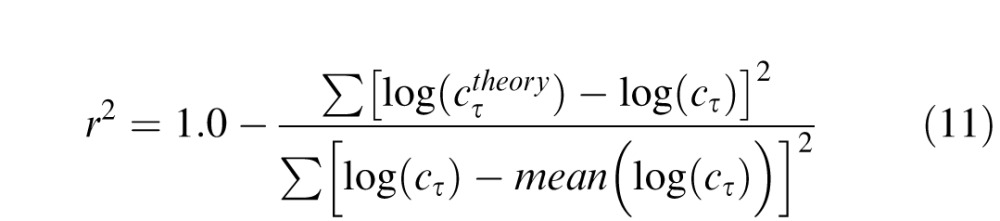where ∑ and mean were collected across three conditions (pre/post/intact) and six levels of external noise, at each performance level (75% or 82% correct). To identify the model with the best account of the data while avoiding potential over-fitting, we followed the method reported by Dosher, Liu, Blair, and Lu (2004). For 25 candidate LAMs and eight PTMs, F tests were used to compare the reduced models to the full model:

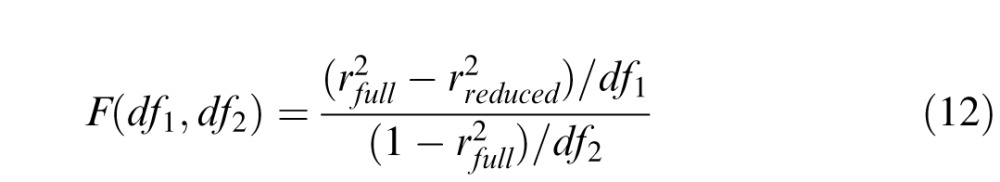where

and

The number of free parameters in each model is k_s, and N is the number of predicted data points. The model with least number of free parameters, which was statistically not different from the full model, was identified as the best-fitting model.

Results

Effect of training on left–right direction discrimination in CB fields

Regardless of their prior training history, CB observers were unable to reliably discriminate leftward or rightward direction of motion of random dot stimuli at the blind field locations chosen for training. Percent correct performance was severely impaired; de novo subjects: 57.5% ± 10.6% correct (M ± SD) versus previously trained by Das et al. (2014): 63.4% ± 5.9%, two-tailed Student's t test, t(5) = −1.0, p = 0.36; direction-trained subjects: 56.67% ± 7.0% versus direction and orientation-trained subjects: 65.5% ± 4.7%, t(5) = −2.01, p = 0.10 (Figure 5A, B). Because performance was generally below 75% correct, thresholds could not be reliably measured on most of the tasks. However, with daily training, subjects improved progressively, requiring an average of 58 ± 45 training sessions until they reached ∼80% correct (Figure 5C). By the end of training, all subjects had achieved comparably good percent-correct performance; de novo subjects: 82.3% ± 2.8% (M ± SD) versus previously trained: 78.7% ± 1.9%, two-tailed Student's t test, t(5) = 2.06, p = 0.09; direction-trained: 81.4% ± 2.5% versus direction- and orientation-trained: 78.4% ± 2.1%, t(5) = 1.76, p = 0.14. At this stage, subjects generated measurable NDR thresholds, which averaged 28% ± 14% (M ± SD). This was not significantly different from thresholds at corresponding locations in the intact hemifield of vision (20% ± 12%, two-tailed paired Student's t test, t(6) = −2.38, p = 0.06 (Figure 5D).

Impact of coarse direction discrimination training on fine direction discrimination

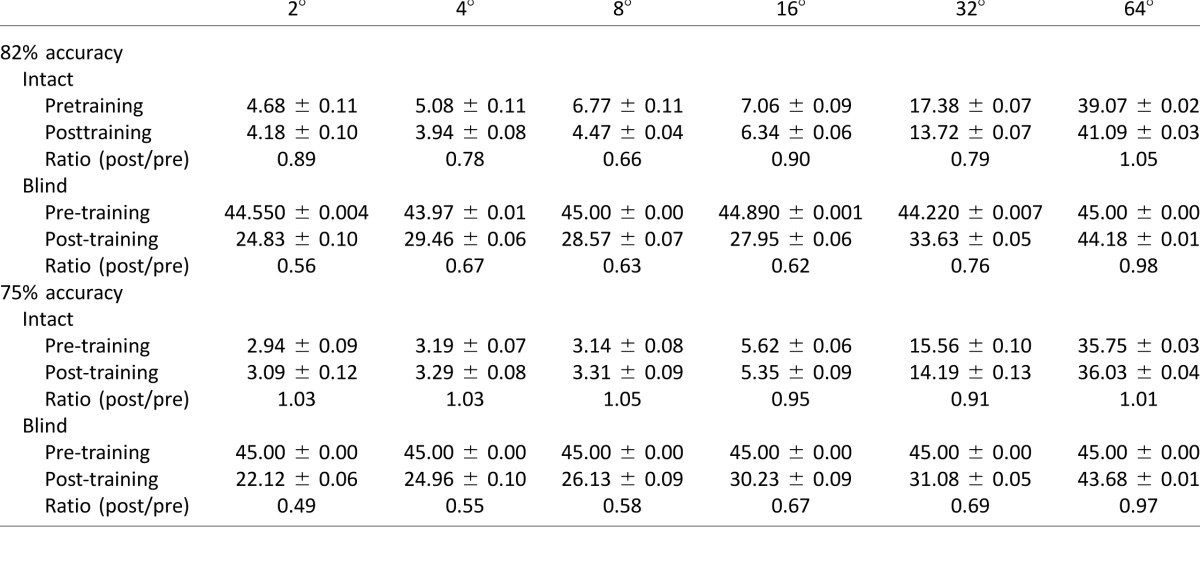
After recovering normal NDR for the left–right, coarse, direction discrimination task, it became possible to measure reliable, fine direction difference thresholds in all trained CB subjects (Table 2). These thresholds averaged 28.3° ± 13.1° (M ± SD) at the trained blind field locations. As previously reported by Das et al. (2014) using a same–different task and random dot stimuli containing 0° range, these values were significantly higher, two-tailed paired Student's t test, t(6) = −4.87, p = 0.003, than those at equivalent locations in the subjects' intact visual fields, where fine difference thresholds averaged 4.6° ± 2.4° (Figure 5E).

Table 2.

Fine direction discrimination thresholds before and after training in intact and blind fields of CB subjects.

Effects of external noise on fine direction discrimination at retrained blind field locations

To better understand residual inefficiencies in fine direction discrimination at trained blind field locations, we measured the effects of added external noise on task performance. The resultant TvN data are shown in Figure 6. Before a detailed analysis with the LAM and PTM, we first conducted a series of ANOVAs to assess the statistical significance of performance differences measured pre- and posttraining in CB subjects (Figure 6A, B), as a function of test and retest in visually intact controls (Figure 6C), and between CB subjects and visually intact controls.

Figure 6.

Effect of training on fine direction discrimination performance. (A) Prior to training, fine direction difference thresholds within the blind field were close to ceiling, hovering just below 45°. Following training, thresholds in the blind field improved. (B) This training had no significant effect on subject performance in the intact field of vision. (C) Likewise, repeated testing of visually intact subjects did not alter performance in the absence of training.

Pretraining, CB subjects exhibited marked difficulties performing this task in their blind field relative to intact regions of their visual field (Table 2). This difficulty was not due to misunderstanding the task requirements because all subjects performed the fine direction discrimination task easily in their intact hemifield of vision. However, whereas they could detect the appearance and disappearance of a stimulus in their blind field, most reported not being able to reliably identify its direction of motion. As a result, direction difference thresholds could not be measured in four out of seven CB subjects because they never reached the requisite percent-correct level. In these instances, a difference threshold “value” of 45° was assigned (the highest possible threshold in our paradigm). A two-way ANOVA comparing performance at 82% correct pretraining in the intact field versus the blind field revealed a main of effect of location, F(1, 60) = 754.5, p < 0.0001, and noise (i.e., direction range), F(5, 60) = 29.53, p < 0.0001, as well as an interaction between them, F(5, 60) = 26.48, p < 0.0001.

Subsequent visual training in the blind field significantly improved fine direction discrimination performance at the trained blind field locations, but not at corresponding locations in the intact field of vision (Table 2). A repeated-measures ANOVA for blind field performance revealed a main effect of training, F(1, 12) = 16.82, p = 0.0015, and directional noise, F(5, 50) = 7.86, p < 0.0001, as well as an interaction between them, F(5, 60) = 6.36, p < 0.0001. This suggests that training significantly improves the ability of CB subjects to process noisy motion stimuli—except at the highest noise levels—at trained blind field locations. In contrast, a two-way ANOVA with pre- and posttraining performance in the intact hemifield of vision as the between-subjects factor (Figure 6B) and noise level as the within-subjects factor revealed a main effect of noise, F(5, 48) = 116.75, p < 0.0001, but no significant effect of training, F(1, 48) = 2.13, p = 0.15, and no significant interaction between them, F(5, 48) = 1.79, p = 0.13. This suggests that noise processing for motion remains unchanged in the intact field of vision following blind field training.

To assess whether the large number of trials necessary to collect TvN curves for modeling with the LAM and PTM changed performance and thus, model outcomes, we collected an entire data set twice on four visually intact, age-matched controls, with ∼30 days between testing sessions (Figure 6C). A repeated-measures ANOVA showed a main effect of noise, F(5, 30) = 92.66, p < 0.0001, but no significant effect of testing, F(1, 6) < 1, and no significant interaction, F(5, 30) < 1, confirming that two separate testing sessions (and the associated large number of trials) did not create a learning effect on their own.

Finally, we also asked whether performance in the intact field of CB subjects was different than that in visually intact controls. A two-way ANOVA of intact field posttraining performance and testing Session 2 in controls revealed a main effect of noise, F(5, 48) = 87.63, p < 0.0001, but neither a significant effect of subject type, F(1, 48) < 1, nor an interaction between them, F(5, 48) < 1, suggesting that the V1 lesion did not impact vision in the intact hemifield, at least for this task.

LAM analysis

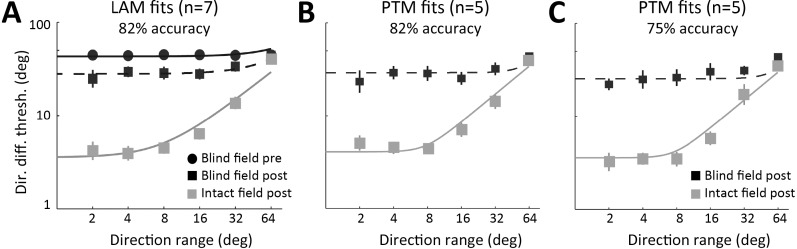
TvN data from the 82% level of performance were first fit using the LAM to determine the nature of observed differences. We focused on the 82% correct data because the LAM does not differentiate mechanisms at different performance levels and we have full datasets for all seven subjects at the 82% level. When comparing performance at the originally selected blind field locations before and after training, as well as with matched locations in the intact field, improved performance in the low external noise conditions would indicate that training reduced the amount of internal noise in the system, whereas improvements across all external noise levels would indicate that training increased sampling efficiency. Among 25 candidate models tested (see Methods), the best-fitting model (R² = 98.1%; four free parameters: A_eq[pre], A_eq[post], N_eq, and E) was the model that assumed a change in equivalent internal noise and no changes in sampling efficiency. Specifically, before training, the blind field had 11.1 times more equivalent internal noise than the intact (good) field (Figure 7A). Visual training reduced the amount of internal noise at the trained blind field locations, but it still remained 6.9 times higher than the estimated internal noise in the intact field of vision (Figure 7A). Statistically, an F test comparing the models revealed that this reduced model was not different from the full model, F(2, 12) = 0.99, p = 0.40, which assumed that both equivalent internal noise and sampling efficiency differed across the three conditions. However, the reduced model was substantially better than the no-difference model, F(2, 14) = 307.7, p < 0.0001, which assumed no changes across the three conditions (Table 3). Other candidate models either provided significantly worse fits compared to the full model, or had more free parameters than the best-fitting model. In summary, in the blind field, the best-fitting LAM suggested that perceptual training in the blind field reduced equivalent internal noise by 38%. However, the recovered visual processing still had ∼7 times more equivalent internal noise than the intact visual field.

Figure 7.

LAM and PTM analysis. (A) LAM analysis (fit lines indicate best-fitting model) of blind field pre- and posttraining data indicated a reduction of internal noise with no change in sampling efficiency. However, despite these improvements, thresholds in the intact field of vision remained significantly better than at the posttraining blind field locations, which were computed to have increased internal noise relative to the intact field. (B) TvN data for 82% and 75% correct levels, contrasting direction difference thresholds in the intact field of vision and blind field posttraining. The best-fitting PTM model (fit lines indicate best-fitting model) showed that following training, blind field locations continued to have more additive internal noise compared to the intact visual field. There was no change in multiplicative noise or external noise processing between the posttraining blind field locations and the intact visual field.

Table 3.

Parameters of LAM fitting. Note: See text for definitions and methodology.

PTM analysis

To better understand residual visual deficits at trained blind field locations relative to vision in intact portions of the visual field, TvN curves measured at 75% and 82% accuracy were analyzed using the PTM. Because blind field thresholds were close to or at ceiling prior to the onset of training, it was not possible to estimate two accuracy levels at that time. Consequently, PTM analysis was restricted to the comparison between trained blind field locations and spatially matched locations in intact regions of the visual field (Figure 7B). The best-fitting model, with R² = 96.94% and five free parameters (γ, β, N_add, N_mul, A_a[post]) assumed only a change in internal additive noise. Specifically, the model estimated that the trained blind field locations contained 90.6 times more internal additive noise than matched, intact field locations (the magnitude difference between PTM and LAM findings is explained in the Discussion). No systematic differences were observed in external noise filtering or multiplicative noise (Table 4). This best-fitting model was not statistically different from the full model, F(2, 17) = 3.01, p = 0.076, but was significantly better than the no-difference model, F(1, 19) = 396.8, p < 0.0001. Particularly, the model that assumed reduced multiplicative noise (which can also predict lower thresholds at low external noise levels) provided a worse fit than the best-fitting model (R² = 33.03% vs. 96.94%), and the ratio of thresholds between the trained blind field locations and the intact field were relatively constant across the two performance levels (M ± SD; 82%: 0.36 ± 0.29 versus 75%: 0.33 ± 0.29, two-tailed Student's t-test, t(5) = 0.99, p = 0.367. These results ruled out the possibility of multiplicative noise reduction contributing to residual inefficiencies at trained blind field locations. In summary, the PTM analysis confirmed findings from the LAM analysis, with both models supporting the notion that residual perceptual deficits at trained blind field locations relative to intact regions of the visual field were due to abnormally high internal noise levels. The PTM suggested that this was additive internal noise and allowed us to ascertain that internal multiplicative noise and external noise exclusion were not significant contributors to these residual inefficiencies.

Table 4.

Parameters of PTM fitting. Note: See text for definitions and methodology.

Discussion

Visual training can improve visual performance in CB fields (Kasten & Sabel, 1995; Sahraie et al., 2006; Raninen, Vanni, Hyvarinen, & Nasanen, 2007; Bergsma & van der Wildt, 2009; Huxlin et al., 2009; Sahraie et al., 2010; Bergsma et al., 2012; Das et al., 2014). However, whereas coarse, global direction discrimination training can recover direction integration thresholds back to intact field levels (Huxlin et al., 2009; Das et al., 2014), fine direction difference thresholds are only partially restored in a comparison task (Das et al., 2014). Here, we verified this fine discrimination deficit in a simple discrimination task and sought to characterize both the computational principles underlying signal processing changes that occur following coarse discrimination training, and those that may underlie residual processing deficits relative to performance in intact hemifields of vision.

Improved internal noise processing underlies visual recovery in CB fields

Damage to the visual system can increase levels of internal processing noise (Hayes & Merigan, 2006). It has also been suggested that elevated internal noise may be responsible for impaired visual performance in people with abnormally developed visual systems (Levi & Klein, 2003). Thus, a reasonable prediction is that training may improve performance by reducing internal processing noise. Supporting this notion, posttraining performance of CB subjects exhibited a LAM signature indicative of less equivalent internal noise relative to pretraining levels, but no change in sampling efficiency. Thus, training primarily created signal-to-noise ratio improvements at trained blind field locations, with thresholds falling by about 40% at the three lowest external noise levels, but only by about 16% at the two highest external noise levels. A potential concern with this finding is that the LAM (and for that matter, any type of model) may not be optimal because of near-chance performance in the blind field before training. Thus, changes in internal processing noise are more likely to be detected by the model fits, because training-induced improvements will probably occur at low noise levels before they occur at more difficult, higher noise levels. Given that internal noise sets the maximum performance level a subject can achieve (Lu & Dosher, 2004), it may be necessary for internal noise levels to change by a minimum amount before changes in sampling efficiency are detected. Continued training of CB subjects may eventually reveal changes in sampling efficiency within the blind field, but they may first require a reduction of internal noise.

We speculate here that in addition to the loss of feed-forward sensory input, elevated internal noise may be one reason why pretraining vision in CB appears dominated by extra-geniculo-calcarine projections (i.e., commonly assumed blindsight pathways; Azzopardi & Cowey, 1997) rather than by residual V1 processing (Papanikolaou et al., 2014). Were that the case, and were there a causal relation between internal noise and reduced conscious vision in CB fields, then decreasing internal noise could represent a restorative mechanism for conscious vision.

Residual visual deficits in CB fields are associated with high residual internal noise

The PTM can separate the impact of internal additive, internal multiplicative, and external noise exclusion on subject performance (Lu & Dosher, 1999) and was used here to further study the residual defects observed in posttraining blind fields. PTM fits of TvN curves confirmed the LAM results that internal noise was indeed elevated in trained blind field locations compared to intact visual field locations. The PTM revealed that this was likely due to internal additive rather than multiplicative noise. This is consistent with the fact that multiplicative noise scales with stimulus intensity and worsens performance at all noise levels, even for high-contrast targets. In CB subjects, posttraining performance was not impaired for high-contrast stimuli (Huxlin et al., 2009; Das et al., 2014). Finally, the PTM revealed no change in external noise exclusion between intact and trained blind field locations.

Overall, in spite of the larger number of free parameters in the PTM relative to the LAM (a key reason why we used both models in the present study), and in spite of different theoretical assumptions, both models converged on the same conclusion and generated consistent, qualitative predictions. We speculate that the reason why quantitative estimates of abnormally high internal noise in the blind field were much higher for the PTM than the LAM lies in the different theoretical assumptions made by the two models. Specifically, the LAM assumes that contrast energy at threshold correlates linearly with internal noise energy. The PTM assumes that input signals and embedded external noise are amplified by a nonlinear rectification process, which increases both external noise and multiplicative noise (Lu & Dosher, 2004). This is mathematically equivalent to lessening internal additive noise (Equation 2). Thus, for the same data, the nonlinearity in the PTM will result in a greater difference in internal noise than LAM fits. This is similar to findings in prior work, in which fitting both the LAM and PTM to the same data set resulted in large differences in fitted values, albeit for a smaller amount of learning than that reported here for CB subjects (Lu & Dosher, 2004).

Normal performance in intact portions of the visual field in CB

External noise manipulations revealed no significant performance differences between the intact field of CB subjects and visually intact controls, indicating that noise processing in fine direction discrimination was unimpaired in the visual field ipsilateral to a V1 lesion. This suggests no significant callosal influence of a unilateral V1 lesion on the intact brain hemisphere's ability to process fine direction differences, even when these are embedded in directional noise.

Putative mechanisms of partial restoration of fine direction discriminations

That coarse direction discrimination training improves fine discrimination thresholds at all in CB fields is impressive. In visually intact subjects, fine direction discrimination can improve by boosting the response gain or by sharpening tuning curves of motion-selective cells. Given that we saw no change in sampling efficiency, we suggest that training reduced internal noise in the residual, motion-selective circuitry primarily by boosting the gain of the population's response (Ling et al., 2009). In fact, the signature of training-induced effects in our CB subjects was similar to that attained following direction discrimination training in high external noise conditions in the fovea of visually intact subjects (Lu et al., 2006). If stimuli presented in CB fields are experienced as noisy and poorly discriminable, then our training may indeed be similar to training under externally noisy conditions.

Nevertheless, residual deficits in fine direction discrimination and contrast sensitivity observed posttraining (Das et al., 2014) could have resulted from the fact that only coarse discriminations were trained. Coarse discriminations are easier to perform than fine discriminations and may not require a major shift in the readout of the population response to recover performance. However, a more precise readout would be required to perform fine direction discriminations. Initial training on easy (coarse) discriminations was necessary in our paradigm because, at first, CB subjects are unable to discriminate even the largest direction differences reliably in their blind field. An interesting question then is whether subjects can ever fully recover fine discriminations in their blind fields. The reverse hierarchy theory posits that learning of easy (coarse) discriminations alters function in higher level visual areas, whereas learning of difficult (fine) discriminations relies on changes in processing within low-level visual areas (Ahissar & Hochstein, 1997), the locus of damage in our subjects. In adult macaque monkeys with aspiration lesions of V1, recordings within a month or two of the striate damage showed a significant reduction in the number of visually responsive MT neurons (down to 66%) and in the response rates of these neurons (Rodman, Gross, & Albright, 1989). However, MT neurons that maintained responsiveness continued to exhibit direction selectivity and relatively normal tuning (Rodman et al., 1989), a result largely recapitulated with reversible inactivation of V1 (Girard et al., 1992). If indeed directional selectivity is preserved in MT, it could provide a substrate for training-induced visual improvements.

Although MT may retain direction selectivity and tuning for a short time after V1 is silenced, a more relevant question regarding CB subjects is whether these properties are maintained more than 6 months after permanent V1 lesions. V1 damage may cause a large reduction of direction selective cells in CB subjects. Strobe-reared cats also have significantly reduced numbers of direction-selective neurons (Cynader, Berman, & Hein, 1973; Olson & Pettigrew, 1974). These cats can perform coarse direction discriminations, but like CB subjects in the present study, they cannot discriminate fine direction differences normally (Pasternak & Leinen, 1986; Pasternak, 1990; Pasternak, Albano, & Harvitt, 1990). However, training these animals to detect rightward motion created direction selectivity, improving their speed sensitivity for trained stimuli, increasing the proportion of direction and orientation-selective cells in their striate cortex (Pasternak, Movshon, & Merigan, 1981). This finding provides hope that if some direction selectivity is maintained in the CB visual system, fine discrimination training may restore this ability in CB subjects.

Such restoration could happen via reweighting or by changing the readout of lower level units by decision-making circuitry (Dosher & Lu, 1998; Dosher, Jeter, Liu, & Lu, 2013). Unlike coarse direction discrimination tasks, which rely on sensitivity of neurons selective for stimulus direction, fine direction discrimination may require more appropriate inference from decision units to lower level representation (Bejjanki, Beck, Lu, & Pouget, 2011). Human psychophysical and monkey neurophysiological studies suggest the most “informative” neurons in fine direction discrimination tasks are those that prefer directions within half a bandwidth of the stimulus direction (Purushothaman & Bradley, 2005; Jazayeri & Movshon, 2007). Computationally, training fine direction discrimination could reweight sensory inputs, assigning more weights to the most informative neurons and reducing weights given to task-irrelevant (or noisy) neurons, thus improving the readout.

Conclusions

The present study shows, for the first time, that training-induced visual discrimination improvements in cortically blind fields are associated with a reduction in internal noise at the trained blind field locations. However, this reduction is not sufficient to return fine direction discrimination performance in the blind field back to normal levels, a factor that may be explained by extremely high, residual, additive, internal noise within these trained locations, relative to the intact hemifield of vision. Future work will investigate if training fine direction discrimination specifically can overcome these residual inefficiencies, or if the loss of a significant proportion of direction selective cells in cortex following V1 damage results in permanent deficits on this task.