Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 Sep 28;5:14581. doi: 10.1038/srep14581

Atomic-scale diffractive imaging of sub-cycle electron dynamics in condensed matter

Vladislav S Yakovlev 1,2,a, Mark I Stockman 1, Ferenc Krausz 2,3, Peter Baum 2,3,b
PMCID: PMC4585944  PMID: 26412407

Abstract

For interaction of light with condensed-matter systems, we show with simulations that ultrafast electron and X-ray diffraction can provide a time-dependent record of charge-density maps with sub-cycle and atomic-scale resolutions. Using graphene as an example material, we predict that diffraction can reveal localised atomic-scale origins of optical and electronic phenomena. In particular, we point out nontrivial relations between microscopic electric current and density in undoped graphene.

Any light-matter interaction is, at its fundamental level, defined by field-driven motion of charges in their atomic-scale environment. Depending on a material’s structure, potential-energy landscape, correlation mechanisms and applied field strength, this motion may be highly complex, and it causes a rich variety of macroscopic optical phenomena, which are at the heart of current laser technologies1, quantum optics2,3, spectroscopy4, nonlinear microscopy5,6, frequency comb metrology7,8, optical information processing9,10, and light-driven electronics11,12,13.

In this paper, we take a real-space/sub-cycle perspective seeking the most direct way to comprehend the nature of optical and electronic phenomena at lightwave frequencies. We consider the following questions: Within a laser cycle, what fraction of the material’s charge density is driven into which direction resulting in which macroscopic response? Are there certain electron densities that are particularly efficient for specific effects? And what experimental approach can possibly reveal such three-dimensional motion of charges in real space? Sub-cell and sub-cycle resolution in space and time, if feasible, would arguably provide the most straightforward access to the basic microscopic effects underlying complex light-matter interaction.

Concept for sub-cycle imaging in real space

The example system considered in this work is graphene, which is well known for its unusual electronic and optical properties14 and high potential for future high-speed electronics. Here, graphene is chosen due to its relatively simple structure and the large number of valence electrons per nucleus. The imaging concept is ultrafast pump-probe diffraction with electron or X-ray pulses of sub-laser-cycle duration, short enough to freeze out the relevant electronic and resultant atomic motion driven by light. Such pulses are achievable with free-electron lasers and, potentially, also with electron pulses, as we discuss below. A series of diffraction snapshots recorded under such conditions for different delays with respect to the driving field can provide real-time insight into rearrangement of electronic charge in condensed matter with spatial and temporal resolution. This idea was introduced earlier15 and modelled in detail for electronic superposition states in atoms and diatomic molecules16,17,18,19,20, as well as for polyatomic molecules on much slower time scales21. Seminal experiments with femtosecond X-rays22,23,24 revealed sensitivity of ultrafast diffraction to light-field-driven electron dynamics, albeit in a cycle-averaged experiment without sufficient temporal resolution. Our main goal here is to demonstrate the feasibility and importance of fully resolving electronic motion driven by the oscillating light fields in space and time. We also show how graphene’s complex relations between atomic- and macroscopic-scale phenomena may be revealed by ultrafast pump-probe diffraction.

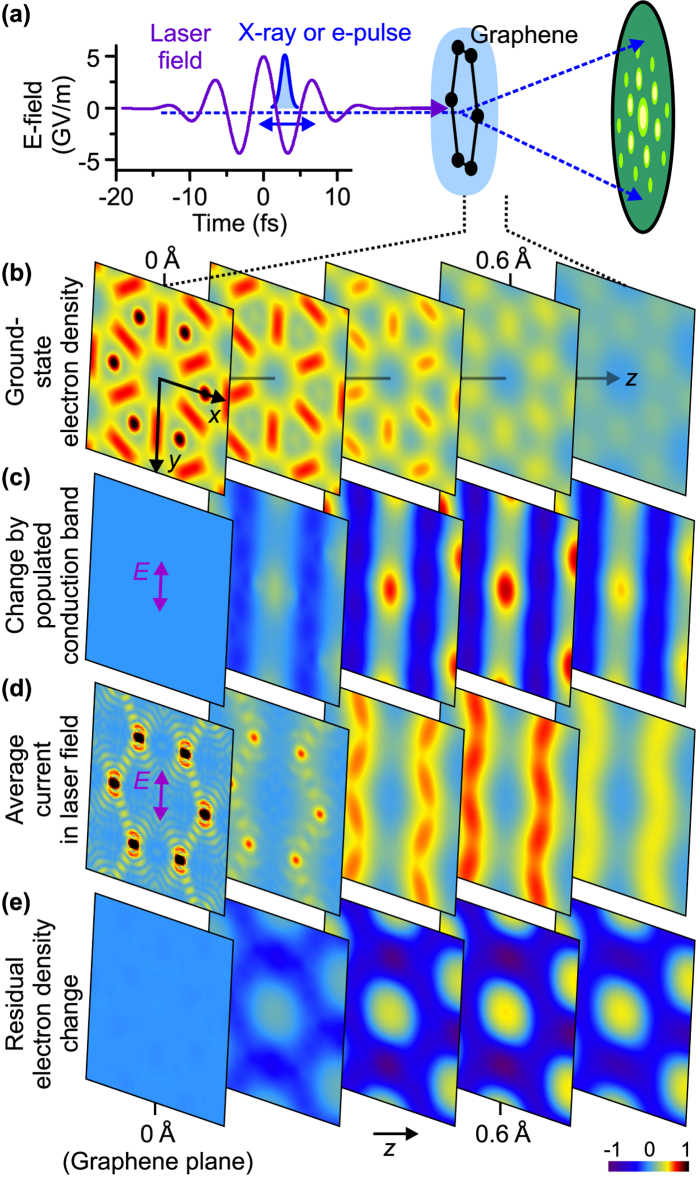
Figure 1(a) depicts a schematic of the proposed experiment. A material (here graphene) interacts with a 10-fs laser pulse carried at a frequency of 140 THz, i.e., a wavelength of 2.1 μm. For such a pulse, the direct excitation of phonons is negligible, and graphene’s response is mostly electronic. The 7-fs optical period of a 2.1-μm pulse is short enough to neglect, in a first approximation, lattice motion; at the same time, it allows for realistic sub-cycle diffraction measurements with few-fs electron and X-ray pulses. As a peak electric field, we use 0.5 V/Å, which is high enough for the onset of nonlinear and strong-field effects25 while still below graphene’s damage threshold26. Current laser technology readily provides such pulses1,27. The optical electric field in our calculations is polarised along graphene’s Γ-K direction, i.e. in real space from the hexagon centre towards the middle of a C-C bond. Snapshots of the moving charges are taken by pump-probe diffraction with ultrashort electron or X-ray pulses of sub-cycle duration for later slow-motion replay.

Figure 1. Real-space imaging of electronic motion in condensed matter.

Figure 1

Open in a new tab

(a) A few-femtosecond electron or X-ray pulse (blue) probes how the charge density in a sample, here graphene, changes under influence of an intense mid-infrared laser pulse (violet). The intensities of Bragg spots (green) are measured for a series of delays between the pulses. (b) Ground-state electron density of graphene’s valence-band electrons in several planes parallel to the sample; the distance to the centre of the atomic layer varies from z = 0 in steps of Δz = 0.2 Å. (c) Change of the electron density caused by excitation from the top 2 eV of the valence band below the Fermi energy to the bottom of the conduction band. (d) Time-averaged magnitude of the atomic-scale electric current. (e) Change of the microscopic electron density after the interaction with the laser pulse. In panels (b–e), the coordinates x and y span the range ±2.1 Å.

Real-space electron dynamics and its complexity

First we report a simulation of graphene’s electron dynamics in real space and discuss its relation to macroscopically observable optical phenomena. The method employed is a numerical solution of the time-dependent Schrödinger equation for a phenomenological lattice potential; see Methods. Figure 1(b) shows the static density of graphene’s valence electrons without the optical field. From a chemical perspective, graphene is a sp2-hybridised structure; each carbon atom, which has electron configuration 1s22s22p2, contributes three of its four valence electrons to three sigma bonds and one to a delocalised electron density above and below the plane of the nuclei.

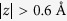Hence, there are two electrons per sigma bond and two delocalised electrons per unit cell. In the computed ground-state charge-density map of Fig. 1(b), these are evident: the sigma bonds form density maxima between carbon atoms, and the pz electrons contribute to an additional delocalised density at larger Inline graphic. For sufficiently large Inline graphic, for example, at Inline graphic, there are local density maxima above/below each C-C bond, not above/below the nuclei. This is a consequence of the overlapping pz orbitals in conjunction with remaining parts of the bond-forming sp2 densities. In other words, the sigma bonds and the delocalised electron density overlap significantly in real space. We note that there is also some remaining density of the valence electrons concentrated around the nuclei.

Electric current in undoped graphene can only exist if some electrons are excited into conduction bands. Let us consider a gedankenexperiment where we transfer valence electrons within a 2-eV energy range from the Fermi level and below into the lowest conduction band conserving the quasi-momentum. Note that this includes the electrons occupying the vicinities of the K points in reciprocal space. Figure 1(c) depicts the change of the electron density upon such excitation. There is no change in the graphene plane, but a maximum change at a distance of 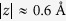Inline graphic above and below it. Remarkably, the electron density is transferred from two localised stripes (dark blue) into a central area (yellow) with a peak (red) at the hexagon centre. This real-space representation of the static band-population change provides the first sign of electronic motion’s complexity in real space.

Next we discuss electron dynamics driven by the laser field. Generally, a material’s response can be separated into localised charge displacements and delocalised charge motion. At low, perturbative fields, the response of dielectrics for frequencies below the bandgap is due to localised charge displacement causing their polarisation. In contrast, electric current in conducting media (metals, doped semiconductors, conjugated polymers, etc.) is caused by delocalised charges. In general, especially in complex materials, both localised and delocalised charges shape the optical response.

In undoped graphene, microscopic (atomic-scale) electron and current densities are, to a significant degree, complementary to each other in real space. This is evident from Fig. 1(d) where we plot magnitude of current density averaged over time. The result looks dramatically different from both the ground-state electron density of Fig. 1(b) and also the excited-state density change of Fig. 1(c). Although the electron density transferred to the conduction band is concentrated in the unit cell centre [Fig. 1(c)], the current is concentrated at its periphery and 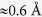Inline graphic above and below the atomic plane where the delocalised and overlapping pz orbitals are situated. Hence, the electric current predominantly flows through regions where these orbitals form continuous chains along the laser polarisation. Note that little or no current flows at the hexagon centre, where carbon orbitals have a negligible overlap. Also, there is no appreciable contribution to graphene’s local or non-local currents originating from any C-C bond electrons in the atomic plane. These combined observations further suggest value of a real-space visualisation approach.

Figure 1(e) identifies the spatial regions associated with optical absorption by depicting the residual change of electron density at t = 20 fs, after the excitation pulse has passed. The deposited energy per pulse is, in our model, 1.9 eV per unit cell. This causes no density change in the plane of the nuclei, but above and below it, charge is transferred towards the carbon hexagon centre where the initial electron density is low. This effect of the intense laser pulse is qualitatively different from that shown in Fig. 1(c) where electrons from the top of the valence band are artificially transferred to the conduction band. This difference is yet another indication of significance of real-space electron distributions.

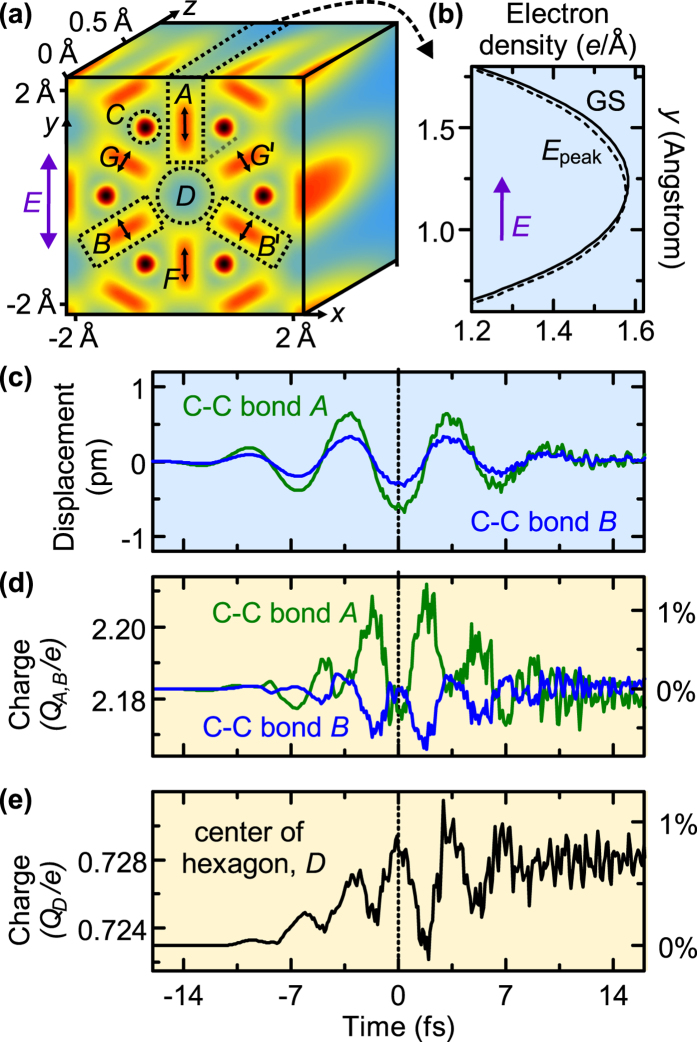
To further elucidate the importance of charge movement in real space, we introduce some regions of interest, labelled A-G in Fig. 2(a). These regions are chosen to encompass distinguishable areas of electron density. The volumes associated with the C-C sigma bonds form two Bravais sub-lattices, one of which contains regions A, B, and 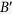Inline graphic, and the other one F, G, and 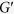Inline graphic. 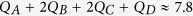Areas A and B are Inline graphic, the radius of area C is 0.26 Å, and that of area D is 0.53 Å. Along the z direction, these volumes extend through the entire simulation space. In the stationary state, volumes A and B contain QA = QB = 2.2 electrons each, which is close to the expected two electrons per the sp2-type sigma bond; volume C contains QC = 0.29 electrons, and there are QD = 0.72 electrons in volume D. Together, Inline graphic electrons per unit cell, close to the overall number of 8 valence electrons of graphene. This indicates that all relevant charges are covered by our assignment.

Figure 2. Real-space analysis of sub-cycle laser-induced perturbations of the charge density in graphene.

Figure 2

Open in a new tab

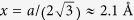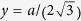(a) Definition of volumes A-D corresponding to distinct types of electrons. The three facets of the cube display the stationary density of valence electrons in the planes z = 0, Inline graphic, and Inline graphic; a = 2.46 Å is the lattice period. Volumes A and B cover the bonds between carbon atoms; volumes C and D cover the nuclei and the hexagon centre, respectively. (b) The displacement and deformation of the charge distribution in volume A in the ground state (GS, solid) and at the peak of the laser field (dashed) along the direction of the laser polarisation (y-axis) and integrated over x and z. (c) Time-dependent displacement of electrons in volumes A (green) and B (blue); the direction is indicated by the black arrows in panel (a). For both bonds, it nearly instantaneously follows the electric field. (d) Time dependence of the charge (number of electrons) in volumes A (green) and B (blue), revealing dynamics at twice the laser frequency. (e) Charge in volume D around the hexagon centre, increasing stepwise with time as a result of electronic excitations.

In each region, the time-dependent effects of the laser field on the charge density are decomposed into two components: local displacement and redistribution between different volumes. We quantified the displacement by evaluating the first momentum (centre of mass) in each volume. For the C-C bond perpendicular to the laser polarisation (region A), Fig. 2(b) compares the ground-state electron density (solid) to that at the instance of maximum field strength (dashed). At this moment, the main effect of the field is displacement of the charge within the bond, though some decrease of the charge is also visible.

Temporal dynamics of displacements and charges are shown in Fig. 2(c–e) for the two types of C-C bonds (volumes A and B) and for the centre of the graphene hexagon (volume D). The field-induced local displacement of the electrons in volumes A and B is about one picometre; see Fig. 2(c). At all times, the shift is approximately proportional to the laser field. The C-C bond represented by volume B also experiences a shift that is proportional to the electric field [Fig. 2(c), green]. The direction of the shift is shown by black arrows in Fig. 2(a) and it is not parallel to the laser field, as one could naively expect. Instead, the centre of mass of volume B moves predominantly along the bond. This is due to the polarisability of a bond being larger along its direction than normal to it. The valence charges around the nuclei (volume C) shift by only ~0.07 pm in the laser field and give/receive a maximum of only ~0.002 electron. These charges are, therefore, negligible for graphene’s optical and electronic dynamics.

Figure 2(d) shows the time-dependent integrated charge in volumes A and B. Both traces start at the same amount of charge, ~2.2 electrons, which is close to the charge expected from chemical considerations: two electrons from a sigma bond plus 60°/360° = 1/6 ≈ 0.167 from the one delocalised electron per carbon in the out-of-plane bonds. The charge 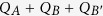Inline graphic is approximately conserved at all times. Also, in a good approximation, the changes of the charge in the individual regions satisfy the relation 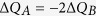Inline graphic. This reflects the symmetry of the system with respect to reflection 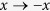Inline graphic in conjunction with pseudo-spin conservation implying charge conservation within each sub-lattice. As each of the two type-A bonds receives its peak charge increase of ~0.03 electrons, each of the four type-B bonds loses ~0.015 electrons. Our results show that this charge transfer mainly takes place at 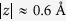Inline graphic, i.e., significantly out of the plane of graphene.

Unlike the charge displacement, the amount of charge in a certain volume is modulated in time with twice the laser frequency, and it is symmetric with respect to the sign of the laser field. Also, the phase of this field-induced charge migration between different types of bonds indicates that the vector potential, rather than the electric field, determines these dynamics: There is little charge transferred at the field extrema, while a maximum amount of charge is transferred between volumes A and B at the zero electric field. The fact that the magnitude of the electric current is also maximal at the zero field suggests that the atomic-scale charge redistribution shown in Fig. 2(d) is a prerequisite for inducing a significant electric current in undoped graphene. 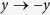The effective charge transfer between regions A and Inline graphic is also largely symmetric with respect to Inline graphic and, consequently, negligibly contributes to net polarisation and current. This charge transfer effect is therefore hidden from far-field spectroscopic characterisation.

Figure 2(e) shows time-dependent charge QD in the centre of the unit cell, volume D. This charge has local maxima at the crests of the laser field and minima at its zero crossings. On a few-femtosecond time scale, there is gradual accumulation of charge in volume D that persists after the pulse end, which is also evident in Fig. 1(e). Physically, this implies that the charge accumulation in the unit cell centre, D, has both an adiabatic component (the local maxima following the absolute strength of the laser field) and a non-adiabatic component caused by resonant absorption. This absorption in graphene is broadband28, causing rapid dephasing (Landau damping), leading to the stationary residual electronic excitation.

Experimental feasibility of sub-cycle electron diffraction

Here we propose an experiment for direct visualisation of purely electronic dynamics in graphene, and discuss its feasibility. The following three considerations are critical. First, the spatial resolution must be atomic. Second, temporal resolution must be sub-cycle. Third, there should be sufficient signal-to-noise ratio for the expected charge density changes, which manifest themselves in diffraction as time-dependent changes of Bragg peak intensities. In our case, sub-cycle means a quarter cycle of the laser, i.e. ~1.75 fs for the 2.1-μm driving laser considered here, in order to temporally resolve the largely nonlinear electron motion driven by a strong field, including, e.g., dynamics responsible for third harmonic generation.

Two currently emerging technologies can provide these prerequisites. Free-electron lasers (FELs) can deliver pulses with attosecond substructures29,30, and significant efforts are being made to scale up the photon energy toward wavelengths that would be sufficiently short for atomic-scale imaging31,32. The low scattering cross section of X-rays is compensated by the superior average photon flux of FELs; note that a particular peak flux is not required since the experiment is reversible. Some ionisation of the graphene sample eventually caused by a pump or a probe pulse will be rapidly replenished33. The second approach is ultrafast electron diffraction34,35. The de Broglie wavelength of electrons is as small as several picometres for kinetic energy of tens of kiloelectronvolts. The scattering efficiency from graphene is high, ~10−3 from the central beam into a typical Bragg spot; see Methods. Ultrashort pulses can be produced by microwave compression36,37 and, in the case of only one or a few electrons per pulse, simulations predict attosecond pulse durations38,39. Indeed, there is indirect experimental evidence40 of an attosecond electron pulse train15.

Here we consider electron diffraction at 30 keV, an energy low enough for efficient scattering and high enough to provide a 7-pm de Broglie wavelength. Diffraction is modelled neglecting inelastic scattering and the electron transit time through the sample, which is a few attoseconds; see Methods. At a realistic 300 kHz pump-probe repetition rate41, about 109 single-electron pulses are incident on the sample within one-hour integration time. With a scattering probability of ~10−3, this allows realistically low shot noise in the Bragg peak intensities.

The inset in Fig. 3 shows the expected Bragg pattern, where we have indicated Miller indices for the two primary reciprocal-space vectors. For the first two diffraction orders, Fig. 3(b,c) show the scattering probabilities as functions of the delay between the laser field [Fig. 3(a)] and a 1-fs electron pulse. Notably, the atomic-scale electron dynamics modulate the scattering probabilities by up to 2% within the first diffraction order and up to 0.2% within the second one. Such values are sufficiently high to be experimentally accessible with state-of-the-art pump-probe electron diffraction42,43.

Figure 3. Simulated pump—probe Bragg diffraction.

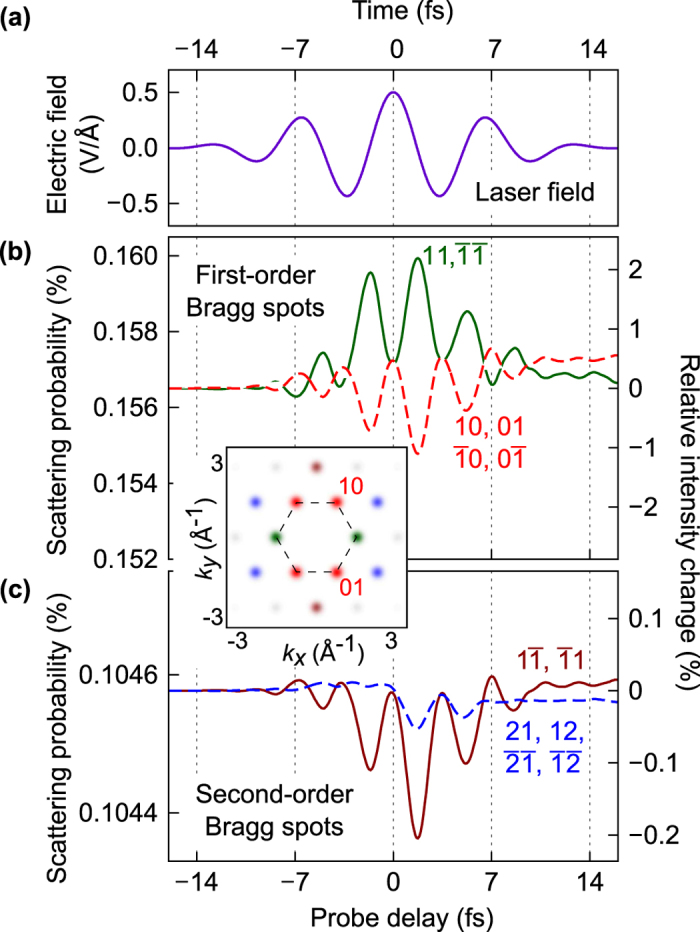
Figure 3

Open in a new tab

(a) Electric field of the laser pulse. (b) Scattering probabilities into first-order Bragg spots as functions of the arrival time of a 1-fs electron pulse with a mean electron kinetic energy of 30 keV. The maximum intensity change is 1–2%. (c) Scattering probabilities for the second-order Bragg spots. The maximum intensity change is 0.05–0.2%. The inset schematically shows the first Brillouin zone and the positions of the Bragg spots, which are coloured in the same way as the curves in panels (b,c).

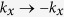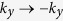The time-dependent scattering probabilities shown in Fig. 3 have symmetry that is specific for our experimental geometry: Inline graphic or Inline graphic, in addition to the general Friedel symmetry of Bragg diffraction. An important observation can be made by comparing Figs 2(d) and 3(b): For Bragg peaks 11 and 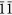Inline graphic, the delay dependence of scattering probabilities looks remarkably similar to the time dependence of the charge in volume A, while the charge in volume B correlates with the intensities of the other first-order Bragg peaks. This similarity encompasses both the modulation period (half of a laser cycle) and the changes that remain after the interaction. This suggests that significant aspects of the real-space light-driven electronic motion can be reconstructed from time-dependent diffraction experiments.

Retrieval of time-dependent charge-density maps

Which details can be retrieved? Bragg-peak intensities represent the magnitudes of complex scattering amplitudes, whose phases are not measured. Many advanced techniques exist to circumvent this problem using prior information, but these techniques may require some adaptation to reveal spatially delocalised changes in electron density, which are in contrast to localised atomic-type scatterers in crystallography.

Therefore, we refrain here from algorithmic procedures and report on a reconstruction specific to the symmetry in our example. First, we assume that the initial microscopic scattering potential is known, for example from ground-state calculations or state-of-the-art crystallography44,45. Second, we assume that the scattering amplitudes maintain their initial phases during the interaction with the laser pulse; see Methods. In this way, we reconstruct the part of the time-dependent electronic motion that is symmetric with respect to the reflection 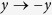Inline graphic, which is hidden from spectroscopy in dipole approximation. We used only the lowest two orders of Bragg scattering as depicted in the inset in Fig. 3.

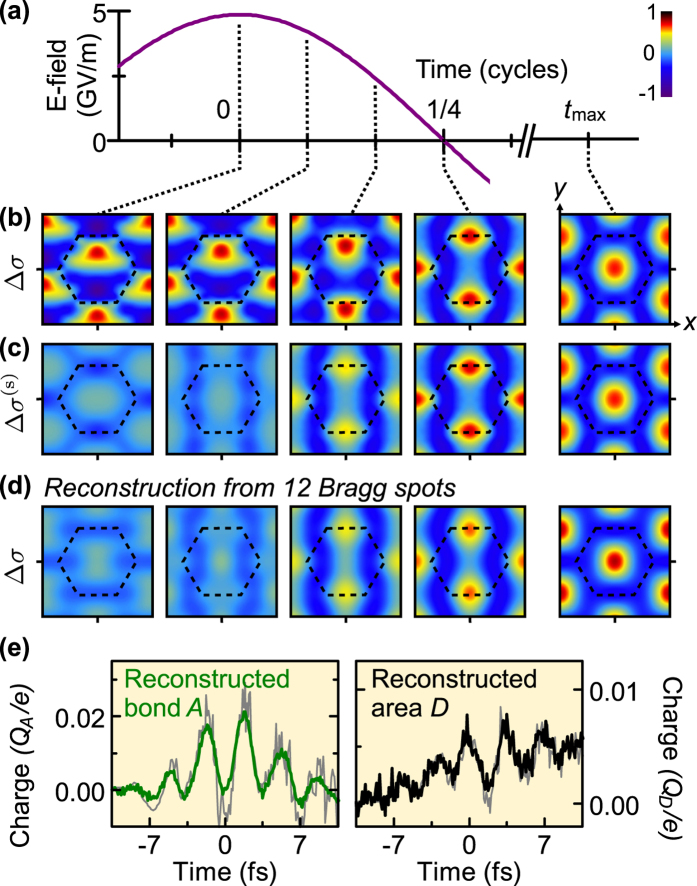
Figure 4 shows the results. In Fig. 4(a), we depict four representative times in the laser cycle and, additionally, a time 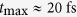Inline graphic, after the pulse end. The electron densities are integrated over z because z-dependent information is absent in diffraction geometry at normal incidence. Figure 4(b) shows changes in the simulated electron density, Δσ, and Fig. 4(c) shows the Δσ(s) that is symmetric with respect to reflection 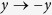Inline graphic, i.e. the part hidden from far-field spectroscopy. The outcomes of the reconstruction are shown in Fig. 4(d). The reconstructed charge-density maps are nearly identical to the y-symmetric parts of the actual electronic motion. Figure 4(e) shows the time-dependent charges in regions A and D, which are reliably reconstructed. A similar quality of reconstruction is also achieved for regions B and C (not shown). The spatial resolution can be further improved by incorporating more Bragg peaks in the reconstruction, provided that the signal-to-noise ratio is sufficiently large.

Figure 4. Reconstruction of the atomic-scale electron dynamics from pump-probe diffraction.

Figure 4

Open in a new tab

(a) Central laser cycle (violet) and five times of reconstruction. (b) Snapshots of the z-integrated electron-density change at the chosen moments of time. (c) Electron density symmetrised with respect to the reflection 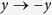Inline graphic. (d) Reconstruction of electron density snapshots from the 12 Bragg spots of Fig. 3 assuming no phase change of the ground-state scattering amplitudes. Whenever the charge distribution is symmetric with respect to the reflection 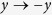Inline graphic, the reconstruction of the real electron density (b) is almost perfect. At other times, the symmetric part (c) is well reconstructed. (e) Time-dependent reconstructed charge in volumes A between carbon atoms (green) and volume D around the hexagon centre (black) in comparison to the actual simulated results (grey). These results confirm the ability of ultrafast diffraction to recover the atomic-scale, real-space origin of macroscopic optical and electronic phenomena.

General value of the real-space approach

We conclude by returning to our initial conjecture on the importance of time-dependent real-space recording of electronic motion. A periodic solid can be fully treated in either reciprocal or real space. However, the simplicity of the description or the feasibility of an experiment can define a preferred perspective. In graphene, our real-space analysis has revealed that electrons in different spatial regions respond to an external field in distinctly different ways. In particular, current flows in stripes above and below the plane of the chemical bonds, absorption populates the hexagon centre, the electrons localised at the bonds are periodically displaced along their structural extensions, and charges are periodically transferred in and out of the conducting stripes. These spatial peculiarities of the light-induced electron dynamics suggest the real-space perspective to be a worthwhile concept exposing features that are not easily discernible otherwise.

Real-space measurements will probably contribute most when applied to problems where spectroscopy does not provide sufficient information. They may give new insights into electronic origins of light-induced structural deformations, for example in graphite46, vanadium dioxide15, charge-density-wave materials47 or nanoparticles42. Knowing the mechanisms of charge transfer on an atomic scale may be indispensable for understanding strongly-correlated systems, i.e. materials where electron-electron interactions play a major role, as well as the build-up of electron-boson interaction, which has recently been shown to be an ultrafast process in high-temperature superconductors48. Identifying structure-function relations for optical phenomena can facilitate design of novel materials and ultrafast electronic devices. Ultrafast electron and X-ray diffraction bear a promise to become important techniques to study light-matter interaction in condensed matter.

Methods

The model

We designed a numerical model adapted for studying ultrafast electron diffraction on an atomically thin sample exposed to a strong field. We solve the time-dependent Schrödinger equation (TDSE) in three spatial dimensions for an ensemble of electrons moving in a local “effective” lattice potential V(r) that is periodic in any plane parallel to the atomic plane: V(r + a1,2) = V(r). Here, a1 and a2 are the lattice unit vectors, both of which are orthogonal to ez. Due to this periodicity, the Bloch theorem applies. We introduce the in-plane crystal momentum 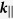Inline graphic, which is a conserved quantity in the velocity gauge. Henceforth we use atomic units and write the TDSE as

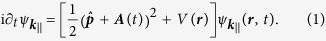graphic file with name srep14581-m23.jpg

Here, A(t) is related to the external electric field by 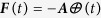Inline graphic. Equation (1) implies the dipole approximation; thus, we neglect the effect of the magnetic field.

Let 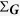Inline graphic denote a sum over vectors of the reciprocal lattice. For each 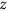Inline graphic, we decompose both the wave function 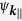Inline graphic and the latice potential in Fourier series:

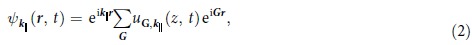graphic file with name srep14581-m28.jpg
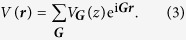graphic file with name srep14581-m29.jpg

For a function f(r) that has the periodicity of the lattice, the decomposition coefficients are

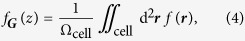graphic file with name srep14581-m30.jpg

where the integration is performed over the unit-cell area 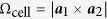Inline graphic. Ansatz (2) translates the TDSE (1) into

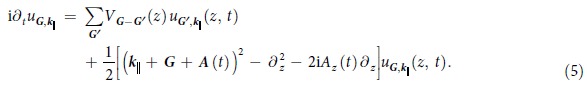graphic file with name srep14581-m32.jpg

This equation is solved for a set of initial conditions, each of which is defined by 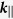Inline graphic and an initial valence band n.

One of the most important physical observables for electron diffraction is the electron density 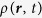Inline graphic, which we decompose into plane waves as well: 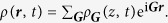Inline graphic Equations (2) and (4) yield

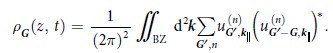graphic file with name srep14581-m36.jpg

The integral here is taken over the first Brillouin zone (BZ), and the contributions from all initial bands are added together; 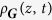Inline graphic is guaranteed to be non-negative.

Our phenomenological lattice potential V(r) is evaluated as a sum of atomic potentials

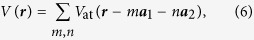graphic file with name srep14581-m38.jpg

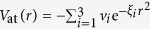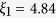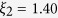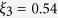each of which is parametrised as Inline graphic with v1 = 27.05, v2 = −10.18, v3 = 2.08, Inline graphic, Inline graphic, and Inline graphic. The band structure for this potential is shown in Fig. 5; it is similar to that obtained in ab initio simulations49. The Fermi velocity in our model is equal to 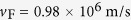Inline graphic in the direction orthogonal to Γ-K, which is close to the literature value: 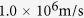Inline graphic50.

Figure 5.

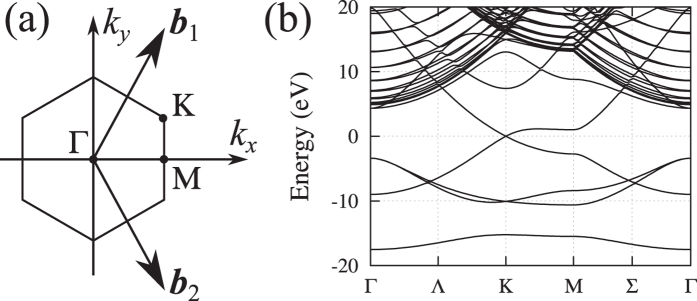
Figure 5

Open in a new tab

(a) The Brillouin zone of graphene and the reciprocal-space vectors. (b) The band structure evaluated with our model (the inner-shell bands are not shown). The Fermi energy is EF = 0. The energy gaps in the continuum spectrum are due to a relatively small size of the simulation box (51.2 at. u. along the z-axis), and they have no impact on electron diffraction.

We note that, unlike most pseudopotential methods, our lattice potential supports core states, which is important for electron diffraction. However, to reduce the required number of plane waves in expansion (2), we allow the 1s states to be less tightly bound as they are in a carbon atom: the 1s state in the potential Vat(r) has an energy of −121 eV, while the K-edge of carbon is at 282 eV. This allows us to consider only the reciprocal-space vectors with 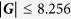Inline graphic. While the presence of the 1s state in the atomic potential is essential for obtaining correct nodal structures in the 2s and 2p states, dynamics of inner-shell electrons in our calculations have a negligible effect on Bragg peaks. Therefore, solving the TDSE, we consider only those initial states that correspond to valence bands.

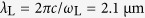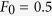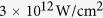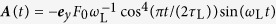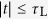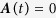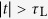The laser pulse in our simulations has a central wavelength of Inline graphic, a full width at half maximum (FWHM) duration of 10 fs, and a peak field of Inline graphic V/Å, which corresponds to a peak intensity of Inline graphic. We define the pulse by its vector potential: Inline graphic for Inline graphic and Inline graphic for Inline graphic.

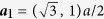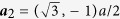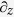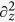For graphene, Inline graphic, Inline graphic, a = 4.65 atomic units. Discretising the crystal momentum, we use a Monkhorst grid51 with 32 × 32 = 1024 nodes. An 8-th order scheme allows us to evaluate Inline graphic and Inline graphic on a relatively coarse z-grid: 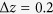Inline graphic. The grid contains 256 nodes, and we apply periodic boundary conditions. For solving the TDSE, we use the 4-th order Magnus propagator52,53, evaluate matrix exponentials using Expokit54, and perform the required sparse-matrix operations with the aid of CXSparse55.

Electron diffraction

We are interested in the intensities of Bragg peaks; their positions do not change as long as the lattice motion can be neglected because the interaction with a laser field preserves lattice periodicity. The first step in modelling elastic scattering of energetic electrons is the evaluation of the scalar potential induced by atomic nuclei, as well as core- and valence-band (VB) electrons. The spatial Fourier transform of the total potential is given by

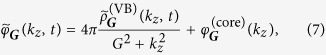graphic file with name srep14581-m58.jpg

where 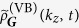Inline graphic is the Fourier transform of Inline graphic with respect to z, and 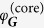Inline graphic is the ionic potential screened by core electrons; for 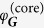Inline graphic, we use the Goedecker-Hartwigsen-Hutter-Teter pseudopotential of carbon56. We assume that atomic positions in the lattice have a root-mean-square uncertainty of 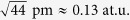Inline graphic resulting from disorder and thermal motion57. We account for this uncertainty by convolving 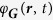Inline graphic with a Gaussian function.

Two factors simplify the evaluation of scattering probabilities: First, an energetic (tens of keV) projectile electron crosses a graphene sheet within just a few attoseconds and, during this time, the scattering potential can be considered constant. Second, integration over a range of angles and energies at a particular Bragg peak suppresses the interference of waves scattered at different moments of time. We also neglect inelastic transitions that give rise to interference effects discussed in19,58,59. In Supplementary Information, we derive, in the first Born approximation, the following expression for the probability of elastic scattering into a certain Bragg peak:

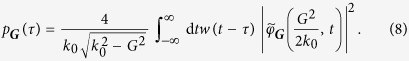graphic file with name srep14581-m65.jpg

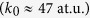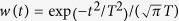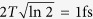Here, w(t) is the probability density for a projectile electron to cross the plane z = 0 at a time t, k0 is the average momentum of projectile electrons, and τ is the delay between the laser and electron pulses. For simulations, we use a kinetic energy of 30 keV Inline graphic and a Gaussian electron wave packet: Inline graphic with a FWHM of Inline graphic.

Reconstruction of electron density

We add a realistic amount of Poisson-distributed shot noise to the scattering probabilities (8) prior to reconstruction. We model the noise assuming that 109 electrons are available to record Bragg-peak intensities for a given delay between the electron and laser pulses. After that, we account for the symmetry of the considered problem by averaging electron counts in Bragg peaks that are symmetric with respect to the reflection off axes kx or ky. This ensures both Friedel’s law and the reflection symmetry in the reconstructed electron density.

For reconstruction, we only use the lowest two diffraction orders because, for higher orders, the shot noise dominates the useful signal. For low diffraction orders, the change of pz upon scattering is negligible: 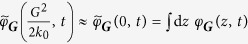Inline graphic in Eq. (8). In this approximation, the diffraction pattern is determined by the electron density integrated over the direction normal to the sample:

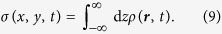graphic file with name srep14581-m70.jpg

Our reconstruction procedure, inspired by60, assumes time-independent phases of scattering amplitudes. In the stationary state of graphene, these amplitudes are real numbers, which reduces the information about their phases to knowing the sign of 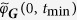Inline graphic. During the laser pulse, 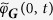Inline graphic are complex numbers, but the sum of each pair 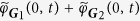Inline graphic is real if 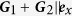Inline graphic. 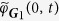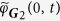Replacing each such pair of Fourier components with their averaged sum is equivalent to neglecting the imaginary parts of both Inline graphic and Inline graphic, and it is also equivalent to symmetrising the charge density:

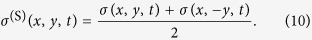graphic file with name srep14581-m77.jpg

Thus, by assuming constant scattering phases, we reconstruct the charge density symmetrised along the y-axis and integrated over z.

Details on the figures

Figures 1(b) and 2b display the sum of electron densities evaluated from all the valence bands:

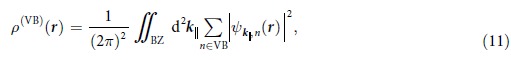graphic file with name srep14581-m78.jpg

where 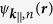Inline graphic are stationary states. Figure 1(c) illustrates how 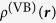Inline graphic would change if all valence-band electrons within a 2-eV energy range under the Fermi level were excited into the lowest conduction band preserving 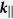Inline graphic. The average current density in Fig. 1(d) is evaluated as

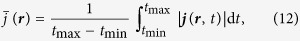graphic file with name srep14581-m82.jpg

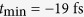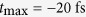where the time interval between Inline graphic and Inline graphic encompasses the laser pulse. The microscopic current density is evaluated using the following equations:

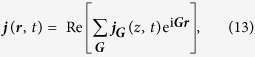graphic file with name srep14581-m85.jpg
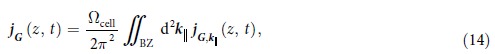graphic file with name srep14581-m86.jpg
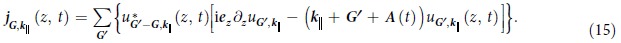graphic file with name srep14581-m87.jpg

The fast oscillations in Fig. 2(c–e) are due to the coherent superpositions of conduction- and valence-band states. They have a broad frequency spectrum, and the period of these quantum beats is much smaller than the duration of the electron pulse. Therefore, they are not time-resolved in the pump-probe measurement (Fig. 3). In Fig. 3(b,c), we plotted 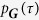Inline graphic given by Eq. (8).

The symmetrised density in Fig. 4(c) is defined as

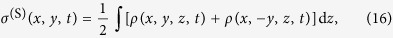graphic file with name srep14581-m89.jpg

which is the same as Eq. (10). The results shown in Fig. 4(d,e) are reconstructed from data obtained by adding shot noise to the scattering probabilities displayed in Fig. 3, see above.

Experimental damage considerations

The deposited energy per pulse at a field of 0.5 V/Å is approximately 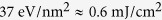Inline graphic. The spot size of the pump laser is determined by the size of the few-femtosecond electron beam, realistically ~50 μm diameter at the sample61. Each pump pulse heats up graphene by < 200 K, which involves electron-phonon and phonon-phonon relaxation processes that take their course within picoseconds62. At 300 kHz pump-probe repetition rate, about 3.5 mW of average power is absorbed. This is sufficiently low to be removed between pump pulses by heat conduction with a finely spaced TEM mesh41. Multiple scattering effects in electron diffraction are negligible because only tiny changes of Bragg intensities are recorded.

Additional Information

How to cite this article: Yakovlev, V. S. et al. Atomic-scale diffractive imaging of sub-cycle electron dynamics in condensed matter. Sci. Rep. 5, 14581; doi: 10.1038/srep14581 (2015).

Supplementary Material

Supplementary Information
srep14581-s1.pdf (84.3KB, pdf)

Acknowledgments

This work was supported by the Munich Centre of Advanced Photonics and the European Research Council. The work of M.I.S. and V.S.Y. was supported primarily by the Chemical Sciences, Biosciences and Geosciences Division (grant no. DEFG02-01ER15213) and additionally by the Materials Sciences and Engineering Division (grant no. DE-FG02-11ER46789) of the Office of the Basic Energy Sciences, Office of Science, US Department of Energy, and by a MURI grant from the US Air Force Office of Scientific Research. We thank Anthony F. Starace and Catherine Kealhofer for valuable discussions.

Footnotes

Author Contributions P.B. triggered and coordinated the investigation. V.S.Y. developed the model and performed the simulations. M.I.S. and F.K. helped to interpret the results and prepare the manuscript.

References

  1. Fattahi H. et al. Third-generation femtosecond technology. Optica 1, 45–63 (2014). [Google Scholar]
  2. Chang D. E., Vuletic V. & Lukin M. D. Quantum nonlinear optics-photon by photon. Nature Photon. 8, 685–694 (2014). [Google Scholar]
  3. Firstenberg O. et al. Attractive photons in a quantum nonlinear medium. Nature 502, 71 (2013). [DOI] [PubMed] [Google Scholar]
  4. Calegari F. et al. Ultrafast electron dynamics in phenylalanine initiated by attosecond pulses. Science 346, 336–339 (2014). [DOI] [PubMed] [Google Scholar]
  5. Hell S. W. Microscopy and its focal switch. Nature Meth. 6, 24–32 (2009). [DOI] [PubMed] [Google Scholar]
  6. Yampolsky S. et al. Seeing a single molecule vibrate through time-resolved coherent anti-stokes Raman scattering. Nature Photon. 8, 650–656 (2014). [Google Scholar]
  7. Cavaletto S. M. et al. Broadband high-resolution X-ray frequency combs. Nature Photon. 8, 520–523 (2014). [Google Scholar]
  8. Burghoff D. et al. Terahertz laser frequency combs. Nature Photon 8, 462–467 (2014). [Google Scholar]
  9. Krausz F. & Stockman M. I. Attosecond metrology: from electron capture to future signal processing. Nature Photon. 8, 205–213 (2014). [Google Scholar]
  10. Moss D. J., Morandotti R., Gaeta A. L. & Lipson M. New CMOS-compatible platforms based on silicon nitride and hydex for nonlinear optics. Nature Photon 7, 597–607 (2013). [Google Scholar]
  11. Schiffrin A. et al. Optical-field-induced current in dielectrics. Nature 493, 70–74 (2013). [DOI] [PubMed] [Google Scholar]
  12. Schultze M. et al. Controlling dielectrics with the electric field of light. Nature 493, 75–78 (2013). [DOI] [PubMed] [Google Scholar]
  13. Wachter G. et al. Ab initio simulation of electrical currents induced by ultrafast laser excitation of dielectric materials. Phys. Rev. Lett. 113, 087401 (2014). [DOI] [PubMed] [Google Scholar]
  14. Castro Neto A. H., Peres N. M. R., Novoselov K. S. & Geim A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162 (2009). [Google Scholar]
  15. Baum P., Yang D. S. & Zewail A. H. 4D visualization of transitional structures in phase transformations by electron diffraction. Science 318, 788–792 (2007). [DOI] [PubMed] [Google Scholar]
  16. Baum P., Manz J. & Schild A. Quantum model simulations of attosecond electron diffraction. Science China: Phys., Mech. & Astr. 53, 987–1004 (2010). [Google Scholar]
  17. Shao H. C. & Starace A. F. Detecting electron motion in atoms and molecules. Phys. Rev. Lett. 105, 263201 (2010). [DOI] [PubMed] [Google Scholar]
  18. Dixit G., Vendrell O. & Santra R. Imaging electronic quantum motion with light. Proc. Natl. Acad. Sci. USA 109, 11636–11640 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Dixit G. & Santra R. Role of electron-electron interference in ultrafast time-resolved imaging of electronic wavepackets. J. Chem. Phys. 138, 134311 (2013). [DOI] [PubMed] [Google Scholar]
  20. Shao H. C. & Starace A. F. Time-resolved ultrafast electron (e, 2e) momentum spectroscopy. Phys. Rev. A 87, 050701 (2013). [Google Scholar]
  21. Bredtmann T., Ivanov M. & Dixit G. X-ray imaging of chemically active valence electrons during a pericyclic reaction. Nature Comm. 5, 10.1038/ncomms6589 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Stingl J. et al. Electron transfer in a virtual quantum state of LiBH4 induced by strong optical fields and mapped by femtosecond X-ray diffraction. Phys. Rev. Lett. 109, 147402 (2012). [DOI] [PubMed] [Google Scholar]
  23. Elsaesser T. & Woerner M. Perspective: Structural dynamics in condensed matter mapped by femtosecond X-ray diffraction. J. Chem. Phys. 140, 020901 (2014). [DOI] [PubMed] [Google Scholar]
  24. Woerner M., Holtz M., Juve V., Elsaesser T. & Borgschulte A. Femtosecond X-ray diffraction maps field-driven charge dynamics in ionic crystals. Faraday Discuss. 171, 373–392 (2014). [DOI] [PubMed] [Google Scholar]
  25. Kelardeh H. K., Apalkov V. & Stockman M. I. Graphene in ultrafast and superstrong laser fields. Phys. Rev. B 91, 045439 (2015). [Google Scholar]
  26. Roberts A. et al. Response of graphene to femtosecond high-intensity laser irradiation. Appl. Phys. Lett. 99, 051912 (2011). [Google Scholar]
  27. Hong K.-H. et al. High-energy, phase-stable, ultrabroadband kHz OPCPA at 2.1 μm pumped by a picosecond cryogenic Yb:YAG laser. Opt. Expr. 19, 15538–15548 (2011). [DOI] [PubMed] [Google Scholar]
  28. Li T. et al. Femtosecond population inversion and stimulated emission of dense Dirac fermions in graphene. Phys. Rev. Lett. 108, 167401 (2012). [DOI] [PubMed] [Google Scholar]
  29. Helml W. et al. Measuring the temporal structure of few-femtosecond free-electron laser X-ray pulses directly in the time domain. Nature Photon. 8, 950–957 (2014). [Google Scholar]
  30. Hemsing E., Stupakov G., Xiang D. & Zholents A. Beam by design: Laser manipulation of electrons in modern accelerators. Rev. Mod. Phys. 86, 897–941 (2014). [Google Scholar]
  31. Bostedt C. et al. Ultra-fast and ultra-intense X-ray sciences: first results from the Linac Coherent Light Source free-electron laser. J. Phys. B 46, 164003 (2013). [Google Scholar]
  32. Schoenlein R. W. et al. Femtosecond X-ray pulses at 0.4 angstrom generated by 90 degrees Thomson scattering: A tool for probing the structural dynamics of materials. Science 274, 236–238 (1996). [Google Scholar]
  33. Fill E. E., Krausz F. & Raizen M. G. Single-molecule electron diffraction imaging with charge replacement. New J. Phys. 10, 093015 (2008). [Google Scholar]
  34. Shorokhov D. & Zewail A. H. 4D electron imaging: principles and perspectives. Phys. Chem. Chem. Phys. 10, 2879–2893 (2008). [DOI] [PubMed] [Google Scholar]
  35. Sciaini G. & Miller R. J. D. Femtosecond electron diffraction: heralding the era of atomically resolved dynamics. Rep. Prog. Phys. 74, 096101 (2011). [Google Scholar]
  36. van Oudheusden T. et al. Compression of subrelativistic space-charge-dominated electron bunches for single-shot femtosecond electron diffraction. Phys. Rev. Lett. 105, 264801 (2010). [DOI] [PubMed] [Google Scholar]
  37. Gao M. et al. Mapping molecular motions leading to charge delocalization with ultrabright electrons. Nature 496, 343–346 (2013). [DOI] [PubMed] [Google Scholar]
  38. Veisz L. et al. Hybrid DC-AC electron gun for fs-electron pulse generation. New J. Phys. 9, 451 (2007). [Google Scholar]
  39. Baum P. Towards ultimate temporal and spatial resolutions with ultrafast single-electron diffraction. J. Phys. B 47, 124005 (2014). [Google Scholar]
  40. Feist A. et al. Quantum coherent optical phase modulation in an ultrafast transmission electron microscope. Nature 521, 200–203 (2015). [DOI] [PubMed] [Google Scholar]
  41. Lahme S., Kealhofer C., Krausz F. & Baum P. Femtosecond single-electron diffraction. Struct. Dynamics 1, 034303 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Schaefer S., Liang W. & Zewail A. H. Structural dynamics of nanoscale gold by ultrafast electron crystallography. Chem. Phys. Lett. 515, 278–282 (2011). [DOI] [PubMed] [Google Scholar]
  43. Chatelain R. P., Morrison V. R., Klarenaar B. L. M. & Siwick B. J. Coherent and incoherent electron-phonon coupling in graphite observed with radio-frequency compressed ultrafast electron diffraction. Phys. Rev. Lett. 113, 235502 (2014). [DOI] [PubMed] [Google Scholar]
  44. Zuo J. M., Kim M., O’Keeffe M. & Spence J. C. H. Direct observation of d-orbital holes and Cu-Cu bonding in Cu2O. Nature 401, 49–52 (1999). [Google Scholar]
  45. Zuo J. M. Measurements of electron densities in solids: a real-space view of electronic structure and bonding in inorganic crystals. Rep. Progr. Phys. 67, 2053 (2004). [Google Scholar]
  46. Carbone F. The interplay between structure and orbitals in the chemical bonding of graphite. Chem. Phys. Lett. 496, 291–295 (2010). [Google Scholar]
  47. Eichberger M. et al. Snapshots of cooperative atomic motions in the optical suppression of charge density waves. Nature 468, 799–802 (2010). [DOI] [PubMed] [Google Scholar]
  48. Dal Conte S. et al. Snapshots of the retarded interaction of charge carriers with ultrafast fluctuations in cuprates. Nature Phys. 11, 421–426 (2015). [Google Scholar]
  49. Trevisanutto P. E., Giorgetti C., Reining L., Ladisa M. & Olevano V. Ab Initio GW Many-Body Effects in Graphene. Phys. Rev. Lett. 101, 226405 (2008). [DOI] [PubMed] [Google Scholar]
  50. Sprinkle M. et al. First Direct Observation of a Nearly Ideal Graphene Band Structure. Phys. Rev. Lett. 103, 226803 (2009). [DOI] [PubMed] [Google Scholar]
  51. Monkhorst H. J. & Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976). [Google Scholar]
  52. Magnus W. On the exponential solution of differential equations for a linear operator. Comm. on Pure and Appl. Math. 7, 649–673 (1954). [Google Scholar]
  53. Blanes S., Casas F., Oteo J. A. & Ros J. A pedagogical approach to the magnus expansion. Europ. J. of Phys. 31, 907 (2010). [Google Scholar]
  54. Sidje R. B. Expokit: A software package for computing matrix exponentials. ACM Trans. Math. Softw. 24, 130–156 (1998). [Google Scholar]
  55. Davis T. A. Direct Methods for Sparse Linear Systems (Society for Industrial and Applied Mathematics, 2006). [Google Scholar]
  56. Hartwigsen C., Goedecker S. & Hutter J. Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys. Rev. B 58, 3641–3662 (1998). [DOI] [PubMed] [Google Scholar]
  57. Shevitski B. et al. Dark-field transmission electron microscopy and the Debye-Waller factor of graphene. Phys. Rev. B 87, 045417 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Dixit G., Vendrell O. & Santra R. Imaging electronic quantum motion with light. Proc. Natl. Acad. Sci. USA 109, 11636–40 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Shao H.-C. & Starace A. F. Imaging electronic motions in atoms by energy-resolved ultrafast electron diffraction. Phys. Rev. A 90, 032710 (2014). [Google Scholar]
  60. Woerner M. et al. Concerted electron and proton transfer in ionic crystals mapped by femtosecond X-ray powder diffraction. J. Chem. Phys. 133, 064509 (2010). [DOI] [PubMed] [Google Scholar]
  61. Kirchner F. O., Lahme S., Krausz F. & Baum P. Coherence of femtosecond single electrons exceeds biomolecular dimensions. New J. Phys. 15, 063021 (2013). [Google Scholar]
  62. Wang H. et al. Ultrafast relaxation dynamics of hot optical phonons in graphene. Appl. Phys. Lett. 96, 081917 (2010). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep14581-s1.pdf (84.3KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES