jModelTest 2: more models, new heuristics and high-performance computing

To the Editor

The statistical selection of best-fit models of nucleotide substitution is routine in the phylogenetic analysis of DNA sequence alignments. The programs ModelTest¹ and jModelTest² are very popular tools to accomplish this task, with thousands of users and citations. The latter uses PhyML³ to obtain maximum likelihood estimates of model parameters, and implements different statistical criteria to select among 88 models of nucleotide substitution, including hierarchical and dynamical likelihood ratio tests, Akaike’s and Bayesian information criteria (AIC and BIC) and a performance-based decision theory method (see ref.⁴). jModelTest also provides estimates of model selection uncertainty, parameter importances and model-averaged parameter estimates, including model-averaged phylogenies⁴.

However, in recent years the advent of NGS technologies has changed the field, and most researchers are now moving from phylogenetics to phylogenomics, where large sequence alignments typically include hundreds or thousands of loci. Phylogenetic resources therefore need to be adapted to a High Performance Computing (HPC) paradigm, allowing demanding analyses at the genomic level. Here we introduce jModelTest 2, which incorporates more models, new heuristics, efficient technical optimizations and multithreaded and MPI-based implementations for statistical model selection.

jModelTest 2 includes several important new features (Supplementary Table 1). We have expanded the set of candidate models from 88 to 1624, resulting from the consideration of the 203 different partitions of the 4 ×4 nucleotide substitution rate matrix (R-matrix) combined with rate variation among sites and equal/unequal base frequencies. Indeed, likelihood computations for a large number of models or for large data sets can be extremely time-consuming, so we have also implemented two different heuristics for the selection of the best-fit model. The first one is a greedy hill-climbing hierarchical clustering that searches the set of 1624 models optimizing at most 288 models (Supplementary Note 1) with almost the same accuracy as an exhaustive search. The second is a heuristic filtering based on a similarity threshold among the GTR rates and the estimates of among-site rate variation (Supplementary Note 2). The program also provides a measure of absolute fit, which is obtained through comparison with the unconstrained (multinomial) likelihood. Moreover, this version adds flexible support for different input alignment formats using the ALTER library⁵, the possibility to use different tree topology search algorithms for ML inference, model-averaged branch lengths, different approximations for the alignment sample size, and automatic html-formatted log that includes topological support summaries (i.e., which topologies are supported by which model) with hyperlinks to PhyloWidget⁶ (http://www.phylowidget.org/) for automatic graphical depiction. jModelTest 2 is written in Java, and can run on Windows, Macintosh and Linux platforms. Source code and binaries are freely available under the GNU GPL version 3 license for download from https://code.google.com/p/jmodeltest2. The software package includes detailed documentation and examples and a forum package exists at https://groups.google.com/forum/#!forum/jmodeltest.

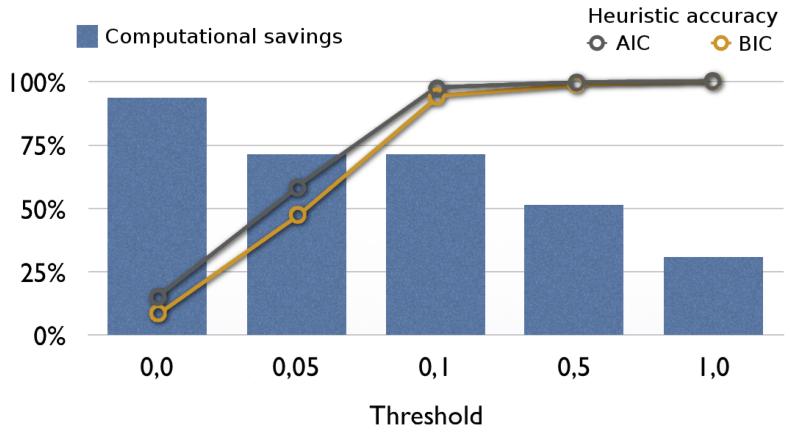
We evaluated the accuracy of jModelTest 2 using 10,000 simulated data sets generated under a large variety of conditions described in Supplementary Note 3. Using BIC as the selection criterion, jModelTest 2 identified the exact generating (true) model 89% of the time (Supplementary Table 2), and in those cases where the model identified was not the generating model, an extremely similar model was selected instead. The structure of the R-matrix (the so-called partition; see Supplementary Note 1) was correctly identified 90% of the time, while the rate variation parameters were properly added in 99% of cases. Accordingly, model-averaged estimates of model parameters like base frequencies, transition rates among nucleotides or proportion of invariable sites were highly accurate, showing small mean square errors in general (Supplementary Table 3). The hierarchical clustering heuristic was tested on 2,000 simulated alignments (as before but considering all 203 R-matrices), finding the same best-fit model as the exhaustive search 95% of the time. The similarity filtering approach was evaluated as a function of the filtering threshold on the same 10,000 simulated alignments above. Here we defined accuracy as the number of times the heuristic found the same best-fit model as the exact procedure evaluating all 88 candidate models (or in other words, the heuristic found the global optimum) (Fig. 1). For example, using a threshold of 0.24 we got an average heuristic accuracy over 99%, while the number of models evaluated was reduced by 60% on average. Complete heuristic accuracy was reached with a threshold of 0.88, affording the computation for 41% of the models. To guarantee a similar trade-off between the accuracy of the heuristic and the computational savings to that depicted in Fig. 1 we developed a general “threshold tuning” using polynomial interpolation (Supplementary Note 2).

Figure 1. Benchmarking of the filtering heuristic in jModelTest 2.

The threshold of the filtering heuristic is directly correlated with the probability of finding the true best-fit model (Heuristic accuracy) and inversely related to the number of models for which we avoided the likelihood calculation (Computational savings).

jModelTest 2 can be executed in HPC environments as: (1) a GUI-based desktop version for multi-core processors; (2) a cluster-based version that distributes the computational load among cluster nodes; and (3) as a hybrid multi-core cluster version that achieves maximum speed through the distribution of tasks among nodes while taking advantage of multi-core processors within nodes. Accordingly, jModelTest 2 offers a significant gain in computational performance compared to the previous version. An experimental study with real and simulated datasets showed important speedups for the estimation of the likelihood scores of all 88 candidate models, the most demanding step in model selection (Supplementary Note 4). In a shared memory architecture with 24 cores, the scalability of the multithreaded implementation was almost linear with up to 8 threads, but also scaled well with 24 threads. In a cluster (distributed memory) the MPI-based application scaled well up to 32 processes, especially for the largest data sets. Here, the fact that some models can be optimized much faster than others, especially when they do not include rate variation among sites, posed a theoretical limit to the scalability. This problem was circumvented when we implemented a hybrid multithread/MPI-based approach (shared and distributed memory), executed on Amazon EC2 cloud, which resulted in speedups of 182-211 (from 182 up to 211 times faster) with 256 processes even for the most complex cases. For relatively large alignments (e.g., 138 sequences and 10,693 sites) this could be equivalent to a reduction of the running time from near 8 days to around 1 hour.

In summary, jModelTest2 facilitates accurate statistical model selection for a comprehensive number of models using large sequence alignments typical in phylogenomic studies, not only for expert cluster users, but also for the owners of standard multicore desktop computers.