Modeling Epistasis in Genomic Selection

Abstract

Modeling epistasis in genomic selection is impeded by a high computational load. The extended genomic best linear unbiased prediction (EG-BLUP) with an epistatic relationship matrix and the reproducing kernel Hilbert space regression (RKHS) are two attractive approaches that reduce the computational load. In this study, we proved the equivalence of EG-BLUP and genomic selection approaches, explicitly modeling epistatic effects. Moreover, we have shown why the RKHS model based on a Gaussian kernel captures epistatic effects among markers. Using experimental data sets in wheat and maize, we compared different genomic selection approaches and concluded that prediction accuracy can be improved by modeling epistasis for selfing species but may not for outcrossing species.

EPISTASIS has long been recognized as an important component in dissecting genetic pathways and understanding the evolution of complex genetic systems (Phillips 2008). It is hence a biologically influential component contributing to the genetic architecture of quantitative traits (Mackay 2014). The influence of epistasis on genome-wide QTL mapping ranges from limited (e.g., Buckler et al. 2009; Tian et al. 2011) to high (e.g., Carlborg et al. 2006; Würschum et al. 2011; Huang et al. 2014). These discrepancies can be explained by the complexities of the examined traits, which are controlled by many loci exhibiting small effects entailing a low QTL detection power. In addition, the estimation of QTL main and interaction effects is very likely biased (Beavis 1994), which makes it challenging to reliably elucidate the role of epistasis through genome-wide QTL mapping studies.

Genomic selection has been suggested as an alternative to tackle complex traits that are regulated by many genes, each exhibiting a small effect (Meuwissen et al. 2001). Genomic selection approaches based on additive and dominance effects have been successfully applied to predict complex traits in human (Yang et al. 2010), animal (Hayes et al. 2009), and plant populations (Jannink et al. 2010; Zhao et al. 2015). Moreover, several genomic selection approaches have been developed to model both main and epistatic effects (Xu 2007; Cai et al. 2011; Wittenburg et al. 2011; Wang et al. 2012). While in some studies prediction accuracies increased (Hu et al. 2011), in others modeling epistasis adversely affected prediction accuracies (Lorenzana and Bernardo 2009).

Despite these first attempts, epistasis is often ignored in genomic selection approaches using parametric models mainly because of the high associated computational load, especially if a large number of markers are available. An attractive solution to reduce the computational load is to extend genomic best linear unbiased prediction (G-BLUP) models (VanRaden 2008) by adding marker-based epistatic relationship matrices [extended genomic best linear unbiased prediction (EG-BLUP)]. Dating back to Henderson (1985), EG-BLUP enables the estimation of epistatic components of the genotypic values without explicitly assessing individually epistatic effects. Applied to predicting daily gain in pigs and the total height of pine trees, EG-BLUP outperformed G-BLUP (Su et al. 2012; Muñoz et al. 2014). The equivalence between G-BLUP and genomic selection approaches, with explicit relevance for modeling marker main effects, has been demonstrated (Habier et al. 2007). However, the association between EG-BLUP and genomic selection approaches explicitly modeling marker main and interaction effects has not been studied.

The use of semiparametric reproducing kernel Hilbert space (RKHS) regression models has been promoted as an alternative powerful option to capture epistasis in genomic selection (Gianola et al. 2006; Gianola and Van Kaam 2008). The RKHS model outperformed linear models that focused exclusively on marker main effects in a number of studies based on simulated data (e.g., Gianola et al. 2006; Howard et al. 2014) and empirical data (e.g., Perez-Rodriguez et al. 2012; Rutkoski et al. 2012; Crossa et al. 2013). Choosing an appropriate kernel, which can be interpreted as a relationship matrix among genotypes (i.e., individuals), is a central element of model specification in RKHS regression (De Los Campos et al. 2010). Among all possible kernels, the Gaussian kernel has been extensively used and is assumed to implicitly portray the genetic effects including epistasis (Gianola and Van Kaam 2008; Morota and Gianola 2014). The exponential function involved in the Gaussian kernel is a nonlinear transformation of the additive inputs, which encodes a type of epistasis (Gianola et al. 2014). Nevertheless, it has not been clarified how RKHS regression based on Gaussian kernels explicitly models epistatic effects among different markers.

In this study, we aimed at (1) explaining how the marker-based epistatic relationship matrix used in EG-BLUP models is related to epistatic effects among markers, (2) unraveling how the RKHS model based on a Gaussian kernel takes epistatic effects among different markers into account, and (3) comparing the prediction abilities of three models (G-BLUP, EG-BLUP, and RKHS), using several published experimental data sets.

Theory

Throughout this article, we use the following notations: Let n be the number of genotypes, m be the number of genotypes having phenotypic records, and p be the number of markers. Let $X=(x_{ij})$ be the $n\times p$ matrix of SNP markers, where $x_{ij}$ equals the number of a chosen allele at the jth locus for the ith genotype. Let $x_i$ be the ith row of the matrix X, which is the marker profile for the ith genotype. Let $p_j$ be the allele frequency of the jth marker. We do not necessarily assume Hardy–Weinberg equilibrium in the population.

The G-BLUP model with additive relationship matrix

The baseline model for comparison was the standard G-BLUP model focusing on additive effects,

$$y=1_m\mu +Zg+e,$$ (1)

where y refers to the m-dimensional vector of phenotypic records, $1_m$ is an m-dimensional vector of ones, μ is the population mean, g is an n-dimensional vector of additive genotypic values, $Z=(z_{ij})$ is the corresponding $m\times n$ design matrix allocating phenotypic records to genotypes (i.e., $z_{ij}=1$ if the jth entry of g corresponds to the ith observation in y, and $z_{ij}=0$ otherwise), and e is an m-dimensional vector of residual terms.

Without loss of generality, we subsequently assume that $m=n$ and that Z is the identity matrix, leading to the simpler form of the model,

$$y=1_n\mu +g+e,$$ (2)

where y, $1_n$, μ, and e are the same as defined in (1). We assume that μ is a fixed parameter, and g, e are random parameters with $e\sim N(0,I{\sigma }_e^2)$ and $g\sim N(0,G{\sigma }_g^2)$. G denotes the $n\times n$ genomic relationship matrix among all genotypes, calculated following VanRaden (2008) as $G=W{W}^{\prime }/\gamma$, where $\gamma =2{\displaystyle {\sum }_{k=1}^p{p}_k\left(1-p_k\right)}$ and $W=(w_{ij})$ is an $n\times p$ matrix with $w_{ij}=x_{ij}-2p_j$. It was proved that the matrix G approaches the well-known numerator relationship matrix A as the number of markers increases (Habier et al. 2007).

EG-BLUP: an extended G-BLUP model comprising additive and additive × additive relationship matrices

Focusing exclusively on additive × additive epistasis, the EG-BLUP model has the form

$$y=1_n\mu +g_1+g_2+e,$$ (3)

where y, $1_n$, μ, and e are the same as defined in (2). For each genotype, not only the additive genotypic values but also epistatic genotypic values are included in the model. Namely, $g_1$ is an n-dimensional vector of additive genotypic values, and $g_2$ is an n-dimensional vector of additive × additive epistatic genotypic values. We assume that μ is a fixed parameter, $e\sim N(0,I{\sigma }_e^2)$, $g_1\sim N(0,G{\sigma }_1^2)$, $g_2\sim N(0,H{\sigma }_2^2)$, and $\mathrm{Cov}\left(g_1,g_2\right)=\mathrm{Cov}\left(g_1,e\right)=\mathrm{Cov}\left(g_2,e\right)=0.$ Here the matrix G is the same as in the G-BLUP model. In an infinitesimal model, Henderson (1985) suggested using the Hadamard product of the additive relationship matrix by itself to obtain the epistatic relationship matrix H. Translated to genomic relationship, this yields

$$H=G\#G.$$ (4)

This extended G-BLUP model was recently used by Su et al. (2012) and Muñoz et al. (2014).

When the number of markers is large, we proved that EG-BLUP is equivalent to the model EG-BLUP* with explicit epistatic effects of markers (see the Appendix),

$$y=1_n\mu +{\displaystyle \sum }_{i=1}^p{W}_i{a}_i+{\displaystyle \sum }_{i=1}^{p-1}{\displaystyle \sum }_{j=i+1}^p\left(W_i\cdot W_j\right)v_{ij}+e,$$ (5)

where y, $1_n$, μ, and e are the same as before; $W_i$ is the ith column of the matrix W; $a_i$ is the additive effect of the ith marker; $W_i\cdot W_j$ is the element-wise product of the two vectors $W_i$ and $W_j$; $v_{ij}$ is the additive × additive epistatic effect of the ith and the jth marker; and e is the vector of residual terms. We assume that μ is a fixed parameter; $a_i\sim N(0,{\sigma }_1^2/\gamma )$; $v_{ij}\sim N\left(0,2{\sigma }_2^2/{\gamma }^2\right)$; $e\sim N\left(0,I{\sigma }_e^2\right)$; and no covariance among $a_i$, $v_{ij}$, and e. The basic setting of EG-BLUP* in Equation 5 appeared in Wittenburg et al. (2011) with different assumptions on the parameters.

Note that the parameters in EG-BLUP* should be considered in the framework of Fisher (1918). Namely, μ is the population mean, $a_i$ is the average effect of an allele for the ith locus, defined as the regression coefficient of the genotypic values on the number of the allele, and $v_{ij} (i\ne j)$ is the epistatic deviation for the ith and the jth loci.

The extension of Equation 3 to include also higher-order additive × additive genotypic values can be deduced using the same method as in Henderson (1985). We need only to note that the ($k-1$)th-order epistatic relationship matrix is given by $G^{\#k}=G\#G\#\cdot \cdot \cdot \#G$ (the Hadamard product of k copies of G).

The RKHS regression model based on a Gaussian kernel

We consider the following model that is equivalent to RKHS regression (De Los Campos et al. 2010):

$$y=1_n\mu +g+e.$$ (6)

The notations are the same as in (2) and the assumptions are $e\sim N(0,I{\sigma }_e^2)$, $g\sim N(0,K{\sigma }_g^2)$, where $K=(k(x_i,x_j))$ is an $n\times n$ kernel matrix whose entries are functions of marker profiles of pairs of genotypes. It is required that K satisfies the semipositive definite property ${\displaystyle {\sum }_{i,j}{\alpha }_i{\alpha }_{j}k(x_i,x_j)\ge 0}$, for all real numbers ${\alpha }_i$, ${\alpha }_j$. Mathematically, a number of matrices would satisfy this property. For example, we may choose $K=G$ whereby the RKHS model is equivalent to G-BLUP.

In this study, we consider only the Gaussian kernel (Gianola and Van Kaam 2008),

$$k\left(x_i,x_j\right)=\exp \left[-\frac{{\Vert x_i-x_j\Vert }^2}{h}\right],$$ (7)

where $\Vert \cdot \Vert$ denotes the norm in the Euclidean space and h is a bandwidth parameter. As the matrix K serves as a genetic relationship matrix among genotypes, the parameter h controls how fast the relationship between two genotypes decays as the distance between the corresponding pairs of marker vectors increases. The choice of the bandwidth parameter can be optimized by applying a cross-validation or a Bayesian approach, treating h as a random variable. Throughout this study, we assume that h is known.

An explicit explanation of why the RKHS model captures epistasis

We start by inspecting the kernel matrix (7) in more detail. Recall that the entries in W are defined as $w_{ij}=x_{ij}-2p_j$. Hence we have

$$\begin{array}{c}{\Vert x_i-x_j\Vert }^2={\displaystyle \sum }_{k=1}^p{(x_{ik}-x_{jk})}^2\\ ={\displaystyle \sum }_{k=1}^p{(w_{ik}-w_{jk})}^2={\displaystyle \sum }_{k=1}^p{w}_{ik}^2+{\displaystyle \sum }_{k=1}^p{w}_{jk}^2-2{\displaystyle \sum }_{k=1}^p{w}_{ik}{w}_{jk}.\end{array}$$

Recall that $G=W{W}^{\prime }/\gamma$. Thus the $\left(i,j\right)$th entry of G is $G_{ij}={{\displaystyle \sum }}_{k=1}^p{w}_{ik}{w}_{jk}/\gamma$. Write ${\beta }_l={\displaystyle {\sum }_{k=1}^p{w}_{lk}^2}$, for all $1\le l\le n$. Then we obtain

$$k\left(x_i,x_j\right)=\exp \left(-\frac{{\beta }_i}{h}\right)\exp \left(-\frac{{\beta }_j}{h}\right)\exp \left(\frac{2\gamma G_{ij}}{h}\right).$$

Let $1_{n\times n}$ be the $n\times n$ matrix of ones and let $\mathrm{\Lambda }=\mathrm{diag}\left(\exp \left(-\left({\beta }_1/h\right)\right),\dots ,\exp \left(-\left({\beta }_n/h\right)\right)\right)$. Note that in terms of power series, $\exp \left(x\right)=1+{\displaystyle {\sum }_{k=1}^{\mathrm{\infty }}\left(x^k/k!\right)}$ (Levi 1968). Rewriting the above steps in matrix form, we have

$$K=\mathrm{\Lambda }\tilde{H}\mathrm{\Lambda },$$ (8)

where

$$\tilde{H}=1_{n\times n}+{\displaystyle \sum }_{k=1}^{\mathrm{\infty }}\frac{{(2\gamma )}^k}{h^{k}k!}{G}^{\#k}.$$ (9)

Therefore, we can see that the epistatic relationship matrices $G^{\#k}$ (for each $k\ge 2$) used in EG-BLUP are all involved in the Gaussian kernel for the RKHS model. In this sense, the Gaussian kernel indeed carries the information of additive × additive epistasis up to any order. But note that in the Gaussian kernel, the proportions of the additive and each epistatic relationship matrix $G^{\#k}$ in the total matrix $\tilde{H}$ are fixed, once the bandwidth parameter is chosen. In contrast, in EG-BLUP, the proportion of $G^{\#k}$ in H depends on the corresponding variance component, which is an unknown parameter to be estimated.

Based on the above observations, we can actually formulate a model with explicit epistasis effects of markers and prove that it is equivalent to the RKHS model with the Gaussian kernel. Let us consider the following model, which seems to be ill-posed as infinitely many unknown parameters are included. But we immediately show that it is equivalent to the RKHS model with Gaussian kernel,

$$y=1_n\mu +\mathrm{\Lambda }{1}_n\nu +{\displaystyle \sum }_{i=1}^p\mathrm{\Lambda }{W}_i{a}_i+{\displaystyle \sum }_{s=2}^{\mathrm{\infty }}{\displaystyle \sum }_{1\le i_1<i_2<\cdots <i_s\le p}\mathrm{\Lambda }({\displaystyle \prod }_{t=1}^s{W}_{i_t})v_{i_1{i}_2\cdots i_s}+e,$$ (10)

where the notations y, $1_n$, μ, $W_i$, $a_i$, and e are the same as in (4). ${\displaystyle {\prod }_{t=1}^s{W}_{i_t}}$ is the element-wise product of the vectors $W_{i_t}$ for $1\le t\le s$. $v_{i_1{i}_2\cdots i_s}$ are the sth-order epistatic effects among the $i_1$, $i_2$, …, and the $i_s$ loci. We assume that μ is fixed, v is an extra random intercept term with $\nu \sim N(0,{\sigma }_0^2)$, $a_i\sim N(0,\left(2/h\right){\sigma }_0^2)$, $v_{i_1{i}_2\cdots i_s}\sim N\left(0,\left(2^s/h^s\right){\sigma }_0^2\right)$, $e\sim N(0,I{\sigma }_e^2)$, and there is no covariance among ν, $a_i$, $v_{i_1{i}_2\cdots i_s}$, and e.

Now, let a be the p-dimensional vector ${(a_i)}_{1\le i\le p}$, $v^{(s)}$ be the $\left(\begin{array}{c}p\\ s\end{array}\right)$-dimensional vector ${(v_{i_1{i}_2\cdots i_s})}_{1\le i_1<i_2<\cdots <i_s\le p}$, and $U^{(s)}$ be the $n\times \left(\begin{array}{c}p\\ s\end{array}\right)$ matrix whose columns consist of the vectors ${\displaystyle {\prod }_{t=1}^s{W}_{i_t}}$ for all $1\le i_1,i_2,\dots ,i_s\le p$. Here $\left(\begin{array}{c}p\\ s\end{array}\right)=\left(p(p-1)\cdots (p-s+1)\right)/s!$ denotes the binomial coefficient. With the above notations, Equation 6 can be rewritten in matrix form as

$$y=1_n\mu +\mathrm{\Lambda }{1}_n\nu +\mathrm{\Lambda }Wa+{\displaystyle \sum }_{s=2}^{\mathrm{\infty }}\mathrm{\Lambda }{U}^{\left(s\right)}{v}^{\left(s\right)}+e,$$ (11)

with assumptions $\nu \sim N(0,{\sigma }_0^2)$, $a\sim N(0,\left(2/h\right)I{\sigma }_0^2)$, $v^{(s)}\sim N(0,\left(2^s/h^s\right)I{\sigma }_0^2)$, and $e\sim N(0,I{\sigma }_e^2)$ and all covariance terms are zero.

Then we have

$$\begin{array}{l}V=\mathrm{var}\left(y\right)=\left(\mathrm{\Lambda }{1}_{n\times n}\mathrm{\Lambda }\right){\sigma }_0^2+\frac{2}{h}\mathrm{\Lambda }W{W}^{\prime }\mathrm{\Lambda }{\sigma }_0^2\\ +{\displaystyle \sum }_{s=2}^{\mathrm{\infty }}\frac{2^s}{h^s}\mathrm{\Lambda }{U}^{(s)}{U}^{(s)}{}^{\prime }\mathrm{\Lambda }{\sigma }_0^2+I{\sigma }_e^2.\end{array}$$

Recall that $G=W{W}^{\prime }/\gamma$. We need to calculate $U^{(s)}{U}^{(s)}{}^{\prime }$ for any $s\ge 2.$ Note that in the case of $s=2$, we have shown in the Appendix that ${\lim }_{p\to \mathrm{\infty }}\left(2U^{(2)}{U}^{(2)}{}^{\prime }/{\gamma }^2\right)={\lim }_{p\to \mathrm{\infty }}G\#G$. This result can be easily generalized for $s>2$, using the same method. That is, for any $s\ge 2$, we have

$$\underset{p\to \mathrm{\infty }}{\lim }\frac{s!U^{(s)}{U}^{(s)}{}^{\prime }}{{\gamma }^s}=\underset{p\to \mathrm{\infty }}{\lim }{G}^{\#s}.$$

Thus, when p is very large, we can approximately treat

$$U^{(s)}{U}^{\left(s\right)}{}^{\prime }\approx \frac{{\gamma }^s}{s!}{G}^{\#s}.$$

Then we can deduce that

$$\begin{array}{l}V=\mathrm{var}\left(y\right)\approx \mathrm{\Lambda }\left(1_{n\times n}+{\displaystyle \sum }_{s=1}^{\mathrm{\infty }}\frac{{(2\gamma )}^s}{h^{s}s!}{G}^{\#s}\right)\mathrm{\Lambda }{\sigma }_0^2+I{\sigma }_e^2\\ =\left(\mathrm{\Lambda }\tilde{H}\mathrm{\Lambda }\right){\sigma }_0^2+I{\sigma }_e^2.\end{array}$$

Note that the matrix $\Lambda \tilde{H}\Lambda$ is exactly the Gaussian kernel K (Equation 8) and that the variance–covariance matrix $V=\mathrm{var}\left(y\right)$ is exactly the same as in the RKHS model with Gaussian kernel.

Using the same approach as in the Appendix, it is straightforward to deduce that the modified RKHS (Equation 11) and the RKHS models give the same predictions for the total genotypic values. Thus, we gave a complete explanation on why the RKHS model takes epistasis into account.

Comparing G-BLUP, EG-BLUP, and RKHS, using experimental data

We used two published data sets each in wheat and maize for our study. The first data set consisted of 599 wheat lines genotyped by 1447 diversity array technology (DArT) markers (Crossa et al. 2010). The second data set comprised 254 advanced wheat breeding lines genotyped by 1576 single-nucleotide polymorphism (SNP) markers (Poland et al. 2012). The third data set consisted of 300 maize lines with 1148 SNP markers (Crossa et al. 2010). The fourth data set comprised two large half-sib maize panels from the flint and dent heterotic pools (Bauer et al. 2013). The dent (flint) panel consists of 847 (833) lines with 31,498 (29,466) SNPs. The phenotypic trait on which we focused in this study was grain yield. More details on the data sets are provided in supporting information, File S1.

Using the four data sets, we tested the option to increase the predicting accuracy by modeling epistasis. To this end, we estimated the prediction accuracy based on the G-BLUP, EG-BLUP, and RKHS models, applying fivefold cross-validations. The prediction accuracy was measured as the Pearson product-moment correlation between predicted and observed genotypic values of the individuals in the test set (more details on methods are included in File S1). We observed that the performance of RKHS was very similar to that of EG-BLUP (Table 1), which fits well with our theoretical findings on the congruency of both models. For the two reanalyzed maize data sets, EG-BLUP and RKHS including epistasis did not outperform G-BLUP ignoring epistasis. In contrast, in the two reanalyzed wheat data sets, we observed that the prediction accuracies for RKHS and EG-BLUP were consistently higher than that for the G-BLUP model.

Table 1. Cross-validated prediction accuracies and standard errors of three genomic selection models (genomic best linear unbiased prediction with additive relationship matrix (G-BLUP), extended G-BLUP with additive and additive × additive relationship matrices (EG-BLUP), and reproducing kernel Hilbert space regression based on the Gaussian kernel (RKHS)] in four data sets.

Data set	Trait–environmente	G-BLUP	EG-BLUP	RKHS
Wheat_1a	GY_E1	0.505 ± 0.034	0.571 ± 0.029	0.576 ± 0.033
	GY_E2	0.493 ± 0.034	0.500 ± 0.034	0.499 ± 0.034
	GY_E3	0.379 ± 0.041	0.421 ± 0.035	0.428 ± 0.034
	GY_E4	0.484 ± 0.033	0.525 ± 0.029	0.526 ± 0.034
Wheat_2b	GY_drought	0.435 ± 0.058	0.445 ± 0.056	0.444 ± 0.054
	GY_irrigated	0.537 ± 0.046	0.550 ± 0.046	0.556 ± 0.042
Maize_1c	GY_drought	0.429 ± 0.044	0.440 ± 0.045	0.449 ± 0.043
	GY_irrigated	0.537 ± 0.038	0.546 ± 0.037	0.544 ± 0.037
Maize_2d dent	DMY	0.632 ± 0.030	0.627 ± 0.031	0.619 ± 0.032
Maize_2d flint	DMY	0.651 ± 0.020	0.649 ± 0.021	0.643 ± 0.021

The highest prediction accuracy for each trait in each data set is underlined.

^aData set previously described in Crossa et al. (2010); 599 lines and 1447 DArT markers were used.

^bData set previously described in Poland et al. (2012); 254 lines and 1576 SNP markers were used.

^cData set previously described in Crossa et al. (2010); 264 lines and 1135 SNP markers were used.

^dData set previously described in Bauer et al. (2013) and Lehermeier et al. (2014); 847 genotypes and 31,498 SNP markers were used for dent lines and 833 genotypes and 29,466 SNP markers were used for flint lines.

^eGY, grain yield; DMY, dry matter yield.

Data availability

This study was based on published datasets. Detailed description and the sources of all data sets were provided in File S1.

Discussion

We focused in our study on digenic additive × additive epistatic effects. Extending the EG-BLUP approach toward additive × dominance and dominance × dominance effects or to higher-order epistasis is straightforward (Henderson 1985). It is important to note, however, that based on the framework used to partition the genotypic variance, additive × additive effects are expected to be the prevailing epistatic effects (Fisher 1918; Lynch and Walsh 1998).

EG-BLUP and RKHS are computational efficient approaches to tackle epistasis in genomic selection

Extending genomic selection models toward epistasis is often hampered by high computational load. We have demonstrated that EG-BLUP is equivalent to genomic selection approaches modeling explicitly epistatic effects (EG-BLUP*, Equation 5). Moreover, RKHS can also be reformulated as a genomic selection model with explicit epistatic effects (modified RKHS, Equation 10). The computational load of EG-BLUP and RKHS mainly depends on the number of genotypes. In contrast, the computational load of EG-BLUP* comprising additive as well as additive × additive epistatic effects depends on the square of the number of markers. Implementing the EG-BLUP and RKHS models for a previously published maize data set (Bauer et al. 2013) with 847 genotypes and 1000 randomly sampled markers is, for instance, up to 130 times faster compared with the corresponding RR-BLUP approach. Consequently, EG-BLUP and RKHS are promising models to routinely integrate epistasis in genomic selection studies.

Modeling epistasis improved the prediction accuracy in selfing but not in outcrossing species

We compared the cross-validated prediction accuracies, using the G-BLUP, EG-BLUP, and RKHS models based on four published data sets. Interestingly, we observed contrast trends for wheat compared with maize on the performance of models including epistasis (EG-BLUP and RKHS) and G-BLUP without considering epistasis. Namely, EG-BLUP and RKHS were superior to G-BLUP for the wheat data sets but not for the maize data sets (Table 1). Hence, our results suggested that modeling additive × additive epistasis can increase the prediction accuracy in genomic selection for selfing but not for outcrossing species. This is in line with recent findings that additive × additive epistasis substantially affects midparent heterosis in the selfing species rice, but contributes only marginally to heterosis in the outcrossing species maize (Garcia et al. 2008). Nevertheless, more experimental data sets are required to examine the role of epistasis in selfing and outcrossing species in more detail. In particular, it seems attractive to study also the role of epistasis involving dominance effects, which entails specific designs such as factorial mating designs (Comstock and Robinson 1952).

In the EG-BLUP model, both the additive and the additive × additive epistatic relationship matrices were derived from molecular markers. If the markers under consideration are in linkage equilibrium (LE), the additive and additive × additive terms in EG-BLUP* are orthogonal in the sense of Cockerham (1954), and hence the estimates of additive and epistatic effects are independent (Álvarez-Castro and Carlborg 2007). However, the assumption of linkage equilibrium may never be true in reality unless only a few loci sparsely distributed on the genome are considered. Hence, we performed a simulation study to investigate whether linkage disequilibrium (LD) among markers, which causes nonorthogonality of the model, has an influence on the performance of EG-BLUP.

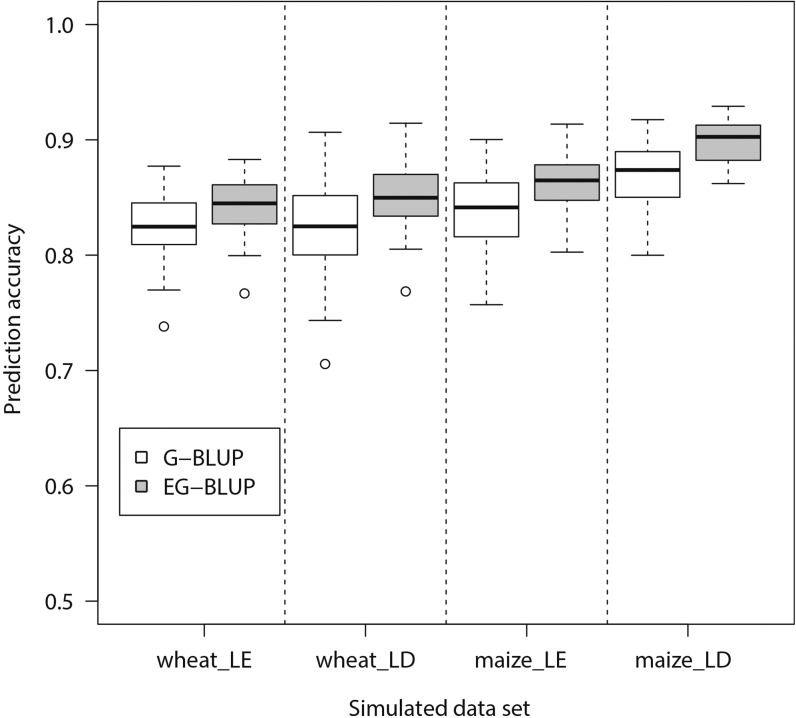
Our simulation was based on the first wheat data set [599 wheat lines with 1447 markers (Crossa et al. 2010)] and the dent panel of the second maize data set [847 lines with 31,498 markers (Bauer et al. 2013)]. We simulated two scenarios: (1) markers contributing to the trait are in LE and (2) markers contributing to the trait are in LD. In all cases, both additive and additive × additive epistatic effects were simulated. The heritability was set to be 0.7. Details for the simulation procedure are presented in File S1. We observed that the prediction accuracy of EG-BLUP was consistently higher than that of G-BLUP in both data sets and both scenarios (Figure 1). Hence, we may conclude that LD among markers has low influence on the effectiveness of EG-BLUP vs. G-BLUP.

Figure 1.

The distribution of prediction accuracies of genomic best linear unbiased prediction (G-BLUP) and extended G-BLUP with additive and additive × additive relationship matrices (EG-BLUP) in simulated data sets. Phenotypic traits were simulated for two data sets (wheat, 599 lines; maize, 847 dent lines) and two scenarios (LE, 100 QTL in linkage equilibrium contributed to the trait; LD, 100 QTL in linkage disequilibrium contributed to the trait). Among 5050 pairs of QTL, 100 pairs were randomly chosen as epistatic QTL. The heritability of the simulated traits was 0.7. For each scenario the simulation was repeated 50 times.

Another factor that may affect the performance of EG-BLUP is inbreeding. In Henderson’s extended BLUP model (Henderson 1985), the derivation of the epistatic relationship matrix being the Hadamard square of the numerator relationship matrix depends on the assumption of random mating (Cockerham 1954), which may never hold for data from plant breeding. In our study, the marker-derived epistatic relationship matrix in EG-BLUP approximately equals the Hadamard square of the marker-derived additive relationship matrix. This result relies only on the assumption that the marker additive and epistatic effects are independent. Maybe this assumption is more likely to hold in noninbred than in inbred populations. If this is true, the superiority of EG-BLUP over G-BLUP would be more pronounced for noninbred than for inbred populations, provided that epistasis substantially contributed to the trait. An investigation of this problem is interesting but beyond the scope of this study. Nevertheless, our results in both simulation and empirical study indicated that EG-BLUP can be effectively applied to noninbred plant data.

Enhancing prediction accuracy across a biparental population through modeling epistasis

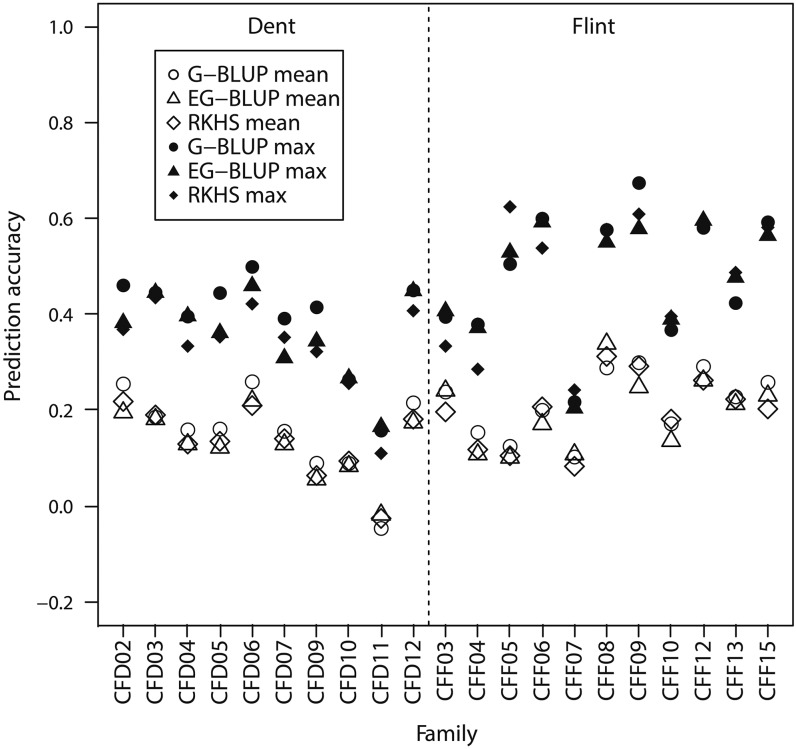
Previous studies have shown that prediction accuracy is impaired when performing genomic selection across connected biparental populations (Zhao et al. 2012; Riedelsheimer et al. 2013). This may be explained at least partially by epistatic effects as the genetic relatedness across connected populations may be better exploited by modeling epistasis in addition to additive effects. Again we used a published maize data set (Bauer et al. 2013) and investigated whether the prediction accuracy across connected biparental families can be increased by modeling additive × additive epistasis. In our scenario, genotypic values of the lines in one family were predicted using lines from each of the other families. We compared the mean and maximal prediction accuracies for each family and observed no superiority for EG-BLUP and RKHS (including epistasis) compared with G-BLUP (ignoring epistasis; Figure 2). The sizes of the biparental populations were small, ranging from 17 to 133. This small population size can substantially reduce prediction accuracy exploiting epistasis, as has been shown previously for QTL mapping (Carlborg and Haley 2004). In addition, maize as an outcrossing species is likely to be influenced only little by additive × additive epistasis in contrast to selfing species (Garcia et al. 2008). Therefore, it will be interesting to investigate in future studies whether prediction accuracy across connected biparental populations can be improved, modeling epistasis using large biparental populations in selfing species.

Figure 2.

Mean and maximal prediction accuracies of maize lines in each family, using lines in each of the other families in the same heterotic group (dent or flint) as the estimation set. The prediction accuracies were evaluated using three different models [genomic best linear unbiased prediction (G-BLUP), extended G-BLUP with additive and additive × additive relationship matrices (EG-BLUP), and reproducing kernel Hilbert space regression based on the Gaussian kernel (RKHS)].

Appendix: A Proof of the Equivalence Between EG-BLUP and EG-BLUP* When the Number of Markers Is Large

Let us start with the EG-BLUP* model (Equation 5). Let a be the p-dimensional vector of the $a_i$’s and v be the $p\left(p-1\right)/2$-dimensional vector of the $v_{ij}$’s. Let U be the $n\times p\left(p-1\right)/2$ matrix whose columns are given by the vectors $\left(W_i\cdot W_j\right)$. Then Equation 5 can be simply written as

$$y=1_n\mu +Wa+Uv+e,$$

with assumptions $a\sim N(0,I\left({\sigma }_1^2/\gamma \right))$, $v\sim N(0,I\left(2{\sigma }_2^2/{\gamma }^2\right))$, and $e\sim N(0,I{\sigma }_e^2)$ and all covariance terms are zero.

Then we have

$$V=\mathrm{var}\left(y\right)=\frac{W{W}^{\prime }}{\gamma }{\sigma }_1^2+\frac{2U{U}^{\prime }}{{\gamma }^2}{\sigma }_2^2+I{\sigma }_e^2.$$ (A1)

The matrix $U{U}^{\prime }$ is an $n\times n$ matrix whose $\left(i,j\right)$ entry is given by

$$\begin{array}{c}{\displaystyle \sum }_{1\le k<s\le p}{u}_{i,ks}{u}_{j,ks}={\displaystyle \sum }_{1\le k<s\le p}{w}_{ik}{w}_{is}{w}_{jk}{w}_{js}=\frac{1}{2}\left({\displaystyle \sum }_{1\le k,s\le p}{w}_{ik}{w}_{is}{w}_{jk}{w}_{js}-{\displaystyle \sum }_{k=1}^p{w}_{ik}^2{w}_{jk}^2\right)\\ =\frac{1}{2}\left[\left({\displaystyle \sum }_{k=1}^p{w}_{ik}{w}_{jk}\right)\left({\displaystyle \sum }_{s=1}^p{w}_{is}{w}_{js}\right)-{\displaystyle \sum }_{k=1}^p{w}_{ik}^2{w}_{jk}^2\right].\end{array}$$

Then it is easy to deduce that

$$U{U}^{\prime }=\frac{1}{2}\left[\left(W{W}^{\prime }\right)\#\left(W{W}^{\prime }\right)-\left(W\#W\right){\left(W\#W\right)}^{\prime }\right].$$

Hence we have

$$\frac{2U{U}^{\prime }}{{\gamma }^2}=G\#G-\frac{\left(W\#W\right){\left(W\#W\right)}^{\prime }}{{\gamma }^2}.$$

Now we claim that

$$\underset{p\to \mathrm{\infty }}{\lim }\frac{2U{U}^{\prime }}{{\gamma }^2}=\underset{p\to \mathrm{\infty }}{\lim }G\#G,$$

which means that when p is very large, we can approximately treat $\frac{2U{U}^{\prime }}{{\gamma }^2}\approx G\#G$. For this purpose we need only to prove

$$\underset{p\to \mathrm{\infty }}{\lim }\frac{\left(W\#W\right){\left(W\#W\right)}^{\prime }}{{\gamma }^2}=0.$$ (A2)

In fact, the $\left(i,j\right)$th entry of the matrix $\left(W\#W\right){\left(W\#W\right)}^{\prime }/{\gamma }^2$ is

$$t_{ij}=\frac{{{\displaystyle \sum }}_{k=1}^p{w}_{ik}^2{w}_{jk}^2}{4{({{\displaystyle \sum }}_{k=1}^p{p}_k(1-p_k))}^2}=\frac{{{\displaystyle \sum }}_{k=1}^p{(x_{ik}-2p_k)}^2{(x_{jk}-2p_k)}^2}{4{({{\displaystyle \sum }}_{k=1}^p{p}_k(1-p_k))}^2}.$$ (A3)

Note that we always exclude monomorphic markers in the analyses. So we can assume that $p_0<p_k<1-p_0$, where $p_0$ is the threshold of minor allele frequency in the quality control (e.g., $p_0=0.01$ or 0.05). Then the numerator of (A3) is a sum of p positive numbers, each belonging to the interval $[0,16{\left(1-p_0\right)}^2]$, while the denominator is a sum of $p^2$ positive numbers, each in the interval $[4p_0^2{\left(1-p_0\right)}^2,0.25]$. Thus we have

$$0\le \underset{p\to \mathrm{\infty }}{\lim }{t}_{ij}\le \underset{p\to \mathrm{\infty }}{\lim }\frac{16{\left(1-p_0\right)}^{2}p}{4p_0^2{\left(1-p_0\right)}^2{p}^2}=\underset{p\to \mathrm{\infty }}{\lim }\frac{4}{p_0^{2}p}=0,$$

which proved (A2).

Hence (A1) is simplified to the following:

$$V\approx G{\sigma }_1^2+(G\#G){\sigma }_2^2+I{\sigma }_e^2.$$

The right-hand side of the above formula is exactly the same as the variance–covariance matrix $\mathrm{var}\left(y\right)$ for Equation 3 in EG-BLUP.

By the results of Henderson (1975), the BLUPs of a and v are given by

$$\widehat{a}=\frac{{\sigma }_1^2}{\gamma }{W}^{\prime }{V}^{-1}\left(y-1_n\widehat{\mu }\right), \widehat{v}=\frac{2{\sigma }_2^2}{{\gamma }^2}{U}^{\prime }{V}^{-1}\left(y-1_n\widehat{\mu }\right),$$ (A4)

where

$$\widehat{\mu }=\frac{{1^{\prime }}_n{V}^{-1}y}{{1^{\prime }}_n{V}^{-1}{1}_n}.$$ (A5)

On the other hand, the BLUPs of $g_1$ and $g_2$ in the EG-BLUP model are given by

$${\widehat{g}}_1={\sigma }_1^{2}G{V}^{-1}\left(y-1_n\widehat{\mu }\right), {\widehat{g}}_2={\sigma }_2^2(G\#G)V^{-1}\left(y-1_n\widehat{\mu }\right),$$ (A6)

where $\widehat{\mu }$ is the same as in (A5) as we have proved that the matrices $V=\mathrm{var}\left(y\right)$ in EG-BLUP and EG-BLUP* are the same.

Comparing (A4) and (A6), we see that ${\widehat{g}}_1=W\widehat{a}$ and ${\widehat{g}}_2=U\widehat{v}$, confirming that EG-BLUP and EG-BLUP* give the same predictions.