Multiple imputation for harmonizing longitudinal non-commensurate measures in individual participant data meta-analysis

Abstract

There are many advantages to individual participant data meta-analysis for combining data from multiple studies. These advantages include greater power to detect effect, increased sample heterogeneity, and the ability to perform more sophisticated analyses than meta-analyses that rely on published results. However, a fundamental challenge is that it is unlikely that variables of interest are measured the same way in all of the studies to be combined. We propose that this situation can be viewed as a missing data problem in which some outcomes are entirely missing within some trials, and use multiple imputation to fill in missing measurements. We apply our method to 5 longitudinal adolescent depression trials where 4 studies used one depression measure and the fifth study used a different depression measure. None of the 5 studies contained both depression measures. We describe a multiple imputation approach for filling in missing depression measures that makes use of external calibration studies in which both depression measures were used. We discuss some practical issues in developing the imputation model including taking into account treatment group and study. We present diagnostics for checking the fit of the imputation model and investigating whether external information is appropriately incorporated into the imputed values.

1 Introduction

Meta-analysis has been used as a tool for synthesizing scientific literature for more than 30 years [1, 2] and is the primary technique used in evidence-based medicine, particularly by the Cochrane Collaboration [3], as it can greatly increase power to detect effects. Cross-study synthesis becomes necessary as a field matures, and findings from individual studies must be combined to approach questions that cannot be answered through studying individual trials in isolation.

Traditionally, meta-analysis involves combining published summary findings across similar studies by placing each of these summaries on a common metric, such as a standardized mean difference or log odds ratio. A single overall measure of impact is then obtained which represents the overall effect across different trials [4–6]. There can be major shortcomings from meta-analyses that are based solely on published results, either from differences in the ways that the individual trials were analyzed or from the use of different outcome measures. Because there are no raw data available, meta-analysis can only synthesize from reported findings, restricting topics of inquiry to those questions that have already been addressed within individual studies. For more sophisticated analyses such as mediation, moderation, growth modeling, and subgroup analysis, published reports of these analyses are rarely available for more than a small proportion of the studies, and even when they are, different modeling and reporting decisions across studies often lead to analytic incompatibility.

In response to limitations of traditional meta-analysis, an increasingly popular approach is individual participant data (IPD) meta-analysis in which the raw individual-level data for each study are obtained and used for synthesis [7]. With the raw data in hand, an analyst can adjust for patient-level covariates and take into account repeated measures, missing values, and differential follow-up times.

However, IPD meta-analysis can introduce challenges of its own. In particular, a common situation is when different outcome measures are used to assess the same construct in different studies [8]. The term harmonization has been coined to describe the procedure of placing variables on the same scale in order to permit pooling of data from a large number of studies [9, 10].

In this article we describe a multiple imputation approach for harmonizing measures across longitudinal intervention trials when there is no overlap in outcome measures within trials. We seek a method that will permit pooling of IPD from studies which use different outcome measures for the same construct, which could greatly increase power for treatment effect analysis. We extend existing methods for harmonization by addressing harmonization in a longitudinal setting where different studies have different follow-up times and the relationships between outcome measures may change over time. Our method makes use of external calibration studies in which IPD are available on both outcomes but the calibration studies are not to be included in final analyses. In addition to providing information on the relationship between outcome measures, the calibration studies facilitate the use of imputation diagnostics to assess the quality of imputations.

This article is organized as follows. In Section 2 we describe the example that motivated this work, a study of five randomized clinical trials investigating the effectiveness of fluoxetine for the treatment of depression among adolescents. We also discuss existing methods for harmonization. In Section 3, we describe our imputation model and diagnostics for checking the quality of imputations when variables are missing for all participants within a study. Section 4 presents the results of applying our methods to the fluoxetine data and Section 5 offers discussion and areas for future work.

2 Motivation and background

2.1 Motivating example

The motivating example for this work are IPD from five randomized controlled trials (RCTs) studying the effectiveness of fluoxetine for the treatment of depression among adolescents. Two different measures of depressive symptoms were used in the trials. Four of the trials used the Children's Depression Rating Scale (CDRS), and one trial used the Hamilton Depression Rating Scale (HDRS). None of the five trials used both the CDRS and the HDRS. The HDRS employs 17 items to assess depressive symptoms and scores range from 0 to 50 [11]. The CDRS also contains 17 items, but was designed to assess depressive symptoms specifically in children ages 6-12 years [12]. Scores on the CDRS range from 17 to 113. Our objective is to combine information from all studies to estimate the effect of fluoxetine on the HDRS.

These five studies consist of all RCTs of fluoxetine in adolescents that included 30 or more patients, all of whom had a diagnosis of major depressive disorder. All five studies were double-blind, placebo-controlled RCTs. Data for four of the 5 fluoxetine trials were obtained from Eli Lilly and Co. Data from the 5th fluoxetine trial came from the Treatment for Adolescents With Depression Study (TADS) [13] and were obtained from the National Institute of Mental Health and do not include participants from a third TADS arm who received cognitive behavioral therapy. Only summary scores were available in all the trials; item-level data for neither the CDRS nor the HDRS were provided.

The top portion of Table 1 displays descriptive statistics by study for the HDRS and CDRS at baseline as well as age, gender, study duration, and sample size, and indicates which studies used which depression measures. Resche-Rigon et al. [14] refer to missing values that are missing for every observation in a study as systematically missing. Across the 5 fluoxetine studies, ages ranged from 7-18 years and trial size ranged from 40 to 221 participants. The length of the trials were from 3 to 12 weeks with anywhere from 3 to 9 assessments during the course of a study.

Table 1.

Descriptive statistics and missing data patterns of fluoxetine and venlafaxine trials at baseline. Not available (NA) indicate trials where the depression measure was not used.

Trial	CDRS (SD)	HDRS (SD)	Age (range)	Male (%)	Duration (wks)	No. Assess.	n
TADS fluoxetine	56 (10.8)	NA	13 (8–18)	51	9	7	221
Eli Lilly fluoxetine 1	44 (12.1)	NA	11 (7–18)	72	3	3	219
Eli Lilly fluoxetine 2	58 (10.3)	NA	13 (7–18)	54	8	9	172
Eli Lilly fluoxetine 3	55 (12.8)	NA	15 (12–18)	47	12	3	96
Eli Lilly fluoxetine 4	NA	22 (3.5)	16 (12–17)	45	6	7	40
Calibration Trials
Wyeth venlafaxine 1	54 (8.7)	18 (5.1)	12 (7–17)	51	8	8	167
Wyeth venlafaxine 2	58 (9.2)	16 (4.8)	12 (7–18)	58	8	8	191

TADS: Treatment for Adolescents With Depression Study

In this setting with no overlap between the CDRS and the HDRS, the partial correlation between the two depression measures after conditioning on background covariates is inestimable [15]. Therefore, in order to estimate the association between the two depression measures, data from two additional placebo-controlled adolescent depression trials were obtained which used a different medication (velanfaxine), but included summary scores for both the CDRS and the HDRS on every participant [16]. Because these trials use a different treatment medication, we are not interested in including them in our final analysis. However, we do want to use the data from these two trials to obtain information on the relationship between the CDRS and HDRS in order to harmonize the CDRS and HDRS data in the fluoxetine trials. For this reason, we refer to these two trials as “external calibration trials.”

The last two rows of Table 1 provide information on the calibration trials, which were both 8 weeks in duration. An interesting and important feature of the external calibration trials is the changing nature of the partial correlation of the CDRS and the HDRS as a function of time. Table 2 displays the partial correlation (controlling for age and gender) of the CDRS and the HDRS as a function of study week. These partial correlations were estimated by using two separate linear regression models to regress CDRS on age and gender and HDRS on age and gender. The correlation between the error terms from these two regression models provides the partial correlation. This procedure was performed separately by time point. As can be seen, the partial correlation increases over the course of the study with an overall correlation of 0.57 at baseline and a correlation of 0.85 by the end of the study. One possible explanation for this increasing correlation is that the distribution of both measures is left-truncated at baseline due to the fact that participants were required to have an elevated depression score in order to meet inclusion criteria.

Table 2.

Partial correlation (controlling for age and gender) between CDRS and HDRS in calibration samples. Baseline (week 0) includes all participants. Subsequent estimates are based only on control participants.

Week	Study 1	Study 2	Overall
0	0.71	0.51	0.57
1	0.74	0.59	0.67
2	0.78	0.71	0.73
3	0.81	0.74	0.76
4	0.83	0.79	0.81
6	0.86	0.77	0.81
8	0.88	0.84	0.85

2.2 Existing data harmonization methods

There are a number of existing methods for data harmonization which make use of the fact that even if different studies use different outcomes, they are attempting to measure the same construct. These methods fall roughly into three general classes: (1) linear or z-transformations to create a common metric across data sets; (2) latent variable methods that identify an underlying latent construct across all studies [17–21]; (3) multiple imputation methods that treat unobserved measures as missing data and replace the missing values with plausible values [14, 22].

Transforming original units into standard deviation units via a z-transformation is a relatively simple solution and does not require common items across studies. A drawback is that this method does not take into account differences in variability across studies and assumes the underlying constructs are the same and measured equally well across studies [9]. Also, the transformed variable may not have the same scientific interpretation and familiarity as the original units with which substantive researchers are better able to interpret results and compare them with other findings in the literature. Latent variable methods solve some of the challenges associated with using z-scores but require strong assumptions about latent structure that can be difficult to check, especially when there are few or no variables of interest measured simultaneously in the data sets to be harmonized. Both approaches, as currently implemented, struggle with repeated observations, and typically assume that repeated observations on the same participant are independent.

Multiple imputation [23] is a natural approach for handling missing data due to un-measured outcomes and has a number of advantages over existing methods. With multiple imputation, missing values are replaced with two or more plausible values to create two or more completed data sets. Analyses are then conducted separately on each data set and final estimates are obtained by combining the results from each of the imputed data sets using rules that account for within-imputation and between-imputation variability. See Harel and Zhou [24] for a review.

In the context of harmonization for IPD meta-analysis, once unmeasured variables have been imputed, analyses and their subsequent inferences are based on existing scales of interest rather than a z-score or a latent variable. In addition, after the data set has been filled in, it can be shared with other investigators and be used for numerous analyses using complete data methods. In fact, once a variable has been multiply imputed, it may be used as an outcome in one analysis, and as a covariate in another analysis.

While multiple imputation was originally conceived for use in single surveys with missing data, the method has been extended to numerous areas. Most relevant to data harmonization in IPD meta-analysis is data fusion where two (or more) data sets from the same population (but different samples) are to be combined and some variables only appear in one data set or the other, but no data set contains all variables of interest [25–27].

For example, in our motivating example of five RCTs where the HDRS and the CDRS are systematically missing, multiple imputation can be used to complete the concatenated data set, by imputing the HDRS in four of the studies and the CDRS in the fifth study. However, in this setting in which the HDRS and CDRS are never jointly observed (as they are in the five fluoxetine trials), the maximum likelihood estimate of the partial correlation between the HDRS and the CDRS, conditioning on background covariates is inestimable [15]. When estimating these parameters and generating imputations in a Bayesian framework, the posterior estimates of the partial correlations will be equal to the prior correlation [28]. Thus, the typical non-informative priors used in Bayesian imputation models would result in partial independence between the HDRS and CDRS. Since the two measures are presumed to be measuring a similar construct, this is unlikely to be a plausible assumption.

Rässler [26] proposed a multivariate normal imputation model for the data fusion setting where imputations are generated by positing a value for the partial correlation between two outcomes that are never jointly observed. Rässler [26] suggests three ways of specifying this correlation: 1) from its prior based on a distributional assumption (e.g. uniform over some range); 2) using several arbitrary values; 3) using values estimated from an external data set with information on the joint distribution between the two variables of interest.

Gelman et al. [22] developed an imputation model to impute missing data from several sample surveys where not all the surveys asked the same questions. Here, a separate imputation model is fit for each survey, but with parameters across the surveys linked using a hierarchical model so that imputations for questions not asked in a survey are determined by data from the other surveys in the population as well as by available responses to other questions in that survey. An advantage of this approach is that covariates may be included in the regression model at both the individual and survey level.

3 Methods

Our approach for harmonizing the depression data across the multiple trials is in the spirit of Gelman et al. [22] and Rässler [26] where the uncollected depression measures are considered missing data and missing observations are multiply imputed. We extend these existing approaches to the case of longitudinal data and we develop methods that make use of external calibration data. Not only do the calibration data provide information on the relationship between the two depression measures, but they also facilitate the use of imputation diagnostics to assess the quality of the imputations.

We begin by concatenating the calibration data sets with the fluoxetine data sets. We then generate multiple imputations for the missing CDRS and HDRS data using an imputation model that estimates the relationship between these two measures based on information from the calibration data. Once the missing data have been imputed, we perform diagnostics to check whether the imputed data are consistent with the observed data. Finally, we remove the calibration data and perform post-imputation analyses on the 5 fluoxetine trials using the multiply imputed completed data sets.

3.1 Imputation Model

Our imputation method is based on a multivariate random-effect model that jointly models the two depression measures over time [29]. Using notation similar to that of Weiss [30], let y_ij and w_ij be the HDRS and CDRS scores, respectively, for participant i measured at time j where j = 1, . . . n_i. Our model is

$$\begin{array}{cc}\hfill y_{ij}=& {\beta }_0+{\beta }_1{\mathrm{age}}_i+{\beta }_2{\mathrm{gender}}_i+{\beta }_{3}tim{e}_{ij}+{\beta }_4(tim{e}_{ij}\times T_i)+{\eta }_{y0i}+{\eta }_{y1i}tim{e}_{ij}+{\epsilon }_{yij}\hfill \\ \hfill w_{ij}=& {\alpha }_0+{\alpha }_1{\mathrm{age}}_i+{\alpha }_2{\mathrm{gender}}_i+{\alpha }_{3}tim{e}_{ij}+{\alpha }_4(tim{e}_{ij}\times T_i)+{\eta }_{w0i}+{\eta }_{w1i}tim{e}_{ij}+{\epsilon }_{wij}\hfill \end{array}$$ (3.1)

where T_i is a variable that indicates whether participant i received fluoxetine or placebo and time_ij is the number of days since baseline, log transformed to approximate linearity and avoid the use of an additional parameter to estimate a quadratic term [31]. The β and α parameters represent fixed effects, while η_y0i and η_y1i are random intercept and slope terms for y and η_w0i and η_w1i are random intercept and slope terms for w. We assume these random effects η_i = (η_y0i, η_y1i, η_w0i, η_w0i) have a multivariate normal distribution η_i ~ N₄(0, Δ), where Δ is a 4 × 4 variance-covariance matrix.

The residual errors ε_ij = (ε_yij, ε_wij) are also correlated and follow a bivariate normal distribution ε_ij ~ N₂(0, Σ). Residual errors ε_ij are independent across participants and time and are independent of the random effects.

This model allows the covariance between the CDRS and HDRS to vary as a function of time as was observed in the external calibration data. We have

$$\begin{array}{cc}\hfill Cov(y_{ij},w_{ij})=& Cov({\eta }_{y0i}+{\eta }_{y1i}tim{e}_{ij}+{\epsilon }_{yij},{\eta }_{w0i}+{\eta }_{w1i}tim{e}_{ij}+{\epsilon }_{wij})\hfill \\ \hfill =& d_{13}+tim{e}_{ij}{d}_{14}+tim{e}_{ij}{d}_{23}+tim{e}_{ij}^2{d}_{24}+{\sigma }_{yw}\hfill \end{array}$$

where d_ij is the ith row and jth column of the random effects variance-covariance matrix and σ_yw is the covariance of the residual errors. In addition to modeling the correlation of the two measures (and its change) over time, the model also estimates the within-subject correlation on the same measure over time, that is, the intra-class correlation.

Note that the imputation model described in Equation 3.1 does not include a term for trial. A fixed effect for trial is not estimable in this model because for some trials all outcomes are missing. There is little information available to estimate random trial effects because the number of trials is small and estimating random effects at the trial level for both the HDRS and the CDRS requires us to estimate the correlation of these two measures at the trial level. With only two calibration trials, we do not have enough degrees of freedom to estimate the study-level correlation between the CDRS and the HDRS. Further complicating our e orts is the fact that the direction of the correlation is negative which is unlikely to be the true direction of this relationship and is more likely due to the small sample size.

3.2 Model assumptions

We highlight four assumptions in the imputation model described in Section 3.1.

Assumption 1

We assume the missing depression data are missing at random (MAR) such that the probability of missingness depends only on observed data included in the model and not on unobserved data. In our setting, the MAR assumption implies that an investigator's decision not to use a depression measure is not related to unobserved variables, in particular the unmeasured depression score itself. The choice of whether to use the HDRS or the CDRS is primarily based on age, where the CDRS was designed to be more relevant to younger children than the HDRS. Since we are able to condition on age in our imputation models and the calibration data are based on an age range comparable to the age ranges in the fluoxetine trials, we are comfortable with this assumption.

Assumption 2

The second assumption relates to the partial correlation between the CDRS and the HDRS. As before, let y_ij and w_ij indicate the HDRS and CDRS scores, respectively, for participant i at time j. The variable T_i is the treatment assignment for participant i, and X_i = (age_i, gender_i) are the age and gender for participant i. Treatment assignment, age, and gender are observed on all participants. Then, at any two time points j and k.

$$\mathrm{Corr}(y_{ij},w_{ik}\mid X_i=x_i,T_i=t_i)=\mathrm{Corr}(y_{ij},w_{ik}\mid X_i=x_i),$$ (3.2)

that is, the partial correlation between the HDRS and CDRS does not depend on treatment group. We make this assumption because the external calibration trials do not use fluoxetine and thus do not provide information on the correlation between measures for fluoxetine participants. We restrict our external calibration trials to placebo participants (and all participants at baseline) and make the assumption in Equation 3.2 that the partial correlation is the same for placebo and fluoxetine participants.

Assumption 3

The third assumption is that the partial correlation between the CDRS and the HDRS does not differ by trial. Let y_ijl and w_ijl indicate the HDRS and CDRS scores, respectively, for participant i at time j in trial l. For two participants i and i′ in trials l and m,

$$\mathrm{Corr}(y_{ijt},w_{ikl}\mid X_i=x_i)=\mathrm{Corr}(y_{i^{\prime }jm},w_{i^{\prime }km}\mid X_{i^{\prime }}=x_i).$$ (3.3)

Assumption 4

Our fourth assumption concerns independence of observations within the same trial in our imputation model. As before, let y_ijl and w_ijl indicate the HDRS and CDRS scores, respectively, for participant i at time j in trial l. Then we make the following assumptions. At any two time points j and k, i≠i′, and conditioning on auxiliary variables age_i, gender_i,

$$\mathrm{Corr}(y_{ijl},y_{i^{\prime }kl})=0$$ (3.4)

$$\mathrm{Corr}(w_{ijl},w_{i^{\prime }kl})=0$$ (3.5)

$$\mathrm{Corr}(y_{ijl},w_{i^{\prime }kl})=0.$$ (3.6)

3.3 Estimation and imputation

We used a Bayesian approach to estimate the parameters of our imputation model and to generate imputations. As noted by Schafer [32], imputations generated from a Bayesian model are proper in the sense that they incorporate both model parameter uncertainty as well as uncertainty due to missingness. We placed non-informative priors (N(0, 10³)) on the regression coefficients of the fixed effects (β, α) in Equation 3.1. For both the random effects covariance matrix and the residual error covariance matrix, we use inverse-Wishart priors with 6 and 4 degrees of freedom, respectively, and a scale parameter equal to the identity matrix.

Markov Chain Monte Carlo (MCMC) via the software OpenBUGS [33], was used to draw model parameters and generate imputations. We diagnosed convergence of the MCMC algorithm using statistics developed by Gelman and Rubin [34] and concluded that the Markov chain converged after 20,000 iterations. OpenBUGS code and MCMC diagnostics for some of the imputation model parameters are included in the supplementary materials. Imputations were generated by running an additional 50,000 iterations on a single chain and drawing a set of parameters from every 500 iterations. This high thinning value was chosen to ensure that imputed values were generated from approximately independent draws of the imputation model parameters [32].

After imputing the missing outcome measures, we removed the calibration data and analyzed only data from the fluoxetine trials. In this setting, when some of the records used to estimate the imputation model are not used for analysis, the usual multiple imputation combining rules variance estimator has positive bias because the conditioning used by the imputer and the analyst are not matched [35]. To address this, we used Reiter's [35] method of two-stage multiple imputation and its associated combining rules which has better performance in this context. First, m values of the parameters in the imputation model are sampled, and then, nested within each set of parameter draws, n imputations are generated for each missing value. This results in mn completed data sets. Analyses are performed separately on each imputed data set and the results are combined using the two-stage imputation rules described in Reiter [35] which are provided in Appendix A. We used m = 100 sets of parameter draws with n = 2 imputations nested within each parameter draw for our application.

3.4 Diagnostics

In our setting, where the amount of missing data is considerable, and where we are imputing values for every participant within a trial, it is particularly important to check the imputation model and the quality of its imputations. We use two general approaches for checking our imputation model: graphical comparisons of the observed data versus the imputed data [22, 36] and posterior predictive checks using numerical summaries based on test statistics [37]. In both cases we focus on diagnostics that capture important features of the data that are relevant to our target analyses.

Graphical exploration consisted of comparing observed (imputed) HDRS values with imputed (observed) CDRS values as a function of time. To do this, we created side-by-side scatterplots of depression scores over time. In one panel, the data are observed, in the other, the data are every participant's average imputed values at each time point. While the scale of the two depression measures is different, we expect to observe similar patterns over time. If not, this suggests a problem with the fit of our imputation model.

The numerical approach follows the posterior predictive checking and re-imputation method of He and Zaslavsky [37] and used the following strategy. First, we duplicated the data from the two external calibration trials and deleted the HDRS values in this duplicated version of the calibration data. Next, we concatenated these duplicated data sets with the original 7 data sets (the 5 fluoxetine trials and the 2 original calibration trials) resulting in a data set containing 9 trials. Finally, we generated imputations using the methods described in Section 3.1, imputing missing values in the fluoxetine studies as well as the missing HDRS values that were deleted in the duplicated calibration data . Let Y be the observed HDRS calibration data and Y^imp the imputed version of Y. To compare observed data to imputed data, we use a test statistic, T(Y,θ), some scalar function of the data and possibly imputation model parameters. Posterior predictive checking consists of comparing T(Y,θ) to the distribution of T(Y^imp,θ). Lack of fit of the imputed data to the observed data can be quantified by the posterior predictive p-value (ppp) [38, 39], the probability that the imputed data are more extreme than the observed data, as measured by the test statistic, that is,

$$ppp=2\times \min (Pr(T(Y^{imp},\theta )>T(Y,\theta )\mid Y),Pr(T(Y^{imp},\theta )<T(Y,\theta )\mid Y))$$ (3.7)

In practice, we can calculate ppp by simulation. For each imputed data set v, v = 1, . . . , V we calculate T(Y^imp,v,θ^v). The estimated two-sided posterior predictive p-value is the proportion of the V test statistics that equal or exceed the test statistic based on the observed data, that is,

$$ppp=\frac{2}{V}\times \min \left(\sum _{v=1}^{V}I(T(Y^{imp,v},{\theta }^v)>T(Y,{\theta }^v)),\sum _{v=1}^{V}I(T(Y^{imp,v},{\theta }^v)<T(Y,{\theta }^v))\right)$$

A small ppp suggests that the proposed imputation model is not adequate to support the targeted post-imputation analysis [37]. We investigated 3 sets of test statistics that capture important relationships linked to our substantive analyses. These test statistics are: 1) the partial correlation (controlling for age and gender) between the HDRS and CDRS at weeks 0, 4, 6, and 8; 2) the HDRS means at weeks 0, 4, 6, and 8; and 3) the fixed intercept and slope terms from a random intercept and slope regression model regressing HDRS on (log) days since baseline.

4 Results based on application to adolescent data

We begin this section by presenting the results of the diagnostics to ensure that our imputations are reasonable and are replicating important relationships relevant to our target analyses. We then analyze the fluoxetine data first using the CDRS as the outcome, then the HDRS.

4.1 Results from diagnostics

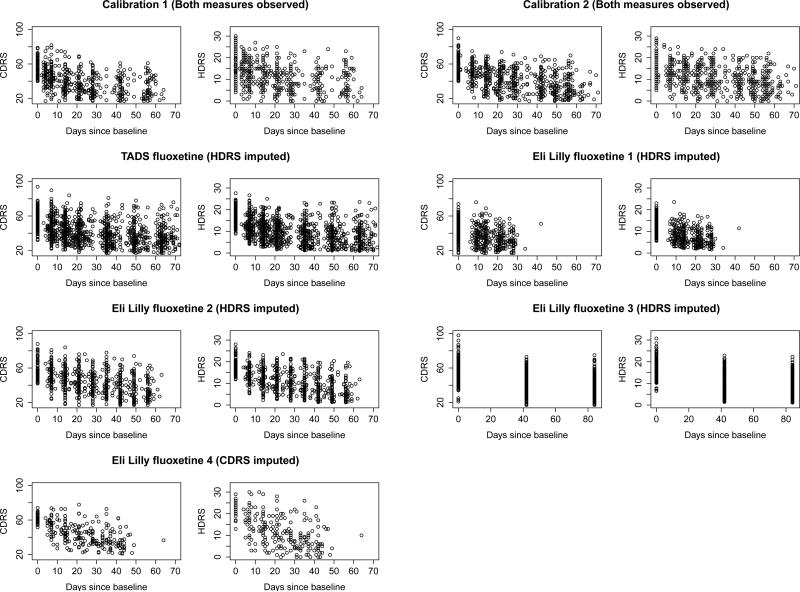
Figure 1 presents scatter plots of CDRS and HDRS data versus time (days since baseline) for each of the trials in Table 1. The first row of the panel are the two calibration data sets in which both the CDRS and the HDRS are observed. The next two rows of the panel are the fluoxetine trials which only used the CDRS. For these trials we have imputed 200 HDRS values for every observation in the trial and displayed the average of these 200 imputations. The last row is the fluoxetine trial which used the HDRS. Here we imputed CDRS values for every participant in the trial. As can be seen, within each trial, the imputed values appear to preserve the relationship that is seen between the observed depression score and time.

Figure 1.

Plot of CDRS scores versus HDRS scores by study. Imputed values are the mean of 200 imputations.

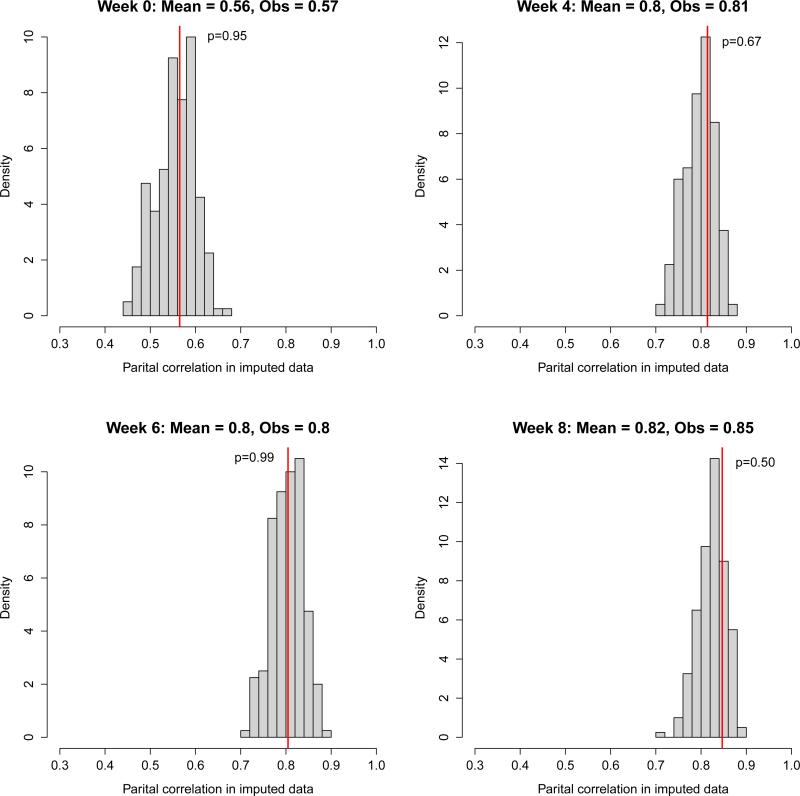
Figure 2 displays the results of posterior predictive checks (based on 200 imputed data sets) on the partial correlation between the CDRS and the HDRS in the duplicated calibration data at weeks 0, 4, 6, and 8. At all time points, the correlation based on imputed values is close to the observed calibration study correlation (indicated by the vertical line) and our imputation model is clearly capturing the increasing correlation over time. Posterior predictive p-values are large at all weeks; thus, we find no evidence that the model generates unreasonable imputations.

Figure 2.

Posterior predictive checks of the partial correlation (controlling for gender and age) between the HDRS and the CDRS in the external calibration data by week. The histogram displays the distribution of partial correlations based on imputed values from 200 imputed data sets. The vertical lines indicate the observed partial correlation. The posterior predictive p-values shown in each histogram are two-sided.

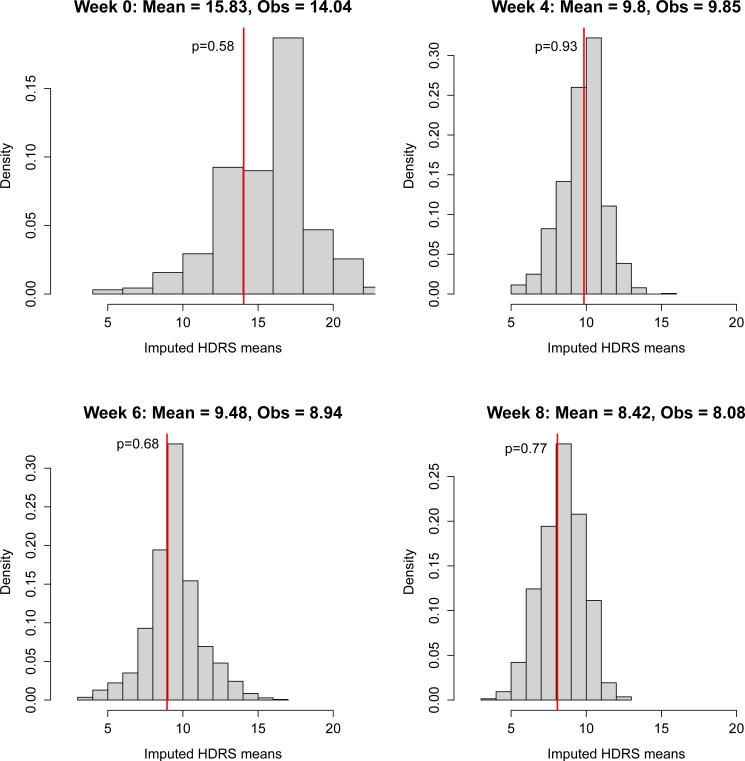
Figure 3 displays the results of posterior predictive checks on the HDRS means in the duplicated calibration data at weeks 0, 4, 6, and 8. At all time points, the imputed mean is close to the observed calibration study mean (indicated by the vertical line). Posterior predictive p-values are large at all weeks. As with the partial correlations, none of these p-values suggest that our imputations are unreasonable. Because the observed correlation between the CDRS and HDRS was lowest at baseline, it is not surprising that our imputations are less accurate at baseline than at other time points.

Figure 3.

Posterior predictive checks of weekly HDRS means in the external calibration data. The histogram displays the distribution of imputed means from 200 imputed data sets. The vertical lines indicate the observed means. Posterior predictive p-values are two-sided.

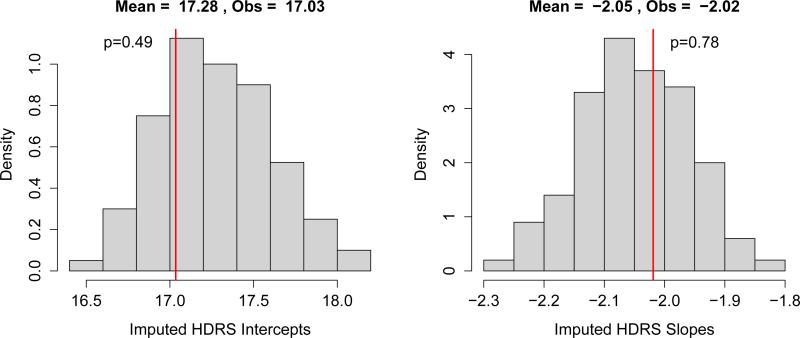
Figure 4 displays the results of posterior predictive checks of the fixed intercept and slope coefficients of a random intercept and slope regression model of HDRS score as a function of log(number of days since baseline + 1) in the calibration data. As with the other posterior predictive checks, the parameters based on imputed values are close to observed values and posterior predictive p-values do not suggest an imputation model that is failing to capture important relationships.

Figure 4.

Posterior predictive checks of regression coefficients from a random intercept and slope regression model estimating the effect of time on HDRS score in the external calibration data. The panel on the left displays the intercept in the model, the panel on the right the slope. The histograms display the distribution of the regression coefficients based on imputed values from 200 imputed data sets. The vertical lines indicate the observed regression coeffcients. Posterior predictive p-values are two-sided. Time is log(number of days since baseline + 1).

4.2 Post-imputation analysis of fluoxetine data

Based on the findings from the imputation diagnostics, we proceeded to discard the calibration data and analyze the 5 fluoxetine trials. Table 3 is the same as Table 1 above but here we have filled in the missing cells with those based on imputed values. Looking at Table 3, those trials with low baseline CDRS scores tended to have low baseline HDRS scores. The Eli Lilly fluoxetine trial 1 had the lowest mean baseline CDRS score of all the trials, including the calibration trials and also has the lowest mean baseline HDRS score. Conversely, the Eli Lilly fluoxetine trial 4 had a high mean baseline HDRS score as compared to the calibration trials and this is also reflected in its imputed mean baseline CDRS score.

Table 3.

Descriptive statistics and missing data patterns of fluoxetine and venlafaxine trials at baseline. Values with an asterisk next to them indicate that they are based on multiple imputations.

Trial	CDRS (SD)	HDRS (SD)	Age (range)	Male (%)	Duration (wks)	No. Assess.	n
TADS fluoxetine	56 (10.8)	17 (5.5)*	13 (8–18)	51	9	7	221
Eli Lilly fluoxetine 1	44 (12.1)	14 (5.6)*	11 (7–18)	72	3	3	219
Eli Lilly fluoxetine 2	58 (10.3)	18 (5.4)*	13 (7–18)	54	8	9	172
Eli Lilly fluoxetine 3	55 (12.8)	17 (5.9)*	15 (12–18)	47	12	3	96
Eli Lilly fluoxetine 4	62 (10.4)*	22 (3.5)	16 (12–17)	45	6	7	40
Calibration Trials
Wyeth venlafaxine 1	54 (8.7)	18 (5.1)	12 (7–17)	51	8	8	167
Wyeth venlafaxine 2	58 (9.2)	16 (4.8)	12 (7–18)	58	8	8	191

TADS: Treatment for Adolescents With Depression Study

^*Based on imputed values

We then analyzed the CDRS scores (both observed and imputed) as a function of treatment and time using the following random-effects regression model. Let CDRS_ijl be the CDRS score for participant i at occasion j, j = 1, . . . , n_i in trial l, l = 1, . . . , N; and let time_ij be the time since baseline and T_i a variable indicating whether participant i received fluoxetine or placebo. Then our model is

$${\mathrm{CDRS}}_{ijl}={\beta }_0+{\beta }_{1}tim{e}_{ij}+{\beta }_2(tim{e}_{ij}\ast T_i)+b_{0l}+b_{0i}+b_{1i}tim{e}_{ij}+{\epsilon }_{ijl}.$$ (4.1)

As in our imputation model, time has been log transformed. The term b_0l is a trial-specific random intercept term which follows a normal distribution and takes into account between-trial variability. The terms b_0i and b_1i are random intercept and slope terms at the participant level, respectively, and follow a bivariate normal distribution independent of the trial-specific random intercept. The error term ε_ijl also follows a normal distribution and is independent of the random effects. The model was fit using the lmer function from the R [40] package lme4 [41].

In this model, inference focuses on the regression coe cient β₂, the time by treatment interaction. This term represents the difference in slopes between treatment and control groups. Our trials are short in duration and this parameterization fits our data well. A more flexible approach to model the effect of treatment would be to treat time as a nominal variable by specifying indicator variables for each time period and interacting these indicator variables with treatment. However, since each study has different follow-up times, we are unable to fit this more flexible model in this particular application.

The top half of Table 4 presents the results of our analysis using only the observed CDRS scores as well as using both observed and imputed CDRS scores. As noted above, post-imputation analyses were based on the two-stage imputation combining rules of Reiter [35]. Not surprisingly, there is very little difference in parameter estimates and their standard errors between the two CDRS analyses. This is because only one trial did not use the CDRS and this was the smallest trial in our data set (n=40). Thus the observed CDRS analysis consists of 708 of the 748 participants in our analysis. Focusing on the treatment by time interaction in Table 4, the treatment effect is significant in both CDRS analyses.

Table 4.

Observed-only and post-imputation analyses of CDRS and HDRS scores in fluoxetine trials. The observed-only HDRS analysis is based on a single trial does not include a random effect at the trial level. All other models include a trial-level random effect.

		Observed				Imputed
Outcome	Parameter	Est	SE	t-val	p-val	Est	SE	t-val	p-val
CDRS	Intercept	54.00	2.56	21.12	<.001	55.20	2.26	24.39	<.001
	Time	−3.79	0.18	−21.34	<.001	−3.97	0.17	−22.77	<.001
	Tx*Time	−1.06	0.21	−4.92	<.001	−0.94	0.21	−4.50	<.001
	SD(b0l)	5.03				4.98
	SD(b0i)	9.91				9.84
	SD(b1i)	2.52				2.58
	Corr(b0i, b1i)	−0.46				−0.45
	SD(εijl)	7.23				7.30
HDRS	Intercept	22.59	0.67	33.48	<.001	17.19	0.77	22.3	<.001
	Time	−3.34	0.42	−7.87	<.001	−1.62	0.04	−45.25	<.001
	Tx*Time	−0.57	0.55	−1.03	.308	−1.22	0.18	−6.95	<.001
	SD(b0l)	NA				1.8
	SD(b0i)	2.11				4.74
	SD(b1i)	1.46				1.23
	Corr(b0i, b1i)	0.13				−0.58
	SD(εijl)	3.97				3.24

SD(b_0l): Standard deviation of random trial-level intercepts

SD(b_0i): Standard deviation of random subject-level intercepts

SD(b_1i): Standard deviation of random subject-level slopes

Corr(b_0i, b_1i): Correlation of random intercepts and slopes

SD(ε_ijl): Standard deviation of residual error

The bottom half of Table 4 presents observed-only and post-imputation analysis of HDRS scores in the fluoxetine trials using the same model in Equation 4.1 but with the HDRS as the outcome. Here, the observed-only results are based on a single trial (n=40) whereas the post-imputation analysis are based on imputing HDRS scores for 708 out of the 748 (95%) participants in our analysis. Because the observed-only HDRS analysis is based on a single trial, the trial-level random intercept term is omitted. There are substantial differences between the observed-only and post-imputation HDRS analyses. In particular, the intercept in the observed analysis is much higher than that of the post-imputation analysis, reflecting the high baseline depression scores in fluoxetine trial 4. Also, the time by treatment interaction term is not significant in the observed-only analysis but it is significant in the imputed analysis. It appears that in trial 4, both treatment and placebo participants improved a great deal and by similar amount, possibly due to their high depression scores at baseline. When including the other 4 trials in the analysis, a treatment effect is detected as the placebo participants in these trials did not improve to the same degree as the placebo participants in trial 4.

Another meaningful difference between the two HDRS analyses in Table 4 is the reduction in standard errors due to the inclusion of the additional data. There is a 67% reduction in the standard error of the time by treatment interaction based on the post-imputation analysis. As a result, the magnitude of the t-value of the treatment effect on the HDRS, −6.95, is similar to the magnitude of the t-value of the treatment effect on the CDRS which is −4.50.

5 Discussion

We have described a multiple imputation approach for harmonizing outcomes across multiple longitudinal trials. In our motivating example, we sought to harmonize two depression measures where there were no studies which used both measures. To do this, we made use of external calibration data in order to estimate key relationships and generate more accurate imputations. Besides providing information on the relationship between the two depression measures, the calibration data facilitate the use of diagnostics to address how well imputed values preserve important relationships related to the target analyses. A benefit of the multiple imputation approach is that once the missing data are filled in, analyses can proceed using complete data methods. This makes the data accessible by a wide variety of researchers, many of whom will not have the background knowledge or the technical expertise to harmonize the data themselves.

Our imputation model is a multivariate linear mixed-effect model and explicitly models the effect of time and treatment on our target variables. This is important so that our imputation model is congenial with our analysis objective [42] which is to investigate the the difference in change over time between treatment and placebo groups. With differential follow-up times across study, attempting to impute missing data at each time point using standard software such as SAS Proc MI [43] or MICE [44] would result in many variables to be imputed and parameters to be estimated. Similarly, an imputation model based on a covariance pattern model rather than random effects would be difficult to fit and unlikely to be parsimonious.

An additional benefit of modeling the effect of time is that if a user of our method wishes to harmonize the assessment time points, they simply need to add a new row for each participant in their data set where the outcome is missing and the time value is set to its desired value. While in our example, the missing values are outcomes in the analysis, our imputation model is flexible and makes no distinction between outcomes or time-varying covariates.

We make several assumptions in developing our imputation model. Most notable is the assumption of no between-study variability. Including random effects at the trial level in our imputation model is dependent upon being able to estimate the correlation between the HDRS and the CDRS at the trial level. With only two calibration trials, this correlation is not estimable. Further complicating our e orts is the fact that the direction of the correlation is negative. Thus, our imputation model assumes that observations on different participants in the same trial are independent. Our analysis model, however, did include a trial-level random effect term and it is interesting to compare the trial-level intra-class correlations between the imputed CDRS analysis and the imputed HDRS analysis. For the CDRS analysis in which data from a single trial is imputed, the baseline ICC is 0.14. For the HDRS analysis in which data from 4 of 5 trials is imputed the baseline ICC is 0.09. So although our imputation model ignores the effect of trial, between-trial variability does not seem to be severely attenuated in post-imputation analyses.

There are several limitations to our approach. Our imputation model is a linear mixedeffects model which assumes the outcomes are normally distributed, although they are actually bounded above and below which can result in imputed values that are out of range. Methods have been developed for handling bounded continuous outcomes [45]. For our data, where the HDRS ranges from 0 to 50 and the CDRS ranges from 17 to 113, the data were relatively symmetric and using a Gaussian-based imputation model resulted in few out-of-range imputations. Only 2.7% of the imputed CDRS values were out of range and only 5.2% of imputed HDRS values were out of range. For these observations, we redrew our imputations until imputed values were in range. Some research has shown that when imputing highly skewed limited-range variables it is best to allow imputed values to remain out of range [46]. For our purposes, in which the normality assumption produced few out-of-range values, this is less of a concern. In addition, the results of our diagnostic checks suggest that our imputations are preserving important features of the data. In settings where outcomes are highly skewed and/or very limited in range, it may be appropriate to allow out-of-range imputed values or use more flexible imputation models that can handle a combination of continuous, ordinal, and binary data [47].

Our method requires calibration data because there is no overlap in depression measures within any of the trials of interest. If overlap does exist, then calibration data are not necessary—although they may still be useful. To investigate the utility of a calibration data set in our setting, we imputed the missing HDRS and CDRS values without using the calibration data and imputed each variable separately using a univariate mixed-effects imputation model [29] as implemented in the R [40] package pan [48]. We then analyzed the imputed data using the analysis model in Equation 4.1. The results are displayed in the supporting information. The results based on imputed data without the calibration sample are similar to the observed-only analyses and suggest that there is little benefit to imputing missing outcomes when the analysis model and imputation model condition on the same set of observed covariates.

Our calibration data were from trials of venlafaxine and as a result do not provide information on the partial correlation between the HDRS and CDRS among participants randomized to fluoxetine. Thus we make the assumption that this partial correlation does not depend on treatment group and we restrict our external calibration trials to only placebo participants (and all participants at baseline). To explore whether use of an antidepressant a ects the partial correlation between the HDRS and CDRS, we compared the partial correlation between the HDRS and CDRS in the calibration trials, stratifying by time, treatment group, and study (included in the supporting information). Post baseline, the partial correlations in the treatment and control groups are similar at each time point. These results suggest that Assumption 2 is a reasonable one, in the sense that use of an antidepressant does not seem to a ect the partial correlation between the HDRS and CDRS. These results also suggest that we would see little change in our results if we were to include both treatment and control groups in the calibration data

Our imputation model is complex and the random-effect covariance matrix itself includes 10 parameters. While it would be possible to fit a more parsimonious model, such as a model with a shared intercept and response specific random slopes, the tradeo for this parsimony is less flexibility in estimating the correlation between the CDRS and HDRS. Since the primary goal of our model is generating imputations rather than inference, we see little advantage to parsimony when our calibration data allows us estimate the parameters from a more complicated model.

Directions for future work include examining harmonization across a larger number of trials and trials with time-varying variables, and developing a 3-level imputation model where repeated observations are nested within participants who are nested within trials. Our application had an insu cient number of trials to support such models. These models may make use of shared parameters [49] and/or use informative priors for situations when calibration data do not exist or are inadequate to model a larger set of parameters.

Increasingly, researchers are collecting data from multiple studies in order to synthesize findings and perform more sophisticated analyses. These projects will continue to grow as U.S. funding agencies encourage data sharing [50, 51] and more journals require the release of data to accompany manuscripts. Methods that harmonize variables across data sets and facilitate analyses by many researchers are increasingly important in order to make full and e cient use of synthesized data and take advantage of the potential of IPD meta-analysis to address new questions not answerable by a single study.

A Nested multiple imputation combining rules

Below we describe the nested multiple imputation approach of Reiter [35]. We use notation that follows closely to that of Shen [52].

Let Q be the quantity of interest. Assume with complete data, inference about Q would be based on the large sample statement that

$$(Q-\widehat{Q})\sim N(0,U)$$

where Q̂ is a complete-data statistic estimating Q and U is a complete-data statistic providing the variance of Q – Q̂. The M × N imputations are used to construct M × N completed data sets, where the estimate and variance of Q from the single imputed data set is denoted by (Q̂^(m,n), U^(m,n)) where m = 1, 2, . . . , M and n = 1, 2, . . . , N. The superscript (m, n) represents the nth imputed data set under the set of parameters m. Let Q̄ be the overall average of all M × N point estimates

$$\stackrel{‒}{Q}=\frac{1}{MN}\sum _{m=1}^M\sum _{n=1}^N{\widehat{Q}}^{(m,n)},$$ (A.1)

and let Q̄_m be the average of the mth model,

$${\stackrel{‒}{Q}}_m=\frac{1}{N}\sum _{n=1}^N{\widehat{Q}}^{(m,n)}.$$ (A.2)

Three sources of variability contribute to the uncertainty in Q. These three sources of variability are:Ū, the overall average of the associated variance estimates

$$\stackrel{‒}{U}=\frac{1}{MN}\sum _{m=1}^M\sum _{n=1}^N{U}^{(m,n)},$$ (A.3)

B, the between-model variance

$$B=\frac{1}{M-1}\sum _{m=1}^M{({\stackrel{‒}{Q}}_m-\stackrel{‒}{Q})}^2,$$ (A.4)

and W, the within-model variance

$$W=\frac{1}{M(N-1)}\sum _{m=1}^M\sum _{n=1}^N{({\widehat{Q}}^{(m,n)}-{\stackrel{‒}{Q}}_m)}^2.$$ (A.5)

The quantity

$$T=\stackrel{‒}{U}+(1+\frac{1}{M})B-(1+\frac{1}{N})W$$ (A.6)

estimates the total variance of (Q – Q̄). Interval estimates and significance levels for scalar Q are based on a Student-t reference distribution

$$T^{-\frac{1}{2}}(Q-\stackrel{‒}{Q})\sim t_v,$$ (A.7)

where v, the degrees of freedom, follows from

$$v^{-1}={\left[\frac{(1+\frac{1}{M})B}{T}\right]}^2\frac{1}{M-1}+{\left[\frac{(1+\frac{1}{N})W}{T}\right]}^2\frac{1}{M(N-1)}.$$ (A.8)

It is possible that T < 0, particularly for small M and N. In this situation, analysts can use T̃ = (1 + 1/M)B. Here inferences are based on a t-distribution with M – 1 degrees of freedom. Generally, negative values of T can be avoided by making M and N large.