Acoustic vibrations contribute to the diffuse scatter produced by ribosome crystals

Lattice vibrations account for the structured component of the diffuse scatter produced by crystals of the 70S ribosome from T. thermophilus.

Abstract

The diffuse scattering pattern produced by frozen crystals of the 70S ribosome from Thermus thermophilus is as highly structured as it would be if it resulted entirely from domain-scale motions within these particles. However, the qualitative properties of the scattering pattern suggest that acoustic displacements of the crystal lattice make a major contribution to it.

1. Introduction  

The X-ray diffraction patterns obtained from macromolecular crystals consist of arrays of Bragg reflections superimposed on backgrounds composed of scattering from the disordered solvent molecules in the crystal and (disordered) gas molecules in the direct beam, Compton scattering and diffuse scattering from the ordered material in the crystal. The diffuse scattering component of the background is the only one that may vary dramatically in intensity as a function of both scattering angle and azimuthal angle (see Glover et al., 1991 ▸).

Owing to thermal motions, if nothing else, the positions of the atoms in the unit cells of a crystal are never exactly the same as those specified by their coordinates, which represent the average distribution of matter in its unit cells. Even though the average displacements of the atoms in a crystal from their mean positions are zero by definition, they do affect diffraction patterns. They make atoms appear larger in electron-density maps than they really are, an effect associated with a systematic fall-off in the intensities of Bragg reflections with increasing scattering angle. They also give rise to diffuse scatter, and the more highly correlated the atomic displacements are in a crystal, the stronger and more strikingly structured its diffuse scattering pattern will be (see James, 1965 ▸).

Even though the activities of most biological macromolecules depend on correlated atomic motions, and many are active in the crystalline state, the information about correlated motions contained in diffuse scattering patterns has largely been ignored over the years, and for a reason. Diffuse scattering patterns, being weak, are hard to measure accurately (Wall et al., 1997 ▸), and in addition no general method exists for interpreting them. Consequently, only a handful of macromolecular diffuse scattering patterns have ever have been analyzed in detail: those of insulin (Caspar et al., 1988 ▸), tropomyosin (Chacko & Phillips, 1992 ▸), lysozyme (Clarage et al., 1992 ▸; Faure et al., 1994 ▸; Héry et al., 1998 ▸), staphylococcal nuclease (Meinhold & Smith, 2007 ▸; Riccardi et al., 2010 ▸; Wall, Van Benschoten et al., 2014 ▸), Feline foamy virus Gag protein (Welberry et al., 2011 ▸) and yeast initiator tRNA (Kolatkar et al., 1994 ▸). For reviews, see Benoit & Doucet (1995 ▸), Moss & Harris (1995 ▸), Thüne & Badger (1995 ▸), Clarage & Phillips (1997 ▸) and Wall, Adams et al. (2014 ▸).

The work described below was undertaken to determine whether anything could be learned about the dynamics of the ribosome from the diffuse scattering patterns produced by ribosome crystals. Although the diffuse scattering patterns obtained from the ribosome crystals discussed below are as strikingly structured as they would be if they were caused by biochemically relevant domain-scale motions, their qualitative properties suggest that they are in a large measure the product of acoustic lattice vibrations, which are unlikely to be biochemically significant. These observations indicate that the possibility that the correlations in atomic displacements responsible for diffuse scattering patterns might extend across unit-cell boundaries is one that should not be lightly dismissed.

2. Methods  

2.1. Extraction of images of the background from frames of oscillation data  

For the purposes of this study, it is assumed that the backgrounds of the frames of oscillation data considered here, which had oscillation angles of either 0.2° or 0.3°, are useful approximations to what would have been observed in stills if the same crystals had been exposed to radiation from the same source, under the same conditions and in the same (average) orientation.

Frames of diffraction data were displayed for inspection and were reformatted for subsequent processing using ADXV (http://www.scripps.edu/~arvai/adxv.html). Processed images were displayed using Gnuplot (http://sourceforge.net/projects/gnuplot). Both experimental and computed amplitudes were scaled so that the color ranges of the false color images shown here would be similar.

A Fortran program was written that uses the information contained in DENZO .x files (Otwinowski & Minor, 1997 ▸) to remove the Bragg reflections present in frames of diffraction data. The algorithm used resembles that devised by Wall and coworkers almost 20 years ago (Wall et al., 1997 ▸). Using the information about the positions of Bragg reflections in a particular frame that is contained in its .x file, it ‘draws’ circles, squares or rectangles around the centers of reflections that are large enough to include entire reflections. The reflection inside the boundary chosen is ‘erased’ by replacing the intensities of pixels inside that boundary with the intensities of adjoining pixels that are outside it.

The area detectors used for macromolecular data collection at synchrotrons are arrays of smaller area detectors that are separated from their neighbors by narrow gaps within which no data can be collected. When appropriate, these gaps were filled using the same local smoothing approach that was used to erase reflections.

All of the data sets analyzed were collected using synchrotron radiation, which is highly polarized. The effects that polarization has on measured intensities were eliminated by dividing the intensities recorded into reflection-free frames of data, pixel by pixel, using the function

where 2θ is the scattering angle appropriate for the pixel, φ is the azimuthal angle of that pixel with respect to the plane of the synchrotron ring and Δp is the fraction by which the degree of polarization of the beam in this plane exceeds 0.5 (Kahn et al., 1982 ▸). Satisfactory results were obtained by setting Δp to 0.5. Frames were corrected for the Lorentz effect by dividing the intensity recorded in every pixel by cos³2θ (Wall et al., 1997 ▸).

2.2. Isolation of the anisotropic component of the background  

The visibility of the local maxima and minima in the images of the background that emerged after the reflections had been erased and Lorentz and polarization (Lp) corrections had been carried out was enhanced by subtracting out the component of the background that depends on scattering angle only (Clarage et al., 1992 ▸). The dependence of the circularly averaged component of the background on the scattering angle was estimated by averaging the data in Lp-corrected, reflection-free frames in narrow annuli of increasing radius that were centered on the positions in those frames identified as their optical centers in the corresponding .x files. The intensities provided by interpolation for pixels in the gaps between the detector panels in the detectors were omitted from these averages, as were the intensities recorded in pixels affected by the shadow of the crystal-mounting apparatus and the beam stop. Some of the frames examined had a strip of pixels that extended across the detector face on the side opposite the shadow of the crystal mount within which the background was obviously reduced in intensity. The intensities recorded for pixels in these regions were also ignored during averaging.

The images of the background that emerged after the circularly averaged background had been subtracted out were characterized by broad regions, i.e. regions that were ∼25% of the width of the detector in at least one direction, within which the local average value was either positive or negative. Not surprisingly, a large strip of pixels near the shadow of the crystal mount and another, smaller, region opposite the shadow of the crystal mount on the other side of the beam stop were often systematically negative, which indicates that both kinds of shadows were considerably wider than was obvious by visual inspection. However, in some cases there were other regions in which the local average value of the background was negative. The locations of the systematically positive regions in these patterns were much less predictable.

These long length-scale features were eliminated from images of the background by high-pass filtering. Two-dimensional Fourier transforms were computed for each image out to a spacing of ∼0.004 reciprocal pixels. Inverse transformation of these transforms yielded images of the features in the image from which they were derived having length scales greater than ∼250 (unbinned) pixels, i.e. low-pass images. The visibility of the shorter length-scale features in these images was enhanced by subtracting these low-pass images, pixel by pixel, from the images from which they were obtained.

The amplitudes of the features in these low-pass images corresponded to ∼±5% of the total background intensity. They were quite reproducible from one frame to the next within a data set, which implies that the features that they display are not crystal-related. However, they did vary considerably from one data set to the next for reasons that are unknown to us (see Supplementary Fig. S1).

2.3. Model computations  

A Fortran program was written to generate images corresponding to the diffuse scatter that would be observed in the still images that would be components of a particular frame of data if (3) (see below) were correct. The inputs for this program are the information about crystal orientation and the identities of the reflections recorded in the frame of concern contained in its .x file. Also required are (i) the wavelength of the radiation used, (ii) the distance from the crystal to the detector, (iii) the mosaic spread of the crystal, (iv) a list of the measured intensities of the relevant reflections and (v) estimates for the velocity of both transverse and longitudinal sound waves in the crystal of concern. The program identifies the Bragg reflection closest to each pixel in the image that it is computing, and estimates the contribution that this reflection should make to the diffuse scatter recorded in the pixel in question. The images provided below for frames of data are the averages of three still images: one corresponding to the still that would have been recorded if the crystal were in the orientation that it was in at the start of the relevant oscillation, another representing the end of this oscillation and a last corresponding to the middle of the oscillation. The program treats intensities in the immediate neighborhoods of Bragg reflections in the same way as the program used to extract images of the background from frames of data, and it was assumed that the mosaic spread function appropriate for these crystals is a square function having a full width equal to the mosaic spread, which was 0.2° in all cases.

The program written to perform these model calculations, as well as the set of programs used to process frames, will be made available on request.

3. Results  

3.1. The backgrounds of 70S ribosome diffraction patterns have an anisotropic component  

The diffuse scattering patterns of concern here derive from oscillation data sets collected from cooled crystals of the 70S ribosome from Thermus thermophilus similar to those that yielded the structure described by PDB entry 4v8i (Polikanov et al., 2012 ▸). The space group of these crystals is P2₁2₁2₁, with two 70S ribosomes per asymmetric unit. The unit-cell parameters are a ≃ 210, b ≃ 449, c ≃ 621 Å. All data sets were collected using Dectris Pilatus 6M detectors either at the Advanced Photon Source (APS), Argonne National Laboratory or at the National Synchrotron Light Source (NSLS), Brookhaven National Laboratory. These detectors are well suited for collecting data of this kind. Their beam-off backgrounds are very low, their dynamic ranges are large and the cross-talk between adjacent pixels is close to zero (Hülsen et al., 2006 ▸).

For reasons that will become clear shortly, the frames of data that are of the greatest interest here were those collected with the incident beam parallel (or antiparallel) to an axis of the crystal lattice. As it happens, these crystals are highly elongated in the a-axis direction and tend to sit in the loops used for mounting crystals with their long axis more or less parallel to the spindle axis and more or less in the plane of the loop. Roughly 350 000 frames of data obtained from over 1000 different crystals were inspected to find a dozen or so that were collected with the crystal aligned appropriately with respect to the beam. Fig. 1 ▸(a) shows a greyscale image of one such frame taken from a data set collected on beamline 24-ID-C at APS. In the horizontal direction, the resolution at the edge of the frame is about 0.40 Å⁻¹. The concentric rings of Bragg reflections in this frame indicate that it was indeed collected with the X-ray beam nearly aligned with one of the unit-cell axes of the crystal. In fact, after processing with HKL-2000 the information in the .x file for this frame indicates that the angle between the beam and the a axis was ∼89.9° and that the corresponding angles for the b and c axes were ∼179.9° and ∼90.1°, respectively.

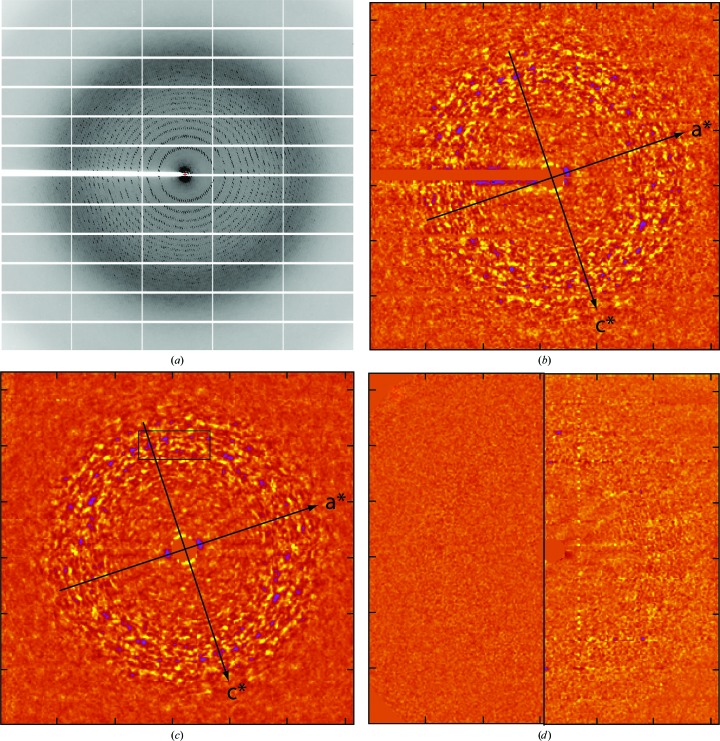
Figure 1.

Extraction of the structured component of the background from frames of diffraction data. (a) A grayscale representation of a single frame of data collected at APS from frozen crystals of 70S ribosome from T. thermophilus. (b) A false color rendering of the background of the frame of data shown in (a) after its Bragg reflections had been erased, Lp corrections performed, the circularly averaged intensity subtracted out and the result high-pass filtered (see §2). Each pixel in this image corresponds to an 8 × 8 array of pixels in the original image (a). In this image yellow is high intensity and blue is low intensity. The projections of the a* and c* axes onto this image are indicated. (c) This image was obtained by mirror-averaging the image displayed in (b) about both its a* and c* directions. The box in the upper center shows the location in this image of the pixels that correspond to the middle panel in the third row down from the top in (a). (d) The left half of this figure is an image of what the shot noise in (a) would contribute to images such as (b) and (c) if this noise could be described using a Gaussian distribution function, the variance of which is the circularly averaged background count per binned pixel in (a). The right half of this image is the difference between the right half of (c) and the right half of (b). Both are plotted using the same scale.

At first glance, the background in this frame appears to vary only with scattering angle, with the broad, gray ring at about 0.3 Å⁻¹ being a typical ‘water ring’. Only after the frame has been fully processed, i.e. after the reflections and panel boundaries evident in Fig. 1 ▸(a) have been suppressed, Lp corrections performed, the circularly symmetric component of the background subtracted out and the image high-pass filtered (see §2), does it become obvious that its background includes a structured component (Fig. 1 ▸ b). The intense, positive features in this image are shown in yellow and its strongly negative features are in blue. The intensity in each pixel in Fig. 1 ▸(b) is the sum of the intensities recorded in an 8 × 8 array of detector pixels. (Data were binned both to make the image array small enough to display conveniently using Gnuplot and to improve its signal-to-noise ratio.)

Prior to binning, the standard error of the pixel-to-pixel fluctuations in the image displayed in Fig. 1 ▸(b) was ∼1.5% of the total background in the range of scattering angles where these fluctuations are strongest, which is only ∼20% of the contribution expected owing to counting statistics alone. The contribution of statistical noise to these fluctuations is suppressed by binning, of course, but the signals of interest are not.

It is important to point out that the linear dimensions of the smallest features removed from this image by the high-pass filtering are very large, ∼30 (binned) pixels. The distance between adjacent tick marks on the edges of these images is 50 (binned) pixels (see Supplementary Fig. S1).

3.2. The diffuse scattering pattern has mirror planes  

Using the indexing information provided by the .x file for the frame shown in Fig. 1 ▸(a), it is easy to work out the locations of the projections of the a* and c* axes in Fig. 1 ▸(b), and when the image is inspected carefully using them as references it becomes clear that it is distinctly mirror-symmetric with respect to both. If this is really the case, its signal-to-noise ratio ought to be improved by mm averaging, a hypothesis that is strongly supported by Fig. 1 ▸(c), which is an mm-averaged version of Fig. 1 ▸(b). (The X-shaped feature in its middle is an artifact of the averaging algorithm used.) All of the strong features in Fig. 1 ▸(b) are evident in Fig. 1 ▸(c) and, in addition, the image obtained by subtracting Fig. 1 ▸(c) from Fig. 1 ▸(b) (Fig. 1 ▸ d, right) is not much different from what would be seen if the non-mm component of Fig. 1 ▸(b) could be attributed entirely to noise (Fig. 1 ▸ d, left).

3.3. The diffuse scattering pattern is reproducible  

The amplitudes of the features in Fig. 1 ▸(b) are so small that their reproducibility cannot be taken for granted. Fortunately, several of the other 70S ribosome data sets available included frames collected with the X-ray beam about as well aligned with the b* axis as in the frame shown in Fig. 1 ▸(a), and their backgrounds are also mirror-symmetric. Figs. 2 ▸(a) and 2 ▸(b) show the fully processed, mm-averaged backgrounds of two such frames that come from two different data sets collected at the same wavelength from two different crystals using beamline X25 at NSLS. The difference in the orientation of the b* axes of the two crystals at the time these frames were collected was ∼0.5°. [Note: the round-off errors in the coefficients reported for orientation matrices are significant when estimating angles this small because cos(0.5°) (= 0.9999619) is hard to distinguish from cos(0) (= 1.0000000).] The axes drawn on these images show the orientations of the planes about which mirror averaging was performed. Setting aside for the moment the fact that the image in Fig. 2 ▸(b) looks like an enlarged version of the image in in Fig. 2 ▸(a), the two images are nearly identical. Their difference in scale is owing to the fact that the data set that yielded Fig. 2 ▸(a) was collected with the crystal 476 mm from the detector, while the corresponding distance for the Fig. 2 ▸(b) data set was 547 mm.

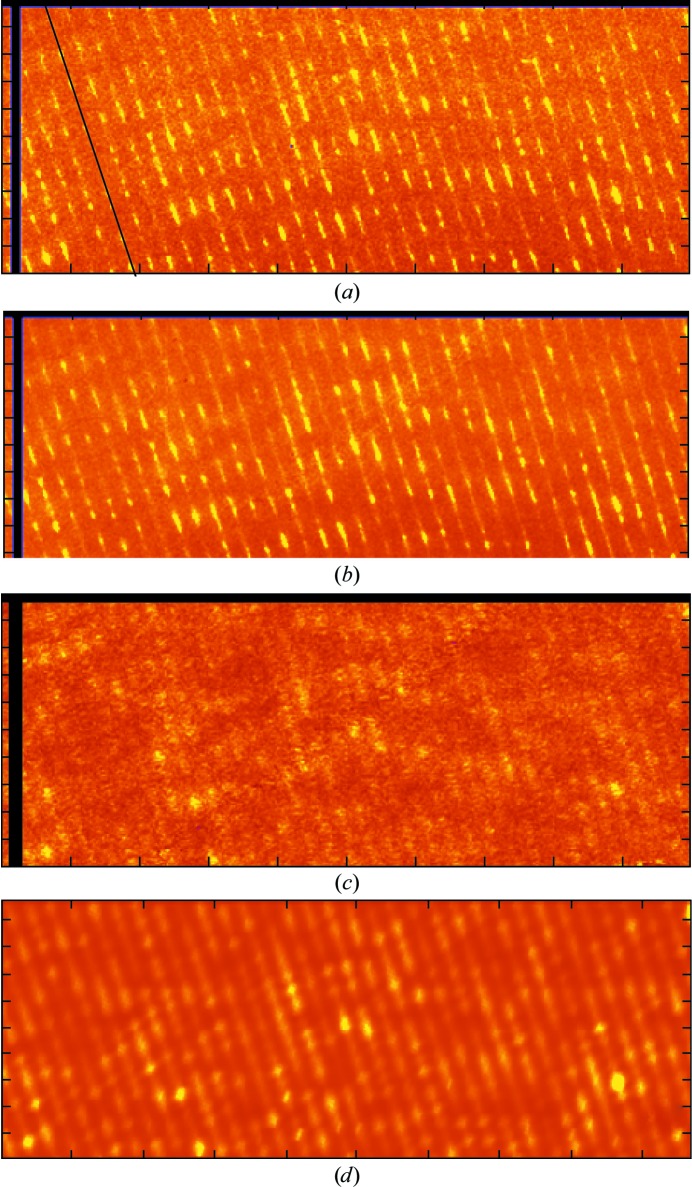
Figure 2.

Tests of the reproducibility of background images. (a) An image of background similar to Fig. 1 ▸(c) that was obtained from a frame belonging to a data set collected at BNL with the crystal orientated in almost exactly the same way with respect to the incident beam. This image has been mm averaged about the axes indicated. (b) A second mm-averaged image that is exactly like that shown in (a) except that it comes from a data set collected at BNL several months later from a different ribosome crystal. (c) An image of the background obtained from a second frame belonging to the data set that yielded (a). The difference in crystal orientation between the two frames is a 15° rotation around an axis parallel to the horizontal direction in both images. (d) A small part of the unbinned image from which (b) derives.

Even though Figs. 1 ▸(c), 2 ▸(a) and 2 ▸(b) all derive from frames taken with the b* axis nearly antiparallel to the X-ray beam, the image in Fig. 1 ▸(c) is not the same as the other two, but this difference is also easy to understand. The data displayed in Fig. 1 ▸(c) were collected using X-rays with a wavelength of 0.975 Å, but the data shown in the other two figures were collected using X-rays with a wavelength of 1.100 Å. Thus, the shell in reciprocal space displayed in Fig. 1 ▸(c) is not the same as the shell shown in both Figs. 2 ▸(a) and 2 ▸(b).

Fig. 2 ▸(c) provides another test of the validity of these images. Fig. 2 ▸(c) shows what the background looks like in another frame taken from the data set that includes the frame that corresponds to Fig. 2 ▸(a). The difference in crystal orientation between the frames is a 15° rotation around an axis parallel to the horizontal axis in both images. Not only are the two images quite different, but there is no indication of mm symmetry in Fig. 2 ▸(c), and for this reason it was not mm averaged. Thus, the background depends on crystal orientation, as it should.

3.4. The three-dimensional diffuse scattering patterns obtained from these ribosome crystals have mmm symmetry  

Because images such as those in Figs. 1 ▸(c), 2 ▸(a) and 2 ▸(b) are representations of spherical surfaces in reciprocal space, rather than planes, the only way that they can display mm symmetry with respect to the projections of their a* and c* axes is if the three-dimensional scattering patterns from which they derive have mmm symmetry, i.e. if

and this must be true both for integer and non-integer values of h, k and l.

It is common knowledge that the three-dimensional distributions of Bragg reflection intensities in the diffraction patterns obtained from crystals belonging to space group P2₁2₁2₁ display mmm symmetry. It is probably less well appreciated that the same is not true of the amplitudes/intensities of the three-dimensional Fourier transforms of the contents of their unit cells. In order for the symmetry of the Fourier transform of the unit-cell contents of a crystal to be the same as that of the Bragg reflections obtained from it, the symmetry operations of the crystal must constitute a point group. This will be the case if (i) the elements of these operations intersect, i.e. the relevant symmetry axes intersect, and (ii) all symmetry operations superimpose the structure of the unit cell onto itself. The symmetry axes of P2₁2₁2₁ crystals do not intersect, and screw axes are not point-group operations because they have a translational component. (The mmm symmetry of the Bragg reflection patterns produced by P2₁2₁2₁ crystals results from the way that the transforms of their unit cells are sampled by the reciprocal lattice.) Thus, the mmm symmetry of these diffuse scattering patterns is not a trivial consequence of crystal symmetry.

3.5. Background intensities correlate with Bragg reflection intensities  

The fact that these diffuse scattering patterns have the same symmetry as the associated patterns of Bragg reflections suggests that they could be artifacts generated by the algorithm used to erase reflections. Fig. 3 ▸(a), which is a false color image of the middle panel in the third row down from the top of Fig. 1 ▸(a) prior to processing, shows that this is not the case. [The location of the panel in question is indicated by the black box in Fig. 1 ▸(c).] Not only is there appreciable intensity evident between the rows of Bragg reflections in this figure, this intensity pattern is mirror-symmetric with respect to the c* axis. Fig. 3 ▸(b) shows what this panel looked like after mm averaging with its Bragg reflections in place, but with no other image processing performed. The last figure in this series, Fig. 3 ▸(c), shows what this panel looked like prior to binning, i.e. after the data that it contains had been fully processed and symmetrized. [Note: pixels corresponding to gaps between panels in Figs. 3(a), 3( ▸ b) and 3 ▸(c) are black to make their locations obvious.] The mmm symmetry evident in these images is not a data-processing artifact.

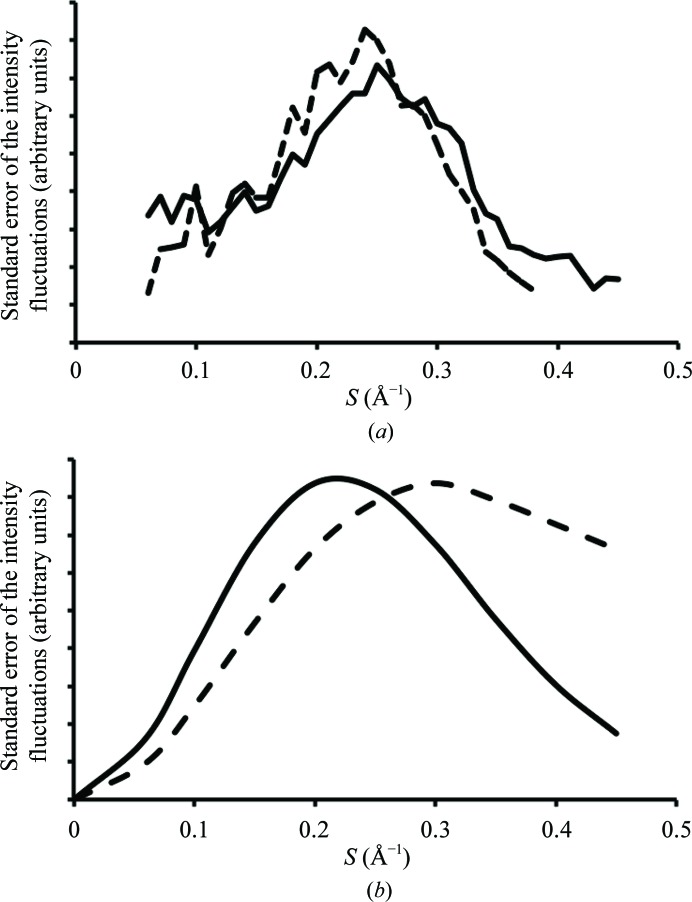
Figure 3.

Single-panel images of the background and predicted images of the background. The unbinned experimental images displayed come from a single panel of the detector face shown in Fig. 1 ▸(a). It is the one that is designated by the box in Fig. 1 ▸(c). (a) Image of this panel prior to data processing. (b) Image of the same panel after mm averaging of the data displayed in Fig. 1 ▸(a) with the reflections left in place but with no other data processing performed. (c) The same image after it had been fully processed. (d) An image of the background for this panel predicted using (3) (see §2).

Nevertheless, it is not just the symmetry of these images that correlates with that of the Bragg reflections associated with them. In regions where Bragg reflections are strong, background levels are high; in regions where Bragg reflections are weak (or absent), the background is low (Fig. 3 ▸ b).

When combined with the observation that these scattering patterns have mmm symmetry, this observation rules out the possibility that this diffuse scattering pattern could be produced by large-scale atomic displacements that do not correlate appreciably from one unit cell to the next. In P2₁2₁2₁ crystals, atomic displacements that do not correlate between unit cells will give rise to diffuse scattering patterns that have exact mmm symmetry only if the distribution functions of the displacements in all of the asymmetric units are the same and do not correlate from one asymmetric unit to the next. However, if this is the case, and the displacements involve translations/rotations of entire domains, the distributions of intensities in the resulting diffuse scattering profiles will be completely unrelated to the intensities of the Bragg reflections of the crystals, which report on the average structure of the entire unit cell rather than on the structures of subassemblies within it.

Even more striking, and much more difficult to explain in terms of displacements that do not correlate between unit cells, are the troughs that run through Fig. 3 ▸(c) parallel to the c* axis, each located exactly between its neighboring rows of reflections. The binning performed to produce images such as Fig. 1 ▸(b) suppresses these troughs, but they are a robust feature of the data that is even more conspicuous in larger scale images of fully processed, symmetrized, but unbinned data (for example Fig. 2 ▸ d) than it is in Fig. 3 ▸(c). [Fig. 2 ▸(d) corresponds to a 125 × 125 pixel portion of the binned image shown in Fig. 2 ▸(b). Adjacent ticks on the axes of Fig. 2 ▸(b) are 50 (binned) pixels apart.]

3.6. Normal-mode models for diffuse scattering  

Many of the models for the atomic displacements in macromolecular crystals that have been developed in the past to explain diffuse scattering patterns have ignored the possibility that correlations in displacements that extend across unit-cell boundaries, which, of course, are unavoidable, might contribute to them significantly (see, for example, Faure et al., 1994 ▸). However, it is hard to imagine how models of this type could possibly explain the diffuse scattering patterns shown above. The troughs between adjacent rows of reflections along c* are strong evidence that these patterns have more to do with the lattice of the crystal than the contents of its unit cells.

Models for diffuse scattering that have the right qualitative properties can be developed by treating the atomic displacements in these crystals as sums of normal-mode vibrations that involve all of the atoms that they contain. If this approach is taken, the following expression can be obtained for the diffuse scatter caused by inelastic scattering events that alter the vibrational energy of crystals by one phonon (Willis & Pryor, 1975 ▸; Moss & Harris, 1995 ▸),

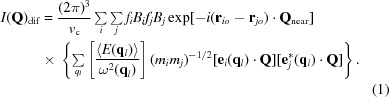Here, v _c is the volume of the unit cell, f_i is the structure factor of the ith atom in the unit cell, the mass of which is m_i, r _io is its average location in the unit cell and Q _near is 2π times the vector between the origin of reciprocal space and the position of the Bragg reflection nearest to Q, which is the corresponding vector specifying the location in reciprocal space where the diffuse scatter is being evaluated. The wavevector of the normal modes that contribute to the scatter at Q is q: q = Q − Q _near. B_i is the temperature factor for the ith atom, evaluated at Q, as f_i should also be, but if |Q _near| >> |q|, as will be the case for most of reciprocal space, the error made by evaluating both quantities at Q _near will be negligible. For every allowable q there are three vibrational modes possible, which are distinguished using a subscript l: one longitudinal and two transverse. 〈E(q _l)〉 is the average thermal energy associated with the vibrations described by the normal mode, the wavevector of which is q _l, and ω(q _l) is the frequency of this mode (in radians per second). e _i(q _l) is the vector that specifies the direction of the movements of the ith atom in the unit cell when the q _l mode is excited, and m_i is the mass of that atom. [Note that 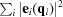= 1.] The first two summations in (1) are over all atoms in the unit cell, and the third summation is over all normal modes.

It takes 3nN − 3 normal modes to represent the (harmonic) motions of the atoms in a crystal composed of N unit cells, each of which contains n atoms. 3(n − 1)N of them are high-frequency, low-amplitude optic modes, the frequencies of which are more or less independent of |q| (Meinhold et al., 2007 ▸). For this reason, the amplitudes of the contributions that they make to diffuse scatter need not correlate strongly with the locations of Bragg reflections. The remaining 3N − 3 modes are lower frequency modes that are called acoustic modes because they are associated with the propagation of sound. Their frequencies increase roughly linearly with |q|, at least for small |q|, which means that the acoustic contribution to diffuse scatter will be strongest near Bragg reflections.

For a crystal consisting of N_a × N_b × N_c (= N) unit cells, where N_a is its length in the direction of unit-cell axis a, measured in number of unit cells, the boundary conditions imposed by the crystal lattice require that the a component of any wavevector, q, that corresponds to a lattice vibration must satisfy the equation |q _a| = 2πm/N_a|a|, where m is any integer other than zero and −N_a/2 ≤ m ≤ N_a/2. (Similar expressions can be obtained for the other two unit-cell axes.) Furthermore, if interactions between adjacent unit cells dominate its lattice motions, which is plausible, it will be true of its acoustic modes that ω(q _l) will have a (roughly) sinusoidal dependence on |q|,

where v _l is the velocity of sound waves of polarization l in the crystal of concern in the direction specified by q, and q _max is the length of the longest vector inside the Brillouin zone that points in the same direction.

It is easy to estimate the value of 〈E(q _l)〉 appropriate for the acoustic modes of a macromolecular crystal. The speed of longitudinal sound waves in macromolecular crystals is of the order of ∼2000 ms⁻¹ and that of transverse sound waves is considerably smaller (see below; Edwards et al., 1990 ▸; Tachibana et al., 2000 ▸). The unit-cell dimensions of the crystals of concern here are about 210 × 450 × 626 Å, which means that the largest possible value of |q| (= q _max) is ∼1.7 × 10⁻² Å⁻¹ [= π(a ⁻² + b ⁻² + c ⁻²)^1/2] and hence ω cannot exceed ∼0.2 THz (2). Since phonons of this frequency have energies of ∼2 × 10⁻²³ J (= hω/2π), and k _B T at room temperature is much larger (∼4.1 × 10⁻²¹ J), 〈E(q _l)〉 will equal k _B T for all of the acoustic modes of these crystals, with k _B being Boltzmann’s constant and T the absolute temperature. Thus, one can rewrite (1) as

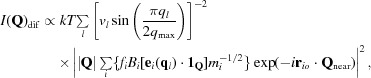where 1_Q is a unit vector in the Q direction.

For acoustic modes with wavelengths that are long compared with the unit-cell dimensions, the e _i(q _i) will be about the same for all of the atoms in the unit cell, and hence |e _i(q _i)| ≃ 1/n ^1/2 for all i. In addition, since m_i ^−1/2 does not vary much for the heavy atoms in macromolecular crystals, the equation above can be approximated as

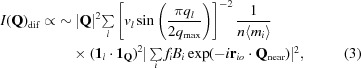where 1 _l is a unit vector in the direction of e _i(q _i). Note that n〈m_i〉 is the mass of the (ordered) contents of the unit cell. Furthermore, for longitudinal sound waves (1 _l · 1 _Q)² = (1 _q · 1 _Q)² and for transverse sound waves (1 _l · 1 _Q)² = (1 _q × 1 _Q)². Note also that 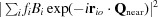is the intensity of the Bragg reflection that appears in the parent diffraction pattern at Q _near. Thus, (3) describes the diffuse scatter that would be caused by the acoustic vibrations of a crystal if all of the atoms in each of its unit cells oscillated as rigid bodies (Cochran, 1969 ▸). It should be reasonably accurate for the long-wavelength acoustic modes of a crystal with unit cells with contents that are not rigid, and it will be used here to approximate the diffuse scatter produced by all acoustic modes.

(3), like the more accurate expressions from which it is derived, predicts that every reflection in a diffraction pattern should be surrounded by a halo of diffuse scatter, the intensity of which is approximately proportional to that of the reflection that it surrounds. [Haloes of this sort are well known in small-molecule diffraction patterns (James, 1965 ▸) and have also been reported in macromolecular diffraction patterns (Glover et al., 1991 ▸).] Furthermore, the [v_lsin(πq _l/2q _max)]⁻² component of (1) guarantees that the acoustic mode contribution to diffuse scatter will be at its weakest at the boundaries of the Brillouin zone, i.e. midway between adjacent reflections. Thus, qualitatively at least, the acoustic contribution to diffuse scatter should resemble the diffuse scattering patterns of concern here.

3.7. Model calculations  

The obvious way to test the validity of (3) is to compare the diffuse scattering pattern that it predicts with observation, but in order to perform these calculations properly, information about the speed of sound in ribosome crystals would be required that simply does not exist. This barrier was surmounted by making two additional assumptions: (i) that the speed of sound in ribosome crystals is the same as it is in crystals of much smaller macromolecules such as ribonuclease A and hemoglobin, and (ii) that the speed of sound in these crystals is independent of direction. Thus, the speed of longitudinal sound waves in ribosome crystals was taken to be 1800 m s⁻¹ and the speed of transverse sound waves was assumed to be 450 m s⁻¹ (Edwards et al., 1990 ▸). It is important to recognize that this difference in velocity between longitudinal and transverse waves, which is unremarkable, implies that the acoustic contribution to the diffuse scattering patterns of macromolecular crystals will be dominated by transverse displacements in atomic positions. Fig. 3 ▸(d) shows what (3) predicts for the portion of reciprocal space displayed in Fig. 3 ▸(c), given these assumptions. [Note: the image in Fig. 3 ▸(d) is smeared by convolution along the c* direction to represent the rather poor resolution of the original data (Fig. 3 ▸ a) in this direction.]

The correspondence between Figs. 3 ▸(c) and 3 ▸(d) is imperfect, but given all of the assumptions made it would have been astonishing if it were otherwise. That said, the two images have some important similarities. Troughs between rows of reflections along c* are evident in both, as required. In addition, Fig. 3 ▸(d) has broad regions of low intensity in about the same locations as in Fig. 3 ▸(c), which it should, irrespective of the relationship between ω and q, if the acoustic disorder model is right and the strongest features in both images are associated with the same, intense Bragg reflections. Thus, there is reason to be optimistic that a computation of this sort that was based on (1) and more complete information about sound velocities in ribosome crystals might give a more convincing result, but this remains to be shown.

3.8. The dependence of the circularly averaged intensity of the diffuse scatter on the scattering angle  

Images such as those shown in Figs. 1 ▸(b), 1 ▸(c), 2 ▸ and 3 ▸ are displays of the fluctuation component of the corresponding diffuse scattering patterns. In all of them, the magnitudes of these fluctuations are largest in the water-ring region and weaken rapidly at larger scattering angles. Using the highly simplified acoustic mode model for diffuse scattering embodied in (3), one predicts that the magnitude of the standard error of the fluctuations in the diffuse background, σ_Eq3(|S|), should vary with the scattering angle as follows,

where I _Br(S) is the measured intensity of a particular Bragg reflection that appears in some frame of data within a narrow annulus of radius |S| that is centered on the origin, 〈I _Br(S)〉 is the average intensity of all such reflections, the summation is over all of the Bragg reflections in that annulus and N is the number of such reflections. The standard deviation profile predicted for the frame shown in Fig. 1 ▸(c) is displayed in Fig. 4 ▸(a) (broken lines). The solid line profile in Fig. 4 ▸(a) is the corresponding plot of the standard deviations of the experimentally observed fluctuations in the background in the same frame, σ_expt(|S|),

Here, σ² _obs(|S|) is the variance per pixel of the intensities within a narrow annulus of constant S estimated using the experimental intensity values recorded in the pixels inside that annulus, and σ² _shot(|S|) is the contribution to σ² _obs(|S|) that is attributable to statistical noise. The intensity scales of the two profiles have been adjusted arbitrarily to make it easy to compare their shapes. Their similarity in shape supports the acoustic model for the diffuse scattering produced by these crystals.

Figure 4.

The dependence of the standard errors of the fluctuations in background intensities on scattering angle. (a) The scattering-angle dependence of the standard errors of the variation in background intensities characteristic of the data represented in Fig. 1 ▸(c) (solid line) is compared with that predicted for these data using (3) and measured Bragg reflection intensities assuming that acoustic lattice vibrations are the primary source of the diffuse scatter seen (broken line; see text). (b) Comparison of the scattering-angle dependence of the standard errors of the variations in background intensity implied by two different models for crystal disorder. The first profile (solid line) is that predicted if acoustic lattice scatter is the dominant source of the diffuse scattering observed. The second profile (broken line) is that expected if the diffuse background is produced by atomic displacements that do not correlate significantly across unit-cell boundaries. The average temperature factor implied by both profiles is the same.

Using Wilson statistics, it is easy to show that at high scattering angles, the standard deviation of the intensities recorded in a narrow shell in reciprocal space is the same as the average intensity within that shell (Wilson, 1949 ▸), namely the sum of the squares of the structure factors of the atoms in the unit cell, i.e. 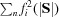. If this were the case at all scattering angles, profiles such as those shown in Fig. 4 ▸(a) would resemble the function

The solid-line profile in Fig. 4 ▸(b) shows what this function would look like if the average temperature factor associated with those fluctuations was 30 Ų. Its similarity to the two profiles in Fig. 4 ▸(a) is obvious.

It is also instructive to compare the solid-line profile in Fig. 4 ▸(b) with the one that can be obtained by similar means for diffuse scattering models based on the assumption that displacements do not correlate across unit-cell boundaries (see, for example, Benoit & Doucet, 1995 ▸). In this case, the profiles obtained should resemble

The broken-line profile in Fig. 4 ▸(b) shows what this function looks like with the average temperature factor set to 30 Ų. Both reach a maximum at about the same Bragg spacing, but beyond this the amplitude of the acoustic disorder profile decreases much more rapidly than the amplitude of the unit-cell disorder profile. Thus, it again appears that the diffuse scatter produced by these ribosome crystals is more likely to be caused by long-range acoustic disorder than by short-range unit-cell disorder.

4. Discussion  

All of the images and profiles displayed above have been scaled in one way or another to facilitate qualitative comparisons of shapes and patterns, and the conclusion that acoustic disorder is responsible for much of the diffuse scatter produced by frozen ribosome crystals rests entirely on these comparisons. It is clear that the qualitative ‘trade marks’ of diffuse scattering patterns produced by acoustic disorder are (i) a strong correlation between Bragg reflection intensities and diffuse scattering intensities, (ii) obvious minima at the edges of Brillouin zones, i.e. between rows of reflections, and (iii) a dramatic fall-off in intensity at high scattering angles.

Although the explanation proposed for these scattering patterns may appear to be plausible, it would be a mistake to conclude that anything like a full understanding of the dynamics of ribosome crystals has been achieved. In the first place, the formalism used here was developed to describe the behavior of crystals of small molecules, and while it is likely that it is also applicable to crystals of macromolecules, it is not clear how the unstructured solvent in these crystals should be treated. Furthermore, the validity of the assumption that the velocity of sound in macromolecular crystals is independent of frequency from 0 Hz to ∼0.1 THz, on which (2) depends, is untested, as is the assumption that sound velocities are independent of direction.

The magnitude of the gap between what is known about these crystals and what would be required to predict their diffuse scattering patterns accurately becomes even more obvious when the acoustic disorder model described above is used to estimate atomic B factors. This can be performed using a slight modification of an equation provided by Edwards et al. (1990 ▸),

Here, B _ac is the acoustic contribution to the average B factor of the atoms in these crystals, ρ is the crystal density, which in this case is about 1250 kg m⁻³, and V _c is the volume of its unit cells. When the temperature and sound velocities used to compute the diffuse scattering pattern shown in Fig. 3 ▸(d) are fed into this formula, the estimate that emerges for B _ac is 0.57 Ų, which is two orders of magnitude smaller than the average B factor of the non-H atoms in the structure obtained using the data set from which the images shown in Figs. 1 ▸ and 3 ▸(a)–3 ▸(c) were drawn: 57 Ų. If B _ac really were 0.57 Ų in these crystals, the acoustic contribution to their diffuse scatter patterns would have been too weak to observe.

The values of three of the five parameters needed to estimate B _ac are problematic: the temperature, and the speed of both longitudinal and transverse sound waves. It is not obvious what temperature should be used because the crystals concerned were flash-cooled prior to data collection. Since roughly 75% of the volume of the unit cells of these crystals is occupied by solvent, i.e. water (see Voss et al., 2006 ▸), it is likely that at the time that the data were collected the mechanical properties of these crystals resembled those of ice. The velocity of longitudinal sound waves in ice is ∼2919 m s⁻¹ and the velocity of transverse sound waves is ∼1788 m s⁻¹ (Smith & Kishoni, 1986 ▸). If these were the correct sound velocities to use, and the relevant temperature was taken to be 100 K, B _ac would be about 0.015 Ų, which is as close to zero as makes no difference. Clearly, these diffuse scattering patterns cannot be the product of acoustic vibrations that were ongoing at the time of data collection.

There are two kinds of atomic displacements in crystals: dynamic and static. Thermal motion is responsible for the time-dependent atomic displacements in crystals. Variations in the time-averaged structure between the unit cells in a crystal, if any, are static and vary only with location. It is commonly assumed that the structure of a flash-cooled crystal is equivalent to a snapshot taken the instant that the crystal froze. If this were the case, freezing would convert dynamic displacements into static displacements without altering their space-averaged variances or covariances, and this would leave B factors and diffuse scattering profiles also unaltered. The right temperature to use would then be ∼273 K, and the appropriate sound velocities would be those of the unfrozen crystal. However, the assumption that the properties of macromolecular crystals are unaffected by flash-cooling is highly questionable (Halle, 2004 ▸; Juers & Matthews, 2004 ▸; Keedy et al., 2014 ▸). For this reason, it would be interesting to know what the diffuse background looks like in data sets collected from the same ribosome crystals at room temperature, which could be a challenge to observe given the high sensitivity of ribosome crystals to radiation damage. In the absence of these data, it cannot be excluded that the diffuse scattering described here is in some way a product of the cooling process itself. If so, it would be an effect specific to these particular crystals because none of the many other diffraction data sets collected from frozen macromolecular crystals that were examined in the course of this work have diffuse backgrounds that resemble that under consideration here.

Even if the effects of fast cooling on the properties of these ribosome crystals were entirely benign, we still would not know enough about their mechanical properties at room temperature to estimate B _ac accurately. The most important missing piece of information is an experimental value for the velocity of transverse sound waves in these crystals, which is the square root of their shear modulus, divided by the crystal density. The shear modulus of ice is about 2.93 GPa, which is unremarkable for a solid, while the shear modulus of crystals of small proteins, which can be estimated from the data provided by Edwards et al. (1990 ▸), is of the order of 0.25 GPa. The shear modulus of water, like that of any other liquid, is effectively zero. Compared with ordinary protein crystals, the water content of ribosome crystals is quite high (∼ 0.75 versus ∼0.5), and RNA molecules are greatly different from protein molecules. The atoms in a protein domain fill space so efficiently that water is largely excluded from their interiors (Richards, 1974 ▸). The packing of RNA atoms in RNA domains, on the other hand, is much less efficient both because it is impossible to fill space efficiently by packing helices together and because RNA helices are so highly charged at neutral pH that they must be surrounded by solvent molecules and counterions if they are to form stable tertiary structures at all. Thus, it would not be surprising if the shear modulus of ribosome crystals at room temperature turned out to be much smaller than that of protein crystals. If it were as low as ∼0.005 GPa, for example, B _ac would be ∼25 Ų, which is about what the standard error profiles in Fig. 4 ▸ suggest that the acoustic contribution to B factors may be.

It is important to point out in closing that even if the shear modulus of these crystals were ∼0.005 GPa, only about half of the B factors of the atoms in these crystals would be explained. Thus, it is highly likely that acoustic lattice vibration is not the only kind of disorder in these crystals. What these other contributions might be remains to be determined, but the argument could be made that the reason why the diffuse scattering pattern predicted by the lattice vibration model used (Fig. 3 ▸ d) does not agree with experiment better (Fig. 3 ▸ c) is because displacements that correlate more weakly across unit-cell boundaries contribute to it significantly. If these displacements correlate on length scales that are much smaller than the dimensions of the ribosome, and are roughly the same everywhere in the unit cell, their contribution to diffuse scatter would probably be dominated by a component that has mmm symmetry, consistent with observation.