Robust, tunable genetic memory from protein sequestration combined with positive feedback

Abstract

Natural regulatory networks contain many interacting components that allow for fine-tuning of switching and memory properties. Building simple bistable switches, synthetic biologists have learned the design principles of complex natural regulatory networks. However, most switches constructed so far are so simple (e.g. comprising two regulators) that they are functional only within a limited parameter range. Here, we report the construction of robust, tunable bistable switches in Escherichia coli using three heterologous protein regulators (ExsADC) that are sequestered into an inactive complex through a partner swapping mechanism. On the basis of mathematical modeling, we accurately predict and experimentally verify that the hysteretic region can be fine-tuned by controlling the interactions of the ExsADC regulatory cascade using the third member ExsC as a tuning knob. Additionally, we confirm that a dual-positive feedback switch can markedly increase the hysteretic region, compared to its single-positive feedback counterpart. The dual-positive feedback switch displays bistability over a 10⁶-fold range of inducer concentrations, to our knowledge, the largest range reported so far. This work demonstrates the successful interlocking of sequestration-based ultrasensitivity and positive feedback, a design principle that can be applied to the construction of robust, tunable, and predictable genetic programs to achieve increasingly sophisticated biological behaviors.

INTRODUCTION

The hallmark of synthetic biology is the ability to design and construct genetic circuits and reprogram natural biological networks. To this end, a diverse array of genetic programs have been constructed ranging from epigenetic switches to multi-layered circuits (1–13). Despite these advances, the design and construction of reliable and predictable artificial genetic programs remains a synthetic biology challenge (14). Many engineered systems fail to function as designed because few design rules are available for robust integration of incompletely characterized genetic parts, and iterative tweaking is often required to implement predictable functions (15,16). In addition, genetic circuits function within specific limits of quantitative parameter regimes (12), but intrinsic fluctuations in the concentrations of key regulatory components compromise networks’ proper functioning (17–19). Our ability to insulate synthetic programs from the inherent noise in gene expression remains limited (20). In contrast, natural biological systems employ complex information-processing algorithms to robustly make developmental decisions (21), control gene expression patterns (22), and implement logical computations (23) in the presence of stochastic fluctuations. The regulatory connectivity among genes, RNAs, and proteins encodes systematic features for robustness against stochastic variations (24–28). A better understanding of regulatory architectures that confer functional robustness is critical for the design and construction of noise-tolerant genetic programs.

Feedback systems are common in natural biological networks and central to maintaining and enhancing cellular behavior (29,30). For example, a negative feedback loop dampens cell-to-cell variability in cell populations (31) and modulates noise frequency (24). A negative feedback loop potentially generates oscillations, but the oscillatory behavior can be affected by stochastic variations, resulting in cells behaving asynchronously (11). This challenge can be addressed by combining negative and positive feedback loops, which increases the robustness and enables tunability of the oscillations (32,33).

A positive feedback loop can create bistable switches (34,35). Bistability arises in a dynamical system where direct (e.g. autoregulation (36)) or indirect (e.g. mutual inhibition (12)) positive feedback is coupled with ultrasensitivity. While most bistable switches built so far are based on cooperativity, a recent report showed that activator-antiactivator pairs can be used to generate sequestration-based ultrasensitivity and bistability (37). In theory, such two-regulator systems with one positive feedback loop are sufficient to construct bistable switches. However, mathematical simulation showed that the system's resistance to noise can be enhanced by interlinking two positive feedback loops (38). Such increased robustness of bistable switches was demonstrated experimentally by using a dual positive feedback topology in the lacZYA operon which relies on cooperativity for ultrasensitivity (39). Natural regulatory networks have evolved into complex forms to increase biological robustness.

Here, we present the bottom-up construction of the tunable bistable switches that are built in Escherichia coli by coupling a three-member sequestration cascade system with dual positive feedback loops. The three-member cascade consisting of Pseudomonas aeruginosa ExsADC regulators allows for finely-tunable bistable behavior which is difficult to achieve in a two-member sequestration system (37). By systematically combining theoretical models and experimentation, we explore the roles of complex regulatory architectures in conferring functional robustness and tunability across the parameter space. Furthermore, we show that interlinking protein sequestration-based ultrasensitivity and dual positive feedback loops generates a predictable bistable switch that is extensively robust over a wide range of parameters.

MATERIALS AND METHODS

Strains and growth media

Escherichia coli DH10B [F- mcrA Δ(mrr-hsdRMS-mcrBC)Φ80lacZΔM15ΔlacX74 recA1 endA1 araΔ139 Δ(ara, leu)7697 galU galK λ-rpsL (StrR) nupG] was used for all the experiments except for the ultrasensitivity analysis (Figure 2), where E. coli DIAL strain JTK164A (40) was used. In all experiments, cells were grown in M9 minimal media supplemented with 1.0 mM thiamine hydrochloride, 0.8 mM l-leucine, 0.2% (w/v) casamino acids, 0.4% (v/v) glycerol, 2.0 mM MgSO₄, and 0.1 mM CaCl₂ (supplemented M9 media). The supplemented M9 medium was filter sterilized and stored at 4ºC. Kanamycin (20 μg/ml), ampicillin (100 μg/ml), and chloramphenicol (34 μg/ml) were added as appropriate. Three inducers were used at the following concentrations: Ara (Arabinose, 0–25 mM), aTc (anhydrotetracyline, 0–1 μg/ml), and 3OC6 (N-(β-ketocaproyl)-l-homoserine lactone, 0–5 μM). All the inducers and chemical reagents used in this study were purchased from Sigma–Aldrich (St. Louis, MO, USA) unless otherwise indicated.

Figure 2.

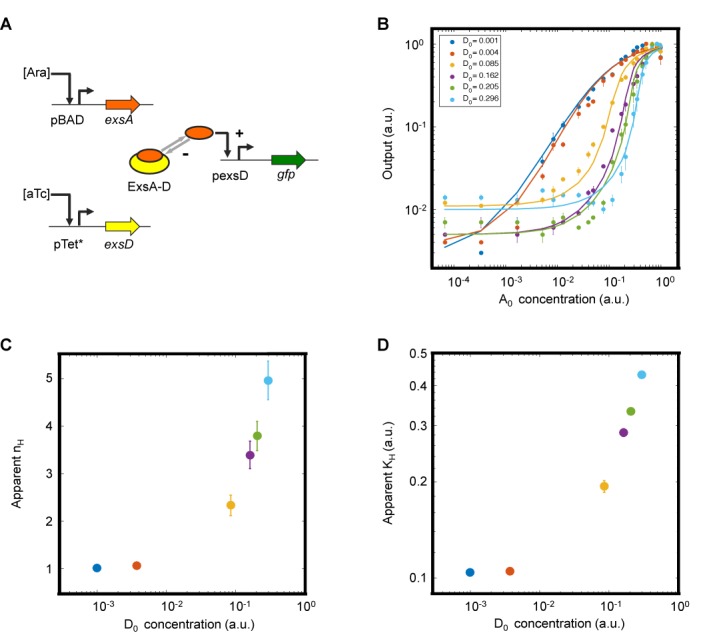
Sequestration-based tuning of ultrasensitivity. (A) Schematic diagram of the genetic circuit constructed to independently control ExsA and ExsD expression. ExsA is sequestered into an inactive complex (ExsA-D), which is the basis of ultrasensitivity. +, activating interaction; –, repressing interaction. (B) Input–output response at different amounts of ExsD (D₀). The total ExsD amount (0.001, 0.004, 0.085, 0.16, 0.21 and 0.30 in a.u.) was calculated using a fitted transfer function model (Supplementary Data). Filled circles and solid curves represent the experimental data and fitted transfer functions (with an R² value of 0.99, Supplementary Table S3), respectively. The experiments were performed at Ara concentrations of 0, 0.0000128, 0.000064, 0.00032, 0.001, 0.0016, 0.0025, 0.005, 0.008, 0.01, 0.016, 0.025, 0.04, 0.05, 0.08, 0.1, 0.15, 0.2, 0.4, 1, 5 and 25 mM and aTc concentrations of 40, 50,000, 250 000, 350 000, 400 000 and 500 000 pg/ml. (C and D) The apparent Hill coefficient (n_H) and the apparent half-maximal concentration (K_H) are shown as functions of the anti-activator levels (D₀). The data and error bars represent the averages and SEM of six replicates performed on three different days, respectively.

Plasmid design and circuit construction

All the genetic circuits were constructed following the Golden-Gate DNA assembly technique (41), using type IIs restriction enzymes (BspMI, BsmBI, and SapI from New England Biolabs, Ipswich, MA). All the regulator genes (exsA, exsD and exsC) and the pTet*, pLux*, and pBAD promoters used in this study were PCR amplified from pTet*-exsDA, pLux*-exsC, and pBAD-sicA* plasmids (13), using Phusion High-Fidelity DNA polymerase (New England Biolabs, Ipswich, MA). The PCR amplified genetic parts were ligated using T4 DNA ligase (New England Biolabs, Ipswich, MA, USA). Constructed plasmid sequences were verified by DNA sequencing (PNACL, Washington University School of Medicine). Electro-competent E. coli DH10B and E. coli DIAL strain JTK164A was transformed with plasmids (Supplementary Table S5) using electroporation (Eppendorf Eporator), and frozen stocks were stored at −80°C (Supplementary Table S6). Zymo DNA isolation kits were used according to the manufacturer's instructions. All the oligonucleotides were purchased from Integrated DNA Technologies (IDT, Coralville, IA, USA). All genetic part sequences used in this study are shown in Supplementary Table S7.

Fluorimetry

Cells were grown overnight in 5 ml supplemented M9 media in 14 ml tubes with appropriate antibiotics at 37ºC and 250 rpm in a New Brunswick Excella E25 shaking incubator. The overnight cultures were subcultured (1:100 dilution) in fresh pre-warmed, supplemented M9 media, grown for 2 h (37ºC, 250 rpm), and transferred to fresh pre-warmed, supplemented M9 media (0.6 ml) in deep 96-well plates (Eppendorf). Each culture (0.6 ml) was grown at inducer concentrations as indicated in Figures 1 and 2. After 8 h, the cells were centrifuged and the cell pellet was re-suspended in 200 μl filtered 0.9% (w/v) saline (pH 8.0). The population level fluorescence measurements (GFP/Abs₆₀₀ where Abs₆₀₀ is an absorbance value at 600 nm) were performed in 96-well microplate (Chimney well and F-bottom, REF-655096, Grenier Bio-One) using a Tecan Infinite M200 PRO plate reader (GFP settings were excitation at 483 nm and emission at 530 nm). Autofluorescence (GFP/Abs₆₀₀ of DH10B lacking GFP) was subtracted from GFP/Abs₆₀₀ of all samples.

Figure 1.

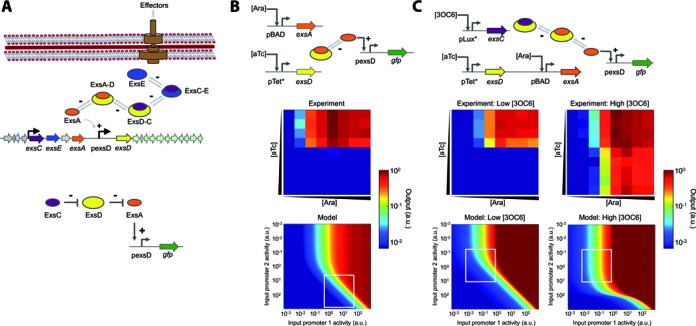
Characterization of the sequestration-based genetic circuits. (A) Schematic diagram of the Pseudomonas aeruginosa T3SS regulatory cascade. Four regulatory proteins control the P. aeruginosa T3SS through partner swapping. A transcription factor ExsA (orange) activates the target promoter and is sequestered by an anti-activator ExsD (yellow) into an inactive complex (ExsA-D). A chaperone ExsC (purple) frees ExsA by sequestering ExsD and forming ExsD-C. ExsE (blue) inhibits T3SS activation by sequestering ExsC and forming ExsC-E. +, activating interaction; –, repressing interaction. A simplified diagram showing the functions of the three ExsADC regulators used in this work is also shown (bottom). (B) A two-member system allows for tunable output. ExsA expressed from an inducible promoter (pBAD) controls GFP expression via the ExsA-inducible promoter (pexsD). Another inducible promoter (pTet*) controls ExsD expression, which represses GFP expression by sequestering ExsA. Heat maps compare the experimental transfer function to a model plotted over a wide range of promoter activities (Supplementary Data). (C) A three-member system enables fine-tuning of output expression. ExsC allows for output tuning by sequestering ExsD (as indicated by low and high 3OC6 concentrations). Heat maps compare the experimental transfer function to a model plotted over a wide range of promoter activities (Supplementary Data). Note that the heat maps cannot be directly compared due to rescaling of the axes from inducer concentration to promoter activity. Supplementary Figure S1 shows a quantitative comparison (with an R² of 0.92 or higher). Output values and input promoter activities are reported in arbitrary units (a.u.). The experiments were performed at arabinose (Ara) concentrations of 0, 0.0016, 0.008, 0.04, 0.2, 1, 5, and 25 mM (from left to right); anhydrotetracycline (aTc) concentrations of 0, 3.2, 16, 80, 400, 2000, 10 000, 50 000, 250 000 and 500 000 pg/ml (from top to bottom); and 3-oxohexanoyl-homoserine lactone (3OC6) concentrations of 0 and 200 nM for low and high [3OC6], respectively. White boxes represent the experiment ranges obtained using the inducible promoters. Experimental data are the averages of nine replicates performed on three different days.

Flow cytometry

Cells were initially grown overnight in 5 ml supplemented M9 media in two conditions, 0 (ON-state) and saturating 1.0 μg/ml aTc (OFF-state), at 37°C and 250 rpm. The method of preparing ON and OFF cells (Figures 3 and 4) was modified from that described by Chen and Arkin (37). Specifically, the uninduced and fully induced overnight cultures (OD₆₀₀ of 0.1, measured by Nanodrop 2000c, Thermo Fischer) were stored in 10% glycerol aliquots (120 μl each in Amplitube PCR Reaction Strips, T320-2N, Simport) at -80ºC. The frozen aliquots were thawed for 1 min at 37ºC, diluted 1-million-fold in fresh pre-warmed, supplemented M9 media, and incubated for 2 h at 37°C and 250 rpm. The resulting cultures were transferred to fresh pre-warmed, supplemented M9 media in deep 96-well plates (Epperndorf Cat. No. 951033405). Each culture (0.6 ml) was induced with different inducer concentrations and grown at 37°C and 250 rpm. After 16 h (final OD₆₀₀ of ∼0.1), sample aliquots, suspended in filtered 0.9% (w/v) saline (pH 8.0) supplemented with 2.0 mg/ml kanamycin, were transferred to 96-well assay microplate (U-bottom, REF-353910 from BD Biosciences, San Jose, CA, USA) for measurements. Flow cytometry analysis was carried out using a Millipore Guava EasyCyte High Throughput flow cytometer with a 488 nm excitation laser (using a blue-laser-only setting) and a 512/18 nm emission filter. The flow rate was 0.59 μl/s. All data contained at least 5,000 events gated by forward and side scatter. FlowJo (TreeStar Inc.) was used to obtain the arithmetic mean of fluorescence distribution. Autofluorescence, the background fluorescence of DH10B lacking GFP, was subtracted from the sample fluorescence, and the averages and s.e.m. of the arithmetic means (with autofluorescence subtracted) were obtained from replicates performed on different days as indicated.

Figure 3.

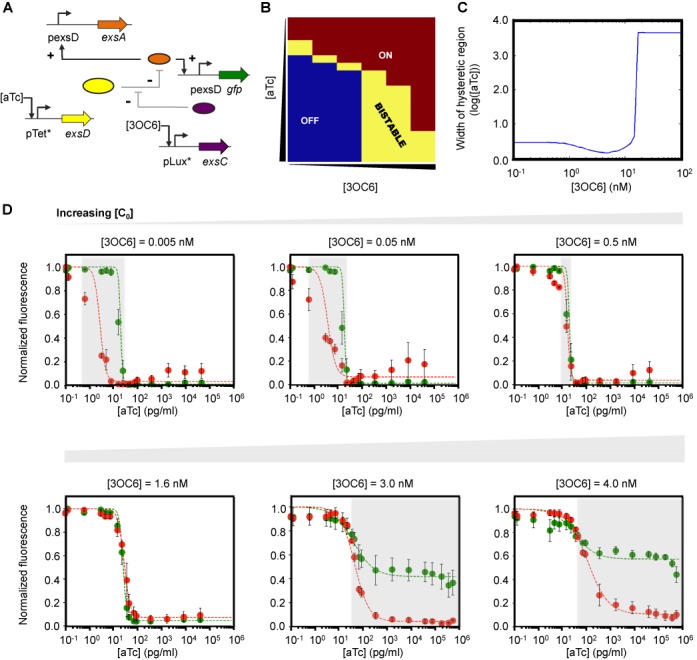
Tuning the hysteretic region by controlling ExsC concentrations. (A) Bistable switch with a positive feedback loop that consists of ExsA, ExsD and ExsC. The expression of exsA is under control of the pexsD promoter, forming a positive feedback loop, while ExsD and ExsC play a role in fine-tuning the concentration of unbound, active ExsA. +, activating interaction; −, repressing interaction. (B) Bifurcation diagram generated by clustering flow cytometry data into BISTABLE (yellow), monostable ON (burgundy), and OFF (dark blue) using an EM algorithm with a GMM model (43) (see Materials and Methods). The experiments were performed at aTc concentrations of 0, 0.128, 0.64, 3.2, 5, 8, 16, 25, 30, 40, 50, 80, 100, 400, 2,000, 10 000, 50 000, 100 000, 250 000 and 500 000 pg/ml (from top to bottom) and 3OC6 concentrations of 0, 0.32, 1.6, 5, 8 and 15 nM (from left to right). (C) Model prediction of the hysteretic region (see Supplementary Figures S3 and S4). (D) Hysteretic responses of the three-member bistable switch determined experimentally. Independent control of ExsC using an inducible promoter (pLux*) enables flexible tuning of the hysteretic region (the shaded area as a guide to the eye) as predicted in Figure 3C. ON and OFF cells (see Materials and Methods) were grown at different aTc and 3OC6 concentrations. Green (ON → OFF) and red (OFF → ON) filled circles represent normalized fluorescence obtained experimentally. The dashed green and red curves correspond to the fit to a mathematical model (Supplementary Data). As predicted and discussed in Supplementary Figure S4, at high 3OC6 concentrations (3.0 and 4.0 nM), the normalized fluorescence of the ON cells does not reach zero even at high aTc concentrations. This reduced, non-zero fluorescence of the ON cells is predicted, and the cells are considered to be in the ON state at high aTc concentrations, rather than OFF (Supplementary Figure S4e). The experiments were performed at aTc concentrations of 0, 0.128, 0.64, 3.2, 5, 8, 16, 25, 30, 40, 50, 80, 100, 400, 2000, 10 000, 50 000, 100 000, 250 000, 500 000 and 750 000 pg/ml and 3OC6 concentrations of 0.005, 0.05, 0.5, 1.6, 3, and 4 nM. For the experiments performed at 3OC6 concentrations of 0.005, 0.05, 0.5 and 1.6 nM, aTc concentrations up to 50 000 pg/ml were tested because sample fluorescence did not change as aTc concentrations increased. Each data point, normalized to the maximum value, and error bars respectively represent the averages and SEM of six replicates performed on three different days.

Figure 4.

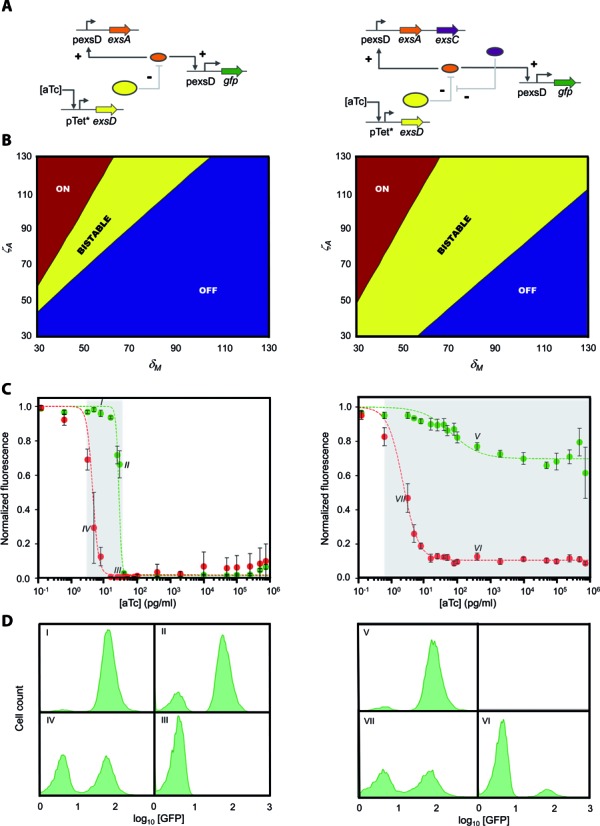
Improving robustness of bistable switches through dual-positive feedback loops. (A) Sequestration-based genetic circuits with one (left) or two (right) positive feedback loops. While ExsA confers direct positive autoregulation on the bistable switches (left and right), an indirect positive feedback loop is formed by ExsC which releases free ExsA by sequestering ExsD (right). The expression of exsA (and exsC for dual-positive feedback loops) is under control of the pexsD promoter. +, activating interaction; -, repressing interaction. (B) Bifurcation diagrams showing that two positive feedback loops (right) generate a larger bistable region than one positive feedback loop (left) (see Supplementary Figure S5 and Table S4). δ_M, non-dimensionalized parameter related to the effective ExsD concentration; ζ_A, non-dimensionalized parameter related to the maximum ExsA concentration (Supplementary Data). (C) Experimental confirmation of the increased hysteretic region (the shaded area as a guide to the eye) through dual-positive feedback loops. Green (ON → OFF) and red (OFF → ON) filled circles represent normalized fluorescence obtained experimentally at different aTc concentrations. The dashed green and red curves correspond to the fit to a mathematical model (Supplementary Data). The experiments were performed at aTc concentrations of 0, 0.128, 0.64, 3.2, 5, 8, 16, 25, 30, 40, 50, 80, 100, 400, 2000, 10 000, 50 000, 100 000, 250 000, 500 000 and 750 000 pg/ml. Each data point, normalized to the maximum value, and error bars respectively represent the averages and SEM of at least six replicates performed on at least three different days. (D) Representative flow cytometry histograms indicating the population distributions at the data points marked in Figure 4C (I–VII).

Analysis and classification of flow cytometry distributions

In order to classify flow cytometry distributions, we employed a clustering algorithm in MATLAB as described previously (42). We classified the flow cytometry data as either ON, OFF or BISTABLE using the Expectation-Maximization (EM) algorithm and a Gaussian Mixture Model (GMM) (43). The model assumes that the data are a mixture of two Gaussian distributions (N₁ and N₂ with the mean μ and the standard deviation σ) such that the probability density function can be described as follows:

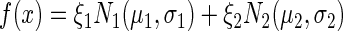where 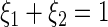. The logarithm of fluorescence data for at least 5000 cells at each combination of aTc and 3OC6 concentrations was used for clustering. The criteria used for classification as BISTABLE are as follows: 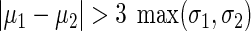and 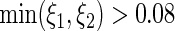. Points were classified as ON 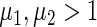if or if 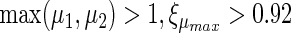. If the points met neither the criteria for BISTABLE nor for ON, they were classified as OFF.

Computational modeling

Numerical simulations, data fitting, and bifurcation analysis were performed using MATLAB 2014b (MathWorks). Equations and derivations relevant to each figure can be found in the Supplementary Data.

RESULTS

Construction and characterization of sequestration-based genetic circuits

We designed sequestration-based genetic circuits by mining genetic parts from the regulatory network of the type III secretion system (T3SS) in Pseudomonas aeruginosa (Figure 1A). Four regulatory proteins control the P. aeruginosa T3SS via a partner swapping mechanism. A transcriptional factor ExsA activates the target promoter (44) and is sequestered by the anti-activator ExsD into an inactive complex (ExsA-D) (45). Because of the higher binding affinity, the chaperone ExsC can sequester ExsD and liberate free ExsA, which activates the pathogenicity machinery (46). A fourth regulator ExsE sequesters ExsC into ExsC-E and prevents ExsC from interacting with ExsD until ExsE is exported (47,48).

We first constructed a two-member circuit in E. coli, which consists of exsA and exsD under the transcriptional control of pBAD and pTet* (13) promoters, respectively, and a green fluorescent protein gene (gfp) fused to the pexsD promoter (Figure 1B). The pBAD and pTet* promoters are respectively activated by arabinose (Ara) and anhydrotetracyline (aTc), and the pexsD promoter is activated by free ExsA. In this circuit, we expect the circuit readout (GFP) to be respectively high and low with increasing Ara (ExsA) and aTc (ExsD). The experimental result shows that independent control of ExsA and ExsD expression using inducible promoters enabled tuning of the output expression (Figure 1B). Furthermore, we developed a mathematical model to which the experimental transfer function was fitted (Supplementary Data). The two-member system was modified by adding ExsC (Figure 1C). The exsC gene was controlled by the pLux* promoter (13) that is activated by N-(β-ketocaproyl)-L-homoserine lactone (3OC6). As shown in Figure 1C, this addition allowed for fine-tuning of the output range, implying the advantage of complex interactions in natural networks over the simpler two-member circuit.

Sequestration-based ultrasensitivity

For the construction of bistable switches, an ultrasensitive input–output response is critical (49). When compared to cooperativity that also leads to ultrasensitivity, molecular sequestration, in which a stoichiometric inhibitor sequesters an activator, has attractive design properties for engineering genetic circuits. First, high-affinity inhibitors serve as buffers which titrate their target activators, and thus increase the system's robustness against input signal noise (i.e. fluctuations in the concentration of activators) (50). Second, molecular sequestration allows for flexible tuning of the response threshold and ultrasensitivity in a predictable and simple manner (e.g. by changing the concentration of inhibitors) while in molecular cooperativity, complicated parameters (e.g. the number of transcription factor binding sites and protein–protein affinity) need to be changed in order to tune ultrasensitivity (50–52). Third, the sequestration-based, molecular titration mechanism is universally found in protein-protein, protein–DNA, RNA–RNA, and enzyme–substrate interactions (51), offering a versatile strategy to construct genetic circuits.

To determine whether the protein sequestration can generate large ultrasensitive responses, we tested the two-member circuit in E. coli DIAL strains (40) which allowed for systematic exploration of a large range of ExsD concentrations (Figure 2). In sequestration-based systems, increasing the anti-activator concentration would increase both the apparent Hill coefficient (n_H) and the apparent half-maximal concentration (K_H) (51). As shown in Figure 2C and D, the expected trend was observed with the apparent n_H values ranging from 1 (at low aTc concentrations) to 5 (at the highest aTc concentration tested). We also confirmed that the activation of pexsD by its activator ExsA is intrinsically non-cooperative in the absence of ExsD (a Hill coefficient of ∼1, Supplementary Figure S2) (53).

Building robust and tunable bistable switches

Previous works have demonstrated that bistability is possible in both natural and artificial systems when ultrasensitivity is combined with positive feedback (36,54). The bistable region in a bifurcation diagram depends on various parameters, including the basal expression of an activator (37). Considering that the ExsADC cascade allows for output fine-tuning (Figure 1C), we asked whether combining the three regulators would allow us to control the bistable region in a tunable manner. To answer this question, we first built and characterized a bistable circuit consisting of the three regulators and a positive feedback loop (Figure 3A). As expected, the experimentally determined bifurcation diagram, in which an EM algorithm with a GMM (43) was used to classify cell population distributions (Methods), shows a bistable region, along with both monostable ON and OFF regions (Figure 3B).

Bistable switches can display a hysteretic region (49) where the output response depends on the previous state. To better understand the effect of fine-tuning by ExsC on the hysteretic region, we developed a mathematical model (Supplementary Data). As shown in Figure 3C, this model predicts that the width of the hysteretic region is a function of 3OC6, the inducer controlling ExsC expression (see also Supplementary Figures S3 and S4). Specifically, as the 3OC6 concentration increases, the hysteretic region first decreases and then sharply increases by several orders of magnitude. This trend is due to the ultrasensitivity of the pTet* transfer function (i.e. big changes in the pTet* promoter activity with small changes in aTc concentrations at certain intermediate aTc concentrations, and saturation at high aTc concentrations). This prediction was experimentally tested by initially growing cells in zero and a high aTc (1.0 μg/ml) concentration (ON and OFF cells, respectively) and then exposing them to different aTc and 3OC6 concentrations as indicated in Figure 3D. In surprisingly good agreement with the computational model, the experimental data shows the trend of shrinkage and sharp increase in the hysteretic width as a function of 3OC6 concentrations. By changing ExsC expression levels, we demonstrated that the three-member, sequestration-based switch can exhibit tunable hysteresis responses in a predictable manner.

Improving robustness through dual-positive feedback loops

Memory switches with broader bistable ranges are more robust against fluctuations in key biochemical parameters (12,18,36,55). In natural regulatory networks, bistable switches often consist of two coupled positive feedback loops (18) although a single positive feedback loop is sufficient for bistability under certain parameter conditions (56). In theory, interlocking direct and indirect positive feedback loops can generate a robust bistable switch (55), and this was experimentally verified by coupling two positive feedback loops, which enhanced the bistability range (39). To test whether this is the case for the sequestration-based system, we used a computational model (Supplementary Data) to generate a bifurcation diagram for a bistable switch with either one or two positive feedback loops (Figure 4A and B). Consistent with other systems, the sequestration-based switch with two positive feedback loops, which consists of the three regulators including ExsC, is expected to show a broader bistable region than its single-positive feedback counterpart, which consists of ExsA and ExsD only. As shown in Figure 4C, the experimentally-determined hysteretic region (in an aTc concentration range) was extensively increased from ∼10-fold (for one positive feedback loop) to >10⁶-fold (for two positive feedback loops). To our knowledge, the 10⁶-fold range is the largest bistable range reported so far. This experimental result demonstrates that the seemingly unnecessary addition of the second positive feedback loop allows us to build a far more robust bistable switch, providing insights into complex natural regulatory networks.

DISCUSSION

Natural biological systems continuously monitor and adapt to fluctuating environmental conditions. These systems use complex regulatory networks to maintain reliable control over biological processes in uncertain environments. Because of the inherent complexity of natural regulatory networks, it remains a challenge to determine how robust, system-level behaviors emerge from such intricate interactions. A bottom-up approach, in which simpler subsystems are built from independently characterized components, can provide a framework that allows for a better understanding of the core design principles that govern reliability and robustness of natural regulatory networks. Our bottom-up approach combined with mathematical modeling was critical in understanding quantitatively how the repurposed regulators from P. aeruginosa (ExsADC) interact in a heterologous host (Figures 1 and 2). Importantly, we demonstrated that by building and characterizing each individual circuit (Figures 1 and 2), the collective behavior of the complete program can be predicted (Figures 3 and 4).

In this study, we have integrated experiments and quantitative modeling to determine how regulatory architecture affects system behavior. By building bistable genetic switches from the bottom-up, we demonstrated that protein sequestration coupled with positive feedback can endow regulatory networks with tunability and robustness (Figures 3 and 4). On the basis of mathematical modeling, we accurately predicted and experimentally verified that the bistable range can be tuned (Figure 3) and even extensively enhanced by increasing complexity of the sequestration cascade (i.e. the number of positive feedback loops; Figure 4). A dual positive feedback topology in the lacZYA operon was reported to be attractive over its single positive feedback counterpart due to remarkable tolerance to parameter variations (39). Our work confirms the previous findings by coupling two positive feedback loops with a different ultrasensitive system (Figure 4), which is based on protein sequestration. Our work is also different from the previous report (39) in that the authors used galactoside permease to provide the second positive feedback loop while we changed circuit topologies in the heterologous host (E. coli) by simply rearranging the repurposed regulators (ExsADC). Because diverse circuit topologies can be easily built using the repurposed regulators and the concentrations of the regulators can be tuned by simply changing corresponding inducer concentrations (Figures 1–4; Supplementary Figure S6), the ExsADC system provides flexible genetic parts for future engineering efforts.

For the first time, we demonstrate experimentally that tunable and robust bistable switches can be built by interlocking the three-member sequestration cascade system and dual positive feedback loops. Previously constructed bistable switches have demonstrated the importance of tunability that can be affected by a variety of factors. While earlier circuits mainly focused on transcriptional level regulation and cooperativity for ultrasensitive responses (12,36,57), more recent circuit constructions have used architectures that incorporate other mechanisms including post-translational, cascading, or hybrid approaches (37,58,59). In addition to circuit topologies, intrinsic parameters, such as protein-protein binding affinities (42), have been shown to affect the bistable region. Those systems could be fine-tuned by changing the cooperativity (e.g. by promoter engineering) and the binding affinity (e.g. by protein engineering), which might be very challenging. One advantage of the three-member sequestration system over previously constructed bistable switches is its tunability, which is quite challenging to achieve in synthetic systems. In our system, the bistable range can be easily and predictably controlled by changing the concentration of ExsC, a member in the sequestration cascade (Figure 3); beyond the threshold level (∼3 nM 3OC6 in Figure 3D), the system remains bistable even in the presence of large changes in aTc concentrations (∼10⁴-fold). In addition, our system is versatile in that it can be easily rewired to generate diverse topologies of interactions that enable different functions (Supplementary Figure S6). Furthermore, protein sequestration is widely found in natural regulatory networks (51) and can easily generate ultrasensitive responses (Figure 2). We expect that our understanding of biological robustness will be increasingly deepened as more complex circuits, based on diverse mechanisms, are constructed and characterized.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Gates Foundation [OPP1087549]; National Science Foundation [CBET-1350498]. Funding for open access charge: National Science Foundation [CBET-1350498].

Conflict of interest statement. None declared.