Sparse Kernel Machine Regression for Ordinal Outcomes

Summary

Ordinal outcomes arise frequently in clinical studies when each subject is assigned to a category and the categories have a natural order. Classification rules for ordinal outcomes may be developed with commonly used regression models such as the full continuation ratio (CR) model (fCR), which allows the covariate effects to differ across all continuation ratios, and the CR model with a proportional odds structure (pCR), which assumes the covariate effects to be constant across all continuation ratios. For settings where the covariate effects differ between some continuation ratios but not all, fitting either fCR or pCR may lead to suboptimal prediction performance. In addition, these standard models do not allow for non-linear covariate effects. In this paper, we propose a sparse CR kernel machine (KM) regression method for ordinal outcomes where we use the KM framework to incorporate non-linearity and impose sparsity on the overall differences between the covariate effects of continuation ratios to control for overfitting. In addition, we provide data driven rule to select an optimal kernel to maximize the prediction accuracy. Simulation results show that our proposed procedures perform well under both linear and non-linear settings, especially when the true underlying model is in-between fCR and pCR models. We apply our procedures to develop a prediction model for levels of anti-CCP among rheumatoid arthritis patients and demonstrate the advantage of our method over other commonly used methods.

1. Introduction

Ordinal outcome data, such as pain scales, disease severity, and quality of life scales, arise frequently in medical research. To derive classification rules for an ordinal outcome y with a p × 1 predictor vector x, one may employ regression models relating x to y and classify future subjects into different categories based on their predicted P(y = c | x). Naive analysis strategies, such as dichotomizing y into a binary variable and fitting multinomial regression models, are not efficient as they do not take into account the ordinal property of the outcome. Commonly used traditional methods for modeling ordinal response data include the cumulative proportional odds model, the forward and backward continuation ratio (CR) models and the corresponding proportional odds version of the CR (pCR) model (Ananth and Kleinbaum, 1997). The forward full CR (fCR) model assumes that

$$\text{logit}P(y=c\mid y\ge c,\mathbf{x})={\mathit{\gamma }}_0^{(c)}+{\mathbf{x}}^{\top }{\mathit{\beta }}^{(c)},c=1,\dots ,C-1$$ (1)

where y is assumed to take C ordered categories, {1, …, C}, ${\mathit{\gamma }}_0^{(c)}$ and β^(c) are unknown regression parameters that are allowed to vary across continuation ratios. When the covariate effects β^(c) are assumed to be constant across c, (1) reduces to the pCR model

$$\text{logit}P(y=c\mid y\ge c,\mathbf{x})={\mathit{\gamma }}_0^{(c)}+{\mathbf{x}}^{\top }\mathit{\beta },c=1,\dots ,C-1$$ (2)

When choosing between these two models, we come across the trade-off between the model complexity and the efficiency in estimating the model parameters. With the fCR model, we might suffer from loss of efficiency due to estimating too many parameters if the true model is a sub-model of (1), especially when the dimension of x is not small. On the other hand, the pCR model might lead to poor prediction performance if the true covariate effects do vary across continuation ratios. However, for many applications, it is reasonable to expect that a compromise between the fCR model and the pCR model might be optimal. That is, β^(c) = β^(c+1) for some c but not all and thus it is possible to improve the estimation by leveraging the sparsity on β^(c) − β^(c−1). Regularization methods can be easily adapted to incorporate sparsity for CR models. Under the pCR model, Archer and Williams (2012) imposed L₁ penalty to incorporate the sparsity of the elements of β. For the fCR model, to leverage the additional sparsity on β^(c) − β^(c−1), one may impose a “fused lasso” type of penalty (Tibshirani et al., 2005), which penalizes the L₁-norm of both β^(c) and β^(c) − β^(c−1).

In the presence of non-linear covariate effects, these existing methods based on linearity assumptions may lead to classification rules with unsatisfactory performance. On the other hand, fully non-parametric methods are often not feasible due to the curse of dimensionality. Alternatively, one may account for non-linearity by including interaction or non-linear basis functions. However, in practice, there is typically no prior information on which non-linear basis should be used and including a large number of non-informative basis could result in significant overfitting. In recent years, kernel machine (KM) regression has been advocated as a powerful tool to incorporate complex covariate effects (Bishop et al., 2006; Schölkopf and Smola, 2001). The KM regression methods flexibly account for linear/non-linear effects, without necessitating explicit specification of the non-linear basis. For ordinal outcomes, some KM based algorithms have also been proposed. For example, in Cardoso and Da Costa (2007), the problem of classifying ordered classes is reduced to two-class problems and mapped into support vector machines (SVMs) and neural networks. In Chu and Keerthi (2005), SVM is used to optimize multiple thresholds to define parallel discriminant hyperplanes for the ordinal scales. Kernel Discriminant Analysis was extended using a rank constraint to solve the ordinal regression problem in Sun et al. (2010). However, none of these existing methods provide a good solution to leverage the potential similarity between sequential logits or to select optimal kernels.

In this paper, we propose a sparse CR KM (sCR_KM ) regression method for ordinal outcomes where we use the KM framework to incorporate non-linear effects and impose sparsity on the differences in the covariate effects between sequential categories to control for overfitting. To improve estimation and computational efficiency, we propose the use of the kernel principal component analysis (PCA) (Mika et al., 1999; Schölkopf et al., 1998) to transform the dual representation of the optimization problem back to the primal form with basis functions estimated from the PCA and reduce the number of parameters by thresholding the estimated eigenvalues. One key challenge in KM regression is the selection of appropriate kernel functions. Here, we propose a data driven rule for selecting an optimal kernel by minimizing a cross-validated prediction error measure. Simulation results suggest that the proposed procedures work well with relatively little price paid for the additional kernel selection. The rest of the paper is organized as the following. We introduce the logistic CR KM model in section 2.1 and detail the estimation procedures under the sparsity assumption in section 2.2. We also describe the model evaluation criteria in section 2.3 and propose a data driven rule for selecting an optimal kernel in section 2.4. Simulation and real data analysis results are given in section 3.1 and 3.2.

2. Continuation Ratio Kernel Machine Regression

Suppose data for analysis consist of n independent and identically distributed random vectors, { ${(y_i,{\mathbf{x}}_i^{\top })}^{\top }$, i = 1, …, n}. The forward fCR KM (fCR_KM ) model assumes that

$$P(y_i=c\mid y_i\ge c,{\mathbf{x}}_i)=g\left\{{\gamma }_0^{(c)}+h^{(c)}({\mathbf{x}}_i)\right\},\text{for}c=1,\dots ,C-1,$$ (3)

where g(x) = e^x/(1 + e^x), h^(c)(·) is an unknown centered smooth function that belongs to a Reproducible Kernel Hilbert Space (RKHS) 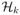, with the Hilbert space generated by a given positive definite kernel function k(·, ·; ρ), and ρ is some tuning parameter associated with the kernel function (Cristianini and Shawe-Taylor, 2000). The kernel function k(x₁, x₂; ρ) measures the similarity between x₁ and x₂ and different choices of k lead to different RKHS. Some of the popular kernel functions include the gaussian kernel $k({\mathbf{x}}_1,{\mathbf{x}}_2;\rho )=exp\{-{\Vert {\mathbf{x}}_1-{\mathbf{x}}_2\Vert }_2^2/2{\rho }^2\}$, which can be used to capture complex smooth non-linear effects; the linear kernel $k({\mathbf{x}}_1,{\mathbf{x}}_2;\rho )=\rho +{\mathbf{x}}_1^{\top }{\mathbf{x}}_2$, which corresponds to h(x) being linear in x; and the quadratic kernel $k({\mathbf{x}}_1,{\mathbf{x}}_2;\rho )={({\mathbf{x}}_1^{\top }{\mathbf{x}}_2+\rho )}^2$, which allows for 2-way interactive effects. Here, we use || · ||_p to denote the L_p norm and || · ||_F to denote Fubini’s norm for matrices. From here onward, for notational ease, we suppress ρ from the kernel function k.

By Mercer’s Theorem (Cristianini and Shawe-Taylor, 2000), any h(x) ∈ 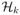has a primal representation with respect to the eigensystem of k. Specifically, under the probability measure of x, k has eigenvalues {λ_l, l = 1, …, 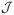} with λ₁ ≥ λ₂ ≥ ··· ≥ 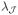and the corresponding eigenfunctions {ϕ_l, l = 1, …, 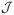} such that $k({\mathbf{x}}_1,{\mathbf{x}}_2)={\sum }_{l=1}^{\mathcal{J}}{\lambda }_l{\varphi }_l({\mathbf{x}}_1){\varphi }_l({\mathbf{x}}_2)$, where 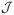could be infinity and λ_l > 0 for any l < ∞. The basis functions, { ${\psi }_l(\mathbf{x})=\sqrt{{\lambda }_l}{\varphi }_l(\mathbf{x})$, l = 1, …, 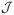}, span the RKHS 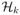. Hence all h^(c) ∈ 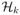has a primal representation, $h^{(c)}(\mathbf{x})={\sum }_{l=1}^{\mathcal{J}}{\beta }_l^{(c)}{\psi }_l(\mathbf{x})$, and (3) is equivalent to

$$P(y_i=c\mid y_i\ge c,{\mathbf{x}}_i)=g\left\{{\gamma }_0^{(c)}+\sum _{l=1}^{\mathcal{J}}{\beta }_l^{(c)}{\psi }_l({\mathbf{x}}_i)\right\},\text{for}c=1,\dots ,C-1.$$ (4)

Assuming ${\beta }_l^{(c)}={\beta }_l^{(c^{\prime })}$ for all l, c, c′ leads to a pCR KM (pCR_KM ) model. Throughout, we assume that x is bounded and k is smooth, leading to bounded {ψ_l(x)} on the support of x.

2.1 Inference under the full model

To make inference about the model parameters with observed data, we may maximize the following penalized likelihood with respect to {( ${\gamma }_0^{(c)}$, h^(c)), c = 1, …, C−1} with penalty accounting for the smoothness of h^(c):

$$\sum _{i=1}^n\sum _{c=1}^{C-1}{\ell }_c\left\{y_i,{\gamma }_0^{(c)},h^{(c)}({\mathbf{x}}_i)\right\}-{\tau }_2\sum _{c=1}^{C-1}{\Vert h^{(c)}\Vert }_{{\mathcal{H}}_k}^2$$ (5)

where τ₂ ≥ 0 is a tuning parameter controlling the amount of penalty,

$${\ell }_c(y_i,{\gamma }_0^{(c)},h_i^{(c)})=I(y_i\ge c)\left[D_i^{(c)}log\{g({\gamma }_0^{(c)}+h_i^{(c)})\}+(1-D_i^{(c)})log\{1-g({\gamma }_0^{(c)}+h_i^{(c)})\}\right]$$

and $D_i^{(c)}=I(y_i=c)$. From the primal representation of h^(c), maximizing (5) is equivalent to maximizing the following penalized likelihood with respect to {( ${\gamma }_0^{(c)}$, β^(c)), c = 1, …, C − 1}:

$$\sum _{c=1}^{C-1}\left[\sum _{i=1}^n{\ell }_c\left\{y_i,{\gamma }_0^{(c)},{\psi }_i^{\top }{\mathit{\beta }}^{(c)}\right\}-{\tau }_2{\Vert {\mathit{\beta }}^{(c)}\Vert }_2^2\right]$$ (6)

Thus, if the basis functions {ψ_l} were known, we can directly estimate h^(c) in the primal form. Unfortunately, in practice the true basis are typically unknown as they involve the unknown distribution of x. On the other hand, by the representer theorem (Kimeldorf and Wahba, 1970), it is not difficult to show that the maximizer in (5) always takes the dual representation with $h^{(c)}({\mathbf{x}}_i)={\mathbf{k}}_i^{\top }{\mathit{\alpha }}^{(c)}$, where k_i = [k(x_i, x₁), …, k(x_i, x_n)]^T and α^(c) is an n × 1 vector of unknown weights to be estimated as model parameters. This representation reduces (6) to an explicit optimization problem in the dual form:

$$\sum _{c=1}^{C-1}\left[\sum _{i=1}^n{\ell }_c\left\{y_i,{\gamma }_0^{(c)},{\mathbf{k}}_i^{\top }{\mathit{\alpha }}^{(c)}\right\}-{\tau }_2{\mathit{\alpha }}^{{(c)}^{\top }}{\mathbb{K}}_n{\mathit{\alpha }}^{(c)}\right]$$ (7)

where 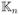= n⁻¹[k(x_i, x_j)]_n×n. Note that unlike the hinge loss in SVM, the logistic loss function is smooth, and consequently the resulting estimate of α^(c) based on (7) is not sparse.

Maximization of (7), however, could be both numerically and statistically unstable due to the large number of (n + 1)(C − 1) parameters to be estimated, especially when the sample size n is not small. On the other hand, if the eigenvalues of k decay quickly, then we may reduce the complexity by approximating k by a truncated kernel $k^{(r)}({\mathbf{x}}_1,{\mathbf{x}}_2)={\sum }_{l=1}^r{\lambda }_l{\varphi }_l({\mathbf{x}}_1){\varphi }_l({\mathbf{x}}_2)$, for some r such that ${\sum }_{l=r+1}^{\mathcal{J}}{\lambda }_l=o({\sum }_{l=1}^{\mathcal{J}}{\lambda }_l)$. The error ${\mathcal{E}}_n=\Vert {\mathbb{K}}_n-{\mathbb{K}}_n^{(r)}\Vert$ can be bounded by $O\{{\lambda }_r+{\sum }_{l=r+1}^{\infty }{\lambda }_l\}$, where ${\mathbb{K}}_n^{(r)}$ is the kernel matrix constructed from kernel k^(r) (Braun et al., 2005, Theorem 3.7). In many practical situations with fast decaying eigenvalues for k, r is typically fairly small and we can effectively approximate 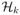by a finite dimensional space 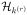. Although k^(r) is generally not attainable directly in practice, we may approximate the space spanned by k^(r) through kernel PCA by applying a singular value decomposition to 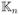: 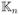= Φ̃Λ̂Φ̃^T, where Φ̃ = (u₁, …, u_n), Λ̂ = diag{a₁, …, a_n}, a₁ ≥ … ≥ a_n ≥ 0 are the eigenvalues of 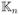and {u₁, …, u_n} are the corresponding eigenvectors. By the relative-absolute bound for the estimated principal values in kernel PCA, the principal values a_l converge to the eigenvalues λ_l and the projection error ${\{{\sum }_{l=r_n+1}^n{a}_l\}}^2$ can be bounded by $O[{\{{\sum }_{l=r_n+1}^{\mathcal{J}}{\lambda }_l\}}^2+{\mathcal{E}}_n]$. Thus, with properly chosen r_n and sufficiently fast decay rate for {λ_l}, 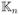can be approximated well by ${\stackrel{\sim }{\mathbb{K}}}_n^{(r_n)}={\stackrel{\sim }{\mathbf{\Phi }}}_{(r_n)}{\stackrel{\sim }{\mathrm{\Lambda }}}_{(r_n)}{\stackrel{\sim }{\mathbf{\Phi }}}_{(r_n)}^{\top }={\stackrel{\sim }{\mathbf{\Psi }}}_{(r_n)}{\stackrel{\sim }{\mathbf{\Psi }}}_{(r_n)}^{\top }$, where Φ̃_(rn) = [u₁, …, u_rn], Λ̂_(rn) = diag{a₁, …, a_rn}, and ${\stackrel{\sim }{\mathbf{\Psi }}}_{(r_n)}={\stackrel{\sim }{\mathbf{\Phi }}}_{(r_n)}\text{diag}\{a_1^{1/2},\dots ,a_{r_n}^{1/2}\}$. Replacing 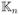with ${\stackrel{\sim }{\mathbb{K}}}_n^{(r_n)}$ and applying a variable transformation ${\stackrel{\sim }{\mathit{\beta }}}_{(r_n)}^{(c)}={\stackrel{\sim }{\mathbf{\Psi }}}_{(r_n)}^{\top }{\mathit{\alpha }}^{(c)}$, the maximization of (7) can be approximately solved by maximizing

$${\widehat{\mathcal{L}}}_0(\mathit{\theta };{\tau }_2)=\sum _{c=1}^{C-1}\left[\sum _{i=1}^n{\ell }_c\left\{y_i,{\gamma }_0^{(c)},{\stackrel{\sim }{\mathit{\psi }}}_i^{\top }{\mathit{\beta }}_{(r_n)}^{(c)}\right\}-{\tau }_2{\Vert {\mathit{\beta }}_{(r_n)}^{(c)}\Vert }_2^2\right]$$ (8)

with respect to $\mathit{\theta }=\{{\gamma }_0^{(c)},{\mathit{\beta }}_{(r_n)}^{(c)},c=1,\dots ,C-1\}$, where ψ̃ is the ith row of Ψ̃_(rn). In practice, we may choose $r_n=min\{r:{\sum }_{l=1}^r{a}_l/{\sum }_{l=1}^n{a}_l\ge \eta \}$ for some η close to 1.

Let $\stackrel{\sim }{\mathit{\theta }}=\{{\stackrel{\sim }{\gamma }}_0^{(c)},{\stackrel{\sim }{\mathit{\beta }}}_{(r_n)}^{(c)},c=1,\dots ,C-1\}$ denote the estimator from the maximization of (8). Then for a future subject with x, the probability π₊(c | x) = P(y = c | y ⩾ c, x) can be estimated as

$${\stackrel{\sim }{\pi }}_{+}(c\mid \mathbf{x})=g\left\{{\stackrel{\sim }{\gamma }}_0^{(c)}+{\stackrel{\sim }{\mathbf{\Psi }}}_{(r_n)}{(\mathbf{x})}^{\top }{\stackrel{\sim }{\mathit{\beta }}}_{(r_n)}^{(c)}\right\}$$

${\stackrel{\sim }{\mathbf{\Psi }}}_{(r_n)}(\mathbf{x})=n^{-1}\text{diag}(a_1^{-1/2},\dots ,a_{r_n}^{-1/2}){\stackrel{\sim }{\mathbf{\Phi }}}_{(r_n)}^{\top }{[k(\mathbf{x},{\mathbf{x}}_1),\dots ,k(\mathbf{x},{\mathbf{x}}_n)]}^{\top }$, by the Nystrom method (Rasmussen, 2004). Subsequently, π(c | x) = P(y = c | x) can be estimated as

$$\stackrel{\sim }{\pi }(c\mid \mathbf{x})={\stackrel{\sim }{\pi }}_{+}{(1\mid \mathbf{x})}^{I(c=1)}{\left\{{\stackrel{\sim }{\pi }}_{+}(c\mid \mathbf{x})\prod _{c^{\prime }=1}^{c-1}\{1-{\stackrel{\sim }{\pi }}_{+}(c^{\prime }\mid \mathbf{x})\}\right\}}^{I(c\ge 2)}$$

A future subject with x can then be classified as ỹ(x) = argmax_c π̃(c | x).

2.2 Estimation Under the sCR_KM Assumption

When the effects of x may differ across some continuation ratios but not all, one may improve the efficiency in estimating h^(c) by imposing sparsity on {h^(c+1) −h^(c), c = 1, …,C −2} in (3), or equivalently on {β^(c+1)–β^(c), c = 1, …,C −2} in (4). To leverage the sparsity in estimation under the sCR_KM assumption, we propose to modify (8) and instead maximize the penalized likelihood,

$$\widehat{\mathcal{L}}(\mathit{\theta };{\tau }_1,{\tau }_2)={\widehat{\mathcal{L}}}_0(\mathit{\theta };{\tau }_2)-{\tau }_1\sum _{c=1}^{C-2}\frac{{\Vert {\mathit{\beta }}_{(r_n)}^{(c+1)}-{\mathit{\beta }}_{(r_n)}^{(c)}\Vert }_2}{{\Vert {\stackrel{\sim }{\mathit{\beta }}}_{(r_n)}^{(c+1)}-{\stackrel{\sim }{\mathit{\beta }}}_{(r_n)}^{(c)}\Vert }_2}$$ (9)

where τ₁ is another tuning parameter controlling the amount of penalty for the differences between adjacent h^(c)’s. The adaptive penalty is imposed here to ensure the consistency in identifying the set of unique h^(c)’s.

To carry out the maximization of (9) in practice, we first obtain a quadratic expansion of the log-likelihood 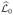(θ; τ₂) around the initial estimator θ̃:

$$n^{-1}{\widehat{\mathcal{L}}}_0(\mathit{\theta };{\tau }_2)\approx n^{-1}{\widehat{\mathcal{L}}}_0(\stackrel{\sim }{\mathit{\theta }},{\tau }_2)-\frac{1}{2}{(\mathit{\theta }-\stackrel{\sim }{\mathit{\theta }})}^{\top }\stackrel{\sim }{\mathbb{A}}(\mathit{\theta }-\stackrel{\sim }{\mathit{\theta }}),$$

where 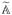= n⁻¹∂ 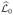(θ; τ₂)/∂θ∂θ^T|_θ=θ̃. Subsequently, we approximate the maximizer of (9) by

$$\widehat{\mathit{\theta }}=\underset{\mathit{\theta }}{\text{argmin}}\left[\frac{1}{2}{(\mathit{\theta }-\stackrel{\sim }{\mathit{\theta }})}^{\top }\stackrel{\sim }{\mathbb{A}}(\mathit{\theta }-\stackrel{\sim }{\mathit{\theta }})+n^{-1}{\tau }_1\sum _{c=1}^{C-2}\frac{{\Vert {\mathit{\beta }}_{(r_n)}^{(c+1)}-{\mathit{\beta }}_{(r_n)}^{(c)}\Vert }_2}{{\Vert {\stackrel{\sim }{\mathit{\beta }}}_{(r_n)}^{(c+1)}-{\stackrel{\sim }{\mathit{\beta }}}_{(r_n)}^{(c)}\Vert }_2}\right]$$ (10)

Such a quadratic approximation has been previously proposed to ease the computation for maximizing LASSO penalized likelihood functions and was shown to perform well in general (Wang and Leng, 2007). Followed by a sequence of variable transformations, we reformulate our optimization problem into a standard group lasso penalized maximization problem (Yuan and Lin, 2006; Wang and Leng, 2008). The detailed algorithm is in Web Appendix A. We tune the 3-tuple parameters (ρ, τ₁ and τ₂) by varying ρ within a range of values. For any given ρ, we first get τ₂(ρ) by GCV criterion in the ridge regression. Subsequently, we select ρ and τ₁ by optimizing the AIC. The detailed tuning procedure is in Web Appendix B.

With $\widehat{\mathit{\theta }}=\{{\widehat{\gamma }}_0^{(c)},{\widehat{\mathit{\beta }}}_{(r_n)}^{(c)},c=1,\dots ,C-1\}$ obtained from (10), h^(c)(x) can be estimated as

$${\widehat{h}}^{(c)}(\mathbf{x})={\stackrel{\sim }{\mathbf{\Psi }}}_{(r_n)}{(\mathbf{x})}^{\top }{\widehat{\mathit{\beta }}}_{(r_n)}^{(c)}$$

We also obtain the corresponding π̂₊(c | x) and π̂(c | x) by replacing θ̃ in π̃₊(c | x) and π̃(c | x) respectively. Then subjects with x can be classified as ŷ(x) = argmax_c π̂ (c | x). We expect that the proposed sparse estimator θ̂ and the resulting classification ŷ will outperform the corresponding estimators and classifications derived from the fCR_KM model based on θ̃ and the reduced pCR_KM model when the underlying model has h^(c) = h^(c+1) for some c but not all. When 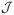= ∞, the convergence rate of ĥ^(c) would depend on the decay rate of the eigenvalues {λ_l}. On the other hand, for many practical settings, 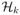with the optimal ρ can be approximated well with a finite dimensional space 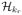with a fixed r. In Web Appendix C, we show that when 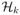is finite dimensional, $\Vert {\widehat{h}}^{(c)}-h^{(c)}\Vert =O_p(n^{-\frac{1}{2}})$). Furthermore, we establish the model selection consistency in the sense that P(ĥ^(c) = ĥ^(c+1)) → 1 if h^(c) = h^(c+1).

2.3 Model Evaluation

To evaluate the prediction performances of different methods for future observations (y⁰, x⁰), we consider three prediction error measures: the overall mis-classification error (OME) P(ŷ(x⁰) ≠ y⁰), the absolute prediction error (APE) E|ŷ(x⁰)–y⁰| and the average size of prediction sets ( 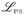) to be defined below. The OME puts equal weights to any error as long as ŷ(x⁰) = y⁰ and APE weights the error by the absolute distance between ŷ(x⁰) and y⁰. When comparing classification rules, one often sees a trade-off between these two error measures as they are capturing slightly different aspects of the prediction performance. In addition to these measures of accuracy based on ŷ(x⁰), we also examine the performance by taking the uncertainty in the classification into account. Specifically, for a given x⁰ with predicted probabilities {π̂(c | x⁰), c = 1, …,C}, instead of classifying the subject according to ŷ(x⁰) = argmax_c π̂(c | x⁰), we construct a prediction set (PS) (x⁰) = {c : π̂(c | x⁰) ⩾ 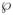}, consisting of all categories whose predicted probabilities exceed 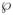, where 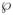is chosen as the largest value such that these prediction sets of all samples achieve a desired coverage level 100(1 – α₀)%, i.e. P{y⁰ ∈ (x⁰)} ⩾ 1 – α₀(Faulkenberry, 1973; Jeske and Harvallie, 1988; Lawless and Fredette, 2005; Cai et al., 2008). The average size of the PS,

$${\mathcal{L}}_{\text{PS}}=E\Vert {\widehat{\mathcal{P}}}_{{\alpha }_0}({\mathbf{x}}^0)\Vert =\sum _{c=1}^{C}P\left\{c\in {\widehat{\mathcal{P}}}_{{\alpha }_0}({\mathbf{x}}^0)\right\},$$

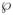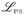can be also used to quantify the prediction performance based on those estimated π̂(c | x⁰) derived from each model. The and can be calculated from the constructed PS’ for all the samples in the testing set. Using the same argument as given in Cai et al. (2008), we may show that 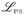is minimized by the true model and hence is a useful measure as a basis for model selection. The use of 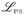allows us to achieve two goals: (i) to obtain a set of potential classifications (x) rather than ŷ(x⁰) to account for the uncertainty in the classification; and (ii) to provide a more comprehensive evaluation for the prediction performance of π̂(c | x⁰) that accounts for the uncertainty.

2.4 Data Driven Rule for Kernel Selection

The choice of kernels is critical in the prediction performance, since different kernels have different features in terms of accounting for the non-linearity properties of the data. For example, the fCR_KM with linear kernel is equivalent to the linear CR model in (1). The quadratic kernel is useful for capturing two-way interactions among predictors; while the gaussian kernel performs well in capturing smooth and complex effects. Unfortunately, in practice, with a given dataset, it is typically unclear which kernel would be the most appropriate. Here we propose to select an optimal kernel via K-fold cross-validation to minimize the 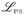. To carry out the K-fold cross-validation for kernel selection, we randomly split the training data into K disjoint subset of about equal sizes and label them as S_k, k = 1, · · ·, K. For each k, we use all observations which are not in S_k to fit our proposed procedures with several candidate kernels and obtain the corresponding estimate θ̂. Then we use samples in S_k to calculate their predicted probabilities π̂ (c | x), c = 1, · · ·, C. After obtaining the predicted probabilities for all the samples from cross-validation, (x) and 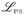can be computed for each of the kernels. The kernel with the smallest 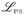will be selected as the optimal kernel and the corresponding estimate θ̂ would then be used for prediction in the validation set. In regards to the choice of K, it is imperative that the size of the training set is large enough to accurately estimate the sCR_KM model parameters. We recommend K = 10 as previously suggested in Breiman and Spector (1992).

3. Numerical Studies

3.1 Simulation Study

We conducted extensive simulations to evaluate the finite sample performance of our proposed methods and compared with three existing methods: the “one-against-one” SVM method (Hsu and Lin, 2002), the L₁ penalized pCR method (Archer and Williams, 2012), denoted by pCR_L1 and the classification tree for ordinal outcomes (CART) (Galimberti et al., 2012). For the “one against-one” SVM, C(C – 1)/2 binary classifiers are trained by SVM, and the appropriate class is found by a voting scheme.

We simulated 5 category ordinal outcome Y with continuous covariates under the CR_KM model in (3). The 20×1 predictor vector X was generated from MVN(0, 3.6+6.4 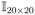).We generate Y | X based on two types of h^(c)(X): (i) linear in X; and (ii) linear effects plus two-way interactions between X_j and X_j+1. The regression coefficients β^(c), c = 1, · · ·, C – 1 were set to be between 0 and 0.4 and the intercept parameters { ${\gamma }_0^{(c)}$, c = 1, · · ·, C − 1} were selected such that there were approximately the same number of observations in each of the five classes. For each setting, we considered three types of h^(c)(X): (a) h⁽¹⁾ ≠ = h⁽²⁾ ≠ = h⁽³⁾ ≠ = h⁽⁴⁾ representing a fCR_KM model; (b) h⁽¹⁾ = h⁽²⁾ ≠ = h⁽³⁾ = h⁽⁴⁾ representing a model between a fCR_KM model and a pCR_KM model; and (c) h⁽¹⁾ = h⁽²⁾ = h⁽³⁾ = h⁽⁴⁾ representing a pCR_KM model. For each simulated data, we let n = 500 in the training set to estimate all model parameters including kernel selection. Then to evaluate the performances of different procedures, we generate independent test sets of sample size 5000 to approximate the expected accuracy of the trained models.

For each scenario, we generate 50 datasets to compare the performance of SVM, pCR_L1, CART, and the three models: sCR_KM, fCR_KM and pCR_KM under the different choices of kernels. Three kernels, including linear, quadratic and gaussian, are considered as candidates for kernel selection. Our recommended procedure would be sCR_KM with adaptive kernel selection, denoted by ${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$. Parameter tuning is performed based on the whole training set, and the selected parameters are fixed and used for the CV as well as building and evaluating the prediction model. We also compare the performance of our proposed procedures with data driven selection of the kernel versus those obtained under the true optimal kernel (linear for setting i and quadratic for setting ii) in each setting to examine the price paid for selecting the kernel.

In Table 1, we present results comparing different procedures when the data are generated from setting i with linear effects. Results for setting ii with interactive effects are given in Table 2. Table 3 shows the percentage of times different kernels being selected as the optimal kernel based on proposed data driven rule for kernel selection. Under both settings, applying our sCR_KM method always results in similar performance as the true model when the underlying model is either (a) the fCR_KM model; or (c) the pCR_KM model. This indicates that little penalty is paid for letting the data determine the underlying sparsity of h^(c+1) – h^(c). When the underlying model is in between the two, sCR_KM performs the best. When the effects are linear, our proposed procedures with adaptive kernel selection perform similarly to those based on linear kernel. In the settings with interaction effects, ${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$ outperforms sCR_KM with linear kernel by capturing non-linear effects. For example, when h⁽¹⁾ = h⁽²⁾ ≠ = h⁽³⁾ = h⁽⁴⁾, the average prediction set size 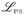was 2.9 for ${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$ and, 4.49 for sCR_KM with linear kernel. In this setting, ${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$ also outperforms both the fCR_KM and the pCR_KM models regardless how kernel was selected for these models. The prediction accuracy from ${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$ was also similar to sCR_KM with quadratic kernel, which is the optimal kernel in this setting, indicating little loss of accuracy for the additional adaptive kernel selection. In general, the kernel selection procedure makes sensible choices of the kernels. When the underlying effects are linear, the linear kernel is selected 100% of the times; when the underlying model involves interactions, either quadratic or gaussian kernels are selected but not the linear kernel. This suggests that the use of cross-validation can overcome the overfitting issue. Under setting ii with interactive effects, the procedures with gaussian kernel appear to perform similarly to those with the quadratic kernel with respect to prediction accuracy. This is not surprising since the gaussian kernel is a universal kernel such that its corresponding RKHS is rich enough to approximate any target function (Steinwart, 2002) and hence could capture quadratic effects reasonably well.

Table 1.

Average prediction performances with respect to average size of the prediction set ( 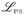), the overall mis-classification error (OME), and the absolute prediction error (APE), for setting i with linear effects.

(a) h(1) ≠ h(2) ≠ h(3) ≠ h(4)
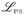
kernel choice			OME	APE
Linear	fCRKM	1.82(0.04)	0.33(0.01)	0.44(0.01)
	sCRKM	1.83(0.04)	0.33(0.01)	0.44(0.01)
	pCRKM	2.29(0.03)	0.46(0.01)	0.53(0.01)
Data Driven	fCRKM	1.82(0.04)	0.33(0.01)	0.44(0.01)
	${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$	1.83(0.04)	0.33(0.01)	0.44(0.01)
	pCRKM	2.29(0.03)	0.46(0.01)	0.53(0.01)
-	SVM	2.00(0.04)	0.34(0.01)	0.46(0.01)
	CART	-	0.56(0.02)	0.80(0.02)
	pCRL1	2.33(0.04)	0.47(0.01)	0.55(0.01)
(b) h(1) = h(2) ≠ h(3) = h(4)
Linear	fCRKM	1.90(0.05)	0.36(0.01)	0.44(0.02)
	sCRKM	1.85(0.04)	0.35(0.01)	0.42(0.02)
	pCRKM	2.21(0.03)	0.44(0.01)	0.51(0.01)
Data Driven	fCRKM	1.90(0.05)	0.36(0.01)	0.44(0.02)
	${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$	1.85(0.04)	0.35(0.01)	0.42(0.02)
	pCRKM	2.21(0.03)	0.44(0.01)	0.51(0.01)
-	SVM	2.04(0.04)	0.38(0.01)	0.47(0.01)
	CART	-	0.55(0.02)	0.76(0.03)
	pCRL1	2.19(0.03)	0.44(0.01)	0.51(0.01)
(c) h(1) = h(2) = h(3) = h(4)
Linear	fCRKM	1.93(0.03)	0.39(0.01)	0.43(0.01)
	sCRKM	1.86(0.03)	0.37(0.01)	0.39(0.01)
	pCRKM	1.85(0.03)	0.36(0.01)	0.39(0.01)
Data Driven	fCRKM	1.93(0.03)	0.39(0.01)	0.43(0.01)
	${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$	1.86(0.03)	0.37(0.01)	0.39(0.01)
	pCRKM	1.85(0.03)	0.36(0.01)	0.39(0.01)
-	SVM	2.03(0.04)	0.42(0.01)	0.46(0.01)
	CART	-	0.55(0.01)	0.68(0.02)
	pCRL1	1.82(0.03)	0.36(0.01)	0.38(0.01)

Table 2.

Average prediction performances with respect to average size of the prediction set ( 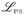), the overall mis-classification error (OME), and the absolute prediction error (APE), for setting ii with interactive effects.

(a) h(1) ≠ h(2) ≠ h(3) ≠ h(4)
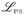
kernel choice			OME	APE
Linear	fCRKM	4.47(0.10)	0.75(0.03)	1.53(0.15)
	sCRKM	4.45(0.11)	0.75(0.03)	1.55(0.16)
	pCRKM	4.44(0.05)	0.76(0.02)	1.65(0.17)
Data Driven	fCRKM	1.99(0.07)	0.36(0.02)	0.52(0.02)
	${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$	2.03(0.09)	0.37(0.02)	0.52(0.02)
	pCRKM	2.70(0.14)	0.53(0.02)	0.67(0.05)
Quadratic	fCRKM	1.93(0.05)	0.35(0.01)	0.51(0.02)
	sCRKM	1.95(0.05)	0.35(0.01)	0.51(0.02)
	pCRKM	2.84(0.06)	0.55(0.01)	0.72(0.02)
-	SVM	2.32(0.06)	0.44(0.01)	0.63(0.02)
	CART	-	0.66(0.03)	1.02(0.04)
	pCR L1	4.05(0.14)	0.79(0.02)	1.72(0.30)
(b) h(1) = h(2) ≠ h(3) = h(4)
Linear	fCRKM	4.50(0.10)	0.75(0.03)	1.42(0.16)
	sCRKM	4.49(0.10)	0.75(0.03)	1.44(0.18)
	pCRKM	4.46(0.04)	0.75(0.03)	1.53(0.19)
Data Driven	fCRKM	2.19(0.07)	0.43(0.02)	0.55(0.02)
	${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$	2.09(0.10)	0.41(0.02)	0.52(0.02)
	pCRKM	2.44(0.07)	0.50(0.01)	0.59(0.03)
Quadratic	fCRKM	2.14(0.04)	0.42(0.01)	0.54(0.02)
	sCRKM	2.00(0.05)	0.39(0.01)	0.50(0.02)
	pCRKM	2.50(0.06)	0.51(0.01)	0.61(0.02)
-	SVM	2.48(0.05)	0.51(0.01)	0.68(0.02)
	CART	-	0.64(0.02)	0.92(0.04)
	pCR L1	4.06(0.18)	0.79(0.02)	1.54(0.34)
(c) h(1) = h(2) = h(3) = h(4)
Linear	fCRKM	4.45(0.09)	0.77(0.02)	1.52(0.13)
	sCRKM	4.44(0.09)	0.77(0.02)	1.55(0.15)
	pCRKM	4.44(0.05)	0.77(0.02)	1.63(0.18)
Data Driven	fCRKM	2.53(0.07)	0.49(0.01)	0.62(0.03)
	${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$	2.34(0.10)	0.46(0.02)	0.57(0.04)
	pCRKM	2.05(0.08)	0.40(0.02)	0.46(0.02)
Quadratic	fCRKM	2.48(0.05)	0.48(0.01)	0.60(0.02)
	sCRKM	2.26(0.06)	0.45(0.01)	0.55(0.02)
	pCRKM	2.03(0.08)	0.40(0.02)	0.46(0.03)
-	SVM	2.76(0.05)	0.56(0.01)	0.80(0.03)
	CART	-	0.64(0.04)	0.87(0.04)
	pCR L1	4.09(0.18)	0.79(0.02)	1.64(0.31)

Table 3.

% of times different kernels being selected as the optimal kernel based on proposed data driven rule for kernel selection.

	setting i with linear effects			setting ii with interaction effects
	Linear	Guassian	Quadratic	Linear	Guassian	Quadratic
h(1) ≠ h(2) ≠ h(3) ≠ h(4)	100	0	0	0	54	46
h(1) = h(2) ≠ h(3) = h(4)	100	0	0	0	50	50
h(1) = h(2) = h(3) = h(4)	100	0	0	0	40	60

Comparing to the three existing methods, our proposed procedures also show great advantage. Across all settings, our proposed ${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$ method outperforms the SVM. For example, in setting ii, when h⁽¹⁾ ≠ h⁽²⁾ ≠ h⁽³⁾ ≠ h⁽⁴⁾, SVM has an average 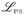of 2.32 vs 2.03 from ${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$; when h⁽¹⁾ = h⁽²⁾ = h⁽³⁾ = h⁽⁴⁾, SVM has an average 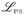of 2.76 vs 2.34 from ${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$. This is in part due to the fact that SVM doesn’t consider the ordinal property of the outcome or the underlying sparsity of h^(c+1) − h^(c). The pCR_L1 performs similarly to pCR_KM with linear kernel because it only considers linear effect of the predictors. However, when the true underlying effects are non-linear as in setting ii, the pCR_L1 performs poorly as expected. The CART method generally provides less accurate prediction compared to both SVM and sCR_KM in both linear and non-linear settings. These comparisons imply the precision gain of our method due to imposing sparsity on the differences in the covariate effects of the sequential categories and incorporating potential non-linear effects via kernel selection.

3.2 Data Example: Genetic Risk Prediction of Shared Autoimmunity

Autoimmune diseases (ADs), roughly defined as conditions where the immune system attacks self tissues and organs, affect 1 out of 31 individuals in the United States (Jacobson et al., 1997). Although ADs encompass a broad range of clinical manifestations, e.g. joint swelling, skin rash, and vasculitis. Recent studies have uncovered shared genetic risk factors across different ADs (Criswell et al., 2005). Epidemiologic studies corroborate with findings from genetic studies demonstrating that autoimmune diseases co-occur within individuals and families (Somers et al., 2006).

The presence of autoantibodies defines the majority of autoimmune diseases. Cyclic Citrullinated Peptide (CCP) antibodies are associated with rheumatoid arthritis (RA), and assays employing CCP to measure antibodies recognizing citrullinated antigens are used as a diagnostic test for RA (Lee and Schur, 2003). Among RA patients, different levels of CCP also indicate different subtypes of RA and are associated with different disease progressions (Kroot et al., 2000). Positive CCP indicates increased likelihood of erosive disease in RA, and high level of CCP may be useful to identify patients with aggressive disease. Given the shared genetic risk factors across autoimmune diseases, we would expect that subjects with one autoimmune disease, would be at higher risk for other autoimmune diseases. For example, CCP may be positive in patients with other autoimmune diseases such as systemic lupus erythematosus (SLE) (Harel and Shoenfeld, 2006). So patients with other autoimmune diseases or with genetic profiles that are indicative of elevated risk of other autoimmune diseases may have worse RA disease progression, which is partially reflected in the CCP levels.

To study the relationship between CCP levels and measurements of autoimmunity, we applied our methods to a dataset of 1265 rheumatoid arthritis (RA) patients of European decsent nested in an EMR cohort at Partner’s Healthcare (Liao et al., 2010). In this RA cohort, all subjects were genotyped for 67 single nucleotide polymorphisms (SNPs) with published associations with RA, Systemic lupus erythematosus (SLE), and celiac disease, and an aggregate genetic risk score (GRS) is calculated for each of the three diseases based on the number of SNPs for the particular diseases (Liao et al., 2013). These three GRSs represent genetic markers of autoimmunity. In addition to genetic information, billing codes of four ADs, RA, JRA and Psoriatic arthritis (PsA), as well as radiology findings of erosions are also available as predictors. For the CCP levels, we categorized into 4 ordinal categories with the total numbers of patients being 353, 266, 312 and 334, in categories 1, 2, 3 and 4, respectively. To construct and evaluate various prediction methods, we randomly split the data into two independent sets (evenly split within each category) with 633 subjects in the training set and 632 subjects in the validation set.

Applying our proposed procedure to the training data, our adaptive kernel selection rule selected the RBF kernel out of the linear, quadratic and RBF kernels, suggesting the presence of non-linear effects. Prediction models using SVM, pCR_L1 and CART were also developed for comparison, and the results are shown in Table 4. When applying the proposed prediction rules to the validation set, the ${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$ method results in the smallest 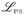(2.58), comparing to the SVM model (3.44) and the pCR_L1 model (3.43). As expected, if we enforce the sCR_KM with quadratic kernel or linear kernel, the procedure yields a larger 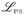(3 and 2.9), highlighting the advantage of kernel selection. With respect to the OME and APE, the ${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$ model also outperforms the three existing methods. The ${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$ has OME of 0.59, versus 0.67 from SVM, 0.66 from pCR_L1 and 0.67 from CART; has APE of 1.02, versus 1.18 from SVM, 1.27 from pCR_L1 and 1.22 from CART. In order to evaluate whether the differences in the prediction is significant, we applied the bootstrap procedure to the validation data to estimate the standard errors for the estimated 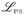, OME, and APE, as well as the differences between ${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$ and other methods with respect to these prediction errors. As shown in Table 4, ${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$ leads to significantly lower prediction errors with p-values < 0.001. Therefore, our ${\text{sCR}}_{\text{KM}}^{\mathbb{S}}$ method leads to a more accurate model for predicting anti-CCP levels compared with existing methods.

Table 4.

Prediction performances with respect to average size of the prediction set ( 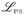), the overall mis-classification error (OME), and the absolute prediction error (APE); differences in performances between sCR_KM and existing methods with standard deviations (SD)

Methods for comparison	Prediction measurements			Differences between sCRKM and other(SD)
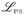
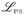
		OME	APE		OME	APE
sCRKM	2.58(0.09)	0.59(0.02)	1.02(0.04)	-	-	-
SVM	3.5(0.05)	0.67(0.02)	1.18(0.04)	−0.92(0.09)	−0.09(0.02)	−0.16(0.04)
pCR L1	3.43(0.05)	0.66(0.02)	1.27(0.04)	−0.85(0.10)	−0.07(0.02)	−0.25(0.04)
CART	-	0.67(0.02)	1.22(0.04)	-	−0.08(0.02)	−0.20(0.04)

4. Discussion

In this paper, we proposed the sCR_KM procedure to construct optimal classification rules for ordinal outcomes. Our proposed method has advantage over existing methods by incorporating potentially non-linear effects while allowing for adaptive selection of optimal kernels. When there is sparsity for the differences in the covariate effects between two sequential categories, our method will also automatically assign the same coefficients to the sequential categories to achieve an optimal balance between model complexity and prediction accuracy. Our numerical studies suggest that when the underlying model is either the fCR_KM model or the reduced pCR_KM model, our proposed sCR_KM method performs similarly to fitting the corresponding model. In the case that the underlying model is in between the full and reduced model, the sCR_KM method performs better than fitting either the fCR_KM or the pCR_KM model. The proposed data driven rule for kernel selection also enables us to choose an optimal kernel for a given dataset. When we select how many components to use in the singular value decomposition of 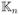, we choose r_n as the largest r such that the estimated proportion of variation explained by the first r_n eigenfunctions, defined as $\frac{\{{\sum }_{l=1}^{r_n}{a}_l\}}{\{{\sum }_{l=1}^n{a}_l\}}$, is at least η ∈ (0, 1]. This selection rule is similar to those considered in the standard PCA literature (Park, 1981). Alternatively, one may treat r_n as an additional tuning parameter and select the appropriate r_n from a certain range to make sure the final AIC reaches its optimal.