Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Sep 23.
Published in final edited form as: Cell Syst. 2015 Sep 23;1(3):238–245. doi: 10.1016/j.cels.2015.09.001

Competitive inhibition can linearize dose-response and generate a linear rectifier

Yonatan Savir 1, Benjamin P Tu 2, Michael Springer 1,*
PMCID: PMC4610030  NIHMSID: NIHMS723884  PMID: 26495436

Summary

Many biological responses require a dynamic range that is larger than standard bi-molecular interactions allow, yet the also ability to remain off at low input. Here we mathematically show that an enzyme reaction system involving a combination of competitive inhibition, conservation of the total level of substrate and inhibitor, and positive feedback can behave like a linear rectifier—that is, a network motif with an input-output relationship that is linearly sensitive to substrate above a threshold but unresponsive below the threshold. We propose that the evolutionarily conserved yeast SAGA histone acetylation complex may possess the proper physiological response characteristics and molecular interactions needed to perform as a linear rectifier, and we suggest potential experiments to test this hypothesis. One implication of this work is that linear responses and linear rectifiers might be easier to evolve or synthetically construct than is currently appreciated.

Keywords: Linear rectifiers, Competitive inhibition, Transcriptional regulation, SAGA, Enzyme kinetics

Introduction

Organisms need to respond to changes in their environment to survive. Response to these changes often involves complex signaling pathways that process information about the environment and directly or indirectly regulate protein concentration and activity. The enzyme kinetics that underlie cellular signaling are typically bimolecular, resulting in a Michaelis-Menten relationship between reactants (inputs) and products (outputs) (Fig. 1A) (Fersht, 1985). This relationship has the disadvantage that it saturates at high input levels, therefore the output is most responsive when the input concentration is low (Fig. 1B). In isolation, this property cannot create the rich signal processing observed in nature (e.g. oscillators or excitable systems). Therefore, signaling pathways combine bimolecular reactions together in ways that result in more complex input-output functions. For example, a switch-like response can be achieved using enzyme cooperativity (Ferrell, 1996; Qian, 2012). A switch is maximally sensitive at a threshold concentration of input and is unresponsive at concentrations both above and below this threshold (Fig. 1C). This response can be advantageous in situations where only one of two outcomes is desired. For example, switches are used to make cell fate decisions (Santos and Ferrell, 2008).

Figure 1.

Figure 1

Open in a new tab

Competitive inhibition combined with mass conservation leads to a linear relationship between the substrate concentration and reaction rate. (A–D) Typical response functions and their sensitivities. (A) Michaelian response (black) and a linear response (red), and (B) their derivatives. The derivative of the linear response highlights that it is sensitive over the entire input range while the Michaelian response saturates at high input values. Neither of these responses have a threshold. (C) Several example rectifiers. Rectifiers are unresponsive below a threshold (dashed horizontal line). Ideal Michaelian rectifier (black), ideal linear rectifier (red), and a Hill function with n = 10 (green) are given along with their derivatives (D). The Hill function and the Michaelian rectifier are akin to a step-like response; each has an ‘on’ and ‘off’ regime with a clear threshold and low sensitivity in each regime. However, the linear rectifier has a threshold that defines an ‘off’ regime while being sensitive to the input across the whole ‘on’ regime; the switch is not sensitive to changes in input concentration within the ‘on’ regime. (E) Kinetic schema of a general enzymatic reaction that is prone to competitive inhibition. Where KM is the Michaelis-Menten constant of the substrate and KI is the inhibitor dissociation constant. (F) When the inhibitor levels are constant (black and green lines), the response is Michaelian. When the total substrate and inhibitor levels are constant, i.e. [S] + [I] = T, the response is linear throughout the entire range of the substrate (red line). (G) A contour plot of the normalized acetylation rate. The dependence of the reaction rate on the substrate and inhibitor levels can be represented as trajectories in the S - I plane. When inhibitor levels are constant (black and green lines) these trajectories are parallel to the substrate axis. When the total level of the substrate and inhibitor is constant (green line), the trajectory has a slope of -1; this slope results in a linearized response.

While switches are useful, there are many situations where it could be desirable to respond above a minimal threshold but still be responsive to graded concentrations of input well above this threshold. A shifted Michaelis-Menten relationship (a Michaelis-Menten response translated to the right along the substrate axis – see black curve in Figure 1C) does not respond below a threshold, is maximally responsive at the threshold, but is still responsive above this threshold. This type of response can be achieved by several mechanisms, such as multisite phosphorylation (Gunawardena, 2005) or a suicide inhibitor (Fersht, 1985). For example, if an inhibitor existed that irreversibly binds the substrate and sequesters it, there could be no response until the substrate concentration was higher than the inhibitor (Elf et al., 2005; Levine et al., 2007; Mehta et al., 2008). At this point the system would behave as if the inhibitor were not there, but the effective concentration of substrate would be the actual concentration minus the concentration of inhibitor. While responsive over a wider dynamic range than a switch-like response, this response still saturates at high input values, and thus the sensitivity to input decreases as input increases above the threshold (Fig 1D).

Signal saturation is a classical engineering problem. One solution is to insert a “pre-distorter” between the input and a system that saturates. If the input-output relationship of the pre-distorter is the inverse of the rest of the system, the resulting input-output relationship will be linear (Becskei, 2009). This type of linearization was demonstrated in a synthetic circuit by the addition of a specific type of negative feedback and negative regulation (Nevozhay et al., 2009). While linear over a broad dynamic range, this system was not intrinsically thresholded, making it sensitive to low concentrations of input, and saturated at high input values.

In contrast to shifted Michaelis-Menten response, a hybrid between the threshold and linear response, termed a linear rectifier, could guarantee that the system has no response below a threshold concentration and is linearly responsive above that threshold concentration. Linear rectifiers could in principle be extremely useful in responses where low levels of input should be ‘ignored’ but the response needs to be maximally responsive over as wide a range of inputs as possible (Fig. 1C,D). Nutrient regulation of growth rate and gene expression is a plausible system in which a linear rectifier could be useful (see Box 1 for discussion), but a linear rectifier could prove useful under any circumstance when a thresholded response is necessary, but linear relationship between input and output is also required over a larger than Michaelian range.

Box 1. Biological case study: histone acetylation.

When cells are faced with low nutrient environments they tend to not grow; as nutrient levels are increased, the growth rate increases proportionally (Yuan et al., 2013). Several studies have suggested that gene expression for a number of genes linearly depends on growth. Expression of 60-90% of genes is correlated with growth rate, implying that there is a global correlation between growth rate and gene expression (Keren et al., 2013). The tight coupling between growth rate and transcription is still not fully understood (Wellen and Thompson, 2012).

A potential mechanistic link could be histone acetylation (Cai et al., 2011; Guan and Xiong, 2011; Haigis and Sinclair, 2010; Morrish, 2010; Schwer and Verdin, 2008; Takahashi et al., 2006; Wellen, 2009). Acetylation of histones is a key transcriptional regulatory step that can have a large effect on gene expression (Wellen and Thompson, 2012). Ac-CoA is the source of the acetyl group used by histone acetyl transferases (HAT) and it is also a key metabolite whose level is affected by nutrients and energy availability, with levels increasing during growth (Cai et al., 2011). Ac-CoA increases have been shown to result in increased acetylation of histones on genes involved in growth, potentially providing a direct link between growth rate and transcription (Cai et al., 2011). Here we outline how the SAGA (Spt–Ada-Gcn5-acetyltransferase) complex from Saccharomyces cerevisiae, a key histone acetyl transferase (HAT) that is conserved from yeast to human (Berndsen and Denu, 2008; Koutelou et al., 2010; Tanner et al., 2000), could be a concrete example of a biological linear rectifier.

It is plausible that SAGA responds linearly to changes in Ac-CoA concentration

Acetylation of histones by SAGA (Grant et al., 1997; Kuo et al., 1996) involves the serial sequential formation of a ternary complex between SAGA, Ac-CoA, and histone (Berndsen and Denu, 2008) (Figure 4A, Supplemental Experimental Procedures, Fig. S1). Two products result from the acetylation reaction: acetylated histone and CoA. Competition for Gcn5 binding between Ac-CoA and CoA may lead to a linear response, given that the following two conditions are met. Condition 1: The CoA dissociation constant for Gcn5, KD,C, (6.7 μM; Fan et al., 2015; Tanner et al., 2000), is very close to the dissociation rate for Ac-CoA, KD,A (5.1 μM). In vivo, CoA and Ac-CoA concentrations are similar both in E. coli (Chohnan et al., 1998) and in mammalian cells (Lee et al., 2014). Thus, CoA is a physiologically relevant inhibitor of Ac-CoA in multiple organisms (Fan et al., 2015; Tanner et al., 2000). Condition 2: the total concentration of Ac-CoA and CoA is conserved. Two lines of evidence support the possibility that in vivo CoA and Ac-CoA levels are interdependent. First, Ac-CoA and CoA levels are mechanistically coupled as there are a number of cellular reactions that interconvert the two species. Second, Ac-CoA and CoA levels were measured in E. coli; while the ratio of Ac-CoA and CoA changed by over ten-fold across several different environmental conditions, the combined amount of these two metabolites varied by under 50% (Chohnan et al., 1998).

When combined with thresholding, a linear SAGA response could produce a linear rectifier

By analogy to multisite phosphorylation, multisite acetylation can impose an activity threshold. In Saccharomyces cerevisiae, at least three components of the SAGA complex are acetylated by the catalytic subunit of SAGA, Gcn5p. Based on chromatin immunoprecipitation, acetylated SAGA interacts more strongly to a ribosomal gene during growth phase relative to the non-acetylated SAGA, suggesting that the auto-acetylation of SAGA might play a role in enhancing its capacity as an acetyltransferase (Cai et al., 2011). In addition, auto-acetylation has been suggested to affect HAT activity in other systems (Yuan and Marmorstein, 2013). A reaction scheme that combines multisite auto-acetylation with conservation of the total levels of Ac-CoA and CoA and competitive binding (Figure 4B) leads to a response that has both a sharp threshold and a linear regime (Figure 4C,D), i.e. a linear rectifier (Supplemental Experimental Procedures, section V).

Future experimental tests

There are several experiments that could help establish SAGA as a linear rectifier. In vitro experiments with purified components can establish whether the SAGA complex is capable of a linear response. While a number of in vitro enzymatic assays have been performed with SAGA, both in the absence and presence of CoA, unusual experiments need to be performed to identify a linear motif. Specifically, assays must be conducted at multiple different CoA levels while the total amount of Ac-CoA and CoA is held constant.

To know whether an intrinsic ability to respond linearly is used in vivo, a different approach must be taken because direct control over intracellular Ac-CoA and CoA is difficult if not impossible. Therefore the intracellular concentration of Ac-CoA needs to be measured in a number of different environments and compared to the amount of histone acetylation. This will directly measure whether the histone acetylation rate is linearly proportional to Ac-CoA. Further support for the proposed mechanism would be given if the total of Ac-CoA and CoA is nearly constant across conditions. Mutants such as acs1 that affect the level of CoA, Ac-CoA, or their ratio would help to separate whether the linear response is directly controlled by CoA/AcCoA levels or by some other nutrient dependent signaling pathway.

Additionally, three classes of mutants should exist: 1) mutants that affect the binding of CoA and AcCoA equivalently, 2) mutants that affect CoA and AcCoA binding differentially, and 3) mutants that affect feedback. The first and third class should shift the activation threshold without compromising the linearity of response; the first class would change the slope of the linear response. These two classes might be achieved, respectively, with a natural variant in gcn5 that affects binding e.g. gcn5 A190T (Langer et al., 2002) and acetylation site mutants of SAGA. This change in threshold should be noticeable in experiments measuring growth rates in different, especially poor, nutrient environments. Additionally, these mutants could have significantly higher cell death at low nutrient levels that should be testable by viability assays. The second class of mutant could potentially be rationally designed with the aide of the crystal structure of Gcn5 (Trievel et al., 1999). A mutant that bound AcCoA much better than CoA might be expected to saturate growth at a lower external nutrient concentration, which should be measurable by competition with wild-type strains in high nutrient environments. These potential decoupling mutants could allow for a deeper mechanistic examination of the regulation of growth control.

Here, we examine an enzyme reaction system that functions as a linear rectifier. It contains two features: 1) a product of the reaction is a competitive inhibitor of the substrate and 2) the total inhibitor and substrate concentration remain roughly constant. This motif had been carefully characterized in the context of ATP, ADP, and AMP binding to enzymes where the ATP binding is much stronger than that of ADP and AMP (Atkinson, 1968). In this regime the system can behave ultrasensitively to changes in ATP levels. We extend previous work on this motif by analytically showing that it can produce a response that is linear across its full dynamic range without saturating. This occurs when an additional constraint is placed on the motif, namely, the binding affinity of the inhibitor and substrate are equal. This motif is robust to modest perturbations in this criterion and in the need to maintain a constant concentration of inhibitor plus substrate. Additionally, we show that combining this motif with a threshold mechanism or positive feedback creates a linear rectifier.

As an example of plausibility, we explain how these features could be biologically implemented in the context of histone acetylation and propose a series of experiments that could test this hypothesis (Box 1). While we describe this motif in the context of histone acetylation, the basic design could be ubiquitous.

Results

Competition between substrate and an inhibitor that are conserved can lead to a linear response. In the case of competitive binding between a substrate and an inhibitor (Figure 1E), the normalized reaction rate (ṽ) is (Supplemental Experimental Procedures, section I) (Fersht, 1998),

v∼=[S][S]+KM+[I]KMKI, (1)

where KM is the Michaelian constant for the substrate and KI is the dissociation constant for the inhibitor. Competition does not change the Vmax of the reaction; instead the effective affinity constant for the reaction is changed. Although the presence of inhibitor affects the reaction rate, if the inhibitor levels are constant the response as a function of substrate is still Michaelian (Figure 1F). However, if the substrate and inhibitor levels are interdependent, a non-Michaelian response is possible, e.g. if the sum of the substrate and inhibitor is constant (Atkinson, 1968). If T = [S] + [I] Eq. (1) can be rewritten as,

v∼=[S][S](1−KMKI)+KM+TKMKI. (2)

When the substrate and inhibitor dissociation constants are similar, KM ≈ KI, the response becomes (Supplemental Experimental Procedures, section I),

v∼≈[S]KM+T (3)

Since KM and T are both constants, the response is linear with respect to substrate over the entire physiological range of substrate concentrations (Figure 1F).

To understand the relationship between the substrate and the reaction rate when the substrate and inhibitor levels are interdependent, it is helpful to visualize the problem as a two-dimensional surface (Figure 1G). As the substrate level changes, the trajectory on the S - I plane in Fig 2C depends on the relationship between the substrate and inhibitor. Horizontal lines in this space, i.e. constant inhibitor, result in a Michaelian relationship between input and reaction rate (green and black lines in Fig. 1F,G). Diagonal lines in this space, S + I = constant, result in a linear relationship between the substrate and the reaction rate (red line in Figure 1F,G).

Figure 2.

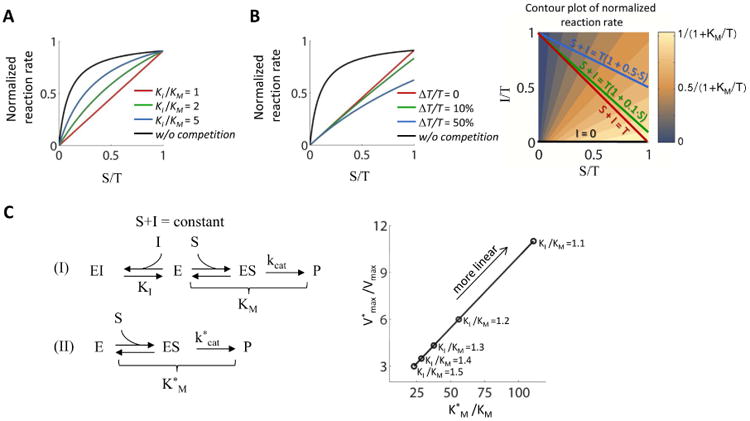
Figure 2

Open in a new tab

Deviations from ideal linearization. (A) The case in which the substrate affinity is higher than the inhibitor affinity, i.e. KI/KM is larger than one. (B) The case in which the total concentration of the substrate and the inhibitor is not constant but rather increases with the substrate levels. As a result, trajectories in the S - I plane might have a slope other than -1. (C) The kinetics constant that lead a linear (I) and Michaelian (II) reaction to behave equivalently in the physiological range, where KI/KM = 1 and T/KM = 10 (similar to the case for the Ac-CoA/CoA system (Biology Box), see text for general relation). A Michaelian scheme (II) needs an affinity that is about 100 times larger and a maximal velocity that is about 10 times larger than the competitive inhibition scheme (I).

While the system is only linear when both KM =KI and [S] +[I] = constant, modest deviations from these equalities are still approximately linear (Figure 2A), even when there are variations in the total sum of the substrate and inhibitor (Figure 2B) (Supplemental Experimental Procedures, section I). Michaelian relationships are also approximately linear when the substrate concentration is well below the KM of the reaction. It is therefore possible to recapitulate the response of competitive inhibition with conservation of the total levels of substrate and inhibitor with a standard Michaelian reaction (Fig. 2C), but this will come at the expense of making the reaction less efficient per unit enzyme (Fig. 2C, Supplemental Experimental Procedures, section II). For example, to achieve the same response in a scenario where KI/KM = 1.3 and T/KM = 10 (similar to the case for the Ac-CoA/CoA system, Box 1) a Michaelian system would need a about 37-fold higher KM and require Vmax to increase about 4.5-fold (Fig. 2C). In general, the affinity of a Michaelian system required to match the linear moti is KM∗=KM(T/KM+KI/KMKI/KM−1) and its maximal velocity is Vmax∗=Vmax(KI/KMKI/KM−1) where the constants without stars are from the linear motif.

Competitive binding combined with a thresholding mechanism can lead to a linear rectifier. The linear motif described above does not intrinsically have a threshold. General mechanisms, such as positive feedback (Alon, 2007) or multisite modification (Gunawardena, 2005), can create a threshold. We therefore asked whether combining the linear motif with these thresholding motifs could create a linear rectifier.

We first considered whether positive feedback can convert a linear response to a linear rectifier. One simple realization of positive feedback in a general catalysis scheme can be achieved by making the enzyme complex increase the level of enzyme (Fig. 3A). In this case, the resulting reaction is a shifted Michaelian with a threshold that depends on the strength of the feedback and the enzyme affinity (Fig. 3A–C, Supplemental Experimental Procedures, section III). Combining competitive inhibition with conservation of the total levels of substrate and inhibitor shifts the threshold toward higher substrate concentrations and linearizes the response (Fig 3B,C, Supplemental Experimental Procedures, section III), thus resulting in a linear rectifier.

Figure 3.

Figure 3

Open in a new tab

Conversion of a linear response to a linear rectifier. (A) A competitive inhibition linearization motif that includes positive feedback. (B) Relationship between substrate and reaction rate with (red) and without (black) positive feedback and with (dashed) or without (solid) linearization. (C) The rate derivate shows how introducing competitive binding with substrate-inhibitor interplay leads to a response that isnot sensitive below a threshold and does not saturate above it. (D) Reaction scheme with auto-activation and competitive inhibition linearization motif. (E) Reaction rate and (F) its derivative with (dashed) and without (solid) competitive binding and with (red) and without (black) multi-site auto-acetylation.

Second, we tested whether a second thresholding mechanism, multisite auto-activation, could also convert a linear response to a linear rectifier (Fig. 3D). In the case of phosphorylation, experimental and theoretical studies (Ferrell, 1996; Gunawardena, 2005; Huang and Ferrell, 1996) have found that multisite phosphorylation in a signaling cascade can lead to a threshold behavior if multiple modifications are needed for the kinase's substrate to gain its activity. This situation is analogous to multisite acetylation. In the Box 1, we discuss the example of histone acetyl transferase auto-acetylation. In its simplest scenario, the ordered distributive case, auto-acetylation results in a shifted Michaelian response. The sharpness of the response depends on the number of auto-activation steps (Fig. 3E, Supplemental Experimental Procedures, section IV). Combining competitive inhibition with substrate-inhibitor conservation retains the threshold of the response but linearizes above the threshold (Fig. 3E, Supplemental Experimental Procedures, section IV). As in the case of the positive feedback, auto-acetylation converts a linear response into a linear rectifier.

Discussion

In this study we found that a relatively simple biological motif is capable of creating a response that is linear throughout the entire physiological range of substrate without saturating. The motif requires three features: 1) the reaction has a competitive inhibitor, 2) the total concentration of substrate and inhibitor is conserved, and 3) the affinity of the inhibitor and substrate for the enzyme is the same. This linear response can be combined with thresholding mechanism (e.g. positive feedback or multisite modification) to create a linear rectifier – a reaction that is linearly responsive over the full dynamic range when the substrate is above a threshold. Both rectification and linearization of a response have been described in other reaction schemes. For example, “suicide inhibition” approximates a rectifier (Elf et al., 2005; Levine et al., 2007; Mehta et al., 2008) and negative feedback with sequestration can result in a linearized response (Becskei, 2009; Nevozhay et al., 2009). Here we show that a common motif, competitive binding, can in certain conditions have the underappreciated function of linearizing the response over the full dynamic range. Additionally, we show how this motif, when combined with thresholding mechanism such as positive feedback or multisite auto-modification, can lead to linear rectifier.

We propose histone acetylation as a plausible biological system that could behave as a linear rectifier (Box 1). A number of physiological and mechanistic experiments suggest that the system might have a linear response and the mechanistic properties required of linear rectifiers. However, the experiments that would be required to convincingly show that this system behaves as a linear motif or a linear rectifier have not been performed. This is not because testing for linearization and linear rectifiers is inherently difficult, but likely because it requires different experiments than are standard (Box 1), for example, in vitro experiments where both the substrate and inhibitor are co-titrated. There are multiple labs that study SAGA that are well positioned for confirming or refuting this hypothesis with respect to histone acetylation.

Many biological reactions form products that have very similar structures to one of the reactants and therefore have the potential to serve as conserved competitive inhibitors. In the case of histone acetylation, this inhibition could result from any of the components of the reaction: the co-factor (e.g. SAM/SAH), a recycled product (e.g. NAD+/NAM), or even the substrate (e.g. a peptide/phosphopeptide). This inhibition may shape metabolic responses in a non-trivial ways (Escalante-Chong et al., 2015). While the relative ratio of substrate and product can change, the timescale of signaling is usually much quicker than changes in total metabolite concentration or protein, making mass conservation likely in many systems. In total, given the numerous ways that the necessary features for a and linear rectifier can be created, there are potentially numerous systems that may have these behaviors.

Linear responses and linear rectifiers have properties that can be useful in a number of biological processes. Linear responses allow for systems to be both proportionally responsive and have high total reaction rates without needing high enzyme levels. This could be a desirable property when the environment could vary over a wide range. For example, this type of linear response might have an advantage in the context of growth regulation: it allows a clear threshold that separates a non-growing state from a growing state while at the same time allows a sensitive growth adjustment in the growth state. Linear rectifiers also have very useful signal processing properties. The thresholding behavior naturally filters noise while the linear response maximizes information transfer; again this could be useful in a process like growth control where a cell might not want to commit to growth when nutrients are below a certain level. Additionally, linear rectifiers have been shown to be more versatile than sigmoidal functions in creating a wide range of output responses in neural networks (Nair and Hinton, 2010), suggesting that linear rectifiers might play useful roles as modules inside more complicated metazoan signaling networks. In total, our work highlights how linear rectifiers can be achieved with biologically simple and potentially common motifs.

Supplementary Material

1
2

Figure 4.

Figure 4

Open in a new tab

Histone acetylation as a linear rectifier: a hypothetical case. (A) Acetylation of histones involves the serial sequential formation of a ternary complex between SAGA, Ac-CoA, and histone. (B) CoA competes with Ac-CoA (top) and multisite auto-acetylation can provide switch-like character (bottom) to the formation of catalytically competent SAGA. Together, this provides a response that has both a sharp threshold (C) and a linear regime (D).

Acknowledgments

We would like to thank S. Boswell, C.M. DeGennaro, L. Cai, L. Shi and members of the Springer lab for valuable discussions. R. Milo provided a critical feedback on the manuscript. This study was supported by the National Science Foundation Grant 1349248 and the P50 GM107618 (M.S.), the Human Frontier Science Program (Y. S.), and award R01GM094314 from the National Institute of General Medical Sciences (B.P.T.).

Footnotes

Author contributions: Y.S., B.P.T and M.S. conceived and designed the study, Y.S and M.S developed the analytical and numerical framework and wrote the paper.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Alon U. Network motifs: theory and experimental approaches. Nature Reviews Genetics. 2007;8:450–461. doi: 10.1038/nrg2102. [DOI] [PubMed] [Google Scholar]
  2. Atkinson DE. Energy charge of the adenylate pool as a regulatory parameter. Interaction with feedback modifiers. Biochemistry. 1968;7:4030–4034. doi: 10.1021/bi00851a033. [DOI] [PubMed] [Google Scholar]
  3. Becskei A. Linearization through distortion: a new facet of negative feedback in signalling. Molecular systems biology. 2009;5:255. doi: 10.1038/msb.2009.14. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Berndsen CE, Denu JM. Catalysis and substrate selection by histone/protein lysine acetyltransferases. Curr Opin Struct Biol. 2008;18:682–689. doi: 10.1016/j.sbi.2008.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cai L, Sutter BM, Li B, Tu BP. Acetyl-CoA induces cell growth and proliferation by promoting the acetylation of histones at growth genes. Mol Cell. 2011;42:426–437. doi: 10.1016/j.molcel.2011.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chohnan S, Izawa H, Nishihara H, TAKAMURA Y. Changes in size of intracellular pools of coenzyme A and its thioesters in Escherichia coli K-12 cells to various carbon sources and stresses. Bioscience, biotechnology, and biochemistry. 1998;62:1122–1128. doi: 10.1271/bbb.62.1122. [DOI] [PubMed] [Google Scholar]
  7. Elf J, Paulsson J, Berg O, Ehrenberg M. Mesoscopic kinetics and its applications in protein synthesis. Systems Biology (Springer) 2005:95–18. [Google Scholar]
  8. Escalante-Chong R, Savir Y, Carroll SM, Ingraham JB, Wang J, Marx CJ, Springer M. Galactose metabolic genes in yeast respond to a ratio of galactose and glucose. Proceedings of the National Academy of Sciences of the United States of America. 2015;112:1636–1641. doi: 10.1073/pnas.1418058112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Fan J, Krautkramer KA, Feldman JL, Denu JM. Metabolic regulation of histone post-translational modifications. ACS chemical biology. 2015 doi: 10.1021/cb500846u. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Ferrell JE. Tripping the switch fantastic: how a protein kinase cascade can convert graded inputs into switch-like outputs. Trends in biochemical sciences. 1996;21:460–466. doi: 10.1016/s0968-0004(96)20026-x. [DOI] [PubMed] [Google Scholar]
  11. Fersht AR. Enzyme structure and mechanism. 2nd. New York: W.H.Freeman and Co.; 1985. 2 edn. [Google Scholar]
  12. Fersht AR. Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding. W. H. Freeman; 1998. [Google Scholar]
  13. Grant PA, Duggan L, Cote J, Roberts SM, Brownell JE, Candau R, Ohba R, Owen-Hughes T, Allis CD, Winston F, et al. Yeast Gcn5 functions in two multisubunit complexes to acetylate nucleosomal histones: characterization of an Ada complex and the SAGA (Spt/Ada) complex. Genes Dev. 1997;11:1640–1650. doi: 10.1101/gad.11.13.1640. [DOI] [PubMed] [Google Scholar]
  14. Guan KL, Xiong Y. Regulation of intermediary metabolism by protein acetylation. Trends Biochem Sci. 2011;36:108–116. doi: 10.1016/j.tibs.2010.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Gunawardena J. Multisite protein phosphorylation makes a good threshold but can be a poor switch. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:14617–14622. doi: 10.1073/pnas.0507322102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Haigis MC, Sinclair DA. Mammalian sirtuins: biological insights and disease relevance. Annu Rev Pathol. 2010;5:253–295. doi: 10.1146/annurev.pathol.4.110807.092250. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Huang CY, Ferrell JE. Ultrasensitivity in the mitogen-activated protein kinase cascade. Proceedings of the National Academy of Sciences. 1996;93:10078–10083. doi: 10.1073/pnas.93.19.10078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Keren L, Zackay O, Lotan-Pompan M, Barenholz U, Dekel E, Sasson V, Aidelberg G, Bren A, Zeevi D, Weinberger A, et al. Promoters maintain their relative activity levels under different growth conditions. Mol Syst Biol. 2013;9:701. doi: 10.1038/msb.2013.59. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Koutelou E, Hirsch CL, Dent SY. Multiple faces of the SAGA complex. Current opinion in cell biology. 2010;22:374–382. doi: 10.1016/j.ceb.2010.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Kuo MH, Brownell JE, Sobel RE, Ranalli TA, Cook RG, Edmondson DG, Roth SY, Allis CD. Transcription-linked acetylation by Gcn5p of histones H3 and H4 at specific lysines. Nature. 1996;383:269–272. doi: 10.1038/383269a0. [DOI] [PubMed] [Google Scholar]
  21. Langer MR, Fry CJ, Peterson CL, Denu JM. Modulating acetyl-CoA binding in the GCN5 family of histone acetyltransferases. J Biol Chem. 2002;277:27337–27344. doi: 10.1074/jbc.M203251200. [DOI] [PubMed] [Google Scholar]
  22. Lee JV, Carrer A, Shah S, Snyder NW, Wei S, Venneti S, Worth AJ, Yuan ZF, Lim HW, Liu S. Akt-dependent metabolic reprogramming regulates tumor cell histone acetylation. Cell metabolism. 2014;20:306–319. doi: 10.1016/j.cmet.2014.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Levine E, Zhang Z, Kuhlman T, Hwa T. Quantitative characteristics of gene regulation by small RNA. PLoS biology. 2007;5:e229. doi: 10.1371/journal.pbio.0050229. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Mehta P, Goyal S, Wingreen NS. A quantitative comparison of sRNA-based and protein- based gene regulation. Molecular systems biology. 2008;4:221. doi: 10.1038/msb.2008.58. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Morrish F. Myc-dependent mitochondrial generation of acetyl-CoA contributes to fatty acid biosynthesis and histone acetylation during cell cycle entry. J Biol Chem. 2010;285:36267–36274. doi: 10.1074/jbc.M110.141606. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Nair V, Hinton GE. Rectified linear units improve restricted boltzmann machines. Paper presented at: Proceedings of the 27th International Conference on Machine Learning (ICML-10) 2010 [Google Scholar]
  27. Nevozhay D, Adams RM, Murphy KF, Josić K, Balázsi G. Negative autoregulation linearizes the dose–response and suppresses the heterogeneity of gene expression. Proceedings of the National Academy of Sciences. 2009;106:5123–5128. doi: 10.1073/pnas.0809901106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Qian H. Cooperativity in cellular biochemical processes: noise-enhanced sensitivity, fluctuating enzyme, bistability with nonlinear feedback, and other mechanisms for sigmoidal responses. Annual review of biophysics. 2012;41:179–204. doi: 10.1146/annurev-biophys-050511-102240. [DOI] [PubMed] [Google Scholar]
  29. Santos SD, Ferrell JE. Systems biology: On the cell cycle and its switches. Nature. 2008;454:288–289. doi: 10.1038/454288a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Schwer B, Verdin E. Conserved metabolic regulatory functions of sirtuins. Cell Metab. 2008;7:104–112. doi: 10.1016/j.cmet.2007.11.006. [DOI] [PubMed] [Google Scholar]
  31. Takahashi H, McCaffery JM, Irizarry RA, Boeke JD. Nucleocytosolic acetyl-coenzyme A synthetase is required for histone acetylation and global transcription. Mol Cell. 2006;23:207–217. doi: 10.1016/j.molcel.2006.05.040. [DOI] [PubMed] [Google Scholar]
  32. Tanner KG, Langer MR, Kim Y, Denu JM. Kinetic mechanism of the histone acetyltransferase GCN5 from yeast. J Biol Chem. 2000;275:22048–22055. doi: 10.1074/jbc.M002893200. [DOI] [PubMed] [Google Scholar]
  33. Trievel RC, Rojas JR, Sterner DE, Venkataramani RN, Wang L, Zhou J, Allis CD, Berger SL, Marmorstein R. Crystal structure and mechanism of histone acetylation of the yeast GCN5 transcriptional coactivator. Proceedings of the National Academy of Sciences. 1999;96:8931–8936. doi: 10.1073/pnas.96.16.8931. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Wellen KE. ATP-citrate lyase links cellular metabolism to histone acetylation. Science. 2009;324:1076–1080. doi: 10.1126/science.1164097. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Wellen KE, Thompson CB. A two-way street: reciprocal regulation of metabolism and signalling. Nat Rev Mol Cell Biol. 2012;13:270–276. doi: 10.1038/nrm3305. [DOI] [PubMed] [Google Scholar]
  36. Yuan HX, Xiong Y, Guan KL. Nutrient sensing, metabolism, and cell growth control. Molecular cell. 2013;49:379–387. doi: 10.1016/j.molcel.2013.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Yuan H, Marmorstein R. Histone Acetyltransferases: Rising Ancient Counterparts to Protein Kinases. Biopolymers. 2013;99:98–111. doi: 10.1002/bip.22128. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1
NIHMS723884-supplement-1.docx (201.5KB, docx)
2
NIHMS723884-supplement-2.pdf (589.5KB, pdf)

RESOURCES