Bayesian evaluation of a physiologically-based pharmacokinetic (PBPK) model of long-term kinetics of metal nanoparticles in rats

Abstract

Biomathematical modeling quantitatively describes the disposition of metal nanoparticles in lungs and other organs of rats. In a preliminary model, adjustable parameters were calibrated to each of three data sets using a deterministic approach, with optimal values varying among the different data sets. In the current effort, Bayesian population analysis using Markov chain Monte Carlo (MCMC) simulation was used to recalibrate the model while improving assessments of parameter variability and uncertainty. The previously-developed model structure and some physiological parameter values were modified to improve physiological realism. The data from one of the three previously-identified studies and from two other studies were used for model calibration. The data from the one study that adequately characterized mass balance were used to generate parameter distributions. When data from a second study of the same nanomaterial (iridium) were added, the level of agreement was still acceptable. Addition of another data set (for silver nanoparticles) led to substantially lower precision in parameter estimates and large discrepancies between the model predictions and experimental data for silver nanoparticles. Additional toxicokinetic data are needed to further evaluate the model structure and performance and to reduce uncertainty in the kinetic processes governing in vivo disposition of metal nanoparticles.

1. Introduction

The use of nanoparticles in commerce has expanded rapidly, with an increase from 803 products in 2008 to 1628 products as of October 2013 in a nanotechnology consumer products database (Project on Emerging Nanotechnologies, 2013). As consumer exposure increases, concerns about toxicity have also been raised, based on effects identified in laboratory animals. As in other areas of chemical toxicology, the development of physiologically based pharmacokinetic (PBPK) dosimetry models has the potential to improve understanding of concerns identified in rodents and the potential relevance to humans, based on comparative internal dosimetry. The fate of nanoparticles is an active area of research.

A biomathematical model was previously developed for the disposition of nanoparticles in rats (MacCalman et al., 2009; MacCalman and Tran, 2009) based on calibration to three data sets (Semmler et al., 2004; Takenaka et al., 2001; Fabian et al., 2008). In the preliminary model, adjustable parameters were calibrated for each data set using least squares methods, with varying values for a given parameter obtained for the different data sets. Some of these parameter values differed radically among data sets. For example, the estimates of fractional translocation from the liver capillaries to the venous blood ( ${\mathrm{\lambda }}_3^2$) were 0.9786 (Semmler), 0.5 (Takenaka) and 0.0001 (Fabian). As these data sets describe the disposition of three different types of nanoparticles, it is unclear whether the parameter differences were due to material-specific differences in disposition, inadequate data to unambiguously identify model parameter values, or an inappropriate model structure.

In the current model, Bayesian population analysis using Markov chain Monte Carlo (MCMC) simulation was performed to provide estimates of the parameter distributions (rather than point estimates), which also allowed for subsequent uncertainty and variability analysis. Bayesian population analysis is an appropriate method for calibrating the rat nanoparticle PBPK model (Bernillon and Bois, 2000; Lunn et al., 2009; Jonsson and Johanson, 2003; Hack, 2006; Hack et al., 2006; Péry et al., 2009). Using this technique, the model parameters were calibrated to one or more data sets simultaneously. Data from one of the three previously-identified studies were used; additional data useful for model calibration were extracted from one of these previously identified studies (described in more detail in the “Methods” section) and from a newly published study of nanoparticle toxicokinetics. The previously-developed model structure was modified and some physiological parameter values modified to improve physiological realism or simplify the model structure, based on published PBPK modeling of nanoparticles in rats and humans.

A sensitivity analysis of the adjustable model parameters was conducted to assess the impact of uncertainty/variability in model parameter values to predictions of output, using the population posterior distribution as inputs for Monte Carlo simulations.

2. Materials and methods

2.1. Key data sets

The preliminary rat PBPK model for nanoparticles (MacCalman et al., 2009; MacCalman and Tran, 2009) was based on calibration to three data sets (Semmler et al., 2004; Takenaka et al., 2001; Fabian et al., 2008). (Key characteristics of these studies and others used in the model calibration are summarized in Table 1). For the preliminary model, the iridium data initially reported in Semmler et al. (2004) (with additional detail reported by Semmler-Behnke et al., 2007) constituted the key data set for understanding rat whole-body disposition of nanoparticles due to the extended follow up time (longer than Takenaka et al., 2001) and the measurement of nanoparticles in most of the tissue regions of interest (particles were not observed in the brain, olfactory, alveolar, and upper airway regions in the i.v. study by Fabian et al., 2008; which was also reported in van Ravenzwaay et al., 2009).

Table 1.

Summary of key studies used in rat nanoparticle PBPK model calibration and testing.

Study	Dosing information	Particle characteristics	Study duration	Available dosimetry information	Animal characteristics
Semmler et al. (2004); Semmler-Behnke et al. (2007) a,b,c	Controlled ventilation via endotracheal intubation of the upper trachea for 60 –100 min, 0.7 mg/m3 (single exposure)	192Ir, count median diameter (CMD) 15–20 nm	168 days	Lung, liver, spleen, and brain burdens, fecal excretion rate	Young adult male Wistar-Kyoto rats
Kreyling et al. (2002, 2009) b	Controlled ventilation via endotracheal intubation of the upper trachea for 60 min, 0.2 mg/m3 (single exposure)	192Ir, CMD 15 nm, geometric standard deviation 1.6	7 days	Lung, liver, kidney, heart, spleen, brain, feces (cumulative), blood, carcass (skeleton and muscle)	Young adult male Wistar-Kyoto rats
Lankveld et al. (2010) b	Five daily iv injections of 23.8 μg	Ag, 20.3 ± 1.9 nm	17 days	Blood, lung, liver, spleen, brain, heart, kidney, testes burdens	6 week-old male Wistar rats
Fabian et al. (2008); van Ravenzwaay et al. (2009) a,b	Single iv injection 5 mg/kg	TiO2 20–30 nm	28 days	Lung, liver, spleen and kidney concentration	Male Wistar rats (200–300 g)

^aData used in earlier model (MacCalman and Tran, 2009).

^bData used in current model development and testing.

^cFeces data and detailed lung time course data from Semmler et al. (2004) (Figs. 3 and 4) were not previously used by MacCalman et al. (2009).

Based on literature searches, additional data sets that could potentially be used to further the development of this model were identified. The studies under consideration were limited to a narrow range of particles sizes (15–30 nm) (Table 1) due to findings that particles of approximately 20 nm diameter behave differently in vivo than larger (80–100 nm) particles (Sarlo et al., 2009; Lankveld et al., 2010). Furthermore, nanoparticles between 6 nm and 34 nm are expected to result in the greatest internal tissue exposure, relative to other particle sizes (Choi et al., 2010). Additional desirable characteristics for candidate studies were the availability of time course data (vs. disposition at a single sampling time) and potential for mass balance (extensive tissue sampling and/or excretion data). Studies with a duration of 7 days or more, and the use of non-functionalized metal particles were preferred due to greater comparability to the key data (Semmler et al., 2004). Potentially applicable new data sets included studies by Zhu et al. (2009) (ferric oxide), Lankveld et al. (2010) (silver), Dziendzikowska et al. (2012) (silver), and Shinohara et al. (2014) (titanium dioxide); the data of Sarlo et al. (2009) could not be used because nanoparticle recovery for most tissues was reported in semi-quantitative form (i.e., 0.005–0.05% of dose). In addition, another study of iridium nanoparticles from the same laboratory as the Semmler et al. (2004) study (Kreyling et al., 2002, 2009) was identified and the additional data deemed useful for the development of this model. The data of Zhu et al. (2009) were not used due to uncertainty regarding the distribution of intratracheally instilled particles within the airway. A portion of the study of Lankveld et al. (2010) was conducted using particles similar in size to the previously identified data, the study duration was similar, and the data were provided in a convenient tabular form, so these data were also used in model development (Table 1). The Dziendzikowska et al. (2012) concentration data were reported in terms of dry weight of tissue or feces; conversion factors were not provided, so this data set could not readily be used for model development. In the Shinohara et al. (2014) study, titanium dioxide was measured as titanium metal (Ti); since Ti in excreta were not elevated above the substantial levels in controls, mass balance could not be adequately characterized.

The data of Semmler et al. (2004), reported in graphical form, were digitized. Whole body retention and fractional excretion rate data were used to compute cumulative fecal excretion of nano-particles (not used in the preliminary model) and fractional retention in the lung (normalized to retention on day 3) was converted to absolute amounts.

The data for the study of Takenaka et al. (2001) were reported in tabular form. We were not able to successfully simulate this scenario, due to simulation errors (negative amounts of mass predicted, most frequently in smaller tissues) encountered when attempting to simulate this study using the MCSim software. Furthermore, this study used a different animal model than other studies under consideration (female F344 rats vs. male Wistar rats), so solutions to the simulation difficulties were not pursued and this data set was not used in the current evaluation.

The data of Lankveld et al. (2010) were reported both in graphical form as concentrations, and in tabular form as whole-organ values. The whole organ values were used, with the exception that the blood values were multiplied by 1/3 to estimate the amount of particles present in the venous blood only, based on rat anatomy and the model structure, which separates venous, arterial, and capillary blood.

The data of Fabian et al. (2008) were reported as tissue concentrations of nanoparticles. These concentrations were scaled to whole-organ values using average organ masses provided in the same paper. On Day 1, the sum of these scaled amounts (1.37 mg) slightly exceeded the administered dose (1.25 mg). To avoid mass balance issues associated with this discrepancy, the amounts of nanoparticles in all tissues on day 1 were adjusted such that the total body burden equaled the administered dose.

2.2. Model structure

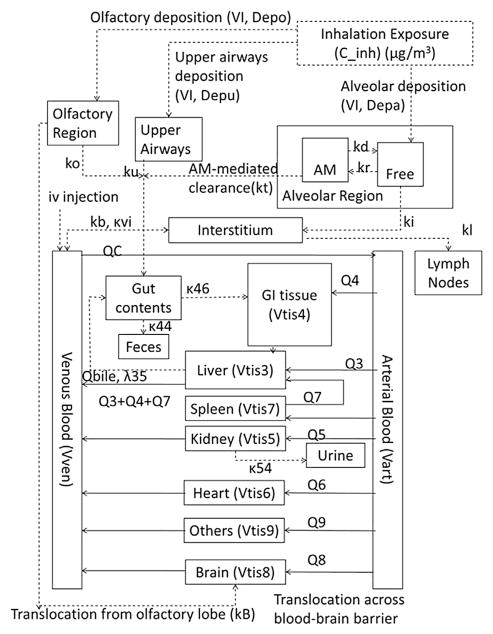
The model structure (Fig. 1) was a revision of the structure proposed by MacCalman and co-workers (MacCalman et al., 2009; MacCalman and Tran, 2009); the MacCalman et al. PBPK model was an extension of earlier models describing the retention and clearance of particles in the lung (Tran et al., 2002; Tran et al., 2001). The multi-compartmental structure (i.e., “splitting” rather. than “lumping”) was dictated by consideration of the data available and physiological processes of interest. For example, the availability of particle concentration data for a number of distinct tissues that are sometimes lumped in PBPK models (e.g., brain, heart, spleen) meant that these tissues could be considered separately. Physiological processes of interest included a realistic representation of arterial plus portal flow to the liver and potential enterohepatic recirculation. Revisions were made to improve the physiological realism of the extrarespiratory portions of the model. Briefly, the model describes each non-respiratory organ as consisting of tissue and tissue capillaries (liver tissue shown in Fig. 2; other tissues have the same subcompartments, but no biliary excretion). Arterial blood carrying nanoparticles enters the tissue capillaries, and nanoparticles diffuse into the tissue. Nanoparticles within the tissue can either be quasi-irreversibly sequestered or diffuse back into the tissue capillaries, from which they may exit in the venous blood. As implemented for this effort, parameter values for diffusion are set such that there is no diffusion limitation. In the revised model structure, the venous blood of the splanchnic tissues (spleen and gastrointestinal tract [GI]) is delivered to the liver capillaries rather than the venous blood, as in the MacCalman et al. model in order to be more physiologically realistic. The GI tract includes a “gut contents” subcompartment in addition to the tissue and capillaries. Nanoparticles may reach the gut contents via gavage; direct oral ingestion; clearance from the olfactory region, upper airways, or alveolar region; or biliary elimination from the liver. The nano-particles in the gut contents may be absorbed into the GI capillaries (and distributed systemically from there) or excreted from the body in the feces. The biliary elimination of nanoparticles from the liver is assumed to occur via partitioning from liver tissue to bile and transport of the bile into the gut contents.

Fig. 1.

Structure of rat nanoparticle PBPK model.

Fig. 2.

Details of liver compartment structure and processes.

The “bound” material in the organs is eliminated from the “sequestered” subcompartment into the feces. This mathematical description is a simplistic description of undetermined processes. The nature of the bound material is unknown, but may be sequestered, phagocytized material in immune cells (Li et al., 2014) or strongly bound to protein. Attempts to describe the entire nanoparticle content of systemic tissues as freely exchangeable with blood or limited by diffusion only were unsuccessful. However, to simulate the long-term time course of nanoparticles in systemic tissues, some form of clearance must be included, although this pathway appears to provide a relatively small contribution to total clearance. It was assumed that, once sequestered, the nanoparticles would not again become “free” particles available for uptake from blood or GI contents. Therefore their tissue clearance was described as direct elimination via feces. Simplified descriptions of elimination pathways for excretion via urinary, fecal, and/or exhaled breath pathways (e.g., Hays et al., 2000; Louisse et al., 2010; Kim et al., 1994; Thrall et al., 2000) are common in PBPK modeling, due to limited data availability for parameterizing clearance (Clark et al., 2004).

2.3. Model parameter values

Anatomical and physiological parameters for a “standard” 250 g rat were generally taken from the preliminary model (MacCalman et al., 2009; MacCalman and Tran, 2009) and are reported in Table 2. The computation of the “other tissues” volume was corrected so that it was calculated by mass balance. Bile flow from the liver to the gut contents was added at a rate of 20 ml/day (RIVM, 2010) so that transfer of nanoparticles from the liver to the gut contents could be calculated based on bile:liver tissue partitioning and bile flow.

Table 2.

Fixed model parameters.

	Value
Anatomical parameters (MacCalman and Tran, 2009; MacCalman et al., 2009)
Volume inhaled, L/min (VI)	0.18 (default)
Liver tissue volume, ml (Vtis3)	10.3
Liver capillary blood, fraction of liver tissue volume (Vcap3C)	0.06
GI tissue volume, ml (Vtis4)	6.0
GI capillary blood, fraction of GI tissue volume (Vcap4C)	0.0265
Kidney tissue volume, ml (Vtis5)	1.2
Kidney capillary blood, fraction of kidney tissue volume (Vcap5C)	0.13
Heart tissue volume, ml (Vtis6)	1.2
Heart capillary blood, fraction of heart tissue volume (Vcap6C)	0.1
Spleen tissue volume, ml (Vtis7)	0.6
Spleen capillary blood, fraction of spleen tissue volume (Vcap8C)	0.1
Brain tissue volume, ml (Vtis8)	1.2
Brain capillary blood, fraction of brain tissue volume (Vcap8C)	0.033
Venous plasma volume (Vven)	5.6
Arterial plasma volume (Vart)	11.3
Other tissues capillary blood, fraction of other tissues volume (Vcap9C)	0.1
Cardiac output, ml/day (QC)	1,201,200
Blood flow to liver (hepatic artery only), ml/day (Q3)	2523
Blood flow to GI tissue, ml/day (Q4)	16,704
Blood flow to kidneys, ml/day (Q5)	13,248
Blood flow to heart tissue, ml/day (Q6)	5616
Blood flow to the spleen, ml/day (Q7)	864
Blood flow to the brain, ml/day (Q8)	1872
Bile output, ml/day (Qbile) (RIVM, 2010)	20
Fecal elimination rate, day−1 (population mean) (Enck et al., 1989)	8.2
Alveolar region parameters (Tran et al., 2002)
Macrophage clearance rate, per day (kt)	0.015
Macrophage phagocytosis rate, per day (kr)	4.0
Macrophage death rate, per day (kd)	0.033
Interstitialization rate, per day (ki)	3.5

The parameters controlling the diffusion of nanoparticles between capillary blood and tissues were set equal to 1 so that the diffusion limitation would effectively be removed. This change was based on the findings of Péry et al. (2009) that diffusion limitations were not necessary to adequately describe the kinetics of ^99mtechnetium-labeled carbon nanoparticles in humans and because in the MacCalman and Tran (2009) optimization to the Semmler et al. (2004) data, most of the values for fractional translocation from capillaries to tissues were similar to 1 (spleen and kidney were exceptions to this finding).

Particle size-specific estimates of airway deposition in the various regions for which calibration data are available were calculated for both normal and endotracheal inhalation using the MPPD2 model (v. 2.11, Applied Research Associates, Albuquerque, NM). Fractional deposition estimates for endotracheal inhalation of iridium were determined using MPPD2 based on the particle and exposure characteristics described in Semmler et al. (2004)/Semmler-Behnke et al. (2007) and Kreyling et al. (2002, 2009). Calculated deposition fractions were 0.2371 for the upper airways (conducting airways, in MPPD) and 0.4203 for the alveolar region for the Semmler study and 0.2657 for the upper airways and 0.4461 for the alveolar region for the Kreyling study. Similar calculations were done to estimate deposition for the Takenaka et al. (2001) data, but are not described here because these data were not used.

In the preliminary model, the fractions of the nanoparticles cleared from the airways into the gut contents were allowed to be adjustable (optimized) parameters. In the current model, 100% transfer of cleared nanoparticles into the gut contents was assumed, an approximation that is likely to be accurate for airway clearance in rats (because it is unlikely that coughing or sneezing would be significant in rats).

In the preliminary model, the rate constants for processes in the alveolar region (particle uptake, release, and clearance by macrophages and the particle interstitialization rate) were taken from an earlier model for silica (Tran et al., 2002; Tran et al., 2001). For the current effort, this assumption was initially relaxed, and attempts were made to estimate these parameter values for nanoparticles. However, it was found that these parameters could not be unambiguously identified from the existing data (i.e., the parameter values did not converge when multiple chains of simulations were completed), so the values used in the preliminary model were used for further analyses.

Urinary elimination of nanoparticles was included in the preliminary model. Lankveld et al. (2010) found that multiple routes of nanoparticle clearance (i.e., urinary and fecal) could not be clearly distinguished in their model (based only on tissue concentrations from their own data set; they did not measure nanoparticle mass in excreta) and Choi et al. (2007) determined that urinary elimination is unlikely for nanoparticles larger than 5.5 nm. Therefore, the urinary clearance in the model was effectively “turned off” by setting the kidney clearance rate (κ54) to zero. In the human nanoparticle PBPK model developed by Péry et al. (2009), the same value was used for all tissue:plasma partition coefficients. Based on their results, the possibility of making all tissue:plasma partition coefficients equal was tested, but did not improve model fits for these data (not shown), so tissue-specific tissue:plasma partition coefficients were retained in the model.

In the preliminary model, sequestration of nanoparticles in tissue was assumed to be irreversible. Because shorter term models (e.g., Péry et al., 2009) were able to simulate nanoparticle tissue kinetics with partition coefficients only (no binding), it was hypothesized that the longer-term declines in tissue nanoparticle levels were due to slow clearance of sequestered material by un-identified processes (possibly via trafficking of phagocytes, or protein turnover). This clearance process was assumed to be governed by first-order kinetics.

The fecal elimination rate was a fully adjustable parameter in earlier versions of the revised model. Because unrealistically high rates for this parameter were estimated in the optimization, the population mean was fixed at 8.2/day, based on the half time for the passage of material from the stomach to the cecum (Enck et al., 1989). The absorption rate from the GI tract to the portal vein blood was allowed to vary for individual studies, within the constraints of the population parameters.

2.4. Model implementation/model calibration

The preliminary rat PBPK model was previously developed by one of the coauthors (Laura MacCalman) in Matlab. The equations were modified per the model structural changes noted above and converted into a format appropriate for MCSim (version 5.3.1). The model text file was converted into a C file using the preprocessor “mod” and was subsequently compiled into the executable program.

The Bayesian approach relies on both prior knowledge, as described in initial parameter distributions (shapes and ranges of values), and information that (if analyzed appropriately) can be deduced from the measured data (Gelman et al., 1996; Bernillon and Bois, 2000). Using a sampling algorithm such as the Metropolis Hastings algorithm, proposed distributions are tested and narrowed to identify distributions that produce the best agreement between the model and the data. In these stochastic simulations, the selection of subsequent random values is influenced by the current parameter values (Bois and Maszle, 2009), with the goal that, on the whole, agreement improves as the simulation progresses. Each chain should be inspected to verify that “equilibrium” has been achieved, and multiple chains with different starting values (seed values) should be executed to test for consistency among chains.

To facilitate the Bayesian MCMC analysis, a statistical model was generated to implement a Bayesian approach to modeling the data. For the statistical model, the parameters to be sampled and optimized were transformed so that the parameters would be described by distributions of the means of the natural logarithm of the parameter value (M_lnParam) and the associated variances (V_lnParam). The variance of the measurement error for the measured covariates was also specified (Ve_Meas). The distribution shapes were modeled after those used in development of the trichloroethylene PBPK model (U.S. EPA, 2009; Evans et al., 2009; Chiu et al., 2009), and reflect to the degree possible the known, empirical distributions of values in variable human populations. The distributions for M_lnParam were generally truncated normal distributions, while the V_lnParam values were assumed to follow an inverse gamma distribution (see “Results”, Table 3, and Supplementary Materials, Tables S-1 and S-2). The Ve_Meas distributions were characterized as log uniform. Highly uninformative prior parameter distributions were used to avoid bias, so that the posteriors were determined by the data alone.

Table 3.

Statistical model parameters for disposition of metal nanoparticles in rats (Bayesian analysis of Semmler et al., 2004/Semmler-Behnke et al., 2007 and Kreyling et al., 2002, 2009).

Data description: all parameters assumed to have lognormal distributions
Measurement	Geometric mean	Variance
AAlvTot (amount in alveolar region, free or in macrophages)	AAlvTot (prediction)	Ve_AAlvTot
AInter (amount in interstitial lung tissue)	AInter (prediction)	Ve_AInter
ALymph (amount in lung-associated lymph nodes [LANL])	ALymph (prediction)	Ve_ALymph
ALungTot (amount in upper airways, alveolar region, interstitial tissue, and LANL)	ALungTot (prediction)	Ve_ALungTot
ALiverTot (amount in liver)	ALiverTot (prediction)	Ve_ALiverTot
AKidTot (amount in kidneys)	AKidTot (prediction)	Ve_AKidTot
AHeartTot (amount in heart)	AHeartTot (prediction)	Ve_AHeartTot
ASplTot (amount in spleen)	ASplTot (prediction)	Ve_ASplTot
ABrTot (amount in brain)	ABrTot (prediction)	Ve_ABrTot
AOthTot (amount in other tissues)	AOthTot (prediction)	Ve_AOthTot
AFeces (cumulative amount excreted in feces)	AFeces (prediction)	Ve_AFeces
CVen (concentration in venous blood)	CVen (prediction)	Ve_CVen

Posterior error distributions: log uniform distribution, prior range of 0.01 (minimum) to 3.3 (maximum)
Measurement	Semmler posterior			Kreyling posterior
	Mean	Avg. variance	R	Mean	Avg. variance	R
Ve_AAlvTot	0.704	0.655	1.0	0.733	0.643	1.0
Ve_AInter	0.772	0.673	1.0	0.692	0.658	1.0
Ve_ALymph	0.746	0.696	1.0	0.776	0.712	1.0
Ve_ALungTot	0.0474	3.4 × 10−4	1.0	0.0422	0.00425	1.0
Ve_ALiverTot	1.32	0.552	1.0	0.499	0.372	1.0
Ve_AKidTot	0.972	0.444	1.0	0.730	0.669	1.0
Ve_AHeartTot	0.699	0.694	1.0	0.672	0.638	1.0
Ve_ASplTot	1.59	0.512	1.0	0.567	0.531	1.0
Ve_ABrTot	0.778	0.395	1.0	0.551	0.530	1.0
Ve_AOthTot	0.681	0.699	1.0	0.526	0.518	1.0
Ve_AFeces	0.0115	2.7 × 10−6	1.0	0.0192	1.5 × 10−4	1.0
Ve_CVen	0.750	0.661	1.0	2.07	0.496	1.0

Model parameters
Partition coefficients	Distribution: truncated normal; mean: M_variable, prior minimum: −5, prior maximum: 5, prior variance: V_variable
Variable	Semmler posterior			Kreyling posterior
	Mean	Avg. variance	R	Mean	Avg. variance	R
lnλ35 (bile:liver partition coefficient [PC])	0.547	2.84	1.1	0.594	2.97	1.1
lnλ31 (plasma:liver PC)	1.48	0.695	1.1	1.39	0.655	1.1
lnλ41 (plasma:GI tissue PC)	0.705	1.71	1.0	0.680	1.69	1.0
lnλ51 (plasma:kidney PC)	−0.530	0.773	1.1	−0.163	0.788	1.1
lnλ61 (plasma:heart PC)	−0.239	1.46	1.0	−0.311	1.09	1.1
lnλ71 (plasma:spleen PC)	−1.00	0.708	1.0	−0.887	0.600	1.0
lnλ81 (plasma:brain PC)	0.287	0.906	1.0	0.349	0.867	1.0
lnλ91 (plasma:other tissue PC)	1.89	0.770	1.4	1.84	0.739	1.4

Tissue sequestration, clearance of sequestered material, upper airway translocation (day−1)	Distribution: truncated normal; mean: M_variable, prior minimum: −10, prior maximum: 10, prior variance: V_variable
Variable	Semmler posterior			Kreyling posterior
	Mean	Avg. variance	R	Mean	Avg. variance	R
lnκ33 (liver sequestration rate)	−1.43	3.71	1.3	−1.24	3.65	1.3
lnκ43 (GI tissue sequestration rate)	−2.62	6.55	1.0	−2.61	6.65	1.0
lnκ53 (kidney sequestration rate)	−0.320	5.14	1.4	−0.387	5.12	1.4
lnκ63 (heart sequestration rate)	−0.383	8.73	1.3	−0.378	9.03	1.3
lnκ73 (spleen sequestration rate)	−2.15	4.22	1.1	−2.10	4.24	1.1
lnκ83 (brain sequestration rate)	0.551	4.50	1.0	0.506	4.59	1.0
lnκ93 (other tissue sequestration rate)	−1.72	4.38	1.5	−1.76	4.35	1.5
lnκ334 (clearance of sequestered material in liver)	−4.73	2.21	1.1	−4.64	2.55	1.1
lnκ434 (clearance of sequestered material in GI tissue)	−1.10	12.7	1.0	−1.11	12.7	1.0
lnκ534 (clearance of sequestered material in kidney)	−0.303	9.99	1.0	−0.219	10.3	1.0
lnκ634 (clearance of sequestered material in heart)	2.23	6.46	1.6	2.22	6.53	1.6
lnκ734 (clearance of sequestered material in spleen)	−5.05	3.03	1.0	−4.97	3.17	1.0
lnκ834 (clearance of sequestered material in brain)	−1.21	2.54	1.1	−1.18	2.90	1.1
lnκ934 (clearance of sequestered material in other tissue)	1.09	13.6	1.1	1.58	0.364	1.2
lnkb (translocation from interstitium to blood)	−1.25	0.360	1.1	−1.18	0.283	1.1
lnku (clearance from upper airways to GI tract)	4.70	3.61	1.0	4.70	3.61	1.0
lnkl (translocation from interstitium to LANL)	−2.61	0.213	1.0	−2.66	0.665	1.0
lnκvi (translocation from blood to interstitium)	−1.90	7.84	1.2	−1.94	7.75	1.2

Tissue sequestration, clearance of sequestered material, upper airway translocation (day−1)	Distribution: truncated normal; mean: M_variable, prior minimum: −10, prior maximum: 10, prior variance: V_variable
Variables with uniform distribution	Posterior
	Prior min.	Prior max.	Group	Mean	Avg. variance	R
lnκ46 (GI absorption rate, day−1)	−10	10	Semmler	0.369	5.03	1.3
			Kreyling	0.598	4.71	1.3
lnκ44 (fecal elimination rate, day−1)		2.11	Semmler	1.40	0.305	1.1
			Kreyling	1.58	0.364	1.2

Population level parameters
Partition coefficients (dimensionless), tissue sequestration (day−1), upper airway translocation (day−1)	Means: M_variable, distribution: truncated normal, prior mean: 0, prior minimum: −5 (partition coefficients) or−10 (rate parameters), prior maximum: 5 (partition coefficients) or 10 (rate parameters), prior variance: 1.7 (partition coefficients) or 4 (rate parameters)
	Variances: V_variable, distribution: Inverse gamma, prior variance shape: 2.25, prior variance scale: 0.3125
Variable	Posterior mean			Posterior Variance
	Mean	Avg. Variance	R	Mean	Avg. Variance	R
lnλ35	0.547	2.61	1.1	0.268	0.0744	1.0
lnλ31	1.39	0.642	1.1	0.245	0.0666	1.0
lnλ41	0.674	1.54	1.0	0.261	0.0726	1.0
lnλ51	−0.349	0.762	1.1	0.267	0.0700	1.0
lnλ61	−0.261	1.15	1.0	0.272	0.0881	1.0
lnλ71	−0.913	0.633	1.0	0.233	0.0639	1.0
lnλ81	0.309	0.852	1.0	0.241	0.0447	1.0
lnλ91	1.78	0.744	1.4	0.266	0.104	1.0
lnκ33	−1.31	3.63	1.3	0.263	0.100	1.0
lnκ43	−2.59	6.44	1.0	0.278	0.115	1.0
lnκ53	−0.352	5.03	1.4	0.264	0.115	1.0
lnκ63	−0.379	8.82	1.3	0.260	0.0610	1.0
lnκ73	−2.12	4.19	1.1	0.260	0.0587	1.0
lnκ83	0.529	4.49	1.0	0.263	0.118	1.0
lnκ93	−1.73	4.18	1.6	0.287	0.154	1.0
lnκ334	−4.64	2.34	1.1	0.296	0.113	1.0
lnκ434	−1.12	12.5	1.0	0.296	0.264	1.0
lnκ534	−0.260	10.1	1.0	0.273	0.0788	1.0
lnκ634	2.21	6.29	1.6	0.263	0.116	1.0
lnκ734	−4.96	3.06	1.0	0.277	0.119	1.0
lnκ834	−1.19	2.59	1.1	0.316	0.234	1.0
lnκ934	1.07	13.3	1.1	0.269	0.103	1.0
Lnkb	0.203	0.0371	1.0	−1.22	0.388	1.1
Lnku	0.262	0.0711	1.0	4.67	3.60	1.0
Lnkl	0.272	0.115	1.0	−2.60	0.446	1.0
Lnkκvi	0.284	0.129	1.0	−1.90	7.56	1.2
lnκ46 (uniform distribution)	0.521	6.28	1.2	3.78	29.7	1.0
lnκ44				4.08	11.3	1.1

Multiple chains of MCMC simulations (10,000 iterations per chain, results reported for every fifth iteration) were produced by using different seed values for the MCMC algorithm. Occasionally chains produced fatal errors; when this happened, such events typically occurred early in the chain and the results were discarded. This problem was encountered more frequently when multiple data sets were considered simultaneously. Preliminary analyses of the chains consisted of evaluating the progress of the chain by viewing the changes in the log likelihood function (LLF) as the iterations progressed (a larger LLF indicates better agreement between the model predictions and experimental data). This inspection ensured that the chain was sufficiently stable that the last 5000 iterations would yield an acceptable set of “optimal” parameter values from the chain. An example of the stabilization of the LLF output is provided in the Supplementary Materials (Fig. S-1). When three acceptable chains had been produced, an initial assessment of the consistency of the results was made by comparing the average of the LLFs. Typically, if there appeared to be disparate results, additional chains were produced (up to a total of six chains) and the three with the highest LLFs were used in subsequent analyses (e.g., convergence, posterior parameter estimates).

2.5. Evaluation of model output

2.5.1. Convergence of model parameter estimates

The convergence (similarity) of results among chains was analyzed by comparing the means and variances of the parameter estimates through the use of the “R” statistic, where R = 1 indicates perfect convergence (Gelman and Rubin, 1992; Gelman, 1996; Gelman et al., 1996). Gelman et al. (1996) indicated that PBPK model parameter value estimates demonstrated acceptable convergence if √R < 1.2 (R < 1.44). In the MCMC output summaries (Table 3, Tables S-1, and S-2), the posterior variances (in the column to the left of the “R” value) reflect the average variance in posterior values the three chains used for a particular data set (or group of data sets). That is, for a series in which the first three chains were deemed to adequately converge, the reported posterior variance is 1/3rd of the sum of variance of posterior values from chain 1, chain 2, and chain 3. These variances among output values of each chain should not be confused with the population parameter variances, the posterior mean value for V_lnParam.

2.5.2. Model sensitivity analyses

Key (sensitive) adjustable model parameters were identified by using the posterior parameter values derived from the MCMC analysis of the Semmler et al. (2004)/Semmler-Behnke et al. (2007) and Kreyling et al. (2002, 2009) data. The model was implemented in acslX (version 3.0.2.1, AEgis Technologies, Huntsville, AL, USA) using the Monte Carlo analysis utility to generate 1000 model iterations. The population means and variances noted in bold in Table 3, Tables S-1, and S-2 and the prior constraints (minimum and maximum values) were used to generate the parameter values for the Monte Carlo simulations. Sensitivity was determined at a limited number of times that corresponded to the times at which experimental data had been collected. Because non-normal distributions were used, inputs and outputs were converted to ranks (i.e., the lowest value is assigned a rank of 1000, whereas the highest value is assigned a rank of 1) prior to correlation analysis (Decisioneering, 1996). The correlation between ranks was determined using Microsoft Excel (“CORREL” function). The contribution of a given parameter to the variance of the forecast value is determined by squaring the correlation coefficients of the input parameters and normalizing each input to a total contribution of 100 percent (Decisioneering, 1996).

2.5.3. Visualization of output

The forecast values from the Monte Carlo simulations were compared to the experimental data using plots generated in Microsoft Excel. Time course simulations of measurements of interest were extracted for the median output of the population simulation and the 16th and 84th percentile values. For normally distributed outputs, the 16th and 84th percentile values approximate values ± one standard deviation from the mean.

2.5.4. Quantification of extent of agreement between model predictions and experimental data

For each experimental data point, the agreement between the model prediction and the experimental value (discrepancy index) was computed as the maximum of the predicted value/experimental value or experimental value/predicted value. In the case of perfect agreement between the model and the data, the discrepancy index would be 1. Geometric mean discrepancy indices were computed to aggregate the discrepancy indices for tissues/excreta over time and for all times and matrices evaluated for a given study. The agreement between the model and data was generally deemed acceptable if, on average, the difference between the model predictions and the mean of the experimental data is not more than a factor of two (International Programme on Chemical Safety [IPCS], 2010).

3. Results

The current model calibration was based mainly on data from three studies, including the Semmler study (Semmler et al., 2004; Semmler-Behnke et al., 2007) that was used in the earlier model (MacCalman and Tran, 2009). The Semmler study was the only study with sufficient detail to adequately characterize the mass balance of inhaled iridium particles. Data from two additional studies were added in a stepwise manner in the current model: a second study of iridium particles (Kreyling et al., 2002, 2009), and a study of silver nanoparticles (Lankveld et al., 2010). Alteration in the agreement between the model predictions and the data was assessed as data sets were added.

Bayesian MCMC analyses were successfully completed for the Semmler data alone (Semmler et al., 2004; Semmler-Behnke et al., 2007) (“S analysis”); the Semmler data plus Kreyling data (Kreyling et al., 2002, 2009) (“SK analysis”), and the Semmler data, Kreyling data, and Lankveld data (Lankveld et al., 2010) (“SKL analysis”). A fourth study (Fabian et al., 2008; van Ravenzwaay et al., 2009) of titanium dioxide nanoparticles, which was also used in the preliminary model, was evaluated in the current model with the other three data sets. It took 32 attempts to find seed values that produced 5 complete chains when all four data sets were used. Several population parameter estimates generated by these chains failed to converge, so no further analysis of this output was conducted.

The statistical model parameters and results for the SK, S, and SKL analyses were summarized in Table 3, Tables S-1, and S-2, respectively. Convergence was seen for all parameters for the S and SKL analyses. A lack of convergence was observed for two parameters for the SK analyses—the sequestration rate in other perfused tissues (κ₉₃) and the clearance of sequestered material from the heart (κ₆₃₄). For the SK and SKL analyses, no substantial differences between the group-specific parameter values for the Semmler data vs. Kreyling data were identified (Table 3, Table S-1). For the SKL analyses, the Lankveld group parameter values were substantially different from those of the Semmler and Kreyling groups for fecal elimination and the plasma:liver partition coefficient (Table S-2).

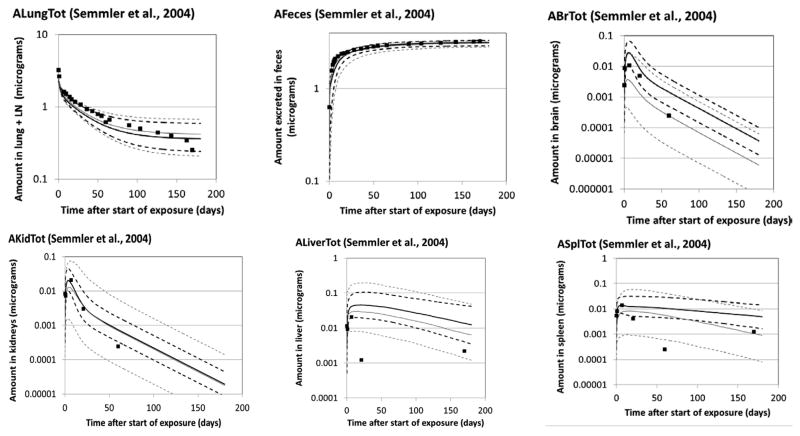
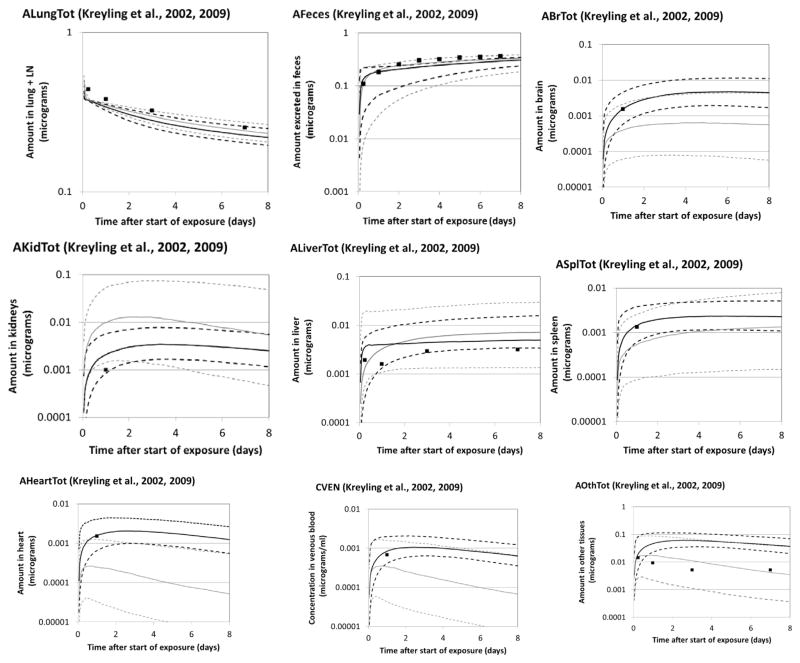
Monte Carlo simulations were conducted based on the population parameters from the S, SK, and SKL analyses. The predictions generated from the central tendency estimates of the population values were compared to the experimental data to generate a quantitative assessment of the agreement between the model and Semmler data (Table 4), Kreyling data (Table 5), and Lankveld data (Table 6). Graphical comparisons of the mean values of the experimental data and the 16th percentile, median, and 84th percentile values of the outputs of the SK and SKL analyses were also generated (Fig. 3—Semmler data, Fig. 4—Kreyling data, and Fig. S-2 in the Supplementary Materials—Lankveld data). Error bars for the experimental data are not shown; standard deviations for the Semmler et al. lung data were small (~17% of the mean, on average). Standard deviations on tissue concentrations appeared to be larger, at times exceeding 100% of the mean value, but could not be determined from the original paper due to lack of clarity in the original figure (overlapping error bars). Outputs from the S analyses were omitted from the figures for clarity and because of their similarity to the SK outputs. A data set not used in parameter estimation (Fabian et al., 2008) was also compared to model forecasts (Table S-3 and Fig. S-3).

Table 4.

Discrepancies between model predictions and experimental data of Semmler et al. (2004) and Semmler-Behnke et al. (2007).

Matrix (n)a	Geometric mean discrepancy indexb
	S Analysis	SK analysis	SKL analysis
Lung (20)	1.2	1.2	1.2
Feces (22)	1.0	1.1	1.1
Brain (4)	1.7	1.9	2.5
Kidney (5)	1.6	1.7	1.9
Liver (5)	2.0	4.4	3.5
Spleen (6)	2.5	3.2	3.1
All (63)	1.3	1.5	1.5

^an = number of experimental data points for a specific matrix.

^bDiscrepancy index = maximum of predicted value/measured value or predicted/measured value. Perfect agreement would have a discrepancy index of 1. Agreement considered acceptable if the discrepancy is, on average, <2 (IPCS, 2010).

Table 5.

Discrepancies between model predictions and experimental data of Kreyling et al. (2002, 2009).

Matrix (n)a	Geometric mean discrepancy indexb
	SK analysis	SKL analysis
Lung (4)	1.1	1.1
Feces (6)	1.2	1.1
Brain (1)	1.0	3.8
Kidney (1)	2.1	9.9
Liver (4)	1.9	1.8
Spleen (1)	1.1	2.5
Heart (1)	1.0	6.1
Venous blood (1)	1.3	2.0
Other tissues (4)	5.1	1.5
All (23)	1.6	1.7

^an = number of experimental data points for a specific matrix.

^bDiscrepancy index = maximum of predicted value/measured value or predicted/measured value. Agreement considered acceptable if the discrepancy is, on average, <2 (IPCS, 2010).

Table 6.

Discrepancies between model predictions and experimental data of Lankveld et al. (2002 ,2009).

Matrix (n)a	Geometric mean discrepancy indexb
	SKL analysis
Lung (7)	10
Brain (7)	16
Kidney (7)	5.4
Liver (7)	2.2
Spleen (7)	9.0
Heart (7)	6.1
Venous blood (5)	1.5
All (47)	5.9

^an = number of experimental data points for a specific matrix.

^bDiscrepancy index = maximum of predicted value/measured value or predicted/measured value. Agreement considered acceptable if the discrepancy is, on average, <2 (IPCS, 2010).

Fig. 3.

Disposition of iridium nanoparticles in rats exposed via a single intratratracheal intubation inhalation at 0.7 mg/m³ for 60–100 min. ■ Mean value of experimental data (Semmler et al., 2004; Semmler-Behnke et al., 2007; n = 8 up through day 59; n = 4 after day 59). Lines: PBPK model Monte Carlo simulations. Solid lines: median; dashed lines: 16th and 84th percentiles; black: SK analysis; gray: SKL analysis.

Fig. 4.

Disposition of iridium nanoparticles in rats exposed via a single intracheal tubation inhalation at 0.2 mg/m³ for 60–100 min. Symbols: mean experimental data of Kreyling et al. (2002, 2009); error bars not shown (fractional excretion and retention were reported graphically in the original data; the following coefficients of variation were estimated from the figures: 0.11 (lung), 0.14 (feces), 0.34 (brain), 0.44 (kidneys), 0.36 (liver), 0.44 (spleen), 0.31 (heart), 1.03 (blood), and 0.18 (skeleton). Lines: PBPK model Monte Carlo simulations; solid lines—median; dashed lines—16th and 84th percentiles; black—SK analysis; gray—SKL analysis.

Overall, the agreement to the Lankveld data was fair to poor, and the model tended to over predict the measured nanoparticle burdens, with the exception of the liver (Table 6, Fig. S-2). Because of this finding, the variability/uncertainty analysis was limited to the SK model to identify contributors to variability in predicted iridium disposition and inform the assessment of parameter identifiability from these data sets. Fixed parameters (Table 2) were not considered in this analysis. The analysis was limited to the population parameters determined through the Bayesian MCMC analysis, with sensitivity determined via rank correlation (i.e. rank of the input, among the 1000 trials vs. the rank of the forecast value derived from that trial) and percent contributions to variability determined from the squares of the correlation coefficients.

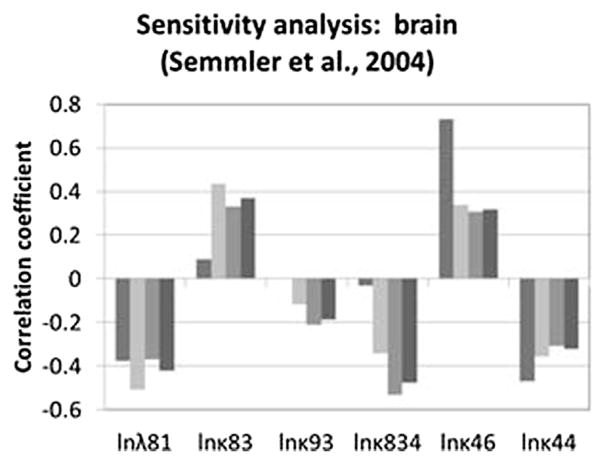
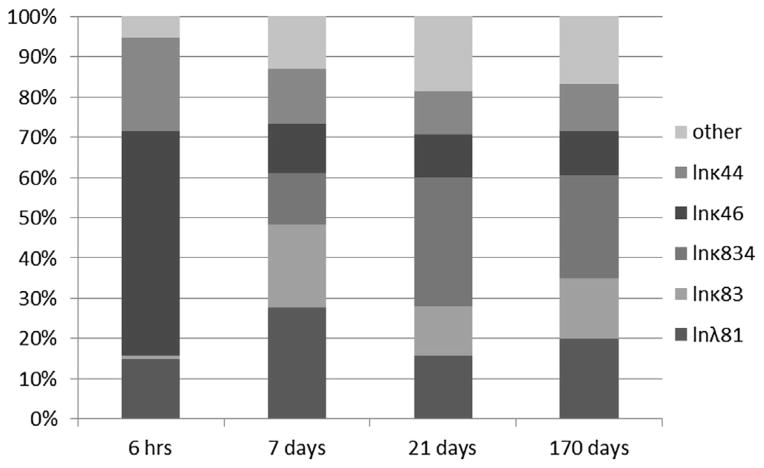
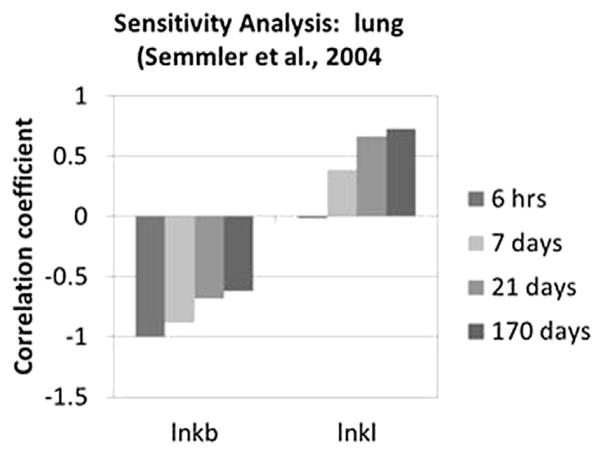
Optimized parameters that had the greatest impact on predicted brain concentration in iridium for the Semmler study are shown in Fig. 5. A larger estimated oral absorption rate tended to increase predicted brain concentrations, especially at the earliest sample time, while the fecal elimination rate had the opposite effect. The tissue-specific sequestration rate (κ83) and clearance rate for sequestered materials (κ834) had little impact at the earliest point, but were more important at later points, with impacts in opposite directions, while the impact of the plasma:brain partition coefficient is fairly consistent over time. The rate of sequestration in “other” tissues has some impact beyond the earliest time point due to its function as a relatively large sink for systemically-delivered nanoparticles. The time-dependent contributions of the various parameters to the variability at each time point are shown in Fig. 6. Other systemic tissue concentrations had similar key determinants (data not shown). The amount in the lung and associated lymph nodes was sensitive to the rates of translocation from the lung to the blood (kb) and into the lymph nodes (kl), and was differentially sensitive over time to these parameters (Fig. 7). The cumulative amount excreted in feces was sensitive to some of the same parameters that drove the forecasted systemic levels (absorption, elimination, and sequestration in other tissues), and the same parameters to which lung burden was sensitive (Fig. 8).

Fig. 5.

Rank correlation coefficient for optimized parameters and brain concentration at 0.25, 7, 21, or 170 days (from left to right, within each cluster) after inhalation exposure to iridium nanoparticles (Semmler et al., 2004; Semmler-Behnke et al., 2007). Only parameters with |rank correlation| >0.2 for at least one sample time are shown.

Fig. 6.

Contributions of various parameters to variability in Monte Carlo-derived population simulations of nanoparticle concentrations in the brain in rats exposed to iridium by inhalation (per Semmler et al., 2004; Semmler-Behnke et al., 2007).

Fig. 7.

Rank correlation coefficient for optimized parameters and lung burden at 0.25, 7, 21, or 170 days after inhalation exposure to iridium nanoparticles (Semmler et al., 2004; Semmler-Behnke et al., 2007). Only parameters with |rank correlation| >0.2 for at least one sample time are shown.

Fig. 8.

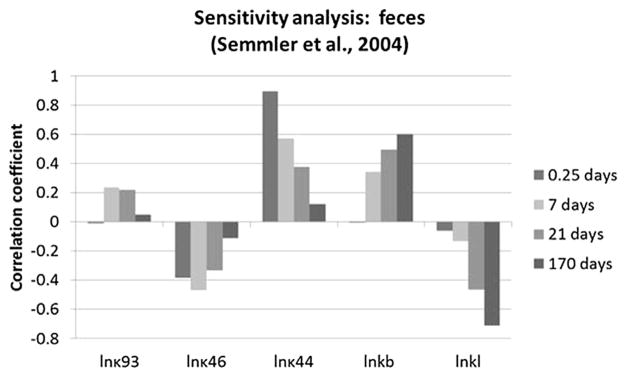
Rank correlation coefficient for optimized parameters and cumulative excretion in feces at 0.25, 7, 21, or 170 days after inhalation exposure to iridium nanoparticles (Semmler et al., 2004; Semmler-Behnke et al., 2007). Only parameters with |rank correlation| >0.2 for at least one sample time are shown.

4. Discussion

The focus on the iridium data of Semmler and co-workers (Semmler et al., 2004; Semmler-Behnke et al., 2007) for these analyses was due to the extended follow up (170 days post dosing) and potential for constraining mass balance (fecal excretion data; urinary excretion was likely minimal for this study due to particle size) and the previous use of these data in PBPK modeling of nanoparticles (MacCalman and Tran, 2009; MacCalman et al., 2009). The addition of the Kreyling et al. (2002, 2009) data was anticipated to better constrain the parameter estimates for systemically distributed iridium because of the availability of data for tissues not characterized by Semmler (e.g., one time point each for heart and blood and four time points for the other tissues compartment). It was determined that the addition of the Kreyling et al. (2002, 2009) data set, did not substantially alter the level of agreement, although optimal parameter values changed. Therefore changes in estimated parameter values between the “S” and “SK” analyses were not necessarily considered indicative of a poor model structure, but rather a reflection of better identification of parameter values due to consideration of additional data. Furthermore, the time course estimates for the median population simulation were still substantially in agreement with the experimental data (Table 4) and the spread of the population simulations (84th vs. 16th percentile values) were narrower for the SK analysis than the S analysis (simulations not shown). The addition of the next data set (Lankveld et al., 2010) did not substantially alter the fit to the iridium data sets, but did not produce adequate agreement between experimental data and simulations for the silver nano-particles. In addition, inclusion of the third data set dramatically increased the spread of the posterior Monte Carlo population simulations of iridium toxicokinetics. This step-wise addition of data sets within the MCMC framework, rather than a single MCMC analysis of all of the data being considered, allowed us to discern the impact of each additional data set on model performance (i.e. fit) and precision of parameter estimates.

The sensitivity analyses for iridium kinetics demonstrated that the forecast values were clearly sensitive to most of the parameters being optimized. The time-sensitivity of the rank correlation co-efficients (Figs. 5 and 7) highlights the importance of time course data for evaluating model structures and parameterization. The determination that tissue burdens were sensitive to the values of many adjustable parameters was not surprising–had the tissue burdens been sensitive to a more limited set of parameters, the simpler model structures that were explored may have sufficed to fit the data.

The Lankveld et al. (2010) data were used to test the applicability of the iridium-derived parameters to the disposition of a similar material (with respect to size, lack of functionalization, etc.) in the same animal model, the young adult male Wistar rat. The fit of the median SKL simulation results to the Lankveld data was not acceptable (Table 6). The impact on simulations of the Semmler and Kreyling studies from the addition of the Lankveld et al. (2010) data to the MCMC analysis was not apparent from the predictions based on the central tendency population parameters values alone (Tables 4 and 5), but was evident in the wider population predictions (Fig. 3) and in an elevated estimate in the variance of the fecal excretion rate (Table S-2). This conclusion could not readily have been drawn from deterministic analyses alone, and helps demonstrate the value of the Bayesian approach. Had data on nanoparticle excretion in feces been available for the Lankveld et al. (2010) study, the fecal excretion rate might have been more narrowly constrained. Dissolution of the silver nanoparticles at some rate may have contributed to poorer model fit and over-prediction compared to the calibration data (Fig. S-2) and an independent data set for titanium oxide nanoparticles (Fig. S-3).

The kinetics of nanoparticles in vivo are, in general, not currently well-understood (Li et al., 2010) and the reasons for the inability of the iridium-derived model parameters to describe the toxicokinetics of silver (Lankveld et al., 2010) data are likewise unclear. One possibility is that there are key differences in the characteristics of the test articles that somehow translate to differences in optimal values for certain parameters; the data sets considered in this analysis were selected primarily based on similarity of particle size, and the lack of additional functional groups. Another possibility is that model structure does not adequately describe the key processes. The PBPK model structure tested here (a flow-limited modification of MacCalman and Tran, 2009; MacCalman et al., 2009), is based largely on model structures used previously for many volatile, soluble compounds, but with limited translocation from the lung interstitial tissue into the blood. A similar model structure was successfully applied to short term (up to 60 min) kinetics of ^99mtechnitium-labeled carbon nanoparticles inhaled by humans (Péry et al., 2009). In contrast, Li et al. (2012) found the kinetics of poly(lactic-co-glycolic acid) nanoparticles prepared with varying amounts of monomethoxypoly (ethylene glycol) in mice were described better by membrane-limited models than flow-limited models. The model structure used herein for iridium particles did not include any saturable processes, and the doses of iridium nanoparticles (~3 μg in Semmler et al., 2004; Semmler-Behnke et al., 2007) were much less than the silver dose in Lankveld et al. (2010) (five injections of 23.8 μg), so the lack of consistency could be due to saturation of key processes at the higher doses in Lankveld et al. (2010). The model does, however, appear to capture the extent of the day-to-day increases in retention of nanoparticles in lung and peripheral tissues, consistent with the repeated-dosing data of Lankveld et al. (2010), the only repeated dosing study considered in this analysis. PBPK models for nanoparticles that integrate diffusion limited uptake and incorporate immune cells as a distinct, capacity-limited subcompartment could provide alternative structures to test against these same data sets (Bachler et al., 2013; Li et al., 2014). In addition, if the majority of systemically distributed nanoparticles are associated with macrophages, rather than “free”, their distribution over the time frame of interest here (several days) might better be described by inter-organ trafficking of the cells of the immune system (Zhu et al., 1996) rather than diffusion from blood alone. The simplistic description of sequestered particles being cleared directly to feces (rather than being trafficked through the lymphatic system or carried in the blood in a non-exchangeable form) contributes uncertainty to the derived parameters. However, since the parameters for clearance of sequestered particles do not have a significant impact on predictions of nanoparticle elimination in feces, the impact, if any, is likely limited to the fit to blood concentrations.

Further modeling work would benefit from well-conducted long-term kinetics studies in rodents, as discussed above. Even without such data, simulation studies may provide more information on the reliability of the current model parameter values as well as the potential to simplify the model structure for poorly-soluble nanoparticles. Moreover, further model development to include particle dissolution pathways (e.g., as described in Bachler et al., 2013) may improve the model predictions for soluble nano-particles. Although a goal of developing a PBPK model in rodents is to provide a biological basis for extrapolation of the model to humans, further data and model evaluations are needed before extrapolation is feasible. Ideally, future in vivo toxicokinetics studies of nanoparticles would incorporate better demonstration of mass balance, by collection of excreta and determination of nano-particle content of all important tissues, including muscle, fat, bone marrow, and the skeleton at multiple time points. Multiple measurements of tissues are important so that both the delivery/distribution and clearance phases can be discerned, but this requires increased numbers of animals and amounts of test article. However, multiple measurements of blood, urine, and feces can be completed without requiring more animals or test article. While the sensitivity of tissue burdens of iridium to values of model parameters was fairly consistent after the initial distribution period (t = 6 h, vs. 7–170 days; Figs. 5–7), the cumulative excretion in the feces showed somewhat different patterns of sensitivity, depending on the parameter. For example, cumulative excretion showed a transient sensitivity to storage in “other” tissues, decreasing sensitivity to the oral absorption rate, and increasing sensitivity to the rate of transfer to the lymph nodes (Fig. 8). Thus, if analytical techniques permit quantitation of nanoparticles in excreta at longer times after administration, these data can provide useful constraints on model parameter values.

5. Conclusions

While the nanoparticle toxicokinetic database continues to expand (Yang et al., 2010), much remains unknown as to the fundamental processes which dictate the systemic uptake, distribution, and clearance from the body. PBPK modeling of nanoparticles is hampered by a lack of thorough mass balance studies with adequate time courses to supply sufficient data sets for comprehensive modeling; this lack may be overcome through better-designed studies, or techniques that allow information to be amalgamated across studies and study designs. In addition, it is important that the test articles be well-characterized so that properties beyond size and elemental composition (e.g., surface properties and other characteristics) be considered as potential key determinants of disposition. Bayesian MCMC techniques have the potential to be applied to test various model structures via the simultaneous consideration of multiple data sets over wide ranges of potential parameter values, facilitating an improved understanding of key determinants of toxicokinetics of different types of nanoparticles.

Appendix A. Supplementary data

Supplementary data related to this article can be found at http://dx.doi.org/10.1016/j.yrtph.2015.06.019.