A novel, Bayesian approach to social structure uncovers cryptic regulation of group dynamics

Abstract

Understanding the mechanisms that give rise to social structure is central to predicting the evolutionary and ecological outcomes of social interactions. Modeling this process is challenging, because all individuals simultaneously behave in ways that shape their social environments—a process called Social Niche Construction [SNC]. In previous work we demonstrated that aggression acts as an SNC trait in fruit flies (Drosophila melanogaster), but the mechanisms of that process remained cryptic. Here, we analyze how individual social group preferences generate overall social structure. We use a combination of agent-based simulation [ABS] and Approximate Bayesian Computation [ABC] to fit models to empirical data. We confirm that genetic variation in aggressive behavior influences social group structure. Furthermore, we find that female “decamping” due to male behavior may play an under-appreciated role in structuring social groups. Male-male aggression may sometimes destabilize groups, but may also be an SNC behavior for shaping desirable groups for females. Density intensifies female social preferences, thus the role of female behavior in shaping group structure may become more important at high densities. Our ability to model the ontogeny of group structure demonstrates the utility of the Bayesian model-based approach in social behavioral studies.

Introduction

The process by which individuals shape their social environment is called social niche construction [SNC] (Flack et al., 2006; Saltz and Foley, 2011; Kohn et al., 2011). In free-living populations, social groups emerge as a consequence of many individuals simultaneously engaging in SNC. These individuals will often vary in important ways, including personality, and sex (e.g. Eldakar et al., 2009; Griffiths and Magurran, 1998; Aplin et al., 2014). This variation may in turn translate into differences in population-wide group structure, such as group size, and sex ratio (Jovani and Mavor, 2011; Sumpter, 2010). Understanding these aspects of group composition is important because social structure affects opportunities for competition, cooperation, or mating. However, modeling SNC is challenging, because an individual’s expressed social phenotype may depend on interactions between sex, genotype, and the available social environment (Saltz and Foley, 2011). In these kinds of diverse groups we need to understand: what are the differences in male and female behavior, how do these differences shape group structure, and how might group structure feed back into subsequent behavior?

The fruit fly, Drosophila melanogaster, is a classic model organism for studying social behavior, sex differences, courtship, and aggression. D. melanogaster interacts in groups on food for mating and egg laying, but the behavioral mechanisms that structure these groups are only partially understood. Aggressive behavior reduces aggregation among males (Saltz and Foley, 2011) and might be expected to reduce local (within patch) competition for mates for territorially successful males. Previous work has shown that across a wide range of conditions, aggressive males gain a mating advantage by excluding other males from the patches of food females use for egg laying (Hoffmann and Cacoyianni, 1989, 1990). However, while these studies focused on the direct outcomes of male-male interactions, they did not measure the way in which female social preferences interacted with male behavior. We have shown that the relationship between male aggressive success and mating success varies across social contexts due to female preferences. Females do not always prefer to mate with terriorial males, and may even mate more often when males are less aggressive (Cabral et al., 2008; Saltz and Foley, 2011; Saltz, 2013). This complexity suggests that we need to understand the social determinants of female behavior, including group choice. Female social preferences for males are likely to be complex, due to several conflicting selective pressures. In order to assess the quality of potential mates, or to mate at all, females need to be in groups with at least some males. However, females only mate every few days, and may often have reasons to actively avoid males. Exposure to males reduces female health (Pitnick and Garcia-Gonzalez, 2002), and females flee unwanted courtship (Spieth, 1974). Female-female interactions may also be important in shaping group composition, since they are thought to aggregate to lay eggs (Sarin and Dukas, 2009). How to model the outcome of varying social interests and their effects on group structure is an important general problem in animal behavior.

Previously, we demonstrated that genetic variation in male-male aggressive behavior acts as a mechanism of SNC in fruit flies (Saltz and Foley, 2011—referred to as ‘S&F’ from here on). In aggressive encounters in D. melanogaster, males chase other males away from food patches. To evaluate whether genetic variation in male aggression can shape group structure, we formed mini-populations, varying density and genotype. Males and females could interact freely and form groups on food patches in each “population”. We found that females tended to form aggregations with other females, but males were more evenly distributed among patches than expected by chance. Overall, flies aggregated more than expected by chance, and male and female presence on patches was highly correlated—there were few groups that had many males in them, but those groups also tended to have large numbers of females in them. Populations of different genotypes had different social structure. Those with the most aggressive genotypes had fewer males on patches, and lower variance in male presence among patches.

While male and female presence on patches was highly correlated, we were unable to assess whether the group choices of males or females were driving that correlation. Additionally, our approach was unable to test for changes in behavior across densities. Because each individual’s behavior can be determined by complex feedback and stochastic dynamics (Sumpter, 2010), linear approximations are often inadequate for higher order group processes (Eriksson et al., 2010). Simulation, however, provides a powerful mechanistic approach to describe complex group formation (Jovani and Mavor, 2011). In particular, Agent Based Simulation [ABS] is a particularly appropriate tool with which to study SNC (Bryson et al., 2007), because it operates at the level of individual behaviors and choices. Quantitative approaches have been successful in model fitting in ABS (Amé et al., 2004; Eriksson et al., 2010; Mann, 2011), particularly in describing patterns of collective movement in schooling or flocking animals (Sumpter et al., 2012; Mann et al., 2014; Ward et al., 2008). While D. melanogaster is not known to engage in collective movement, the methodology seems well suited for describing outcomes of individual interactions.

In situations where the potential state space is small, the model is reasonably simple, or there are no missing data, exact methods of model fitting are appropriate. For example, Aplin et al. (2014) applied a maximum-likelihood approach to fit stochastic models of empirical group behavior, while Mann et al. (2014) used Bayesian model selection. Our data, however, comprise multiple sampled states, and are sampled at discrete time-points rather than being observed continuously. Furthermore, because we need to model male and female social preferences independently, our state space is quite large. Since exact methods are not tractable in our context, we utilize Approximate Bayesian Computation [ABC] with Monte Carlo Markov Chain [MCMC] sampling (Marjoram et al., 2003; Beaumont et al., 2009). ABC is an approach that allows us to estimate model parameters in a principled manner, even in contexts that are analytically intractable. In essence we replace calculation of the likelihood with simulation, and use a Euclidean distance metric to assess model fit. In this way, it is a formalized version of the maximum likelihood approach sometimes used in fitting complex behavioral models (e.g. Ward et al., 2008). While a number of sampling schemes are possible in ABC, MCMC is a well worked-out approach that allows us to efficiently sample high-dimensional parameter space (e.g. Mann et al., 2013, 2011).

Materials and Methods

The 6 D. melanogaster genotypes used in S&F spanned a range of aggression. Of these, 4 (W23, W58, W89 and W145) were nearly isogenic lines collected in Winters California in 1998. The other 2 were high-aggression selected (A), and neutral control (N) genotypes, kindly supplied by Ralph Greenspan. These were created from the common laboratory wildtype stock Canton-S, as described in (Dierick and Greenspan, 2006).

Simulation

Simulations were designed after the assay of S&F, and mimicked the experimental conditions of these assays. We simulated the results of experiments using our 6 different genotypes at 5 different densities. Each experimental density×genotype combination is considered a “treatment”. Each simulation comprised 4 food patches, among which flies were able to freely assort (as well as an “off patch” state). Each simulated trial contained an equal number of males and females. The density (total number) of flies in the arena ranged from 12 to 20 flies. We did not attempt to model the lowest 3 densities of S&F since the sampling variance for these replicates was high. We simulated group choice using a simple joining-and-leaving model (Amé et al., 2004). We modelled group behavior for each fly as a function of a joining rate, a baseline leaving rate, as well as social preferences (Figure 1). Social preferences were a fly’s affinity for males, and their affinity for females. Parameters were sex specific, so for each simulation there was a total of 8 parameters, 4 male and 4 female, comprising the parameter set Θ (Figure 1B). While it is possible to construct simpler models with fewer parameters, we found highly significant sex differences in these estimates (Supplemental Material) suggesting that male and female social preferences should be modelled separately. Events were modeled as a continuous time Markovian Process, with rates determined by rate equations (Otto and Day, 2007).

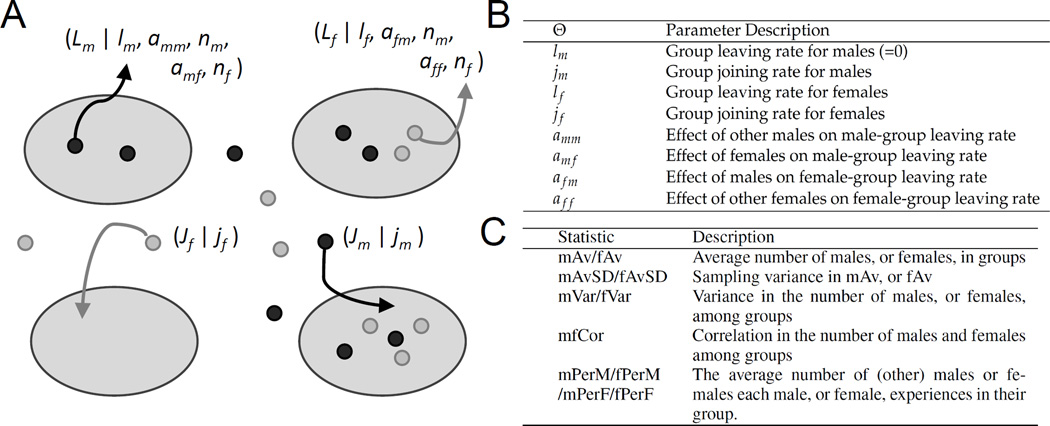
Figure 1.

Schematic of the Agent Based Simulation. Females are denoted as light gray, and males as dark gray. A) Food patches constitute social groups, and individuals may choose to join a patch at random, or leave a patch and be off-patch, at characteristic rates governed by the model parameters we are estimating. Female and male joining rate (J_i) for sex i are each a function of a single parameter, j_f and j_m. Leaving rate (L_i) is a function of the sex-specific leaving rate, l_s, the number of non-self males and females in a group, and the sex-specific social parameters describing female attraction to males (a_fm) and females (a_ff), and male attraction to males (a_mm) and females (a_mf) [Equation 1]. B) Table of model parameters. C) Table of group-level summary statistics S, calculated from the experiments of S&F. These statistics were used to estimate the parameters Θ.

Flies who were off-patch could join a group. Group joining J_i was taken to be a simple rate exp(j_s) for a focal individual i of sex s. Group joining was random with respect to patch (Figure 1A) since (at least over short distances) fruit flies do not appear to use social cues before landing on patches, but instead respond to social cues within groups (Saltz, 2011). We fixed the male joining parameter j_m at 0 throughout all replicate simulations, rather than attempting a post hoc scaling of rate parameters. Priors for j_f were flat between −3.3 and 3.3, which represents a possible difference of joining rates of more than 700 fold. Flies who were off-patch were not considered to belong to any group.

Flies who were on-patch left at a rate L_i proportional to their sex-specific leaving rate, l_s, modified by their group context and social parameters as described in Equation 1 (Figure 1B). The particular form of our leaving rate equation was a simplified version of the leaving rate equation of (Amé et al., 2004), which is a very general rate equation that has been shown to describe group choice very well, in cockroaches for example. In order to reduce the number of parameters we needed to fit, we did not include their term k, effectively setting the intercept at the sex-specific baseline leaving rate l_s. This means that every additional fly (of a given sex) added to a patch has the same proportional effect as the one before on the leaving rate of a focal fly.

The leaving rate L_i for an on-patch focal individual, i of sex s is thus

$$L_i=\mathit{\text{exp}}(l_s)\prod n_r^{-a_{sr}}$$

given the number of non-focal individuals n_r of sex r, and the sex-specific affinity a_sr of the focal individual for them. For the affinity parameters this results in easily interpretable values that are symmetric around 0. A preference value of 0 represents a lack of preference for members of a given sex, a negative value represents a negative affinity (the leaving rate increases) and a positive value represents a positive affinity (the leaving rate decreases). The prior for l_s was identical to j_s, while the prior for a_sr was flat and ranged between −10 and 10 (Supplemental Material). The simulation design was chosen to mimic the experimental set-up of S&F (see Supplemental Material for details). Summary statistics (Figure 1C and Supplemental Material) were chosen to comprehensively describe male and female distributions among patches, male and female covariance among patches, and sampling variance among measurements. We measured the average number of males and females on patches (mAv, fAv), the variance of their distribution among patches (mVar, fVar) and their covariance on patches (mfCovar). We also considered several metrics which were not included in S&F, including the mean individual-level group composition statistics: the number of males or females per-male (mPerM, fPerM) and per female (mPerF, fPerF), since these are better descriptors of individual experience (Jovani and Mavor, 2011). We also included the standard deviations of our mAv and fAv metrics (mAvSD, fAvSD), since these provide estimates of movement between measurements. This results in a total of 11 summary statistics.

ABC

In a Bayesian framework, we describe our certainty about our parameter values, Θ, conditional on the observed data, D, by the posterior distribution, f (Θ | D). We write f(Θ | D) = f (D | Θ)π(Θ)/f(D), where π(Θ) is a prior distribution that reflects our existing beliefs regarding the parameters, and f(D) is a normalizing constant. This normalizing constant can be calculated by observing that f (Θ | D) is a probability distribution, and must therefore integrate to 1. The likelihood term f(D | Θ), however, is not calculable in this context, because D is composed of broad summary statistics, and does not include the stochastic individual movements described by Θ. We can instead replace the calculation step by a simulation step, generating a pseudo-likelihood between the statistics from the data, and statistics from the simulation.

We used an ABC Markov Chain Monte Carlo [MCMC] approach to estimate the parameter posterior distributions (Marjoram et al., 2003; Sisson et al., 2007, 2009; Beaumont et al., 2009) (for full details see Supplemental Material). The use of MCMC has an advantage in high-dimensional space of searching efficiently, rather than estimating the entire set of possible solutions (as in Perez-Escudero and de Polavieja, 2011). We did this using the set of summary statistics given earlier. As is common in ABC analyses, we used the Euclidean distance metric and define a tolerance, [220A], that determines the level of agreement required between simulated and observed statistic values during the analysis. Choice of [220A] represents a trade-off between computational efficiency and accuracy of results. The analysis returned a joint-posterior distribution of these parameter values for each treatment. The underlying model did not include explicit parameters governing genetic differences or differences due to density. We instead expected that correlations between preference parameters and density or aggression would reveal the bases of SNC at the level of individual preferences.

For speed, we opted to implement our simulation and ABC algorithm in a custom C++ program. For full details on implementation, stationarity diagnostics, and model validation see Supplemental Material.

Multimodality

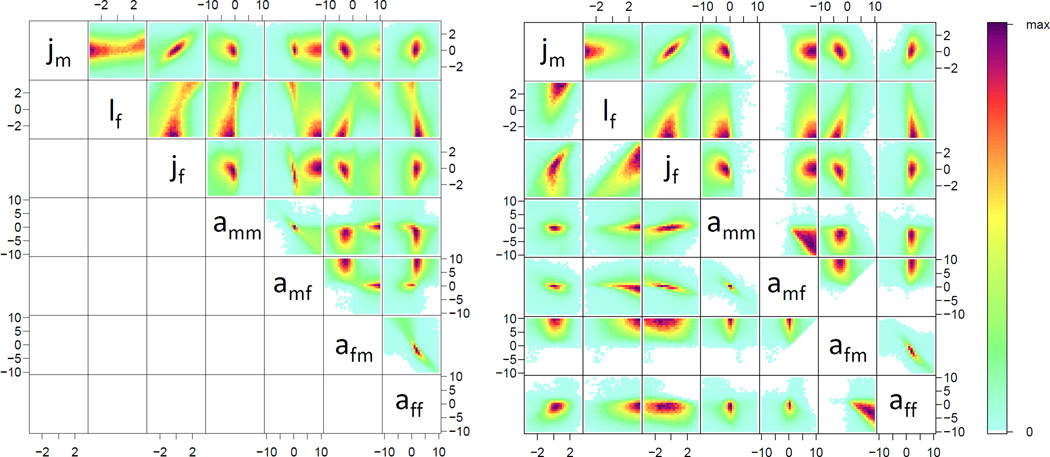
In a majority of treatments, we found that two distinct, mutually-exclusive models fit the data, reflected in multivariate bimodal distributions for several parameters (Figure 2A). All but 2 treatments showed evidence of multimodality in at least 1 parameter (peaksIDPmisc in R, see Supplemental Material). The 2 parameters that showed the strongest evidence of multimodality were a_mf and a_fm, that is the affinity (or social preference) of males for females, and females for males. In one of the modes, males exhibited a strong social affinity towards females, in the other, females exhibited a strong affinity to males. When we fit these two models separately (model “mfHigh”: a_mf> a_fm; model “mfLow”: a_mf< a_fm), evidence of multimodality disappeared in all parameters for all treatments (Figure 2B). Thus, we have a problem of identifiability.

Figure 2.

Bivariate heat map pooling the posterior distributions of parameter estimates of all 30 genotype×density treatments. There is bimodality within a_fm a_mf and l_f. Bimodal distributions like this may represent a lack of identifiability (see Supplemental Material). Here, for the combination of a_mf and a_fm, the two peaks fall into two distinct categories: one in which a_mf is higher than a_fm(mfHigh), and one in which the opposite is true (mfLow). Because the joint probability of mfHigh is effectively 1, we conduct subsequent analyses only on mfHigh. On the left plot we show the full dataset. On the right, the model mfHigh is above the diagonal and mfLow is below.

In each treatment we calculated the Bayes factor representing the relative likelihood of the mfHigh model by splitting the posterior distribution into mfHigh and mfLow samples, and dividing the number of samples representing the mfHigh model by those representing the mfLow. A Bayes factor of 1 means the models are equally likely. The Bayes factor for mfHigh ranged from 0.66 to 17.80 across all treatments. In only two treatments, (W23×d14, 0.66; W58×d12, 0.90) was the Bayes factor lower than 1. Given the general level of support for mfHigh, we determined whether we were justified in disregarding the mfLow model. We calculated the joint probability of mfHigh by multiplying the probability of the mfHigh model across all treatments, and the probability of the mfLow model across all treatments, then recalculated the overall Bayes factor. The Bayes factor for the joint probability of mfHigh is 10¹⁷, therefore there is no reason to consider mfLow further.

Corrections for Multiple Testing

When testing for associations between variation in Θ and the predictors aggression, genotype and density (Results), we performed a number of tests which required correction for multiple testing. For the Wilcoxon Signed-Rank test, we were primarily interested in establishing that our method was sensitive enough to find significant differences in our parameters for the most conservative comparisons between posteriors. Because we were less interested in accurate, global P-values we opted for the simplest method of calculating the Bonferroni cutoff, that is for the total number of tests performed without accounting for the dimensionality of the data. For the regression analysis, because the model parameters had evident covariance structure, we first calculated the effective number of independent dimensions (Cheverud, 2001). We performed Principal Components Analysis on the concatenated dataset comprising all posteriors for all treatments in the mfHigh model. The first 5 PCs explained 96.7% of the total variance in the parameters. Since we tested 3 predictors, this indicates approximately 15 independent tests and we therefore set the global Bonferroni correction for the regression of Θ on predictors at 0.003.

Results

The ABC output comprised 30 replicates of Θ, with posterior distributions for our 7 movement and social preference parameters, for each of our density×genotype combinations.

Variation among posteriors

We first established that the posteriors of Θ varied among genotypes and densities (treatments), and that we had the power to detect these differences, given our sampling rate. We thus performed a series of Wilcoxon Signed-Rank Tests for pairs of posteriors. We compared the distributions of all posteriors for a given parameter that were either within genotype, but different by one unit of density; or within density, between genotypes that were closest pairs in aggression levels. These comparisons were those we expected to be most similar. Even these conservative comparisons showed that posteriors varied greatly among treatments. Among the 24 density pairs for all 7 parameters (168 comparisons), only 53 comparisons did not show significant differences after Bonferroni correction. Among the 25 aggression pairs for all 7 parameters (175 comparisons), only 54 comparisons were not significantly different after Bonferroni correction. Two parameters (female leaving rate, l_f, and male affinity for females, a_mf) accounted for over half of the non-significant results—28 and 30 comparisons, for density and aggression respectively. This suggests that 5 of our 7 parameters might be particularly important in shaping variation in group outcomes.

Genotype and aggression effects

Given significant differences in parameter estimates among treatments, we explored whether this variation was a result of genotype and density. Because we also had genotypic values for aggression (S&F), we used aggression as an additional predictor. In order to detect the directional effects of our predictors across all treatments, we used a summary (the marginal mean of each posterior) for each treatment and parameter combination. Subsequent calculations are performed using these summaries. We further investigated whether the differences in parameter estimates could be used to explain observed patterns of group structure.

Male and female group joining rates j_m and j_f, as well as male-male affinity, a_mm, were all correlated with both genotype and aggression (Figure 3A, B). The strongest correlation for both aggression and genotype was with a_mm. Aggression is male-directed behavior toward other males in Drosophila (see (Nilsen et al., 2004; Chen et al., 2002; Dierick and Greenspan, 2006; Cabral et al., 2008)). We therefore expected that aggression would be most correlated with a_mm in our analysis. It serves as a validation of the model that this is the case (est=−0.37, F_(1,28)=14.95, P<0.001, adjrsq=0.32), and was significant at the global Bonferroni threshold (Materials and Methods). Because our lines were chosen for their extreme genetic values in male-male aggression, it is likewise encouraging that we found evidence for genetic variation in a_mm among the lines in our treatments (F_(5,24)=4.52, P=0.005, adjrsq=0.38). Although this did not quite meet the global Bonferroni threshold of P<0.0033, the consistency of the effect among predictors suggests the association between a_mm and genotype is real.

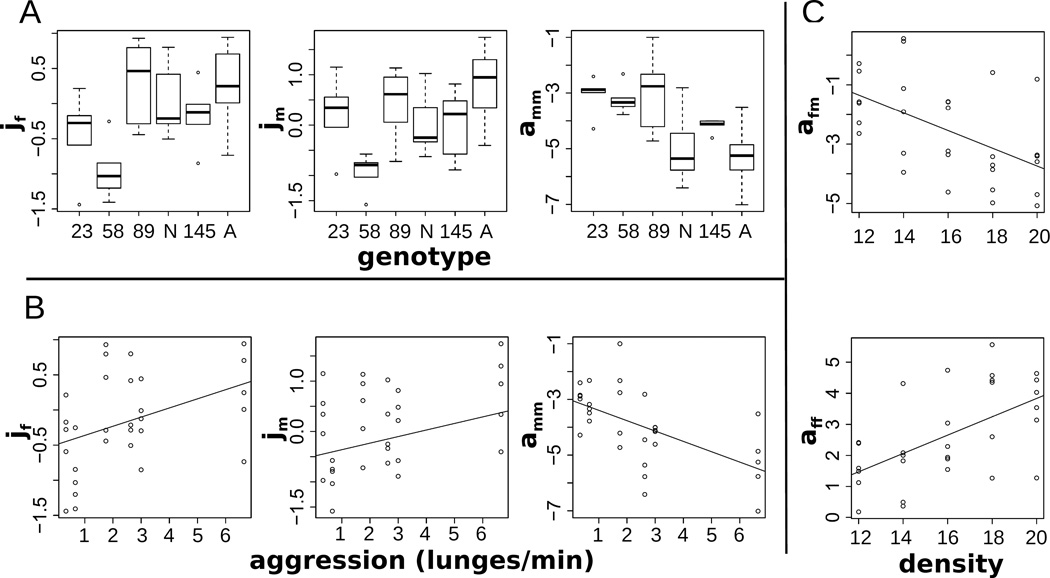
Figure 3.

Plots for parameters showing significant correlations with predictors. Sub-figure axes are denoted by the sub-headings as y ~ x. In linear models with genotype as a factor, significant effects were found for male joining rate, j_m, female joining rate, j_f, and male-male affinity, a_mm (A). In linear models with genotypic aggression values as a quantitative trait, effects were found for male joining rate, j_m, female joining rate, j_f, and male-male affinity, a_mm (B). In linear models with treatment density (number of individuals), effects were found for female-male and female-female affinity, a_fm and a_ff (C).

Having established that a_mm is significantly related to aggression and likely varies with genotype, we attempted to understand what elements of group structure are shaped by male-male interactions. We tested for an effect of parameter estimates on group-level outcomes among our treatments using linear models, with density as a covariate (Figure 3C). We found that males with low values of a_mm had fewer other males in their groups (lower mPerM) (est=0.18, t=3.72, P<0.001, df=27). Likewise, low values of a_mm correlated with overdispersion, or decreased variance in the numbers of males among patches, (lower mVar), (est=0.16, t=3.56, P=0.001, df=27). This is consistent with one definition of aggression as a male-male displacement strategy in D. melanogaster (Wang and Anderson, 2010). One might assume that aggression is a competitive strategy males engage in to gain access to females (Hoffmann and Cacoyianni, 1989). But, in fact, both increased aggression (est=− 0.08, t=−2.73, P=0.011, df=27), and the corresponding low a_mm (est=0.14, t=3.12, P=0.004, df=27), had a slightly negative relationship with our empirical measure of the number of females per on-patch male (fPerM).

In addition to a_mm, sex-specific joining rates for males and females, j_m and j_f, varied significantly among the genotypes (F_(5,24)=3.36, P=0.019, adjrsq=0.29; F_(5,24)=3.44, P=0.017, adjrsq=0.30) and with aggression (est=0.49, F_(1,28)=5.72, P=0.024, adjrsq=0.14; est=0.39, F_(1,28)=5.63, P=0.025, adjrsq=0.14). The higher the overall aggression levels were, the higher the group joining rates were. The consistency of the effects of multiple predictors on these parameters supports their significance, although individually they do not meet the Bonferroni cutoff. The relationship between j_m or j_f and group structure was complex, and differed between their corresponding sexes. Higher values of j_m and j_f should result in a higher average number of males (mAv) and females (fAv) respectively on patches because increased joining rates were not offset by correlated higher leaving rates. We found support for this prediction for males, (est=0.05, t=4.29, P<0.001), but not females (est=0.03, t=1.84, P=0.07). Higher values of j_f did correspond with one aspect of group structure: reduced male-female correlation on patches (mfCor) (est=−0.3, t=−3.73, P<0.001, adjrsq=0.51), suggesting one way in which females might shape their group context.

Male disruption of preferred female groups

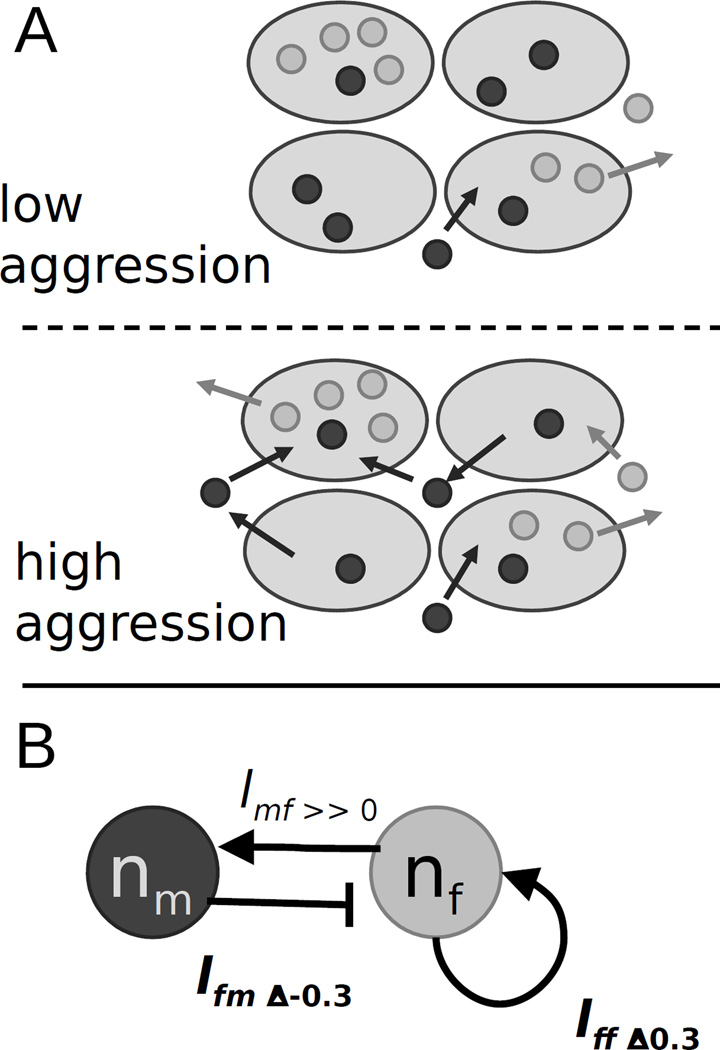
Analysis in an agent-based simulation framework allows us to evaluate the plausibility of proposed hypotheses relating parameter values to group structure. We can vary one or more parameters in a series of test simulations, and examine the effects without needing to explicitly redefine all the interacting dynamics (Supplemental Material). Here we manipulate the 3 aggression-related parameters, holding the other parameters constant. This enables us to determine whether these parameters by themselves can explain the patterns we see, and whether there is a plausible mechanism underlying the effect. In this case, we investigate changes in movement rates to evaluate social dynamics. Because aggression is a behavioral interaction where males displace other males, we might expect overall male movement rates to be higher in aggressive environments.

We simulated a ‘high aggression” and “low aggression” treatment, using typical values of parameters from our set of posterior distributions. All conditions in these simulations were identical, but we mimicked high-aggression versus low-aggression values of j_f, j_m and a_mm. Our simulations include an internal “clock” against which fly movement rate is calculated. We recorded the length of time between fly moves, as well as the relative number of male and female fly moves. In the set of parameters mimicking the high-aggression conditions, overall fly movement rate was significantly greater, compared to the low-aggression scenario (est=−21.38, t=−18.45, P<0.001, sf=58). Moreover, the proportion of times males moved in the high aggression treatment was higher (est=0.02, t=5.72, P<0.001, df=58). These results are consistent with the idea that aggressive males are driving each other off patches more frequently than nonaggressive males.

It is not immediately obvious why female moving rates should co-vary with male aggression. But given that males seem to move more often in high aggression treatments, we hypothesized that male-female encounter rates are higher in these treatments. Female reaction to males is mediated by the term a_fm, and a_fm is consistently negative (Figure 2B, above diagonal), indicating that females will respond to increased numbers of males on patches by leaving.

To test the role of displaced-males in disrupting female group structure, we set the preference of males for females, a_mf, to 1 (nearly neutral) in the “high aggression” simulation. This will reduce the confounding effects of overall mobility with male social preferences for female groups. The average number of females on patches increased dramatically with lowered a_mf (est=0.86, t=33.07, P <0.001, df=58), and the ratio of female to male movement decreased (est=−0.29, t=−52.22, P <0.001, df=58).

Together these results suggest a plausible mechanism for the relationship between aggression and female group preferences. More-mobile males preferentially aggregate with females, disrupting female groups in turn. In this scenario, the negative correlation between j_f and mfCor, and the lack of correlation between j_f and fAv indicate that females are reacting to non-preferred groups by modifying their group-choice parameters (Figure 4A). If so, the correlation between genotype and j_f is an example of an Indirect Genetic Effect (IGE) (Moore et al., 1997).

Figure 4.

Graphical representation of our proposed mechanisms comprehensively explaining group-level outcomes from variation in individual-level parameters. Females are denoted as light, and males as dark. A) Our proposed mechanism for how variation in aggression indirectly affects female group joining parameters. When aggression is high (male-to-male affinity, a_mm is low), males move between groups more often. They are thus more likely to encounter groups of females. Because female-to-male affinity, a_fm, is consistently negative, when males join these groups are destabilized and females leave and must find a new patch. B) We found that density affects both female-to-male and female-to-female affinity, a_fm and a_ff, in opposing ways. We propose that the effects of this change cancel out at the group-level via a negative feedback loop involving male preferences for females. An arrow indicates a positive effect, a bar headed line an inhibitory effect.

Density effects

We found significant density effects (after global Bonferroni correction) in the 2 female social preference parameters. Female preference for males, a_fm (est=−0.59, F_(1,28)=10.733, P=0.003, adjrsq=0.25), was more negative at higher density; female preference for females, a_ff (est=0.59, F_(1,28)=13.57, P=0.001, adjrsq=0.30), was increasingly positive at higher densities (Figure 3C). In S&F, using conventional analyses, these differences in female behavior across densities were cryptic.

We expected to see more females in groups with other females in those treatments where we estimated high a_ff, as described by our summary statistics fPerF, and fVar. Instead, we found that fVar did not correlate with a_ff. Moreover, the correlation between a_ff and fPerF was in the opposite direction to our expectation (est=−0.098, t=−2.40, P=0.024, df=27). Likewise, we expected females would be less often on patches with males in treatments where we estimated low values of a_fm. This would be reflected in a lower value of our male-female correlation statistic mfCor and sex ratio statistics of males-per-female (mPerF) and females-per-male(fPerM). However, among the treatments, only mfCor varied with a_fm in the predicted direction (est=0.035, t=2.35, P=0.026, df=27), and we did not detect any correlation between a_fm and fPerM or mPerF. Because the differences in a_fm and a_ff across densities were equal in magnitude and in the opposite direction, we hypothesized that they might, in effect, cancel each other out, via a mechanism similar to that described above (see “Male disruption of preferred female groups”). An increased value of a_ff will lead to groups with more females. But, because a_mf is uniformly large and positive, groups with more females will come to attract more males. Since a_fm is highly negative, this will make the group less attractive to females (Figure 4B).

Additional simulations confirmed that our proposed mechanism could plausibly account for the group structure we observed. We ran simulations with a_ff and a_fm corresponding to either high density or low density values, holding all other parameter values constant. We first tested the effects of changing a_ff and a_fm together and independently. We found that when we changed them independently, the values of fVar or fPerF changed significantly (Supplemental Material). But, when we changed the values of a_fm and a_ff simultaneously, the values of these summary statistics did not change. We then evaluated whether male preferences for females might play a role in regulating this process. We set the male preference for females, a_mf, to 1 (nearly neutral). When we then tested high-density and low-density values of a_ff and a_fm, there was a large difference in group structure. In particular fVar increased, as did fPerF, that is, a very few groups became increasingly female biased. This result indicates that opposing social preferences between the sexes may regulate group structure through a process of negative feedback, and that increasingly extreme female preferences may help to buffer this process with increasing density.

Discussion

Understanding the behavioral mechanisms that give rise to group structure—i.e., Social Niche Construction—is central to predicting the evolutionary and ecological outcomes of social interactions. These interactions are best modeled at the level of individual choices, therefore we used ABS with ABC model-fitting techniques. Using this approach in D. melanogaster, we found that effects of density and aggression on group structure that were ambiguous when we examined group-level summary statistics were more transparent when we modeled them at the individual level. We have shown that there is an effect of female group choice on overall social structure. This has important implications for understanding male aggressive behavior. While some studies have shown that males who directly exclude other males from food may directly increase their mating success (Hoffmann and Cacoyianni, 1989), there are a number of exceptions to this pattern (S&F, Cabral et al., 2008). Our current results highlight the importance of the indirect effects of male behavior on female group choice. In particular, we found that heightened aggression might degrade the desirability of social environments for females, which may help explain why there are multiple successful social strategies for male D. melanogaster.

Our results give novel insight into the way that differences between the sexes define social structure in D. melanogaster, and point to a dynamic process of SNC, actively involving both sexes. The consistent negative affinity of females for males was not a priori predictable. While males can damage females with intense courtship or mating (Pitnick and Garcia-Gonzalez, 2002), it is not obvious that males should behave in ways that drive females away from patches. In fact, we found extremely strong, positive affinity of males for females, consistent with the effort males spend in courtship behavior (Greenspan and Ferveur, 2000). As well as between-sex interactions, within-sex interactions were also important in shaping group structure. We found that females tended to have positive affiliative tendencies, consistent with descriptions of egg-laying aggregation (Sarin and Dukas, 2009). For males, the strongly negative male-male affinity we found was consistent with the role of male-male aggression as an SNC behavior previously reported in S&F.

We found that complex male-female behavioral interactions that depended on density generated the social structures we observed in S&F. In our previous work, we were unable to demonstrate a role of female behavior, or response to the social environment, in SNC. Here, changes in female parameters with changes in male aggression and density show that female social group choice plays an active role in shaping group structure. The effects of female group choice were not directional however, and were more easily interpreted as buffering the effects of directional male preferences. Strong male preferences for being in groups with females apparently led to disruption of females’ preferred groups at both high aggression and high density. Joining rates in both sexes were perturbed under high aggression. Our model suggests that displaced males preferentially aggregate in groups with more females, influencing the females to leave in turn. The fact that females seem to be increasing their joining rates without changing their overall time spent on patches is consistent with results showing individuals have a baseline preference for the proportion of time they spend on patches (Saltz, 2011). At high densities, female social preferences were increasingly strong. Our predictions based on changes of a_ff and a_fm with density were that at high densities, larger, more female biased groups should form. Models suggest that male affinity for females disrupts these groups. Together, these results are consistent with published observations (Hoffmann and Cacoyianni, 1990) showing that mobile, non-territorial males may even chase females between patches.

The effects of the opposing male-female group dynamic points to an underappreciated role of decamping (or female negative group choice) as an SNC trait, and as an important component of courtship (Spieth, 1974). Mating can only occur in groups with both males and females in them. Therefore, preventing female decamping has an important role in male mating success. For males, aggression directly removes competitors from a group, by displacing other males. It may also have an important indirect role in increasing the numbers of females in a group, via females’ preferences for fewer males. Open ended selection for increased aggression does not seem to occur, however. According to indirect genetic effect theory, the net SNC effects of aggression is expected to depend on the behavior of all other males in the population (Moore et al., 1997). It is telling that increased aggression has the unexpected effect of disrupting preferred groups for both sexes. We found in S&F that the least aggressive genotypes had large groups, with more males, and high mating success. There may, then, be emergent social niches for stable, relatively large groups, containing less-aggressive males.

The study of complex systems, including social systems, is of growing importance. Our paper demonstrates the power of a model-based analysis in such contexts. Power is gained because behavior is modeled in detail, at the individual level. However, where individual level modeling is not accompanied by individual level data, an explicit solution is generally impossible. Simulation, and Bayesian methods have proven their worth in the field of behavior, particularly where there is complete information (cf Perez-Escudero and de Polavieja, 2011; Arganda et al., 2012; Mann et al., 2014; Aplin et al., 2014; Mann, 2011). However the form of our data—multiple sampled states describing spatial distributions across time—is common in animal behavior research. For instance, field observations may be restricted to spot-sampling distributions of individuals, or patterns of group membership (e.g. Oh and Badyaev, 2010; Jovani et al., 2008; Wittemyer et al., 2005), and tools to analyze this kind of data will be valuable. Here, we invoked ABC methodology, an approach that has gained traction in recent years in a variety of fields. The ABC method may be complementary to other emerging methods of model building and fitting (Franz and Nunn, 2009; Pratt et al., 2005). For example, we used simple dynamic models from the animal behavior to characterize variation resulting from genotype, density and a candidate behavior (aggression) in many replicate data sets. Once the basic dynamics of a system has been described, one could use ABC with these models to estimate the underlying parameter values which lead to patterns of group behavior such as schooling or hierarchy development (Hemelrijk, 1999); or in human social sciences (Smith and Conrey, 2007); or in complex social groups such as flies.