Properties of different selection signature statistics and a new strategy for combining them

Abstract

Identifying signatures of recent or ongoing selection is of high relevance in livestock population genomics. From a statistical perspective, determining a proper testing procedure and combining various test statistics is challenging. On the basis of extensive simulations in this study, we discuss the statistical properties of eight different established selection signature statistics. In the considered scenario, we show that a reasonable power to detect selection signatures is achieved with high marker density (>1 SNP/kb) as obtained from sequencing, while rather small sample sizes (~15 diploid individuals) appear to be sufficient. Most selection signature statistics such as composite likelihood ratio and cross population extended haplotype homozogysity have the highest power when fixation of the selected allele is reached, while integrated haplotype score has the highest power when selection is ongoing. We suggest a novel strategy, called de-correlated composite of multiple signals (DCMS) to combine different statistics for detecting selection signatures while accounting for the correlation between the different selection signature statistics. When examined with simulated data, DCMS consistently has a higher power than most of the single statistics and shows a reliable positional resolution. We illustrate the new statistic to the established selective sweep around the lactase gene in human HapMap data providing further evidence of the reliability of this new statistic. Then, we apply it to scan selection signatures in two chicken samples with diverse skin color. Our analysis suggests that a set of well-known genes such as BCO2, MC1R, ASIP and TYR were involved in the divergent selection for this trait.

Introduction

In the classical view of natural selection, beneficial mutations that can improve the chance of individuals to survive and reproduce tend to become more frequent in populations over time (Darwin and Beer 1859). However, the process of adaptive evolution has been largely beyond our understanding, especially so in domestic animals. The process of evolution contains a series of unknown demographic events, including population bottleneck, admixture of populations, migration, inbreeding and genetic drift, which further increase the difficulty of detecting selection signatures. If successful, the detection of selection signatures can provide a straightforward insight into the mechanisms creating diversity across populations and contribute to mapping the causal mechanisms related to selected traits in the genome (Andersson and Georges 2004; Oleksyk et al., 2010).

Recently with the advent of high throughput and cost-effective genotyping techniques, the ability of detecting selection signatures at the genome level has made a major breakthrough; correspondingly, a series of statistical tests have been developed to detect directional selection signatures based on different demographic models or selection models (Vitti et al., 2013). Theoretically, a novel beneficial variant that has been under pressure of selection will generate distinct signatures in the respective region of the genome such as: (i) the allele frequency spectrum is shifted towards extreme (high or low) frequencies; (ii) there is an excess of homozygous genotypes, (iii) long haplotypes exist with high frequency, and (iv) local population differentiation is extreme. All selection signature statistics that have been suggested pick up one or a combination of these signatures, for example, iHS (Voight et al., 2006) is based on the frequency of extended haplotypes within a population, whereas F_ST (Wright, 1949) uses the divergence of allele frequencies among populations. Viewed from this perspective, statistics and P-values obtained with those methods should exhibit a certain degree of correlation if they reflect fully or partly the same underlying pattern caused by selection or if they are derived from the same basic statistics, such as allele frequency spectrum. On the other hand, different methods have their own characteristics, for example, iHS is known to be sensitive in the ongoing or incomplete selection signatures, whereas XPEHH is best at revealing the selection signatures close to fixation (Sabeti et al., 2007). Accordingly, some studies used multiple methods to detect selection signatures to benefit from advantageous complementarities across methods in hope of improving the statistical power (Staubach et al., 2012; Qanbari et al., 2014).

Grossman et al. (2010) have suggested combining various signals into a composite of signals (termed CMS) mainly to improve the resolution of the detected selection signatures. A keystone of this approach is the ability to simulate data according to calibrated demographic models using the coalescent approach. For most livestock species, the actual demography is largely unknown and, if it was known, would probably be hardly suited for simulation using a coalescent approach. Beyond that, the general applicability of coalescent theory in livestock genomics was questioned by Woolliams and Corbin (2012). Driven by the basic concept of the CMS approach, Utsunomiya et al. (2013) suggested a new combined statistic, termed meta-SS, merging different genome-wide scan statistics by combining P-values using a method suggested by Whitlock (2005). It does not require any forward or backward simulation of demography and thus no assumptions on the demographic history. Randhawa et al. (2014) suggested another method termed Composite Selection Signals (CSS) which unifies the multiple pieces of selection evidence from the rank distribution of its diverse constituent tests and was successfully applied to detect selection signatures in cattle and sheep. Both meta-SS and CSS do not account for the covariance structure of the different single statistics, though.

In view of the above description, we propose an alternative strategy to combine the outcomes of several complementary tests that takes the covariance structure of the different single statistics into account. As a by-product, we will discuss the properties of the different methods based on a comprehensive simulation varying the key factors underlying the performance of the different tests. We show that in the simulation, our new method outperforms all single statistics in most of scenarios and also has higher power than the two alternative combining strategies in most cases. We then illustrate the novel combining strategy with an analysis of known selection signatures in the human and the chicken genome.

Materials and methods

Elementary selection signature statistics used

Eight different elementary selection signature statistics from three categories were computed for each single nucleotide polymorphism (SNP) position or window.

Allele frequency spectrum-based methods

As a classical neutrality test, Tajima's D compares the difference between the mean pairwise difference and the number of segregating sites in nucleotide polymorphism data to detect selection signatures (Tajima, 1989). As extensions of Tajima's D, Fu and Li's F* statistic detects selection signatures through the comparison of the number of singleton mutations and the mean pairwise difference between sequences (Fu and Li 1993). Similarly, Fu and Li's D* statistic compares the number of singleton mutations to the total number of nucleotide variants in a genomic region to reveal selection signatures (Fu and Li 1993). The three statistics were calculated for nonoverlapping sliding windows of 50 kb across the simulation data and later the whole genome in real data.

Different from these three methods, the composite likelihood ratio (CLR) statistic does not only evaluate the skewness of the frequency spectrum across multiple loci, but also incorporates information on the recombination rate to distinguish selection from other demographic events (Nielsen et al., 2005). In this study, the sofware ‘SweepFinder' (Nielsen et al., 2005) was used to calculate the CLRs.

Haplotype-based methods

As a representative for haplotype-based methods, the integrated haplotype score (iHS) was calculated for each single SNP (Voight et al., 2006) using the R package ‘rehh' (Gautier and Vitalis, 2012). Absolute values of iHS were averaged into nonoverlapping sliding windows of 50 kb across the simulation and real data.

The Cross Population Extended Haplotype Homozogysity (XPEHH) statistic (Sabeti et al., 2007) compares the amount of extended haplotype homozygosity at each locus contrasting an observed with a reference population. We used the script XPEHH (Pickrell et al., 2009) available at http://hgdp.uchicago.edu. In general, a negative XPEHH score suggests that selection happened in the reference population, whereas selection happened in the observed population. This statistic has a high power to detect selection signatures with almost or fully fixed haplotypes and also approximately follows a standard normal distribution (Sabeti et al., 2007).

Population differentiation-based methods

We calculated Wright's fixation index (F_ST) (Wright, 1949) as a widely used method to test the population differentiation with values ranging from 0 (homogeneous population) to 1 (complete differentiation). We used the two-step approach to calculate F_ST—values proposed by Gianola et al. (2010).

As a further method assessing population differentiation, the cross-population composite likelihood ratio (XPCLR) statistic was applied (Chen et al., 2010). In this study, the script XPCLR available through http://genepath.med.harvard.edu/reich was used. The corresponding parameters included: grid size 2 kb, window size 0.5 cm, maximum of SNPs within a window 200 and correlation level from which the SNPs contribution to XPCLR result was down weighted 0.25. And then, the XPCLR scores were averaged into nonoverlapping sliding windows of 50 kb across the simulation and real data.

It should be noted that the XPEHH method described above is also a method that is based on population differentiation.

A new combining strategy

When presenting the CMS approach, Grossman et al. (2010) suggested that ‘If each signature provides distinct information about selective sweeps, combining the signals should have greater power for localizing the source of selection than any single test.', which is an inspiring idea for us to reveal selection signature as comprehensively as possible. To be specific, the original CMS was developed to detect selection in each candidate region and an important assumption is that exactly one selected SNP in each localized region was assumed. Later, Grossman et al. (2013) modified this original method to scan for potential selection regions across the genome. The modified CMS did not assume any prior hypothesis and computed the Bayes factor for each test directly. The composite of multiple signals is expressed as

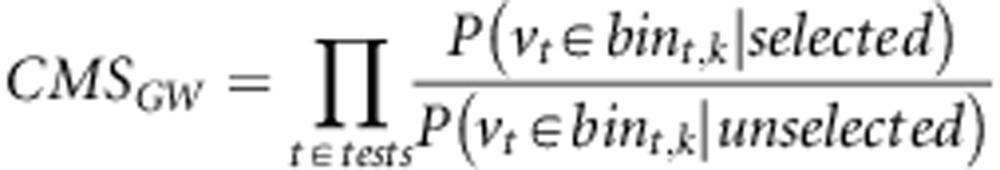Following the concept of the CMS approach (Grossman et al., 2010, 2013), we tried to promote this method to identify selection signature in domestic animals. However, coalescent simulations to derive posterior probabilities for certain values of the test statistics under selection and neutral scenarios are questionable in farm animal studies (Woolliams and Corbin, 2012) and thus calculating the posterior probabilities for calculating the Bayes factor in domestic animals is a challenge. We also note that some of the used methods reflect similar phenomena caused by selection and some degree of correlation between the statistics is expected even under the null hypothesis of no selection. Hence, we suggest a novel statistic called ‘de-correlated composite of multiple signals' (DCMS) to combine several statistics while accounting for the respective correlation. In the novel statistic, we used the ratio of (1- p_lt)/ p_lt in the place of the Bayes factor for each test in CMS for hypothesis testing directly. p_lt is the P-value in each position l for each statistic t. Correspondingly, the ‘de-correlated composite of multiple signals' at position l then is calculated as

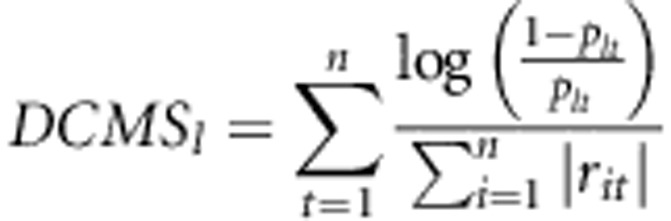where r_it is the genome-wide correlation coefficient between the test statistic of the i^th and the t^th used method. n represents the total number of used methods.

The weight factor, 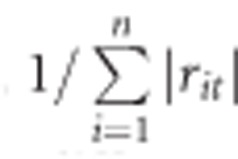suggested here, ranges from 1/n to 1. Consider a situation with n=3 different test statistics. If all of them are uncorrelated (r_i≠j=0), the weight factor will be 1 and DCMS will just be the sum of the log((1- p_lt)/ p_lt). If all of them are perfectly correlated (r_i≠j=1), the weight factor will be 1/3 and the (1- p_lt)/ p_lt will be averaged. If, say, statistics of method 2 and 3 are highly correlated (for example, r_2,3=1), but uncorrelated to method 1 (r_1,2= r_1,3=0) the respective vector of weights will be (1 1/2 1/2), thus the (1- p_lt)/ p_lt obtained with method 2 and 3 will get the same weight as the (1- p_lt)/ p_lt obtained with method 1.

Simulation

We simulated three different scenarios: the neutral case with no selection at all, a case in which two subpopulations were considered of which one was selected and the other was not (like divergent selection), and a case in which two subpopulations were considered and both were selected for the same allele (like parallel selection). Overall, we expected to match the simulated scenarios to real scenarios as closely as possible. The program msms (Ewing and Hermisson, 2010) was used to simulate population datasets under a neutral model (Neu, Neu_1 and Neu_2 after fission) and a single locus selection model (noSel, Sel, Sel_1 and Sel_2 after fission), respectively. Each simulation scenario represents a 10 Mb genomic fragment with a constant recombination rate (1cM/Mb). In the selection model, a selected allele was positioned in the center of the considered fragment (see Supplementary Information).

Table 1 summarizes different parameters applied in each simulated populations. The neutral population was modeled only with two parameters: the sample size and marker distance. Then, we defined the ‘reference scenario' for the selected populations with the following parameters: the selection coefficient was s=0.02, data for analysis were sampled when the frequency of the selected allele reached a predefined value P=0.8, selection signature statistics then were computed for sample size N=50 gametes in each selected or unselected subpopulations, and the average marker distance was d=2.5 kb. Starting from this reference setting, every parameter was varied over a range of values on a linear or exponential scale listed in Table 1, while all other parameter/levels were kept at the reference setting.

Table 1. Parameter settings varied in the simulated selection scenarios.

Parameter	Range of values
Selection coefficient s	0.005, 0.01, 0.02, 0.04, 0.08
Allele frequency P	0.2, 0.4, 0.6, 0.8, 1.0
Sample size N	10, 30, 50, 70, 90
Marker distance d	0.1, 0.5, 2.5, 12.5, 62.5 kb

Reference values are underlined.

For the neutral, the divergent selection and the parallel selection case the combinations Neu_1 vs Neu_2, Sel vs noSel, and Sel_1 vs Sel_2 were considered for between-population analysis, respectively. As to the tests without population comparisons, the Neu scenarios were used to acquire the empirical distribution and the Sel scenarios were treated as observed population for scan selection signature.

To calculate the weights in DCMS, the correlation matrix for all elementary test statistics under the null hypothesis is required. In the simulation, this correlation matrix was calculated from the data generated under the neutral model. We found that the pairwise correlations between Tajima's D, Fu and Li's D* and Fu and Li's F* are all above 0.60 and the correlation between XPCLR and F_ST is 0.10. To avoid the influence of the difference in genomic structure between simulation and real data, we also computed the correlation in real data removing all loci located at the top 5% quantile in any of the used statistics. Similarly, the pairwise correlations between Tajima's D, Fu and Li's D* and Fu and Li's F* are also high and the correlation between XPCLR and F_ST is 0.23 (0.26) in the chicken data (Table 2).

Table 2. The absolute values of correlation coefficient of the eight statistical methods were under the null hypothesis (upper triangular) and chicken data (lower triangular), respectively.

	XPEHH	XPCLR	|iHS|	CLR	Tajima D	FuLi D	FuLi F	FST
XPEHH		0.04	0.03	0.00	0.05	0.03	0.04	0.05
XPCLR	0.03 (0.03)		0.01	0.00	0.01	0.01	0.01	0.10
|iHS|	0.13 (0.08)	0.01 (0.02)		0.02	0.05	0.07	0.04	0.01
CLR	0.03 (0.02)	0.00 (0.01)	0.01 (0.02)		0.03	0.03	0.03	0.00
Tajima D	0.16 (0.13)	0.05 (0.05)	0.18 (0.16)	0.17 (0.19)		0.61	0.75	0.02
FuLi D	0.03 (0.01)	0.03 (0.02)	0.17 (0.13)	0.12 (0.10)	0.07 (0.18)		0.97	0.01
FuLi F	0.11 (0.09)	0.01 (0.02)	0.04 (0.03)	0.20 (0.20)	0.82 (0.80)	0.63 (0.73)		0.01
FST	0.03 (0.03)	0.23 (0.26)	0.05 (0.07)	0.01 (0.02)	0.02 (0.03)	0.07 (0.04)	0.03 (0.01)

Abbreviations: CLR, composite likelihood ratio; iHS, integrated haplotype score; XPCLR, cross-population composite likelihood ratio; XPEHH, cross population extended haplotype homozogysity.

Note: the correlation coefficients in lower triangular were calculated using those statistic which deleted all loci located at the top 5% quantile in any of the used statistics. Correspondingly, the scores out and in bracket represent the correlation coefficients in yellow skin population and white skin population, respectively. The absolute values of correlation coefficient of the eight statistical methods in human population were displayed in Supplementary Table S6.

Identifying potential selection signatures in simulation data

To obtain the empirical distributions of the eight elementary test statistics and the novel combined statistic, one thousand calculations for each method were run in which case neutral was assumed in the corresponding populations, and the maximum observed value of each test statistic in each run was stored. The value cutting off the upper 5 percent quantile of each statistic was used as an empirical significance threshold value that corresponded to a 5% false positive rate (FPR) in simulations.

To assess the power of eight elementary test statistics and the novel combined statistic, one thousand replicates were simulated under the considered selection scenario. A selection signature was assumed to be detected, if at least one SNP within a 500 kb window around the selected locus exceeded the empirical significance threshold. This window size was determined by the extent of linkage disequilibrium in the simulated dataset (Supplementary Figure S1). The percentage of detected signatures among all replicates is reported as empirical power. To visualize the control of FPR, half of the neutral replicates were chosen to derive the empirical distribution as described above and the remaining replicates were used to compute the FPR in accordance with the process of power calculation. In addition, the signatures outside the 500 kb window around the selected locus were also used to assess the control of FPR and a random 500 kb window located in either side of selection scenario was chosen to scan the unexpected selection signatures in each replicate. The percentage of unexpected signatures among all replicates was defined as the FPR of selection scenario.

Analysis of human HapMap data

In addition to the simulation results, we examined the potential of the different approaches in human data at the well-known locus for the lactase enzyme LCT, positioned at 135.78–135.83 Mb on chromosome 2. For this, a total of 116 582 SNPs covering the whole chromosome 2 in ‘Maasai in Kinyawa, Kenya' (MKK) population (180 individuals), ‘Utah residents with Northern and Western European ancestry from the CEPH collection' (CEU) population (165 individuals) and ‘African ancestry in Southwest USA' (ASW) population (83 individuals) were downloaded from the HapMap FTP server (ftp://ftp.ncbi.nlm.nih.gov/hapmap/genotypes/2009-01_phaseIII/plink_format/) to validate the feasibility and effectiveness of the novel combining strategy.

We examined all statistics with a similar windowing strategy as in the simulation data. The ASW population was selected as the reference population in between-population analysis. We later derived the P-value of each test from the normal distribution after normalization. Correspondingly, the DCMS was calculated in nonoverlapping sliding windows of 50 kb across the whole chromosome as described above.

Analysis of chicken data

Further to the verification of DCMS on human HapMap data, we applied the novel combining strategy to scan selection signatures in the chicken genome in a sample of chickens differing in skin color. Genotypes obtained with the Affymetrix chicken 600 k Axiom-SNP-array were used for a total of 139 chicken individuals from seven different breeds, comprising 87 individuals (Araucana, Italiener, Zwerg-Cochin and Shamo) with yellow skin color and 52 individuals (Gallus Gallus Spadiceus, Rheinländer and Vorwerkhühner) with white skin color. In the analysis, the yellow skin population was treated as observed population and the white one was treated as reference population. This study was carried out in strict accordance with the German Animal Welfare regulations. The blood-taking protocol was approved by the Committee of Animal Welfare at the Institute of Farm Animal Genetics of the Friedriech-Loeffler-Institut. Blood sampling was also notified to the Lower Saxonian authorities according to 1 8a para.1 of the German Animal Welfare Act. The blood takings were registered at the Lower Saxony State Office for Consumer Protection and Food Safety (Registration Number 33.9-42502-05-10A064).

Quality control of SNP data applied the following criteria: (i) individual call rate > 0.95; (ii) SNP call rate >0.99; (iii) SNPs in Hardy–Weinberg equilibrium in each breed (P>10e–6); (iv) SNP minor allele frequency > 0.01; (v) only autosomal SNPs with known positions were used. After quality control, we imputed the missing genotypes and inferred haplotypes using BEAGLE (Browning and Browning, 2009). The final dataset consisted of 392 280 SNPs at 28 chromosomes with an average inter-marker spacing of 2.44 kb. We calculated all eight statistics and DCMS to examine the capability of novel combining strategy for detecting selection signatures in the chicken genome as described above.

Functional annotation for chicken

On the basis of the detected selection signatures in the chicken data analysis, further bioinformatics analyses were carried out to reveal the potential biological function of genes located in putatively selected regions. This analysis involved all candidate genes/ESTs in a bracket of 250 k around the outlier signals. The program BioMart (http://www.biomart.org/, Kasprzyk, 2011) was used to search the candidate genes located in selected regions. In addition, an enrichment analysis including cellular component, molecular function, biological process and the KEGG pathway, was performed for the list of genes located in putatively selected regions using DAVID 6.7 (http://david.abcc.ncifcrf.gov/).

Results and Discussion

Simulation scenarios

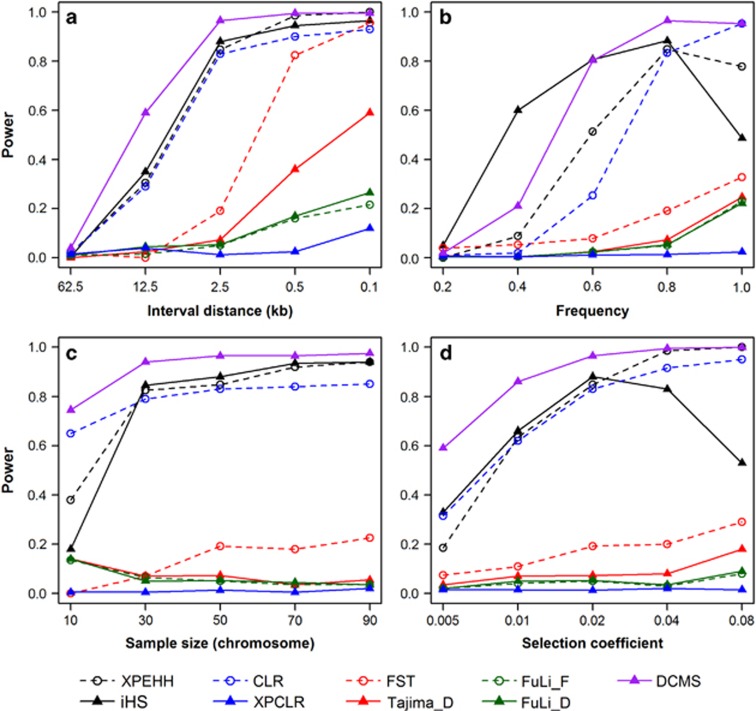
Figure 1 summarizes the power of applied selection signature statistics along with the novel combining strategies in different scenarios varying (i) marker interval distance; (ii) frequency of the selected allele; (iii) sample size; (iv) selection coefficient. Considering the results obtained with the eight elementary selection signature statistics in the differential selection scenario first, we find that there is a clear separation between the considered statistics regarding the power in the reference scenario. Three methods (XPEHH, |iHS| and CLR) have a power >70%, while for all other methods the power is <20%. Correspondingly, the FPR is approximately controlled at the targeted level (5%) for all methods (Supplementary Figure S2). Furthermore, the FPR of selection scenario can also reflect the control of FPR in this study, even though the neutral loci located at either end of a fragment may be influenced by the selected locus owing to linkage disequilibrium in selection scenario (Supplementary Figure S3).

Figure 1.

Power of eight different selection signature test statistics and the novel combining strategy when varying four different parameters: (a) Marker interval distance; (b) frequency of the selected allele; (c) sample size; (d) selection coefficient. The selected scenarios in simulation data were treated as observed population in all methods and the neutral (or no selection) scenarios was treated as reference population when the between-population was performed.

Figure 1a shows that the power of all methods increased with the decrease of marker interval. With a marker interval d=62.5 kb, which is approximately the resolution obtained when genotyping mammals with 50 k SNP arrays, all methods have low power <10% (Figure 1a). Higher resolutions (note that in Figure 1a the scale of the x axis is exponential) quickly lead to better results for the three ‘high power methods' (XPEHH, |iHS| and CLR), but in general, all methods show an improved performance with resolution d=0.1 kb, which is approximately what is obtained in sequence data. These results suggest that a denser panel of SNPs, as is assessed by re-sequencing data, is essential for detecting selection signatures. It should be noted that the power of Tajima's D and F_ST comes close to the three top methods with the highest marker density considered (Figure 1a). The low reproducibility of the results reported in some of the first genome-wide selection studies in farm animal data (Qanbari and Simianer 2014) based on medium density SNP arrays (~50 k SNPs) may be due to the lack of power demonstrated here. To further investigate the low power of all methods in the scenario with a marker interval 62.5 kb, a special empirical significance threshold value was separately defined as 1 percent of the rank of all scores in all selection replicates for each method, which is a widely used ‘outlier' approach in real data analysis. Correspondingly, we found that although the power of each method was improved and ranged from 11 to 28%, the FPRs were also increased and ranged from 40 to 93% (Supplementary Table S1). This result suggested that we can detect selection signature using high marker interval data, but at the expense of generating more serious FPR.

Regarding the frequency of the selected allele (Figure 1b), |iHS| appears to be the most powerful elementary selection signature statistic to detect ongoing selection processes when the target allele has an intermediate frequency (0.4 < P < 0.8). However, at fixation (P=1), |iHS| has limited power (~40%), while XPEHH and CLR have 98% power. The results are generally consistent with those of Sabeti et al. (2007). Furthermore, our results suggest that most of used methods, such as Tajima's D and CLR, are most sensitive in detecting fixed selection signatures (Figure 1b).

Regarding the impact of sample size (Figure 1c), it appears that a rather limited value (N=30 gametes, equivalent to 15 diploid individuals) is sufficient to reach reasonable power with the three ‘high power methods'. In contrast, the performance of the other statistics does not benefit from increased sample size (at least within the considered and rather limited range). It should be noted that nowadays in many farm animal application, much larger samples (thousands of gametes) are available (Utsunomiya et al., 2013), whereas the present study cannot provide any insight into the power of the considered methods in such a setting. However, the range of sample sizes discussed here reflects the amount of data usually available in whole genome resequencing studies in farm animals providing the most informative marker density (see Figure 1a).

In Figure 1d it is shown that the power of XPEHH and CLR monotonically increases with an exponentially increasing selection coefficient, while |iHS| has highest power with an intermediate (s=0.02) selection coefficient in this research, but the power erodes both with stronger and weaker selection. Most of the other statistics show a slight increase of power with growing selection coefficient, but overall, the power of those statistics also stays at a low level. In general, it is difficult to judge which of the simulated selection coefficients reflects selection intensities of practical relevance in livestock populations, because a wide range of selection intensities is applied. Although selection for some of the main production traits is very intense, leading to up to 1 percent improvement through genetic progress per year (Hill, 2010), selection for some functional traits, such as fertility or disease resistance, is weak, but has operated over long periods, even as ‘natural selection' prior to the actual domestication event.

For all considered scenarios, the XPCLR test displayed a weak power in comparison with the other used methods, including population differentiation-based methods and frequency spectrum-based methods (Figure 1). We speculate that this unexpected performance may be caused by the following reasons: (i) the divergent selection considered here is weaker than the completely divergent selection, in which both alleles were separately selected in different directions after fission, resulting in fixation of alternative alleles in the divergently selected lines. (ii) The XPCLR test is so sensitive that it tends to show high values in many positions, preventing the derivation of a suitable empirical significant threshold. An example can be seen in Figure 2, where XPCLR produces signals in the selected position, but almost equally strong signals in other positions as well.

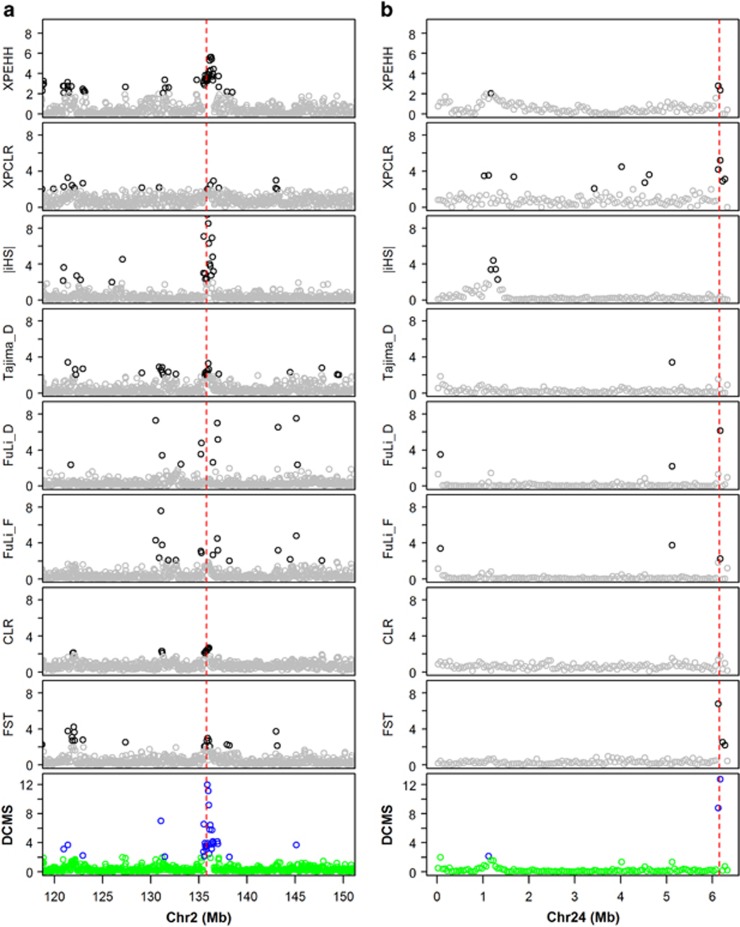
Figure 2.

Selection signature detected by DCMS in (a) Chromosome 2 in human HapMap data in the analysis of the CEU population vs the ASW population, (b) Chromosome 24 in the comparison of yellow skin vs white skin populations. The y axis reflects the −log (P-values). The red dashed line in (a) marks the location of the LCT gene in the human genome, and the red dashed line in (b) marks the location of the BCO2 gene in the chicken genome. The deep-colored symbols represent the P-value of statistical scores for each statistic less than 1%.

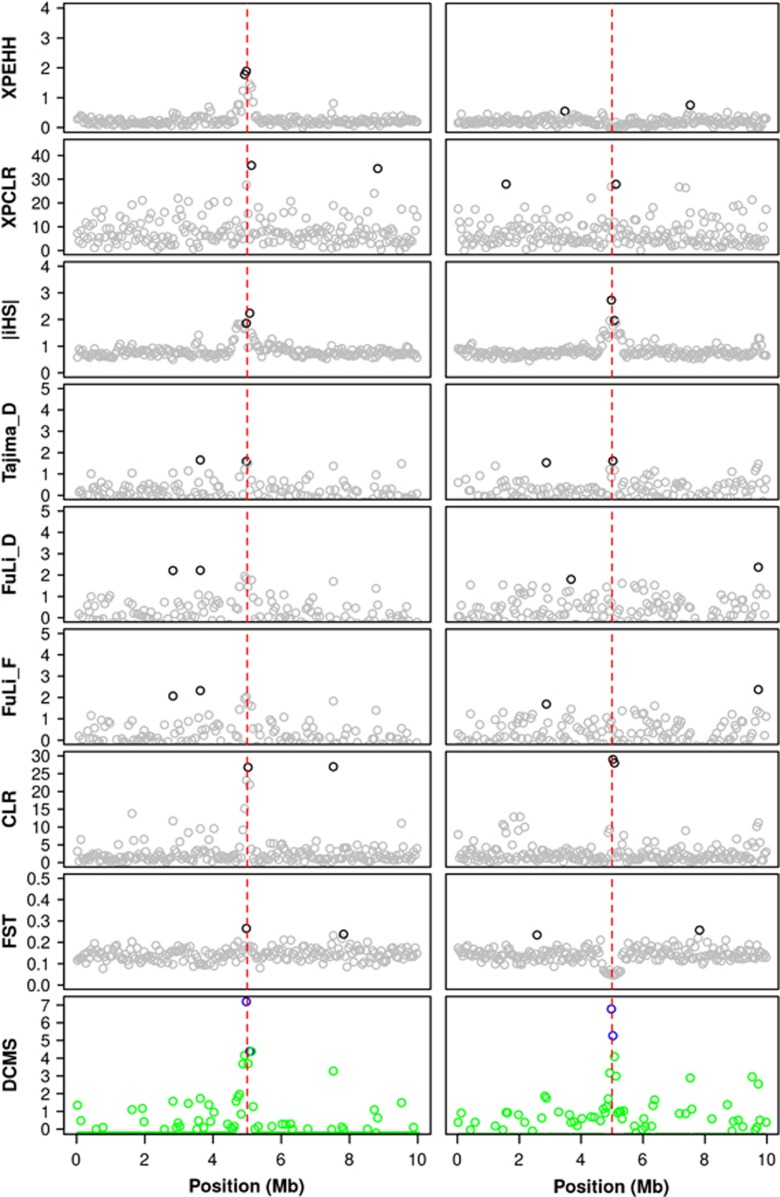
Very similar results are obtained in the parallel selection scenario when within-population methods were performed to detect selection signature in the scenarios of Sel_1 and Sel_2, respectively (Figure 1,Supplementary Figure S4). However, the two between-population methods F_ST and XPEHH have little (XPEHH) or no (F_ST) power in this case (Supplementary Figure S4). The results are consistent with those reported by Voight et al. (2006): The loci with high within-population method score in one population, but low in another population are likely to have a high between-population method score, which is similar with the scenarios of Sel_1 vs Neu_1 in this study. On the contrary, the extreme within-population method scores in both populations will contribute to the low between-population methods scores, which correspond to the results in the parallel selection scenario (Sel_1 as observed population, Sel_2 as reference population). This phenomenon is demonstrated in Figure 3, where results for two replicates (Neu_1 vs Sel_1, and Sel_1 vs Sel_2) of the simulated selection scheme under reference assumptions are depicted. Note that the loss power of those between-population methods only has a little effect on the novel combining strategy (Figure 3, Supplementary Figure S4).

Figure 3.

Observed values of the eight test statistics and the combining strategy in two replicates of the simulated reference scenario. The red dashed lines indicate the position of the SNP under selection. In the left column, the statistic was calculated between the selected population and a no selection population (Sel vs noSel), while in the right column, both populations were under selection (Sel_1 vs Sel_2). The deep colored symbols represent the top 1% quantile of statistical scores for each statistic.

Regarding the novel combining strategy, it is observed that almost all considered scenarios DCMS has highest power as the locally most powerful single test (Figure 1, Supplementary Figure S4). While the empirical power of DCMS is >50% across the whole range of sample sizes and selection coefficients considered, it is markedly reduced for marker spacings >12.5 kb and allele frequencies <0.6. However, it should be noted that DCMS even has high power (>55%) in cases where none of the elementary statistics has a power >38% (for example, with selection coefficient 0.005 both in the divergent selection case). Averaged across all scenarios, the empirical power of DCMS is 3.5 percent higher compared with the power of the respective best elementary selection signature statistic. While we see a considerable dependency even of the high power elementary statistics on the scenario (for example, iHS losing power towards fixation and high selection coefficients, and CLR and XPEHH losing power with low to intermediate allele frequencies), DCMS is more robust in that it combines the strengths of all considered elementary statistics.

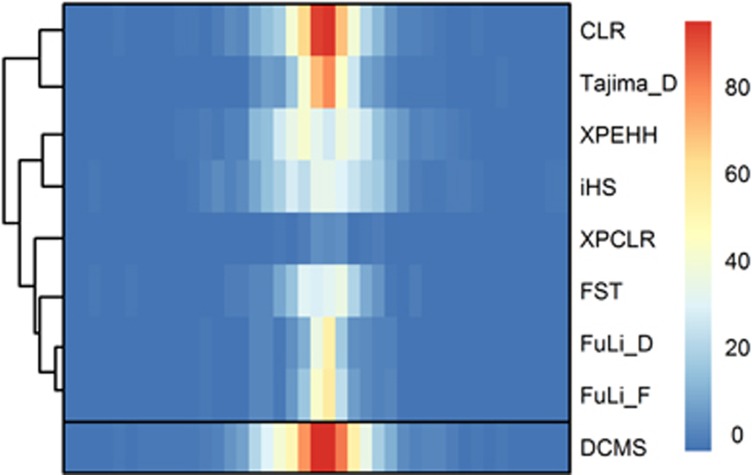
A further aspect that deserves consideration is the positional resolution of the selection signature statistic. Figure 4 shows the power of the eight statistics in a scenario with maximum marker density (d=0.1 kb) reported for intervals of 50 kb. It becomes evident that for most statistics, the highest power is concentrated around the selected position, while especially for XPEHH and |iHS|, the region of highest power is quite broad, indicating that the positional resolution is limited. Note that the |iHS| statistic was examined up to a final frequency of the selected allele at P=0.8, because under fixation (P=1), this statistic has a massive loss of power (cf. Figure 1b). Further analysis suggests that the resolutions of the methods based on frequency spectrum are better than the methods based on haplotype across the eight elementary statistics in most scenarios. Among the three ‘high power statistics', CLR has the best resolution. The spatial resolution of DCMS is comparable with it and is even better in some scenarios (Supplementary Table S2). In spite of this, we consider the power of a method to be more important than its positional resolution, because the successful detection of a region carrying a selection signature is the primary task of selection signature analysis. On the left margin of Figure 4, the clustering of the eight used elementary statistics reflecting the correlation structure is shown.

Figure 4.

Heat map of the empirical power (in per cent) of eight different selection signature test statistics and the novel combining strategy in 50 kb intervals. The simulated scenario was s=0.02, N=50, d=0.1 kb and P=1.0 (for |iHS|, P=0.8). The middle of this graph indicates the position of the SNP under selection. The clustering of the test statistics is indicated on the left margin for eight used methods.

Comparing DCMS with other combining strategies

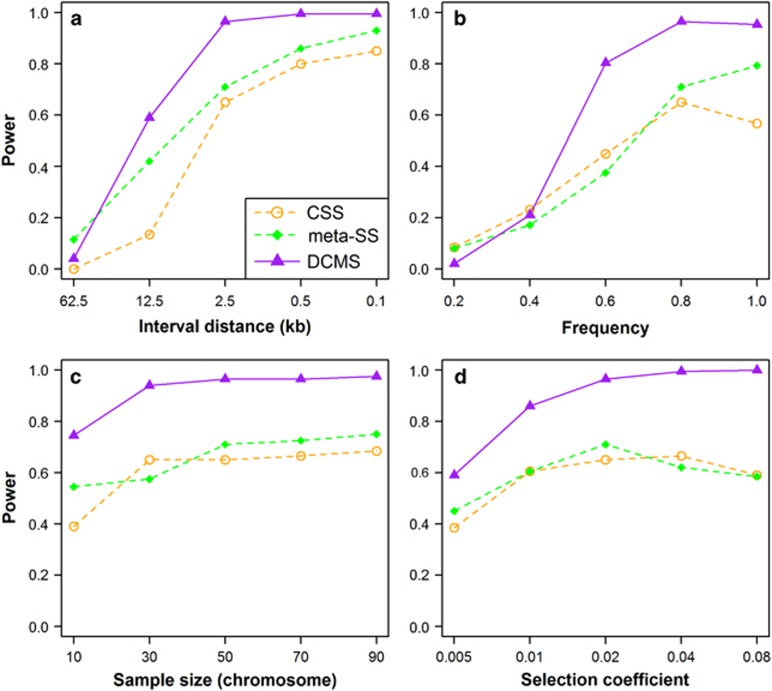
In a further step, we compared DCMS strategy to two previously reported combining methods: CSS (Randhawa et al., 2014) and meta-SS (Utsunomiya et al., 2013). As shown in Figure 5, the power of DCMS is higher than any of them in most scenarios in our simulation data, with the exception of the largest interval distance d=62.5 kb and the smallest allele frequency P=0.2 considered, in which meta-SS and CSS has some power whereas the competing methods have not. Across all scenarios considered, DCMS, on average, has 21.32 (21.82) percent more power than meta-SS (CSS). As described above, meta-SS and CSS are based on the P-values and the test statistics of the elementary tests, respectively. It should be noted that some of the underlying assumptions of DCMS and meta-SS using P-values of the elementary statistics are hardly met, as the P-values of some of the single tests are not P-values in the classical statistical sense, but reflect quantile values from the empirical distribution of test statistic values under selection.

Figure 5.

Comparison of the novel combing strategy DCMS and alternative combining methods CSS (Randhawa et al., 2014) and meta-SS (Utsunomiya et al., 2013) when varying four different parameters: (a) Marker interval distance; (b) frequency of the selected allele; (c) sample size; (d) selection coefficient.

In the meta-SS approach, Utsunomiya et al. (2013) assumed scan statistics to be largely uncorrelated, although in their case study Pearson correlations of Z-transformed P-values partly were in the range of 0.5. In our case, different statistics are partly highly correlated as well. We also note that ‘one-sided upper tail P-values' may increase the FPR in real data analysis for those methods that can distinguish selection directions correctly, for example, the positive scores in XPEHH generally suggests that selection happened in the observed population, otherwise with negative scores, selection happened in the reference population. In addition, the uniform penalization for eight single statistics may decrease the contribution of selection loci with small P-values in the process of combination. Different from the methods based on P-values, the CSS method combines the test statistics directly through obtaining the inverse cumulative distribution function for a normal distribution after ranking the statistics for each used method (Randhawa et al., 2014). This method may enlarge or reduce the true effect of selection for some methods, especially for the methods with unknown distribution of the test statistic. In comparison with the meta-SS, the novel combining strategy does not only remove (partly) duplicated information through a weight factor, but also decreases the influence from uniform penalization, which may be the key point why the power of DCMS is better than meta-SS. A potential cause for the limited power of the CSS method may lie in the fact that information reflected by outstanding signals of an elementary statistic (or, equivalently, extremely low P-values at this location) is partly leveled out when using the ranks.

To evaluate the DCMS approach in comparison with the CMS approach, we used data on the five elementary statistics reported in Figure 2 of the study by Grossman et al. (2010) around the MATP gene, a well-characterized region under positive selection in humans. Totally, the data contain 702 loci and extend approximately 1 Mb genome region on chromosome 5. Correspondingly, the DCMS scores were calculated in each locus and the distribution of normalized DCMS without log transformation showed the similar trend as the results of CMS (Supplementary Figure S5). Note that the selected location around 51.78CM identified by DCMS is the same as the location detected by CMS, and the corresponding DCMS score (26.06) is even a little higher than the CMS score (22.93). It should be noted that the DCMS strategy yields very similar results as CMS while bypassing the complex demographic simulation process, which, as was argued before, might be not applicable in species of unknown or too complex demography, such as farm animals.

Results obtained with human HapMap data

To further validate the DCMS approach, we applied this novel strategy to detect the selection signatures on chromosome 2 in human HapMap data to target the established selection sweep around the lactase gene LCT. As an established sweep, the selection of the lactase gene was usually explained as lactose tolerance (Bersaglieri et al., 2004). The corresponding allele nearly has an allele frequency P=0.8 among the population with European descent, and there is evidence of a selection signature spanning roughly 1 Mb (Bersaglieri et al., 2004). As expected, extreme scores of DCMS around the location of the LCT gene were observed in this region in CEU population (Figure 2a), whereas the ASW population did not show any extreme signal (Supplementary Figure S6A). Although some of the elementary methods also detect the selection signature in the CEU population correctly, the DCMS provides the strongest signal (Figure 2a). Correspondingly, the −log(P-value) of DCMS (11.97) around the location of LCT gene is greater than any of used statistic, including the highest −log(P-value) of |iHS| (9.46). A very similar result was also found in MKK population (Supplementary Figure S6C), pastoral people in Kenya, whose traditional diet of milk is rich in lactose (Wagh et al., 2012).

Results obtained with chicken data

The novel combining strategy was also applied to scan selection signatures in two sets of chicken populations with different skin color. In the chicken genome, a cis-regulatory mutation in BCO2 gene has played a significant role in the evolution of skin color (Eriksson et al., 2008). This gene has therefore been treated as a proof of principle displaying that ZHp could identify selection signatures by Rubin et al., (2010). As an established sweep, the region around BCO2 gene was also detected as being under selection in both populations using the novel combining strategy in this study (Figure 2b and Supplementary Figure S6B).

In general, the classical features of selection signatures should contain two major elements: a long range haplotype and a high allele frequency (Sabeti et al., 2002). In this potential selection region, the mean value of pairwise r² is 0.604 exceeding the mean value of 0.209 in whole genome as well as the mean value of 0.221 in most selection regions. At the region of 6.10–6.20 Mb, the heterozygosity in yellow skin population (red) is almost 0 which suggests that the corresponding alleles have been nearly fixed, on the contrary, the divergently selected haplotype was observed in white skin population (green) (Supplementary Figure S7C). Correspondingly, the divergent allele frequency around BCO2 gene in two populations can be observed in Supplementary Figure S7A and S7B, respectively. A further exploration suggests that a total of seven SNPs fell into the BCO2 gene in our research. Note that the corresponding haplotype of ‘CGCCGCG' with the frequency of 0.874 was observed in yellow skin population. However, those SNPs were divided into three different haplotypes in white skin population.

Through scanning selection signatures in chicken genome, a total of 18 396 windows in each population were combined by the DCMS approach (Supplementary Table S3). After normalization, the empirical distributions of those statistical methods approximately follow a normal distribution with a small skew (Supplementary Figure S8). Correspondingly, the scores that reached to the significant level (⩽0.05) were treated as outliers for further analysis. In pooled populations of yellow skin chickens, 1013 outlier regions were detected spanning over 50.65 Mb of the genome. Similarly, 1013 outlying windows covering 50.65 Mb of the genome were found in white skin pool (Supplementary Table S4). On basis of candidate selection signatures identified by combining strategy, the genes close to the putative outliers were explored using the available annotation of the chicken genome (Annotation Release 102). The results of enrichment analysis did not show any intuitive information on selection. However, many of genes recognized under selection were observed in our list (Supplementary Table S5). It is noteworthy that a series of genes associated with pigmentation were summarized in Table 3, which should be credited to the experimental populations with different skin color in this study. Among them, another famous gene, the melanocortin 1 receptor (MC1R), located between 18.287 and 18.288 Mb on GGA11 was also identified under selection in this research. Traditionally, MC1R is an important candidate gene relevant to the regulation of coat and feather color in chicken and other mammals. The complex function of this gene determines which type of color is produced through gene switching and copy number variation of MC1R variant alleles and some reports also suggest that this gene may play a role in the regulation of skin color in chicken (Guo et al., 2010; Dalziel et al., 2011). In addition to those two well-known genes, a set of windows with extreme P-value coincide with a cluster of genes involved in melanogenesis and pigmentation, including the dopachrome tautomerase (DCT) gene and the tyrosinase (TYR) gene located on GGA1, the osteopetrosis associated transmembrane protein 1 (OSTM1) gene located on GGA3, the orthodenticle homeobox 2 (OTX2) gene located on GGA5 and the endothelin 3 (EDN3) gene located on GGA20.

Table 3. A partial list of candidate genes revealed by DCMS analysesa.

Chr.	Gene b	Position (kb)2	P-value	Skin color	Function/association (Reference)
1	DCT	145325;145275;	0.011;0.037;	Y;W;	Pathway: Melanogenesis, organism-specific biosystem, Pigmentation (Anno et al., 2010)
1	TYR	187125;	0.017;	Y;	Melanogenesis (Anno et al., 2010)
3	OSTM1	67325;65875;	<0.001;0.047;	Y;W;	Pigmentation (Anno et al., 2010)
5	OTX2	51375;	0.003;	W;	The developing retinal pigment epithelium (Nishihara et al., 2012)
11	MC1R	18275;18275;	<0.001;0.044;	Y;W;	The regulation of coat, skin and feather color (http://www.chickencolours.com/Pigment%20holes%20Paint%20Silkies.pdf)
12	MITF	15375;15425;	0.008;0.021;	Y;W;	Regulating the differentiation of pigment cells (Tsukiji et al., 2009)
20	ASIP	1425;	<0.001;	Y;	Pigmentation in skin (yellow) and feather (Nadeau et al., 2008)
20	EDN3	11175;	0.003;	Y;	Promoting melanoblast proliferation (Dorshorst et al., 2011)
24	BCO2	6125;6125;	<0.001;0.003;	Y;W;	The deposition of yellow carotenoids in the skin (Eriksson et al., 2008)

^aAll related genes are close to potential selection regions. See Supplementary Table S4

.

^bThis column presents the middle position of selection regions, the bold and italics represent the genes without detailed annotation in chicken.

Conclusions

In this study, we discussed the statistical properties of eight different elementary selection signature statistics based on extensive simulations. Most remarkable is the clear evidence for the usefulness of high density markers in selection signature analysis, suggesting that whenever possible, such studies should be based on sequence data—even at the cost of small sample size—whereas results obtained with low to medium density SNP arrays appear to be of limited reliability, explaining partly the limited reproducibility of selection signature results reported in the literature (Qanbari and Simianer 2014). Although all elementary statistics are shown to have little power in some areas of the examined parameter space, the suggested novel DCMS statistic uniformly has the locally highest power and thus should be preferably considered. Compared with other combining strategies, it has the advantage to be easily computable even in populations with not sufficiently known demography (compared with CMS), and to account for correlations of the elementary test statistics, which were found to be too large to be ignored. When applying DCMS, the detailed results of all elementary statistics will be available, such that the overall decision whether a selection signature is detected can be made on basis of the DCMS statistic, while the nature of the signature, for example, whether it was caused by within or between breed selection, can be assessed through a closer inspection of the profiles of the elementary statistics.

Selection signature analysis is a relatively novel and highly promising approach in livestock population genomics, an accurate and comprehensive set of selection signatures will be the basis for a better understanding of the forces driving artificial selection and will help to design more efficient livestock breeding programs.

Data archiving

Data deposited in the HapMap FTP server: ftp://ftp.ncbi.nlm.nih.gov/hapmap/genotypes; Chicken data are available from the Dryad data repository: http://dx.doi.org/10.5061/dryad.pf093

The authors declare no conflict of interest.