Dispersion corrected DFT approaches for Anharmonic Vibrational Frequency Calculations: Nucleobases and their Dimers

Abstract

Computational spectroscopy techniques have become in the last years effective means to analyze and assign infrared (IR) spectra for molecular systems of increasing dimensions and in different environments. However, transition from compilations of harmonic data to full anharmonic simulations of spectra is still under way. The most promising results for large systems have been obtained, in our opinion, by perturbative vibrational approaches based on potential energy surfaces computed by hybrid (especially B3LYP) density functionals and medium size (e.g. SNSD) basis sets. In this framework, we are actively developing a comprehensive and robust computational protocol aimed to a quantitative reproduction of the spectra of nucleic acid bases complexes and their adsorption on solid supports (organic/inorganic). In this contribution we report the essential results of the first step devoted to isolated monomers and dimers. It is well known that in order to model the vibrational spectra of weakly bound molecular complexes dispersion interactions should be taken into proper account. In this work, we have chosen two popular and inexpensive approaches to model dispersion interaction, namely the semi-empirical dispersion correction (D3) and pseudopotential based (DCP) methodologies both in conjunction with the B3LYP functional. These have been used for simulating fully anharmonic IR spectra of nucleobases and their dimers through generalized second order vibrational perturbation theory (GVPT2). We have studied, in particular, isolated adenine, hypoxanthine, uracil, thymine and cytosine, the hydrogen-bonded and stacked adenine and uracil dimers, and the stacked adenine-naphthalene heterodimer. Anharmonic frequencies are compared with standard B3LYP results and experimental findings, while the computed interaction energies and structures of complexes are compared to the best available theoretical estimates.

1 Introduction

The study of the adsorption of nucleic acid bases on organic and inorganic substrates and the detailed characterization of their supra-molecular structure, orientation and dynamics have numerous applications in different areas, such as materials science, nanotechnology, surface science, catalysis, biosensing, cell biology, etc.^1-8. A comprehensive analysis of the properties of these systems could be very useful for designing highly biocompatible materials and specific biosensors^9-14. DNA-based biosensors, for example, can consist of probes attached to functionalized substrates with the capability of recognizing and capturing specific DNA targets. In these hybrid systems, the nature of the interactions between purines/pyrimidines and the substrates is critical for the effective functionality of the devices and thus its characterization is a mandatory starting point for developing and improving high quality technologies^15-20 and finely tuned therapies^21,22.

Moreover, nucleic acid bases are powerful biomaterials for realizing rationally designed and functionally enhanced nanostructures for homogeneous dense surface coatings, bottom-up nanopatterning, and 3D nanoparticle lattices²³.

The investigation of the adsorption of nucleobases on different substrates is also particularly relevant in the prebiotic context to identify the role played by solid supports in the processes that led to the emergence of life, which is one of the open questions of the astro-biological research. As already reported in previous works, these molecules are prebiotically available and their adsorption on solid interfaces could be correlated to their effective preservation and resistance to degradation as well as to the improvement of their prebiotic conversion into complex biologically functional molecules^24-30. Indeed, self-organization and self-interactions of biomolecules at interfaces were most likely responsible for the evolution from inanimate matter to biological systems.

The binding of nucleobases to substrates can be affected by a large variety of factors such as the type of material which the interface is composed of and the exposed superficial area, the presence of water and electrolytes, the concentration of the adsorbates. Adsorption of organic molecules onto surfaces is a complex thermodynamic process, in which the mutual orientation of the molecules should be energetically favourable. Molecules can adopt highly anisotropic distributions and be self-organized in disordered arrangements, they can lay flat on the surfaces forming various types of layers, be inclined or even aligned with certain directions of the interfaces. The competition between molecule-surface and molecule-molecule interactions can control their behaviour. Molecular organization usually depends on the synergistic combination of specific and nonspecific interactions, e.g., ionic, covalent, van der Waals, hydrogen bonding, solvophobic, etc. As a consequence, in order to investigate and identify possible adsorption mechanisms and the final configurations, many factors should be taken into account.

Among the various types of investigations, vibrational spectroscopy can be used to characterize, at the molecular level, the forces acting on the various components of the nucleobase-surface complexes. This is important for the analysis of functionalized nanostructures and of particular relevance for prebiotic processes, interpretation of astronomical data and detection of organic compounds in extraterrestrial environments.

However, due to the great variety of interactions between the adsorbate and the interface and to complex environmental factors, the results of experimental spectroscopic studies on these kinds of systems are difficult to interpret³⁰. Even though some hints can be obtained through the comparison with available gas-phase spectroscopic data, these are not sufficient for a complete characterization of their properties. The main problem is related to the presence of the substrate, which could influence intra-molecular interactions in comparison with the gas phase scenario and could be responsible for the formation of supra-molecular complexes and thus the appearance of new spectroscopic features. Considering these premises, it is extremely difficult to identify the geometrical arrangement of the nucleobases on the surface and their interaction sites from the analysis of the experimental data only, especially at low coverage.

A factual determination of the geometry of molecular adsorbates may be better achieved by employing quantum mechanical (QM) computations. Recent improvements in computational methods have led to better understanding, at the atomic level, of nucleic acid base properties, their tautomerization, conformation and pairing and have also shown to be a powerful tool to interpret and predict experimental spectroscopic results^31-42. This is especially useful in the case of IR spectra where it is often difficult to attribute some frequencies to a particular vibrational mode of the molecule, and becomes even more important for complex systems, where differently oriented/adsorbed molecules have specific spectral patterns. For example computational spectroscopy studies of a hybrid organic-inorganic system, namely glycine adsorbed on silicon⁴³, lead to a more correct interpretation of the experimental results⁴⁴.

The present work is aimed at identifying a general, reliable and effective computational strategy, based on fully anharmonic computations of the vibrational wavenumbers and IR intensities, to analyze and assign IR spectra of nucleic acid bases-solid-support complexes. A plausible way of studying the intricate interactions mentioned above is through a multistep strategy. This consists in performing a series of studies on the isolated bases, base pairs and multicomponent configurations (nucleobases in various environments such as adsorbed on inorganic and organic substrates, in aqueous solution, etc.). The present investigation describes the first two stages, focussing on: the isolated nucleobases adenine, hypoxanthine, uracil, thymine and cytosine, the hydrogen-bonded and stacked dimers of adenine and uracil and, finally, a first example of interaction with a substrate that is the stacked adenine-naphthalene heterodimer.

Vibrational frequency calculations are necessary to verify if the optimized geometries of the chosen compounds are minima on their potential energy surfaces (PES) and are used to characterize the thermodynamic properties of the molecular system. In these calculations molecular conformations play a central role for determining the harmonic frequencies, and reliable structures are necessary starting points for further calculations, while accuracy requirements increase moving from simple confirmation of the nature of stationary points to the analysis of vibrational spectra through computed data (frequencies and intensities) which could be compared to experimental measurements. The common approach to correct frequencies for anharmonicity and improve their agreement with the experimental findings is obtained by using simple scaling factors^45-49, or more sophisticated scaling methods^50-52. Mode specific scaling improves the agreement between computed and experimental vibrational frequencies, but the uncertainty of the optimized scaling factors cannot be lower than 0.02⁴⁷ and the problem of transferibility is not trivial. Furthermore, due to the different role played by anharmonicity in vibrational frequencies, zero-point vibrational energies (ZPVE), and partition functions, different scaling factors must be used. As a consequence, the definition of a consistent procedure becomes rather cumbersome^47,53,54. On the contrary, consistent procedures can be derived from QM computations of vibrational properties beyond the harmonic approximation. Recently, exact solutions for the treatment of few active modes to the vibrational problem for a generic system has been proposed⁵⁵ and effective schemes to compute vibrational frequencies within the second order vibrational perturbative (VPT2)^56-75 or vibrational self-consistent field (VSCF) based^76-85 approaches have been developed and implemented. In particular, a general VPT2 framework to compute thermodynamic properties, vibrational energies and transition intensities from the vibrational ground state to fundamentals, overtones and combination bands^66,67,86-88 has been developed in our group. It should be noted that information about the intensities of overtones and combination transitions, not available from any computations based on the double-harmonic approximation, is required to reproduce the overall band pattern, and might be necessary to correctly analyze experimental outcomes, for example to distinguish low-intensity features related to non-fundamental transitions of the most populated species present in experimental mixtures from fundamental transitions of the less abundant species^89,90. The fully ab initio VPT2⁸⁸ approach allows also inclusion of non-specific solvent effects by means of the polarizable continuum model (PCM) essentially without any additional cost⁹¹, and has been also extended to take into account non-equilibrium solvent effects on vibrational (e.g. IR or VCD) transition intensities^92-94.

The VPT2 model, combined with a semi-diagonal fourth-order polynomial representation of the anharmonic force field in terms of normal modes, evaluated by means of Density Functional Theory (DFT) using hybrid or double-hybrid functionals with polarized double- or triple-zeta basis sets, is particularly appealing to treat medium-size semirigid systems. Indeed, it has been shown that this methodology provides very accurate vibrational properties at a relatively low computational cost (see for example Refs.^90,95-99). As gathered from literature, B3LYP^100,101 with double-zeta plus polarization functions basis sets^{33,41,65,73,90,95,102-107} is a cost-effective approach providing accurate vibrational spectra of medium-size semirigid systems.

However, when dealing with molecular complexes of aromatic compounds, such as nucleobases and their dimers, it should be taken into account that, depending on the relative position of the molecules, dispersion interactions could play a major role in determining the stability of the systems. Unfortunately, standard functionals fail in describing such non-local and non-classical electronic interactions¹⁰⁸. Instead, this type of interactions can be modelled at a relatively low computational cost by using dispersion-corrected DFT methods^109-111 and new functionals^112-115. However, some of the most successful last-generation functionals (M06-2X¹¹³ and ωB97X^114,116) do not predict vibrational wavenumbers with an accuracy sufficient for spectroscopic studies^31,89,90,117. On the other hand addition of semi-empirical dispersion corrections to B3LYP (leading to B3LYP-D^109,110) showed better promises for accurate computation of vibrational properties for larger weakly bound molecular systems where dispersion/stacking interactions cannot be neglected^31,41,117. Considering also other B3LYP-based dispersive methods, we have chosen the improved version of Grimme’s correction, B3LYP-D3^111,118 coupled to the SNSD basis set and the last version of dispersion-correcting potentials by Di Labio (B3LYP-DCP^119-122 with the companion 6-31+G(2d,2p) basis set), for calculating anharmonic frequencies of nucleobases and their dimers. The results have been compared with both B3LYP data and experimental findings in order to identify which DFT-based dispersion-corrected model was the most reliable for simulating vibrational spectra. Both DFT-D3 and DCP have shown good performance in predicting structural parameters and binding energies of non-covalent adducts but they have not been validated yet for anharmonic vibrational frequencies. In particular, the DFT-D3 approach, which is the last refined version of DFT-D^110,123,124 parameterized for the 94 elements of the periodic table, has been used successfully to describe tripeptide-folding, metallic systems, graphene, benzene on the Ag(111) surface and other molecular complexes¹¹¹. Then, the recently proposed B3LYP-DCP method (developed for H, C, N, and O), which corrects B3LYP by using atom-centered effective core potentials (dispersion-correcting potentials - DCPs) composed of Gaussian-type functions^119-121, is able to model satisfactorily π-stacking, steric repulsion noncovalent interactions and also hydrogen bonding¹²².

The paper is organized as follows: after providing a short description of theoretical models applied for computation of vibrational wavenumbers and IR intensities (section 2), we analyse in detail spectra of isolated nucleobases by comparison with experimental data (section 3.1). The computed interaction energies and structures of complexes provided by both dispersion-corrected models are compared with the best available theoretical estimates in section 3.2, along with effects of intermolecular interactions on vibrational spectra, considering both frequency and intensity changes. General conclusions and perspectives are given in the last section.

2 Computational Details

Geometry optimizations together with harmonic and anharmonic vibrational frequency calculations of isolated nucleobases were performed at the B3LYP/SNSD, B3LYP-D3/SNSD and B3LYP-DCP/6-31+G(2d,2p) levels.

The B3LYP-D3 and B3LYP-DCP methods have shown good performances in predicting structural parameters and binding energies of chemical systems involving mainly dispersion interactions but they have not been validated yet for vibrational frequencies. In particular, the DFT-D3 approach is the last refined version of DFT-D, which models dispersion by adding to the density functional a semi-empirical dispersion term (DFT-D), that is a long-range attractive pair-potential (inversely proportional to the sixth power of the intermolecular distance) multiplied by a damping function which determines the range of the dispersion correction in order to avoid near singularities for very small distances and double-counting of correlation effects at intermediate distances^110,123-124. In DFT-D3, atom-pairwise specific dispersion coefficients and cutoff radii computed from first principles have been introduced together with dispersion coefficients dependent on coordination numbers (geometry). These modifications lead to an improved accuracy and a wider range of applicability¹¹¹.

Instead, the recently developed B3LYP-DCP method corrects B3LYP by using atom-centered effective core potentials (dispersion-correcting potentials - DCPs) which model dispersion by modifying the environment in which the valence electrons move^119-121, composed of Gaussian-type functions, with the following general form:

$$U_l\left(r\right)=r^{-2}\sum _{i=1}^{N_l}{c}_{li}{r}^{n_{li}}{e}^{-{\zeta }_{li}{r}^2}$$

where N_l is the number of Gaussian functions, n_li is the power of r (set to 2 throughout this work), c_li is the coefficient of the Gaussian, and ξ_li is its exponent. Functions are local (l = p for H and l = f for C, N, O) or are semilocal (l = s for H and l = s, p, or d for C, N, O), and operate on electron density in specific angular momentum channels. The DCPs used in this work were developed by optimizing c_li and ξ_li values such that the error in the predicted interactions chosen from a set of noncovalently bonded dimers (the “fitting” set) was minimized relative to those obtained by CCSD(T)/CBS-quality methods¹²².

Effective core potentials are normally used in simulations involving metals and other heavy atoms, and in this case they are employed to account for dispersion interaction.

B3LYP-based approaches have been chosen because this hybrid functional has been extensively validated for the prediction of vibrational frequencies with the accuracy necessary for a quantitative comparison with experimental data. The B3LYP/N07D method has been employed to calculate anharmonic frequencies of several closed- and open-shell molecular systems^{43,90,117,125-131}, and a recent extension of N07D, the SNSD basis set, with the inclusion of diffuse s functions on all atoms and one set of diffuse polarized functions, d on heavy and p on hydrogen atoms, has improved its performance (Double and triple-ζ basis sets of SNS and N07 families, are available for download. 2012; visit http://dreamslab.sns.it)^132,133.

All structures have been optimized using tight convergence criteria. Anharmonic frequencies at optimized geometries have been obtained, with the DFT methods mentioned above, by means of the fully-automated, second-order vibrational perturbation approach (VPT2), as implemented in the GAUSSIAN package. Recently, the method has been extended to compute anharmonic infrared and Raman intensities of the fundamentals, overtones and combination bands^66,67,87,90. In order to calculate anharmonic frequencies and IR intensities, the underlying semi-diagonal quartic potential energy and cubic electric dipole moment surfaces have been derived through numerical differentiations on geometries displaced from equilibrium along the normal modes (with a 0.01 Å step). Vibrational wavenumbers have been computed within the generalized VPT2 model (GVPT2), where nearly-resonant contributions are removed from the perturbative treatment (leading to the deperturbed model, DVPT2) and treated in a second step variationally^61,66,68. This model, as implemented in the GAUSSIAN package⁸⁶, provided accurate vibrational wavenumbers for several semi-rigid systems^{31,32,90,97-99,103,104,117,129,130,132,134,135}. Such an approach relies on semi-empirical thresholds for Fermi and Darling-Denninson resonances. In the present work, the criteria proposed by Martin et al.⁶⁸ for Fermi resonances have been chosen as they provide accurate results for fundamental bands¹³⁴, overtones and fundamental transitons¹³⁶. Within GVPT2 computations the force constants related to the strongly anharmonic out-of-plane vibrations of amino group, poorly described by Cartesian normal modes, have been excluded from the vibrational perturbative treatment (SKIPT2 option). Moreover, considering the computations of IR intensities within the DVPT2 model, the values of the threshold for 1-1 resonances have been varied between 2 and 10 cm⁻¹, in order to get converged results.

Geometry optimizations followed by harmonic and anharmonic vibrational frequency calculations were performed also for the hydrogen-bonded and stacked homodimer structures of uracil and adenine, and the stacked heterodimer structure of adenine-naphthalene, starting from geometries reported in the literature^137-140. Dimer binding energies have been computed as differences between dimer total energies and the sums of the total energies of isolated monomers, taking into account the basis set superposition error (BSSE) via counterpoise correction (CP)¹⁴¹. Moreover, the anharmonic zero-point vibrational energies (ZPVE) of monomers and dimers have been computed by means of our resonance-free formulation^86,142 and used to obtain anharmonic ZPVE corrections to the interaction energies.

All calculations have been carried out employing a locally modified version of the GAUSSIAN suite of programs¹⁴³.

3 Results and discussion

3.1 Monomers

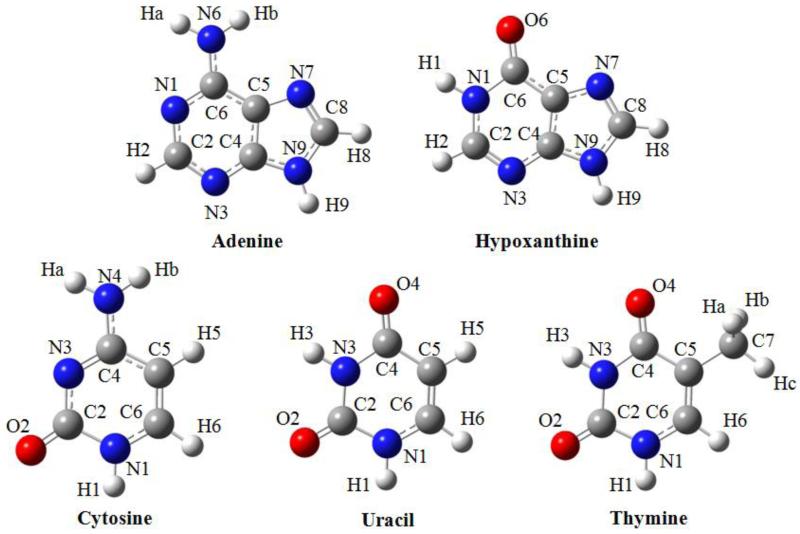
B3LYP optimized geometries and atom numberings of the investigated nucleobases are shown in Figure 1. The detailed results of harmonic and anharmonic frequency DFT calculations for the isolated nucleobases are reported in the supplementary material (Tables 1-5) where they are compared with the available experimental data. Assignments of vibrational modes were performed by visual inspection of the atomic displacements along normal modes and by comparison with the assignments reported in the literature^{31,32,34-36,39,144-147}.

Figure 1.

Geometries optimized using B3LYP and numbering schemes of nucleobases investigated.

3.1.1 DFT and hybrid CC/DFT approaches: Uracil

We start our analysis from the uracil molecule, devoid of problems related to the description of out-of-plane NH₂ vibrations, and for which highly accurate theoretical studies are available³². For uracil we have considered also M06-2X¹¹³, ωB97XD¹¹⁴ and B2PLYP^130,148 functionals, in order to further check their performances for anharmonic frequency computations. Table 1 compares harmonic frequencies computed at the DFT level to the best theoretical estimates of CCSD(T)/CBS quality³², while DFT and hybrid anharmonic frequencies are compared to experimental results. In line with previous studies, B3LYP provides fairly accurate anharmonic frequencies, with a Mean Absolute Error (MAE) of about 12 cm⁻¹, and maximum discrepancies lower than 35 cm⁻¹. The overall result is due to the good quality of both harmonic contributions and anharmonic corrections, and not to a fortuitous cancellation of errors. The overall accuracy can be improved by hybrid computations, with the harmonic part computed at higher levels of theory, here B2PLYP/aug-cc-pVTZ and CCSD(T)/CBS, which in both cases lead to MAEs within 10 cm⁻¹. Moreover the best theoretical estimates at the CC/DFT level lower maximum discrepancies to 25 cm⁻¹. It is noteworthy that, although harmonic frequency computations at the CCSD(T)/CBS level are at present limited to systems with up to 10-15 atoms, the B2PLYP/B3LYP model can be applied also for larger systems of biological and/or technological interest^40,90. Concerning dispersion-corrected DFT approaches, B3LYP-D3 provides results essentially equal to B3LYP, for both harmonic frequencies and anharmonic corrections, so the same improvements can be obtained by hybrid models. All the other DFT models, B3LYP-DCP, M06-2X and ωB97XD yield less accurate harmonic frequencies, with MAEs of about 20 cm⁻¹ and maximum discrepancies larger than 50 cm⁻¹. Moreover, for M06-2X and ωB97XD the quality of results is worsened for anharmonic corrections. Although for uracil the MAEs shown by M06-2X and ωB97XD are slightly lower than those previously reported for other systems^31,89,90,117, both functionals show again non-systematic maximum deviations (MAX) larger than 100 cm⁻¹, accompanied by large errors (50-100 cm⁻¹) for several important spectral features (e.g. N-H or C=O stretching vibrations). On the other hand, the large MAE of anharmonic B3LYP-DCP frequencies can be essentially attributed to the errors in the harmonic part. Thus, in the following we will focus on B3LYP, B3LYP-D3 and B3LYP-DCP results, considering B3LYP as a reference for both harmonic frequencies and anharmonic corrections.

Table 1.

Experimental, harmonic and anharmonic vibrational frequencies (cm⁻¹) for uracil molecule. Mean absolute error (MAE), maximum positive (MAX) and negative (MIN) deviations with respect to CCSD(T) for harmonic frequencies, and with respect to experiment for anharmonic GVPT2 values (in bold).

	Exp.	Calculated
	Ar matrixa	B3LYP		B3LYP-D3		B3LYP-DCP		M06-2X		ωB97XD		B2PLYP/B3LYP		CCSD(T)/B3LYPb		Assignmentc
Mode		harm	anharm	harm	anharm	harm	anharm	harm	anharm	harm	anharm	harm	anharm	harm	anharm
1	3482	3639	3473	3639	3473	3643	3475	3671	3511	3691	3589	3650	3494	3653	3472	νN1H
2	3433	3594	3427	3595	3430	3598	3429	3623	3437	3647	3545	3602	3442	3602	3430	νN3H
3	3130	3246	3111	3246	3109	3293	3162	3280	3120	3270	3064	3266	3134	3253	3113	νC5H
4		3205	3062	3203	3060	3252	3118	3233	3197	3229	3060	3225	3090	3218	3062	νC6H
5	1762	1798	1771	1799	1770	1832	1801	1855	1814	1845	1822	1789	1752	1790	1771	νC2=O
6	1733	1764	1749	1765	1749	1801	1773	1828	1796	1814	1802	1754	1734	1762	1747	νC4=O
7	1644	1673	1640	1672	1638	1728	1694	1714	1674	1710	1679	1673	1643	1678	1640	νC5=C6
8	1473	1499	1463	1500	1463	1535	1492	1523	1491	1527	1484	1503	1464	1505	1455	ν ring, δN1H
9	1401	1417	1386	1417	1386	1430	1396	1433	1409	1437	1409	1423	1406	1427	1390	δN3H + δCH
10	1389	1403	1372	1405	1371	1450	1418	1420	1385	1427	1405	1411	1384	1414	1367	ν ring, δN1H, δN3H
11	1359	1381	1349	1383	1350	1401	1362	1394	1365	1402	1378	1388	1365	1394	1349	ν ring, δN3H, δCH
12	1219	1227	1202	1230	1204	1225	1203	1238	1210	1250	1217	1235	1229	1248	1204	ν ring, δNH, δCH
13	1186	1195	1167	1199	1165	1277	1242	1208	1191	1220	1208	1204	1184	1205	1167	ν ring, δNH, δCH
14	1076	1085	1064	1087	1062	1109	1091	1095	1090	1103	1080	1091	1065	1084	1064	ν ring, δCH, δN1H
15	987	992	977	991	976	1005	979	997	982	1002	990	996	984	995	978	δ ring
16	963	964	942	968	946	994	973	982	962	983	968	984	951	968	947	ν ring, δN3H, δCH
17	958	973	949	972	948	1005	981	994	973	991	978	969	959	973	946	γCH
18	806	822	803	822	803	845	830	833	827	832	818	826	796	814	803	γC4=O, γCH
19	757	769	746	769	745	792	778	784	768	782	766	771	750	773	753	γC2=O
20	759	770	753	769	752	794	780	783	769	782	765	768	753	765	748	ring breathing
21	718	731	713	731	712	745	732	739	741	740	726	736	716	728	714	γCH
22	662	689	643	687	641	699	679	685	766	689	658	688	666	670	659	γN3H
23	562	571	530	569	528	581	577	567	597	570	550	570	556	559	558	γN1H
24	551	559	550	561	560	572	563	567	559	567	568	559	550	545	549	δ ring
25	537	542	535	542	535	555	548	547	542	551	543	541	531	541	534	δC=O
26	516	521	515	523	516	531	525	523	515	526	523	520	510	517	515	δ ring
27	391	387	387	389	387	396	395	399	403	402	398	401	397	388	395	δC=O, δ ring
28	411	401	391	400	390	411	407	395	395	394	395	386	374	387	387	torsion
29	185	170	163	170	162	170	168	168	163	168	161	167	154	159	165	torsion
30		155	147	154	146	153	152	154	151	154	151	149	128	140	147	torsion
MAE		8	12	8	12	25	19	17	19	18	24	7	8		10
MIN		−21	−32	−18	−34	−24	−17	−10	−22	2	−66	−13	−37		−24
MAX		18	16	16	16	72	56	67	104	55	112	18	12		14

^aFrom Ref.^145,157,158.

^bBest estimated harmonic frequencies evaluated by composite scheme at CCSD(T)/CBS(T,Q+aug)+CV level from Ref.³².

^cAbbreviations: ν = stretching; δ = in-plane bending; γ = out-of-plane bending; τ = torsional; sciss = scissoring; rock = rocking; wagg = wagging; asym = asymmetric; sym = symmetric.

B3LYP and B3LYP-D3 approaches give better predictions than B3LYP-DCP, with MAE and MAX of 11.8 and 32 cm⁻¹, 12.3 and 34 cm⁻¹, 18.7 and 56 cm⁻¹, respectively. Moreover, B3LYP and B3LYP-D3 anharmonic frequencies all agree with respect to experiments within 20 cm⁻¹ range, while larger discrepancies (over 30 cm⁻¹) have been observed only for the vibrational mode γN₁H at 562 cm⁻¹. For B3LYP-DCP errors larger than 30 cm⁻¹ have been observed for several vibrations in higher frequency range (νC-C, νC=O and νC₅H) and ν ring, δNH, δCH at ~ 1240 cm⁻¹.

3.1.2. B3LYP and its dispersion corrected counterparts

A statistical analysis of the deviations of computed vibrational frequencies for all nucleobases with respect to experimental data and B3LYP results is presented in Table 2.

Table 2.

Deviations of computed vibrational frequencies (cm⁻¹) of all nucleobases with respect to experimental data^a and B3LYP results.

	Calculated vs Experimentala	Calculated vs B3LYP
	Δanharmf	Δharme	Δanharmf	ΔGVPT2g
	MAEb
B3LYP	11.1
B3LYP-D3	11.4	1.4	1.7	1.5
B3LYP-DCP	22.6	21.6	26.4	6.1
	MINc
B3LYP	−38
B3LYP-D3	−41	−14	−17	−19
B3LYP-DCP	−80	−103	−102	−23
	MAXd
B3LYP	27
B3LYP-D3	28	15	18	20
B3LYP-DCP	72	82	75	52

^aFrom Ref. ^{31,32,34-36,39,145,147,157,158}.

^bWeighted Mean Absolute Error.

^cMinimum negative deviation.

^dMaximum positive deviation.

^eDeviation between harmonic frequencies.

^fDeviation between anharmonic frequencies.

^gDeviation of anharmonic shift for the selected method respect to B3LYP method.

Inspection of Table 2 shows that B3LYP and B3LYP-D3 results agree fairly well with experiments, with MAEs of about 11 cm⁻¹ for the whole set of molecules and maximum positive (MAX) and negative (MIN) discrepancies not exceeding 30 cm⁻¹ and 41 cm⁻¹, respectively. It should be also noted that larger discrepancies observed for N-H stretching vibrations can be attributed to red-shifts of about 20 cm⁻¹ due to the Ar matrix environment. The relative errors for B3LYP-DCP are significantly larger, with MAE, MAX and MIN of 23, 72 and 80 cm⁻¹ respectively. The accuracy of B3LYP results confirms that it can stand as a reference for comparison between the two dispersive methods B3LYP-DCP and B3LYP-D3. Direct comparison between the theoretical models allows to analyze different contributions to each overall anharmonic frequency, namely the harmonic part and the anharmonic correction. The accuracy of the latter is of particular interest as the harmonic part can be corrected by more expensive computations within hybrid schemes, as shown above for the case of uracil. It emerges that harmonic and anharmonic frequencies obtained with B3LYP and B3LYP-D3 methods are nearly equivalent. On the other hand, major deviations appear in the case of B3LYP-DCP frequencies, with weighted mean absolute errors of 22 and 26 cm⁻¹ respectively for the harmonic and anharmonic frequencies of all the nucleobases; a small deviation (6 cm⁻¹) of the anharmonic shifts is, instead, observed. On the whole, B3LYP and B3LYP-D3 approaches provide more accurate vibrational wavenumbers with respect to B3LYP-DCP. In particular, the high accuracy of B3LYP, fully sufficient for the analysis of experimental spectra, is retained by computations with B3LYP-D3. However, even if less accurate than B3LYP-D3, B3LYP-DCP computations perform significantly better than most of the other dispersion-corrected DFT models^31,90 and, most importantly, provide reliable anharmonic corrections. In the following a more detailed analysis for remaining molecules is provided.

Adenine

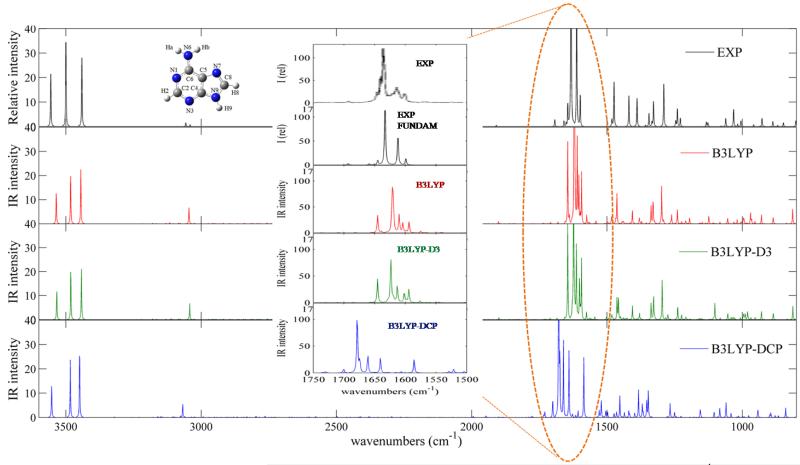
Adenine vibrational wavenumbers are well reproduced in the whole spectral range with MAE and MAX of 12.0 and 26 cm⁻¹, 12.3 and 25 cm⁻¹, 24.0 and 55 cm⁻¹, for B3LYP, B3LYP-D3 and B3LYP-DCP, respectively (see Table 6 in the supplementary material). However, the region of the experimental spectrum³⁴ between 500 and 600 cm⁻¹, corresponding to out-of-plane vibrational modes such as τNH2, γN₉H,γC₂H, τR, τr, shows several features which are not reproduced. In particular, a very intense doublet of bands at 591 and 583 cm⁻¹ was tentatively assigned to the out-of-plane vibrations of the amino group, split into two components due to matrix effects. Thus, the direct comparison between simulated and experimental³⁴ infrared spectra of isolated adenine molecule has been restricted to the 800-3600 cm⁻¹ spectral range, as shown in Figure 2.

Figure 2.

Computed anharmonic and experimental infrared spectra of isolated adenine molecule in the 800-3600 cm⁻¹ spectral range. Experimental IR spectrum recorded in the low-temperature Ar matrix have been generated using the data of Table 3 of Ref.³⁴. IR spectra line-shapes (both theoretical and experimental) have been convoluted using Lorentzian functions with a half-width at half-maximum (HWHM) of 1 cm⁻¹. The inset shows the 1500-1700 cm⁻¹ spectral range, with both the experimental spectrum obtained by convolution of fundamental vibrational modes (EXP FUNDAM) and the experimental spectrum shown in Figure 3 of Ref.³⁴ (EXP).

In the lower frequency range B3LYP and B3LYP-D3 anharmonic frequencies provide major discrepancies in relation to experiments for the following vibrational modes: δ_scissNH2, νC₄C₅, νC₅C₆ at ~ 1565 cm⁻¹, δ_rockNH2, νN₁C₆ at ~ 994 cm⁻¹, γC₈H, τR, τr, γC₆N₆ in the 777-814 cm⁻¹ region, γN₉H, γC₂H, τR, τr at ~ 545 cm⁻¹, γ_waggNH2, τRr in the 205-240 cm⁻¹ region. Nevertheless also in these cases the errors are of the order of about 20-30 cm⁻¹, and mainly involve out-of-plane modes of the amino group.

In the 900-1500 cm⁻¹ spectral region a very good agreement between experimental data and calculated B3LYP and B3LYP-D3 anharmonic frequencies and intensities is observed. Instead, B3LYP-DCP anharmonic frequencies show larger deviations from experimental values.

Direct comparison with simulated spectra shows that experimental spectroscopic features in the 1500-1750 cm⁻¹ spectral range are well reproduced by B3LYP and B3LYP-D3 anharmonic calculations taking into account also the presence of relatively intense non-fundamental transitions. The difference between the full experimental spectra (EXP) and the ones resulting from the fundamental transitions only (EXP FUNDAM) is also highlighted. It should be noted that such result could not be obtained by scaling the harmonic frequencies, as in this case only fundamental bands are present instead of complex pattern, including combination bands at 1604 cm⁻¹ (δ_rockNH2, νN₁C₆ + δr, νC₅C₆, δR), 1610 cm⁻¹ (δC₂H, νC₈N₉, δC₈H, νC₆N₆ + δC₆N₆, δR, δr), 1645 cm⁻¹ (δr, νC₄C₅ + ring breathing) (Figure 2: inset). The B3LYP-DCP anharmonic frequencies also result in rather complex spectra but the band positions show larger deviations from experimental values, and different band patterns.

As it could be expected, larger discrepancies between computed anharmonic frequencies and experiment are observed for the higher-frequency vibrational modes at ~ 3500 cm⁻¹, ν_asymNH2 and νN₉H, with about 30 cm⁻¹ shifts in the case of B3LYP and B3LYP-D3, and about 20 cm⁻¹ shifts for B3LYP-DCP. It was noted that larger discrepancies in the high-wavenumber region are related to the Ar matrix effects. On the other hand X-H vibrations are also more sensitive to the PES description and can be systematically emended by hybrid computations with harmonic frequencies corrected at higher-level of theory (CCSD(T) or B2PLYP) with basis sets of at least triple-zeta quality⁹⁰.

Cytosine

Globally, B3LYP and B3LYP-D3 approaches give better predictions than B3LYP-DCP, with MAE and MAX of 11.2 and 27 cm⁻¹, 11.0 and 28 cm⁻¹, 18.4 and 46 cm⁻¹, respectively (see Table 6 in the supplementary material). However, B3LYP and B3LYP-D3 anharmonic frequencies show remarkable differences from the experimental values (with shifts in the 20-30 cm⁻¹ range) for the vibrational modes: ν_asymNH2 and N₁H at ~ 3500 cm⁻¹ which are better predicted by B3LYP-DCP, probably due to the fortuitous cancellation of errors. In the lower frequency range we note νC₂N₃ at ~ 1225 cm⁻¹, δC₅H, νC₆N₁, νC₅C₆ at ~ 1111 cm⁻¹, δ_rockNH2 at ~ 1066 cm⁻¹ which is better predicted by B3LYP-DCP, δC₄N₄, δC₂O at ~ 357 cm⁻¹.

Hypoxanthine

B3LYP and B3LYP-D3 methods give much better predictions than B3LYP-DCP, with MAE and MAX of 11.3 and 26 cm⁻¹, 11.2 and 25 cm⁻¹, 31.9 and 66 cm⁻¹, respectively (see Table 6 in the supplementary material). However, B3LYP and B3LYP-D3 anharmonic frequencies deviate from experiments (with shifts in the 17-36 cm⁻¹ range) for the following vibrational modes: νC₂N₃, δC₂H at ~ 1590 cm⁻¹, νN₇C₈, νC₄C₅ at ~ 1494 cm⁻¹, νN₇C₈, δN₁H at ~ 1441 cm⁻¹, δN₉H, δC₂H at ~ 1367 cm⁻¹, νN₁C₆, δC₆O at ~ 1032 cm⁻¹, γC₆O, τR, τr at ~ 766 cm⁻¹, δr, νC₅C₆ at ~ 599 cm⁻¹, γN₉H at ~ 524 cm⁻¹.

Thymine

Once again B3LYP and B3LYP-D3 anharmonic frequencies agree much better with experiment than their B3LYP-DCP counterparts, with MAE and MAX of 9.3 and 7 cm⁻¹, 9.9 and 8 cm⁻¹, 20.3 and 57 cm⁻¹, respectively (see Table 6 in the supplementary material). However, B3LYP and B3LYP-D3 anharmonic frequencies show major discrepancies with respect to experiment (with shifts in the 19-40 cm⁻¹ range) for the following vibrational modes: ν_asymCH3 at ~ 2964 cm⁻¹, ν_out-of-planeCH3 at ~ 2945 cm⁻¹, inv CH3, δN₁H, νC₂N₃ at ~ 1386 cm⁻¹, νC₅-CH3, νN₁C₆ at ~ 1197 cm⁻¹, γ_waggN₃H, γ ring, γ_waggN₁H, γ_waggC₂O at ~ 633 cm⁻¹ and γ_waggN₁H, γ_waggN₃H, γ_waggC₄O, γ ring at ~ 507 cm⁻¹ (which are much better predicted by B3LYP-DCP with shifts of the anharmonic frequencies of only 14 cm⁻¹ and 21 cm⁻¹, respectively).

3.2 Dimers

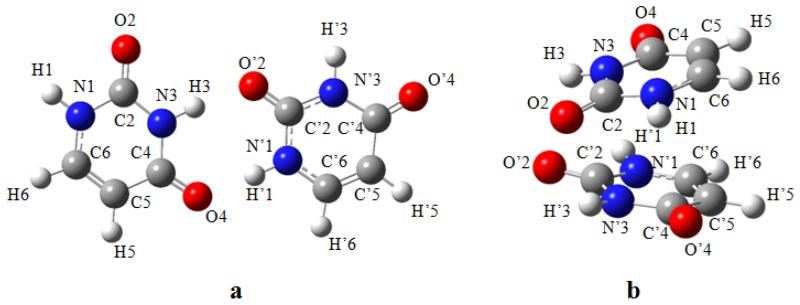
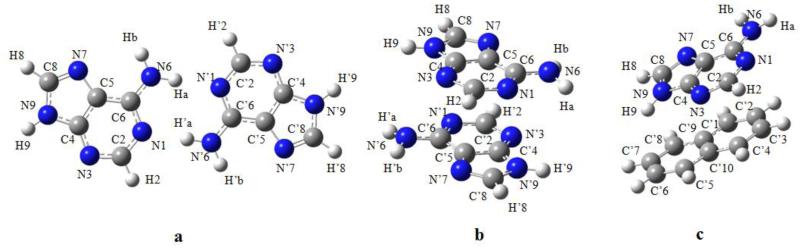
Optimized geometries and atom numberings of the investigated dimers are shown in Figures 3 - 4.

Figure 3.

Geometries optimized using B3LYP-D3 and numbering schemes of the hydrogen-bonded (a) and stacked (b) uracil dimers.

Figure 4.

Geometries optimized using B3LYP-D3 and numbering schemes of the hydrogen-bonded (a), stacked (b) adenine dimers and stacked adenine-naphthalene dimer (c).

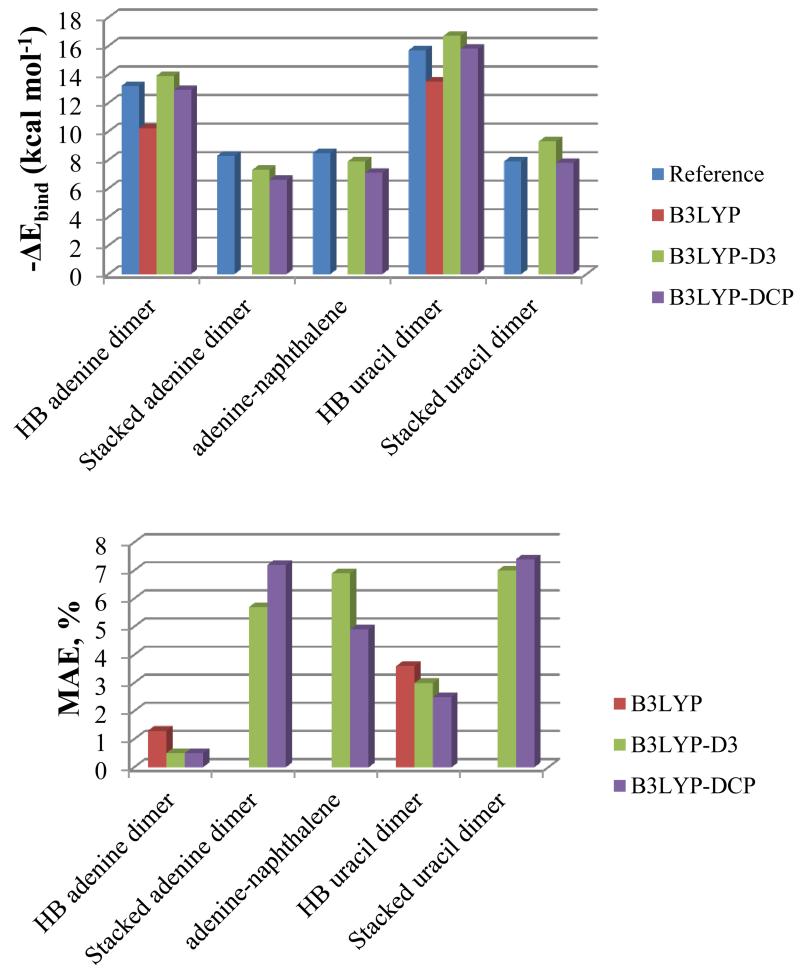
Counterpoise-corrected binding energies (ΔE_bind) of hydrogen-bonded and stacked dimer structures were calculated and compared to reference values^137-140 in Figure 5 (detailed data are reported in Table 8 in the supplementary material). The comparison between the optimized structures of the dimers and the reference ones is reported in Tables 9 in the supplementary material, while the percentage mean absolute errors (MAE, %) of rotational constants of dimer structures are shown in Figure 5. The anharmonic Zero Point Vibrational Energies (ZPVE) for monomers and dimers, along with anharmonic ZPVE corrections to the binding energies are reported in Table 3.

Figure 5.

Counterpoise-corrected binding energy (ΔE_bind) of hydrogen-bonded and stacked dimer structures in kcal mol⁻¹ compared to reference values, and percentage mean absolute errors (MAE, %) of rotational constants of optimized dimer structures computed with B3LYP, B3LYP-D3 and B3LYP-DCP methods.

Table 3.

Zero-point vibrational energies (ZPVE) (in cm⁻¹) and ZPVE corrections to the binding energy (ΔZPVE) (in kcal mol⁻¹) for all dimers, computed with B3LYP-D3 and B3LYP-DCP methods.

	B3LYP-D3		B3LYP-DCP
	harm	anharm	harm	anharm
	ZPVE
Uracil	19077	18842	19410	19204
Adenine	24517	24199	24888	24612
Napthalene	32266	31888	33004	32633
Uracil-Uracil hydrogen-bonded	38581	37923	39166	38727
Uracil-Uracil stacked	38402	38002	39042	38567
Adenine-Adenine hydrogen-bonded	49649	48910	50378	49689
Adenine-Adenine stacked	49260	48638	50097	49455
Adenine-Naphthalene stacked	56998	56253	58140	57507
	ΔZPVE
Uracil-Uracil hydrogen-bonded	1.2	0.7	1.0	0.9
Uracil-Uracil stacked	0.7	0.9	0.6	0.5
Adenine-Adenine hydrogen-bonded	1.8	1.5	1.8	1.3
Adenine-Adenine stacked	0.6	0.7	0.9	0.7
Adenine-Naphthalene stacked	0.6	0.5	0.7	0.7

The results of the anharmonic frequency calculation obtained through the three DFT methods for the hydrogen-bonded and stacked homodimers of uracil are reported in Table 4 for the vibrational modes which exhibit the largest anharmonic frequency shifts with respect to the isolated nucleobase (complete anharmonic frequency results both for uracil and adenine dimers are reported in Tables 12-16 in the supplementary material).

Table 4.

Anharmonic vibrational frequencies (cm⁻¹) of hydrogen-bonded and stacked uracil dimer, computed using B3LYP, B3LYP-D3 and B3LYP-DCP approaches, and corresponding shifts with respect to the isolated molecule (Δ).

B3LYP		B3LYP-D3		B3LYP-DCP		Assignmenta
anharm	Δ	anharm	Δ	anharm	Δ
hydrogen-bonded uracil dimer
3002	−424.6, −470.4	2926	−503.1, −546.4	2947	−482.0, −527.5	νN3H (M1), νN1H (M2)
2897	−530.0, −575.8	2870	−559.7, −546.4	2880	−549.4, −594.9	νN3H (M1), νN1H (M2)
1700	−49.9	1699	−49.4	1735	−38.4	νC2=O, νC4=O, δNH (M2)
1679	−70.8	1676	−72.4	1715	−58.1	νC4=O, ν ring, δN3H (M1)
1511	48.6	1515	52.3	1535	42.3	δN1H (M2)
1474	102.0	1475	104.9	1514	95.4	ν ring, δN1H, δN3H (M1)
543	156.1	543	155.8	558	162.1	δC=O, δ ring (M2), δ ring (M1)
527	140.0	527	139.9	539	143.2	δC=O, δ ring (M1), δ ring (M2)
stacked uracil dimer
		3362	−111.1	3465	−9.6	νN1H (M1, M2)
		3374	−98.5	3465	−9.5	νN1H (M1, M2)
		1727	−21.6	1745	−27.9	νC4=O (M1, M2)
		1689	−59.3	1734	−39.2	νC4=O (M1, M2)
		700	59.1	687	7.9	γN3H (M1, M2)
		686	44.9	690	11.1	γN3H (M1, M2)
		824	296.1	587	10.4	γN1H (M1, M2)
		651	123.7	584	7.5	γN1H (M1, M2)

^aAbbreviations: ν = stretching; δ = in-plane bending; γ = out-of-plane bending; τ = torsional; sciss = scissoring; rock = rocking; wagg = wagging; asym = asymmetric; sym = symmetric; M1 = Monomer 1; M2 = Monomer 2.

Assignments of vibrational modes were performed by means of visual inspection of the atomic displacements along normal modes and through comparison with the assignments of the isolated nucleobases.

A detailed statistical analysis of the deviations of the harmonic and anharmonic frequencies computed with B3LYP-D3 and B3LYP-DCP methods is presented in Table 5. The mean absolute difference (MAD) has been computed considering all normal modes, while MIN e MAX have been evaluated by excluding 10 of the 341 vibrational modes which exhibit exceptionally large discrepancies. The small values of MADs prove that such modes do not play a major role in the weighted average.

Table 5.

Deviations of harmonic and anharmonic vibrational frequencies (in cm⁻¹) of dimers computed with B3LYP-DCP with respect to the B3LYP-D3 method.

	MADa			MINb			MAXc
	Δharmd	Δanharme	ΔGVPT2f	Δharmd	Δanharme	ΔGVPT2f	Δharmd	Δanharme	ΔGVPT2f
Uracil-Uracil hydrogen-bonded	20.3	31.7	14.9	−6	−2	−22	60	65	51
Uracil-Uracil stacked	20.6	28.1	13.5	−15	−16	−20	55	59	14
Adenine-Adenine hydrogen-bonded	21.4	29.2	13.2	−63	−63	−37	47	63	46
Adenine-Adenine stacked	22.1	22.2	3.3	−1	−3	−16	53	55	14
Adenine-Naphthalene stacked	24.2	25.4	5.9	−65	−65	−23	52	67	33
all	21.5	27.3	10.3	−65	−65	−37	60	67	51

^aMean absolute difference.

^bMinimum negative deviation, evaluated by excluding 10 of 341 vibrational modes.

^cMaximum positive deviationevaluated by excluding 10 of 341 vibrational modes.

^dDeviation between harmonic frequencies.

^eDeviation between anharmonic frequencies.

^fDeviation of anharmonic shift.

3.2.1 Structures and energies: comparison of computational methods

The structures and energies of all dimers considered in the present study have been previously evaluated by highly accurate computational strategies, mainly by combination of MP2 and Coupled Cluster (CCSD(T)) approaches along with extrapolation to the complete basis set limit (CBS), allowing the comparison and assessment of the performance of less computationally demanding B3LYP-based models. First of all it can be observed that B3LYP calculations fail for stacked dimers, as expected for systems that mainly interact through dispersion forces. Instead, both B3LYP-D3 and B3LYP-DCP models predict reliable binding energies and structural parameters with similar good accuracy.

As shown in Figure 5 and in Tables 8-11 in the supplementary material, even in the case of hydrogen-bonded structures B3LYP shows the largest deviations for both binding energies and structural parameters with respect to the best theoretical estimates^137-140, while B3LYP-D3 and B3LYP-DCP show very good performances and provide rather similar values, making both approaches of essentially equal accuracy. The slight differences between B3LYP-D3 and B3LYP-DCP results suggest that each method has its pros and cons and none of them can be considered clearly superior to the other.

As far as the energies of the optimized geometries are concerned, B3LYP underestimates the binding energies of the hydrogen bonded structures^137,138 by about 14 % for the uracil dimer and 22% for the adenine dimer, B3LYP-D3 slightly overestimates by up to 6 % for the uracil dimer and 5% for the adenine dimer, whereas B3LYP-DCP gives energies with the best agreement. Indeed, an overestimation within 0.6% of the reference, in the case of the uracil dimer, and an underestimation of 2%, in the case of adenine dimer, are observed. For stacked structures^137,139,140, in most cases B3LYP-D3 and B3LYP-DCP underestimate interaction energies (exception: uracil dimer at the B3LYP-D3 level), and in all cases the difference from the reference is at most 2 % (see Table 8 in the supplementary material).

Regarding the optimized structures, all methods give rotational constants which reflect the overall accuracy of geometry parameters within 5% of the reference (see Table 9 in the supplementary material), whereas for structural parameters the difference is at most 11 % (see Table 11 in the supplementary material). In the case of hydrogen bonded dimers B3LYP shows the largest errors, which are about 4 % for rotational constants and 5 % for structural parameters in the case of the uracil dimer, and 1 % for both rotational constants and structural parameters in the case of the adenine dimer. On the contrary, B3LYP-D3 and B3LYP-DCP provide quite similarly small deviations, i.e. 3 % for rotational constants and 4 % for structural parameters in the case of the uracil dimer and 0.5 % for rotational constants and 0.3 % for structural parameters in the case of the adenine dimer. Stacked dimers show, instead, larger deviations with respect to reference values. This reflects the difficulty of obtaining a proper description of geometry when the overall structures are largely influenced by dispersion interactions. However, both B3LYP-D3 and B3LYP-DCP show deviations within about 7% for rotational constants and 11% for structural parameters, and no clear preference of one over another can be observed.

3.2.2 Vibrational properties

Unfortunately, reliable reference data regarding vibrational properties are not available in the literature. To the best of our knowledge, anharmonic computations at the Coupled Cluster level for the systems considered in this work (except uracil molecule) have not yet been performed. Additionally, experimental spectroscopy studies of weakly bound nucleobase complexes or similar systems are still rather scarce^149,150 and most importantly results might be biased by interpretations, thus being not fully adequate for benchmark purposes. As an example it could be quoted the study by Kleinermanns and coworkers¹⁵⁰ on adenine dimers, performed by IR-UV double-resonance spectroscopy, where the assignment of the observed spectra in the N-H stretching frequency range has been performed with the aid of harmonic computations at the HF/6-31G(d,p) level, and the most stable symmetric structure has been excluded due to the disagreement between computed and experimental spectra. A similar analysis, based on very limited spectroscopic data, namely the comparison of experimental and theoretical OH vibrational frequencies, lead to an incorrect proposal of a non planar equilibrium structure for the anisole-water complex¹⁵¹. This was corrected by high-resolution laser induced fluorescence spectroscopy (LIF) measurements of the rotational constants, which showed that water is located in the anisole symmetry plane and is bound to the molecule by a conventional hydrogen bond¹⁵² and further confirmed by experimental^153-155 and computational^155,156 findings. As a consequence, for a proper benchmark reference it is necessary to combine structure identification of the complexes (by means, e.g., of rotational spectra) with an analysis of the vibrational transitions. To the best of our knowledge such experimental studies for the nucleobase complexes are not available and the present work could be useful for supporting future investigations. Experimental data on dimers are largely related to the X-H stretching vibrations, at high-wavenumbers, which are more difficult to describe at the DFT level. Moreover, while isolated X-H stretching vibrations are accurately described at the VPT2 level, which is an exact solution for a Morse-like potential energy curve, this might not be the case for strongly anharmonic vibrations within hydrogen bonded bridges. Thus, benchmark studies based on the high-frequency spectral zone would unbalance the accuracy of the lower-wavenumbers regions, which are, instead, more relevant for the current project. For that reasons, the performances of both dispersion-corrected models for prediction of vibrational properties have been validated by comparison with well-established data for monomers. In this section, vibrational properties for complexes, computed with both B3LYP-D3 and B3LYP-DCP, are discussed and a critical comparison between both models is made.

Considering the absolute values of ZPVE’s (Table 3), the differences between B3LYP-D3 and B3LYP-DCP are mainly related to the harmonic part, while anharmonic corrections vary by up to 50 cm⁻¹ for monomers and 250 cm⁻¹ for dimers. The latter value refers to the uracil hydrogen bonded dimer and leads to the largest differences in the ZPVE correction to the binding energy. B3LYP-D3 predicts a decrease of ΔZPVE by 0.5 kcal mol⁻¹ when anharmonic correction is considered while for B3LYP-DCP harmonic and anharmonic ΔZPVEs are very similar. On the contrary, in the case of the adenine stacked dimer B3LYP-D3 yields similar values of harmonic and anharmonic ΔZPVEs while for B3LYP-DCP both values differ by about 0.25 kcal mol⁻¹. Considering the similar performances of B3LYP and B3LYP-D3, for the latter an accuracy of anharmonic corrections to ZPVE of about 0.05 kcal mol⁻¹ can be expected⁸⁶. By comparison with B3LYP-D3 we can estimate for anharmonic ΔZPVEs computed with B3LYP-DCP an average error of about 0.2 kcal mol⁻¹, with maximum discrepancies of up to 0.5 kcal mol⁻¹. In summary, for accurate estimates of complexes binding energies ΔZPVEs computed at the B3LYP-D3 level should be recommended, while computations at harmonic level and/or with B3LYP-DCP yield results well within the so called chemical accuracy.

Comparison of harmonic and anharmonic frequencies obtained with both dispersive methods (Table 5) indicates a MAD of about 20 cm⁻¹ for the deviations between the harmonic frequencies, about 30 cm⁻¹ for the deviations between the anharmonic frequencies and about 10 cm⁻¹ for the deviations of anharmonic shifts. It can be noted that the relative performance of these two methods in calculating vibrational frequencies in the case of the dimers is the same as that just observed for monomers (with respective MADs again of about 20 cm⁻¹, 30 cm⁻¹ and 10 cm⁻¹). Absolute maximum deviations of 65 cm⁻¹, 67 cm⁻¹ and 51 cm⁻¹ are obtained for harmonic frequencies, anharmonic frequencies and the anharmonic shifts, respectively, excluding 10 of the 341 vibrational modes which exhibit exceptionally large discrepancies. The vibrations excluded from the statistical analysis are indeed the ones which are the most difficult to describe properly due to both PES requirements and limitations of perturbative treatment. In particular, the most significant deviations between the harmonic frequencies calculated through B3LYP-DCP and B3LYP-D3 methods are observed for the torsional vibrational mode of the amino group in the hydrogen-bonded adenine dimer (−78 cm⁻¹), and the ring stretching of hydrogen-bonded uracil dimer (60 cm⁻¹). The largest deviations between the anharmonic frequencies are observed for the out-of-plane bending of N₁H group in the stacked uracil dimer (−236 cm⁻¹) and the out-of-plane bending of N₁H, CH and N₃H groups in the hydrogen-bonded uracil dimer (139 cm⁻¹). The maximum negative deviation of anharmonic shifts is due to the out-of-plane bending of N₁H group in the stacked uracil dimer (−257 cm⁻¹), while the maximum positive deviation of anharmonic shifts is due the torsional vibrational mode of the amino group in the hydrogen-bonded adenine dimer (196 cm⁻¹). However, as it can be inferred by the MADs evaluated taking into account all the vibrational modes, the role of such modes is negligible in the weighted average, justifying their exclusion in the evaluation of MAX and MIN.

3.2.3 Effect of intermolecular interactions

Given the better performance of B3LYP-D3 in calculating vibrational frequencies for the monomeric nucleobases, this method has been chosen to compare IR spectra of the monomers and the dimers in order to investigate the effect of the intermolecular interactions on the vibrational frequencies of nucleobases.

The anharmonic infrared spectra, calculated through B3LYP-D3 approach, of adenine dimers compared with that of isolated adenine molecule are presented in Figure 6.

Figure 6.

Anharmonic IR spectra of adenine dimers computed with B3LYP-D3 method, compared with IR spectrum of isolated adenine molecule, in the 800-3600 cm⁻¹ energy range, along with the assignment of most pronounced bands. Theoretical spectra line-shapes have been convoluted with Lorentzian functions with a HWHM of 1 cm⁻¹.

The two major effects of intermolecular interactions observed on the IR spectra are the frequency shifts and the intensity changes.

The anharmonic frequency shifts of adenine dimers with respect to the isolated adenine molecule are reported in bold italic in the supplementary material in Tables 14-16.

In the hydrogen-bonded adenine dimer, the most significant shifts of anharmonic vibrational frequencies concern some vibrational modes of the amino group, which is indeed involved in the hydrogen-bonding interaction. These are: ν_symNH2 at 2965 cm⁻¹ with a considerable shift of ~ −500 cm⁻¹ and a large intensity increase giving the most intense band in the spectrum, δ_scissNH2, νC₆N₆ at 1495 cm⁻¹ with a shift of −70 cm⁻¹, γ_waggNH2, τRr at ~ 152 cm⁻¹ with a shift of ~ −53 cm⁻¹. It is noteworthy that all these shifts are negative indicating that hydrogen bonds weaken the force constants of the amino group for such vibrations. Other bands which gather intensity include the ν_asymNH2 vibrational mode at 3502 cm⁻¹, the νC₈H vibrational mode at 3101 cm⁻¹, the νC₂H vibrational mode at 3030 cm⁻¹, the δ_scissNH2, νC₅C₆, νC₆N₆ vibrational mode at 1647 cm⁻¹ and 1592 cm⁻¹, the δ_scissNH2, νC₄C₅, νC₅C₆ vibrational mode at 1583 cm⁻¹, the νC₂N₃, νN₁C₂ vibrational mode at 1311 cm⁻¹.

In the stacked adenine dimer, the main anharmonic frequency shifts involve out-of-plane vibrational modes, such as τNH2, γN₉H at 425 cm⁻¹ with a shift of −66 cm⁻¹ and γ_waggNH2 at ~ 280 cm⁻¹ with a shift of ~ 77 cm⁻¹. The most intense band in the spectrum of the dimer corresponds to the δC₈H, νN₇C₈, δN₉H vibrational mode at 1242 cm⁻¹, which acquires intensity with respect to the case of the isolated adenine molecule.

In the present study the stacked adenine-naphthalene heterodimer may be considered as a first step in the investigation of the interactions between nucleobases and graphene-like solid supports. Therefore the effects determined by the naphthalene support on the vibrational frequencies and band intensities of the spectrum of the adenine molecule have been examined. In particular, the most relevant anharmonic frequency shift concerns the γ_waggNH2, τRr vibrational mode of the adenine molecule at 330 cm⁻¹ with a shift of 125 cm⁻¹, which shows also an intensity increase. Other shifts are observed for the ν_asymNH2 vibrational mode at 3520 cm⁻¹ (−14 cm⁻¹), νN₉H vibrational mode at 3463 cm⁻¹ (−19 cm⁻¹), ν_symNH2 vibrational mode at 3425 cm⁻¹ (−18 cm⁻¹), γC₈H vibrational mode at 824 cm⁻¹ (+11 cm⁻¹), γC₈H, τR, τr, γC₆N₆ vibrational mode at 810 cm⁻¹ (+30 cm⁻¹), γN₉H, γC₂H, τR, τr vibrational mode at 567 cm⁻¹ (+23 cm⁻¹) which has vanishing intensity in the spectrum of the isolated nucleobase, but gather intensity when adenine interacts with naphthalene, δR, γN₉H vibrational mode at 523 cm⁻¹ (+18 cm⁻¹) which undergoes to a remarkable intensity increase leading to the most intense band in the spectrum of the adenine-naphthalene heterodimer, τNH2, γN₉H vibrational mode at 518 cm⁻¹ (+20 cm⁻¹) which is one of the most intense bands in the spectrum of the isolated nucleobase, but decreases its intensity when adenine interacts with naphthalene, γN₉H vibrational mode at 522 cm⁻¹ (+31 cm⁻¹) which shows also an intensity increase, τNH2, δR vibrational mode at 461 cm⁻¹ (−25 cm⁻¹) which decreases in intensity, τRr, γ_waggNH2 vibrational mode at 218 cm⁻¹ (−21 cm⁻¹) which is subjected to a significant decrease, γ_waggNH2, τRr vibrational mode at 168 cm⁻¹ (−37 cm⁻¹) which is subjected to a significant decrease. Other bands which gather intensity when adenine interacts with naphthalene include the νC₂H vibrational mode at 3034 cm⁻¹ which becomes the second most intense band in the spectrum, the νN₁C₆, δC₂H, νC₂N₃, νC₆N₆ vibrational mode at 1464 cm⁻¹ and the δN₉H, δC₂H, νC₄N₉, νC₈N₉ vibrational mode at 1379 cm⁻¹ which becomes particularly intense.

The main anharmonic frequency shifts of uracil dimers with respect to the isolated uracil molecule are reported in bold italic in Table 4 (detailed anharmonic frequency shifts are reported in the supplementary material in Tables 12-13).

In the hydrogen-bonded uracil dimer, the most significant shifts of anharmonic frequencies are observed for some vibrational modes of the functional groups involved in the hydrogen-bonding interaction. In particular, the stretching modes of the N₃H and νN₁H groups at about 3000 cm⁻¹ show very pronounced shifts to lower frequencies of ~ −500 cm⁻¹, and the νC₂=O, νC₄=O, ν ring, δNH vibrational modes at ~ 1700 cm⁻¹ display red-shifts up to ~ −70 cm⁻¹; whereas the ν ring, δN₁H, δN₃H vibrational modes at ~ 1500 cm⁻¹ and the δC=O, δ ring vibrational modes in the 527-560 cm⁻¹ region present blue-shifts up to ~ 160 cm⁻¹.

In most cases B3LYP-DCP yields similar results as B3LYP-D3. Only for stacked uracil dimer B3LYP-DCP anharmonic calculations do not predict any significant shift of vibrational frequencies of the dimer with respect to the isolated molecule, while using B3LYP-D3 noteworthy frequency shifts are observed. These involve the stretching mode of the N₁H group at about 3370 cm⁻¹ with shifts to lower frequencies of ~ −100 cm⁻¹, the stretching mode of the C₄=O group at 1689 cm⁻¹ with a shift of ~ −60 cm⁻¹, and out-of-plane vibrational modes which undergo shifts to higher frequencies, that are: γN₃H at ~ 700 cm⁻¹ with shifts up to 59 cm⁻¹, γN₁H at 824 cm⁻¹ with a shift of 296 cm⁻¹ and at 651 cm⁻¹ with a shift of 124 cm⁻¹.

As expected, comparison of the IR spectra of the monomer and the dimers shows important shifts of the vibrational frequencies and/or IR intensity variations of specific functional groups. These correspond to proton donor and acceptor moieties which could interconnect the molecules through intermolecular hydrogen bonds. Even in the stacked structures and in the heterodimer significant changes in the spectral features are noticed for some out-of-plane vibrational modes, which are most influenced by the stacked configuration.

4. Conclusions

Computational spectroscopy studies are often indispensable for the interpretation of experimental spectra of complex molecular systems, such as nucleobase complexes characterized by different kinds of intermolecular interactions which may deeply influence the vibrational frequencies of the isolated molecules. Therefore, it is necessary to define a viable yet accurate computational procedure for the description not only of isolated monomers but especially of dimers with the aim of studying multicomponent configurations such as isolated nucleobases or layers of nucleobases adsorbed on solid supports in vacuum or in aqueous environments.

For such systems the dominant intermolecular interactions to be taken into account are the relatively weak hydrogen bonding and van der Waals interactions. In order to model the vibrational spectra of weakly bound molecular complexes, we have tested the performances of two popular and inexpensive approaches, namely the semi-empirical dispersion correction (D3) and pseudopotential based (DCP) methods both in conjunction with the B3LYP functional, for calculating anharmonic frequencies of the nucleobases adenine, hypoxanthine, uracil, thymine, cytosine, the hydrogen-bonded and stacked adenine and uracil dimers and the stacked adenine-naphthalene heterodimer. These methods have already shown good performances for structural parameters and binding energies of non-covalent adducts, but they have not been validated yet for vibrational anharmonic frequencies, so we decided to use these two approaches for simulating fully anharmonic infrared spectra of nucleobases and their dimers.

Our investigation indicates that in the case of isolated nucleobases B3LYP and B3LYP-D3 lead to a very good agreement with experiments, with MAEs of about 12 cm⁻¹ for the whole set of molecules and maximum discrepancies not exceeding 45 cm⁻¹. Larger deviations are observed instead for B3LYP-DCP, with MAE of 24 cm⁻¹and maximum discrepancy of 80 cm⁻¹. Direct comparison between theoretical models shows that harmonic and anharmonic frequencies obtained with B3LYP and B3LYP-D3 methods are nearly equivalent, while B3LYP-DCP frequencies differ more from B3LYP ones with a weighted mean absolute error of 22 cm⁻¹ on the harmonic frequencies and of 26 cm⁻¹ on the anharmonic frequencies of all the nucleobases. However, the deviation between the anharmonic shifts is only 6 cm⁻¹, suggesting that the main difference between the performances of the two dispersive methods concerns the harmonic part of the overall vibrational frequencies.

In the case of dimers, our study points out the failure of B3LYP calculations in describing stacked structures, as expected for systems that mainly interact through dispersion forces. Even in the case of hydrogen bonded dimers B3LYP behaves worse both for calculating binding energies and structural parameters. On the contrary, B3LYP-D3 and B3LYP-DCP predict reliable binding energies, rotational constants and structural parameters with similar good accuracy both for hydrogen bonded and stacked dimers, indicating that such methods may be effectively used for describing these kinds of systems.

Regarding vibrational spectra, examination of harmonic and anharmonic frequencies of the dimers obtained with both dispersive methods yields about the same deviations obtained in the case of isolated nucleobases, with a MAE of about 20 cm⁻¹ for the deviations between the harmonic frequencies, about 30 cm⁻¹ for the deviations between the anharmonic frequencies and about 10 cm⁻¹ for the deviations of anharmonic shifts. This result indicates that the relative performances of these two methods in calculating vibrational frequencies does not change increasing the complexity of the system. Then, the effect of intermolecular interactions on the vibrational frequencies of nucleobases has been investigated comparing the IR spectra of the dimers with those of the monomers, observing significant shifts of the vibrational frequencies and the increase of band intensity of specific functional groups. As expected, in the hydrogen bonded dimers major effects are observed for the groups involved in the hydrogen bonds, i.e. the proton donor and acceptor moieties. But even in the stacked structures significant shifts have been observed for some out-of-plane vibrational modes, which are more influenced by the stacked configuration.

As a consequence, when considering nucleobases in condensed-phases or adsorbed onto surfaces, assignments of spectroscopic features based on gas-phase data could be misleading³⁰, bringing to an incorrect interpretation of the spectra and thus of the actual groups involved in the interactions. Therefore, for a correct assignment of vibrational frequencies it is fundamental to carry out computational spectroscopy studies not only for isolated molecules but especially for the complexes.

Our investigation indicates that the two dispersive methods, B3LYP-D3 and B3LYP-DCP, are capable of predicting reliable values for binding energies and structural parameters, both for hydrogen bonded and stacked structures. For vibrational frequencies B3LYP-D3 yields more accurate results, yet B3LYP-DCP outperforms several other dispersion-corrected DFT approaches, and provides reliable anharmonic corrections. However, considering also its applicability for essentially all elements from the periodic table, B3LYP-D3 can be suggested as the method of first choice.

From the present investigation it emerges that spectra simulated with dispersion-corrected B3LYP approaches may be used confidently to interpret experimental data of nucleobase complexes, or nucleobase solid-support molecular systems in order to get hints on their function and properties, of relevance to astrophysical research (prebiotic interactions, the detection of such compounds in extraterrestrial environments) as well as to improve the characterization of biomolecular devices that are particularly appealing in materials science and biotechnologies.