Abstract
In situations with redundant or competing sensory information, humans have been shown to perform cue integration, weighting different cues according to their certainty in a quantifiably optimal manner. Ants have been shown to merge the directional information available from their path integration (PI) and visual memory, but as yet it is not clear that they do so in a way that reflects the relative certainty of the cues. In this study, we manipulate the variance of the PI home vector by allowing ants (Cataglyphis velox) to run different distances and testing their directional choice when the PI vector direction is put in competition with visual memory. Ants show progressively stronger weighting of their PI direction as PI length increases. The weighting is quantitatively predicted by modelling the expected directional variance of home vectors of different lengths and assuming optimal cue integration. However, a subsequent experiment suggests ants may not actually compute an internal estimate of the PI certainty, but are using the PI home vector length as a proxy.
Keywords: optimal cue integration, Bayesian, navigation, insects, ants
1. Introduction
All animals have to deal with multiple sensory cues that provide information of varying consistency and reliability about the external world. An increasingly popular explanation of how this is done is based on Bayesian reasoning: that the degree to which different information sources contribute to judgements should be weighted relative to their respective certainty. The view that human brains operate in this way has been substantiated by studies of optimal cue integration [1], in which a perceptual judgement or action depends on at least two sensory inputs, both with some associated noise. Assuming normally distributed noise and a uniform prior distribution, the optimal estimate under Bayes rules is the same as the maximum-likelihood estimate and is obtained by averaging the inputs weighted by the inverse of their relative variance. Weighted averaging can be deduced from perceptual judgements that fall between conflicting cues, and optimality tested by systematically altering the variance of one of the cues, and looking for a corresponding alteration in the judgement. For example, in a classic study by Ernst & Banks [2], the height of an object could be judged using independently manipulated haptic and visual depth cues. As increasing noise was introduced to the visual cue, the height judgement shifted gradually from a visual to a haptic bias, to a degree that was quantitatively predicted by the relative variance of the cues. Many subsequent psychophysical studies in humans have produced comparable results (reviewed in [3]) and the possibility that other animals, even insects, may also perform optimal cue integration is discussed by Cheng et al. [4].
Navigating ants have a ‘toolkit’ for foraging [5]. One element is path integration (PI), which by constant integration of heading direction (derived from the celestial compass) and distance walked (from a stride integrator and ventral optic flow) maintains a PI home vector pointing to the origin of the path [6]. A second element is visual memory of the surrounding scenery, which can be used independently of PI to determine an appropriate direction of travel (reviewed by Collett et al. [7]). PI and visual memory can be set in conflict experimentally by displacing ants [8–11], rotating the sky polarization pattern [12,13] or rotating the visual scene [14,15]. Ants in these experiments tend to take a compromise direction between those indicated by their PI and visual memories. Collett [9] found the intermediate directions were systematically altered by the degree of discrepancy and argued that the weighting of the cues could approximate optimality, but did not attempt to directly manipulate the relative certainty of the cues. Legge et al. [11] found that ants took a compromise direction which was more biased towards the PI direction when the visual scenery at the release point was less familiar, and argued that this represents an optimal strategy of reduced weighting of a less certain cue. However, this experiment had only two levels of cue reliability, and no clear means of quantifying their relative degree of certainty.
In human cue integration studies, the certainty of different cues and the effects of manipulation (e.g. adding visual blur) are measured directly by a large number of repeated trials on individuals. This would be difficult for ants. Individuals make insufficient foraging trips in their lifetime, especially if estimates under several different conditions are needed; and recording the heading of ants under field conditions introduces additional noise that could swamp changes in variance due to the cue. However, for PI, the relative certainty of the PI home vector as distance walked increases can, under very general assumptions, be directly deduced [16] (see Material and methods). This provides an elegant method to manipulate the relative certainty of the PI cue: allow ants to run different distances before setting the directions indicated by the PI and visual memory in conflict. We find the heading direction they take closely matches the expected direction given by optimal integration of the cues. In a further experiment, we attempt to manipulate the directional uncertainty of the PI independently from the home vector length to establish what information about the uncertainty the ant actually uses to weight cues.
2. Material and methods
All experiments were conducted in June 2014, on a field site on the outskirts of Seville, Spain (37°20′ N, 5°59′ W), using the species Cataglyphis velox, a thermophilic ant. These ants are solitary foragers and learn idiosyncratic routes using terrestrial and celestial visual cues, rather than pheromones [17]. Two ant nests located approximately 100 m apart were chosen for experimentation. A route corridor approximately 1.5 m wide and 8 m long, enclosed by a small plastic barrier (approx. 4 cm high), was cleared around each nest, and cookie crumbs and meal worm pieces were provided ad libitum 7 m away from the nest. The corridors of the two nests pointed in different compass directions (nest 1: NW; nest 2: SW).
(a). Experimental procedure
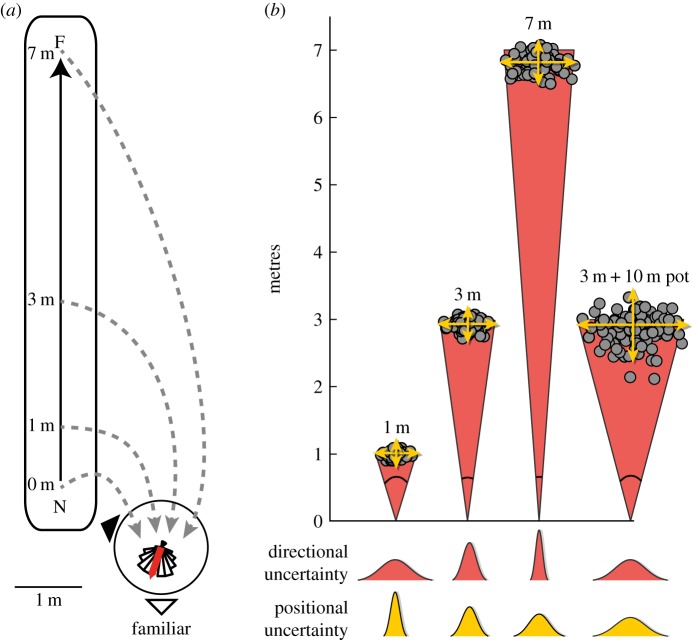
Ants were trained by allowing them to forage freely between the nest and feeder for at least 1 day. In experiment 1, individuals leaving the nest and running rapidly towards the feeder (i.e. ants familiar with the route) were captured in a small opaque tube at different locations along their outbound route: 0 m (i.e. just after their departure from the nest), 1 m, 3 m or 7 m (i.e. arriving at the feeder); capture locations were randomly interleaved. To trigger homing motivation, captured ants were provided with food before being released on a goniometer partitioned into 5° bins, either at a visually familiar location 1.5 m from the nest (110° from the nest-to-feeder direction; see figure 1a and electronic supplementary material, figure S1, for views from nests and release points) or at a completely unfamiliar location (see electronic supplementary material, figure S3). Their heading direction was recorded by two observers as they crossed a circle of 60 cm radius around the release point.
Figure 1.
Experimental protocol and modelling uncertainty. (a) Ants were trained to forage from their nest (N) along a straight route to a feeder (F) 7 m away. Experienced foragers were captured on their outward journey at either 0, 1, 3 or 7 m, provided with food, and released on a goniometer 1.5 m from the nest, and their direction of travel recorded 60 cm from the release point. In experiment 2, some 3 m ants were made to run for an additional 5 min in a pot before testing. (b) Ants will accumulate uncertainty during PI, so the positional variance of their estimate will increase (larger scatter of dots, yellow distributions) with distance. However, as the increase is proportional to distance, the angular error of the estimate (red angles and red distributions) will decrease inversely to distance (see Material and methods). For the pot condition in experiment 2, the additional accumulation of uncertainty should lead to a larger angular error for the same home vector length. The illustrated scatter was produced using a particle filter model (see the electronic supplementary material). (Online version in colour.)
In the second experiment, outbound ants were always captured 3 m away from the nest. Control ants were given a food item and immediately released on the goniometer at either the familiar or unfamiliar release points, as for experiment 1. For the experimental group, ants were confined for 5 min (without food) in a circular, opaque, fluon-lined pot (diameter: 10.5 cm; height: 8.5 cm) with a clear view of the sky but all terrestrial cues obscured. Video recording reveals the total distance walked within the pot was around 10 m. They thus should have accumulated additional noise in PI without increasing the length of the home vector. They were subsequently given a food item and released at either the familiar or unfamiliar release point.
(b). Estimating uncertainty
To estimate the expected variance in the home vector for ants that have travelled different distances, their outbound path can be modelled as an allothetic directed walk [16]: at each time-step, the ant takes a step of equal length (L) in the same direction, from its nest towards the food. Noise can be considered equivalently as arising in the motor system (i.e. variance in the ant's actual location after a series of steps) or sensory system (i.e. variance in the ant's estimate of its location after a series of steps) or both. Because the ant has an external celestial compass, the angular error on each step is independent. Following [16], if we denote the noisy step lengths as L1, L2…, and the noisy angles as Δ1, Δ2…, and take the X-axis as the direction of intended travel, then for the ant's position perpendicular to the direction of intended travel, Y, the expected variance after n steps is given by
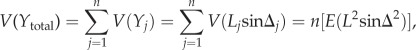 |
2.1 |
where E denotes the expected value. Thus, variance increases proportionally to the number of steps taken, n, or equivalently for steps of equal length, the distance travelled (dT) (figure 1b). The directional variance (i.e. the variance in the heading direction indicated by the home vector) is given by the angle θ = arctan(y/dH), where dH is the direct distance home. As arctan(y/dH) ≈ y/dH for 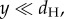 the directional variance is given by
the directional variance is given by
| 2.2 |
For an ant moving in a relatively straight line (e.g. on a learned route from nest to feeder), dT ≈ dH, and thus, perhaps surprisingly, V(θ) will decrease with distance, proportionally to 1/dH. This analysis was confirmed using a particle filter simulation (electronic supplemental material, S4).
For experiment 2, if we assume the ant has travelled 13 m while the distance home remains 3 m, the directional variance should be
| 2.3 |
This means the variance would be equivalent to the variance of straight run of less than 1 m (V(θ) proportional to 1/dH = 1.4, hence dH = 0.71). This estimate was also confirmed using the particle filter simulation.
To compare the model to our data, we assume the ant is using a weighted sum of the directions given by its view towards the nest and its PI system. According to maximum-likelihood estimation, the optimal weighting should be inversely proportional to the variance, or equivalently
| 2.4 |
and
| 2.5 |
The same optimal estimate can be derived from Bayes's theorem if we assume a uniform prior. Ants with no view or PI information appeared to head equally often in every direction (electronic supplementary material, figure S1). Ants could have acquired a prior that coincides with the PI direction, due to repeated travel back from the food. However, in our experiment, this would not be distinguishable from a reduced relative weighting of the view, and hence would make no difference to the fit.
We compare the fit with optimal weighting based either on the positional variance (i.e. variance is proportional to distance) or the directional variance (i.e. direction is proportional to 1/distance); these fits have one free parameter, the variance of the view. We also look at the fit of a simple (non-optimal) linear weighting by distance: 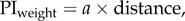 which also has one free parameter; or a linear weighting by distance with an upper threshold beyond which the weight is 1:
which also has one free parameter; or a linear weighting by distance with an upper threshold beyond which the weight is 1: 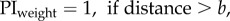 which has two free parameters. We compare the fit of these four models using the Akaike information criterion [18].
which has two free parameters. We compare the fit of these four models using the Akaike information criterion [18].
3. Results
(a). Experiment 1
By capturing ants on their route to a feeder and releasing them with food at a novel location, we set into conflict the directional information provided by the view (release-point-to-nest direction) with the direction indicated by their PI system (feeder-to-nest direction): a difference of 110° in our experimental configuration (figure 1a). By capturing the outbound ants at different distances (0, 1, 3 and 7 m), the relative certainty of their PI should be altered, as described in the Material and methods section.
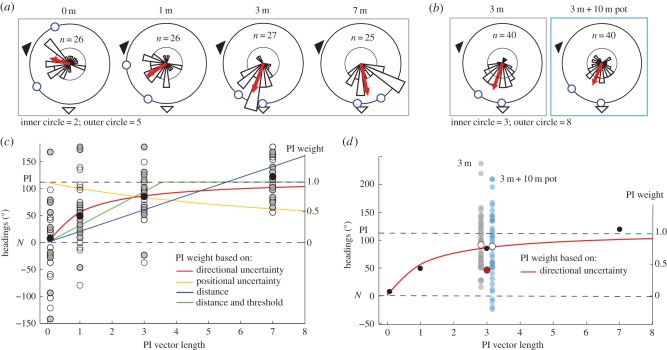
The procedure for the two nests was identical and no significant differences between them were observed, so they were grouped for analysis using circular statistics [19]. All groups showed oriented distributions (Rayleigh test p-values < 0.0008; z-values > 6.84), but the groups headed in significantly different directions from each other (Mann–Whitney U: p < 0.0001, 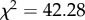 ). The further ants had travelled before capture, the closer the mean direction to the PI direction. On average, the 0 m group headed towards the nest (i.e. in accordance with the view), 1 and 3 m groups moved in intermediate directions, and the 7 m group followed the feeder-to-nest direction (PI) (figure 2a). The 1 and 3 m heading distributions show no signs of bimodality. Figure 2c shows the data described above with the heading direction relative to the nest chosen by each ant plotted against the distance travelled before capture. Both nests show the same pattern of results (compare grey and white dots), with increased weighting of the PI direction as distance increases. As described in the Material and methods section, we examined the fit of four different models to this data. The best fit (table 1) is given by assuming optimal weighting of the cues based on the directional variance of PI, which decreases proportionally with increasing distance. This fit has only one free parameter, the assumed (relative) variance of the view, and the best fit is obtained when this is set as equivalent to PI at 0.95 m.
). The further ants had travelled before capture, the closer the mean direction to the PI direction. On average, the 0 m group headed towards the nest (i.e. in accordance with the view), 1 and 3 m groups moved in intermediate directions, and the 7 m group followed the feeder-to-nest direction (PI) (figure 2a). The 1 and 3 m heading distributions show no signs of bimodality. Figure 2c shows the data described above with the heading direction relative to the nest chosen by each ant plotted against the distance travelled before capture. Both nests show the same pattern of results (compare grey and white dots), with increased weighting of the PI direction as distance increases. As described in the Material and methods section, we examined the fit of four different models to this data. The best fit (table 1) is given by assuming optimal weighting of the cues based on the directional variance of PI, which decreases proportionally with increasing distance. This fit has only one free parameter, the assumed (relative) variance of the view, and the best fit is obtained when this is set as equivalent to PI at 0.95 m.
Figure 2.
Ants integrate sensory cues using uncertainty. (a,b) Circular histograms show the orientations taken by ants with various PI lengths (a), and for the 3 m control and 3 m ‘pot’ groups (b). Black and white arrowheads indicate view direction (nestwards) and PI direction, respectively. Red arrows indicate the mean directions and blue circles the 90% CI. (c,d) The headings at the familiar release point are replotted linearly. Left axis shows the angle from the nestward heading with PI direction at 110°, and the right axis shows the weighting given to PI. Overlaid are the best fits of the various models. (c) Ants' headings with various PI lengths for nest 1 (grey) and nest 2 (white). Mean headings (black) match best weightings predicted by optimal integration based on PI directional uncertainty (red curve). (d) Ants' headings for the 3 m (grey) and 3 m ‘pot’ (blue) groups. Red dot shows the weighting predicted by PI directional uncertainty for 3 m ‘pot’ group. Instead, mean headings of both groups (white dots) closely match previous data (black dots), suggesting that ants use the vector length to weigh PI. (Online version in colour.)
Table 1.
Comparing models of PI weighting, ordered by lower AIC = nlog(error) + 2K, where K is the number of free parameters for each model. A difference of more than 3 between the first and subsequent models suggests they have considerably less support. Performance of models to explain how directional dictate of PI is weighted. The smaller the AIC the better the fit.
| model | equation | best fit | no. free parameters | residual error | AIC |
|---|---|---|---|---|---|
directional uncertainty 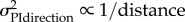
|
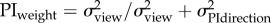 |
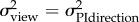 at 0.95 m at 0.95 m |
1 | 0.0686 | −6.0366 |
| distance and threshold |
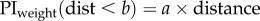
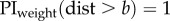
|
a = 0.2717 b = 3.5 | 2 | 0.1050 | −2.7600 |
| distance | 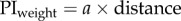 |
a = 0.1731 | 1 | 0.2364 | −2.3266 |
positional uncertainty 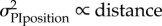
|
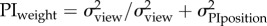 |
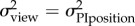 at ∼ 10 m at ∼ 10 m |
1 | 0.4583 | −0.3406 |
The headings also show significant difference in scatter around the mean (O'Brien test: p = 0.0178, F = 3.52), with variability reduced as the PI vector length increases. Note that this inter-individual variability should not be taken to reflect individual variability, but rather this change in scatter is also consistent with increased weighting of PI with increasing vector length, as previous results have shown larger inter-individual variability in use of learnt views than PI [20], with the former affected by individual foraging history, whereas use of PI is not [21,22].
(b). Experiment 2
In our second experiment, we decoupled distance walked and PI vector length by capturing outbound ants 3 m from the nest and making them spend 5 min walking in a pot. Video analysis of nine ants showed they walked on average 10 m in the pot (min. 8 m, max. 15 m). Assuming ants are still performing PI during this time, we predicted their directional uncertainty should increase, to around the same variance as 1 m ants in experiment 1 (see Material and methods and figure 1b) and hence (assuming optimal weighting) they should make a similar directional choice. We used a higher n (= 40) to ensure experiment 2 should have power to detect the predicted difference.
Figure 2c shows the heading directions of control (3 m) ants and ‘pot’ (3 m + 10 m) ants. Both groups headed in the same intermediate direction (WWtest: p = 0.8485; F = 0.0367). This suggests the two cues are combined with a weighting that depends on the home vector distance, not the directional uncertainty; that is, it is highly consistent for all groups with a PI length of 3 m, irrespective of total distance covered (or time spent), and different to groups with a different PI length (experiment 1). It is possible that ants in the pot stopped integrating their paths, or that for some reason the expected accumulation of error in their PI estimate did not occur. Below we propose instead that ants do not maintain an internal estimate of their PI uncertainty, but weight cues optimally based on a proxy for uncertainty: the length of their PI.
4. Discussion
A number of ant species have been shown to combine information from PI and their visual memory so as to head in intermediate directions when these cues are set in conflict [9–11,13,23]. Here, we tested whether this cue combination is optimal by varying the relative certainty of the PI cue.
(a). Assessing optimality without measuring individual variance
Quantifying the variance associated with different cues, and with manipulation of those cues, usually requires estimation based on multiple trials for individuals [4]. It is crucial to note that although we use only single measurements on individual ants in this experiment, we can nevertheless obtain from first principles a quantitative expression for how the individual directional variance should change relative to distance travelled. This depends only on the well-justified assumption that ants are performing PI using an external compass reference [6], which means variance perpendicular to the home direction increases proportionally to distance [24]; from basic trigonometry, it follows that the variance of the angle subtended with the home position decreases inversely with distance. This allows us to determine, for a given certainty of a directional visual memory cue, how the relative weighting of the directional PI cue should change with distance, and hence predict the intermediate direction that ants should take when these are in conflict.
It could be argued that the use of group data is not sufficient to demonstrate that individual ants are altering their weighting of the two cues (optimally or otherwise). However, the absence of bimodality in the distributions suggests we are not simply seeing the group average of single cue choices by individuals; individual ants took compromise directions. Although the precise weighting (and possible influence of other factors) varies across individuals, the population statistic can be estimated with the mean. All ants received similar training and were randomly assigned to one of the four groups, so the only factor that could explain the significant group differences in the mean heading direction is their differing PI state.
(b). Combining multiple strategies
Previous work [11] suggests that ants can also modulate the weight attributed to their visual memory. At locations where the view is more familiar, the directional choice appears more strongly biased to the view. There may also be innate species differences, or environmental influences on the certainty of visual memory. Assuming optimal integration, we can predict how the relative weighting should vary with PI vector length for different levels of visual certainty (electronic supplementary material, figure S2). At strongly familiar locations, visual memories could be favoured even for large PI vector length, and this has been observed in ants [17,25–27]. Conversely, PI should dominate behaviour at visually unfamiliar locations, consistent with present (electronic supplementary material, figure S3) and previous data [10,11,23,28]. Although we only consider the initial bearing of ants in our experiment, note that movement towards home will alter the relative certainty of the cues, and thus a changing path direction (see for instance fig. 8 of [29]) could still be consistent with optimal integration.
(c). Do ants weight path integration optimally?
Cataglyphis velox ants show increasing bias towards the PI direction as home vector length increases (figure 2a,c) in a manner quantitatively predicted by optimal cue integration based on the decrease in PI directional uncertainty (figure 2c). We examined several alternative models of how the PI state might have affected directional choice (table 1) but none provide as close a fit to the data as the assumption that the cues are weighted inversely to the predicted directional variance of PI. We thus have equivalent evidence of optimal cue combination in ants such as has been provided in many psychophysical studies in humans [3].
However, the results of our second experiment suggest that ants may not compute the actual directional certainty of their PI. Ants that should have accrued substantially more uncertainty (figure 1b, ‘3 m + 10 m pot’) gave equivalent weighting to the PI cue as ants with the same PI length (figure 2b,d), contrary to the prediction of optimal integration.
One potential explanation of this result is that ants did not update their PI during the extra walking time spent in the pot, and the observed behaviour is still optimal, as the PI directional uncertainty is unchanged. Indeed, ants may well be aware that they are trapped in a pot, although previous studies suggest that PI is continuously running when ants are constrained by narrow channels or forced into making a detour [30]. A second explanation is that ants do not explicitly maintain an estimate of PI certainty, but use PI home vector length as a proxy for certainty when weighting PI with other cues. The use of such a proxy would spare the need for their small brains to support the representation of, or calculation with, the actual uncertainty of PI. Supporting this view, we note that the ‘uncertainty’ revealed by nest search distributions in ants [31], in a study where the outward path was unconstrained, also appears to be dependent on PI home vector length rather than absolute path length, even though the latter modifies the actual uncertainty of PI.
Nevertheless, the correct weight to associate with this proxy cue to obtain optimal integration is not trivial: as we have shown, the ant does not simply use a linear weighting (figure 2c). We think it is unlikely that individual ants in our experiment could have acquired the correct tuning of the weighting from individual experience, as their foraging experience consisted of a small number of trips within a cleared corridor, which would seem insufficient to collect meaningful measures of PI variance. We suggest that evolution has come up with an optimal weighting rule that reflects long-term average levels of certainty, encompassing the sensory-motor noise and typical meander of natural paths in a short-cut estimate. Different species might thus have evolved different tunings reflecting the reliability of their sensory-motor systems in their natural environments [32]. It remains possible that a pre-wired weighting rule could be further tuned by experience.
If optimal weighting in ants is due to use of a proxy rather than explicit measure of uncertainty, this raises the question of whether the same could be the case in at least some vertebrate and human examples of cue integration. Many studies assume that perceptual judgements that fit the predictions of optimal integration necessitate probabilistic processing. Ma [33] suggests that strong evidence for Bayesian processing dependent on explicit representation of uncertainty is provided by experiments in which unpredictable changes in the level of uncertainty on individual trials produces appropriate alterations in the weighting. However, if the estimate of uncertainty for a single trial can be based on some aspect of the cue that covaries with cue uncertainty in a consistent manner (a proxy or ‘valid cue’ [34]) then it is possible that an appropriate mapping to the ‘optimal’ weighting could have been learnt or evolved. However, it is notable that both here and in previous studies [11,23], ants appear to combine cues even when they indicate very discrepant directions. That is, ants do not appear to be making a ‘meta-Bayesian’ computation to determine the likelihood that the cues come from a single source versus independent sources [16]. This may reflect a significant difference in the flexibility of cue integration in the invertebrate and vertebrate brain.
Supplementary Material
Acknowledgements
We thank Luigi Acerbi, Matthew Collett and Peggy Series for their comments, and Nadia Kolewa, Chris Elmes and Xim Cerda for field assistance. Allen Cheung advised on modelling ant uncertainty; Paul Graham and Andy Philippides on early experimental design.
Competing interests
The authors declare no conflict of interest.
Funding
This work was supported by the BBSRC grant ‘Bayesian ants’.
References
- 1.Kording KP. 2014. Bayesian statistics: relevant for the brain. Curr. Opin. Neurobiol. 25, 130–133. ( 10.1016/j.conb.2014.01.003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ernst MO, Banks MS. 2002. Humans integrate visual and haptic information in a statistically optimal fashion. Nature 415, 429–433. ( 10.1038/415429a) [DOI] [PubMed] [Google Scholar]
- 3.Ernst MO. 2006. A Bayesian view on multimodal cue integration. In Human body perception from the inside out, vol. 131 (eds Knoblich G, Thornton IM, Grosjean M, Shiffrar M), pp. 105–131. Oxford, UK: Oxford University Press. [Google Scholar]
- 4.Cheng K, Shettleworth SJ, Huttenlocher J, Rieser JJ. 2007. Bayesian integration of spatial information. Psychol. Bull. 133, 625–637. ( 10.1037/0033-2909.133.4.625) [DOI] [PubMed] [Google Scholar]
- 5.Wehner R. 2009. The architecture of the desert ant's navigational toolkit (Hymenoptera: Formicidae). Myrmecol. News 12, 85–96. [Google Scholar]
- 6.Wehner R, Srinivasan MV. 2003. Path integration in insects: biological basis of navigation. Oxford, UK: Oxford University Press. [Google Scholar]
- 7.Collett M, Chittka L, Collett TS. 2013. Spatial memory in insect navigation. Curr. Biol. 23, R789–R800. ( 10.1016/j.cub.2013.07.020) [DOI] [PubMed] [Google Scholar]
- 8.Fukushi T, Wehner R. 2004. Navigation in wood ants Formica japonica: context dependent use of landmarks. J. Exp. Biol. 207, 3431–3439. ( 10.1242/jeb.01159) [DOI] [PubMed] [Google Scholar]
- 9.Collett M. 2012. How navigational guidance systems are combined in a desert ant. Curr. Biol. 22, 927–932. ( 10.1016/j.cub.2012.03.049) [DOI] [PubMed] [Google Scholar]
- 10.Narendra A, Gourmaud S, Zeil J. 2013. Mapping the navigational knowledge of individually foraging ants, Myrmecia croslandi. Proc. R. Soc. B 280, 20130683 ( 10.1098/rspb.2013.0683) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Legge ELG, Wystrach A, Spetch ML, Cheng K. 2014. Combining sky and Earth: desert ants (Melophorus bagoti) show weighted integration of celestial and terrestrial cues. J. Exp. Biol. 217, 4159–4166. ( 10.1242/jeb.107862) [DOI] [PubMed] [Google Scholar]
- 12.Jander R. 1957. Die optische Richtungsorientierung der Roten Waldameise (Formica ruea L.). Z. Vgl. Physiol. 40, 162–238. ( 10.1007/BF00297947) [DOI] [Google Scholar]
- 13.Reid SF, Narendra A, Hemmi JM, Zeil J. 2011. Polarised skylight and the landmark panorama provide night-active bull ants with compass information during route following. J. Exp. Biol. 214, 363–370. ( 10.1242/jeb.049338) [DOI] [PubMed] [Google Scholar]
- 14.Graham P, Cheng K. 2009. Ants use the panoramic skyline as a visual cue during navigation. Curr. Biol. 19, 935–937. ( 10.1016/j.cub.2009.08.015) [DOI] [PubMed] [Google Scholar]
- 15.Wystrach A, Beugnon G, Cheng K. 2011. Landmarks or panoramas: what do navigating ants attend to for guidance? Front. Zool. 8, 21 ( 10.1186/1742-9994-8-21) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cheung A, Zhang S, Stricker C, Srinivasan MV. 2007. Animal navigation: the difficulty of moving in a straight line. Biol. Cybern. 97, 47–61. ( 10.1007/s00422-007-0158-0) [DOI] [PubMed] [Google Scholar]
- 17.Mangan M, Webb B. 2012. Spontaneous formation of multiple routes in individual desert ants (Cataglyphis velox). Behav. Ecol. 23, 944–954. ( 10.1093/beheco/ars051) [DOI] [Google Scholar]
- 18.Burnham KP, Anderson DR. 2002. Model selection and multimodel inference: a practical information-theoretic approach. New York, NY: Springer Science & Business Media. [Google Scholar]
- 19.Batschelet E. 1981. Circular statistics in biology. London, UK: Academic Press. [Google Scholar]
- 20.Wystrach A, Beugnon G, Cheng K. 2012. Ants might use different view-matching strategies on and off the route. J. Exp. Biol. 215, 44–55. ( 10.1242/jeb.059584) [DOI] [PubMed] [Google Scholar]
- 21.Cheng K, Narendra A, Sommer S, Wehner R. 2009. Traveling in clutter: navigation in the Central Australian desert ant Melophorus bagoti. Behav. Process. 80, 261–268. ( 10.1016/j.beproc.2008.10.015) [DOI] [PubMed] [Google Scholar]
- 22.Merkle T, Wehner R. 2009. How flexible is the systematic search behaviour of desert ants? Anim. Behav. 77, 1051–1056. ( 10.1016/j.anbehav.2009.01.006) [DOI] [Google Scholar]
- 23.Wystrach A, Schwarz S, Schultheiss P, Baniel A, Cheng K. 2014. Multiple sources of celestial compass information in the Central Australian desert ant Melophorus bagoti. J. Comp. Physiol. A Neuroethol. Sensory Neural Behav. Physiol. 200, 591–601. ( 10.1007/s00359-014-0899-x) [DOI] [PubMed] [Google Scholar]
- 24.Vickerstaff RJ, Cheung A. 2010. Which coordinate system for modelling path integration? J. Theor. Biol. 263, 242–361. ( 10.1016/j.jtbi.2009.11.021) [DOI] [PubMed] [Google Scholar]
- 25.Andel D, Wehner R. 2004. Path integration in desert ants, Cataglyphis: how to make a homing ant run away from home. Proc. R. Soc. Lond. B 271, 1485–1489. ( 10.1098/rspb.2004.2749) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kohler M, Wehner R. 2005. Idiosyncratic route-based memories in desert ants, Melophorus bagoti: how do they interact with path-integration vectors? Neurobiol. Learn. Mem. 83, 1–12. ( 10.1016/j.nlm.2004.05.011) [DOI] [PubMed] [Google Scholar]
- 27.Wystrach A, Schwarz S, Schultheiss P, Beugnon G, Cheng K. 2011. Views, landmarks, and routes: how do desert ants negotiate an obstacle course? J. Comp. Physiol. A Neuroethol. Sensory Neural Behav. Physiol. 197, 167–179. ( 10.1007/s00359-010-0597-2) [DOI] [PubMed] [Google Scholar]
- 28.Schwarz S, Albert L, Wystrach A, Cheng K. 2011. Ocelli contribute to the encoding of celestial compass information in the Australian desert ant Melophorus bagoti. J. Exp. Biol. 214, 901–906. ( 10.1242/jeb.049262) [DOI] [PubMed] [Google Scholar]
- 29.Zeil J, Narendra A, Stürzl W. 2014. Looking and homing: how displaced ants decide where to go. Phil. Trans. R. Soc. B 369, 20130034 ( 10.1098/rstb.2013.0034) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wehner R. 2003. Desert ant navigation: how miniature brains solve complex tasks. J. Comp. Physiol. A Neuroethol. Sensory Neural Behav. Physiol. 189, 579–588. ( 10.1007/s00359-003-0431-1) [DOI] [PubMed] [Google Scholar]
- 31.Merkle T, Wehner R. 2010. Desert ants use foraging distance to adapt the nest search to the uncertainty of the path integrator. Behav. Ecol. 21, 349–355. ( 10.1093/beheco/arp197) [DOI] [Google Scholar]
- 32.Cheng K, Schultheiss P, Schwarz S, Wystrach A, Wehner R. 2014. Beginnings of a synthetic approach to desert ant navigation. Behav. Process. 102, 51–61. ( 10.1016/j.beproc.2013.10.001) [DOI] [PubMed] [Google Scholar]
- 33.Ma WJ. 2012. Organizing probabilistic models of perception. Trends Cogn. Sci. 16, 511–518. ( 10.1016/j.tics.2012.08.010) [DOI] [PubMed] [Google Scholar]
- 34.Barthelmé S, Mamassian P. 2010. Flexible mechanisms underlie the evaluation of visual confidence. Proc. Natl Acad. Sci. USA 107, 20 834–20 839. ( 10.1073/pnas.1007704107) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.