Computational modeling of subdural cortical stimulation: A quantitative spatiotemporal analysis of action potential initiation in a high density multicompartment model

Abstract

Objectives

Computational modeling studies were performed to identify presynaptic elements of cortical neurons that are activated by subdural electrical stimulation.

Materials and Methods

The computer model consists of layers of multicompartmental neurons arranged in 3D space in an anatomically realistic fashion inside a 4.8×4.8×3.4 mm volume of gray matter modeled as a homogenous and isotropic medium. The model was subjected to an electric field generated by a circular disk electrode.

Results

The initiation of presynaptic action potentials (PAPs) in neurons takes place predominantly in the axon initial segment (AIS) or ectopically in axonal branch terminals. PAPs that were initiated in only one axonal terminal were typically followed by a second PAP (spike duplet) resulting from the activation of the AIS by the antidromically propagating initial PAP. There were significant time delays (up to 0.5 ms) in the propagation of these ectopically initiated PAPs along the axons to non-activated axonal branches and, associated with these delays, latencies in the occurrence of spike duplets in different axonal terminals. The effect of the dendritic arbor 3D structure on the AIS activation threshold was contingent on whether the net axonal and somato-dendritic current flows made an antagonistic or synergetic contribution.

Conclusions

This study examines the effects of subdural electrical stimulation on a high density network consisting of several populations of multicompartment cell types. The effect of dendritic arbor structure on the axonal activation threshold is prominent in the case of multipolar neurons with large-diameter symmetric dendrites (basal/apical) that are oriented parallel to the electric field lines. The timing of presynaptic terminal activation after stimulation is not determined solely by the axonal delay (orthodromic propagation) but depends on the details of the applied stimulation field and axonal branching structure, which may be important factors in characterizing the effects of electrical stimulation in neuromodulation systems.

Introduction

Direct cortical brain stimulation has emerged as a relevant clinical tool for mapping of eloquent cortex ¹, and for neuromodulation attempts at stopping seizures². Since its introduction in the late nineteenth and early twentieth centuries³, the electrical stimulation of the cortex has been used predominantly in an empirical way due to the lack of methodology for quantifying the effects on cellular populations. The cellular and network mechanisms underlying the effect of electrical stimulation in the brain remain poorly understood, mostly due to the inability to capture and quantify the high variability in the responses of stimulated neurons. As a result, many new therapeutic and clinical applications of brain stimulation are introduced without a clear understanding of the mechanisms necessary for the determination of clinical efficacy or safety of these interventions. For these reasons, a better understanding of the mechanisms underlying electrical stimulation is needed.

At the single neuron level, it is recognized that the axon initial segment (AIS) and nodes of Ranvier are sites of activation of neurons subjected to electrical stimulation^4-7. In contrast, everything occurring in a network, above the level of a single neuron, is far from being well understood. This is mostly due to the complex interactions of the ongoing activity (in an unperturbed network) with the activity evoked by the stimulation in the network. The effect of an electrical field applied to a limited cortical area for example is difficult to precisely predict because of the existence of intracortical connectivity through which locally evoked activity will propagate to adjacent and remote areas. The volume directly targeted by the electric field is also characterized by a high variability in the response of stimulated neurons, which results from many factors such as the distributed orientation of axons and spatial variation of current density under the stimulating electrode. Along with the cellular, membrane and volume effects, the application of an electric field primarily results in the generation of presynaptic action potentials (PAPs) in a large number of neuronal axons. These PAPs are prime movers that initiate the complex effect of an electrical stimulation in a network. Identification of sites of initiation of these PAPs right after the stimulation and how they conduct into various local proximal and distal axonal collaterals is important for understanding the mechanism of action underlying electrical stimulation.

Studies of brain stimulation in laboratory models are difficult but often invaluable ⁸ and the efficacy of newly introduced therapies can only be established through invasive clinical trials. Computer simulations of the modulatory effect of electrical stimulation in neuronal network models offer a promising alternative that can be used for studying a wide-range of stimulation parameters in order to improve stimulation efficacy. Neuronal network models offer the great advantage of allowing modification of various stimulation parameters while at the same time monitoring the resultant behavior of many neurons in the network. After the application of the electric field, the effects on individual neurons are manifested in changes in network behavior. Studies at the network level, which are difficult in biological systems, are needed in order to fully understand the mechanisms of stimulation.

In the past decade, several computer models of the modulatory effects of electrical stimulation have been developed as attempts to understand various factors influencing stimulation and the recruitment of neurons in cortical^9-13, hippocampal¹⁴, and thalamic networks^15,16 as well as in dorsal column fibers¹⁷. All of these studies have dealt mostly with non-active networks and have focused on current distribution and voltage threshold effects for action potential induction in myelinated or unmyelinated axons (i.e. AIS, nodes of Ranvier). In the recent most advanced cortical models¹³ a 3D folded layer of realistically reconstructed multicompartmental pyramidal neurons is considered which allows for the investigation of how geometry and the location of neurons contribute to the induced effects of the electric field. In contrast, only a very few studies ^18-21 have made attempts to investigate the effects of electrical stimulation in the context of active neural networks. Early studies, however, suffer either from not explicitly modeling the effects of the electric field on axonal processes of simulated neurons (single compartment neurons were modeled¹⁸) or from considering a very generic network architecture^19-20. Recent and more sophisticated large scale cortical models propose a realistic cortical architecture with several neuronal populations and intrinsic cortical connectivity guided by anatomic data while employing neuronal models of various complexity^12,21.

In this paper we describe the modeling study of a realistic neuronal cellular array subjected to an electric field. The effect of the applied electric field is simulated in a multi-layer cortical network model of unfolded cortex consisting of a several different types of multicompartmental cortical neurons (excitatory and inhibitory). The proposed model has several advantages. This multi-type and high cell density network model allows for better quantification of the effects of stimulation in terms of depth, focality, and spatial extent of the recruited neuronal volume by the stimulating electrode as well as for the creation of maps of direct neural activation. In particular, the developed model allows for studying how the effects of stimulation vary across neuronal populations in various neuron types. It allows for identification of axonal sites where PAPs are initiated in each neuronal type and for the statistical analyses of these recruited PAPs. Based on these analyses, the effect of changing various stimulation parameters on neuronal recruitment across the single neuronal population and types are demonstrated. These include the effect of changing the amplitude of the stimulating current and varying the polarity sequence of the charge-balanced pulse. The relatively high density of neurons in our model (10³/mm³) compared to densities in similar previously studied models, permits the quantification of how the electrode size affects the number of recruited neurons. These analyses indicate that this number is not very sensitive to the electrode diameter as long as the applied current to the electrode does not change.

In 3D cortical models when a population of axons is considered^9,13 the location and orientation of the axons relative to the electrode position are major factors in determining the site of PAP initiation. In contrast, the addition of various neuron types in our model allowed the demonstration of cell-class specific neuronal recruitment, in addition to location and orientation factors. The electrical stimulation then can selectively activate different neuron types in various cortical layers and therefore produce various inhibitory/excitatory responses in superficial and deep layers (relative to the direction of a current flow).

Unmyelinated and branched neuronal axons in our model are intended to represent the fraction of axons projecting locally within gray matter. The addition of the branching structure in axons allows for the analysis of temporal axonal responses in these neurons after stimulation. Such investigations were not carried out in previous published studies which dealt mostly with long myelinated fiber axons. These analyses show that PAPs initiated in distal axonal segments of stimulated neurons can cause retrograde axonal activation which occurs in a nonphysiological fashion and produces a more convoluted temporal post-stimulation neuronal response. The latter finding may represent an initial step toward understanding the direct effects of electric stimulation on neurons in addition to “synaptic and network” post-stimulation components, which are not studied in this paper. Our long-term goal is to develop a fairly realistic model of neocortex linked by synaptic connections and subjected to an electric field, which will be the focus of future studies. Such studies based on theoretical computer models may in the future provide justification for the choice of stimulation parameters in clinical trials, or aid studies of animal models.

Methods

Neuron models that have been adapted for these studies were used previously to study high frequency gamma oscillations, sleep spindles and epileptogenic bursts²². This simulated network model differs from the original single-column thalamocortical network model in that horizontal (parallel to the pia) size scale has been applied throughout the modeled volume. Both the vertical and the horizontal size for the modeled volume are chosen as an approximate representation of human cortex, with a total simulated thickness of 2340 μm and 25 μm interspacing between cortical minicolumns^23,24 respectively. Compared to the original single-column network model, the number of neurons in a single minicolumn has been scaled down. Neuronal structural differences that have been imposed include dendritic/axonal 3D representations along the neuron’s normal axis with axons directed perpendicular to the pia rather than the tangential plane. Neuronal model structures are determined by their 3D compartmental representations and have been implemented in the GENESIS 2.3 simulation platform. Details of the neuron morphologies have been described earlier and can be found elsewhere^22,25. The conductance densities of various compartmental regions for all simulated neurons are listed in Table 1, for comparison with other models. All simulations were performed in pGENESIS 2.3 (parallel GENESIS).

Table 1.

Membrane conductance densities (mS/cm²):

Supragranular pyramidal neurons22 (layer II/III)
	gNa(F)	gNa(P)	gK(DR)	gK(C)	gK(A)	gK(M)	gK2	gK(AHP)	gCa(L)	gCa(T)	gAR
axon	400	0	400	0	2	0	0.1	0	0	0	0
soma	187.5	0.12	125	12	30	7.5	0.1	0.04	1	0.1	0.25
proximal	12.5-93.75	0.008-0.06	6.25-125	12	2-30	7.5	0.1	0.04	1	0.1	0.25
distal	12.5	0.008	6.25	12	2	7.5	0.1	0.04	1	0.1	0.25

Supar- and infragranular basket neurons25 (layer II/III & V)
	gNa(F)	gNa(P)	gK(DR)	gK(C)	gK(A)	gK(M)	gK2	gK(AHP)	gCa(L)	gCa(T)	gAR
axon	400	0	400	0	1	0	0	0	0	0	0
soma	60	0	100	25	1	0	0	0	0.1	0	0
proximal	60	0	100	25	1	0	0	0	0.1	0	0
distal	10	0	10	25	1	0	0	0	0.2	0	0

Internal granular stellate neurons22 (layer IV)
	gNa(F)	gNa(P)	gK(DR)	gK(C)	gK(A)	gK(M)	gK2	gK(AHP)	gCa(L)	gCa(T)	gAR
axon	400	0.4	400	0	2	0	0.1	0	0	0	0
soma	150	0.15	100	10	30	3.75	0.1	0.1	0.5	0.1	0.25
proximal	75	0.075	75	10	2-30	3.75	0.1	0.1	0.5	0.1	0.25
distal	5	0.005	0	10	2	3.75	0.1	0.1	0.5	0.1	0.25

Infragranular pyramidal neurons22 (layer V)
	gNa(F)	gNa(P)	gK(DR)	gK(C)	gK(A)	gK(M)	gK2	gK(AHP)	gCa(L)	gCa(T)	gAR
axon	450	0	450	0	0.6	30	0.5	0	0	0	0
soma	200	0.16	170	28.8	20	8.5	0.5	0.2	1.6	0.1	0.1
proximal	75-15	0.06-0.012	0-75	0.9-28.8	0.6-8	13.6	0.5	0.2	0.4-1.6	0.1	0.1
distal	3	0.0024	0	2.16	0.6	4	0.5	0.2	0.4		0.1

Infragranular pyramidal neurons22 (layer VI)
	gNa(F)	gNa(P)	gK(DR)	gK(C)	gK(A)	gK(M)	gK2	gK(AHP)	gCa(L)	gCa(T)	gAR
axon	450	0	450	0	4	0	0.1	0	0	0	0
soma	200	0.08	170	15	122.5	4.2	0.1	0.2	0.2	0.1	0.25
proximal	75	0.03	75	15	13.6	4.2	0.1	0.2	0.2	0.1	0.25
distal	5	0.002	0	0	13.6	4.2	0.1	0.2	0.2	0.1	0.25

The spatial arrangement of neurons is based on our previous implementations of single compartment neurons arranged around a minicolumnar square lattice format¹⁸. The current network model differs from previous models in two aspects. 1) In comparison to previous studies of single compartment neurons, each neuron now has a 6-compartment axon and multiple dendritic compartments that replicate spatially diffuse dendritic arborization. 2) Stimulations of neurons by the disk electrode were performed in a network without resting (sparse) activity and with no active synaptic connections. This approach allows the investigation of the direct recruitment of neurons resulting from delivered stimulation without the interference of synaptic and network (post-stimulation) components, which will be investigated in a later paper.

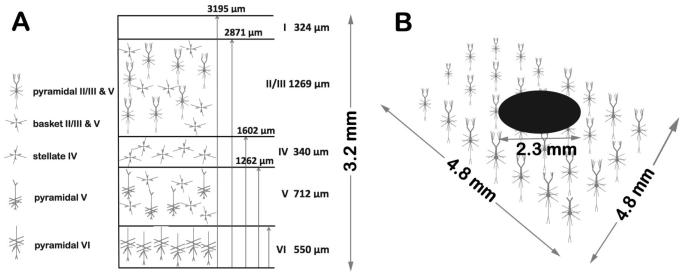
The modeled cortical volume was divided into a three layers as shown in Fig. 1A: supragranular (basket and pyramidal neurons in layers II/III), internal granular layer (stellate neurons in layer IV) and infragranular (basket in layer V and pyramidal neurons in layers V and VI). The position of a neuron within a simulated volume is defined by the Cartesian coordinates of the soma. Coordinates of proximal and distal compartments are calculated relative to the position of the soma. The vertical location of a neuron within a minicolumn is random within a given range that is pre-determined for each cell type and each neuron is rotated about its normal axis by a random angle from 0 to 360 degrees. This allows for the vertical arrangement of neuron types into a layered structure within a simulated volume similar to that found in corresponding cortical layers. In horizontal directions we use an array of repeating minicolumns^23,24 to create the modeled cortical volume. The arrangement of neurons in layers and minicolumns provides a spatial scale in both vertical and horizontal directions. An array of 40×40 repeating minicolumns represents approximately 1 mm × 1 mm of cortex. The cellular density in the model varies from 630 (basket) to 5043 (pyramidal) neurons/mm³.

Figure 1.

(A) Distribution of compartmental models of cortical neurons in the x-z plane in the simulated cortical volume. The supragranular layer consists of basket and pyramidal neurons in layers II/III, the internal granular layer is represented by stellate neurons in layer IV, and the infragranular layer consists of basket cells in layer V and pyramidal neurons in layers V and VI. The position of a neuron within a simulated volume is defined by the Cartesian coordinates [x,y,z] of the soma. The vertical arrangement of neuron types into a layered structure was obtained by assigning z coordinates of neurons within a given range that is pre-determined for each cell type. The z coordinate of each neuron within a given layer was randomized and each neuron is rotated about its normal axis by a random angle from 0 to 360 degrees. In horizontal directions we use an array of repeating minicolummns. The arrangement of neurons in layers and minicolumns provides a spatial scale in both vertical and horizontal directions. An array of 40×40 repeating minicolumns represents approximately 1 mm × 1 mm of cortex and the total simulated volume corresponds to 4.8 × 4.8 × 3.195 mm of gray matter. The cellular density in the model varies from 630 (basket) to 5043 (pyramidal) neurons/mm³. (B) Schematic illustration of electrode position in respect to pyramidal neurons in the supragranular layer. Note: Sizes of neuron and electrode along with neuron-to-neuron distances were scaled for better visualization.

Neurons were electrically stimulated with a realistic circular disk electrode (0.7 - 2.3 mm diameter) positioned in the simulations 0.2 mm above and parallel to the top surface of the modeled gray matter volume (4.8 × 4.8 × 3.195 mm). The electric potential of the disk due to electrical charge is assumed to be a V₀ (transient value) relative to a ground electrode at infinity. The values of the extracellular potentials under the electrode at the points matching the positions of neuronal compartments have been calculated from a voltage distribution for an infinitely thin charged disk sitting atop an infinite half-plane²⁶ according to the following equation:

$$V(r,z)=\{\begin{array}{cc}\frac{2V_0}{\pi }{\mathit{sin}}^{-1}\left(\frac{\mathrm{d}}{\sqrt{{\left(r-\frac{d}{2}\right)}^2+z^2}+\sqrt{{\left(r+\frac{d}{2}\right)}^2+z^2}}\right)\hfill & z\ne 0\hfill \\ V_0\hfill & z=0,r\le \frac{d}{2}\hfill \end{array}\phantom{\}}$$ (1)

where r and z are radial coordinates of a given compartment, d is the diameter of the disk electrode and V₀ is the potential applied to the electrode. The volume is modeled as a homogeneous and isotropic medium with uniform conductivity σ = 0.24 S/m²⁷ with no reactive capacitance component interacting with the flow of currents. Discretization of the neuron compartment coordinates and the knowledge of the potential distribution in the space under the electrode allow for the calculation of equivalent intracellular current sources for compartments that are injected at the time of stimulation^28,29. The potential V₀ value was used to calculate the equivalent current sources but the results of simulations are reported for current-controlled stimulation. The total current I₀ applied to the electrode was a product of V₀ and the electrode resistance R = 1/2σd where d is the electrode diameter³⁰. The amplitude of the delivered current I₀ to the electrode varies in the range 1 - 15 mA³¹ which corresponds to a V₀ value applied to disk in a range 1 - 7 V. It should be noted that the I₀ value is arbitrary since it depends on the choice of σ value. The applied current has the form of a charge-balanced square wave (positive /negative, 0.15 ms each). Stimulation parameters used in simulations are consistent with those used in a typical cortical mapping session. In this paper, only the case of monopolar disk electrode stimulation was considered. Analysis of other electrode configurations will be the subject of a future work.

Results

Neuronal population recruitment

Fig.2 illustrates input-output curves for the axonal activation of pyramidal and basket neurons in supragranular layer II/III obtained for a 0.3 ms long charge-balanced current pulse sequence (anodal-cathodal vs. cathodal-anodal). In the case of pyramidal neurons, PAPs were initiated in either the AIS (with the exception of a low current amplitude < 3 mA) or in the axon branch terminal compartments. The simultaneous occurrence of PAPs in the AIS and the axon terminal compartment or in both terminal compartments was observed in less than 6% of activated axons for stimulating currents larger than 3 mA (anodal-cathodal pulse). In contrast, in basket neurons, the initiation of PAPs in the AISs took place only in a small fraction of these neurons and only in the case of cathodal-anodal stimulation (Fig. 2D). In the case of anodal-cathodal pulse stimulation, PAPs in basket neurons were solely initiated in the axon terminal compartments. In the case of cathodal-anodal pulse stimulation, a strong reduction in the numbers of neurons activated in axonal terminals was observed in both pyramidal and basket neurons (Fig. 2C and D)

Figure 2.

Input-output characteristics of axonal activation for pyramidal (diamonds) and basket neurons (squares) in the supragranular layer (II/III) as a function of the current amplitude (range 2-15 mA) applied to the electrode. Legends (left insets) show neuronal axons along with sites of axonal activations indicated in red. Line color next to the axon matches the corresponding input-output activation curve for a given axonal site. Blue line corresponds to a total number of recruited neurons (sum of input-output activation curves for all axonal sites). A single 0.3 ms long anodal-cathodal (top panels) and cathodal-anodal (bottom) pulse was applied.

Lateral and vertical extent of recruited volume

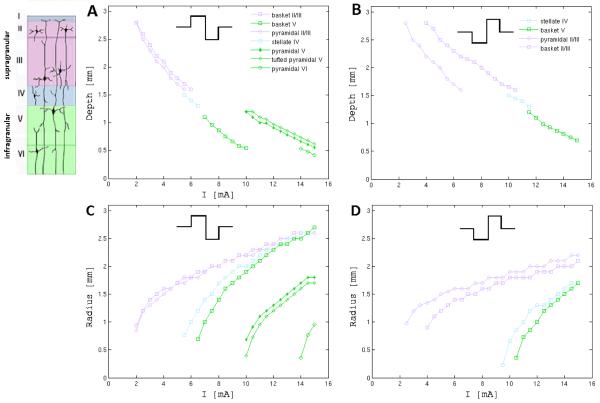
The depth of the spatial extent of neuron recruitment in the vertical direction (perpendicular to the electrode surface) varied for neuron types. Fig. 3 illustrates depth recruitment curves (superimposed) for all types of simulated neurons in supra, inter, and infragranular layers as a function of the applied current amplitude to the electrode for a 0.3 ms long anodal-cathodal (A) and cathodal-anodal (B) pulse sequences. Neuron type specific differences in the depth of recruitment are clearly visible in the infragranular layer where pyramidal neurons in layers V and VI at a given cortical depth need approximately 30% larger current amplitude of the stimulating pulse sequence than basket neurons in order to be activated.

Figure 3.

Depths (A,B) and radii (C,D) of a spatial extent of neuron recruitment under the electrode as functions of the applied current. Depths and radii were measured in directions perpendicular and parallel (on a plane) to the pia respectively. Colors of curves correspond to simulated neuron in supra, internal and infragranular layers indicated on left inset.

The volume of recruited neurons under the electrode has a radial symmetry (Fig. 4) and similar to the depth of spatial extend distribution (Fig. 3A and B), the radius of the lateral extent of the recruited neurons can be estimated by measuring the distance between the center of the electrode and the position of the most distal recruited neuron in planes parallel to the electrode surface. Fig. 3C and D show radii of the lateral extent of neuron recruitment under the electrode as a function of the applied current amplitude for all simulated neuron types. With the exception of pyramidal neurons in the infragranular layers, there is a convergence of curves describing the radii of recruitment volumes as the amplitude of the applied current increases (supra- and inter-granular layers).

Figure 4.

A plot summarizing recruitment of neurons in layers II-V in in a plane perpendicular to the electrode surface and including the electrode center line. The volumes corresponding to recruited neurons (blue - pyramidal, turquoise - stellate, yellow - tufted pyramidal V, red - basket) may overlap (supragranular layer) but in general are not equal. The volumes of recruited pyramidal neurons in the infragranular layer are notably smaller than the volume of recruited basket neurons (red). The position of the electrode is indicated by the top black line. The applied current amplitude was I₀ = 12.5mA and the stimulation pulse was 0.3 ms (anodal-cathodal). The pyramidal neurons in layer VI are not activated at this particular value of I₀ and neurons in layer I were not simulated.

Pulse polarity sequence

In terms of the total number of recruited neurons the, anodal-cathodal pulse sequence was found to be more efficient than the equivalent cathodal-anodal pulse (Fig 2A,B and Fig.5A,B,C). The anodal-cathodal pulse as mentioned earlier in general recruited more neurons in the axon terminals than the cathodal-anodal pulse. This can be seen in Figs. 2A and B (green line) as well as in Figs. 5A,B and C (cadet blue colored cloud) where in the case of the anodal-cathodal pulse a considerably larger number of neurons activated in the axonal terminals was observed among all recruited neurons. The anodal-cathodal pulse sequence was also found more effective for the activation of neurons in deeper layers than the analogous cathodal-anodal pulse. This can be seen in Fig. 3A where pyramidal neurons in layers V and VI (green lines) were recruited for I₀ > 10 mA by the anodal-cathodal pulse while these neurons were not recruited at all by the equivalent cathodal-anodal pulse (Fig. 3B).

Figure 5.

3D maps of recruitment (direct axonal activation) of pyramidal neurons in the supragranular layer by a single 0.3 ms pulse. Stimulating current amplitudes (3, 6 and 12 mA), and stimulus polarization along with the position of the electrode are indicated at the top of each subset. Colors representing the corresponding sites of axonal initiation (indicated in red) are shown on the right.

Neuron-type specific recruitment

Curves describing the lateral and vertical extent of the recruited neuron volumes (Fig. 3C and D) depend on neuron type, which suggests that the recruitment volumes will not be identical. The plot summarizing the volumes and distribution of recruited neurons in layers II-V in a plane vertical to the electrode surface including the electrode center line is shown in Fig. 4. In the supragranular layers the volume of the recruited pyramidal neurons (blue) overlaps almost exactly with the volume of recruited basket neurons (red) which is consistent with Fig. 3C for I₀ = 12.5 mA current amplitude applied to the electrode. The recruitment of neurons in the infragranular layer (V) provides an example of unequal volumes. Particularly the volumes corresponding to the recruitment of two types of pyramidal neurons (regular pyramidal - blue and tufted pyramidal - yellow) lay within the volume of the recruited basket neurons. The latter however extends far beyond the volume of recruited pyramidal neurons.

Sites of PAP initiation

Besides the neuronal class specific differences in neuron recruitment, the response of a neuron to stimulation varies within each neuron type (Fig. 2). The factors affecting the site of initiation of PAPs in a given neuron type include the position and orientation of the neuron relative to the electrode and the amplitude of the applied current to the electrode. Fig. 5 illustrates 3D maps showing the distribution of sites of axonal AP initiation obtained for pyramidal neurons in supragranular layers and subjected to 3, 6, and 12 mA charge-balanced current pulse sequences (anodal-cathodal and cathodal-anodal). Axons that are closest and directly under the electrode are predominantly activated in AISs (blue core). The initiation within axon terminals takes place solely in the basket like area (light blue/green) that is adjacent and surrounds the core (AIS activation). Simultaneous initiation of PAPs in the AIS and terminal(s) is also demonstrated in Fig. 5 (yellow/orange). These take place mostly in the area between the core and the surrounding basket. It must be noted that the activation maps do not illustrate instantaneous activation of axonal compartments. The points used to create the maps in Fig. 5 were collected over a 4 ms interval after the onset of the stimulation pulse and might be associated with latencies up to 3.1 ms (in the case of a cathodal-anodal pulse).

Temporal response of neurons to stimulation

Analyses of the temporal response of a single neuron to the applied stimulation pulse are illustrated in Fig. 6A and B. The temporal sequences of excitation occurring in neurons are shown by plotting voltage traces in all axonal, somatic, and most proximal dendritic compartments in two basket neurons (A and B) after a 0.3 ms long current pulse. PAPs are initiated in one (A) or simultaneously in both axonal branch terminals (B). A single stimulation pulse sequence typically induces a PAP duplet at axon terminals, with the second PAP arising from AIS activation by antidromic propagation (towards the soma) from the initial PAP. In panel B, these duplets (the initial and the second PAP) arrive at both terminals at the same time, while in panel A there is latency (0.5 ms) in the arrival of these spike duplets at axonal branch terminals.

Figure 6.

Sequence of excitation of compartments in a model of a basket cell neuron resulting from a single pulse of stimulation. Presynaptic spikes are generated in one (panel A, left top insets shows branch marked in red color) or simultaneously in both distal axonal branches (panel B, left top insets branches marked in red) and propagate antidromically to the soma and later to the dendritic compartments. The second PAP occurs at the axon terminal approximately 1.5 ms after the initial spike and results from orthodromic propagation that follows somatic depolarization (yellow). The pulse timing and duration are indicated at the bottom by the blue trace. In panel A, the PAP is generated in the left distal axonal branch (turquoise) and propagates antidromically towards the distal axon (red) and next to the right axonal branch (green and pink) and somatic/dendritic compartments (yellow/black). Current pulse amplitude in 6 mA; duration 0.3 ms

Electrode diameter

In the current-controlled configuration (constant current) for the simulations used in this work, the electrode diameter has a minor effect on the recruitment of neurons. Fig. 7 illustrates input-output curves of neuronal activation obtained for three different electrode diameters. The slope of the input-output curves as well as the number of recruited neurons are relatively unaffected by the electrode diameter for the 4 -6 mA range of the stimulation current. However the input-output curves diverged for stimulation currents below 4 mA and when the applied current to the electrode is above 6 mA.

Figure 7.

Effect of changing electrode diameter on numbers of activated neurons. Input-output curves of axonal activation for pyramidal neurons in the supragranular layer (II/III) vs. the current amplitude applied to the electrode (range 2.5-12.5 mA) are shown for 0.7, 1.5, and 2.1 mm electrode diameters. A single 0.3 ms long anodal-cathodal (A) and cathodal-anodal (B) pulse was applied.

Discussion

In order to understand the effects of electrical stimulation applied to the cortical surface we wish to know how the electric field modulates the activities of several morphological types of neurons in the cerebral cortex. In these modeling studies several types of cortical neurons were subjected to a non-uniform electric field. The novelty of these studies is twofold: we can make a prediction about the membrane polarization at each compartment of each individual neuron and at the same time obtain valuable statistical information on the number of recruited neurons along with the initiation sites of the induced PAPs. This approach differs from earlier studies in which either a lower numbers of neurons were used^10,32 or just investigated a few neurons positioned in different locations⁹. In contrast to these previous studies, which provided valuable but more qualitative description, our approach allows obtaining a detailed quantitative statistical study as shown in Fig. 2.

It should be emphasized that the neuron models used in this work were initially developed to mimic the intrinsic synaptic activity of interneurons and principal cortical neurons and were not used before in studies of electrical stimulation. The spatially distributed neuronal model we employ here represents neurons and cortical organization in relatively great detail with the exception of synaptic connections, which are not simulated. This approach is similar to that proposed by Markram³³ where behaviors of a cortical network are investigated by modeling the complex behavior of real neurons, rather than using phenomenological neuron models³⁴. Efforts to simulate the effect of an electric field in this type of neuronal network face frequent criticism that questions the ability of the compartmental model to mimic the interaction of the electric field with neurons. This often includes claims that either the neuron models used in the simulations involves too much or too little complexity for emulating this phenomenon. The choice of these particular neuron models is partly motivated to fill the need for easy coding implementation while preserving prominent elements of the 3D cellular architecture. This means that the simulated neurons do not represent fully 3D reconstructed cells, but on the other hand they are not limited to only axonal initial and proximal dendritic compartments. The reduction of the neuronal model however is notable, including the simplified, but not completely neglected, axonal structure. The use of a simplified axonal structure here might be partially justified by the results of previous studies^4-7showing that after electrical stimulation, the majority of the induced PAPs will be generated in AISs. Adding synaptic contacts, which are not present in the current model, may further justify the axonal simplification. In the current case, the lack of synapses helps in identification of the sites of PAP origin. Lastly, the degree of cellular complexity reduction in the model is optimal for large-scale network simulations such as presented in this work. Previous studies that were based on a fully 3D reconstructed neuron model, due to its complexity, were more suited for simulation of one¹⁵ or considerably lower numbers of neurons^9,10.

Additionally, we consider here an idealized network without resting or background activity. Modeling of stimulation paradigms in an unconnected network is a common modeling approach, which may help us in understanding the direct effects that electric stimulation has on neurons without a “synaptic and network” post-stimulation component^9-11,32. As our understanding of this phenomenon becomes more mature we will introduce connectivity to the simulated network in order to understand the induced network effects, with the current study a first step in this direction.

These studies confirmed that the sites of direct activation of neurons are AISs but also indicate that more distal axon segments in the proximity of the AIS (below the first branchpoint) are likely locations where PAPs can originate regardless of the state of the AIS (sup- or sub-threshold activation, hyperpolarization). After the stimulation, the level of polarization of a given axon compartment depends on the net contribution of current inputs introduced by all the remaining axonal compartments. In the case of the AIS, in addition to the net axonal contribution, the proximal dendritic arbor has a significant impact on the polarization of this compartment. This is different from the activation of the myelinated axon in remote nodes of Ranvier, which are in electrical isolation from the soma or the AIS.

The results suggest that despite the relatively high soma->axon resistance (small axon diameter) the mutual somato-dendritic polarization may contribute to the activation of the AIS. Depending on the orientation of a neuron relative to the electrode position and stimulus polarity, different compartments along the neuron will respond with either a positive or a negative polarization of a different magnitude. For the AIS (a perisomatic axonal compartment) it is important whether the net axonal and somato-dendritic current flows make an antagonistic or synergetic contribution. This in turn will be determined by the neuron morphology, orientation relative to the electrode position, and the stimulus polarization. For example the absence of the AIS activation in basket neurons in Fig. 2B by an anodal-cathodal pulse (for comparison see pyramidal neurons in Fig. 2A) can be explained by the morphological differences in the dendritic arborization of basket and pyramidal neurons. The pyramidal neuron model has large diameter apical dendrites and several small diameter basal dendrites. The basket neuron model, contrary to the pyramidal neuron, has four symmetrical (across the neuron main axis) large diameter dendritic branches (Fig. 6). For this stimulation paradigm and the electrode configuration, the neuron’s normal axes are perpendicular to the electrode surface meaning that the electric field lines directly under the electrode remain parallel to these axes. The low resistance between the soma, the apical dendritic, and in the case of basket neurons, the basal dendritic branches creates an easy pathway for the flow of axial currents in the direction that is determined by the stimulus polarization. During the anodal stimulation the somal compartment of pyramidal neurons would be more depolarized because a smaller volume of axial current flows into the basal compartments. In the basket neuron, the somal compartment is hyperpolarized rather than depolarized during the same anodal pulse because the current can easily flow into the large diameter and basally oriented compartment. The hyperpolarization of the soma in basket neurons affects the polarization of the AIS by increasing the threshold for activation of this compartment. This may explain the lack of PAP in the AISs in basket neurons subjected to an anodal-cathodal pulse in Fig 2B.

The effect of dendritic currents on the AIS polarization might be important in the case of cortical neurons generating dendritic spikes (which were omitted and not simulated here). For instance some bursting pyramidal neurons in layer V can generate large dendritic calcium currents^35,36 or N-Methyl-D-aspartate (NMDA) spikes³⁷. It is likely that the dendritic initiation zone of calcium spikes may potentially interact with the AIS segment. As in interneurons, the flow of dendritic currents associated with calcium and N-Methyl-D-aspartate (NMDA) spikes might contribute to the polarization of the AIS in these neurons. These dendritic currents may have an effect on the total number of recruited neurons in layer V and the overall excitability of this layer. This effect however needs to be investigated in a connected and active network.

In the case of the most distal axon compartments (below the first branchpoint), in addition to the net current contribution from the adjacent axon compartments, the sealed-end effect will also contribute to the polarization of these compartments. As mentioned earlier, for this stimulation paradigm, the neuron’s normal axes are perpendicular to the electrode surface. The axonal terminals will always represent more distal compartments for the neurons (relative to the electrode position) and therefore they will be the most depolarized in the case of anodal stimulation and the most hyperpolarized compartments after cathodal stimulation respectively. This effect is clearly evident in Fig. 2C and D where the number of neurons activated in axon terminals in both types of neurons by cathodal-anodal pulses is lower compared to anodal-cathodal pulses (Fig. 2A,B). There is no rebound excitation in these compartments after the cathodal phase of the stimulus because the width of the pulse phase (0.15 ms) is too short to induce anodal break excitation. This is also evident in Fig. 5D-F where the volume representing activation of axonal terminals is notably smaller.

This model allows for the creation of detailed 3D maps of axonal activation in order to visualize the spatial extent of PAP initiation and the volume of tissue of recruited neurons. Fig. 2 and Fig. 4 show that the repertoire of axonal activation varies depending on the neuron orientation and the stimulating current parameters. The total number of recruited neurons by the cathodal-anodal pulse in general is lower compared with the anodal-cathodal pulse (Fig. 2). The main difference is in the number of neurons recruited that have PAPs initiated in the axon terminals (Fig. 2C and D). The total number of recruited neurons might be an important factor that determines the effects of stimulation but is not an exclusive one. The initiation of PAPs in axonal terminals generates spike duplets (Fig. 6A and B). In addition if a neuron is recruited only in one axon terminal this introduces an offset in the arrival of these spike duplets in both terminals (Fig. 6A). In this case, the applied stimulation does not only result in the spatial activation of neurons in the network but also produces more complex temporal responses in the postsynaptic neurons. Particularly in the case of GABAergic neurons it seems that both, the number of recruited neurons and the temporal variation in the arrival of PAPs may be important factors determining the ability of stimulation to disrupt synchrony in a network. Given that the anodal-cathodal pulse sequence in general recruits more neurons and, in the case of basket neurons, recruitment is solely at axon terminals we can expect that the anodal-cathodal pulse sequence will have a qualitatively different effect than the equivalent cathodal-anodal pulse.

The anodal-cathodal pulse was also found to be more effective in the recruitment of pyramidal neurons in deeper layers V and VI (Fig 3A green lines). This is in agreement with the experimental data from monopolar stimulation of rat motor cortex³⁸ where deeper layers were found to be more sensitive to anodic stimulation and responded earlier after stimulation than upper layers. This is consistent with our results presented in Fig. 3A where pyramidal neurons from layers V and VI were recruited solely after anodal-cathodal pulse while they were not recruited by the equivalent cathodal-anodal pulse at all (Fig. 3B). The results shown in Fig.3 however represent the aggregated activation of neurons over a 0.6 ms time window and therefore cannot show which layers were activated first. Despite the fact that our neurons were inactive and only a single stimulation pulse was used, our results can still qualitatively reproduce what was observed in vivo in the active rat motor cortex³⁸.

Electrode size

When changing the electrode diameter, the total number of recruited neurons does not change notably as long as the current I₀ applied to the electrode remains the same (which is the case in current-controlled stimulation). The results in Fig. 7 are consistent with those reported by Wongsarnpigoon and Grill¹⁰, although in those earlier studies the input-output curves of neuronal recruitment did not diverge noticeably as the amplitude of the stimulation current increases. The modest impact of the electrode diameter on the number of recruited neuron can be explained by the fact that the lateral and vertical extent of the recruited neuron volume is inversely correlated to the electrode diameter. In general, electrodes with larger diameters, besides providing a larger lateral extent of field effects, will offer a smaller extent of the recruitment volume in the vertical direction. Electrodes with smaller diameters will offer a larger vertical field effect but with a smaller lateral extent. The latter suggests that for a given I₀ smaller electrodes will generally provide better recruitment of neurons in the vertical direction. It should be noted that this is only a theoretical supposition because for a given amplitude of I₀ (constant-current stimulation), when the electrode diameter d decreases, the V₀ potential at the electrode will increase as 1/r (r=d/2 is an electrode radius). Therefore small diameter electrodes will require larger V₀ potentials in order to activate the same number of neurons. For that reason the simulations described in this work with small diameter electrodes in situ may be associated with a higher risk of tissue damage since a larger current density will be delivered from a small electrode area.

Limitation

While 3D representations of neurons adopted for these studies replicate many details of the dendritic morphologies of neurons found in cortical layers, axons are represented by a six unmyelinated compartments. The reduced axonal model takes into account the AIS, the compartment before the main branchpoint, and the two main branches, each consisting of two compartments. The total length of the unmyelinated section of the axon does not exceed 0.2 mm (measured along the neuron normal axis). This is consistent with an estimation of the first maximum in the myelin sheath density function reported for pyramidal neurons, which is 0.2 mm below the level of a neuron body^39,40. However other data indicate that pyramidal neurons in infragranular layers (V) have a 0.1 mm long myelin sheath section located between the AIS and the branchpoint⁴¹. Therefore this reduced form of the axonal model cannot replicate all characteristics of the axonal arbor in neurons. This is important since axonal elements have a lower threshold for excitation and represent the potential sites of direct activation of neurons subjected to electrical stimulation. As long as the network model considered here is idealized without resting or background activity, the lack of synaptic connections in the model can partly justify the reduced form of the axonal model. Despite the axonal model simplicity, these simulations allow us to show that electrical stimulation can create temporal patterns (PAP duplet sequence in axons) that are qualitatively different from the patterns resulting from dendritic processing of postsynaptic potentials (Fig. 6A).

The perpendicular orientation of neuronal axons to the electrode surface is the other limitation. The current computer model does not reflect the broad diversity of the cortical neuronal alignment. Although the vertical alignment of axons may be a fairly valid approximation for pyramidal neurons whose main axons project vertically into the white matter, it is less valid in the case of interneurons which form local connections and may have main axons projecting in any direction (including the direction traversing cortical columns). This indicates that the results presented for basket neurons may not be as easily generalized as the case of pyramidal neurons. On the other hand the larger diversity in orientation of interneurons may not be that important given that the morphology of the dendritic arbor of these neurons may be more symmetric (Fig. 6). In contrast to pyramidal neurons, the net soma-dendritic current contribution to the AIS polarization in interneurons would be relatively unaffected by neuron rotation because all four dendritic trunks project along the neuron’s main axes.

In this work we solely analyzed the responses of neurons to a single biphasic pulse, however in clinical practice the majority of therapeutic interventions rely on periodically delivered repeating pulses. We limited our analyses to a single pulse because in the current network configuration (unconnected neurons), the initiation and propagation of the induced PAPs in both orthodromic and antidromic directions typically occur in a less than a 4 msec time window, which is below the intervals between the two consecutive pulses in a typical range of stimulation frequencies used for therapeutic interventions.

Furthermore, Eq. (1) used to calculate the electric potential under the electrode does not take into account the capacitance of the intercellular medium. The cortical volume is modeled as a homogeneous and isotropic ohmic medium that has no reactive component⁴². This approach creates major obstacles for the analysis of the effects of periodic stimulation because it does not allow for the calculation of voltage transients produced by biphasic current pulses delivered at various frequencies. However in the case of single pulse analysis it gives a fairly sufficient approximation. Since the tissue-electrode impedance cannot be currently taken into account, we limited our analysis to a single pulse. Repeating pulses are certainly required for the stimulation of active fibers or eloquent tissue and we reserve these analyses for our future simulations of connected neurons with an improved method of calculation of the electric potential under the electrode.

An additional limitation of the present studies is the assumption that the gray matter conductivity is homogenous and isotropic. The conductivity of gray matter varies in cortical layers⁴³ because layers consist of different neuronal types that vary in size, density, and orientation. Beside the laminae, the cortex has also a horizontal architecture with spatially clustered patch projections⁴⁴. These are a few mechanisms for the reported horizontal anisotropy in the gray matter conductivity⁴⁵. As described earlier this cortical stimulation study dealt with several populations of unconnected and thus synaptically inert neurons. This is an apparent limitation because the neuronal post-stimulation response is also determined by a large number of synaptic currents, gap junctions and ephaptic coupling. The intracortical horizontal connectivity through which locally evoked activity will propagate to adjacent and remote areas is also neglected. For example, previous modeling studies of motor cortex stimulation for pain management¹² indicated that stimulation of M1 area can lead to a suppression of activity of neurons in S1 somatosensory cortex area which receive outputs from neurons in the M1 area.

Lastly, the existing model does not take into account the conductivity of cerebrospinal fluid (CSF), which may be considerably greater than the conductivity of cortical layers⁴⁶. The current from the subdural electrode entering the cortical layers through the top CSF space may be shunted and this may result in reshaping of the field potential distribution in all layers below and thus affect the lateral and vertical extent of neuron recruitment. A finite element model (FEM) incorporating several stacked conductive tissue layers may provide a more meaningful model for the study of neuron recruitment in a cortical volume. The application of FEM methods however may impose certain limits on the density of neurons that are simulated in the modeled volume.

Finally, the fact that this cortical model does not take into account the folded structure of the cortex is another limitation. Because the surface of the cortex is highly folded, the orientation of cortical columns will not be perpendicular to the electrode surface as well. In addition, the orientation of columns that form the cortical slab may not be perpendicular to the surface of the cortex per se⁴⁷. This geometrical simplification in the model is a consequence of the methods used for the calculation of a potential distribution under the stimulating disk electrode (analytical solution for a half infinite plane). The application of FEM methods would allow for the consideration of more arbitrary geometries of the cortex, as well as accounting for the heterogeneities in the tissue.

Comparison with other modeling studies

Previous studies^9,10,32 have examined the effects of electrode placement, geometry, and polarity during cortical stimulation and addressed mostly epidural stimulation. The subdural cortical stimulation has not been studied in great detail because in general the extradural electrode placement is preferred in many types of therapies. As the stimulation methods are being continuously improved^48,49 and new therapies are being introduced the rationale for the placement of the electrode extradurally becomes debatable. Previous theoretical studies^50,51 have suggested that epidural stimulation would only reach the outer cortical layers and likely recruit only the axons parallel to the direction of the electric field (bipolar stimulations). Another comparative epidural vs. subdural stimulation modeling study³² suggests that epidural stimulation is more effective in the activation of cortical efferent (pyramidal) axonal tracts but in fact these studies might not take into account the recruitment of neurons in the internal and infragranular layers by the subdural electrode. Studies presented in this work provide several new insights showing that subdural monopolar stimulation can recruit neurons in deeper cortical layers. Besides the different site of the electrode placement (epidural), these previous studies differ from the present work in several aspects. These mainly include the way the electric field was calculated (FEM or Finite Difference Method), the density of neurons/axons in a simulated cortical volume (number of simulated neurons < 10³), the presence of different neuron types, as well as taking into consideration the curvature of the cortex (gyral/sulcal folding pattern). Despite these differences, the results of previous studies are consistent with the results of the present study in many points. The three studies are all in agreement in showing that: 1) during anodal stimulation, the most distal axonal compartments on the border of the gray matter, are sites where PAPs are initiated (besides AISs). 2) cathodal stimulation activates neurons predominantly at AISs. These observations are in agreement with our results showing that the anodal-cathodal pulse sequence is more effective in the recruitment of axons in the terminals, while cathodal-anodal pulses initiate PAPs predominantly in AISs (Fig. 2 and 5). Previous studies also indicated that the electrode diameter has a modest impact on the input-output neuronal recruitment curves, which is also consistent with our results (Fig. 7).

While previous studies ignored the effect of the 3D structure of the neuronal dendritic arbor on the axonal activation threshold, our study suggests that the morphology of the dendritic arbor can affect this threshold in certain conditions. This effect will be particularly prominent in the case of multipolar neurons with large-diameter symmetric dendrites (basal/apical directions) that are oriented parallel to the electric field lines. The basket neurons used in this study (Fig. 6) are examples of such neurons. The symmetric structure of the dendritic arbor in these neurons creates the passage for an easy flow of axial current that will either hyperpolarize or depolarize the soma compartment and affect the polarization of the AIS by increasing or decreasing the threshold for activation of this compartment (see discussion).

Finally, the large density of simulated neurons in the present study allows for the creation of detailed maps describing the distribution of sites of axonal initiation, their spatial extent, and the volume of a tissue with recruited neurons (Fig. 4 and 5).

Conclusion

The initiation of PAPs in simulated neurons takes place predominantly in the AIS or ectopically in axonal branch terminal compartments, below the main branchpoint. The site of initiation of PAPs in the axon depends on the orientation of the neuron relative to the electrode, and the amplitude and polarization of the applied current. Coincident PAP initiations in more than one (adjacent or distant) axonal compartment were less frequent and occurred mostly in axon terminals. The total number recruited by a single charge-balance current pulse exhibits an S-shape growth curve as the amplitude of the applied current to the electrode increases. The number of recruited neurons is not sensitive to the electrode diameter change. The anodal-cathodal pulse sequence was more effective in neuron recruitment however the increase in the number of recruited neurons was selective with respect to the number of neurons recruited solely in axonal terminals. The effect of 3D dendritic arbor structure on the AIS activation threshold is prominent in the case of multipolar neurons with large-diameter symmetric dendrites (basal/apical) that are oriented parallel to the electric field lines. PAPs that were ectopically initiated in only one axonal terminal were typically followed by a second PAP (spike duplet) resulting from the activation of the AIS by the antidromically propagating initial PAP. There were up to 0.5 ms time delays in the propagation of these ectopically initiated PAPs along the axons to non-activated axonal branches and, associated with these delays, latencies in the occurrence of both spike duplets in the main axon branch terminals. This suggests that after stimulation, the time of activation of postsynaptic neurons at presynaptic terminals is not determined solely by the axonal delay (orthodromic propagation) but depends on details of the applied stimulation field. The fact that after stimulation, PAPs arrive at the presynaptic terminals of various branches at different times might be important in characterizing the effects and evaluating the efficacy of electrical stimulation. The temporal variability of PAPs can contribute to desynchronizaton of the neural activity and therefore may underlay desynchronizing or anti-epileptic effects of stimulation.