The Net Reclassification Index (NRI): a Misleading Measure of Prediction Improvement Even with Independent Test Data Sets

Abstract

The Net Reclassification Index (NRI) is a very popular measure for evaluating the improvement in prediction performance gained by adding a marker to a set of baseline predictors. However, the statistical properties of this novel measure have not been explored in depth. We demonstrate the alarming result that the NRI statistic calculated on a large test dataset using risk models derived from a training set is likely to be positive even when the new marker has no predictive information. A related theoretical example is provided in which an incorrect risk function that includes an uninformative marker is proven to erroneously yield a positive NRI. Some insight into this phenomenon is provided. Since large values for the NRI statistic may simply be due to use of poorly fitting risk models, we suggest caution in using the NRI as the basis for marker evaluation. Other measures of prediction performance improvement, such as measures derived from the ROC curve, the net benefit function and the Brier score, cannot be large due to poorly fitting risk functions.

1 Introduction

The Net Reclassification Index (NRI) was introduced in 2008 [11] as a new statistic to measure the improvement in prediction performance gained by adding a marker, Y, to a set of baseline predictors, X, for predicting a binary outcome, D. The statistic has gained huge popularity in the applied biomedical literature. On March 13, 2013 through a search with Google Scholar we found 840 papers (44 since January 2012) that contained the acronym ‘NRI’ and referenced Pencina et al. (2008) [11]. The measure has been extended from its original formulation [13,9]. In this note we demonstrate a fundamental technical problem with use of the NRI in practice.

2 Illustration with Simulated Data

Consider a study that fits the baseline model risk(X) = P(D = 1|X) and the expanded model risk (X, Y) = P(D = 1|X, Y) using a training dataset. The fitted models that we denote by riŝk(X) and riŝk(X, Y) are then evaluated and compared in a test dataset. as

$$\text{NRI}=2\{P[\text{ri}\widehat{\mathrm{s}}\mathrm{k}(X,Y)>\text{ri}\widehat{\mathrm{s}}\mathrm{k}(X)|D=1]-P[\text{ri}\widehat{\mathrm{s}}\mathrm{k}(X,Y)>\text{ri}\widehat{\mathrm{s}}\mathrm{k}(X)|D=0]\}$$ (1)

the proportion of cases in the test dataset for whom riŝk(X, Y) > riŝk(X) minus the corresponding proportion of controls, multiplied by 2. The categorical NRI [11] is discussed later.

We generated data from a very simple simulation model described in the Supplementary Materials where X and Y are univariate and the logistic regression models hold:

$$\text{logit}P(D=1|X)={\alpha }_0+{\alpha }_{1}X$$ (2)

$$\text{logit}P(D=1|X,Y)={\beta }_0+{\beta }_{1}X+{\beta }_{2}Y.$$ (3)

We used a small training set and fit logistic regression models of the correct logistic forms in (2) and (3). Using a large test dataset we calculated the continuous NRI statistic for the training set derived models:

$$\begin{array}{c}\text{logit}\text{ri}\widehat{\mathrm{s}}\mathrm{k}(X)={\hat{\alpha }}_0+{\hat{\alpha }}_{1}X\\ \text{logit}\text{ri}\hat{\mathrm{s}}\mathrm{k}(X,Y)={\hat{\beta }}_0+{\hat{\beta }}_{1}X+{\hat{\beta }}_{2}Y.\end{array}$$

For the simulation results in Table 1 the data were generated under the null scenario where Y does not add predictive information, i.e., β₂= 0 and α₁ = β₁ is chosen so that X has the area under the ROC curve in the second column. The results indicate, however, that the NRI statistic is positive on average in the test dataset. Moreover, in a large portion of simulations the NRI statistic was positive and statistically significant in the test dataset using the standard test based on the empirically estimated NRI divided by the standard error provided in [11,13]. Thus the NRI statistic calculated on the test dataset tends to indicate the erroneous result that Y contributes predictive information when in fact it does not.

Table 1.

Measures of improvement in prediction when risk models, logitP(D = 1|X) = α₀ + α₁X and logit P(D = 1|X, Y) = β₀ + β₁X + β₂Y, are fit to a training dataset and applied to a test dataset. The novel marekr Y does not improve prediction: the true models are linear logistic (2) and (3) with coefficients: β₂ = 0, β₁ = α₁ and β₀ = α₀. Data generation is described in Supplementary Materials. Performance measures are averaged over 1000 simulations. Standard errors are small and are shown in Table A.1 of the Supplementary Materials. In parentheses are shown the % of simulations where the NRI was found to be statistically significantly positive.

One Uninformative Marker
Simulation Scenario					Average Performance Increment ×100
ρ = P(D = 1)	AUCaX	N-trainingb	N-testc	NRId	ΔROC(0.2)	ΔAUC	ΔBrier	ΔSNB(ρ)
0.1	0.6	250	25,000	0.27(12.7)	−1.70	−1.28	−0.044	−1.85
0.1	0.7	250	25,000	1.38(29.4)	−1.37	−0.86	−0.049	−1.31
0.1	0.8	250	25,000	3.22(46.8)	−0.90	−0.48	−0.058	−0.80
0.1	0.9	250	25,000	7.72(60.3)	−0.52	−0.25	−0.066	−0.57
0.5	0.6	50	5,000	0.57(21.3)	−1.67	−1.19	−0.479	−1.69
0.5	0.7	50	5,000	2.78(40.5)	−2.59	−1.69	−0.540	−2.49
0.5	0.8	50	5,000	6.56(55.2)	−1.83	−1.00	−0.492	−1.62
0.5	0.9	50	5,000	17.09(69.0)	−1.11	−0.56	−0.433	−1.17

^aArea under the ROC curve for the baseline model (X)

^bSize of training dataset

^cSize of test dataset

^d% of simulations with NRI statistically significantly positive shown in parentheses

We also calculated more traditional measures of performance improvement. Define

$$\begin{array}{l}\text{AUC}(\text{risk})=P({\text{risk}}_i\ge {\text{risk}}_j|D_i=1,D_j=0)\\ \text{ROC}(f,\text{risk})=P({\text{risk}}_i\ge \tau (f)|D_i=1)\text{where}\tau (f):P({\text{risk}}_j\ge \tau (f)|D_j=0)=f\\ S\text{NB}(t,\text{risk})=P(\text{risk}>t|D=1)-\frac{P(D=0)}{P(D=1)}\frac{t}{1-t}P(\text{risk}>t|D=0)\\ \text{and}\\ \text{Brier}(\text{risk})=E{(D-\text{risk})}^2.\end{array}$$

The AUC is the area under the receiver operating characteristic (ROC) curve. The ROC(f, risk) measure is the proportion of cases classified as high risk when the high risk threshold is chosen as that exceeded by no more than a proportion f of controls. This is closely related to the PCF statistic proposed by Pfeiffer and Gail [17,14] that is defined as the proportion of cases classified as high risk when the high risk threshold is chosen so that a fixed proportion of the population is classified as high risk. The standardized net benefit, SNB(t), is a weighted average of the true and false positive rates associated with use of the risk threshold t to classify subjects as high risk. This is a measure closely related to the decision curve [21,2] and the relative utility [1]. The Brier score is a classic sum of squares measure. Differences in these measures calculated with baseline and expanded fitted models are traditional measures of prediciton improvement: ΔAUC = AUC(riŝk(X, Y)) − AUC(riŝk(X)); ΔROC(f) = ROC(f, riŝk(X, Y)) − ROC(f, riŝk(X)); ΔSNB(t) = SNB(t, riŝk(X, Y)) − SNB(t, riŝk(X)) and ΔBrier = Brier(riŝk(X)) − Brier(riŝk(X, Y)). Like the NRI, positive values of these measures (including Δ Brier by our definition) indicate improved performance. In the tables they are given as percentages. We used their empirical estimates calculated in the test dataset. We set f = 0.2 for ΔROC(f) and t = P [D = 1], the average risk for ΔSNB(t).

In contrast to the NRI statistic, we found that changes in the two ROC based measures, the standardized net benefit and the Brier score were negative on average in the test datasets, in all simulation scenarios (Table 1). Negative values for measures of performance improvement in the test dataset are in fact appropriate because, given that Y is not predictive we expect that the fitted model riŝk(X, Y) is further from the true risk, P(D = 1|X), than is riŝk(X). In particular, the model giving rise to riŝk(X) requires estimating only 2 parameters and takes advantage of setting β₂ at its true value, β₂ = 0. In contrast, by fitting the three parameter model (3) that enters Y as a predictor, we incorporate noise and variability into riŝk(X, Y). The ΔBrier score, ΔROC(f), ΔAUC and ΔSNB(t) quantify the reduced performance of riŝk(X, Y) relative to riŝk(X) in different ways. In contrast, the NRI statistic tends to mislead us into thinking that the expanded model is an improvement over the baseline model.

3 Illustration with a Theoretical Example

Using Monte-Carlo studies as well as a breast cancer dataset, Hilden and Gerds (2013) [6] constructed some examples of risk functions that do not fit data and showed that the NRI statistic can be artificially inflated and hence misleading. We now consider a simplified version of one of the examples from that paper and prove a theoretical large sample result. The example provides some insight into our simulation study results. Specifically, let Y be a constant, Y = 0 say, and consider a model risk*(X, Y) that is a distorted version of the true baseline risk function risk(X) but that obviously contains no additional predictive information:

$${\text{logit risk}}^{\ast }(X,Y)=\text{logit risk}(X)+\epsilon \text{if risk}(X)>\rho$$ (4)

$${\text{logit risk}}^{\ast }(X,Y)=\text{logit risk}(X)-\epsilon \text{if risk}(X)>\rho$$ (5)

where ρ = P(D = 1) and ε is some positive constant. Result 1 below shows that the NRI > 0 for comparing the model risk*(X, Y) with the baseline model risk(X). Here the training and test datasets are considered to be very large so there is no sampling variability, but the expanded risk function risk*(X, Y) is clearly not valid in the sense that it does not reflect P[D = 1|X, Y] while the baseline risk funciton is valid.

Result 1

Assume that the baseline model is not the null model,

$$P(\text{risk}(X)\ne \rho )>0.$$

Then NRI > 0 for the model (4)–(5).

Proof

Observe that P(risk(X) ≠ ρ > 0 implies that P(risk(X) > ρ) > 0 because the average risk is equal to ρ by definition.

Since the baseline model is valid in the sense that it correctly specifies P(D = 1|X) and

$$P(D=1|\text{risk}(X)>\rho )=E(\text{risk}(X)|\text{risk}(X)>\rho ),$$

we have

$$P(D=1|\text{risk}(X)>\rho )=\rho +\delta \text{for some}\delta >0.$$

$$\text{NRI}=2\{P({\text{risk}}^{\ast }(X,Y)>\text{risk}(X)|D=1)-P({\text{risk}}^{\ast }(X,Y)>\text{risk}(X)|D=0)\}=2\{\frac{P(D=1|\text{risk}(X)>\rho )P(\text{risk}(X)>\rho )}{P(D=1)}-\frac{P(D=0|\text{risk}(X)>\rho )P(\text{risk}(X)>\rho )}{P(D=0)}\}=2P(\text{risk}(X)>\rho )\{\frac{\rho +\delta }{\rho }-\frac{1-\rho -\delta }{1-\rho }\}=2P(\text{risk}(X)>\rho )\{\frac{\delta }{\rho }+\frac{\delta }{1-\rho }\}=\frac{2\delta P(\text{risk}(X)>\rho )}{\rho (1-\rho )}>0$$

We see that even in an infinitely large test dataset, the NRI associated with the expanded model in (4)–(5) is positive despite the fact that the expanded model contains no more predictive information than the baseline model. The integrated discrimination improvement (IDI) statistic was also proposed by Pencina et al. [11] and is quite widely used [7]. Hilden and Gerds (2013) [6] proved that the IDI> 0 for a different theoretical example of an uninformed expanded model.

4 Further Results

The expanded risk function in Result 1 is an extreme form of an invalid risk function, invalid in the sense that it does not reflect the true risk, P(D = 1|X, Y). Similarly, in the simulated data examples, the expanded model derived from the small training dataset is likely to be overfit and therefore not a good reflection of P(D = 1|X, Y) in the test dataset. This phenomenon is likely to be exacerbated by inclusion of multiple novel markers in the expanded model fit to training data. We see in Table 2 that the effects on NRI are more pronounced in the presence of multiple novel markers that are not predictive.

Table 2.

Measures of improvement in prediction ×100 when risk models are fit to a training dataset of 50 observations and assessed on a test dataset of 5000 observations where P(D = 1) = 0.5. The linear logistic regression models fit to the training data are (i) baseline logitP(D = 1|X) = α₀ + α₁X; (ii) model(X, Y₁) : logitP(D = 1|X, Y₁) = β₀ + β₁X + β₂Y₁; (iii) model(X, Y₁, Y₂) : logitP(D = 1|X, Y₁, Y₂) = γ₀ + γ₁X + γ₂Y₁ + γ₃Y₂. Data generation is described in Supplementary Materials. Shown are averages over 1000 simulations. Neither Y₁ nor Y₂ are informative — the true values of β₂, γ₂, and γ₃ are zero.

Two Uninformative Markers
Average PerformanceIncrement ×100
	NRI		ΔROC(0.2)		ΔAUC		Δ Brier		ΔSNB(ρ)
Model	(X, Y1)	(X, Y1, Y2)	(X, Y1)	(X, Y1, Y2)	(X, Y1)	(X, Y1, Y2)	(X, Y1)	(X, Y1, Y2)	(X, Y1)	(X, Y1, Y2)
AUCX
0.60	0.61	0.78	−1.81	−2.91	−1.30	−2.18	−0.55	−1.12	−1.84	−3.06
0.70	2.08	3.63	−2.63	−4.55	−1.66	−2.95	−0.52	−1.08	−2.44	−4.36
0.80	6.18	10.60	−1.75	−3.50	−0.95	−1.89	−0.47	−0.96	−1.61	−3.14
0.90	17.83	28.00	−1.33	−2.57	−0.65	−1.27	−0.51	−1.03	−1.36	−2.63

We next considered a scenario where a marker Y does add predictive information. The true expanded model in Table 3 is

Table 3.

Measures of improvement in prediction when risk models are fit to a training dataset of N-training=50 observations and assessed on a test dataset of N-test=5000 observations where P(D = 1) = 0.5. The linear logistic regression models fit to the training datasets are (i) baseline logitP(D = 1|X) = α₀ + α₁X; (ii) model(X, Y) : logitP(D = 1|X,Y) = β₀ + β₁X + β₂Y; (iii) model(X, Y, XY) : logitP(D = 1|X,Y) = γ₀ + γ₁X + γ₂Y + γ₃XY. The baseline model is correct. The marker Y is informative and the correct expanded model is model(X, Y) while the model(X, Y, XY) is overfit. Data generation is described in Supplementary Materials. Shown are the true values of the performance measures (True) that use the true risk, as well as averages of estimated performance using training and test data over 1,000 simulations. All measures shown as %.

One Informative Marker
		NRI			ΔROC(0.2)			ΔAUC			ΔBrier			ΔSNB(ρ)
AUCX	AUCY	True	Model (X,Y)	Model (X,Y,XY)	True	Model (X,Y)	Model (X,Y,XY)	True	Model (X,Y)	Model (X,Y,XY)	True	Model (X,Y)	Model (X,Y,XY)	True	Model (X,Y)	Model (X,Y,XY)
0.7	0.7	28.32	23.37	22.74	3.25	0.99	−0.89	1.98	0.64	−0.69	0.61	0.16	−0.41	3.21	0.98	−0.40
0.8	0.7	28.39	23.37	27.03	1.97	0.14	−1.13	1.03	0.06	−0.80	0.47	0.01	−0.45	1.84	0.15	−0.90
0.8	0.8	57.84	55.65	55.82	7.73	6.09	4.99	3.94	3.12	2.25	1.89	1.48	1.00	7.10	5.39	4.59
0.9	0.7	28.41	27.16	39.92	0.88	− 0.31	−1.15	0.43	−0.16	−0.77	0.29	−0.16	−0.59	0.92	−0.33	−1.25
0.9	0.8	57.87	57.13	63.05	3.40	2.31	1.61	1.69	1.14	0.53	1.19	0.74	0.30	3.79	2.49	1.71
0.9	0.9	89.58	87.02	88.18	7.35	6.46	5.59	3.74	3.23	2.54	2.81	2.40	1.95	8.85	7.50	6.74

$$\text{model}(X,Y):\text{logit}P(D=1|X,Y)={\beta }_0+{\beta }_{1}X+{\beta }_{2}Y.$$

We fit this model and a model with superfluous interaction term to the training data

$$\text{model}(X,Y,XY):\text{logit}P(D=1|X,Y)={\gamma }_0+{\gamma }_{1}X+{\gamma }_{2}Y+{\gamma }_{3}XY.$$

The test set NRIs comparing each of these fitted models with the fitted baseline model are summarized in Table 3. For comparison we display the NRI calculated using the true risk model parameter values. In some scenarios the NRI derived from the overfit model with interaction is substantially larger than the true NRI. For example, when AUC_X = 0.9 and AUC_Y = 0.7, the average NRI is 39.92% compared with the true NRI of 28.41%.

Considering the fact that the models fit to training data should be observed to perform worse than the true risk models, their tendency to appear better than the true risk models is particularly disconcerting. We see from Table 3 that the ROC based measures, the Brier Score and the net benefit all indicate that the performances of both of the expanded models fit to training data are worse than the performance of the true risk model. Moreover, as expected, the overfit model, model(X, Y, XY), is generally shown to have worse performance than the model without interaction. The NRI statistic however, only rarely conforms with this pattern. In five of the six scenarios considered, the NRI statistic for the overfit model(X, Y, XY) was larger than that for the model(X, Y). We conclude that overfitting of the expanded model by including superfluous covariates is problematic for the NRI statistic not only when the new marker is uninformative but also when the new marker is informative. In particular, overfitting can lead to inappropriately large values for the NRI in the test dataset.

5 Insights

In each of our simulation studies expanded models were fit to training data that included superfluous covariates. In other words the models were overfit to the training data. Although we cannot fully explain why the NRI statistic tends to be large when the model for risk(X, Y) is overfit to training data, we can share a few relevant observations.

5.1 NRI is not a Proper Measure of Performance Improvement

Hilden and Gerds (2013) [6] attribute the problem with the NRI statistic to the possibility that it is not based on a ‘proper scoring rule.’ See Gneiting and Raftery (2007) [3] for an in-depth discussion of proper scoring rules.

In our context we need to expand on the definition of propriety. Let a population prediction performance improvement measure (PIM) comparing r*(X, Y), a function of (X, Y), to the true baseline risk function r(X) = P(D = 1|X), be denoted by S:

$$\text{PIM}=S(r^{\ast }(X,Y),r(X),F(D,X,Y))$$

where F is the population distribution of (D, X, Y).

Definition

The PIM is proper if for all F and r*(X, Y):

$$S(r(X,Y),r(X),F(D,X,Y))\ge S(r^{\ast }(X,Y),r(X),F(D,X,Y)).$$ (6)

In other words, a prediction improvement measure is proper if it is maximized at the true risk function of (X, Y), r(X, Y) = P(D = 1|X, Y). If the inequality in (6) is strict, then r(X, Y) is the unique function that maximizes S and the PIM is said to be strictly proper.

Propriety is generally considered a desirable attribute in the decision theoretic literature [6,3]. An unquestionably appealing attribute of a proper PIM is that improvement in performance cannot be due simply to use of an expanded risk function that doesn't fit the test data set. Result 1 proves with a large sample counter example that the NRI is not proper because NRI > 0 with use of the function risk*(X, Y) while NRI = 0 with use of the true risk function risk(X, Y) that in this example is the same as risk(X). On the other hand, it is well known from the theory of least squares that the change in the Brier score is proper, a fact that follows from the equality E(D|X, Y) = risk(X, Y). In addition, the ΔAUC and ΔROC(f) measures are proper since the ROC curve for (X, Y) is maximized at all points by the risk function [10]. Interestingly, these are not strictly proper measures because ROC curves are also maximized by any monotone increasing function of the risk. We show in supplementary materials that the change in the standardized net benefit, ΔSNB(t), is proper. Being proper measures of prediction improvement appears to translate into more sensible comparisons of risk models in our simulation studies. In particular, distortion of the baseline model by adding unnecessary predictors to the model does not increase the estimated values of the proper performance measures but can increase the NRI.

5.2 Manifestations of Overfitting

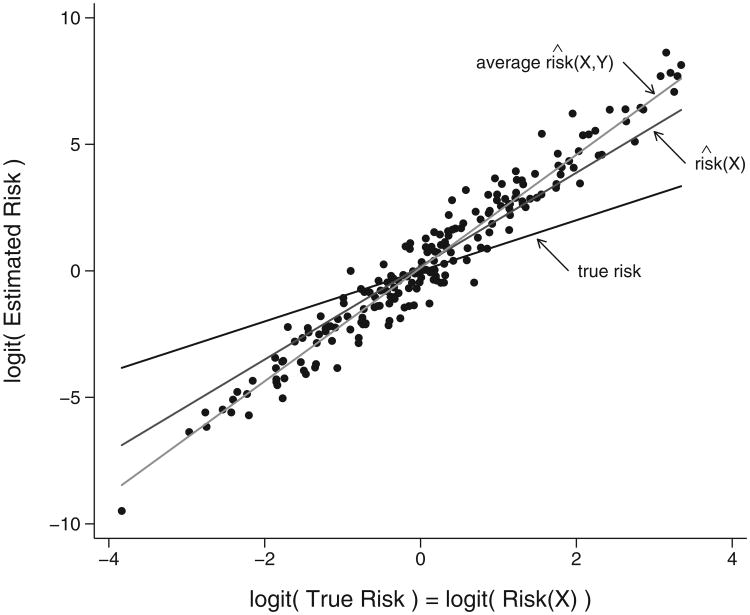
When risk models include superfluous predictor variables, predictions are apt to predict more poorly in test data than predictions derived from models without them. In Figure 1 we demonstrate this for one simulated dataset corresponding to the scenario in the second-to-last row of Table 1. Observe that the predictions from the baseline model, riŝk(X), are seen to be closer to the true risk, risk(X), than are the more variable predictions based on risk(X, Y), where Y is an uninformative variable that is therefore superfluous. The NRI statistic does not acknowledge the poorer predictions while the other performance improvement measures do (Figure 1 caption).

Fig. 1.

Risk estimates calculated using models fit to training data, and applied to a test data set of 5000 observations. Data were simulated from the scenario shown in the second to last row of Table 1. Shown are results for one simulation in which values of performance improvement statistics are: NRI= 56.21%, ΔROC(0.2) = −1.48%, ΔAUC= −0.59%, ΔBrier= −1.10% and ΔSNB(ρ) = −1.49%. A random sample of 200 test set estimates, riŝk(X,Y), are shown, as well as a line fit to all 5000 values. The baseline fitted model, logit riŝk(X), is linear in X and the true risk, risk(X) is the 45° line.

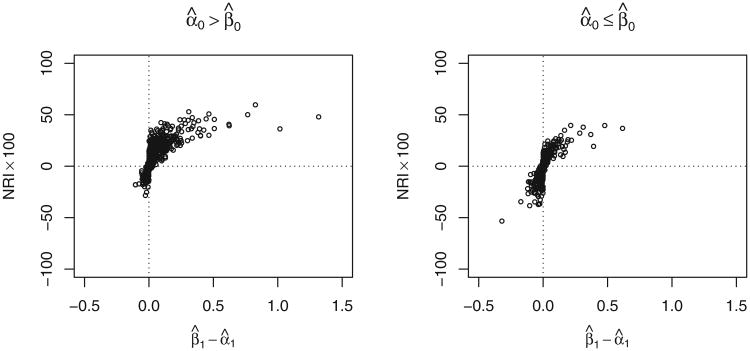
We compared the estimated odds ratios for X in the overfit models described in Table 2 with those in the fitted baseline model. Results shown in Table 4 indicate that odds ratios associated with X are biased too large in the overfit models. This phenomenon doesn't appear to be widely known. Nevertheless it provides some rationale for use of shrinkage techniques to address problems with overfitting (Hastie [2001], section 10.12.1 [4]). Interestingly, we see from Figure 2 that when the odds ratio for X is larger in an overfit model than in the baseline model, the NRI statistic is generally positive and vice versa. We now attempt to provide some intuition for this observation. Note that the NRI statistic compares riŝk(X, Y) with riŝk(X) for each individual. Assuming that the intercept terms center X at 0 but otherwise can be ignored, the NRI statistic adds positive contributions when

Table 4.

Average estimated odds ratios for X in models fit to training data generated using the same settings as in Table 2. Both Y₁ and Y₂ are uninformative markers.

	True	Baseline Model	Model (X,Y1)	Model (X,Y1,Y2)
AUCX	exp(α1)	exp(α̂1)	exp(β̂1)	exp(γ̂1)
0.6	1.43	1.56	1.58	1.60
0.7	2.10	2.46	2.55	2.63
0.8	3.29	4.02	4.24	4.49
0.9	6.13	6.78*	7.37*	8.23*

^*medians displayed when distribution is highly skewed

Fig. 2.

Scatterplots showing the relationship between the NRI statistic (× 100) and β̂₁–α̂₁ in 1000 simulated datasets generated according to the scenario shown in the second to last row of Table 1. The coefficients are calculated by fitting the models logit P(D = 1|X) = α₀ + α₁X and logit P(D = 1|X, Y) = β₀ + β₁X + β₂Y to the training data. The NRI is calculated using the test dataset.

$${\widehat{\beta }}_{1}X+{\widehat{\beta }}_{2}Y>{\widehat{\alpha }}_{1}X\text{and}D=1$$ (7)

and when

$${\widehat{\beta }}_{1}X+{\widehat{\beta }}_{2}Y<{\widehat{\alpha }}_{1}X\text{and}D=0.$$ (8)

But since X is large (positive) in cases and small (negative) in controls, the inequalities (7) and (8) tend to hold because of the tendency for β̂₁ > α̂₁. Note that Y is centered at 0 and β̂₂ is likely to be small in the simulations because β₂ = 0. In the simulation scenario corresponding to Figure 2 (and the second-to-last rows of Tables 1 and 4) we found that β̂₁ > α̂₁ in 66.4% of simulated datasets leading to NRI> 0 in 66.9% of datasets and an average NRI of 6.56% (Table 1). In supplementary materials (figure A.1-A.4) we see that for the same scenario, the ΔROC(0.2), ΔSNB(ρ), ΔAUC and ΔBrier statistics were generally negative regardless of the comparative values of α̂₁ and β̂₁.

6 Discussion

The simulation and theoretical results provided here and in Hilden and Gerds (2013) [6] demonstrate that the NRI statistic can be biased large by use of risk models that do not fit the test data. Of particular concern is the fact that models overfit to training data tend to appear to improve prediction performance by having positive NRI values when evaluated with test data even when the models do not actually improve prediction performance. Even small amounts of overfitting, by adding a single unnecessary predictor, lead to biased test set evaluations in our simulation studies. The problem was exacerbated by including multiple unnecessary predictors. Following the same logic, this sort of bias is likely also to be manifested in internally cross-validated estimates of the NRI when test set data are unavailable although we have not specifically investigated the phenomenon here.

Hilden and Gerds [6] demonstrated the principle that the NRI statistic can spuriously yield positive values. They did so by constructing risk functions that do not fit specific illustrative data sets. On the other hand by performing simulation studies with large numbers of simulated datasets we investigated the average behavior of the NRI in some classic scenarios. In particular we investigated the tendency for incorrect conclusions to be made with the NRI when models are fit to training data and evaluated on test data. Moreover, this paper adds to Hilden and Gerds [6] by addressing a scenario that is by far the most commonly applied in practice. We fit nested logistic regression models to data and compared them using the NRI. Note that the model forms were correctly specified in our simulations in the sense that the data were generated from logistic models of the same form as those that are fit. The fact that we show poor behavior for the NRI in this classic and ideal setting provides compelling evidence for it being a flawed risk prediction performance measure.

The simulation scenarios we investigated employed a small training dataset size with 25 events expected and no more than 3 predictors (2 in Table 1). This is a reasonable ratio of events to predictors according to standard rules of thumb for model fitting. Using a larger training set while keeping the number of predictors fixed resulted in less bias as can be seen in the columns of Table A.2 in Supplementary Materials. This result is not surprising since over fitting is likely to be reduced when the ratio of observations to predictors is increased. On the other hand, by using a larger training set but also including a proportionately larger number of covariates, the magnitude of positive bias in the NRI remained high and in fact the bias increased somewhat. In particular, we see from the highlighted diagonals of Table A.2 that when the ratio of observations to predictors remained constant at 25, larger training sets did not result in reduced bias in the NRI. The phenomenon of bias in the NRI is therefore not simply a small sample phenomenon. We employed very large test datasets in all of our simulation studies in order to examine bias without its magnitude being overwhelmed by sampling variability in the test dataset.

The scenarios that we simulated are well within the range of those encountered in practice. Consider first the baseline risk functions. The strength of the baseline risk function can be characterized by its AUC. We included baseline risk functions with AUCs in the range of 0.6-0.9. For comparison we note that the long standing Framingham Risk score for cardiovascular disease has an AUC of approximately 0.75 [20] which is in the middle of this range. In regards to the novel marker Y, we focused on uninformative novel markers in Tables 1 and 2. Unfortunately, uninformative markers are all too common in biomarker research. In Table 3, we simulated novel markers with AUCs in the range of 0.7-0.9. An example of a biomarker with this sort of predictive power is prostate specific antigen [19], one of the few cancer biomarkers currently used in cancer screening.

When an independent test dataset is not available, it is common practice to report the empirical NRI evaluated with the same data used to fit the risk models. Fitting and evaluating models with the same data is well known to yield over-optimistic estimates of performance. Results in Table A.3 in the Supplementary Material demonstrate the severe bias for uncorrected estimates under the same simulation scenarios considered in Table 1. We focused on the setting where independent validation data are available in the body of the paper because it is generally held that unbiased estimates of performance can be calculated with such data. The fact that the NRI statistic tends to be positive even in this setting points to a fundamental problem with the statistic.

The simulations and examples in this paper have focused on the continuous NRI statistic. However the phenomenon is not unique to the continuous version of the NRI statistic. Categorical NRI statistics were also shown to suffer from optimistic bias even in independent test datasets when models are overfit to training data [16].

In practice, one should not use the NRI statistic, or other prediction improvement performance measures such as ΔAUC, ΔROC(f), ΔSNB(t), or ΔBrier for that matter, to determine if there is predictive information in a novel marker Y. We and others have argued previously that testing the null hypothesis about the regression coefficient associated with Y in the risk model risk(X, Y) is equivalent and more powerful to tests based on estimates of prediction improvement performance measures [15,23].

On the other hand, for quantifying the improvement in prediction performance one must choose summary statistics. A variety of statistics have been proposed and there has been some debate in the literature about which measures are most appropriate [14,22]. Arguments have centered on the interpretations and clinical relevance of various measures. We encourage further dialogue about the conceptual bases of prediction improvement statistics and their relative merits for quantifying prediction performance. Kerr et al. have recently provided a critical review of the NRI statistic that focuses on conceptual aspects [8]. See also commentaries by Hilden [5] and Vickers and Pepe [24]. The results in this paper and in Hilden and Gerds (2013) [6] however add another dimension to the debate. NRI is also problematic from a technical point of view. Its potential for being inflated by over-fit models is a very serious concern.

Our results underscore the need to check if risk functions fit the test data set as a crucial part of the exercise of evaluating risk prediction models.[18] In additional simulation studies (results not shown) we found that after recalibrating the training set models to the test dataset, problems with inflated NRIs were much reduced. However, guaranteeing well fitting risk models in practical applications is not always possible. Moreover, methods for making inference about the NRI are not available when risk models are estimated or recalibrated in the evaluation data and markers are non-predictive or weakly predictive because regularity conditions fail to hold for the NRI when the novel markers Y are non-predictive. Other statistical measures of prediction improvement that cannot be made large in test data by use of poorly fitting risk functions may be preferred for practical application. We especially encourage use of the change in the standardized net benefit statistic and its components, the changes in true and false positive rates, calculated at a relevant risk threshold, because, not only is it a proper prediction improvement statistic, as we have shown, but unlike ΔAUC and ΔBrier, it quantifies prediction performance in a clinically meaningful way [14,21,1,2].