SEX, LIES AND SELF-REPORTED COUNTS: BAYESIAN MIXTURE MODELS FOR HEAPING IN LONGITUDINAL COUNT DATA VIA BIRTH-DEATH PROCESSES

Abstract

Surveys often ask respondents to report non-negative counts, but respondents may misremember or round to a nearby multiple of 5 or 10. This phenomenon is called heaping, and the error inherent in heaped self-reported numbers can bias estimation. Heaped data may be collected cross-sectionally or longitudinally and there may be covariates that complicate the inferential task. Heaping is a well-known issue in many survey settings, and inference for heaped data is an important statistical problem. We propose a novel reporting distribution whose underlying parameters are readily interpretable as rates of misremembering and rounding. The process accommodates a variety of heaping grids and allows for quasi-heaping to values nearly but not equal to heaping multiples. We present a Bayesian hierarchical model for longitudinal samples with covariates to infer both the unobserved true distribution of counts and the parameters that control the heaping process. Finally, we apply our methods to longitudinal self-reported counts of sex partners in a study of high-risk behavior in HIV-positive youth.

1. Introduction

When survey respondents report numeric quantities, they often recall those numbers with error. Respondents sometimes round up or down, for example to the nearest integer, decimal place or multiple of 5 or 10. This kind of misreporting is called heaping, and when the probability of heaping depends on the true value of the unheaped variable, the mechanism is non-ignorable (Heitjan and Rubin, 1991). Heaping is a well-known problem in many survey settings, and robust inference for heaped data remains an important problem in statistical inference (Heitjan, 1989; Wang and Heitjan, 2008; Wright and Bray, 2003; Crockett and Crockett, 2006; Schneeweiss, Komlos and Ahmad, 2010). Reporting errors are frequently observed for a variety of measurements, including self-reported age (Myers, 1954; Stockwell and Wicks, 1974; Myers, 1976), height and weight (Rowland, 1990; Schneeweiss and Komlos, 2009), elapsed time (Huttenlocher, Hedges and Bradburn, 1990) and household purchases (Browning, Crossley and Weber, 2003). Respondents may be inclined to misreport when the survey addresses topics that seem private, embarrassing or culturally taboo (Schaeffer, 1999). For example, there may be significant misreporting in studies of drug use (Klovdahl et al., 1994; Roberts and Brewer, 2001), cigarette use (Brown et al., 1998; Wang and Heitjan, 2008) or number of sex acts or sexual partners (Westoff, 1974; Golubjatnikov, Pfister and Tillotson, 1983; Wiederman, 1997; Weinhardt et al., 1998; Fenton et al., 2001; Ghosh and Tu, 2009).

Several authors have proposed approximations to correct estimates using heaped data (Sheppard, 1897; Schneeweiss and Komlos, 2009; Schneeweiss, Komlos and Ahmad, 2010; Schneeweiss and Augustin, 2006; Tallis, 1967; Lindley, 1950). Others have explored smoothing techniques for heaped data on the grounds that smoothing may have the effect of “spreading out” grouped responses (Hobson, 1976; Singh, Suchindran and Singh, 1994). Heitjan (1989) and Heitjan and Rubin (1990, 1991) provide an important unifying perspective on heaped and grouped data by introducing the concept of coarsening, in which one observes only a subset of the complete data sample space. Based on this paradigm, Wang and Heitjan (2008) formulate a model for heaped cigarette counts and apply these ideas to study impact of a drug treatment on smoking. Jacobsen and Keiding (1995) discuss extensions of the coarse data concept to more general sample spaces than those considered by Heitjan and Rubin (1991). Wright and Bray (2003) model heaped nuchal translucency measurements as samples from a mixture model and propose a Gibbs sampling scheme to draw from the joint distribution of the true counts and unknown rounding parameters. Bar and Lillard (2012) model the age at which subjects quit smoking by supposing that heaping takes place on a grid of multiples of 5 or 10.

Most attempts to disentangle heaped count responses from latent true values can be understood as mixture models. To illustrate, suppose each subject draws their latent true count x from a distribution with mass function f(x|ϕ) on the non-negative integers that depends on parameters ϕ and then reports a possibly different value y from a reporting distribution with mass function g(y|x, θ) that depends on the true count x and parameters θ. Because the reporting distribution g depends on the latent true count x, the heaping mechanism is non-ignorable. The likelihood contribution of an observed count y is therefore

$$L(\mathit{\theta },\mathit{\varphi };y)=\sum _{x=0}^{\infty }g(y\mid x,\mathit{\theta })f(x\mid \mathit{\varphi }).$$ (1)

Figure 1 shows a graphical representation of this mixture model for heaped counts. The objects of inference are often the true counts x and the parameters ϕ underlying the true count distribution f(x|ϕ).

Fig. 1.

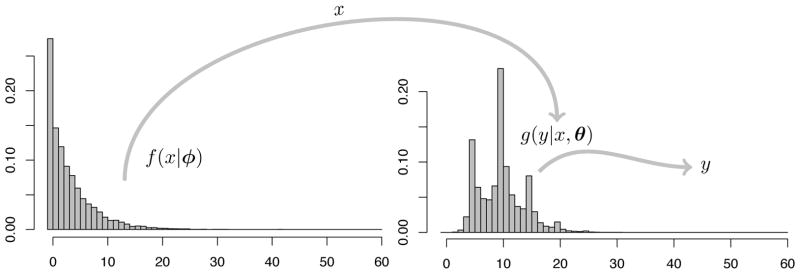
Mixture model schematic for reported counts. Each subject chooses their true count x from the distribution f(x|ϕ), then reports the possibly different count y drawn from the distribution g(y|x, θ).

Many approaches characterize the reporting mechanism as a choice between reporting truthfully and misreporting at suspected heaping grid points (for example, Wang and Heitjan, 2008; Wright and Bray, 2003; Wang et al., 2012; Bar and Lillard, 2012). The probability of reporting a particular heaped value depends on the value of the latent true value: Wang and Heitjan (2008) use a proportional odds model for different heaping grids; Bar and Lillard (2012) propose a multinomial distribution governing the choice of different heaping rules; McLain et al. (2014) propose a semi-parametric model for heaping (digit preference) of duration-time data in which subjects are equally likely to round up or down. Most models for count data only allow exact heaping to the multiple of 5, 10, or 20 that is nearest to the latent true count, and the heaping rule is the same for all subjects. However, limiting heaped responses to the nearest grid point can produce inferences of true counts that are unrealistically constrained. For example, if the reported count is y = 35 and the model only allows heaping to multiples of 5, then one must infer x ∈ {33, …, 37}. Furthermore, established models do not allow for misremembering as a function of the true count or quasi-heaping to counts close to, but not equal to, the specified grid values (for example, a subject whose true count is 93 may report 101 or 99 instead of the heaped value 100).

In this paper, we relax several of these restrictive assumptions and incorporate rigorous analysis of heaped data into a hierarchical regression model. In Section 2 we propose a novel reporting distribution by imagining the true count x as the starting point of a continuous-time Markov chain on the non-negative integers known as a general birth-death process (BDP). The ending state of this Markov chain after a specified epoch is the reported count y. Jumps from integer state k to k + 1 or k − 1 occur with instantaneous rates λ_k and μ_k respectively, with μ₀ = 0 to keep the process on . We specify λ_k and μ_k so that the process is attracted to nearby heaping grid points. Our BDP heaping model characterizes an infinite family of reporting distributions g(y|x, θ) that is 1) indexed by the true count x; 2) controlled by a small number of parameters θ that are readily interpretable; and 3) can be computed quickly to provide a reporting likelihood. The model permits heaping to values beyond the nearest grid point, provides for multiple heaping grids and continuous transitions between them, allows misremembering and quasi-heaping, and accommodates subject-specific heaping intensities. In Section 3, we outline a Bayesian hierarchical model for longitudinal counts and a Metropolis-within-Gibbs scheme for drawing inference from the joint posterior distribution of the unknown parameters. We are interested in learning about the parameters ϕ underlying the true counts, the true counts x themselves, and the parameters θ that govern the reporting/heaping process. Finally, in Section 5, we demonstrate our method on longitudinal self-reported counts of sexual partners from a study of HIV-positive youth.

2. Constructing the Reporting Distributions

Let x be the true count for a subject and let y be their reported count. Let g(y|x, θ) be the probability of reporting y, given that their true count is x under the parameter vector θ. To parameterize g(y|x, θ) to allow heaping, suppose y represents the state of an unbounded continuous-time Markov random walk, taking values on 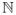, starting at x and evolving for a finite arbitrary time. We accomplish this task by defining the birth and death rates λ_k and μ_k of a general BDP in a novel way so that the process is attracted to grid points on which we expect heaping to occur. The transition probabilities of this process give rise to the family of reporting distributions g(y|x, θ). We extend the proportional odds framework of Wang and Heitjan (2008) to allow heaping to different grid values depending on the magnitude of the count. First we present background on general BDPs and show how to use the transition probabilities of a general BDP to model heaping.

2.1. General birth-death processes

A general BDP is a continuous-time Markov random walk on the non-negative integers 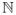(Feller, 1971). Let U(t) ∈ 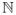be the location of the walk at time t. Define the transition probability P_ab(t) = Pr(U(t) = b | U(0) = a) to be the probability that the process is in state b at time t, given that it started at state a at time 0. A general BDP obeys the Kolmogorov forward equations

$$\frac{\mathrm{d}{P}_{ab}(t)}{\mathrm{d}t}={\lambda }_{b-1}{P}_{a,b-1}(t)+{\mu }_{b+1}{P}_{a,b+1}(t)-({\lambda }_b+{\mu }_b)P_{ab}(t),$$ (2)

for all a, b ∈ 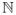, where P_ab(0) = 1 if a = b, P_ab(0) = 0 if a ≠ b, and μ₀ = λ₋₁ = 0 to keep the BDP on 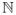. In this setting, t is arbitrary; for example, halving t and multiplying all birth and death rates by two does not change the distribution of U(t)|U(0). The forward equations (2) form an infinite sequence of ordinary differential equations describing the probability flow into and out of state b within a small time interval (t, t + dt). Karlin and McGregor (1957) provide a detailed derivation of properties of general BDPs. Unfortunately, it remains notoriously difficult to find analytic expressions for the transition probabilities in almost all general BDPs, and often one must resort to numerical techniques (Novozhilov, Karev and Koonin, 2006; Renshaw, 2011). Appendix A gives an overview of the Laplace transform technique we use to numerically compute the transition probabilities efficiently.

In our heaping parameterization, we model the true count U(0) = x as the starting state of a BDP and U(t) = y as the ending state. We therefore set t = 1 and define g(y|x, θ) = P_xy(1) so that P_xy is a function of the unknown parameter vector θ, where the {λ_k} and {μ_k} are all functions of θ. We emphasize that the time parameter t is meaningless in this context, because scaling t by a constant and dividing the birth and death rates by the same constant does not change the transition probabilities.

2.2. Specifying the jumping rates λ_k and μ_k

Grunwald et al. (2011) and Lee, Weiss and Suchard (2014) model under- and over-dispersion in count data using a simple linear BDP with λ_x = μ_x = λx, but do not address heaping. In addition to modeling dispersion, BDPs can be used to parameterize general families of probability measures on 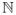(Klar, Parthasarathy and Henze, 2010). In our heaping model, we imagine errors in self-reported counts to come from two sources: dispersion due to misremembering and heaping. Misremembering adds variance by spreading reported counts around the true count. Heaping results in preference for reporting certain counts, for example on a grid of values such as multiples of 5 or 10. We specify both of these sources of misreporting error using a BDP with jumping rates {λ_k} and {μ_k} that are modeled as functions of the finite-dimensional parameter vector θ.

To motivate development of our general BDP model for heaping, suppose for now that heaping occurs at multiples of 5. We wish to define a random walk on 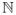that is dispersed around its starting point and attracted to multiples of 5, with this attraction increasing with proximity to each multiple of 5. For example, if the true count is x = 49, then the reported count y is more strongly attracted to 50 than 45, because 49 is closer to 50. Here, attraction to a given multiple means that the likelihood of the BDP moving toward that multiple is greater than that the likelihood of moving in the other direction. Informally, we wish to assign birth and death rates such that

$$\begin{array}{l}{\lambda }_k=(\text{dispersion}\text{around}k)+(\text{attraction}\text{to}\text{multiple}\text{of}5\text{above}),\\ {\mu }_k=(\text{dispersion}\text{around}k)+(\text{attraction}\text{to}\text{multiple}\text{of}5\text{below}).\end{array}$$ (3)

One way to quantify the strength of attraction to the multiple of 5 immediately above k is (k mod 5). Likewise, the attraction to the multiple of 5 immediately below k is (−k mod 5), which is equal to 5 − (k mod 5). In both directions, the closer k is to the nearby multiple of 5, the greater its attraction to it.

Subjects whose true number of sex partners is greater than 100, for example, may be less able to accurately recall this number than subjects whose true count is less than 10. We therefore model dispersion around the true count in the reported counts due to misremembering as increasing the true count. Consider a general BDP with jumping rates

$$\begin{array}{l}{\lambda }_k={\theta }_{\text{disp}}(1+k)+{\theta }_{\text{heap}}(kmod5),\\ {\mu }_k={\theta }_{\text{disp}}k+{\theta }_{\text{heap}}(-kmod5),\end{array}$$ (4)

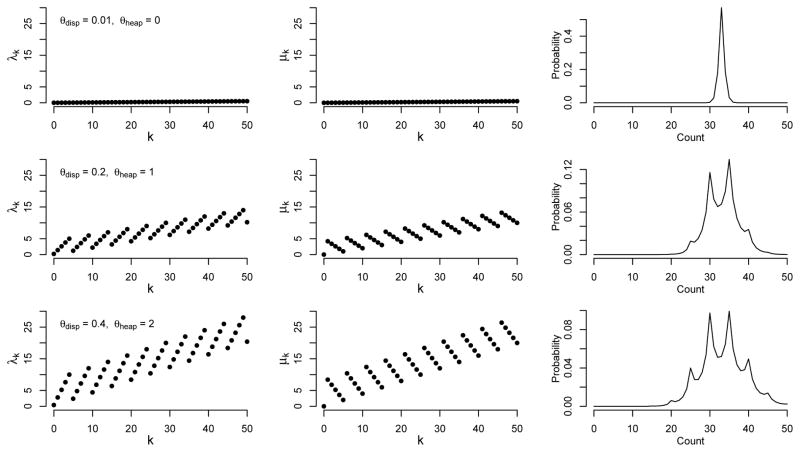
where the (1+k) in the birth rate arises because we wish to allow the BDP to escape from zero with positive rate. In this formulation of the birth and death rates, the dispersion parameter θ_disp ≥ 0 is the propensity to over- or under-report and θ_heap ≥ 0 is the propensity of rounding up or down to multiples of 5. Figure 2 shows the birth rates λ_k, death rates μ_k, and reporting probabilities with true count x = 33 for this heaping model. The complexity of the reporting distributions generated by the heaping model is evident in Figure 2; the BDP tends toward multiples of 5 and the magnitude of θ_heap controls the severity of heaping. The BDP heaping model exhibits subtler behavior than a dispersion distribution with added mass at the heaping points.

Fig. 2.

Birth rates λ_k (left), death rates μ_k (center), and reporting probabilities for true count x = 33 (right) in the heaping model (4) for different values of the dispersion parameter θ_disp and heaping intensity θ_heap. Larger values of θ_disp result in more dispersion about the true count. Larger values of θ_heap result in more heaping to nearby multiples of 5.

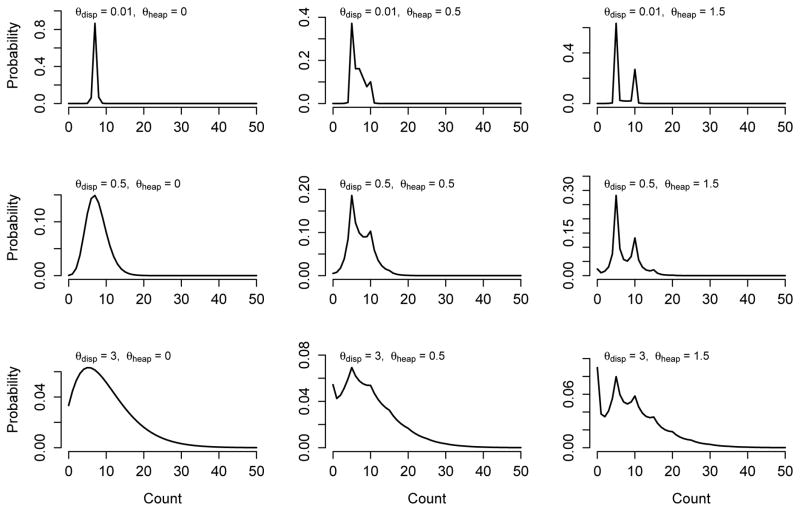
Figure 3 shows reporting distributions for true count x = 7. When θ_heap = 0, the reporting distribution only adds variance to the true count. As θ_heap becomes larger, the peaks in the reporting distribution at the heaping points become more pronounced. When θ_heap is large and θ_disp is small, the reporting distribution is sharply peaked at nearby multiples of 5 and the values between heaping points have little probability mass.

Fig. 3.

Reporting probabilities for heaping at multiples of 5 with true count x = 7 using different values of the dispersion parameter θ_disp and the heaping parameter θ_heap. Larger values of θ_disp allow reports closer to zero; when θ_heap is positive, heaping occurs at zero, providing a mechanism for zero-inflated reports.

In general, suppose that heaping occurs at equally-spaced grid points mk where m ∈ 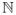is the grid spacing; for example, m could be one of 5, 10, 20, 25, or 100. Analogous to (4), the birth and death rates become

$$\begin{array}{l}{\lambda }_k={\theta }_{\text{disp}}(1+k)+{\theta }_{\text{heap}}(\mathit{k}modm)\\ {\mu }_k={\theta }_{\text{disp}}k+{\theta }_{\text{heap}}(-\mathit{k}modm).\end{array}$$ (5)

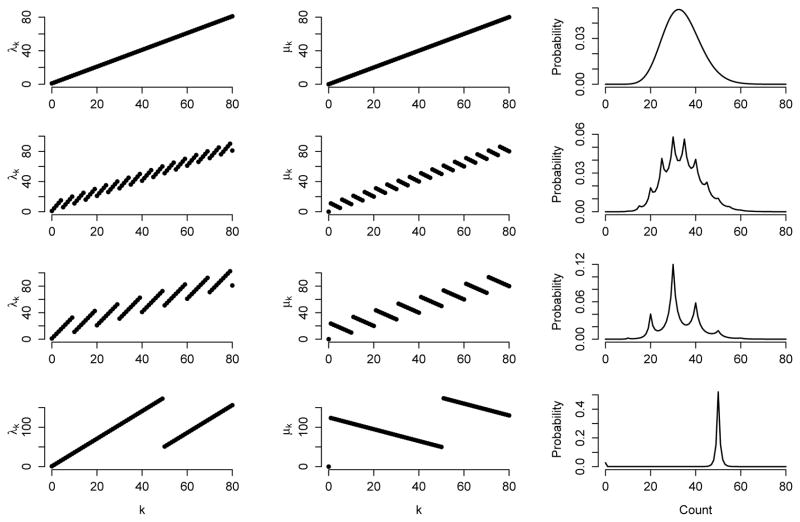
Figure 4 shows birth and death rates for several heaping grid spacings m.

Fig 4.

Birth rates λ_k (left), death rates μ_k (center), and reporting probabilities (right) for different heaping grids with true count x = 33 and θ_disp = 1. The first row shows the reporting distribution for θ_heap = 0. Subsequent rows show the birth and death rates and reporting probabilities with θ_heap = 2.5 with heaping at multiples of 5, 10, and 50. When heaping is to multiples of 50 (bottom row), reporting is concentrated at y = 50.

We can analytically characterize the properties of the reporting distribution when θ_heap is zero. Given the true count x, the mean and variance of the reported count y are

$$\begin{array}{ll}\hfill \mathbb{E}[y\mid x]& =x+{\theta }_{\text{disp}},\text{and}\\ \hfill \text{Var}[y\mid x]& =(2x+1){\theta }_{\text{disp}}+{\theta }_{\text{disp}}^2.\end{array}$$ (6)

Appendix B provides a derivation of these expressions. It is evident that both the mean and variance of y|x increase linearly with the true count x, consistent with our belief that the severity of misremembering scales in proportion to the magnitude of the true count.

2.3. Heaping regimes

As true counts become larger, coarseness often increases; small counts appear to be heaped at multiples of 5, then 10, and finally 50 or 100 for larger counts. Models such as (4) that enforce heaping to the same grid regardless of the magnitude of the count may provide insufficient rounding behavior when the coarseness increases with x. Consider J distinct heaping grids and suppose m_j is the grid spacing for regime j, where j = 1, …, J. Let v_j(x) be the intensity of regime j as a function of the true count x. Regime 0, with intensity v₀(x), is the probability of accurately reporting the true count. Regime j, with intensity v_j(x), corresponds to heaping at multiples of m_j. We follow Wang and Heitjan (2008) to develop a proportional odds model for smooth transitions between heaping grids.

Define birth and death rates

$$\begin{array}{l}{\lambda }_k={\theta }_{\text{disp}}(1+k)+{\theta }_{\text{heap}}\sum _{j=1}^J{v}_j(x)(kmod{m}_j)\\ {\mu }_k={\theta }_{\text{disp}}k+{\theta }_{\text{heap}}\sum _{j=1}^J{v}_j(x)(-kmod{m}_j),\end{array}$$ (7)

where the heaping regime probabilities are

$$\begin{array}{ll}\hfill v_0(x)& ={(1+e^{{\gamma }_1+{\gamma }_{0}x})}^{-1},\hfill \\ \hfill v_1(x)& ={(1+e^{{\gamma }_2+{\gamma }_{0}x})}^{-1}-{(1+e^{{\gamma }_1+{\gamma }_{0}x})}^{-1},\hfill \\ \hfill v_2(x)& ={(1+e^{{\gamma }_3+{\gamma }_{0}x})}^{-1}-{(1+e^{{\gamma }_2+{\gamma }_{0}x})}^{-1},\hfill \\ \hfill ⋮& \hfill \\ \hfill v_J(x)& =1-{(1+e^{{\gamma }_J+{\gamma }_{0}x})}^{-1},\hfill \end{array}$$ (8)

and we restrict the regime transition parameters γ₀ > 0 and γ₁ > γ₂ > ⋯ > γ_J. We have, by construction,

$$\sum _{j=1}^J{v}_j(x)=1,$$ (9)

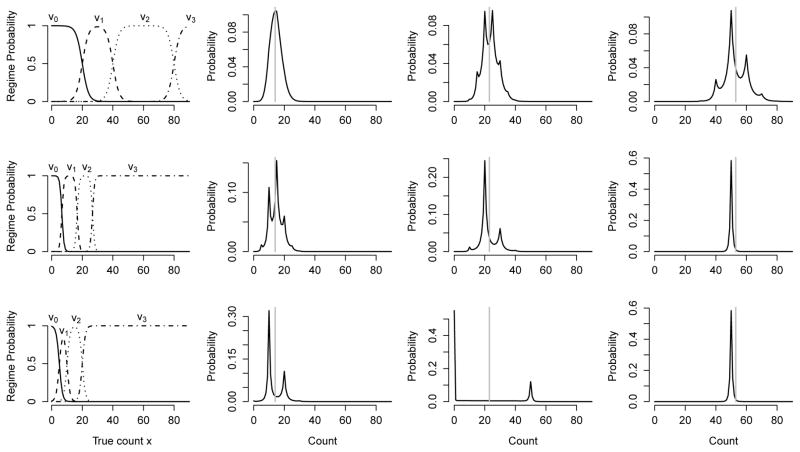
for every x ∈ 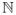. In this proportional odds model, γ₀ determines the transition rate between regimes and γ_j/γ₀ controls the midpoint of the transition between regimes j − 1 and j. Figure 5 shows the heaping regime model defined above. Each row shows a different heaping regime model and reporting distribution g(y|x, θ, γ) where γ = (γ₀, …, γ_J) for x = 14, 23, 53 and θ = (0.5, 1.5).

Fig 5.

Heaping regimes. Each row shows a different heaping regime model with reporting probabilities for θ_disp = 0.5 and θ_heap = 1.5. A gray line denotes the true counts x = 14, 23, 53. In the first row, the regime intensities are shown with regime parameters γ = (0.5, −10, −20, −40). For x = 14, the reporting distribution is dominated by regime 0, which specifies no heaping. For x = 23, the reporting distribution is dominated by regime 1, so rounding to nearby multiples of 5 is evident. At x = 53, regime 2 is dominant, and the reporting distribution is peaked at multiples of 10. In the second row, γ = (1.5, −10, −25, −40), and the reporting distribution for x = 53 is dominated by regime 3, so the model exhibits heaping to multiples of 50. In the third row, γ = (1, −5, −10, −20).

2.4. Justification for the BDP heaping model

We formulate the heaping model as a continuous-time Markov process for three reasons: mathematical convenience, diversity of reporting distributions, and parsimony in parameterization. First, the theory of general BDPs is well-developed and efficient methods now exist for computing transition probabilities for any specification of the birth and death rates (Crawford and Suchard, 2012). The heaping probability mass function g(y|x) is automatically normalized to integrate to one (since it is the likelihood of a Markov process), so the mixture model (1) is always well-defined. Second, the model described in (7) and (8) exhibits a great diversity in reporting distributions, from no heaping, to always-heaping, under a wide variety of magnitude-based regimes (see Figures 2–5 for examples). Third, the general BDP achieves this complex behavior using only two parameters for the heaping process and four in the regimes specification. Additionally, the specification of heaping regimes via (7) and (8) results in an appealing property: the reporting distribution can by highly asymmetrical when the true count is subject to two heaping regimes. For example, the third row of Figure 5 shows how the true count x = 14 can be pulled toward 10 and 20 with very different probabilities.

3. A hierarchical model for longitudinal counts

We describe a generalized linear mixed model (GLMM) for longitudinal counts. Label subjects i = 1, …, N, with each subject’s true count X_it and self-reported count Y_it at real calendar time points t_ij for j = 1, …, n_i. We record d-dimensional covariates W_it and c-dimensional Z_it for each subject at each time point. Consider the following hierarchical model

$$X_{it}~\text{Poisson}({\eta }_{it}),$$ (10)

$$log{\eta }_{it}={\mathbf{W}}_{it}\mathit{\alpha }+{\mathbf{Z}}_{it}{\mathit{\beta }}_i,$$ (11)

and

$${\mathit{\beta }}_i~\text{Normal}(\mathbf{0},{\mathbf{\sum }}_{\beta }),$$ (12)

where the vector of regression coefficients α is d × 1, the subject-specific random effect β_i is c × 1 with the covariance matrix Σ_β is c×c, and η_it is the subject-timepoint-specific mean of the outcome distribution in the GLMM.

A model without heaping arises when we set Y_it = X_it for all i and t. To incorporate heaping, let

$$Y_{it}~\text{BDP}(X_{it},\mathit{\theta },\mathit{\gamma }).$$ (13)

We allow the BDP heaping model to have a separate heaping intensity parameter θ_heap,i for each subject. If X_it = x, the birth and death rates for subject i are

$$\begin{array}{l}{\lambda }_k={\theta }_{\text{disp}}(1+k)+{\theta }_{\text{heap},i}\sum _{j=1}^3{v}_j(x)(kmod{m}_j),\text{and}\\ {\mu }_k={\theta }_{\text{disp}}k+{\theta }_{\text{heap},i}\sum _{j=1}^3{v}_j(x)\left(m_j-((k-1)mod{m}_j)\right),\end{array}$$ (14)

where m₁ = 5, m₂ = 10, m₃ = 50, and v₁(x), v₂(x), and v₃(x) are defined above in (8). The subject-specific heaping intensity is

$$log{\theta }_{\text{heap},i}={\mathbf{H}}_i\mathit{\omega }+{\xi }_i,$$ (15)

where H_i is a heaping covariate vector for subject i, ω is an unknown parameter vector of corresponding dimension, and ξ_i is a subject-specific random effect, with distribution

$${\xi }_i~\text{Normal}(\mathbf{0},{\sigma }_{\xi }).$$ (16)

To complete our Bayesian hierarchical model for longitudinal studies, we specify conditionally conjugate prior distributions for α and Σ_β,

$$\begin{array}{ll}\hfill \mathit{\alpha }& ~\text{Normal}(\mathbf{0},{\mathbf{V}}_{\alpha }),\hfill \\ \hfill {\theta }_{\text{disp}}& ~\text{Inverse-Gamma}(a,b),\hfill \\ \hfill \mathit{\omega }& ~\text{Normal}(\mathbf{0},{\mathbf{\sum }}_{\omega })\hfill \\ \hfill \mathit{\gamma }& ~\text{Normal}(\mathbf{0},{\mathbf{V}}_{\gamma })\text{subject}\text{to}{\gamma }_0<\cdots <{\gamma }_J,\text{and}\hfill \\ \hfill {\mathbf{\sum }}_{\beta }& ~\text{Inverse}-\text{Wishart}(A_{\beta },{\mathbf{m}}_{\beta }),\hfill \end{array}$$ (17)

where V_α, a, b, V_γ, A_β and m_β are fixed hyperparameters of corresponding dimension that we specify in Section 5.

Finally, we fit an alternative model of Wang and Heitjan (2008) in which responses not equal to a heaping point are assumed to be reported accurately. The model for the latent counts X_it is identical to (10)-(12), but the heaping distribution is different. If x is the true count, then y is reported as

$$y=\{\begin{array}{ll}x\hfill & \text{with}\text{probability}{v}_0(x)\hfill \\ \text{nearest}\text{multiple}\text{of}5\hfill & \text{with}\text{probability}{v}_1(x)\hfill \\ \text{nearest}\text{multiple}\text{of}10\hfill & \text{with}\text{probability}{v}_2(x)\hfill \\ \text{nearest}\text{multiple}\text{of}50\hfill & \text{with}\text{probability}{v}_3(x).\hfill \end{array}$$ (18)

Once the heaping regime in (18) has been determined, the reported count y arises deterministically.

3.1. Posterior inference

We estimate the joint posterior distribution with Markov chain Monte Carlo (MCMC). We describe standard Gibbs and Metropolis-Hastings samplers for the full conditional distributions of α, β = (β₁, …, β_N), θ, γ, and Σ_β in the supplemental article (Crawford, Weiss and Suchard, 2015). Sampling from the conditional posterior distribution of the true counts is more challenging because of the lack of conjugacy between Pr(X_it|Z_it, W_it, α, β_i) and g(Y_it|X_it, θ). Fortunately, the discrete nature of count data makes some simplifications possible. The conditional distribution of the unobserved true count X_it is

$$Pr(X_{it}\mid Y_{it},{\mathbf{Z}}_{it},{\mathbf{W}}_{it},{\mathbf{H}}_i,\mathit{\theta },\mathit{\alpha },{\mathit{\beta }}_i)\propto g(Y_{it}\mid X_{it},\mathit{\theta })Pr(X_{it}\mid {\mathbf{Z}}_{it},{\mathbf{W}}_{it},{\mathbf{H}}_i,\mathit{\alpha },{\mathit{\beta }}_i).$$ (19)

It is computationally costly to evaluate g(y|x, θ) hundreds of times to construct the distribution of X_it. In the Appendix we present a method for approximating this density by a discretized normal distribution derived from the dynamics of the BDP with θ_heap = 0, allowing efficient sampling. We then employ a Metropolis-Hastings accept/reject step to sample from the correct posterior.

4. Simulation study

To validate the proposed heaping model and the associated Bayesian inference framework, we simulate data under a simplification of the hierarchical model described in Section 3,

$$\begin{array}{ll}\hfill Y_{it}& ~\text{BDP}(X_{it},\mathit{\theta },\mathit{\gamma }),\hfill \\ \hfill X_{it}& ~\text{Poisson}({\eta }_{it}),\hfill \\ \hfill log{\eta }_{it}& =\alpha +{\beta }_i,\text{and}\hfill \\ \hfill {\beta }_i& ~\text{Normal}(0,{\sigma }_{\beta }^2),\hfill \end{array}$$ (20)

for subjects i = 1, …, n and repeated measures t = 1, …, 5, with α and β_i scalars. The heaping parameter θ_heap,i = θ_heap is constant for every subject. Setting α = 2, ${\sigma }_{\beta }^2=1.21$, γ = (0.5, −5, −10, −20), and θ_disp = 0.5 and θ_heap = 2 yields observed counts qualitatively similar to those we observe in the Application section below. From this model, we simulate datasets with N = 100, 250, and 500 total observations from n = N/5 subjects. Using 100 replicates, table 1 reports true parameter values, average posterior means, average posterior variances, and mean squared error (MSE) for each dataset. Standard deviations are given in parentheses. As expected, simulations with larger N give, in general, more accurate parameter estimates, with posterior variance and MSE decreasing with N. Posterior mean estimates of the heaping regimes parameters γ₂ and γ₃ parameters are close to their true values, but their MSE does not appear to decrease monotonically with N. The regime parameters may be only weakly identified in datasets with few large reported counts. Since these parameters control the midpoints of transitions between heaping regimes, they may be highly variable unless many counts fall near these transitions. In addition to larger N, it may be necessary to observe a greater proportion of heaped counts near regime transitions in order to achieve a substantial reduction in posterior variance for γ₂ and γ₃.

Table 1.

Summary of estimated parameters from 100 simulated datasets of size N = 100, 250, and 500 under the heaping model given by (20). Averages of the posterior means, averages of the posterior variances, and mean squared errors are shown with standard deviations in parentheses.

	True	N = 100			N = 250			N = 500
		Mean	Var	MSE	Mean	Var	MSE	Mean	Var	MSE
α	2.00	1.991 (0.28)	0.059 (0.03)	0.078	1.970 (0.14)	0.026 (0.01)	0.021	2.030 (0.12)	0.013 (0.00)	0.014
${\sigma }_{\beta }^2$	1.21	1.368 (0.32)	0.210 (0.12)	0.123	1.270 (0.22)	0.081 (0.03)	0.052	1.211 (0.16)	0.037 (0.01)	0.027
θdisp	0.50	0.516 (0.17)	0.026 (0.01)	0.030	0.508 (0.09)	0.011 (0.00)	0.008	0.492 (0.08)	0.006 (0.00)	0.007
θheap	2.00	2.013 (1.11)	0.572 (0.68)	1.220	2.288 (0.89)	0.615 (0.90)	0.858	2.157 (0.71)	0.368 (0.61)	0.527
γ0	0.50	0.494 (0.08)	0.004 (0.01)	0.007	0.497 (0.07)	0.003 (0.00)	0.005	0.492 (0.06)	0.003 (0.00)	0.004
γ1	−5.00	−5.022 (1.37)	0.840 (0.56)	1.867	−5.204 (0.92)	0.657 (0.48)	0.881	−5.231 (0.86)	0.616 (0.46)	0.790
γ2	−10.00	−9.677 (1.70)	1.617 (1.31)	2.949	−9.916 (1.41)	1.516 (0.98)	1.985	−10.282 (1.50)	1.418 (0.91)	2.290
γ3	−20.00	−19.603 (2.21)	2.343 (2.05)	4.969	−19.388 (2.17)	3.126 (2.58)	5.050	−19.351 (2.26)	3.250 (2.09)	5.486

5. Application to self-reported counts of sex partners

To illustrate the effectiveness of our mixture model and general BDP characterization of the reporting distributions g(y|x, θ), we analyze a survey of HIV-positive youth regarding their sexual behavior from the Choosing Life: Empowerment, Action Results (CLEAR) longitudinal three-arm randomized intervention study designed to reduce HIV transmission and improve quality of life (Rotheram-Borus et al., 2001). Respondents (175, interviewed between 2 and 5 times for 816 total observations) report the number of unique sex partners they had during the previous three months. Figure 6 summarizes the reported counts. There are several striking features of the reported counts: 1) a fair proportion (27%) of the counts are zero; 2) the histogram shows peaks at integer multiples of 10; and 3) a few counts are very large.

Fig 6.

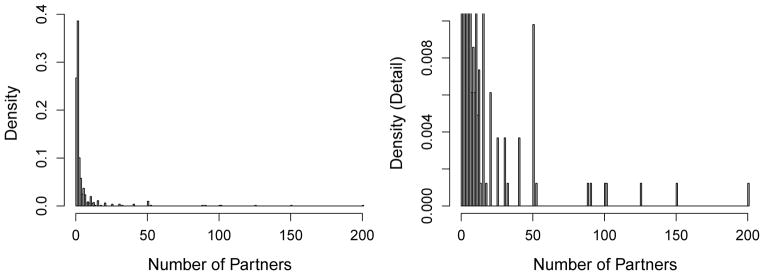
Summary of self-reported counts of sex partners. At left, the histogram shows aggregate reported number of partners in the previous three months, for all subjects, at all time points. At right is the same histogram with the vertical axis limited to (0, 0.01) to show greater detail. There is an apparent preference for reporting counts in multiples of 5, 10, and 50.

We let W_it in (11) be an 8 × 1 vector of covariates for subject i at time t by including subject baseline age, gender (1 for male, 0 for female), an indicator for men who have sex with men (MSM), an indicator for injection drug use, time since baseline interview, an indicator for post-baseline educational intervention and an indicator for use of methamphetamine or other stimulant drugs. Time since baseline interview, use of drugs, and post-baseline intervention, depend on the timepoint t. To facilitate comparison of estimated effects, subject age and time since baseline interview were standardized by subtracting the mean and dividing by the standard deviation. We let Z_it = 1, making β_i a scalar; this provides a subject-specific random intercept. We fit two subject-specific heaping models. In the first, we let H_i = 1 so that θ_heap,i is a subject-specific random intercept. In the second, H_i = (1, gender). Based on the histogram of aggregate counts in Figure 6, we use the BDP rate model in Equation (7) with J = 3 regimes corresponding to heaping at grid points at multiples of 5, 10, or 50.

We assign hyperparameters as follows: for the fixed effects α, α₀ = 0 and Σ_α = 10I where I is the identity matrix; for the heaping parameters θ, a = 0.001 and b = 0.001, such that each has a prior expectation of 1 and variance 1000; for γ, ${\sigma }_{\gamma }^2=100$. Since the subject-specific random effects β_i are scalars, β_i has inverse gamma distribution with parameters A_β = 4 and m_β = 5.

5.1. Results

To evaluate the usefulness of our heaping distributions and to compare to previous approaches, we fit six hierarchical Bayesian models: 1) Poisson mixed effects (PME) with X_it = Y_it and no heaping; 2) the model of Wang and Heitjan (2008) (WH08) as defined by (18); 3) BDP with dispersion and no heaping; 4) BDP model with dispersion and global heaping parameter θ_heap; 5) BDP model with subject-specific heaping intensity; and 6) BDP model with subject-specific heaping intensity and a fixed effect controlling heaping propensity for male and female subjects. In each case, the model for the underlying true count is identical to (10)–(12). The priors on equivalent parameters are also the same for all models.

Table 2 shows posterior summaries for each model. The first eight rows are regression coefficients for the fixed effects α. Estimates of fixed effects in the WH08 model are similar to those found in the PME model without heaping. In general, fixed effects estimates all have larger variance in the heaping models because the BDP reporting distribution induces over-dispersion. Use of stimulants is positively associated with increased true count. While the intervention is not significantly associated with decreased reported counts in the model without heaping and in the Wang and Heitjan (2008) model, the intervention has a clear association with reduced true counts in the BDP heaping models. This result suggests that heaping in reported counts may obscure important associations between covariates and count outcomes. Figure 7 plots the posterior distribution of true counts X_it versus their corresponding reported values Y_it. The points are slightly jittered to show the density of samples. The gray dashed line traces X_it = Y_it. Larger reported counts often correspond to smaller estimated true counts, possibly because the same subjects also reported very low counts at other timepoints.

Table 2.

Parameter estimates, intervals, and goodness-of-fit measures the CLEAR data. We fit six models, each using the basic Bayesian Poisson regression setup (10) for the true counts. In the model without heaping the reported counts are assumed to be equal to true counts. In the dispersion-only model, the BDP allows misremembering but not heaping. The Wang and Heitjan (2008) model involves deterministic heaping under different regimes (18). The BDP heaping model has global dispersion and heaping parameters, the subject-specific BDP heaping model allows subject-specific effects (15), and the subject-specific model with covariates includes a fixed effect for the influence of gender on heaping behavior. Parameter estimates (posterior means) and 95% posterior quantiles are shown for each parameter. The fixed effects are age, gender, men who have sex with men (MSM), injection drug user, intervention, stimulant use, and trading sex. The random intercept variance ${\sigma }_{\beta }^2$ is also shown. The heaping parameters θ_disp and θ_heap control dispersion and heaping for the BDP models. The heaping regime parameters γ₀, γ₁, γ₂, and γ₃ are shown for the heaping models. The heaping random intercept variance ${\sigma }_{\xi }^2$ and the gender-specific heaping fixed effect ω are also shown. Finally, we provide two measures of goodness-of-fit for each model: deviance information criterion (DIC) and the sum of squared mean prediction errors, and the sum of squared prediction errors (SSPE).

	No heaping	WH08	Dispersion-only	Heaping	Subject-specific heaping	Subject-specific heaping+gender
Age	−0.11 (−0.27,0.08)	−0.07 (−0.25,0.1)	−0.15 (−0.56,0.25)	−0.20 (−0.58,0.14)	−0.12 (−0.55,0.23)	−0.14 (−0.43,0.22)
Male	−0.26 (−0.78,0.25)	−0.24 (−0.74,0.28)	−1.48 (−2.77, −0.27)	−0.85 (−1.81,0.12)	−1.01 (−2.16, −0.01)	−0.98 (−2.05, −0.02)
MSM	0.82 (0.33,1.32)	0.81 (0.3,1.32)	0.57 (−0.59,1.75)	0.89 (−0.06,1.85)	0.99 (0.03,1.99)	0.92 (−0.06,1.95)
Inject	−0.37 (−0.88,0.11)	−0.29 (−0.72,0.18)	−0.38 (−1.45,0.65)	−0.29 (−1.2,0.56)	−0.35 (−1.3,0.55)	−0.38 (−1.54,0.44)
Time	−0.89 (−1.06, −0.72)	−0.85 (−1.03, −0.66)	−1.72 (−2.27, −1.18)	−1.02 (−1.46, −0.6)	−1.09 (−1.51, −0.67)	−1.06 (−1.5, −0.61)
Intv	−0.24 (−0.57,0.05)	−0.18 (−0.5,0.1)	−1.29 (−2.05, −0.6)	−1.07 (−1.76, −0.45)	−1.09 (−1.85, −0.32)	−1.16 (−2.06, −0.47)
Stim	1.00 (0.88,1.12)	0.97 (0.84,1.1)	1.51 (1.14,1.88)	1.09 (0.82,1.39)	1.15 (0.83,1.47)	1.05 (0.77,1.36)
Trade	1.32 (1.2,1.45)	1.21 (1.08,1.35)	2.49 (1.98,3)	1.81 (1.41,2.21)	1.79 (1.44,2.15)	2.00 (1.65,2.34)
${\sigma }_{\beta }^2$	1.15 (0.88,1.48)	1.07 (0.82,1.36)	3.63 (2.2,5.66)	2.77 (1.75,4.47)	2.93 (1.79,4.81)	2.93 (1.93,4.45)
θdisp			1.57 (1.4,1.75)	1.04 (0.86,1.22)	1.08 (0.9,1.27)	1.06 (0.91,1.24)
θheap				0.82 (0.59,1.12)
γ0		0.07 (0.05,0.11)		0.42 (0.26,0.84)	0.29 (0.21,0.4)	0.45 (0.28,0.79)
γ1		−2.37 (−2.86, −1.95)		−4.51 (−6.09, −3.46)	−4.66 (−5.78, −3.68)	−5.50 (−8.43, −4.16)
γ2		−2.90 (−3.47, −2.42)		−5.44 (−8.75, −3.95)	−5.40 (−6.87, −4.21)	−7.23 (−10.11, −5)
γ3		−4.07 (−4.9, −3.39)		−6.81 (−12.47, −4.75)	−6.22 (−7.68, −5.1)	−8.40 (−11.55, −6.36)
${\sigma }_{\xi }^2$					0.74 (0.61,0.98)	0.94 (0.87,1)
ω						−0.03 (−0.69,0.54)
DIC	4585	524	3329	3214	3195	3175
SSPE	47773	55078	28005	25371	25336	24364

Fig 7.

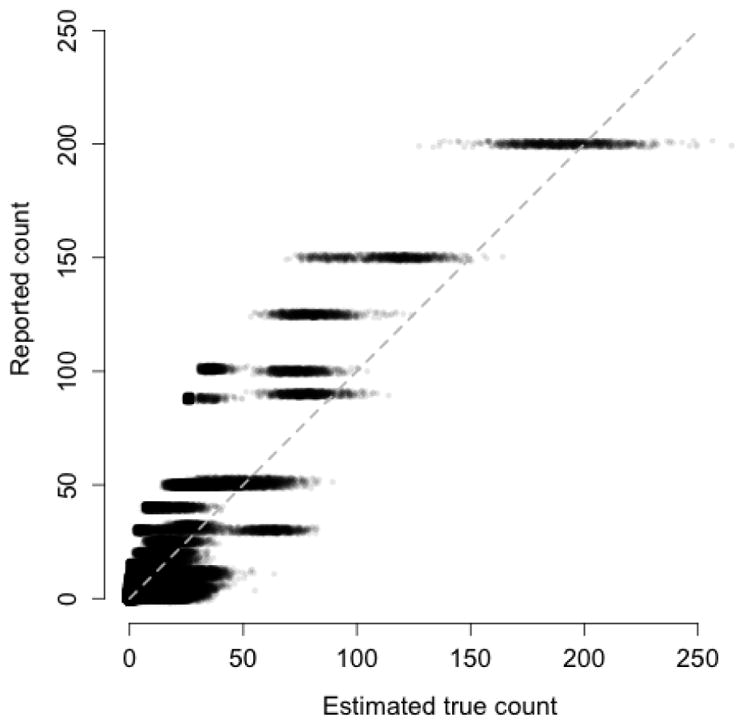
Posterior samples of true counts on the horizontal axis versus reported counts on the vertical axis for the CLEAR data under the BDP heaping model. The points have been slightly jittered to show the density of posterior samples. A gray dashed line is shown on the diagonal.

Estimates of θ_disp are similar for all BDP models with heaping, suggesting that dispersion or misremembering carries information that is distinct from heaping or rounding in the data. The regime parameters γ₀, …, γ₃ are similar for all the BDP heaping models, but likely not comparable to the WH08 model, as the heaping mechanism is different. Estimates of the regime parameters can be interpreted by transforming them into their regime transition midpoints −(γ₁, γ₂, γ₃)/ γ₀. For example, the posterior mean estimates for the “Heaping” model indicate that the “no heaping” regime dominates when the true count is between 0 and −γ₁/γ₀ = 10.7 (posterior mean), and heaping to multiples of 50 dominates when the true count is greater than −γ₃/γ₀ = 16.2. Between these values, heaping to multiples of 5 or 10 dominates. Estimates of γ₁, γ₂, γ₃ exhibit fairly large posterior variance, and posterior intervals for γ₁ and γ₂ show substantial overlap. This indicates that there is not strong evidence of heaping to multiples of 5 and 10 in the data; rather, small counts exhibit little heaping, and large counts show strong heaping to multiples of 50.

We find that there is no significant difference in heaping by gender under our model: the gender-specific effect ω in the last model is not significantly different from zero. This finding is in contrast to those of other researchers who see a strong effect of gender on reporting of sexual behaviors (Wiederman, 1997). One of the goals of the CLEAR study was to show that educational intervention for HIV-positive youth could reduce risky behaviors. While heaping behavior may differ with respect to gender among subjects in the CLEAR study, the small number of reported counts per subject does not permit us to detect such a difference under the BDP heaping model. The intervention tended to reduce true counts, and Pr(α_intv < 0) > 0.95 for every model.

We report two goodness-of-fit measures. The first is deviance information criterion (DIC), computed by conditioning on posterior samples of the parameters that directly affect the outcome Y_it. For the “no heaping” model, these parameters are α and β; for the WH08 model, the X_it’s and γ; for the “dispersion-only’ model, the X_it’s and θ_disp, for the ‘heaping’ model the X_it’s, θ_disp, θ_heap, and γ; for the ‘subject-specific heaping’ model the X_it’s, θ_disp, γ, and ${\sigma }_{\xi }^2$; and for the ‘subject-specific heaping+gender’ model the X_it’s, θ_disp, γ, ${\sigma }_{\xi }^2$, and ω. The second goodness-of-fit measure is the sum of squared mean prediction errors, $\text{SSPE}={\sum }_{i=1}^n{\sum }_{t=1}^{n_i}{(Y_{it}-{\widehat{Y}}_{it})}^2$, where Ŷ_it the mean posterior predictive value of Y_it, calculated by conditioning on the same parameters as used to calculate the DIC. The Wang and Heitjan (2008) model is unique because Y_it|X_it depends only on the four rounding regimes parameters γ, so the DIC is low, and the heaping models all show similar DIC. The SSPE tells a different story: the dispersion-only model shows the worst fit, and the BDP heaping models outperform the WH08 model. These goodness-of-fit measures should be interpreted carefully since the WH08 and BDP heaping models have somewhat different structure.

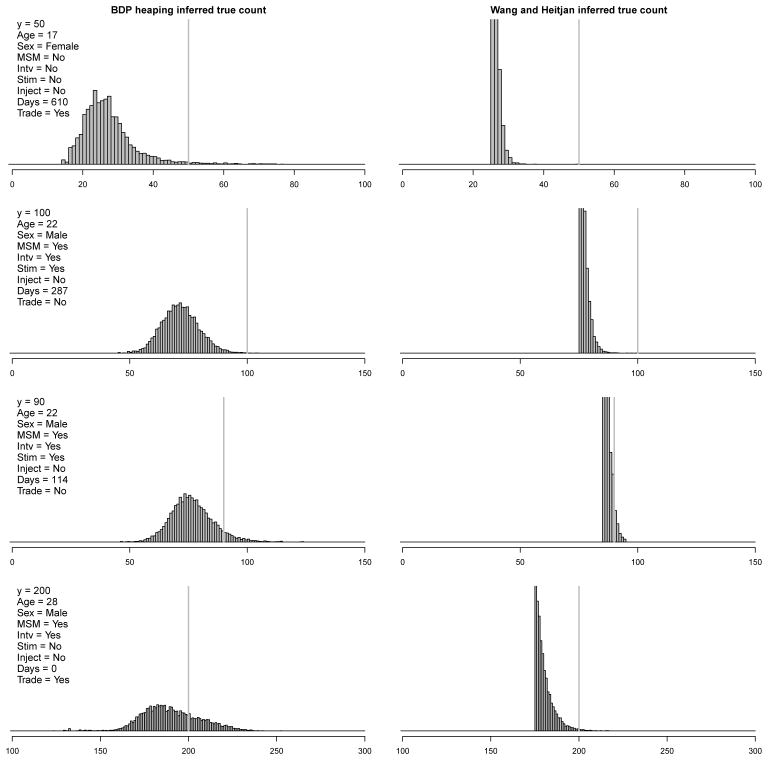
The proportional odds model for different heaping regimes (rounding to 5, 10, and 50) introduced by WH08 proves to be an essential ingredient in our analysis. The apparent heaping pattern observed in the CLEAR counts of sex partners suggests that heaping to multiples of 50 happens often as counts become larger than 30 or 40. We find that heaping models that required rounding to multiples of 5, even for large counts, provide a very poor fit (results not shown). However, in our analyses, the model of WH08 has a serious drawback; when only one heaping regime is in effect, it places a nearly uniform distribution on the true count. The inferred true count distribution is proportional to the product of this uniform distribution and the posterior predictive distribution of the true count. Figure 8 illustrates the problem for specific subjects. Both the WH08 model and the subject-specific BDP heaping model have similar predictive distributions f(x|α, β) for the latent true count x, and in both cases only the v₃ regime (rounding to the nearest multiple of 50) is in effect. But the rounding model of WH08 assumes that rounding is always to the nearest grid point, so for example, a reported value of y = 200 means that x ∈ {175, …, 225} with probability one. The heaping distribution g(y = 200|x, θ, γ) implicitly places a nearly uniform distribution on this set, so the inferred posterior distribution of the true count x is a truncated version of f(x|α, β). In contrast, the BDP heaping model provides a reporting distribution g(y = 200|x, γ, θ) that has support on all of and preferentially places more mass on those x that are most likely to deliver the reported count y. In settings where the true counts themselves might be the objects of inference, we believe the BDP heaping model provides more realistic and useful estimates.

Fig 8.

Marginal posterior distributions of true counts X_it for individual subjects under the BDP heaping model with subject-specific heaping parameters and the model of Wang and Heitjan (2008). The subject- and timepoint-specific covariate values are listed with each plot. A gray vertical line denotes the reported count Y_it = y. Not all inferred true count distributions are centered at the reported count. Moreover, the inferred true counts become more dispersed as the reported count increases. The Wang and Heitjan (2008) model does not allow responses beyond the nearest heaping point and effectively puts a uniform prior distribution on responses that fall within this window. This results in inferred true counts whose posterior distribution is a truncated version of the predictive distribution of X_it.

6. Discussion

In this paper, we have illustrated how researchers can infer the posterior distribution of true integer counts from reported counts using a general BDP reporting distribution within a hierarchical modeling framework. Our most substantial innovation is the novel reporting distribution g(y|x, θ) based on the BDP with specially defined jumping rates that make the Markov chain attracted to heaping grid points. Use of simple linear BDPs to model over-dispersion or reporting error has been proposed before (Grunwald et al., 2011; Lee, Weiss and Suchard, 2014). However, we have substantially expanded the possibilities for general birth-death models of reporting error to explicitly incorporate both over-dispersion and heaping, while providing a computational method to evaluate likelihoods and sample from the posterior distribution of the true counts. This approach has the benefit of providing a sophisticated and highly configurable family of reporting distributions indexed by the true count and just a few unknown parameters θ and γ.

Statisticians may understandably be wary of parametric assumptions about the way study participants report data. However, applied and methodological research in public health offers some clues into reporting mechanisms. Researchers in this field often address the problem of reporting error in surveys related to sexuality and other taboo topics (Schaeffer, 1999). Wang and Heitjan (2008) discuss validation of reported counts of cigarettes smoked by measuring tobacco products in the blood. In related work, Wang et al. (2012) compare instantaneous and retrospective self-reports of cigarette consumption under a similar model for heaping. Other survey methods are possible, including using diary-like surveys or repeated questionnaires to assess reporting error. Studies like these can provide useful information about the parameters θ and γ in our BDP heaping model. Armed with prior information about rounding propensities, perhaps stratified by personal attributes such as gender, age or sexual orientation, public health researchers could proceed with a Bayesian analysis similar to the one outlined in this paper to jointly estimate true counts and regression parameters. Designing a model that accommodates various assumptions about both the mechanism generating the true counts and the cognitive processes that give rise to the reported counts can be challenging. The BDP model for heaped counts presented in this paper is one promising step in this direction.

APPENDIX A: NUMERICAL EVALUATION OF REPORTING PROBABILITIES

We efficiently find the transition probabilities P_ab(t) by first applying the Laplace transform to both sides of the forward equations (Karlin and McGregor, 1957; Murphy and O’Donohoe, 1975). This turns the infinite system of differential equations (2) into a recurrence relation whose solution yields an expression for the Laplace transform of the transition probability P_ab(t). To illustrate, let the Laplace transform h_ab(s) of the transition probability P_ab(t) be

$$h_{ab}(s)={\int }_0^{\infty }{e}^{-st}{P}_{ab}(t)\mathrm{d}t.$$ (21)

Then differentiating h_ab(s) with respect to t and setting a = b = 0, (2) becomes

$$\begin{array}{ll}\hfill s{h}_{00}(s)-P_{00}(0)& ={\mu }_1{h}_{01}(s)-{\lambda }_0{h}_{00}(s),\text{and}\\ \hfill s{h}_{0b}(s)-P_{0,b}(0)& ={\lambda }_{b-1}{h}_{0,b-1}(s)+{\mu }_{b+1}{h}_{0,b+1}(s)-({\lambda }_b+{\mu }_b)h_{0b}(s)\end{array}$$ (22)

for b ≥ 1. Rearranging (22), we find the recurrence

$$\begin{array}{c}{h}_{00}(s)=\frac{1}{s+{\lambda }_0-{\mu }_1\left(\frac{h_{01}(s)}{h_{00}(s)}\right)},\text{and}\\ \frac{h_{0b}(s)}{h_{0,b-1}(s)}=\frac{{\lambda }_{b-1}}{s+{\mu }_b+{\lambda }_b-{\mu }_{b+1}\left(\frac{h_{0,b+1}(s)}{h_{0,b}(s)}\right)}.\end{array}$$ (23)

From this recurrence, we arrive at the well-known continued fraction representation for h₀₀(s),

$$h_{00}(s)=\frac{1}{s+{\lambda }_0-\frac{{\lambda }_0{\mu }_1}{s+{\lambda }_1+{\mu }_1-\frac{{\lambda }_1{\mu }_2}{s+{\lambda }_2+{\mu }_2-\cdots }}},$$ (24)

(see Murphy and O’Donohoe, 1975; Crawford and Suchard, 2012, for further details). This is the Laplace transform of the transition probability P₀₀(t). From (24), we can derive similar continued fraction representations for h_ab(s) for any U (0) = a and U (t) = b. These expressions are given in the supplemental article (Crawford, Weiss and Suchard, 2015). Crawford and Suchard (2012) present a numerical method for inverting transforms (24) to compute the transition probabilities in any general BDP with arbitrary jumping rates ${\{{\lambda }_k\}}_{k=0}^{\infty }$ and ${\{{\mu }_k\}}_{k=1}^{\infty }$. The supplementary material of Crawford, Minin and Suchard (2014) shows how numerical error is controlled in the computation. Section B of this Appendix gives an approximation to the reporting distribution that is useful for sampling.

APPENDIX B: APPROXIMATION OF REPORTING PROBABILITIES

In this Appendix, we derive an approximation to the conditional distribution of the reported count given the true count, Y_it|X_it. The full conditional distribution of the ith subject’s true count X_it at timepoint j is

$$\begin{array}{l}Pr(X_{it}=x\mid Y_{it},{\mathbf{Z}}_i,{\mathbf{W}}_{it},\mathit{\alpha },{\mathit{\beta }}_i,\mathit{\theta })\propto Pr(Y_{it}\mid X_{it}=x,\mathit{\theta })Pr(X_{it}=x\mid {\mathbf{W}}_{it},{\mathbf{Z}}_i,\mathit{\alpha },{\mathit{\beta }}_i)\\ =P_{x,Y_{it}}(\mathit{\theta })\frac{{\eta }_{it}^x{e}^{-{\eta }_{it}}}{x!}\\ =g(y\mid x,\mathit{\theta })f(x\mid {\eta }_{it}),\end{array}$$ (25)

where η_it = exp(W_itα + Z_itβ_i) and P_xy(θ) = g(y|x, θ) is the general BDP transition probability under the model described in Section 2.2. Under a Metroplis-Hastings scheme, we need to propose a new value of X_it efficiently; we approximate the density P_xy(θ) as normal. Let θ_heap = 0 and θ_disp > 0. Then this simplified BDP has birth and death rates

$${\lambda }_k={\theta }_{\text{disp}}+{\theta }_{\text{disp}}k\text{and}{\mu }_k={\theta }_{\text{disp}}k.$$ (26)

This is a linear process with immigration that has an asymptotically normal distribution. Similar to Section 2.1, let U(t) be a BDP starting at U(0) = a. Following Lange (2010), we form the probability generating function (PGF)

$$H(s,t)=\sum _{b=0}^{\infty }{s}^b{P}_{ab}(t).$$ (27)

where s is a “dummy” variable and P_ab(t) = Pr(U (t) = b | U (0) = a) is the transition probability. Although H(s, t) has a closed-form solution that can be inverted to obtain the P_ab(t) in analytic form, the details are somewhat complicated, and we only require a normal approximation to this density. The mean m_a(t) = 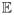(U (t) | U (0) = a) is given by

$${\frac{\partial H(s,t)}{\partial s}|}_{s=1}=\sum _{b=0}^{\infty }j{P}_{ab}(t)=\mathbb{E}[U(t)]=m_a(t),$$ (28)

and likewise the second factorial moment e_a(t) is given by

$${\frac{{\partial }^{2}H(s,t)}{\partial s^2}|}_{s=1}=\sum _{b=1}^{\infty }b(b-1)P_{ab}(t)=\mathbb{E}[U{(t)}^2]-\mathbb{E}[U(t)]=e_a(t),$$ (29)

where the expectations are conditional on the process beginning in state U(0) = a. This suggests that we can determine the mean and variance of U(t) | {U(0) = a} by finding the partial derivatives of H with respect to the dummy variable s. To derive these quantities, we form a partial differential equation for the solution of the PGF

$$\frac{\partial H(s,t)}{\partial t}={\theta }_{\text{disp}}\left[{(s-1)}^2\frac{\partial H(s,t)}{\partial s}+(s-1)H(s,t)\right].$$ (30)

See Lange (2010), Bailey (1964) and Renshaw (2011) for the details of deriving this generating function. Now, the time-derivative of the mean falls out as

$$\frac{\mathrm{d}{m}_a(t)}{\mathrm{d}t}={\frac{{\partial }^{2}H(s,t)}{\partial t\partial s}|}_{s=1}={\theta }_{\text{disp}},$$ (31)

and the time-derivative of the second factorial moment is

$$\frac{\mathrm{d}{e}_a(t)}{\mathrm{d}t}={\frac{{\partial }^{3}H(s,t)}{\partial t{\partial }^{2}s}|}_{s=1}=4{\theta }_{\text{disp}}(a+{\theta }_{\text{disp}}t).$$ (32)

Solving these differential equations with the initial conditions m_a(0) = a and e_i(0) = a² − a yields

$$m_a(t)=a+{\theta }_{\text{disp}}t\text{and}{e}_a(t)=a(a-1)+4a{\theta }_{\text{disp}}t+2{\theta }_{\text{disp}}^2{t}^2.$$ (33)

From these, we determine that

$$\begin{array}{ll}\hfill \mathbb{E}[U(t)\mid U(0)=a]& =a+{\theta }_{\text{disp}}t,\text{and}\hfill \\ \hfill \text{Var}[U(t)\mid U(0)=a]& =(2a+1){\theta }_{\text{disp}}t+{\theta }_{\text{disp}}^2{t}^2,\hfill \end{array}$$ (34)

where the second line arises because Var[U(t) | U(0) = i] = e_a(t) + m_a(t) − m_a(t)². Therefore a reasonable approximation to the probability mass function of U(t) | {U(0) = a} is the normal distribution with the mean and variance above. This approximation serves as an effective proposal within a Metropolis-Hastings accept/reject step.