Genome-wide modeling of transcription kinetics reveals patterns of RNA production delays

Significance

Gene transcription is a highly regulated dynamic process. Delays in transcription have important consequences on dynamics of gene expression and consequently on downstream biological function. We model temporal dynamics of transcription using genome-wide time course data measuring transcriptional activity and mRNA concentration. We find a significant number of genes exhibit a long RNA processing delay between transcription termination and mRNA production. These long processing delays are more common for short genes, which would otherwise be expected to transcribe most rapidly. The distribution of intronic reads suggests that these delays are required for splicing to be completed. Understanding such delays is essential for understanding how a rapid cellular response is regulated.

Abstract

Genes with similar transcriptional activation kinetics can display very different temporal mRNA profiles because of differences in transcription time, degradation rate, and RNA-processing kinetics. Recent studies have shown that a splicing-associated RNA production delay can be significant. To investigate this issue more generally, it is useful to develop methods applicable to genome-wide datasets. We introduce a joint model of transcriptional activation and mRNA accumulation that can be used for inference of transcription rate, RNA production delay, and degradation rate given data from high-throughput sequencing time course experiments. We combine a mechanistic differential equation model with a nonparametric statistical modeling approach allowing us to capture a broad range of activation kinetics, and we use Bayesian parameter estimation to quantify the uncertainty in estimates of the kinetic parameters. We apply the model to data from estrogen receptor α activation in the MCF-7 breast cancer cell line. We use RNA polymerase II ChIP-Seq time course data to characterize transcriptional activation and mRNA-Seq time course data to quantify mature transcripts. We find that 11% of genes with a good signal in the data display a delay of more than 20 min between completing transcription and mature mRNA production. The genes displaying these long delays are significantly more likely to be short. We also find a statistical association between high delay and late intron retention in pre-mRNA data, indicating significant splicing-associated production delays in many genes.

Induction of transcription through extracellular signaling can yield rapid changes in gene expression for many genes. Establishing the timing of events during this process is important for understanding the rate-limiting mechanisms regulating the response and vital for inferring causality of regulatory events. Several processes influence the patterns of mRNA abundance observed in the cell, including the kinetics of transcriptional initiation, elongation, splicing, and mRNA degradation. It was recently demonstrated that significant delays attributable to the kinetics of splicing can be an important factor in a focused study of genes induced by tumor necrosis factor (TNF-α) (1). Delayed transcription can play an important functional role in the cell, for example, inducing oscillations within negative feedback loops (2) or facilitating “just-in-time” transcriptional programs with optimal efficiency (3). It is therefore important to identify such delays and to better understand how they are regulated. In this study, we combine RNA polymerase (pol-II) ChIP-Seq data with RNA-Seq data to study transcription kinetics of estrogen receptor (ER) signaling in breast cancer cells. Using an unbiased genome-wide modeling approach, we find evidence for large delays in mRNA production in 11% of the genes with a quantifiable signal in our data. A statistical analysis of genes exhibiting large delays indicates that splicing kinetics is a significant factor and can be the rate-limiting step for gene induction.

A high-throughput sequencing approach is attractive because it gives broad coverage and thus allows us to uncover the typical properties of the system. However, high-throughput data are associated with significant sources of noise, and the temporal resolution of our data is necessarily reduced compared with previous studies using more focused PCR-based assays (1, 4). We have therefore developed a statistically efficient model-based approach for estimating the kinetic parameters of interest. We use Bayesian estimation to provide a principled assessment of the uncertainty in our inferred model parameters. Our model can be applied to all genes with sufficiently strong signal in both the mRNA and pol-II data with only mild restrictions on the shape of the transcriptional activation profile (1,814 genes here).

A number of other works studying transcription and splicing dynamics (e.g., refs. 1, 5, and 6) forgo detailed dynamical modeling, which limits the authors’ ability to properly account for varying mRNA half-lives. Our statistical model incorporates a linear ordinary differential equation of transcription dynamics, including mRNA degradation. Similar linear differential equation models have been proposed as models of mRNA dynamics previously (4, 7, 8) but assuming a specific parametric form for the transcriptional activity. In contrast, we apply a nonparametric Gaussian process (GP) framework that can accommodate a quite general shape of transcriptional activity. As demonstrated previously (9–11), the linearity of the differential equation allows efficient exact Bayesian inference of the transcriptional activity function. Before presenting our results, we outline our modeling approach.

Model-Based Inference of Transcriptional Delays

Our modeling approach is summarized in Fig. 1. We model the dynamics of transcription using a linear differential equation,

$$\frac{\text{d}m\left(t\right)}{\text{d}t}=\beta p\left(t-\mathrm{\Delta }\right)-\alpha m\left(t\right),$$ [1]

where $m\left(t\right)$ is the mature mRNA abundance and $p\left(t\right)$ is the transcription rate at the 3′ end of the gene at time t, which is scaled by a parameter β because we do not know the scale of our $p\left(t\right)$ estimates. The parameter $\mathrm{\Delta }$ captures the delay between transcription completion and mature mRNA production. We refer to this as the RNA production delay, defined as the time required for the polymerase to disengage from the pre-mRNA and be fully processed into a mature transcript. The parameter α is the mRNA degradation rate, which determines the mRNA half-life ($t_{1/2}=\ln 2/\alpha$). We infer all model parameters (α, β, $\mathrm{\Delta }$, and the noise variance and parameters of the GP covariance function discussed in Materials and Methods) using a Markov chain Monte Carlo (MCMC) procedure. The posterior distribution of the model parameters quantifies our uncertainty, and we use percentiles of the posterior distribution when reporting credible regions around the mean or median values.

Fig. 1.

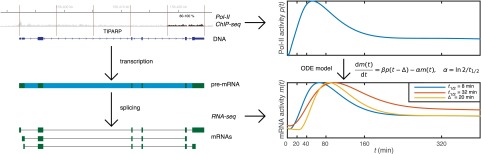
Cartoon illustrating the underlying biology and data gathering at a single time point (Left) and time series modeling (Right). The data are from pol-II ChIP-Seq, summarized over the last 20% of the gene body, and RNA-Seq computationally split to pre-mRNA and different mRNA transcript expression levels. The modeling on the right shows the effect of changing mRNA half-life ($t_{1/2}$) or RNA production delay ($\mathrm{\Delta }$) on the model response: both induce a delay on the mRNA peak relative to the pol-II peak, but the profiles have otherwise distinct shapes.

We measure the transcriptional activity $p\left(t\right)$ using pol-II ChIP-Seq time course data collected close to the 3′ end of the gene (reads lying in the last 20% of the transcribed region). Our main assumption is that pol-II abundance at the 3′ end of the gene is proportional to the production rate of mature mRNA after a possible delay $\mathrm{\Delta }$ attributable to disengaging from the polymerase and processing. The mRNA abundance is measured using RNA-Seq reads mapping to annotated transcripts, taking all annotated transcripts into account and resolving mapping ambiguities using a probabilistic method (12) (see Methods for details). As we limit our analysis to pol-II data collected from the 3′ end of the transcribed region, we do not expect a significant contribution to $\mathrm{\Delta }$ from transcriptional delays when fitting the model. Such transcriptional delays have recently been studied by modeling transcript elongation dynamics using pol-II ChIP-Seq time course data (13) and nascent mRNA (GRO-Seq) data (14) in the same system. Here, we instead focus on production delays that can occur after elongation is essentially complete.

Existing approaches to fitting models of this type have assumed a parametric form for the activation function $p\left(t\right)$ (4, 7, 8). We avoid restricting the function shape by using a nonparametric Bayesian procedure for fitting $p\left(t\right)$. We model $p\left(t\right)$ as a function drawn from a GP that is a distribution over functions. The general properties of functions drawn from a GP prior are determined by a “covariance function,” which can be used to specify features such as smoothness and stationarity. We choose a covariance function that ensures $p\left(t\right)$ is a smooth function of time because our data are averaged across a cell population. Our choice of covariance function is nonstationary and has the property that the function has some persistence and therefore tends to stay at the same level between observations (see the SI Appendix for further details). The advantage of using a nonparametric approach is that we only have to estimate a small number of parameters defining the covariance function (two in this case, defining the amplitude and time scale of the function). If we were to represent $p\left(t\right)$ as a parametrized function, we would have to estimate a larger number of parameters to describe the function with sufficient flexibility. The Bayesian inference procedure we use to associate each estimated parameter with a credible region would be more challenging with the inclusion of these additional parameters.

We have previously shown how to perform inference over differential equations driven by functions modeled using GPs (9–11). The main methodological novelty in the current work is the inclusion of the delay term in Eq. 1 and the development of a Bayesian inference scheme for this and other model parameters. In brief, we cast the problem as Bayesian inference with a GP prior distribution over $p\left(t\right)$ that can be integrated out to obtain the data likelihood under the model in Eq. 1 assuming Gaussian observation noise. This likelihood function and its gradient are used for inference with a Hamiltonian MCMC algorithm (15) to obtain a posterior distribution over all model parameters and the full pol-II and mRNA functions $p\left(t\right)$ and $m\left(t\right)$.

Results

We model the transcriptional response of MCF-7 breast cancer cells after stimulation by estradiol (E2) to activate ER-α signaling. Fig. 2 shows the inferred pol-II and mRNA profiles for all genes with sufficient signal for modeling, along with some specific examples of fitted models and estimated delay parameters. Before discussing these results further below, we describe the application of our method to realistic simulated data to assess the reliability of our approach for parameter estimation under a range of conditions.

Fig. 2.

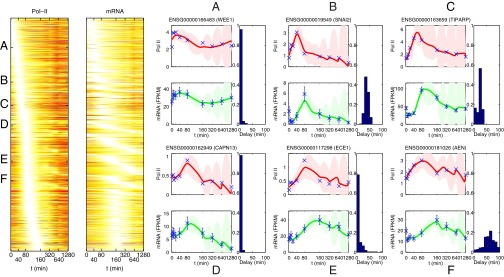
(Left) Heat map of inferred pol-II and mRNA activity profiles after MCF-7 cells are stimulated with E2. Genes with sufficient signal for modeling are sorted by the time of peak pol-II activity in the fitted model. (Right) Examples of fitted model for six genes (genes A to F). For each gene, we show the fit using the pol-II ChIP-Seq data (collected from the final 20% of the transcribed region) representing the transcriptional activity $p\left(t\right)$ (Eq. 1) and using the RNA-Seq data to represent gene expression $m\left(t\right)$. Solid red and green lines show the mean model estimates for the pol-II and mRNA profiles, respectively, with associated credible regions. In each case, we show the posterior distribution for the inferred delay parameter $\mathrm{\Delta }$ to the right of the temporal profiles. Note that the final measurement times are very far apart (the x axis is compressed to aid visualization), leading to high uncertainty in the model fit at late times. However, this does not significantly affect the inference of delays for early induced genes.

Simulated Data.

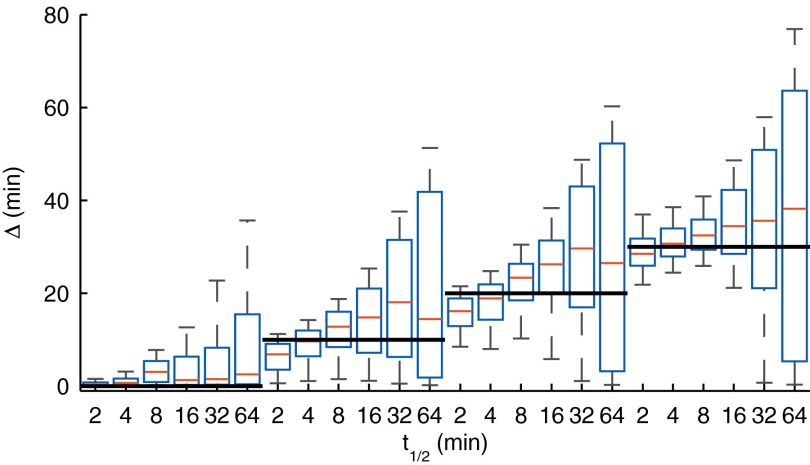
We applied our method to data simulated from the model in Eq. 1 using a $p\left(t\right)$ profile inferred using pol-II data from the TIPARP gene (gene C in Fig. 2; see SI Appendix for further details about the simulated data). We simulated data using different values of α and $\mathrm{\Delta }$ to test whether we can accurately infer the delay parameter $\mathrm{\Delta }$. Fig. 3 shows the credible regions of $\mathrm{\Delta }$ for different ground truth levels (horizontal lines) and for different mRNA degradation rates (half-lives given on the x-axis). The results show that $\mathrm{\Delta }$ can be confidently inferred with the ground truth always lying within the central part of the credible region. The maximum error in posterior median estimates is less than 10 min, and when positive, the true value is always above the 25th percentile of the posterior. We observed that as the mRNA half-life increases, our confidence in the delay estimates is reduced. This is because the mRNA integrates the transcriptional activity over time proportional to the half-life leading to a more challenging inference problem. We also note that inference of the degradation parameter α is typically more difficult than inference of the delay parameter $\mathrm{\Delta }$ (SI Appendix, Fig. S1). However, a large uncertainty in the inferred degradation rate does not appear to adversely affect the inference of the delay parameters which are the main focus here. More time points, or a different spacing of time points, would be needed to accurately infer the degradation rates. Additional results of delay estimation in a scenario where the simulated half-life changes during the time course are presented in SI Appendix, Fig. S2. These results demonstrate that the obtained delay estimates are reliable even in this scenario.

Fig. 3.

Boxplots of parameter posterior distributions illustrating parameter estimation performance on synthetic data for the delay parameter $\mathrm{\Delta }$. The bolded black lines indicate the ground truth used in data generation. The box extends from 25th to 75th percentile of the posterior distribution, whereas the whiskers extend from ninth to 91st percentile. The results show that delay estimates are accurate and reliable, with the true value always in the high posterior density region.

ER Signaling.

We applied our method to RNA-Seq and pol-II ChIP-Seq measurements from MCF-7 cells stimulated with E2 to activate ER-α signaling (Methods). The measurements were taken from cells extracted from the same population to ensure that time points are directly comparable across technologies. Example fits of our model are shown in Fig. 2. The examples in Fig. 2 show a number of different types of behavior ranging from early-induced (A to C) to late-induced (D to F) and from very short delay (A, D, and E) to longer delays (B, C, and F). Example E in Fig. 2, ECE1, is illuminating because visual inspection of the profiles suggests a possible delay, but a more likely explanation according to our model is a longer mRNA half-life, and the posterior probability of a long delay is quite low. Indeed, it is well known that differences in stability can lead to delayed mRNA expression (16), and therefore delays in mRNA expression peak relative to pol-II peak time are not sufficient to indicate a production delay. Changes in splicing can be another potential confounder, but our transcript-based analysis of RNA-Seq data can account for that. An example of how more naive RNA-Seq analysis could fail here is presented in SI Appendix, Fig. S3.

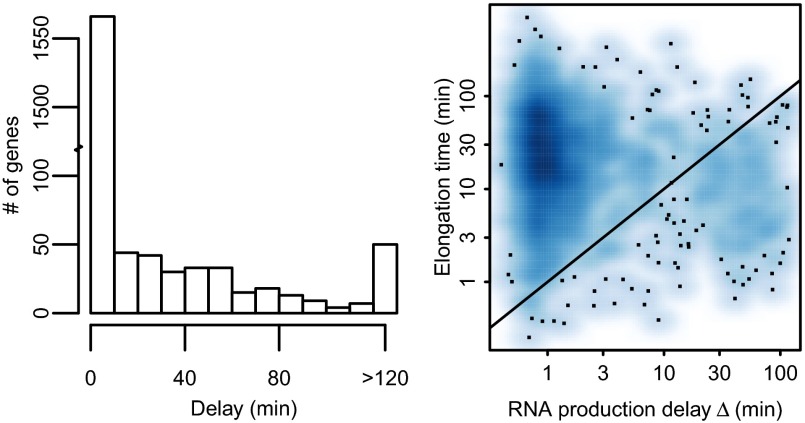
The parameter estimates of the models reveal a sizeable set of genes with strong evidence of long delays between the end of transcription and production of mature mRNA. We were able to obtain good model fits for 1,864 genes. We excluded 50 genes with posterior median delay >120 min, given that these genes are unreliable because of sparse sampling late in the time course, which is apparent from broad delay posterior distributions. Out of the remaining 1,814 genes with reliable estimates, 204 (11%) had a posterior median delay larger than 20 min between pol-II activity and mRNA production, whereas 98 genes had the 25th percentile of delay posterior larger than 20 min, indicating confident high delay estimates. A histogram of median delays is shown in Fig. 4 (Left). The 120-min cutoff for long delays was selected by visual observation of model fits, which were generally reasonable for shorter delays. Note that late time points in our dataset are highly separated because of the exponential time spacing used, and thus the model displays high levels of uncertainty between these points (Fig. 2). Therefore, genes displaying confident delay estimates are typically early-induced such that time points are sufficiently close for a confident inference of delay time. Our Bayesian framework makes it straightforward to establish the confidence of our parameter estimates.

Fig. 4.

(Left) Histogram of delay posterior medians from 1,864 genes found to fit the model well. Estimated delays larger than 120 min are considered unreliable and are grouped together. These 50 genes were excluded from further analysis, leaving 1,814 genes for the main analysis. (Right) Estimated gene transcriptional delay for the longest transcript plotted against the estimated posterior median RNA production delay. The transcriptional delay is estimated assuming each gene follows the median transcriptional velocity measured in ref. 14. The solid line corresponds to equal delays.

Genomic Features Associated with Long-Delay Genes.

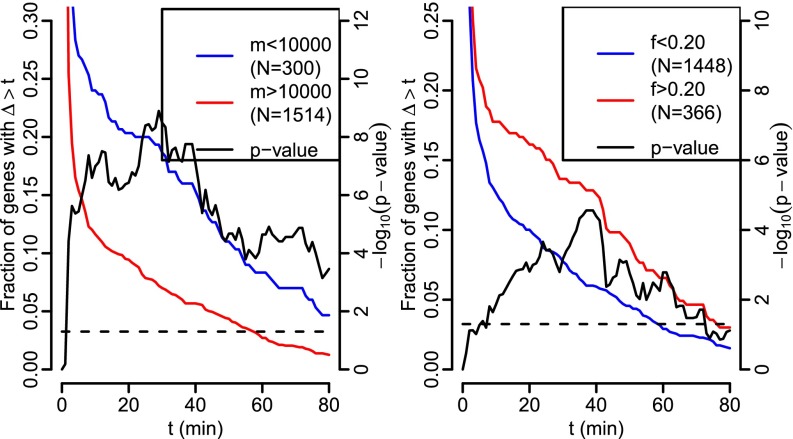
Motivated by previous studies (5, 6, 17), we investigated statistical association between the observed RNA production delay and genomic features related to splicing. We found that genes with a short pre-mRNA (Fig. 5, Left) are more likely to have long delays. We also found that genes where the ratio of the final intron’s length in the longest annotated transcript over the total length of the transcript is large (Fig. 5, Right) are also more likely to have long delays, but this effect appears to be weaker. These two genomic features, short pre-mRNA and relatively long final introns, are positively correlated, making it more difficult to separate their effects. To do so, SI Appendix, Fig. S6 shows versions of the right panel of Fig. 5 but only including genes with pre-mRNAs longer than 10 or 30 kb. The number of genes with long final introns in these sets is smaller, and the resulting P values are thus less extreme, but the general shape of the curves is the same. We did not find a significant relationship with the absolute length of the final intron. This may be because the two observed effects would tend to cancel out in such cases. We also checked whether exon skipping is associated with long delays as previously reported (6). The corresponding results (SI Appendix, Fig. S7) show no significant difference in estimated delays in genes with and without annotated exon skipping.

Fig. 5.

Tail probabilities for delays. (Left) Genes whose longest pre-mRNA transcript is short (m is the length from transcription start to end). (Right) Genes with relatively long final introns (f is the ratio of the length of the final intron of the longest annotated transcript of the gene divided by the length of that transcript pre-mRNA). The fraction of genes with long delays $\mathrm{\Delta }$ is shown by the red and blue lines (left vertical axis). In both subplots, the black curve denotes the P values of Fisher’s exact test for equality of fractions depicted by the red and blue curves conducted separately at each point (right vertical axis), with the dashed line denoting P < 0.05 significance threshold. Similar plots for other values of m and f, as well as different gene filter setups, are given in SI Appendix, Figs. S4 and S5.

Analysis of the Intronic Read and pol-II Distribution.

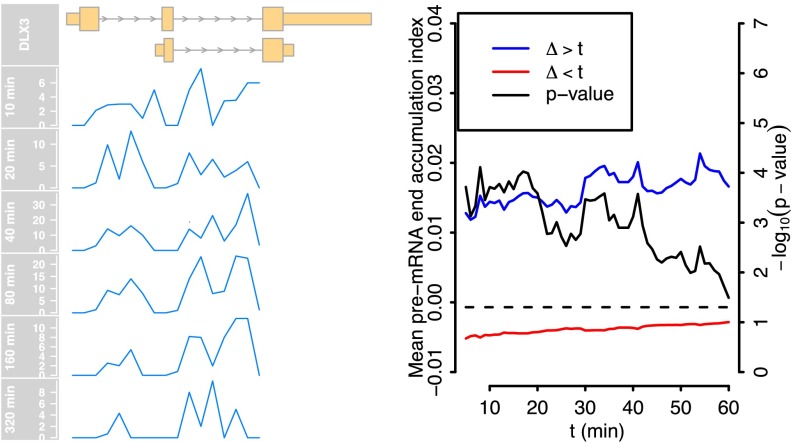
We investigated whether there was evidence of differences in the pattern of splicing completion for long-delay genes. To quantify this effect, we developed a pre-mRNA end accumulation index: the ratio of intronic reads in the last 50% of the pre-mRNA to the intronic reads in the first 50% at late (80–320 min) and early (10–40 min) times. Fig. 6 shows that genes with a long estimated delay display an increase in late intron retention at the later times. There is a statistically significant difference in the medians of index values for short and long delay genes (P < 0.01; Wilcoxon’s rank-sum test P values for different short/long delay splits are shown in Fig. 6). The example on the left of Fig. 6, DLX3, is a relatively short gene of about 5 kb, and thus differences over time cannot be explained by the time required for transcription to complete. The corresponding analysis for pol-II ChIP-Seq reads as well as GRO-Seq reads is in SI Appendix, Fig. S8. The analysis shows a clear delay-associated accumulation to the last 5% nearest to the 3′ end, whereas for pol-II in the last 50%, the accumulation is universal. These results suggest our short-delay genes tend to be efficiently spliced, whereas long-delay genes are more likely to exhibit delayed splicing toward the 3′ end. There is also evidence of some accumulation of pol-II near the 3′ end, although the effect appears relatively weak. We note that Grosso et al. (18) identified genes with elevated pol-II at the 3′ end, which were found to be predominantly short, consistent with our set of delayed genes, and with nucleosome occupancy consistent with pausing at the 3′ end.

Fig. 6.

(Left) We show the density of RNA-Seq reads uniquely mapping to the introns in the DLX3 gene, summarized in 200-bp bins. The gene region is defined from the first annotated transcription start until the end of last intronic read. The ratio of the number of intronic reads after and before the midpoint of the gene region is used to quantify the 3′ retention of introns. The pre-mRNA end accumulation index is the difference between averages of this ratio computed over late times (80–320 min) and early times (10–40 min). (Right) Differences in the mean pre-mRNA accumulation index (left vertical axis) in long delay genes (blue) and short delay genes (red) as a function of the cutoff used to distinguish the two groups (horizontal axis). Positive values indicate an increase in 3′ intron reads over time. The black line shows the P values of Wilcoxon’s rank sum test between the two groups at each cutoff (right vertical axis).

Relative Importance of Production and Elongation Delays.

To better understand what are the rate-limiting steps in transcription dynamics, we assessed the relative importance of the observed RNA production delays in comparison with transcriptional delays attributable to elongation time. We estimated elongation times for each gene using assumed transcriptional velocity corresponding to the 2.1 kb/min median estimate from ref. 14 combined with the length of the longest annotated pre-mRNA transcript. Others (e.g., ref. 13) have reported higher velocities; so this approach should provide reasonable upper bounds on actual elongation time for most genes. A comparison of these delays with our posterior median delay estimates is shown in Fig. 4 (Right). The figure shows the majority of genes with short production delays and moderate elongation time in the upper left corner of the figure, but 14.3% (260/1,814) of genes have a longer RNA production delay than elongation time.

Discussion

Through model-based coupled analysis of pol-II and mRNA time course data, we uncovered the processes shaping mRNA expression changes in response to ER signaling. We find that a large number of genes exhibit significant production delays. We also find that delays are associated with short overall gene length, relatively long final intron length and increasing late-intron retention over time. Our results support a major role for splicing-associated delays in shaping the timing of gene expression in this system. Our study complements the discovery of similarly large splicing-associated delays in a more focused study of TNF-induced expression (1), indicating that splicing delays are likely to be important determinants of expression dynamics across a range of signaling pathways.

It is known that splicing can strongly influence the kinetics of transcription. Khodor et al. (5) carried out a comparative study of splicing efficiency in fly and mouse and found a positive correlation between absolute gene length and splicing efficiency. This finding suggests that efficient cotranscriptional splicing is facilitated by increased gene length and is consistent with our observation that delays are more common in shorter genes. In these genes, it appears that the mature mRNA cannot be produced after transcription until splicing is completed; it is splicing rather than transcription that is the rate-limiting step for these genes. In the same study, it was also observed that introns close to the 3′ end of a gene are less efficiently spliced, which is consistent with our observation that the relative length of the final intron may impact on splicing delays. A further theoretical model supporting a link between long final introns and splicing inefficiency was recently suggested (19), but it is unclear whether the model can fully explain the observed relationships.

Our model assumes a constant mRNA degradation rate, which may be unrealistic. Given the difficulty of estimating even a single constant degradation rate for simulated data where the true rate is constant, it seems infeasible to infer time-varying rates with the current data. On the other hand, estimated delays were quite reliably inferred even when we simulated data with a time-varying degradation rate (SI Appendix, Fig. S2), and hence the potentially incorrect degradation model should not affect the main results significantly.

It is important to differentiate the delays found here with transcriptional delays required for pol-II elongation to complete. Elongation time can be a significant factor in determining the timing of gene induction, and elongation dynamics has been modeled using both pol-II ChIP-Seq (13) and nascent RNA (GRO-Seq) (14) time course measurements in the system considered here. However, in this study we limited our attention to pol-II data at the 3′ end of the gene (i.e., measuring polymerase density changes in the region where elongation is almost completed). Therefore, we will not see transcription delays in our data, and the splicing-associated delays discussed above are not related to elongation time. Indeed, the splicing-associated delays observed here are more likely to affect shorter genes where transcription completes rapidly. These splicing-associated delays are much harder to predict from genomic features than transcriptional delays, which are mainly determined by gene length, although we have shown an association with final intron length and gene length. In the future, it would be informative to model data from other systems to establish associations with system-specific variables (e.g., alternative splice-site use) and thereby uncover context-specific mechanisms regulating the delays that we have observed here.

Materials and Methods

Data Acquisition and Mapping.

MCF-7 breast cancer cells were stimulated with E2 after being placed in E2-free media for 3 d, similarly to the method described previously (13). We measured pol-II occupancy and mRNA concentration from the same cell population collected at 10 time points on a logarithmic scale: 0, 5, 10, 20, 40, 80, 160, 320, 640, and 1,280 min after E2 stimulation. At each time point, the pol-II occupancy was measured genome-wide by ChIP-Seq and mRNA concentration using RNA-Seq. Raw reads from the ChIP-Seq data were mapped onto the human genome reference sequence (NCBI_build37) using the Genomatix Mining Station (software version 3.5.2; further details are in the SI Appendix). On average, 84.0% of the ChIP-Seq reads were mapped uniquely to the genome. The RNA-Seq reads were mapped using bowtie to a transcriptome constructed from Ensembl version 68 annotation allowing at most three mismatches and ignoring reads with more than 100 alignments. The transcriptome was formed by combining the cDNA and non-coding RNA transcriptomes with pre-mRNA sequences containing the full genomic sequence from the beginning of the first annotated exon to the end of the last annotated exon. On average, 84.7% of the RNA-Seq reads were mapped.

RNA-Seq Data Processing.

mRNA concentration was estimated from RNA-Seq read data using BitSeq (12). BitSeq is a probabilistic method to infer transcript expression from RNA-Seq data after mapping to an annotated transcriptome. We estimated expression levels to all entries in the transcriptome, including the pre-mRNA transcripts, and used the sum of the mRNA transcript expressions in fragments per kilobase of exon per million fragments mapped (FPKM) units to estimate the mRNA expression level of a gene. Different time points of the RNA-Seq time series were normalized using the method in ref. 20.

pol-II ChIP-Seq Data Processing.

The ChIP-Seq data were processed into time series summarizing the pol-II occupancy at each time point for each human gene. We considered the last 20% of the gene body nearest to the 3′ end. The gene body was defined from the start of the first exon to the end of the last exon in Ensembl version 68 annotation. The data were subject to background removal using manually selected empty regions in Dataset S1 and normalization of time points. The gene regions were refined for a small subset of genes using active transcripts listed in Dataset S2. (Full details are in the SI Appendix.)

Filtering of Active Genes.

We removed genes with no clear time-dependent activity by fitting time-dependent GP models to the activity curves and only keeping genes with Bayes factor at least 3 in favor of the time-dependent model compared with a null model with no time dependence. We also removed genes that had no pol-II observations at two or more time points. This process left 4,420 genes for which we fitted the models.

Modeling and Parameter Estimation.

We model the relationship between pol-II occupancy and mRNA concentration using the differential equation in Eq. 1, which relates the pol-II time series $p\left(t\right)$ and corresponding mRNA time series $m\left(t\right)$ for each gene. We model $p\left(t\right)$ in a nonparametric fashion by applying a GP prior over the shapes of the functions. We slightly modify the model in Eq. 1 by adding a constant ${\beta }_0$ to account for the limited depth of pol-II ChIP-Seq measurements, yielding $\text{d}m\left(t\right)/\text{d}t={\beta }_0+\beta p\left(t-\mathrm{\Delta }\right)-\alpha m\left(t\right)$. This differential equation can be solved for $m\left(t\right)$ as a function of $p\left(t\right)$ in closed form. The pol-II concentration function $p\left(t\right)$ is represented as a sample from a GP prior, which can be integrated out to compute the data likelihood. The model can be seen as an extension of a previous model applied to transcription factor target identification (11). Unlike ref. 11, we model $p\left(t\right)$ as a GP defined as an integral of a function having a GP prior with RBF covariance, which implies that $p\left(t\right)$ tends to remain constant between observed data instead of reverting back to the mean. Additionally we introduce the delay between pol-II concentration and mRNA production, as well as model the initial mRNA concentration as an independent parameter. In the special case where $\mathrm{\Delta }=0$ and $m_0={\beta }_0/\alpha$, SI Appendix, Eq. 3 reduces to the previous model (equation 4 in ref. 11). To fit the model to pol-II and mRNA time course data sampled at discrete times, we assume we observe $m\left(t\right)$ and $p\left(t\right)$ corrupted by zero-mean Gaussian noise independently sampled for each time point. We assume the pol-II noise variance is a constant ${\sigma }_p^2$ inferred as a parameter of the model. The mRNA noise variances for each time point are sums of a shared constant ${\sigma }_m^2$ and a fixed variance inferred by BitSeq by combining the technical quantification uncertainty from BitSeq expression estimation with an estimate of biological variance from the BitSeq differential expression model (full details are in the SI Appendix).

Given the differential equation parameters, GP inference yields a full posterior distribution over the shape of the pol-II and mRNA functions $p\left(t\right)$ and $m\left(t\right)$. We infer the differential equation parameters from the data using MCMC sampling, which allows us to assign a level of uncertainty to our parameter estimates. To infer a full posterior over the differential equation parameters ${\beta }_0$, β, α, $\mathrm{\Delta }$, $m_0$, and $E\left[p_0\right]={\mu }_p$, the observation model parameters ${\sigma }_p^2$ and ${\sigma }_m^2$ and a magnitude parameter $C_p$ and width parameter l of the GP prior, we set near-flat priors for the parameters over reasonable value ranges, except for the delay $\mathrm{\Delta }$, whose prior is biased toward 0 (exact ranges and full details are presented in the SI Appendix). We combine these priors with the likelihood obtained from the GP model after marginalizing out $p\left(t\right)$ and $m\left(t\right)$, which can be performed analytically. We infer the posterior over the parameters by Hamiltonian MCMC sampling. This full MCMC approach uses gradients of the distributions for efficient sampling and rigorously takes uncertainty over differential equation parameters into account. Thus, the final posterior accounts for both the uncertainty about differential equation parameters and uncertainty over the underlying functions for each differential equation. We ran four parallel chains starting from different random initial states for convergence checking using the potential scale reduction factor ref. 21. We obtained 500 samples from each of the four chains after discarding the first half of the samples as burn-in and thinning by a factor of 10. Posterior distributions over the functions $p\left(t\right)$ and $m\left(t\right)$ are obtained by sampling 500 realizations of $p\left(t\right)$ and $m\left(t\right)$ for each parameter sample from the exact Gaussian conditional posterior given the parameters in the sample. The resulting posteriors for $p\left(t\right)$ and $m\left(t\right)$ are non-Gaussian and are summarized by posterior mean and posterior quantiles. Full details of the MCMC procedure are in the SI Appendix.

Filtering of Results.

Genes satisfying the following conditions were kept for full analysis (full implementation details of each step are in the SI Appendix): (i) $p\left(t\right)$ has the maximal peak in the densely sampled region between 1 min and 160 min; (ii) estimated posterior median delay is less than 120 min; and (iii) $p\left(t\right)$ does not change too much before t = 0 min to match the known start in steady state.

Analysis of the Gene Annotation Features Associated with the Delays.

Ensembl version 68 annotations were used to derive features of all genes. For each annotated transcript, we computed the total pre-mRNA length m as the distance from the start of the first exon to the end of the last exon and the lengths of all of the introns. Transcripts consisting only of a single exon (and hence no introns) were excluded from further analysis. For each gene, we identified the transcript with the longest pre-mRNA and used that as the representative transcript for that gene. The final intron share f was defined as the length of the final intron of the longest transcript divided by m.

Pre-mRNA End Accumulation Index.

For this analysis, we only considered reads aligning uniquely to pre-mRNA transcripts and not to any mRNA transcripts. We counted the overlap of reads with 200-bp bins starting from the beginning of the first exon of each gene ending with the last nonempty bin. We compute the fraction $r_{e,i}$ of all reads in the latter half of bins in each sample i and define the index as the difference of the means of $r_{e,i}$ over late time points (80–320 min) and over early time points (10–40 min).

Availability.

Raw data are available at GEO (accession no. GSE62789). A browser of all model fits and delay estimates is available at www.cs.helsinki.fi/u/ahonkela/pol2rna/. Code to reproduce all of the experiments is available at https://github.com/ahonkela/pol2rna.