Abstract
This article describes the application of a change-point algorithm to the analysis of stochastic signals in biological systems whose underlying state dynamics consist of transitions between discrete states. Applications of this analysis include molecular-motor stepping, fluorophore bleaching, electrophysiology, particle and cell tracking, detection of copy number variation by sequencing, tethered-particle motion, etc. We present a unified approach to the analysis of processes whose noise can be modeled by Gaussian, Wiener, or Ornstein-Uhlenbeck processes. To fit the model, we exploit explicit, closed-form algebraic expressions for maximum-likelihood estimators of model parameters and estimated information loss of the generalized noise model, which can be computed extremely efficiently. We implement change-point detection using the frequentist information criterion (which, to our knowledge, is a new information criterion). The frequentist information criterion specifies a single, information-based statistical test that is free from ad hoc parameters and requires no prior probability distribution. We demonstrate this information-based approach in the analysis of simulated and experimental tethered-particle-motion data.
Introduction
The problem of determining the true state of a system that transitions between discrete states, and whose observables are corrupted by noise, is a canonical problem in statistics with a long history (e.g., Little and Jones (1)). The approach we discuss in this article is called “change-point analysis” and has been applied widely (1–5), including previous applications to single-molecule biophysics problems (6–10). We have recently developed an information-based approach to model selection, one that is new to our knowledge: the frequentist information criterion (FIC), an approach that greatly simplifies the analysis (C. H. LaMont and P. A. Wiggins, unpublished). This approach reconciles two previously disparate approaches (information-based versus frequentist), and fixes a series of flaws with previous applications (C. H. LaMont and P. A. Wiggins, unpublished).
From an information-theoretic perspective, model selection is performed by minimizing estimated information loss. FIC provides a single, objective statistical test for the existence of a change point that greatly simplifies the statistical analysis of change-point problems. A detailed development and description of this theory is too long to include here and is therefore described elsewhere (C. H. LaMont and P. A. Wiggins, unpublished). The primary goal of this article is to provide an explicit example of the application of this information-based approach to both simulated and experimental data to demonstrate the power of information-based inference in a biophysical context.
The article is organized as follows: we define an explicit noise model applicable to many biophysical systems and introduce the information criterion. We then present the application of these results to experimental tethered-particle-motion (TPM) data. The application of change-point analysis to simulated TPM data is presented in the Supporting Material. The development of the theory, the computation of the FIC approximation of the complexity, and the applications of change-point analysis to other biophysical systems are discussed in C. H. LaMont and P. A. Wiggins (unpublished).
Materials and Methods
A noise model for biophysical signals
We begin by making three broad assumptions about the character of the noise in a given state: 1) the probability distribution describing the noise is approximately Gaussian, 2) the noise is Markovian, and 3) the parameters describing the noise are stationary (time-independent). The Markovian property dictates that the probability distribution of the ith measurement depends only on the last measurement (i − 1) and no other proceeding measurements. (Note that we do not expect any of these conditions to be met exactly in a true experiment. These assumptions can and should be checked experimentally. We will give examples below of experimental data where we explicitly demonstrate that these assumptions are weakly and strongly violated.) When the three criteria listed above are met, the observations can be modeled by the discrete stochastic time-evolution equation, as
| (1) |
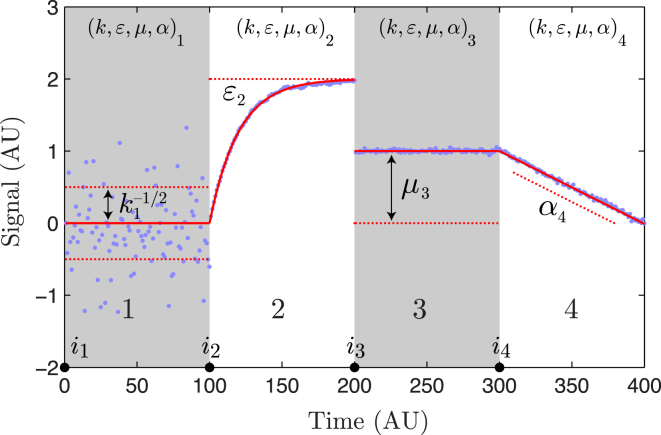
where the stochastic processes are parameterized by the parameter vector , and the values are independent D-dimensional, normally distributed random variables with zero mean and unit variance for each component of the vector. The parameter k is the stiffness, which parameterizes the standard derivation of the noise; ε is the nearest-neighbor coupling and parameterizes the statistical correlation between the ith and the (i − 1)th observations; μ is the level mean; and α is the level slope in time. (Of course it is possible to give the level means a more complicated time dependence than a constant slope, but this form is sufficient to analyze many problems. Another important generalization is to make k- and ε-tensors. It is straightforward to extend the results for these generalized models.) Finally, i∗ is a redundant parameter added for convenience and is analogous to putting the equation for a line in point-slope form. The role of these parameters in shaping the noise is illustrated schematically in Fig. 1. The noise parameters θ would be called “emission parameters” in the context of a hidden Markov model (11).
Figure 1.
State model schematic. The state model signal is characterized by four model parameters that are written as the vector θ ≡ (k, ε, μ, α). Above, we schematically illustrate the role of each parameter in shaping the signal. The parameter k, state 1, parameterizes the standard deviation of the noise (σ = k−1/2). State 2 illustrates the effect of the finite lifetime of fluctuations in models with autoregression (0 < ε < 1). State 3 illustrates the role of the level mean μ. State 4 illustrates of the role of the level slope (α). To see this figure in color, go online.
Now we define a model for the signal corresponding to a system transitioning between a set of discrete states. We define the discrete time index corresponding to the start of the Ith state as iI. The model parameters describing the noise in the Ith interval are θI. Together these two sets of parameters (iI and θI) parameterize the model . The model parameterization for the signal (including multiple states) can then be written explicitly as
| (2) |
where n is the number of states. By definition, we set i1 ≡ 1. The dependence of the model on these two sets of parameters (θI and iI) is fundamentally different. The noise model parameters θI are continuous harmonic parameters. (Note that harmonic parameters have the property that the likelihood is well approximated by a Gaussian distribution about the maximum likelihood estimator (C. H. LaMont and P. A. Wiggins, unpublished) because they always have nonzero Fisher information (C. H. LaMont and P. A. Wiggins, unpublished).) By contrast, the change-point indices iI are discrete and typically nonharmonic parameters. These properties will have important consequences for model selection (C. H. LaMont and P. A. Wiggins, unpublished).
The model dimension
A critical consideration for analysis will be the dimension of the model. The most important dimension will be the dimension of an individual state. At this point, it is important to make the distinction between two types of model parameters, i.e., local and global. For instance, if we set , we will model a system with global parameter values (global is state-independent) of ε and , and local parameter values (local is state-dependent) of k and . In spatial dimension D, the parameters k and ε have dimension 1 because they are scalars, whereas and both have dimension D because they are vectors. In this example, the dimension of the model for an individual state is where d is identical for all states (if there is only a single state, there is no distinction between local and global parameters, i.e., d = dM, as defined below), and therefore does not need a subscript I. Due to their discrete nature, the change-point indices do not contribute to the parameter counting for the model dimension. (The failure of the change-point indices to contribute to the model dimension is not universally true under all scenarios. For long-lived states with very small changes in the model parameters, the change-point index does become effectively continuous, which will therefore contribute to the state dimension (C. H. LaMont and P. A. Wiggins, unpublished).)
The likelihood and information
The likelihood of model , with parameterization Θ given observations X, is defined to be the probability density of observing X in the model parameterized by Θ, as
| (3) |
where X is short-hand notation for the ordered list of observations , Q is the probability density of observations X, and is the model parameterized by parameters Θ. (We give explicit analytic formulas for Q in the Supporting Material.) It is most convenient to work in terms of the encoding information, defined as the minus-log likelihood,
| (4) |
which can be interpreted as the information required (see C. H. LaMont and P. A. Wiggins, unpublished, for a more in-depth explanation of this statement), in natural units of information (Nats), to encode the observations X given a model parameterized by Θ. Model predictivity is measured most naturally by the Shannon cross entropy for N observations,
| (5) |
where X is the expectation over observations X taken with respect to the true probability distribution of the observed stochastic process (C. H. LaMont and P. A. Wiggins, unpublished).
The information and entropy are understood in this context as follows: the information is understood as the number of characters (information) required to encode a particular observed data-set X using the model to some specified precision. If the model is perfectly predictive, no additional information is required to encode the observations X. The average amount of information to encode N observations is the entropy (e.g., see C. H. LaMont and P. A. Wiggins, unpublished). Naturally, the information h is said to be an estimator of entropy H.
Model fitting by maximum likelihood
To fit the model, we use a maximum-likelihood procedure. The maximum-likelihood procedure selects the model parameters that maximizes the likelihood (and equivalently minimizes the information) with respect to the model parameters,
| (6) |
| (7) |
where the hat on the parameters denotes that they are the maximum likelihood estimators (MLEs) of the information and model parameters. We can divide the optimization processes for change-point analysis into two coupled steps: 1) determining the model noise parameters (θI) given a set of change-point indices (iI), and 2) determining the change-point indices themselves. The first step is computationally trivial: we derive explicit algebraic equations for the MLEs of the continuous parameters, which are convex given any set of change-point indices iI. (See the Supporting Material for the explicit expressions.) This operation is order N computationally.
In contrast, the optimization of the change-point indices themselves is nonconvex and must be performed numerically. A simultaneous optimization of n + 1 states would require the computation of roughly Nn/n! sets of MLE parameters. To simplify the optimization problem, we use a greedy binary-segmentation algorithm that is applied recursively to each segment, subdividing segments until the model selection criterion is satisfied. This procedure is generically referred to as “model nesting”. The algorithm is described in Box 1. The nesting procedure of optimizing with respect to the position of a single change-point index only requires the computation of order N MLEs. Because the MLE parameters can be computed algebraically, the greedy optimization process is computationally trivial and extremely rapid.
Box 1. Greedy Binary-Segmentation Algorithm.
-
1)
Initialize the change-point vector: i ← {1}
-
2)Segment model
-
a)Compute the entropy change that results from all possible new change-point indices j:
(8) -
b)Find the minimum entropy change Δhmin, and the corresponding index jmin.
-
c)If the entropy change plus the nesting complexity is <0:
(9) - Then accept the change point jmin.
-
i)Add the new change point to the change-point vector:
(10) -
ii)Segment model
-
i)
-
d)Else terminate the segmentation process.
-
a)
A schematic description of the greedy algorithm for determining change-point indices. The nesting complexity is defined as the difference in the complexity on model nesting: k_ ≡ Kn+1 – Kn. In the expressions above, the information estimator is evaluated at the respective MLE parameters given the change-point indices i.
Model selection and the information criterion
One might hope to estimate the size of the model, corresponding to the number of states n, using the ML procedure, but this procedure is flawed in the following sense: additional parameters always increase the likelihood due to overfitting. The solution we advocate can intuitively be understood as maximum predictivity (C. H. LaMont and P. A. Wiggins, unpublished). In maximum predictivity, one does not optimize the likelihood of observing the data-set fit in the ML procedure, but rather the probability of unobserved data generated by the same stochastic process. This modified procedure can be understood as minimizing an information criterion, an approximation for the unbiased estimator of the entropy (12). The canonical information criterion is called the “Akaike information criterion” (AIC) (12,13). It has long been appreciated that AIC fails to correctly estimate the bias in the context of change-point analysis. We recently demonstrated that this failure is due to the presence of unidentifiable parameters (e.g., Watanabe (14)).
We have proposed an information criterion, the FIC, which accounts for parameter unidentifiability (C. H. LaMont and P. A. Wiggins, unpublished). FIC is defined as
| (11) |
where is intuitively understood as a complexity function that penalizes the addition of new parameters but is rigorously defined as the bias in the estimator of the cross entropy. (Note that this complexity is analogous to the AIC complexity, but the FIC complexity is evaluated using an approximation that is more generally applicable, including in the context of singular models.)
The power of the information-based approach is as follows: naïvely, one might expect to have to compute the complexity for the entire range of possible parameter values (e.g., Kerssemakers et al. (8)). This is not the case for change-point analysis. Surprisingly, the complexity K has a generic asymptotic form that depends only on the number of observations and the dimension of the model, greatly simplifying the analysis. This change-point complexity can be estimated analytically or computed numerically via Monte Carlo (C. H. LaMont and P. A. Wiggins, unpublished). The analytic limit can be related to the extrema of discrete-time Brownian bridges in d dimensions (C. H. LaMont and P. A. Wiggins, unpublished).
The optimal model, which maximizes the expected model predictivity, is the model that minimizes FIC:
| (12) |
Again, the power of the information-based approach is clear: the comparison of the information criterion (FIC value) can be made between any two models (as long as FIC is computed with respect to the same data-set X), regardless of differences in the model parameterization or the number of model parameters (12). The numerical minimization of FIC using the algorithm described above is effectively instantaneous, facilitating the exploration of many possible model realizations with minimal effort, as we will demonstrate below.
Results
Change-point analysis applied to tethered particle motion
In this section, we apply the change-point algorithm to a biological problem. In the interest of brevity, we will consider the analysis of one specific example: experimental tethered-particle-motion (TPM) data in the main text. We analyze TPM data because it provides a rich signal, which incorporates three of the four parameters that we have introduced into our state model, while remaining an in vitro experiment. To demonstrate the breadth of applicability of the change-point algorithm, we present the analysis of three other problems (single-molecule-bleaching analysis, molecular-motor-stepping analysis, and the analysis of cell motility) in C. H. LaMont and P. A. Wiggins (unpublished).
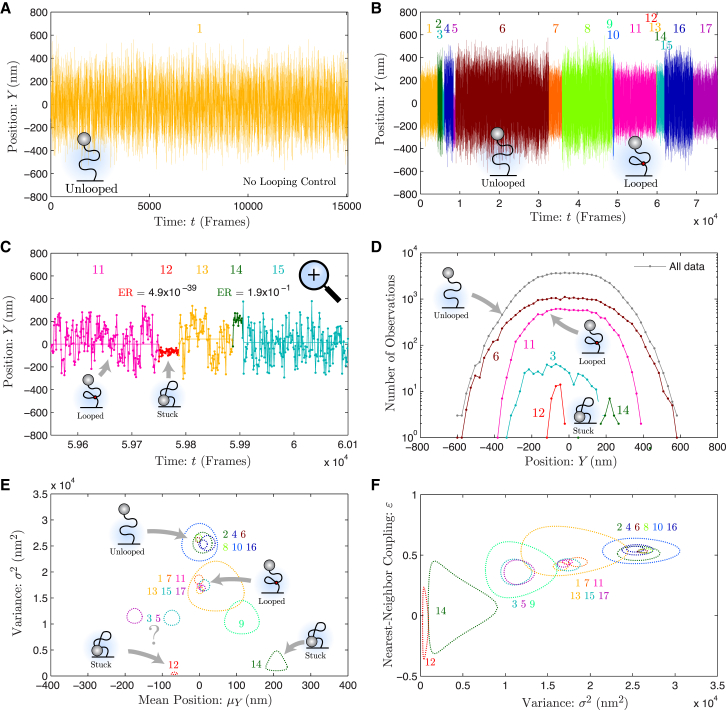
Finzi and Gelles (15) developed the TPM experiment to observe DNA looping with single-molecule resolution. In the assay, beads are immobilized to a coverslip using DNA tethers a few kilobytes in length. The DNA tether behaves like a spring, confining the motion of the bead that undergoes the tethered Brownian motion. The longer the DNA tether is, the larger the typical Brownian excursions of the bead from its average position. Protein-induced DNA looping reduces the effective length of the tether and therefore changes the character of the bead motion. The effective tether length is inferred by the analysis of the bead trajectory. The configuration (looped versus unlooped) is then inferred from the effective DNA tether length. See the schematic in Fig. 2 B.
Figure 2.
Analysis of experimental TPM data: protein-induced DNA looping measured by TPM. (A) Position trace for the no-looping control. The y position of the bead shown for 1.5 × 104 frames. In the absence of protein-induced looping, only a single state is identified by change-point analysis, corresponding to the unlooped configuration. (B) Position trace for protein-induced DNA looping. The y position of the bead shown for 7.5 × 104 frames. Seventeen states were identified by change-point analysis. The trace is colored by state and the state number is shown above the trace. A representative example of the unlooped and looped state is shown. (C) High-resolution time trace. At t ≈ 5.98 × 104 frames, a high-time-resolution trace is shown, which reveals two short-lived states, states 12 and 14. The ER for each of these states is shown. The statistical evidence for state 12 is extremely strong whereas the evidence for state 14 is marginal. (D) Histogram of bead position by state. The histogram for all data and selected states is shown. States 6 and 11 are representative of the unlooped and looped states, respectively. Neither state is well approximated by a Gaussian distribution, as demonstrated by the flatness of the peak of the probability density functions. (E) Mean position and variance by state. The 95% confidence region is shown for each state. The states cluster into two clearly identifiable groups corresponding to the unlooped (2, 4, 6, 8, 10, and 16) and looped (1, 7, 11, 13, 15, and 17) states. In addition to these clusters, there are low-mobility and moderate-mobility states with mean positions offset from zero. The short-lived states with low mobility correspond to sticking events (12 and 14). (F) Variance and nearest-neighbor coupling by state. The 95% confidence region is shown for each state. Again, the states form clusters analogous to (E). For states 12 and 14, ε is approximately zero, consistent with bead sticking. To see this figure in color, go online.
Application to simulated data
In the Supporting Material, we model simulated data to demonstrate the performance of the technique because we can check the fit model against the true simulated model. Not only is the truth known, but the true model is one of the candidate models. In short, the analysis demonstrates that: 1) The change-point algorithm analysis of simulated data accurately estimates the change-point index positions. 2) The change-point algorithm analysis of simulated data accurately estimates the noise model parameters in each state. 3) The information criterion correctly identifies which parameters are global (equal for all states) versus local (at least one distinct value among the states) in our simulated model. 4) FIC predicts that the most predictive model is a model in which all the states can be identified or clustered into two sets of states with identical parameters corresponding to the looped and unlooped states, exactly as simulated. A detailed description of these simulations is presented in the Supporting Material.
Application to experimental data
It is important to note that the existence of a true model exactly equal to one of the candidate models is an unrealistic convenience of simulated data. In practice, experimental data is always extremely complex and TPM data is no exception. Therefore, the application of change-point analysis to experimental data is a more important and an interesting test of the techniques discussed in this article.
We apply the change-point analysis to experimental data from the lab of D. Dunlap (Emory University, Atlanta, GA). The data captures the DNA looping dynamics of the lac repressor (LacI) with a 2231-bp DNA construct and a 320-nm-diameter bead. On loop formation, the loop size is 1200 bp and residual DNA tether length is 1031 bp. We show two data sets in Fig. 2: in Fig. 2 A, we show the y-position trace for the no-protein control for 1.5 × 104 frames. In Fig. 2 B, we show the y-position trace for the protein-induced DNA looping for 7.5 × 104 frames. The frame delay in both data sets is 20 ms.
As a first step in the data analysis, we need to determine which family of nested change-point models to analyze. We set the level slope α = 0 by hand. Now, we need to determine whether to fit the remaining parameters (k, ε, and μ) as local (L) or global (G) parameters. We perform change-point analysis for each possibility: in each case, we minimize FIC for the family of nested models to find the optimal model in the model family. We use an ordered triplet of L and G parameters to label a model family to denote whether the parameter vector (k, ε, and μ) is described by local or global parameters in the state model. For instance, LGL describes a model with local values of k and μ, but a global value for ε. Note that the relation between the discrete time parameters (k, ε, and μ) and the underlying physical parameters is discussed in the Supporting Material.
Once the family optimum model has been determined, we record the FIC value for this model, which is the unbiased estimate of information loss. We also consider a model that is constrained to be a Gaussian process (ε = 0) rather than Ornstein-Uhlenbeck, with a global mean (model L0G) because this was essentially the model employed by Manzo and Finzi (10). A summary of the analysis of the simulated data is shown in Table 1. The FIC values have a large constant offset and therefore only the FIC values relative to the minimum FIC value (ΔFIC) are shown in the table. The model with the lowest FIC is the model with the strongest statistical support. The relative difference between the FIC values for each model encodes the relative strength of the statistical support for the model (remember that because this is a likelihood-based measure, the absolute scale of the likelihood has no meaning, and therefore it cannot be understood as a statistical test of the model).
Table 1.
Model selection for experimental TPM data
| Model M (k, ε, μ) | Information Criterion ΔFIC (Nats) | Number of States n | Parameters per State d |
|---|---|---|---|
| L0G | 22,920 | 11 | 1 |
| GLG | 1977 | 7 | 1 |
| GGL | 1975 | 7 | 1 |
| GLL | 1833 | 9 | 3 |
| LGG | 691 | 13 | 1 |
| LGL | 364 | 15 | 3 |
| LLG | 355 | 13 | 2 |
| LLL, clustered | 35 | 17 | 4 |
| LLL | 0 | 17 | 4 |
We considered eight families of models where the parameters k, ε, and μ were either optimized locally for each state (L) or globally for all states (G). For each family of models, the FIC value for the optimal model is shown. The large FIC values for all but the all-local model (LLL) offer strong statistical support for changes in all model parameters between states. Unlike the simulated data, the parameters describing the states corresponding to the looped and unlooped configurations are statistically distinct because the IC value for the clustered model is larger than the value for the LLL model.
Our initial expectation (as simulated) was that both the mean bead position and the stiffness k, which parameterize the diffusion coefficient at high time resolution, would be global parameters while ε, which is controlled by the tether length, would be a local parameter. To our surprise, only models with local parameters for k, ε, and (LLL) resulted in acceptable information criterion, despite incurring a larger complexity for adding states for all local parameters. The large information criterion for all models except the LLL model imply that at least some of the states violate our assumption that the diffusion constant and mean bead positions are constant throughout the experiment. We will examine both the experimental data and the LLL model in detail to understand this failure. The L0G model (similar to that employed by Manzo and Finzi (10)) leads to the largest information loss of the models considered. Despite the poor fit, it does identify all sufficiently long-lived states, but misses short-lived states and leads to oversegmentation due to a failure to correctly model the correlation between successive bead positions. This model also does not identify bead-sticking events, which typically have a mean position offset. (Note that in this data set, the lifetime of the fluctuations, as parameterized by ε, is sufficiently short as to not result in the identification of many false-positive states. If the frame rate was significantly increased or a larger bead was used at the same frame rate, the oversegmentation described for the simulated data would occur in the experimental data.)
The data and the LLL model are shown in Fig. 2. Fig. 2 A shows the analysis of the no-protein control, where the bead should only be found in the unlooped configuration. This control is critical in the context of the experimental data to demonstrate that the change-point analysis does not identify nonexistent states. Because the true distribution was known for the simulated data, this control was not required in the analysis of the simulated data. As expected, no change points were detected in the no-protein control, consistent with the algorithm successfully rejecting false-positive states.
Fig. 2 B shows the y-position trace for protein-induced DNA looping. Although this data may qualitatively appear similar to the simulated data, it is significantly more complex: 17 states were determined by change-point analysis and the trace is colored by state with the corresponding state number plotted above the trace. The characteristics of the 17 states are varied not only in the state parameters but in the state lifetimes.
Fig. 2 C shows a high time-resolution y-position trace in which two short-lived states were identified (states 12 and 14). One immediate concern is whether these states are the result of stochastic fluctuations rather than true transitions. We apply simple statistical metric to answer this question: the evidence ratio (ER) (12), which is described in the Supporting Material. In short, the ER is the ratio of the model likelihood in the absence of the state over the model likelihood in the presence of the state corrected for bias; therefore, a small ER for a state corresponds to strong statistical support. The ER values for each state are plotted in Fig. 2 C. State 12 shows extremely strong statistical support whereas the support for state 14 is much weaker. We shall discuss the physical significance of these states in more detail shortly.
Fig. 2 D shows the y-position histograms for all data and selected states. States 6 and 11 are representative of the unlooped and looped states, respectively. Compared with the histogram of the simulated data, it is immediately clear that the experimental probability distributions are too flat to be Gaussian probability distributions. This is an explicit example of the added complexity of the analysis of experimental data. We show the histograms for three other states (3, 12, and 14), two of which we have already discussed. All three of these states show a significant offset from the mean position of the majority of the data (μy ≈ 0 nm nm). Although states 12 and 14 show low mobility, state 3 shows an intermediate mobility between state 12 and the looped states.
Fig. 2, E and F, shows the model parameters plotted by state. The dotted lines represent 95% confidence regions computed with respect to the model parameters (k, ε, and μ). As modeled in the simulated data, there are two well-defined clusters of states corresponding to the unlooped {2, 4, 6, 8, 10, 16} and looped {1, 7, 11, 13, 15, 17} states, but there appears be at least one additional loose cluster. States 12 and 14 are clearly consistent with bead-sticking events: 1) The variance (k−1) for both states is small. 2) The mean position is offset from zero. 3) The nearest-neighbor coupling is consistent with zero (remember that in the limit where the relaxation time of the bead position is shorter than the frame delay, ε goes to zero, whereas in the limit that the relaxation time is infinite, the motion is diffusion-dominated and ε goes to one). States 3, 5, and 9 appear neither to be stuck, nor to exhibit the expected motion about a mean position of zero. It is therefore likely that the tether is stuck to the coverslip, both shortening the tether and shifting the equilibrium position. Interestingly, these transitions always occur during the unlooped state. Because the no-protein data does not show any such states, it appears likely that this adhesion (sticking) is protein-mediated.
State clustering
In analogy with the simulated data, we now propose a model in which the looped and unlooped state clusters are described by the same model parameters, respectively. We constrain these parameters to be equal over the states in each cluster (as defined above). The resulting model (LLL-clustered) leads to an increase in the FIC, suggesting that in fact not all states in these proposed clusters can be described by the same parameters. Again, these observations reveal that the experimental true distribution is far more complex than the simulated model.
Discussion
In the previous section, we applied FIC to determine the optimal models for experimental TPM data by minimizing the estimated information loss. Simulated TPM data is discussed in the Supporting Material. The analysis of both simulated and experimental data demonstrated both the ability of the model selection approach to eliminate unnecessary parameters (in the context of the simulated data) while retaining necessary parameters (in the experimental context). The analysis provides clear statistical evidence for a complexity in experimental data which, to date, has been mostly overlooked. Our central focus is not on the data we have discussed in the article, but rather to demonstrate an analytical tool (change-point analysis with FIC model selection) that we believe will be widely applicable to biophysical and cell biology problems.
A number of competing methods have been used to analyze TPM data: half-amplitude thresholding (16–18), hidden Markov models (19,20), and variational Bayes (21). Indeed, our work is not the first application of the change-point analysis to TPM data: in 2010, Manzo and Finzi (10) performed a beautiful analysis that harnessed some of the advantages of change-point analysis. Our analysis improves upon the published change-point analysis in three respects: 1) We improve the resolution of the analysis by analyzing more of the experimental information by approximating the underlying physics with a better microscopic model. 2) The improved model results in the statistical inference of more physically relevant model parameters: the diffusion constant and the relaxation time for each state identified by the analysis, as well as the level means that correspond to the tether location. 3) Finally, because our analysis is based on an information criterion, rather than explicit individual likelihood ratio tests, the analysis of the statistical significance of the results is dramatically simplified.
As described above (L0G Model), Manzo and Finzi (10) previously used a change-point analysis to analyze TPM data, approximating the process as Gaussian (rather than Ornstein-Uhlenbeck) with a global mean. Clearly, there are two very important shortcomings of analysis with the incorrect noise model: 1) As we demonstrated above, the determination of both the local diffusion constant (variance) and local mean position allows sticking event to be resolved and identified. 2) As most clearly demonstrated in the analysis of the simulated TPM data in the Supporting Material, the failure to correctly model the correlations among bead positions (in an Ornstein-Uhlenbeck process) can lead to severe oversegmentation of the data. Therefore, the use of FIC and the correct Ornstein-Uhlenbeck noise model significantly improves the analysis.
But, it is important to note that even when the underlying physical model is not correct in detail, the analysis can still result in strong statistical inferences. For instance, if the TPM experiment really was well approximated by an Ornstein-Uhlenbeck process, the histogram for the individual states would be Gaussian. In fact, the probability distributions corresponding to individual states are clearly poorly approximated by Gaussian distributions. The relative stability of the method to nonideal data is an important quality because true experimental processes are generically much more complicated than the simulated distributions that are typically invoked to test algorithms (12). It is therefore natural to ask why the Gaussian process approximation described in the previous paragraph leads to significant information loss, while the difference in the modeled and observed distribution functions is benign. The key differentiator is the effective temporal duration of the model-violating fluctuations. The Gaussian process approximation failed because the bead relaxation time was long enough for the change-point algorithm to model the physics with additional states (in the Gaussian process model), whereas the temporal duration of the distribution-function-violating perturbations is much too short to result in oversegmentation. If the true distribution function for the TPM process had very long tails, there would be very long-lived model-violating fluctuations and the change-point algorithm (using the Ornstein-Uhlenbeck approximation) would lead to oversegmentation of the data. In this case, a more complicated analysis would be required.
The surprising feature of the TPM analysis was the diversity of states detected and the failure of these states to be clustered into a small number of statistically identical states (corresponding to looped and unlooped configurations). Had we designed a model based on our physical intuition, we might not have included this possibility. A strength of our approach is the low computational cost of our algorithm, which facilitated a less-biased approach whereby we considered a large number of candidate models. We expect the data from in vivo experiments to be less ideal still. Cells may switch between behaviors that are approximately discrete in nature, but in reality the system is transitioning between states that are all distinct and cells never truly transition back to an identical state. Change-point analysis is well suited to these problems because the algorithm does not use the trajectory history, except locally, when determining statistical support for a transition. This is not to say that building a quantitative model for the system does not require the clustering of states. On the contrary, we suggested such a clustering in order to interpret the TPM data. In the context of our analysis, we first studied the distribution of state parameters that resulted from the change-point analysis and then made a decision about how to cluster the states, which was informed both by the distribution of parameters and by our biophysical knowledge of the system. A large number of distinct states is probably generically justified for biological problems.
Competing techniques
In short, change-point analysis using FIC model selection has many practical advantages over existing tools. As we have already discussed, our implementation of change-point analysis leads a significant reduction in information loss in the context of TPM analysis than the previous implementation proposed by Manzo and Finzi (10), and is much more generally applicable than previous approaches (e.g., Watkins and Yang (6) and Kalafut and Visscher (9)).
The Bayesian information criterion (BIC), which can be understood as the weak-prior limit of a Bayesian approach, has recently been used for a biophysical change-point application by Kalafut and Visscher (9). BIC is already known to be an asymptotic result that is applicable only at large N (22), but it is particular poorly suited to the change-point problem because the BIC complexity is too small for small N and much too large for large N, and therefore it is difficult to recommend this approach under any circumstance. (See the Supporting Material.)
Little, Jones, and co-workers (1,5,23,24) have recently introduced a number of convex methods closely related to change-point analysis. Although convexity is clearly a desirable property of an algorithm, the mathematical meaning of the convexified optimization is less clear. Furthermore, the regularization constant (the complexity) in these techniques is an adjustable parameter. Therefore these analyses are subject (in principle) to the value of an ad hoc regularization constant. In FIC, the complexity, although an approximation, is rigorously defined in terms of the bias of the estimator of the cross entropy, and is therefore not an adjustable parameter.
Hidden Markov models (HMM) provide a powerful approach to the analysis of systems that transition between states with unknown emission spectrums (e.g., Rabiner (11)). Like the change-point algorithm, a maximum likelihood approach to HMMs is also subject to the problem of overfitting, but a Bayesian approach is free from these shortcomings. For that reason, a significant number of authors have either undertaken a fully Bayesian HMM analysis (e.g., Johnson et al. (21), and references therein) or invoked Bayesian arguments implicitly by a maximum likelihood approach to HMM, coupled with BIC model selection (e.g., Greenfield et al. (25)). The Bayesian approach has a number of drawbacks: in general, Bayesian approaches to model selection have the disadvantage that they depend upon prior probability distributions for the model parameters (and models). Like the adjustable regularization constants for the convex methods, the Bayesian analysis is dependent, at least in principle, on the choice of prior probability distributions. We expect the fully Bayesian approach will not result in models that are optimally predictive, and in particular will result in underfitting for vague priors (C. H. LaMont and P. A. Wiggins, unpublished). In fact, the underfitting problem may be especially severe in the context of biophysical problems where, as we have demonstrated in the context of TPM, the assumption that the system returns to a state that is statistically identical to a previous state is flawed. Finally, even approximate Bayesian approaches, like variational Bayes, are computationally demanding.
Conclusions
We have developed an information-based approach to change-point analysis, which is computationally efficient, applicable, tractable, and statistically principled. As illustrated by applications to both experimental and simulated data, the approach is widely applicable to many important problems in biophysics and cell biology. In analogy to AIC, FIC is an approximation for the unbiased estimator of information loss. The proposed change-point model selection criterion can be rigorously understood as minimizing expected information loss, in analogy to the use of AIC in other contexts. We expect that this proposed information-based approach to change-point analysis will prove attractive to investigators who wish to use a statistically principled approach free from ad hoc parameters or prior probability distributions.
Author Contributions
P.A.W. designed research, performed research, contributed analytic tools, analyzed data, and wrote the article.
Acknowledgments
The author thanks C. LaMont for teaching him about information-based techniques; K. Burnham, J. Wellner, L. Weihs, and M. Drton for advice and discussions; D. Dunlap and L. Finzi for experimental data; and M. Lindén and N. Kuwada for advice on the manuscript.
This work was supported by National Science Foundation Molecular and Cellular Biosciences grant No. 1243492.
Editor: Fazoil Ataullakhanov.
Footnotes
Supporting Materials and Methods, two figures, and two tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)00552-4.
Supporting Material
References
- 1.Little M.A., Jones N.S. Generalized methods and solvers for noise removal from piecewise constant signals. I. Background theory. Proc. Math. Phys. Eng. Sci. 2011;467:3088–3114. doi: 10.1098/rspa.2010.0671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Page E.S. A test for a change in a parameter occurring at an unknown point. Biometrika. 1955;42:523–527. [Google Scholar]
- 3.Page E.S. On problems in which a change in a parameter occurs at an unknown point. Biometrika. 1957;44:248–252. [Google Scholar]
- 4.Chen J., Gupta A.K. On change point detection and estimation. Comm. Stat. Simul. Comput. 2007;30:665–697. [Google Scholar]
- 5.Little M.A., Jones N.S. Generalized methods and solvers for noise removal from piecewise constant signals. II. New methods. Proc. Math. Phys. Eng. Sci. 2011;467:3115–3140. doi: 10.1098/rspa.2010.0674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Watkins L.P., Yang H. Detection of intensity change points in time-resolved single-molecule measurements. J. Phys. Chem. B. 2005;109:617–628. doi: 10.1021/jp0467548. [DOI] [PubMed] [Google Scholar]
- 7.Montiel D., Cang H., Yang H. Quantitative characterization of changes in dynamical behavior for single-particle tracking studies. J. Phys. Chem. B. 2006;110:19763–19770. doi: 10.1021/jp062024j. [DOI] [PubMed] [Google Scholar]
- 8.Kerssemakers J.W.J., Munteanu E.L., Dogterom M. Assembly dynamics of microtubules at molecular resolution. Nature. 2006;442:709–712. doi: 10.1038/nature04928. [DOI] [PubMed] [Google Scholar]
- 9.Kalafut B., Visscher K. An objective, model-independent method for detection of non-uniform steps in noisy signals. Comput. Phys. Commun. 2008;179:716–723. [Google Scholar]
- 10.Manzo C., Finzi L. Quantitative analysis of DNA-looping kinetics from tethered particle motion experiments. Methods Enzymol. 2010;475:199–220. doi: 10.1016/S0076-6879(10)75009-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rabiner L.R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE. 1989;77:257–284. [Google Scholar]
- 12.Burnham K.P., Anderson D.R. 2nd Ed. Springer; New York: 1998. Model Selection and Multimodel Inference. [Google Scholar]
- 13.Akaike H. Information theory and an extension of the maximum likelihood principle. In: Petrov B.N., Csaki F., editors. 2nd International Symposium of Information Theory. Akademiai Kiado; Budapest, Hungary: 1973. pp. 267–281. [Google Scholar]
- 14.Watanabe S. Cambridge University Press; New York: 2009. Algebraic Geometry and Statistical Learning Theory. [Google Scholar]
- 15.Finzi L., Gelles J. Measurement of lactose repressor-mediated loop formation and breakdown in single DNA molecules. Science. 1995;267:378–380. doi: 10.1126/science.7824935. [DOI] [PubMed] [Google Scholar]
- 16.Colquhoun D., Sigworth B. Plenum Press; New York: 1983. Fitting and Statistical Analysis of Single-Channel Recording. [Google Scholar]
- 17.van den Broek B., Vanzi F., Wuite G.J.L. Real-time observation of DNA looping dynamics of type IIE restriction enzymes NaeI and NarI. Nucleic Acids Res. 2006;34:167–174. doi: 10.1093/nar/gkj432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Vanzi F., Broggio C., Pavone F.S. Lac repressor hinge flexibility and DNA looping: single molecule kinetics by tethered particle motion. Nucleic Acids Res. 2006;34:3409–3420. doi: 10.1093/nar/gkl393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Beausang J.F., Nelson P.C. Diffusive hidden Markov model characterization of DNA looping dynamics in tethered particle experiments. Phys. Biol. 2007;4:205–219. doi: 10.1088/1478-3975/4/3/007. [DOI] [PubMed] [Google Scholar]
- 20.Beausang J.F., Zurla C., Nelson P.C. DNA looping kinetics analyzed using diffusive hidden Markov model. Biophys. J. 2007;92:L64–L66. doi: 10.1529/biophysj.107.104828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Johnson, S., J. W. van de Meent, …, M. Lindén. 2014. Multiple Lac- mediated loops revealed by Bayesian statistics and tethered particle motion. ArXiv14020894 Phys. Q-Bio. [DOI] [PMC free article] [PubMed]
- 22.Kass R.E., Raftery A.E. Bayes factors. J. Am. Stat. Assoc. 1995;90:773–795. [Google Scholar]
- 23.Little M.A., Steel B.C., Jones N.S. Steps and bumps: precision extraction of discrete states of molecular machines. Biophys. J. 2011;101:477–485. doi: 10.1016/j.bpj.2011.05.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Little M.A., Jones N.S. Signal processing for molecular and cellular biological physics: an emerging field. Philos. Trans. A Math. Phys. Eng. Sci. 2013;371:20110546. doi: 10.1098/rsta.2011.0546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Greenfeld M., Pavlichin D.S., Herschlag D. Single molecule analysis research tool (SMART): an integrated approach for analyzing single molecule data. PLoS ONE. 2012;7:e30024. doi: 10.1371/journal.pone.0030024. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.