Maxwell’s Mixing Equation Revisited: Characteristic Impedance Equations for Ellipsoidal Cells

Abstract

We derived a series of, to our knowledge, new analytic expressions for the characteristic features of the impedance spectra of suspensions of homogeneous and single-shell spherical, spheroidal, and ellipsoidal objects, e.g., biological cells of the general ellipsoidal shape. In the derivation, we combined the Maxwell-Wagner mixing equation with our expression for the Clausius-Mossotti factor that had been originally derived to describe AC-electrokinetic effects such as dielectrophoresis, electrorotation, and electroorientation. The influential radius model was employed because it allows for a separation of the geometric and electric problems. For shelled objects, a special axial longitudinal element approach leads to a resistor-capacitor model, which can be used to simplify the mixing equation. Characteristic equations were derived for the plateau levels, peak heights, and characteristic frequencies of the impedance as well as the complex specific conductivities and permittivities of suspensions of axially and randomly oriented homogeneous and single-shell ellipsoidal objects. For membrane-covered spherical objects, most of the limiting cases are identical to—or improved with respect to—the known solutions given by researchers in the field. The characteristic equations were found to be quite precise (largest deviations typically <5% with respect to the full model) when tested with parameters relevant to biological cells. They can be used for the differentiation of orientation and the electric properties of cell suspensions or in the analysis of single cells in microfluidic systems.

Introduction

Impedance characterization is a common method in chemistry, colloid sciences, and biology (1, 2, 3, 4, 5, 6, 7, 8, 9). The persistent interest in characterizing suspensions of colloidal objects, biological cells, or tissues (10, 11, 12) calls for intuitive models and characteristic equations. Generally, the geometric and electric structures of the samples are too complex for a full analytical description by Maxwell’s equations. Mixing equations allow for deducing the effective properties of the suspended objects from the impedance properties of the suspension. In his treatise, Maxwell (13) derived a first expression for the static resistance of a dilute suspension of shelled spheres. Wagner (14) introduced complex specific conductivities into Maxwell’s theory and slightly simplified Maxwell’s mixing equation using a Taylor-series development in the particle concentration around zero concentration. Alternatively, the polarization effects governing the impedance properties can be modeled by numerical methods (15, 16, 17); however, the tremendous geometrical differences of the samples (mm-range), cell bodies (up to tens of μm), subcellular structures (μm- to nm-range), and the thickness of biological membranes (nm-range) call for a high number of mesh-elements and result in long computational times.

Resistor-capacitor (RC) networks are an ideal start-point to describe the impedance and the electric potential distributions of structured biological systems. In the 1920s of the last century, equivalent circuit diagrams had already been developed for the impedance of blood (18, 19). Networks of RC-pairs, i.e., parallel circuits of a resistor and a capacitor, can be considered a crude version of a numerical description of the passive electric properties of biological material. Usually, the precision of the models correlates to the number of elements used. Special models use a limited number of elements, e.g., in cubic arrangements of RC-pairs (3, 4, 20, 21, 22, 23, 24). Even though the models may allow for a qualitatively good description of experimental impedance data, they are usually too crude to allow for the extraction of the electric parameters of particle, cell, or tissue structures.

It was to the merit of H. P. Schwan to insist on the introduction of the media parameters into the RC-models to allow for the extraction of physiologically relevant properties such as cytoplasmic conductivity or membrane capacitance (25). His model was derived from a simplified analytical solution of Laplace’s equation for a spherical cell model (20, 26). It was also H. P. Schwan who proposed the search for passive RC-models for AC-electrokinetic effects such as the dielectrophoresis and electrorotation of cells (H.P. Schwan (deceased), University of Pennsylvania, personal communication, 1985). A first qualitatively correct RC-model unifying the impedance of cell suspensions, the induced transmembrane potential, dielectrophoresis, and electrorotation was developed by us in 1998 (27).

Neglecting magnetic properties, it started from RC-pairs describing any volume element of a homogeneous, isotropic medium. The resistor and capacitor values, R and C, of the (e.g., cubical) volume element are given by a geometry factor and the complex specific conductivity,

$${\sigma }^{\ast }=\sigma +j\omega {\epsilon }_0{\epsilon }_r,$$ (1)

where j, ε₀, and ω stand for (−1)^0.5, vacuum permittivity, and circular frequency, respectively. The values ε_r and σ are the relative permittivity and the specific direct current (DC)-conductivity of the medium, respectively. Here and in the following, complex parameters are designated by an asterisk.

Besides the correspondence of RC-pairs to the dispersion relation (Eq. 1) (5, 6, 27, 28), the success of the RC-models to describe suspensions of cells (6, 18, 20, 29) is based on the fact that the field inside a spherical homogeneous body is homogeneous and constant. This also applies to the so-called Maxwellian equivalent body of spherical objects with confocal shells (13). The Maxwellian equivalent body is a hypothetical homogeneous body showing the same polarization as the shelled object at a given frequency. Moreover, for a multishell spherical object the effective fields inside the spherical boundaries of every shell (30) are homogeneous and constant. Maxwell’s idea also applies to ellipsoidal objects (31, 32, 33) when all media in the model are described by complex isotropic or even anisotropic properties (34, 35, 36, 37, 38).

The properties of Maxwell’s equivalent body are the result of the structure of Laplace’s equation in combination with the used geometries (13, 33). Generally, the Laplace equation can be analytically solved for confocal surfaces of the second degree. Naturally, only closed, i.e., ellipsoidal, surfaces are of interest to describe the shapes of particles and biological cells. Depending on the problem, either potential or field distributions are considered to derive, e.g., the induced transmembrane potential or the dipole moment. It is especially simple to obtain these distributions for spherical objects or for an external field orientation in parallel to one of the principal axes of a spheroidal or ellipsoidal object (3, 39, 40). For the general orientation, the distributions of three orthogonal field components can be obtained by summing up their induced transmembrane potential components (41, 42, 43) or by a linear superposition of the induced dipole moment components (28). For the latter, the effective field for the whole object can be calculated from the frequency-dependent potentials at the three poles. These potentials represent the three constant field contributions inside the Maxwellian equivalent body along the principal axes of the ellipsoidal object (44). Please note that even though the resulting fields inside the cytoplasm or the equivalent body are constant, their orientation is not necessarily in parallel to the external field or to one another.

While the classical Laplace solution assumes isotropic membrane conductivity, the current conduction inside biological membranes is anisotropic because membranes are double-lipid layers with integrated ion-channel proteins (35, 36). The ion-channel pores are normally oriented with respect to the membrane surface, resulting in a membrane current that mainly flows perpendicular to the surface, i.e., for biological membranes, tangential currents inside the membrane can be neglected. Our axial longitudinal element (ALE) approach only considers membrane-conductivity contributions, which are oriented in parallel to the considered field component. Nevertheless, for the ionic membrane current, the argument holds that the anisotropic ion conductivity is correctly described at membrane sites in the vicinity of the considered pole, i.e., at sites with the highest contributions to the impedance of the suspension.

Another point is the different membrane thickness at the poles. While the thickness of a biological membrane is constant (∼8 nm for protein-rich membranes) closed analytical Laplace descriptions assume confocal surfaces, resulting in a thickness variation of the membrane for nonspherical objects (3, 4, 33, 44, 45). Poles of longer axes possess a thinner membrane-shell than poles with shorter axes. For objects with extreme axis ratios, e.g., elongated cells, some bacteria or colloids, the Laplace description may lead to larger errors.

Generally, field-induced force effects, such as deformation, orientation, dielectrophoresis, and electrorotation, all of which can be used to move, separate, trap, or manipulate objects or cells, are governed by the dipole moment (8, 10, 11, 17, 27, 30, 44, 46, 47). To describe the impedance of a suspension of monodisperse objects by mixing equations, it is sufficient to know the Clausius-Mossotti factor (CMF) of the suspended objects, which is the frequency-dependent term of their dipole moment. Sometimes the different research communities dealing with polarization effects of particles or biological cells were not aware of the work that had already been done in other communities dealing, e.g., with the impedance of suspensions (6), the physics of ponderomotive forces (48), dielectrics (49), meteorology (31), or AC-electrokinetics (50, 51).

Simplified expressions for the impedance of suspensions of ellipsoidal, spheroidal, or spherical cells, or objects with or without a single shell, are presented in Appendix A. Appendix B presents expressions for the characteristic frequencies of the suspensions, and Appendix C gives an overview on references of existing equations. The impedance behavior is analyzed introducing the ALE description for the CMF into Maxwell’s mixing equation (28, 44). Simplification of the RC schemes obtained from the ALE approach in certain frequency ranges allows us to easily obtain analytical solutions for certain features of the impedance spectra of the suspensions, such as plateau levels and characteristic frequencies.

Our equations can be used to differentiate variously shaped or oriented cells or colloids with differing electric properties in suspensions, as well as in single-cell analysis in microfluidic systems, e.g., by dielectrophoresis-activated cell sorting, etc. (12, 52, 53, 54). They may also describe the polarization of atmospheric dust particles by light (31). We think that the limiting cases of the equations, describing the limiting ratios of the relative polarizabilities of the external medium and the objects may be of technological relevance, e.g., for particles or droplets in gas or air streams (see air/fuel ratio), for particles in waste gases, or for gas bubbles in liquids (44, 55, 56).

Materials and Methods

General idea

Usually, the Laplace equation is solved for a given geometry assuming boundary conditions at the interfaces containing the actual electric properties of the media (3, 5, 29, 30). Here, we separate the geometric and electric problems using the limiting case of the Laplace solution for an ellipsoidal object of very low polarizability (vacuum) surrounded by a highly polarizable medium. For such an object the potentials induced by the external field at the three poles would be at maximum and solely determined by the object’s geometry. For a single-shell cell model, the actual potentials at the interfaces are determined by the electric properties of cytoplasm, membrane, and external medium as well as the field frequency. In our model, these three media form voltage-divider elements oriented along the three principal axes. The maximum possible pole-potentials depend on the length of the external medium elements. We designated the distances from the center of the ellipsoidal object of the three points at which the external medium elements grip the external potential influential radii (28). The three influential radii are related to the three depolarizing factors of an ellipsoidal body (44, 57, 58, 59, 60).

We define the orthonormal coordinate systems (x, y, z) with x, y, and z being oriented along the principal semiaxes a, b, and c of the ellipsoidal object. Along semiaxis a the influential radius is

$$a_{\text{inf}}=\frac{a}{1-n_{\text{a}}},$$ (2)

for the depolarizing factor n_a, and so on.

For a biological cell with a nonconductive membrane the maximum potentials at the three poles occurring for a vacuum object would be approached at low field frequencies. In this case, the potential at the pole of semiaxis a is

$$\left(\begin{array}{c}{a}_{\text{inf}}\\ 0\\ 0\end{array}\right)\overrightarrow{E}=\left(\begin{array}{c}{a}_{\text{inf}}\\ 0\\ 0\end{array}\right)\left(\begin{array}{c}{E}_{\text{a}}\\ E_{\text{b}}\\ E_{\text{c}}\end{array}\right),$$ (3)

i.e., the potential at the site of the pole in the absence of the object is increased by the maximum amplification factor a_inf/a (32). Please note that in the following all components of Eq. 3, as well as the semiaxes a, b, and c of the objects and variables derived thereof, e.g., ξ_a, ξ_b, and ξ_c (see Eq. 7), are considered as scalar components.

The mixing equation for suspensions

In chapter IX of his treatise, Maxwell derived an expression for the effective DC-resistance of “…a hollow sphere having a nucleus resistance k₁ surrounded by a shell of resistance k₂” (13). The effective resistance is that of a uniform homogeneous sphere of the radius of the outer surface, i.e., of Maxwell’s equivalent sphere. The fields inside a homogeneous sphere as well as inside the equivalent sphere of a shelled confocal object are homogeneous and constant. Maxwell derived an expression (see Eq. 4) for the static resistance of a dilute suspension of spherical objects using specific resistances of the media.

Substituting the specific resistances by specific complex conductivities (for simplicity designated “conductivity” in the following) for alternating currents, the well-known notation of the Maxwell-Wagner mixing equation can be obtained (14):

$$\frac{{\sigma }_S^{\ast }-{\sigma }_e^{\ast }}{{\sigma }_S^{\ast }+2{\sigma }_e^{\ast }}=p\frac{{\sigma }_p^{\ast }-{\sigma }_e^{\ast }}{{\sigma }_p^{\ast }+2{\sigma }_e^{\ast }}.$$ (4)

The indices S, e, and p refer to the whole suspension, the external medium, and the effective particle conductivities, respectively. Both, the left- and right terms of Eq. 4 resemble the structure of the CMF for a spherical object. The particle volume fraction p at the right term weighs the contribution of the particle-polarizabilities with respect to the polarizability of a larger suspension sphere (left term) containing a number of these objects (compare to Maxwell (13) and Wagner (14)). For spherical objects, the mixing equation (Eq. 4) is valid up to a maximum volume fraction of p = 10%.

In a suspension, the averaged conductivity is determined by a linear superposition of the contributions of each ellipsoidal object. For randomly oriented three axial objects, the three different CMFs along the three principal axes are evenly distributed in space. Therefore, each of the CMFs along the three axes contributes to the averaged conductivity of the suspension by one-third (3, 4, 61, 62). The CMFs can be introduced for the right term of Eq. 4 (3, 62),

$$\frac{3\left({\sigma }_S^{\ast }-{\sigma }_e^{\ast }\right)}{{\sigma }_S^{\ast }+2{\sigma }_e^{\ast }}=p\frac{1}{3}\sum _{\text{dir}=a,b,c}CM{F}_{\text{dir}}^{\ast },$$ (5)

where dir stands for the semiaxes a, b, or c oriented in the field direction. Please note the factor 3 in the left term. It stems from our CMF-definition, which conserves the volume term and can be easier expanded to nonspherical objects (28, 44).

The CMF for a homogeneous (Maxwellian equivalent-) ellipsoid in a direction can be expressed using fields or the potentials induced at the poles of the object, e.g., Ψ_a^∗ at the membrane surface at pole a (for details, see Gimsa and Wachner (28) and Gimsa et al. (33)),

$$CM{F}_a^{\ast }=\frac{1}{n_a}\left(\frac{E_a-E_{loc,a}^{\ast }}{E_a}\right)=\frac{1}{n_a}\left(\frac{{\Psi }_{0,a}-{\Psi }_a^{\ast }}{{\Psi }_{0,a}}\right),$$ (6)

where Ψ_0,a is the undisturbed potential at the site of the pole a in the absence of the object, i.e., $E_{\text{loc},a}^{\ast }={\Psi }_a^{\ast }/a$ and $E_a={\Psi }_{0,a}/a$ reflect the effective local field of the object and the external field strength, respectively. All above potentials refer to a potential of 0 V at the symmetry planes of the object without restriction in generality (Fig. 1 B).

Figure 1.

(A) Tilted top-side view sketching the shape relations of three spheroidal objects of the same volume with their symmetry axes c being vertically oriented. (Left and right top, and right bottom) Prolate, oblate, and spherical objects with axis ratios a/b/c of 1:1:5, 5:5:1, and 1:1:1, respectively (see Table 1). (B) Sketch of the chain of volume elements for the principle semiaxis a of an ellipsoidal object. The labels A, d, a, and a_inf are the cross-sectional area, membrane thickness, equatorial radius, and the influential radius in the a direction, respectively. The internal and external media and the membrane are marked by i, e, and m. The value E_a is the strength of the external field (component), which is oriented in the a direction. It induces a reference potential of 0 V at the symmetry plane and Ψ_a^∗ at pole a. In the absence of the object, Ψ_a^∗ changes to Ψ_a^∗ = a E and the potential at the a_inf distance from the symmetry plane is Ψ_inf,a= a_infE. The RC-chain describes the behavior of the potentials at the interfaces of internal, membrane, and external media.

ALE approach

We use our approach (28, 44) to derive the potentials in Eq. 6 for single-shell ellipsoidal objects (Fig. 1 A). In short: chains of three RC-pairs for the internal (i) and external (e) media and the membrane (m) form potential dividers along each principle semiaxis (Fig. 1 B). Their parameters are determined by the media properties (Eq. 1) and their geometries defined by a cross-sectional area A and a length. The value A is arbitrarily small, and equal and constant along each principal semiaxis.

The value Ψ_inf,a is the undisturbed potential at the a_inf distance from the symmetry plane. It is the maximum potential that occurs at pole a of an object with a very low effective polarizability, e.g., an equivalent vacuum body or a biological cell at low frequency. Ψ_inf,a can be considered as the input from the separated geometric problem of the Laplace solution. It allows us to define the length of the external medium element forming the external RC-pair of the voltage divider along axis a (Fig. 1 B). Its relative length is ξ_a:

$${\xi }_a=\frac{a_{\text{inf}}}{a}-1.$$ (7)

For randomly oriented three-axial objects, we average the three ξ-factors along the main axes:

$$\overline{\xi }=\frac{{\xi }_a+{\xi }_b+{\xi }_c}{3}.$$ (8)

Please note that this expression (Eq. 8) is the first of a set of mixed terms introduced for the simplification of the equations given in the Appendices. For the special case of a spherical object, we obtain $\overline{\xi }={\xi }_a={\xi }_b={\xi }_c=0.5$. The impedances of the RC-pairs of the external and internal media along axis a are $Z_{e,a}^{\ast }=(a_{\inf }-a)/(A\cdot {\sigma }_e^{\ast })=a\cdot {\xi }_a/(A\cdot {\sigma }_e^{\ast })$ and $Z_{i,a}^{\ast }=a/(A\cdot {\sigma }_i^{\ast })$. The complex conductivities of the media are defined by Eq. 1. The electric properties of the membrane can be described by $Z_m^{\ast }=1/(A\cdot g_m^{\ast })$. The complex area-specific membrane conductance of the membrane is g_m^∗ = g_m + jωC_m, with C_m and g_m being the sectoral capacity and the area-specific membrane conductance. The use of area-specific terms for the negligibly thin membrane avoids uncertainties in the definition of the membrane thickness. Given by the low conductance of biological membranes, i.e., the specific membrane conductivity is <1 μS/m (8, 63) and the area-specific membrane conductance is of 1–100 S/m² (5, 8), it is usually justified to assume that g_m = 0 Sm⁻².

CMF in the ALE model

Expressing the potentials in Eq. 6 by the voltage-divider properties of the ALE scheme in Fig. 1 B leads to (28)

$$CM{F}_a^{\ast }=\frac{1+{\xi }_a}{{\xi }_a}\left(1-\frac{Z_{i,a}^{\ast }+Z_{m,a}^{\ast }}{Z_{i,a}^{\ast }+Z_{m,a}^{\ast }+Z_{e,a}^{\ast }}\left(1+{\xi }_a\right)\right).$$ (9)

The mixing equation

Combining the left term of Eq. 5 with Eq. 9 results in

$$\frac{3\left({\sigma }_S^{\ast }-{\sigma }_e^{\ast }\right)}{{\sigma }_S^{\ast }+2{\sigma }_e^{\ast }}=p\frac{1}{3}\sum _{\text{dir}=a,b,c}\left(\frac{1+{\xi }_{\text{dir}}}{{\xi }_{\text{dir}}}\left(1-\frac{Z_{i,\text{dir}}^{\ast }+Z_{m,\text{dir}}^{\ast }}{Z_{i,\text{dir}}^{\ast }+Z_{m,\text{dir}}^{\ast }+Z_{e,\text{dir}}^{\ast }}\left(1+{\xi }_{\text{dir}}\right)\right)\right).$$ (10)

Derivations

The softwares Maple, Version 12 (Maplesoft, Waterloo, ON, Canada) and SigmaPlot, Version 11 (Systat Software, San Jose, CA) were used for model considerations, the derivation of simplified equations, and the generation and plotting of theoretical curves. The characteristic equations presented in the Appendices were derived from Eq. 10, starting from the full ALE model (Fig. 1 B) or, alternatively after simplification of the RC-pair chain for certain frequency ranges (28). These before-the-event simplifications reduced the complexity of the derivation and ad hoc, led to simpler expressions. For further information, please see the Supporting Material.

Model parameters

We validated our model for differently shaped objects. As exemplary shapes, we used oblate, prolate, and spherical single-shell objects of the same volume (Fig. 1 A). Furthermore, as a biological example for a single-shell ellipsoid, a three-axial chicken red blood-cell (CRBC) model was used. For the CRBC, the dimensions of the axes correspond to experimental values given by Maswiwat et al. (42). All axis ratios and electric properties are summarized in Table 1.

Table 1.

Axis lengths of single-shell model objects of different shapes and electric media properties

Description	Semiaxis a/μm	Semiaxis b/μm	Semiaxis c/μm
Model Geometry
Sphere	6.66	6.66	6.66
Oblate spheroid (ratio 5:5:1)	11.39	11.39	2.28
Prolate spheroid (ratio 1:1:5)	3.89	3.89	19.47
Three axial ellipsoid (CRBC)	6.66	4.17	1.43
Volume fraction of objects		p = 0.1
Media properties
Internal conductivity		σi = 0.5 Sm−1
Internal permittivity		εi = 50 ε0
External conductivities		σe = 0.1 Sm−1 or σe = 1.3 Sm−1
External permittivity		εe = 80 ε0
Area-specific membrane capacitance		Cm = 0.01 Fm−2
Area-specific membrane conductance		gm = 0 Sm−2 or gm ≠ 0 Sm−2

Results and Discussion

Comparison of the ALE and Laplace models, parameter definitions

We compared our ALE approach with the original Maxwell-Wagner model. The results are shown in Figs. 2 and 3 for a suspension of spherical cells (for parameters, see Table 1). The model differences in the real and imaginary parts of the impedance (Fig. 2) as well as between the conductivities and permittivities (Fig. 3), are negligible.

Figure 2.

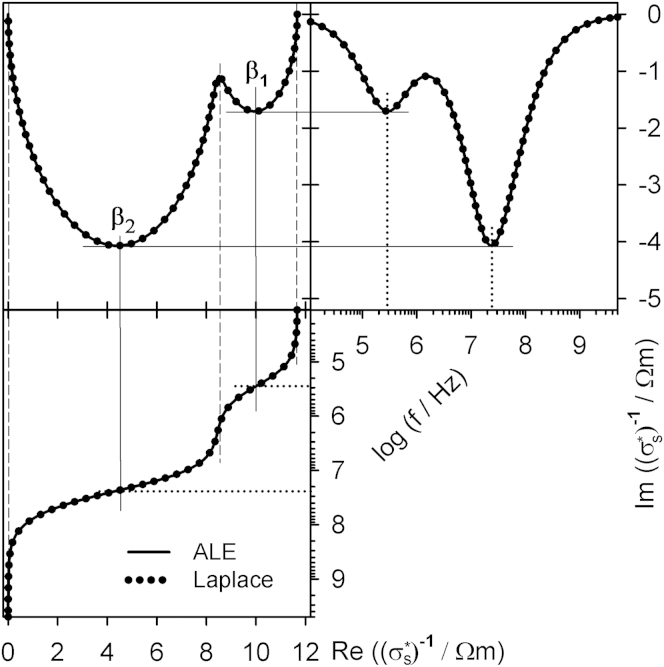
Real and imaginary parts of the complex specific impedance for a suspension of single-shell spheres obtained from the Maxwell-Wagner mixing equation (Eq. 5) solved with the ALE model (solid line) and the Laplace model (solid circles). The Cole-Cole plot (top-left) merges the frequency-dependent plots of the real (lower-left) and imaginary (top-right) parts. The three plateaus in the real part (vertical dashed lines) correspond to low absolute magnitudes in the imaginary parts. The inflection points (solid lines) correspond to peaks in the imaginary part at the two characteristic frequencies (dotted lines) of the membrane (β₁) and the bulk conductivity (β₂) dispersions. For parameters, see Table 1 for σ_e = 0.1 Sm⁻¹ and g_m = 0 Sm⁻².

Figure 3.

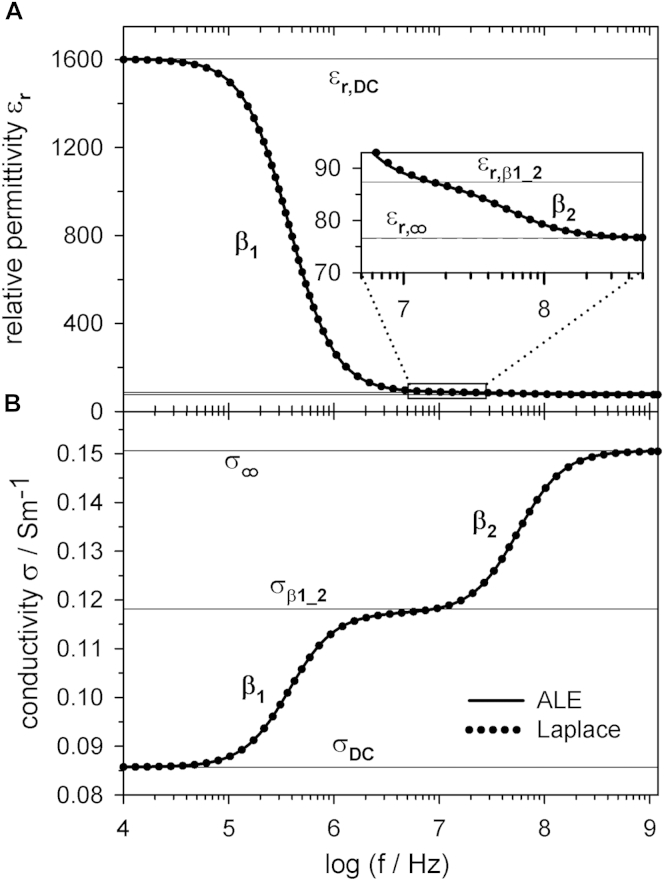
Frequency dependencies of the relative permittivity (A) and the conductivity (B) for the parameters used in Fig. 2. Two dispersion processes (β₁ and β₂) and characteristic plateaus for DC (ε_r,DC, σ_DC) and infinitely high frequencies (ε_∞, σ_∞) as well as an intermediate plateau (ε_{r,β1_2}, σ_{β1_2}) are clearly visible in (A) and (B).

Figs. 2 and 3 show two significant dispersion processes (β₁ and β₂) that are generally based on the fact that the capacitive membrane and bulk conductivity contributions of certain relaxation processes that follow the external field at lower frequencies disperse at higher ones. Consequently, the permittivity of cell suspensions drops over some frequency decades by orders of magnitude while the conductivity increases (Fig. 3). For a classification of the contributing processes, two different approaches exist: the dispersions were sorted according to their physical nature, e.g., as Maxwell-Wagner and Debye dispersions, or according to the frequency range in which they occur (27).

Nonspherical objects

Simplified equations for characteristic plateaus of the conductivities and permittivities of a suspension of randomly oriented single-shell ellipsoidal objects are shown in Appendix A1. For further simplifications of the equations, mixed terms were introduced for the objects’ geometries that simplify the description of the superposition of the ellipsoidal object orientations (see Appendix A2; compare to Eq. 8). Similarly, mixing ratios for the conductivities and permittivities were introduced that are related to the geometrical mixed terms (see Appendix A2). For objects of rotational symmetry (spheroids), the mixing ratios can further be simplified assuming an approximation function for the influential radii (41, 42).

It is known that objects can be oriented by electric fields (42, 44, 64) or fluid motion (65). In the presence of a linear AC field, nonspherical objects may orient with a certain axis into the direction of the field depending on the frequency (44). The axis with the highest induced dipole moment is frequency dependent. In linear fields, it is oriented in the field direction. For objects oriented with the same axis in parallel to the electric field, the equations of Appendix A1, reduce to the equations of Appendix A3.

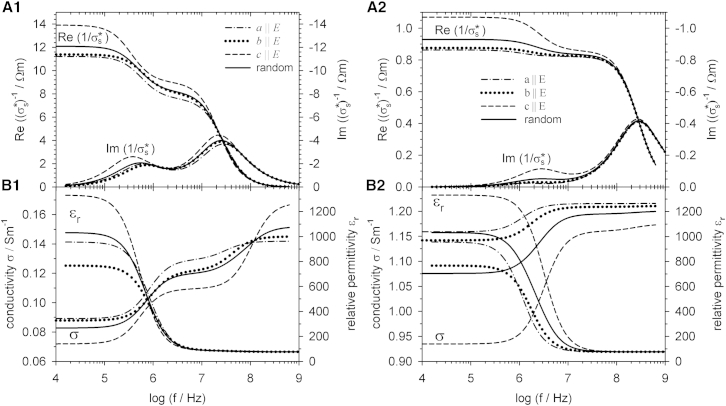
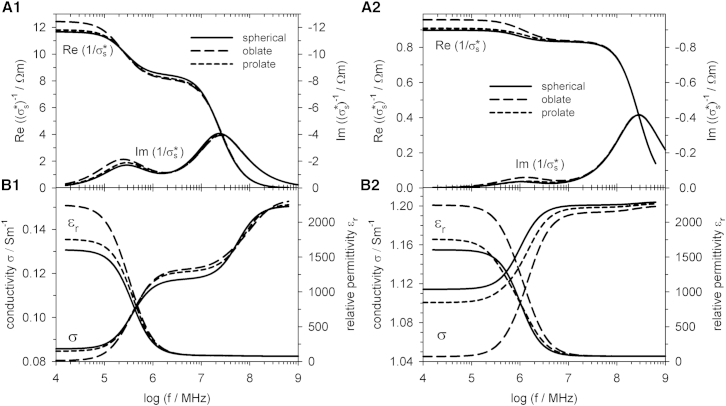
Fig. 4 shows the results for the real and imaginary parts of the specific complex impedance as well as for the conductivity and relative permittivity for different orientations of the main axes of CRBCs at two external conductivities. It can be seen that the different axes lengths and corresponding ξ-values can be distinguished at low and high external conductivities, especially in the lower frequency range. The real and imaginary parts of the impedance are showing differences in the frequency range up to 100 MHz. Above 100 MHz, different orientations of the objects are hard to distinguish. The same applies to the permittivity. In the conductivity case, the object orientations can be distinguished over the whole frequency range.

Figure 4.

Comparison of the electric properties of suspensions of CRBCs oriented in the a, b, or c direction with g_m = 0 Sm⁻². The external media conductivity was σ_e = 0.1 Sm⁻¹ (A1 and B1) and σ_e = 1.3 Sm⁻¹ (A2 and B2). For further parameters, see Table 1. Please note that the function plots touch the ordinates to which they refer.

For simplicity, we neglected the membrane conductivity in the above considerations. In the following, we will check the influence of the membrane conductance on the specific complex impedance, conductivity, and relative permittivity for the CRBC geometry.

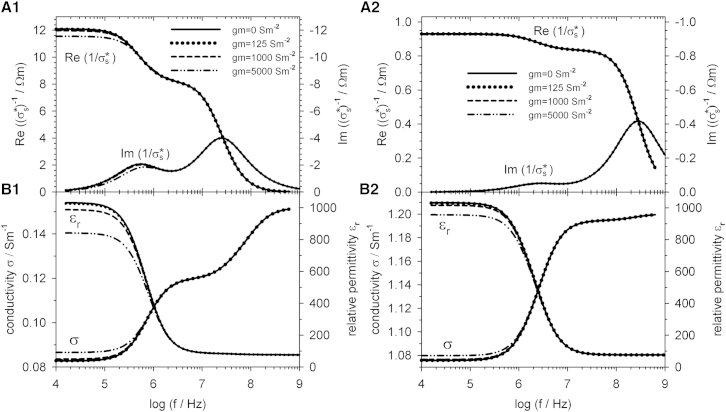
As can be seen in Fig. 5, the membrane-conductance influence for an external conductivity >0.1 Sm⁻¹ is almost negligible at <1000 Sm⁻², a value above standard biological parameters. Nevertheless, membrane conductivities above this level only reduce the dispersion strength of the membrane (β₁) dispersion, leaving the β₂ dispersion unchanged. This is a result of the very small volume contribution of the membrane to the overall cell volume. Please note that for very small objects such as liposomes or viruses, the membrane volume fraction is higher and may no longer be neglected at frequencies above the membrane dispersion (66).

Figure 5.

Comparison of the electric properties of suspensions of CRBCs of random orientation with membrane conductances of g_m = 0, 125, 1000, and 5000 Sm⁻². The external medium conductivity was σ_e = 0.1 Sm⁻¹ (A1 and B1) or σ_e = 1.3 Sm⁻¹ (A2 and B2). For further parameters, see Table 1.

Spheres and oblate and prolate spheroids

For a sphere with ξ = 0.5 along each axis, the equations of Appendix A3 result in the equations of Appendix A4 and A5 for an area-specific membrane conductance of g_m = 0 Sm⁻² and g_m ≠ 0 Sm⁻², respectively. Originally, Pauly and Schwan (7) solved the full mixture equations for spherical single-shell objects by hand, throwing out small terms, which led to the famous Pauly-Schwan expressions. Later, Foster and Schwan (5) used a Pade approximation, keeping terms to first-order in the membrane-thickness/cell-diameter ratio (K.R. Foster, University of Pennsylvania, personal communication, 2014). In the ALE model, the membrane thickness is fully neglected and area-specific properties provide transition conditions between the internal and external bulks.

Our equations for suspensions of spherical single-shell objects (see Appendix A4 and A5) include the special cases for the conductivity and permittivity already provided by Foster and Schwan (5), and Schwan (6), proving the feasibility of the ALE approach.

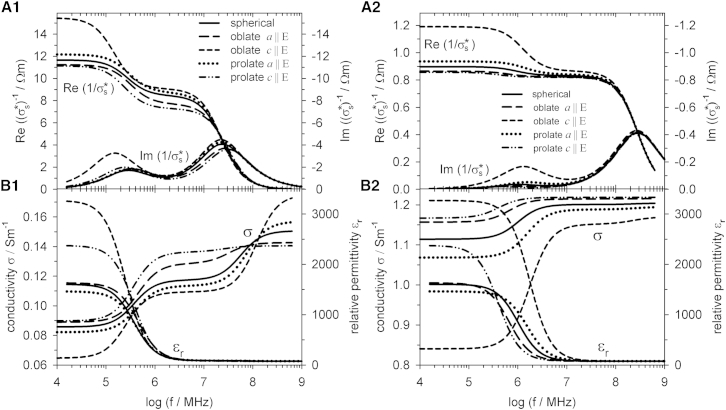
Fig. 6 compares impedance spectra for spherical as well as oblate and prolate spheroidal objects. As can be seen in Fig. 6, A1 and A2, the real and imaginary parts of the specific impedance of a suspension do not very sensitively depend on the shape of randomly oriented oblate or prolate single-shell spheroids or single-shell spheres. Interestingly, both deviations from the spherical shape lead to concordant changes in the specific impedance. Whether the deviation from the spherical shape leads to an increase or decrease in the impedance depends on frequency and external conductivity. For a given axis ratio, impedance changes are larger for deviations toward the oblate than the prolate shape.

Figure 6.

Comparison of suspensions of single-shell spheres with randomly oriented oblate and prolate single-shell spheroids for g_m = 0 Sm⁻². All objects had the same volume and volume fraction. The external medium conductivity was σ_e = 0.1 Sm⁻¹ (A1 and B1) and σ_e = 1.3 Sm⁻¹ (A2 and B2). For further parameters, see Table 1.

Fig. 6, B1 and B2, shows that relative permittivities and conductivities are more sensitive to shape changes. While a transition from the spherical to an oblate shape results in a change of the low-frequency plateaus of the specific impedance changes by <10%, relative permittivity and conductivity are changed by >50 and 10%, respectively. At frequencies above the membrane dispersion, differences in the conductivities are more pronounced than in the relative permittivities.

As suggested in Fig. 4 for the general ellipsoidal shape, axis-length variations in field direction can be sensitively detected. In Fig. 7, different orientations of oblate and prolate objects are compared with spherical objects.

Figure 7.

Comparison of the electric properties of suspensions of single-shell spheres with oriented oblate and prolate single-shell spheroids for g_m = 0 Sm⁻². The external medium conductivity was σ_e = 0.1 Sm⁻¹ (A1 and B1) and σ_e = 1.3 Sm⁻¹ (A2 and B2). For further parameters, see Table1.

As can be seen in Fig. 7, A1 and A2, the specific impedance reflects the shape of oblate and prolate spheroids more sensitively when the objects are oriented (compare to Fig. 6, A1 and A2). Clearly, oblate and prolate spheroids lead to increased impedances relative to spheres when their longer axes are oriented perpendicular to the field direction. Qualitatively, an increase or decrease in the impedance induced by a shape deviation of the oriented objects does not depend on frequency and external conductivity. For a given object orientation, this effect is also independent from the effective impedance of the object relative to that of the external medium (compare β_{1_2} plateaus in Fig. 7, where the internal conductivity is higher (Fig. 7 A1) or lower (Fig. 7 A2) than that of the external medium). For a given shape, the two orientations determine limits for the impedance obtained for incomplete or random orientations (Fig. 6).

Relative permittivities are more sensitive to shape changes than the specific impedance, as can be seen from the spreading of the spectra in Fig. 7, B1 and B2. The value ε_r,DC is increased by >50% when moving from prolate to oblate objects with their symmetry axes oriented in the field direction. Nevertheless, at first glance, a systematics in the permittivity change is not as intuitive as in Fig. 6, B1 and B2.

The sensitivities of σ_DC and specific impedance are comparable. Clearly, the conductivity is increasing with the length of the axis oriented in the field direction below the β₂-dispersion (compare to Table 1 and Fig. 1 A). Above the β₂-dispersion, the systematics is reversed (Fig. 7 B1). This suggests conductivity to be the ideal parameter for differentiating the shapes of oriented objects.

In summary, Figs. 6 and 7 suggest that a prerequisite for the experimental differentiation of different object shapes will require largely monodisperse suspensions, especially for the random orientation. It would be of strong advantage, if electric measurements could be conducted on the same suspension for different object orientations, e.g., induced by AC fields of certain frequencies. Such an approach would be similar to electrooptic measurements, which combine the electrically induced orientation of objects with the detection of changes in the turbidity of the suspension (64). Even more sensitive might be the detection of single objects, e.g., in microfluidic impedance chambers (12, 52, 53, 54).

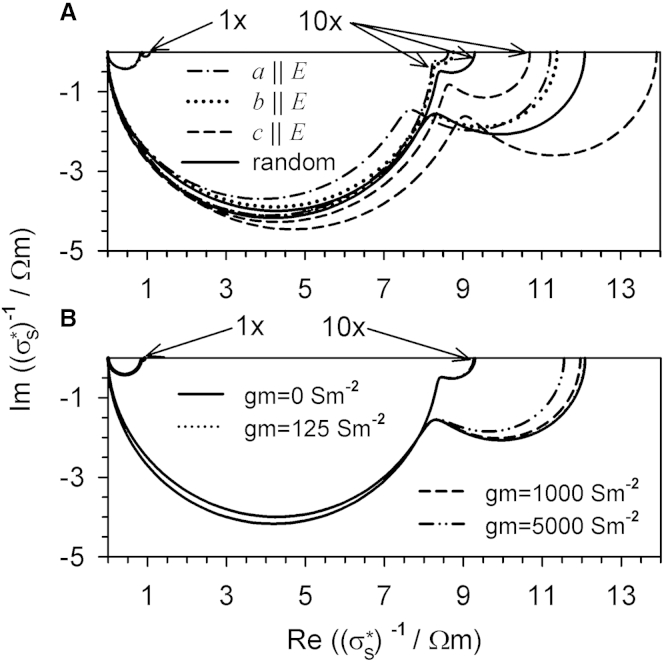
Complex plot summaries

Fig. 8 summarizes the spectra of CRBC suspensions (Figs. 4 and 5) in complex plots of the specific impedance in dependence on the cell orientation (Fig. 8 A) and membrane conductance of the randomly oriented CRBCs (Fig. 8 B). Comparison clearly shows a higher resolution for both parameters at the low external conductivity, as already discussed in relation to Figs. 4 and 5.

Figure 8.

Complex plots of the specific impedances for oriented CRBCs with zero membrane conductance (A; compare to Fig. 4) as well as randomly oriented CRBCs of different specific membrane conductances (B; g_m = 0, 125, 1000, and 5000 Sm⁻²; compare to Fig. 5). The spectra were calculated for σ_e = 0.1 Sm⁻¹ and σ_e = 1.3 Sm⁻¹ (small semicircles in the top-left corners of A and B designated by “1×”). For other parameters, see Table 1. For a better comparability with the larger σ_e = 0.1 Sm⁻¹ plots, σ_e = 1.3 Sm⁻¹ plots were upscaled by a factor of 10 and designated by “10×”. For reference, the random orientation for g_m = 0 Sm⁻² (solid line) is included in (A) and (B).

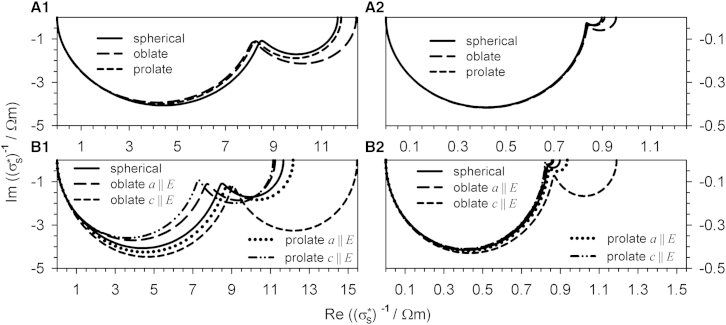
Fig. 9 summarizes the spectra of Figs. 6 and 7 for suspensions of single-shell spheroids with different axis ratios (Fig. 1 A; Table 1). The specific impedances are considered for objects, which are randomly oriented (Fig. 9 A) or pointing in the field direction with certain axes (Fig. 9 B).

Figure 9.

Complex plots of the specific impedances of suspensions of randomly oriented (A1 and A2; compare to Fig. 6A) as well as oriented (B1 and B2; compare to Fig. 7A) single-shell spheroids of oblate, spherical, and prolate shapes and g_m = 0 Sm⁻². The external medium conductivity was σ_e = 0.1 Sm⁻¹ (A1 and B1) or σ_e = 1.3 Sm⁻¹ (A2 and B2). For further parameters, see Table 1. (Please compare the factor-of-10 scaling between the abscissas of A and B with Fig. 8.)

Comparison of the ALE approach with other model approaches

Here we show that the same CMF expressions can be employed in impedance and AC-electrokinetic models. A closed Laplace solution for a single-shell object of the general ellipsoidal shape requires two confocal interfaces (for internal medium, membrane; for membrane, external medium) to describe the membrane. The assumption of the correct thickness of the membrane shell at each of the poles of the three principal semiaxes of nonspherical objects would lead to nonconfocal membrane surfaces, hindering a consistent Laplace solution. In the classical derivations of the CMF of single-shell ellipsoidal objects, exact depolarizing factors are introduced for the inner- and outer-confocal membrane-shell interfaces (3, 31, 40).

A simple way to partly correct for the nonconstant membrane thickness of confocal models is the combination of three (or two for the rotational symmetry) different Laplace solutions for three different ellipsoidal models (31). Each of the models should exhibit the same correct membrane thickness at the poles of the principal axis, which is oriented in parallel to the considered field component. For multishell spheroidal objects, a solution for the simultaneous thickness correction for the multitude of shells has been given by Sokirko (67). A way to correct for the nonconstant membrane thickness may be the assumption of anisotropic membrane properties (Jones (51); see also Simeonova and Gimsa (34) and Sukhorukov et al. (36)).

Generally, for biological cells the assumption of the same depolarizing factors for the inner and outer ellipsoids, which form the two membrane interfaces, is justified because of their negligible geometry differences. While the model of Asami et al. (3) still contains the small difference between the volumes of the two ellipsoids, this difference is neglected in the ALE approach by the introduction of area-specific membrane parameters. The combination of three different Laplace solutions for three geometries is inherent to the ALE approach. This allows for the assumption of the same membrane properties at the poles for each field component. Naturally, the highest contribution of each field component to the impedance of the suspension stems from the respective poles, especially below and in the frequency range of membrane dispersion (28).

Precision of the ALE model

For the parameters given in Table 1, the full ALE approach (Eqs. 9 and 10) shows no differences with the spectra calculated with the spherical models of Schwan (Foster and Schwan (5)), as well as with the ellipsoidal models of Asami et al. (3) and Bohren and Huffman (31) within the numerical accuracy (compare to Fig. 3).

To explore the limits of the ALE model, we considered a suspension of single-shell spheres with a very high area-specific shell conductance of 6.25 × 10¹⁶ Sm⁻², which was calculated from the specific conductivity of gold of 5 × 10⁷ Sm⁻¹ assuming a membrane-shell thickness of 8 nm. The ALE results were compared with the classical Laplace solution at σ_e = 0.1 Sm⁻¹ (see Table 1 for other parameters). For the three plateaus (DC, β_{1_2}, and infinitely high frequencies), respective percentage differences $\left(({\text{value}}_{\text{ALE}}-{\text{value}}_{\text{Laplace}})/{\text{value}}_{\text{Laplace}}\right)$ of −12, 0, and −7% (conductivity spectra), as well as −19, 0, and 0% (permittivity spectra) were found. We suppose that the main reason for the differences stem from the Cartesian anisotropy in the membrane properties inherent to the ALE model, which excludes membrane currents tangentially oriented to the considered field component. As a result, the current conduction through an ALE suspension as well as its conductivity and permittivity are slightly reduced. Nevertheless, an elaborate investigation of this relation is beyond the scope of this article, especially because conductances of the order of gold are unrealistic for biological membranes. Whether the actual properties of biological membranes with protein and aqueous pores being normally oriented to the membrane surface are even better reflected in the ALE model, remains to be elucidated.

There is at least one further problem to be considered. It concerns Maxwell’s requirement that the concentration of the objects has to be low enough to avoid mutual electrical interactions of the objects. It is known that the potential far from spherical objects vanishes, which is not necessarily the case for spheroidal or ellipsoidal objects (68). Accordingly, Maxwell’s requirement cannot simply be assumed as fulfilled for nonspherical objects. For simplicity, we neglected this problem, based on the fact that the shape of biological objects is close to spherical. Nevertheless, especially for the random orientation, it is uncertain whether a 10% volume fraction will be low enough to fulfill Maxwell’s condition. The investigation of the shape and orientation dependencies on the limiting concentrations is beyond the scope of this article and will need separate attention. We are not aware of any work on such limits.

Conclusions

Many of the characteristic or limiting equations given in Appendices A and B for the impedance of suspensions of ellipsoidal, spheroidal, and spherical objects are given here for the first time, to our knowledge. A summary is given in Table C1. It is amusing that the derivation of characteristic equations using the ALE approach applies the philosophy of ancient analog computing: to separate time constants, certain electric elements of the complete RC-chain model are neglected in the considered frequency range. We think that this philosophy is closer to the electric character of the problem, and facilitates the identification of negligible terms with respect to, for example, Taylor or Pade approximations. For an illustration, please compare the differences in the simplified equations derived in Gimsa et al. (69) with those in Gimsa and Wachner (28) and see discussion in Gimsa et al. (33). Naturally, our model provides all solutions for suspensions of homogeneous objects. In this case, the RC-chain is reduced to two RC-pairs for the internal and external media and the described object is identical to Maxwell’s equivalent body (see Appendices A and B and Maxwell (13) and Gimsa et al. (33)).

Table C1.

Reference chart for characteristic equations of parameters of suspensions of single-shell and homogeneous objects for random and axial orientations

Description	σ∗	ε∗	σDC	σP	σ∞	εDC	εP	ε∞	τc1	τc2	σDC−∞	εDC−∞
Single Shell
Ellipsoids
Oriented	—	(71)	new	new	new	new	new	new	new	new	—	—
Random	—	(3) n.e.	new	new	new	new	new	new	—	—	—	—
Spheroids
Oriented	—	—	new	new	new	new	new	new	new	new	—	—
Random	—	—	new	new	new	new	new	new	—	—	—	—
Spheres	—	—	(5)	new	new	new	new	(5)	(5, 33)	(72)	—	(5)
Homogeneous
Ellipsoids
Oriented	—	(4)	new	new	new	new	new	new	—	new	—	—
Random	—	(4)	new	new	new	new	new	new	—	—	—	—
Spheroids
Oriented	(61)	(61)	new	new	new	new	new	new	—	new	—	—
Random	—	—	new	new	new	new	new	new	—	—	—	—
Spheres	(14)	(14)	(5)	new	new	new	new	(5)	—	(72)	(5)	(5)

n.e., no explicit expression given.

Author Contributions

J.G. provided most of the general theoretical ideas and concepts, the line of arguments, and the choice of parameter combinations for the figures. M.S. did the MAPLE software programming, derivation of the characteristic equations, calculations, and plotting of the results. The writing of the article was a joint effort.

Editor: Jochen Guck.

Appendix A: Conductivity and Permittivity Plateaus

Here, we present collections of characteristic equations of conductivity and permittivity plateaus for suspensions of randomly oriented, axially oriented single-shell spheroidal and three axial ellipsoidal objects as well as spheres with and without membrane conductance. Plateau equations were derived for the static case (index DC), the plateau beyond membrane dispersion (index β_{1_2}), and the plateau at infinitely high frequency (index ∞, Figs. 2 and 3). Below, we introduce the mixed terms $\overline{\xi }$, $\overline{\overline{\xi }}$, and ξ_abc as well as $\overline{\sigma }$ and $\overline{\epsilon }$ for randomly oriented objects.

1. Characteristic equations of conductivity and permittivity plateaus for a suspension of randomly oriented single-shell spheroidal and three-axial ellipsoidal objects with zero membrane conductance

$${\sigma }_{DC}=\left(\frac{3-2p\left(1+\overline{\xi }\right)}{3+p\left(1+\overline{\xi }\right)}\right){\sigma }_e,$$ (A1)

$${\epsilon }_{DC}=\left(\frac{3-2p\left(1+\overline{\xi }\right)}{3+p\left(1+\overline{\xi }\right)}\right){\epsilon }_e+\left(\frac{3}{{\left(3+p\left(1+\overline{\xi }\right)\right)}^2}\right)p{C}_m\left(a{\left(1+{\xi }_a\right)}^2+b{\left(1+{\xi }_b\right)}^2+c{\left(1+{\xi }_c\right)}^2\right),$$ (A2)

$${\sigma }_{\beta 1\_2}=\left(\frac{3\overline{\sigma }-2p\left({\sigma }_e-{\sigma }_i\right)\left({\sigma }_e^2\left(1+\overline{\xi }\right)+2{\sigma }_e{\sigma }_i\left(\overline{\xi }+\overline{\overline{\xi }}\right)+{\sigma }_i^2\left({\xi }_{\text{abc}}+\overline{\overline{\xi }}\right)\right)}{3\overline{\sigma }+p\left({\sigma }_e-{\sigma }_i\right)\left({\sigma }_e^2\left(1+\overline{\xi }\right)+2{\sigma }_e{\sigma }_i\left(\overline{\xi }+\overline{\overline{\xi }}\right)+{\sigma }_i^2\left({\xi }_{\text{abc}}+\overline{\overline{\xi }}\right)\right)}\right){\sigma }_e,$$ (A3)

$${\epsilon }_{\beta 1\_2}=\left(\frac{{\left({\sigma }_e+\overline{\xi }{\sigma }_i\right)}^2+p\overline{\xi }{\left({\sigma }_e-{\sigma }_i\right)}^2}{{\left({\sigma }_e+\overline{\xi }{\sigma }_i+p\overline{\xi }\left({\sigma }_e-{\sigma }_i\right)\right)}^2}\right)\left(1-p\right){\epsilon }_e+\left(\frac{{\left(1+\overline{\xi }\right)}^2{\sigma }_e^2}{{\left({\sigma }_e+\overline{\xi }{\sigma }_i+p\overline{\xi }\left({\sigma }_e-{\sigma }_i\right)\right)}^2}\right)p{\epsilon }_i,$$ (A4)

$${\sigma }_{\infty }=\left(\frac{{\left({\epsilon }_e+\overline{\xi }{\epsilon }_i\right)}^2+p\overline{\xi }{\left({\epsilon }_e-{\epsilon }_i\right)}^2}{{\left({\epsilon }_e+\overline{\xi }{\epsilon }_i+p\overline{\xi }\left({\epsilon }_e-{\epsilon }_i\right)\right)}^2}\right)\left(1-p\right){\sigma }_e+\left(\frac{{\left(1+\overline{\xi }\right)}^2{\epsilon }_e^2}{{\left({\epsilon }_e+\overline{\xi }{\epsilon }_i+p\overline{\xi }\left({\epsilon }_e-{\epsilon }_i\right)\right)}^2}\right)p{\sigma }_i,$$ (A5)

$${\epsilon }_{\infty }=\left(\frac{3\overline{\epsilon }-2p\left({\epsilon }_e-{\epsilon }_i\right)\left({\epsilon }_e^2\left(1+\overline{\xi }\right)+2{\epsilon }_e{\epsilon }_i\left(\overline{\xi }+\overline{\overline{\xi }}\right)+{\epsilon }_i^2\left({\xi }_{abc}+\overline{\overline{\xi }}\right)\right)}{3\overline{\epsilon }+p\left({\epsilon }_e-{\epsilon }_i\right)\left({\epsilon }_e^2\left(1+\overline{\xi }\right)+2{\epsilon }_e{\epsilon }_i\left(\overline{\xi }+\overline{\overline{\xi }}\right)+{\epsilon }_i^2\left({\xi }_{abc}+\overline{\overline{\xi }}\right)\right)}\right){\epsilon }_e.$$ (A6)

2. Mixed terms for randomly oriented nonspherical objects

Please note that further simplification is possible for the spheroidal shape with ξ_a = ξ_b.

$${\xi }_{\text{abc}}={\xi }_a{\xi }_b{\xi }_c,\overline{\xi }=\frac{\left({\xi }_a+{\xi }_b+{\xi }_c\right)}{3}\overline{\overline{\xi }}=\frac{\left({\xi }_a{\xi }_b+{\xi }_b{\xi }_c+{\xi }_c{\xi }_a\right)}{3}=\frac{{\xi }_{\text{abc}}}{3}\left(\frac{1}{{\xi }_a}+\frac{1}{{\xi }_b}+\frac{1}{{\xi }_c}\right)$$ (A7)

$$\overline{\sigma }=\left({\xi }_a{\sigma }_i+{\sigma }_e\right)\left({\xi }_b{\sigma }_i+{\sigma }_e\right)\left({\xi }_c{\sigma }_i+{\sigma }_e\right)$$ (A8)

$$\overline{\epsilon }=\left({\xi }_a{\epsilon }_i+{\epsilon }_e\right)\left({\xi }_b{\epsilon }_i+{\epsilon }_e\right)\left({\xi }_c{\epsilon }_i+{\epsilon }_e\right)$$ (A9)

3. Characteristic equations of conductivity and permittivity plateaus for a suspension of axially oriented single-shell spheroidal and three-axial ellipsoidal objects with zero membrane conductance

$${\sigma }_{DC}=\left(\frac{3-2p\left(1+{\xi }_a\right)}{3+p\left(1+{\xi }_a\right)}\right){\sigma }_e,$$ (A10)

$${\epsilon }_{DC}=\left(\frac{3-2p\left(1+{\xi }_a\right)}{3+p\left(1+{\xi }_a\right)}\right){\epsilon }_e+\left(\frac{3}{{\left(3+p\left(1+{\xi }_a\right)\right)}^2}\right)p{C}_m\left(3a{\left(1+{\xi }_a\right)}^2\right),$$ (A11)

$${\sigma }_{\beta 1\_2}=\left(\frac{3\left({\sigma }_e+{\xi }_a{\sigma }_i\right)-2p\left({\sigma }_e-{\sigma }_i\right)\left(1+{\xi }_a\right)}{3\left({\sigma }_e+{\xi }_a{\sigma }_i\right)+p\left({\sigma }_e-{\sigma }_i\right)\left(1+{\xi }_a\right)}\right){\sigma }_e,$$ (A12)

$${\epsilon }_{\beta 1\_2}=\left(\frac{9{\left({\sigma }_e+{\xi }_a{\sigma }_i\right)}^2-p\left(1+{\xi }_a\right)\left(3\left({\sigma }_e^2+2{\sigma }_e{\sigma }_i\left(2{\xi }_a+1\right)-{\xi }_a{\sigma }_i^2\right)+2p\left(1+{\xi }_a\right){\left({\sigma }_e-{\sigma }_i\right)}^2\right)}{{\left(3\left({\sigma }_e+{\xi }_a{\sigma }_i\right)+p\left({\sigma }_e-{\sigma }_i\right)\left(1+{\xi }_a\right)\right)}^2}\right){\epsilon }_e+\left(\frac{9{\sigma }_e^2{\left(1+{\xi }_a\right)}^2}{{\left(3\left({\sigma }_e+{\xi }_a{\sigma }_i\right)+p\left({\sigma }_e-{\sigma }_i\right)\left(1+{\xi }_a\right)\right)}^2}\right)p{\epsilon }_i,$$ (A13)

$${\sigma }_{\infty }=\left(\frac{9{\left({\epsilon }_e+{\xi }_a{\epsilon }_i\right)}^2-p\left(1+{\xi }_a\right)\left(3\left({\epsilon }_e^2+2{\epsilon }_e{\epsilon }_i\left(2{\xi }_a+1\right)-{\xi }_a{\epsilon }_i^2\right)+2p\left(1+{\xi }_a\right){\left({\epsilon }_e-{\epsilon }_i\right)}^2\right)}{{\left(3\left({\epsilon }_e+{\xi }_a{\epsilon }_i\right)+p\left({\epsilon }_e-{\epsilon }_i\right)\left(1+{\xi }_a\right)\right)}^2}\right){\sigma }_e+\left(\frac{9{\epsilon }_e^2{\left(1+{\xi }_a\right)}^2}{{\left(3\left({\epsilon }_e+{\xi }_a{\epsilon }_i\right)+p\left({\epsilon }_e-{\epsilon }_i\right)\left(1+{\xi }_a\right)\right)}^2}\right)p{\sigma }_i,$$ (A14)

$${\epsilon }_{\infty }=\left(\frac{3\left({\epsilon }_e+{\xi }_a{\epsilon }_i\right)-2p\left({\epsilon }_e-{\epsilon }_i\right)\left(1+{\xi }_a\right)}{3\left({\epsilon }_e+{\xi }_a{\epsilon }_i\right)+p\left({\epsilon }_e-{\epsilon }_i\right)\left(1+{\xi }_a\right)}\right){\epsilon }_e.$$ (A15)

4. Characteristic equations of conductivity and permittivity plateaus for a suspension of single-shell spheres with zero membrane conductance

$${\sigma }_{DC}=\left(\frac{2-2p}{2+p}\right){\sigma }_e,$$ (A16)

$${\epsilon }_{DC}=\left(\frac{2-2p}{2+p}\right){\epsilon }_e+\left(\frac{9}{{\left(2+p\right)}^2}\right)pr{C}_m,$$ (A17)

$${\sigma }_{\beta 1\_2}=\left(\frac{2{\sigma }_e+{\sigma }_i-2p\left({\sigma }_e-{\sigma }_i\right)}{2{\sigma }_e+{\sigma }_i+p\left({\sigma }_e-{\sigma }_i\right)}\right){\sigma }_e,$$ (A18)

$${\epsilon }_{\beta 1\_2}=\left(\frac{{\left(2{\sigma }_e+{\sigma }_i\right)}^2+2p{\left({\sigma }_e-{\sigma }_i\right)}^2}{{\left(2{\sigma }_e+{\sigma }_i+p\left({\sigma }_e-{\sigma }_i\right)\right)}^2}\right)\left(1-p\right){\epsilon }_e+\left(\frac{9{\sigma }_e^2}{{\left(2{\sigma }_e+{\sigma }_i+p\left({\sigma }_e-{\sigma }_i\right)\right)}^2}\right)p{\epsilon }_i,$$ (A19)

$${\sigma }_{\infty }=\left(\frac{{\left(2{\epsilon }_e+{\epsilon }_i\right)}^2+2p{\left({\epsilon }_e-{\epsilon }_i\right)}^2}{{\left(2{\epsilon }_e+{\epsilon }_i+p\left({\epsilon }_e-{\epsilon }_i\right)\right)}^2}\right)\left(1-p\right){\sigma }_e+\left(\frac{9{\epsilon }_e^2}{{\left(2{\epsilon }_e+{\epsilon }_i+p\left({\epsilon }_e-{\epsilon }_i\right)\right)}^2}\right)p{\sigma }_i,$$ (A20)

$${\epsilon }_{\infty }=\left(\frac{2{\epsilon }_e+{\epsilon }_i-2p\left({\epsilon }_e-{\epsilon }_i\right)}{2{\epsilon }_e+{\epsilon }_i+p\left({\epsilon }_e-{\epsilon }_i\right)}\right){\epsilon }_e.$$ (A21)

5. Characteristic equations of conductivity and permittivity plateaus for a suspension of single-shell spheres with nonzero membrane conductance

For g_m ≠ 0, the derivations were restricted to the DC plateaus because the complexity of the obtained expression for the other cases makes their usefulness questionable:

$${\sigma }_{DC}=\left(\frac{1-p+\frac{r{g}_m}{{\sigma }_e{\sigma }_i}\left({\sigma }_e+\frac{{\sigma }_i}{2}+p\left({\sigma }_i-{\sigma }_e\right)\right)}{1+\frac{p}{2}+\frac{r{g}_m}{{\sigma }_e{\sigma }_i}\left({\sigma }_e+\frac{{\sigma }_i}{2}-\frac{p}{2}\left({\sigma }_i-{\sigma }_e\right)\right)}\right){\sigma }_e,$$ (A22)

$${\epsilon }_{DC}=\left(\frac{1+\frac{p}{2}+\frac{2r{g}_m}{{\sigma }_e{\sigma }_i}\left({\epsilon }_e-\frac{{\epsilon }_i}{2}+\frac{p}{2}\left({\epsilon }_i+{\epsilon }_e\right)\right)}{{\left(1+\frac{p}{2}+\frac{r{g}_m}{{\sigma }_e{\sigma }_i}\left({\epsilon }_e+\frac{{\epsilon }_i}{2}-\frac{p}{2}\left({\epsilon }_i-{\epsilon }_e\right)\right)\right)}^2}\right)\left(1-p\right){\epsilon }_e+\left(\frac{9}{4{\left(1+\frac{p}{2}+\frac{rgm}{{\sigma }_e{\sigma }_i}\left({\epsilon }_e+\frac{{\epsilon }_i}{2}-\frac{p}{2}\left({\epsilon }_i-{\epsilon }_e\right)\right)\right)}^2}\right)prCm.$$ (A23)

Appendix B: Time Constants of Membrane and Bulk Media Polarizations For Objects with Zero Membrane Conductance

Membrane dispersion

The following derivations were restricted to oriented and spherical objects, because the relaxation time is not well defined for suspensions of nonoriented objects with orientation-dependent relaxation times. To obtain the membrane-time constants, the RC-chain in Fig. 1 B has been reduced to R_i, C_m, and R_e (28) (Eq. 10). The final expressions were obtained by approximating the Taylor series in p by the first-order term. They were numerically checked for their correspondence with the full expressions assuming geometrical and electric parameters relevant for biological cells.

For the membrane-relaxation time ${\tau }_{c1}^{\text{IMP}}$ of suspensions of ellipsoidal (or spheroidal) single-shell objects oriented with their a axis in the field direction, we obtain

$${\tau }_{c1}^{\text{IMP}}=C_m^{\text{spec}}a\left(\frac{1}{{\sigma }_i}+\frac{{\xi }_a}{{\sigma }_e}\right)\left(\frac{{\sigma }_i+\frac{{\sigma }_e}{{\xi }_a}}{\left(1-p\frac{{\left({\xi }_a+1\right)}^2}{6{\xi }_a}\right){\sigma }_i+\frac{{\sigma }_e}{{\xi }_a}}\right),$$ (B1)

with ${\omega }_{c1}^{\text{IMP}}=1/{\tau }_{c1}^{\text{IMP}}$ being the characteristic circular frequency. For spherical objects with ξ_a = ξ_b = ξ_c = 0.5, Eq. B1 simplifies to (33)

$${\tau }_{c1}^{\text{IMP}}=C_m^{\text{spec}}r\left(\frac{1}{{\sigma }_i}+\frac{1}{2{\sigma }_e}\right)\left(\frac{{\sigma }_i+2{\sigma }_e}{\left(1\mathrm{-}\frac{3}{4}p\right){\sigma }_i+2{\sigma }_e}\right).$$ (B2)

For the limiting case of p = 0, Eq. B1 reduces to the membrane-time constant of a single cell τ_c1,

$${\tau }_{c1}^{\text{IMP}}\left(p=0\right)={\tau }_{c1}=C_m^{\text{spec}}a\left(\frac{1}{{\sigma }_i}+\frac{{\xi }_a}{{\sigma }_e}\right),$$ (B3)

which is known from the induced transmembrane potential or the membrane-dispersion peak of spheroidal cells in electrorotation (28). For spherical cells, Eq. B3 is simplified to the well-known equation (5, 50, 70):

$${\tau }_{c1}^{\text{IMP}}\left(p=0\right)={\tau }_{c1}=C_m^{\text{spec}}r\left(\frac{1}{{\sigma }_i}+\frac{1}{2{\sigma }_e}\right).$$ (B4)

In contrast to the equation given by Foster and Schwan (5), Eqs. B1 and B2 predict a slight increase of ${\tau }_{c1}^{\text{IMP}}$ for increasing cell fractions. Because of these differences, we checked that the limiting cases of the time constants for σ_i >> σ_e, σ_i = σ_e, and σ_i << σ_e correspond for ellipsoidal (left) and for spherical objects (right):

$${\tau }_{c1}^{\text{IMP}}=C_m^{\text{spec}}a\frac{{\xi }_a}{\left(1-p\frac{{\left({\xi }_a+1\right)}^2}{6{\xi }_a}\right){\sigma }_e}\text{and}{\tau }_{c1}^{\text{IMP}}=C_m^{\text{spec}}r\frac{2}{{\sigma }_e\left(4\mathrm{-}3p\right)}\text{for}{\sigma }_i\mathrm{\gg }{\sigma }_e,$$ (B5)

$${\tau }_{c1}^{\text{IMP}}=C_m^{\text{spec}}a\frac{{\xi }_a+1}{\left(1-p\frac{\left({\xi }_a+1\right)}{6}\right){\sigma }_e}\text{and}{\tau }_{c1}^{\text{IMP}}=C_m^{\text{spec}}r\frac{6}{{\sigma }_e\left(4\mathrm{-}p\right)}\text{for}{\sigma }_i={\sigma }_e,$$ (B6)

$${\tau }_{c1}^{\text{IMP}}=C_m^{\text{spec}}a\frac{1}{{\sigma }_i}\text{and}{\tau }_{c1}^{\text{IMP}}=C_m^{\text{spec}}r\frac{1}{{\sigma }_i}\text{for}{\sigma }_i\mathrm{\ll }{\sigma }_e.$$ (B7)

For a more detailed discussion, please see Gimsa et al. (33).

Conductivity dispersion of the bulk media

Beyond the membrane dispersion, Z_m contributions can be neglected. For the bulk media-time constants, the RC-chain in Fig. 1 B can be reduced to R_i, C_i, R_e, and C_e (28). The final expressions were obtained by approximating the Taylor series in p by the first-order term and numerically checked for parameters relevant for biological cells. For suspensions of oriented ellipsoidal (or spheroidal) single-shell (or homogeneous) objects, we obtain

$${\tau }_{c2}^{\text{IMP}}=\frac{{\xi }_a{\epsilon }_i+{\epsilon }_e}{{\xi }_a{\sigma }_i+{\sigma }_e}\left(\frac{1}{1-\frac{1}{6}p\frac{\left({\epsilon }_i{\sigma }_e-{\epsilon }_e{\sigma }_i\right){\left(1+{\xi }_a\right)}^2}{\left({\xi }_a{\epsilon }_i+{\epsilon }_e\right)\left({\xi }_a{\sigma }_i+{\sigma }_e\right)}}\right).$$ (B8)

For spherical objects, Eq. B8 can be simplified to

$${\tau }_{c2}^{\text{IMP}}=\frac{{\epsilon }_i+2{\epsilon }_e}{{\sigma }_i+2{\sigma }_e}\left(\frac{1}{1-\frac{3}{8}p\frac{\left({\epsilon }_i{\sigma }_e-{\epsilon }_e{\sigma }_i\right)}{\left({\epsilon }_i+2{\epsilon }_e\right)\left({\sigma }_i+2{\sigma }_e\right)}}\right).$$ (B9)

For oriented ellipsoidal objects and the limiting case of p = 0, Eq. B8 can further be reduced to

$${\tau }_{c2}^{\text{IMP}}\left(p=0\right)={\tau }_{c2}=\frac{{\xi }_a{\epsilon }_i+{\epsilon }_e}{{\xi }_a{\sigma }_i+{\sigma }_e}.$$ (B10)

For spherical cells, Eq. B10 reduces to (50, 51, 67)

$${\tau }_{c2}^{\text{IMP}}\left(p=0\right)={\tau }_{c2}=\frac{{\epsilon }_i+2{\epsilon }_e}{{\sigma }_i+2{\sigma }_e}.$$ (B11)

The τ_c2 expressions are already known from electrorotation (28, 50, 69). For oriented objects of the general ellipsoidal, spheroidal, and spherical shapes the limiting conditions σ_i >> σ_e and σ_i << σ_e can be fulfilled assuming zero conductivity for the lower or, alternatively, infinite conductivity for the higher parameter. Nevertheless, as can be seen from Eqs. B8–B11 the relaxation times will become infinitely short (${\tau }_{c2}^{\text{IMP}}$ = 0) for the assumption of infinitely high conductivities. From the experimental point of view, the assumption of σ_e = 0 and σ_i = 0 for the cases σ_i >> σ_e and σ_i << σ_e is more reasonable. In analogy to the ${\tau }_{c1}^{\text{IMP}}$ considerations, we obtain

$${\tau }_{c2}^{\text{IMP}}=\frac{{\left({\xi }_a{\epsilon }_i+{\epsilon }_e\right)}^2}{\left({\xi }_a\left({\xi }_a{\epsilon }_i+{\epsilon }_e\right)+\frac{1}{6}p{\epsilon }_e{\left(1+{\xi }_a\right)}^2\right){\sigma }_i}\text{and}{\tau }_{c2}^{\text{IMP}}=\frac{{\left({\epsilon }_i+2{\epsilon }_e\right)}^2}{2\left({\epsilon }_i+2{\epsilon }_e\left(1+\frac{3}{4}p\right)\right){\sigma }_i}\text{for}{\sigma }_i\mathrm{\gg }{\sigma }_e,$$ (B12)

$${\tau }_{c2}^{\text{IMP}}=\frac{{\left({\epsilon }_i+{\epsilon }_e\right)}^2}{\left(\left({\xi }_a{\epsilon }_i+{\epsilon }_e\right)\left(1+{\xi }_a\right)-\frac{1}{6}p\left({\epsilon }_i-{\epsilon }_e\right){\left(1+{\xi }_a\right)}^2\right){\sigma }_e}\text{and}{\tau }_{c2}^{\text{IMP}}=\frac{{\left({\epsilon }_i+2{\epsilon }_e\right)}^2}{3\left(1-\frac{1}{2}p\frac{{\epsilon }_i-{\epsilon }_e}{{\epsilon }_i+2{\epsilon }_e}\right){\sigma }_e}\text{for}{\sigma }_i={\sigma }_e,$$ (B13)

$${\tau }_{c2}^{\text{IMP}}=\frac{{\left({\xi }_a{\epsilon }_i+{\epsilon }_e\right)}^2}{\left(\left({\xi }_a{\epsilon }_i+{\epsilon }_e\right)-\frac{1}{6}p{\epsilon }_i{\left(1+{\xi }_a\right)}^2\right){\sigma }_e}\text{and}{\tau }_{c2}^{\text{IMP}}=\frac{{\left({\epsilon }_i+2{\epsilon }_e\right)}^2}{2\left(\left(1-\frac{3}{4}p\right){\epsilon }_i+2{\epsilon }_e\right){\sigma }_e}\text{for}{\sigma }_i\mathrm{\ll }{\sigma }_e.$$ (B14)

We think that these limiting cases may be of technological relevance (see Introduction).

Appendix C: References for Characteristic Equations

We collected references with simplified equations as derived in this article, to the best of our knowledge. Table C1 gives a summary. Nevertheless, in many cases the authors presented only general derivations for the complex impedance, conductivity, or permittivity of suspensions, and did not give explicit expressions or characteristic equations for the DC, intermediate (β_{1_2}), and infinitely high frequencies’ plateaus. In some cases, differences of the DC and infinitely high frequency plateaus are described (designated by index DC–∞ in Table C1), thereby ignoring the β₁-membrane dispersion. Especially in older works, dispersions are discussed in terms of loss angles (61).