Torsional Behavior of Axonal Microtubule Bundles

Abstract

Axonal microtubule (MT) bundles crosslinked by microtubule-associated protein (MAP) tau are responsible for vital biological functions such as maintaining mechanical integrity and shape of the axon as well as facilitating axonal transport. Breaking and twisting of MTs have been previously observed in damaged undulated axons. Such breaking and twisting of MTs is suggested to cause axonal swellings that lead to axonal degeneration, which is known as “diffuse axonal injury”. In particular, overstretching and torsion of axons can potentially damage the axonal cytoskeleton. Following our previous studies on mechanical response of axonal MT bundles under uniaxial tension and compression, this work seeks to characterize the mechanical behavior of MT bundles under pure torsion as well as a combination of torsional and tensile loads using a coarse-grained computational model. In the case of pure torsion, a competition between MAP tau tensile and MT bending energies is observed. After three turns, a transition occurs in the mechanical behavior of the bundle that is characterized by its diameter shrinkage. Furthermore, crosslink spacing is shown to considerably influence the mechanical response, with larger MAP tau spacing resulting in a higher rate of turns. Therefore, MAP tau crosslinking of MT filaments protects the bundle from excessive deformation. Simultaneous application of torsion and tension on MT bundles is shown to accelerate bundle failure, compared to pure tension experiments. MAP tau proteins fail in clusters of 10–100 elements located at the discontinuities or the ends of MT filaments. This failure occurs in a stepwise fashion, implying gradual accumulation of elastic tensile energy in crosslinks followed by rupture. Failure of large groups of interconnecting MAP tau proteins leads to detachment of MT filaments from the bundle near discontinuities. This study highlights the importance of torsional loading in axonal damage after traumatic brain injury.

Introduction

Traumatic brain injury (TBI) is a major public health issue worldwide, with >500,000 diagnosed cases per year and a societal cost of approximately $85,000,000,000 in the United States (1). Transportation accidents, falling incidents, and sport collisions are the leading causes of TBI. TBI is responsible for greater than one-third of all traumatic deaths (2), yet is also one of the most neglected causes of death (3). TBI is defined as an impact to the brain tissue from an external mechanical force such as rapid acceleration and deceleration, contact forces, or penetration of a projectile, causing transient or permanent neurological dysfunction (4). These rapid deformations of the brain result in a cascade of pathological events and ultimately neurodegeneration. Therefore, TBI might result in impairment of cognitive, physical, and psychological abilities (5). In many cases of TBI, widespread disruption of axons occurs through a phenomenon known as “diffuse axonal injury” (DAI). DAI is caused by overstretching and torsion of axons, particularly in the white matter region (6). While today’s imaging methods are not able to detect these microscopic damages to axons (7,8), computational modeling can efficiently simulate the brain tissue behavior subjected to external forces and substantially improve contemporary understanding of the underlying damage mechanisms.

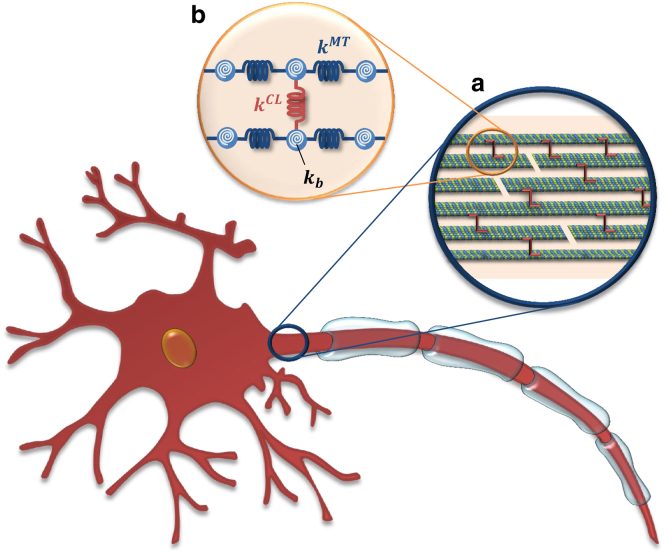
Axons are long slender projections of neurons that conduct electrical impulses away from the cell body. Their shape and mechanical integrity are maintained by a network of filaments comprising the cytoskeleton. Microtubules (MTs), the stiffest elements of the axonal cytoskeleton, are responsible for various essential biological functions such as axonal transport of cargos (9,10). MTs are long and hollow cylinders, made up of 13 parallel longitudinally oriented protofilaments composed of polymerized α- and β-tubulin heterodimers (11–14). Axonal MTs are found to be arranged in organized polarized arrays (15,16), with an average length of 4 μm (17). These hexagonally packed MT bundles are crosslinked by microtubule-associated protein (MAP) tau (16,18), as sketched in Fig. 1. It is worth mentioning that some experimental studies on axonal MTs suggest that they are bundled in a somewhat linear fashion, rather than in a hexagonal shape (called “fasciculated MTs”) (19). Typically, a bundle contains 10–100 MTs per cross-section (20).

Figure 1.

Schematic of a neuron cell along with dendrites and its axon. (a) A zoomed-in view of the axon initial segment showing the bundled MTs. MT filaments, represented by helical structures of heterodimers (blue and green beads), are bundled by MAP tau crosslinks (red). Discontinuities are randomly placed along the length of the filaments. (b) A zoomed-in view of two MT filaments and one MAP tau protein, showing a detailed schematic of the bead-spring model. Bundle filaments are represented by a network of beads (blue) connected by spring elements of axial constant k^MT (dark blue). Torsional springs (white), representing bending stiffness of k_b, were also included for each MT element. Crosslinks (red) are modeled as spring elements with axial spring constant k^CL. (Not drawn to scale.) To see this figure in color, go online.

Rotational acceleration of the brain is a major cause of TBI (1,21), and is suggested as the principal mechanical force responsible for DAI in animal models (22–24). Investigating the mechanical effect of torsion on neuronal axons due to this rotational acceleration would improve contemporary understanding of the underlying mechanism of DAI, which could enhance the effectiveness of future protective devices (25,26). It is believed that axonal swelling is initiated due to breaking of MTs, eventually leading to axonal degeneration (27). Along with uniaxial forces, torsional loads are substantially damaging to MT filaments in DAI, and are suggested to facilitate MT failure (6,28). For instance, rotation of the brain stem may result in torsion of the nerve fibers in the reticular activating system (29). Moreover, breaking and twisting of MTs is observed near the maximum curvatures of axonal undulations, preceding formation of varicosities and degeneration of the axons (30). Some portions of MTs are twisted with a spiral or curling configuration and the collective MT polymers appeared twisted and tortuous, suggesting severe disruption near the breakage points (27). Twisting and misalignment of broken MTs at multiple sites along injured axons appears to hinder relaxation of axons back to their original straight orientation (31).

We have previously investigated the mechanical response of MT bundles under tension and compression (32,33). Our former study on tension of MTs showed that the failure of MT bundles occurs primarily due to the failure of MAP tau proteins. This failure mode is proposed as MT pullout, and is characterized by MTs being pulled past each other and out of the tightly bundled configuration. It was also observed that crosslinked axonal MT bundles demonstrate a stiffening behavior, similar to a power-law relationship from nonaffine network deformations. In our subsequent study of MT buckling behavior (33), we investigated the response of individual MTs as well as MT bundles under compressive forces. Both individual and bundled configurations showed tip-localized, decaying, and short-wavelength buckling. This behavior highlights the role of the surrounding cytoplasm and MAP-tau crosslinks on MT buckling behavior, which allows MT filaments to bear much larger compressive forces without being bent or buckled.

The torsional behavior of axonal cytoskeleton has remained understudied. In practice, torsion of filaments is a very tricky experiment (14,34), suggesting computational modeling as an efficient method to study mechanical behavior of axonal MTs under torsion. This study focuses on the behavior of the MT bundle under torsion as well as combined tension and torsion, the two major loading conditions in DAI (6). A linear torque is applied along the length of the MT bundle so that the bundle undergoes a certain number of turns. To the best of our knowledge, there is no experimentally reported data on the number of possible turns experienced by axons or MTs.

However, a critical buckling angle of 610° for an 8-μm-long MT, which is equivalent to 1.7 turns, is reported by Yi et al. (35). We chose to explore a wider range of up to seven turns to consider extreme twisting conditions of the bundle. We study mechanical behavior of MT bundles, their relaxation behavior, and the influence of crosslink spacing under pure torsion. Moreover, the combination of tension and torsion is examined with particular attention paid to the influence of torsion on bundle failure, in contrast to our previous studies (32,33). The bundle energy distribution is monitored in all different case studies. Finally, the stretching of pretwisted MT bundle is explored to shed light on how mechanical properties of twisted bundles are affected.

Materials and Methods

Discrete bead-spring model

Discrete bead-spring models are often employed to model the mechanical behavior of polymers or filamentous networks (36,37). Our previously developed model has proven useful in studying the mechanical behavior of MTs under external tensile and compressive forces (32,33). We further developed this model to explore the behavior of MTs under torsional stress (Fig. 1). In this model, filaments are represented by bead-spring chains, where neighboring beads are connected by linear springs interacting via elastic forces. Bending stiffness of the filaments is included by introducing torsional springs along the length of the filament. Crosslinks between MTs are represented by elastic springs as well (38). As intrinsically disordered proteins, MAP tau proteins are characterized by a lack of stable secondary and tertiary structure (39). As of this writing, there is not enough evidence that they can bear compressive forces. Therefore, although some MAP tau proteins experience compressive forces in our simulations, they are modeled to only resist in tension in this study. The model includes random discontinuities along the length of the filaments, which are believed to play a significant role in mechanical behavior of MT bundles (40). For a more detailed description of the bead-spring model, please see Section B in the Supporting Material.

An MT bundle was modeled as a hexagonal network of 19 filaments with a center-to-center MT spacing of 45 nm, corresponding to a 20-nm edge-to-edge spacing (18,32). The bead spacing was set to 10 nm to sufficiently resolve bending between MT elements. Each filament was 8-μm long and contains a single discontinuity, resulting in 38 separate MT filaments with an average continuous length of 4 μm. Discontinuities were placed within the central 80% of the filaments, away from the edges of the bundle. Crosslinks were randomly distributed along the length of MTs throughout the bundle to obtain the desired crosslink spacing, i.e., δ_CL. The tau crosslink mass was added to the mass of the beads where crosslink elements were added. Because, in discrete bead-spring models, beads are represented by points (as opposed to spheres) and are connected to each other from their centers, initial length of tau crosslinks are set to 45 nm, equal to the center-to-center distance of MT filaments. To account for failure of MT and MAP tau elements, a critical strain of 0.5 was assigned to MT elements while the critical strain of MAP tau elements was set to 1.0, corresponding to the jump-out length obtained from a study on MAP tau dimerization (16,41). (For a complete set of parameters, please see Table S1A in Supporting Material.) To assess the sensitivity of the model to input parameters, a sensitivity analysis was previously performed on different parameters (32) (please see Section F in the Supporting Material).

The presence of a viscous cytoplasm with viscosity μ was modeled by applying tangential and normal drag forces on MT filaments and MAP tau proteins. MT and MAP tau drag coefficients (C^MT, C^CL) determine the amount of drag force experienced by each element. A numerical integration algorithm, Velocity Verlet, was used to calculate bead trajectories over the duration of the simulations (42). A time step of 0.1 ps was used for stability and computational efficiency.

Application of torsional load

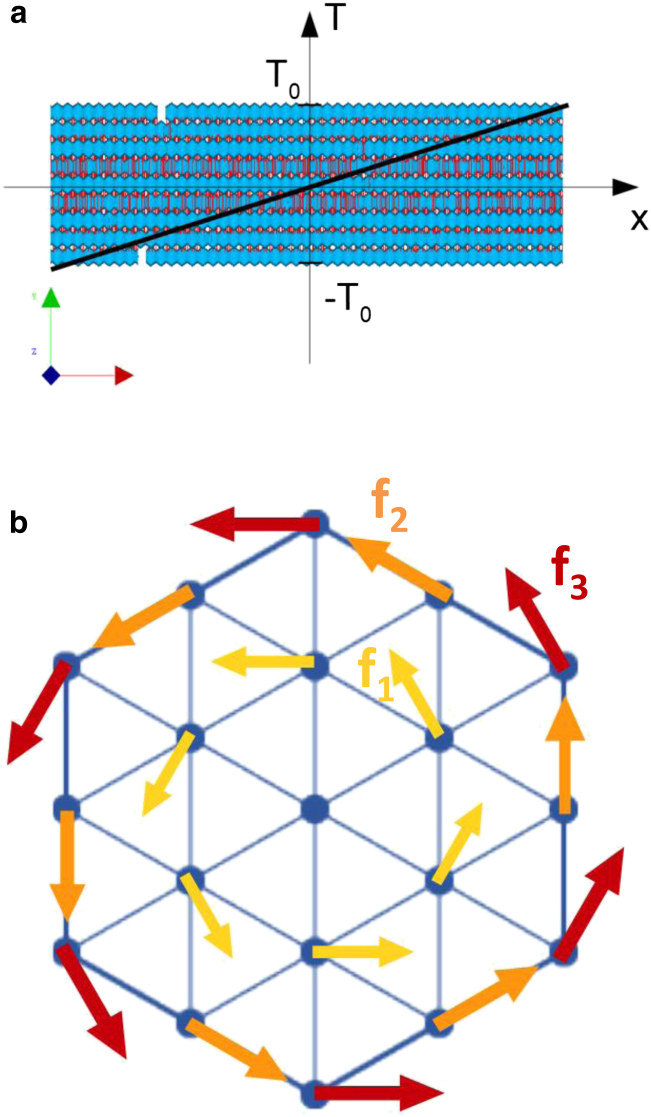
The bundle was twisted along its longitudinal axis. Assuming that cross-sectional planes do not penetrate each other and remain parallel over the course of simulations, a linear torque was applied to the bundle. In each cross-section of the bundle, an orthoradial force was applied to each bead, with its magnitude proportional to the distance between the bead and the center of the bundle. The torque was applied linearly, with its highest values at the two ends of the bundle and zero in the middle (Fig. 2).

Figure 2.

Schematic of the mechanical model used to apply torsional forces. (a) The applied torque is a linear function of x, parallel to the long axis of the bundle. (b) Cross-section of the bundle with orthoradial forces f₁, f₂, and f₃, proportional to the corresponding radii R₁, R₂, and R₃, which are initially 45 nm, $45\sqrt{3}$ nm ≈ 77.0, and 90 nm, respectively. To see this figure in color, go online.

The torque was applied in a ramp-and-hold manner and was distributed evenly among the 18 filaments, excluding the central filament (Eq. 1) (43). The bundle was assumed to maintain its hexagonal configuration during the simulation (see Section D in the Supporting Material). Therefore, the beads were located in three circles of radii R₁, R₂, and R₃, corresponding to applied torsional forces f₁, f₂, and f₃, respectively:

$$T=6R_1{f}_1+6R_2{f}_2+6R_3{f}_3.$$ (1)

Assuming small deformations, shear stress was considered as a linear function of the bundle radius and different radii were assumed to maintain their ratio. An average radius of the bundle inner circle (R₁) was calculated (R_avg). Therefore, the torsional force applied to each bead can be calculated by Eq. 2 (for a more detailed explanation of torsion application, please see Section C in the Supporting Material):

$$f_i=R_i\frac{T}{48R_{\text{avg}}^2}.$$ (2)

A previous theoretical study has reported a critical torque of 77 pN.nm (44), while another study on actin filaments has reported a value of 30 pN.nm (34). Simulations are 5 μs in length with the applied torques of magnitude 0.1–50 nN.nm. The aforementioned assumptions are continuously monitored, to hold valid throughout the simulations (see Section D in the Supporting Material). The applied torques allow for a wide range of 0–7 turns of the bundle during the simulation period. Furthermore, bundle angle was calculated by averaging the angles formed by each of the 12 external MT filaments with respect to the central axis (see Section C in the Supporting Material).

Results and Discussion

Pure torsion

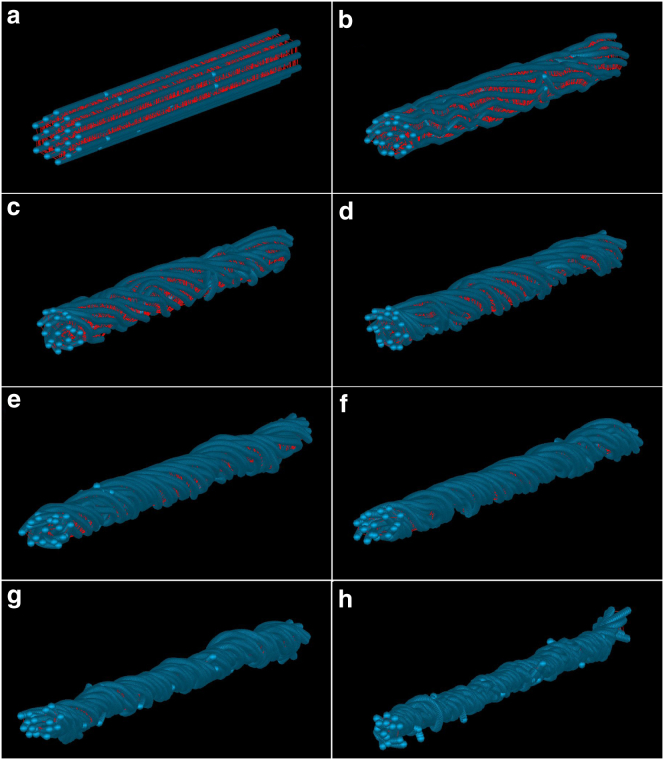
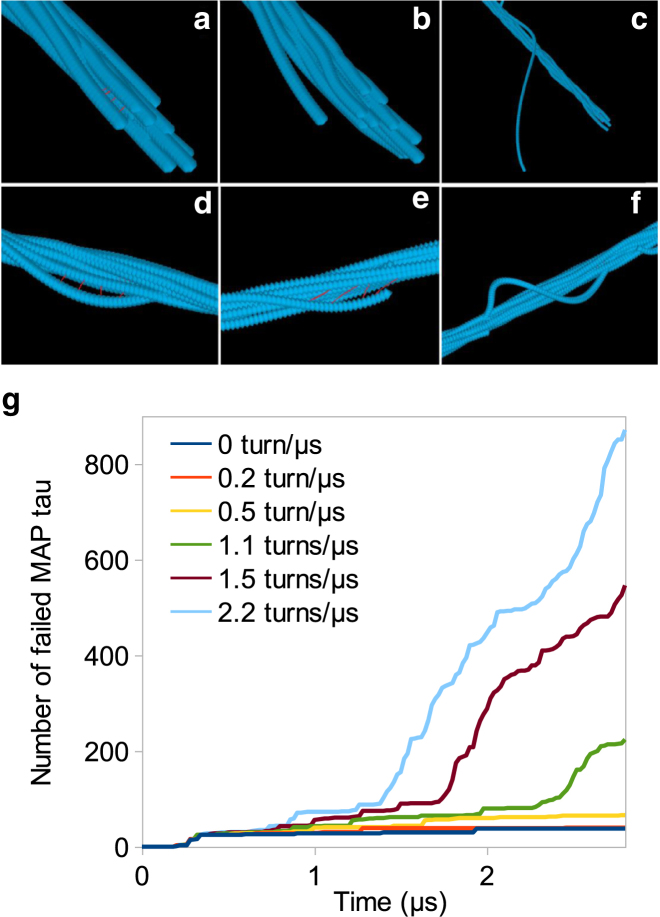
The torsion of the bundle is clearly observable in Fig. 3. During the first three turns, local undulations appear along the length of MT filaments, featuring some instabilities near discontinuities of the filaments. It is also noticeable that filaments do not show the same behavior, which is presumably due to the uneven distribution of MAP tau proteins and discontinuities along the length of the filaments. Upon further twisting, the bundle is smoothed out, undulations are progressively stretched, and the bundle gradually shrinks. Up to three turns, the number of bundle turns increases linearly with time, while afterwards the rate of change in the number of turns increases and becomes a nonlinear function of time (see Section C in the Supporting Material).

Figure 3.

Progressive twisting of MT bundle. (a) 0 turn; (b) 0.83 turn; (c) 1.7 turns; (d) 2.7 turns; (e) 4 turns; (f) 5.1 turns; (g) 7 turns; and (h) >8 turns. Shrinking of the bundle happens at three turns (d and e), and after seven turns (g), the bundle radius is significantly reduced. To see this figure in color, go online.

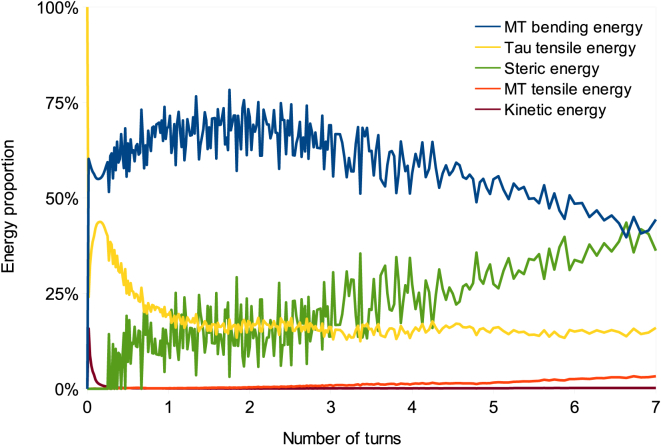
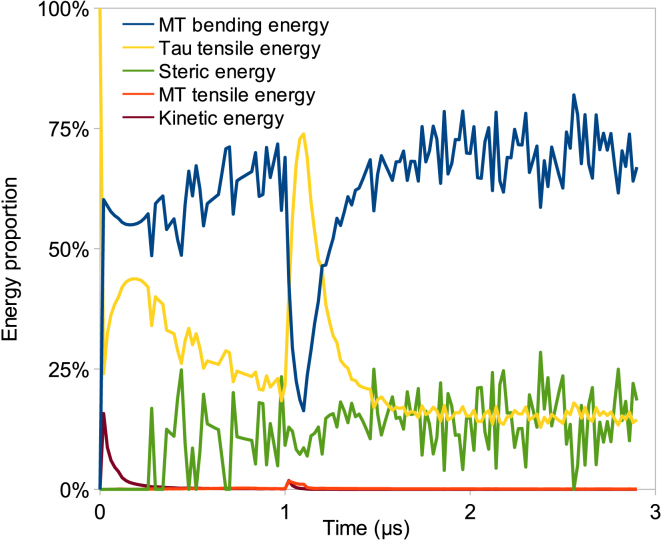
Energy distribution analysis reveals that MT bending and MAP tau tensile energies are the two dominant energy modes (Fig. 4). MT bending energy is dominant throughout the simulations except in the first-half of a turn, where MAP tau tensile energy is almost equal to MT bending energy. Because MT filaments approach each other under torsion, steric energy comprises a significant portion of the total energy of the bundle. In fact, MAP tau proteins that are longitudinally stretched during torsion bring MT filaments together. As steric energy increases during the simulation, two transition points are observed in Fig. 4. The first transition occurs after three bundle turns, where steric energy becomes larger than MAP tau tensile energy and the rate of increase of steric energy clearly increases. At this point, the role of MAP tau proteins is taken over by an increasing repulsion between MT filaments, as MT filaments are approaching each other. Moreover, upon three turns, the number of bundle turns is changed from a linear to a nonlinear function of time (see Section C in the Supporting Material). The second transition happens at around seven turns, where steric energy reaches MT bending energy. This is considered as the criterion of a particular phenomenon occurring during torsion of the bundle, which shall be referred to as “shrinking” of the bundle. Because steric energy becomes too high after seven turns, results are considered inaccurate after this point.

Figure 4.

Energy distribution in the case of pure torsion for seven bundle turns. Energy proportion is defined as the ratio of each type of energy to the total energy of the bundle. MT filament bending and tensile energies, MAP tau protein tensile energy, steric energy, and kinetic energy are given. Gradual increase of steric energy is observed, exceeding MAP tau tensile energy at three bundle turns and reaching MT bending energy at seven turns. Kinetic energy and MT tensile energy do not play a significant role, because the movement of beads is limited in torsion experiments. To see this figure in color, go online.

To conduct a more detailed analysis, the bundle is divided into 10 axial and two radial zones. MAP tau proteins are stretched more in the middle of the bundle compared to the two ends (data not shown). During the first turn, MAP tau proteins in the inner radial zone are more stretched, while afterwards, crosslinks within the outer radial zone are generally more stretched. However, upon further twisting of the bundle, more MAP tau proteins are compressed, reaching 100% in some regions of the bundle, e.g., at the two ends of the bundle and within the inner radial zone.

The influence of MAP tau spacing

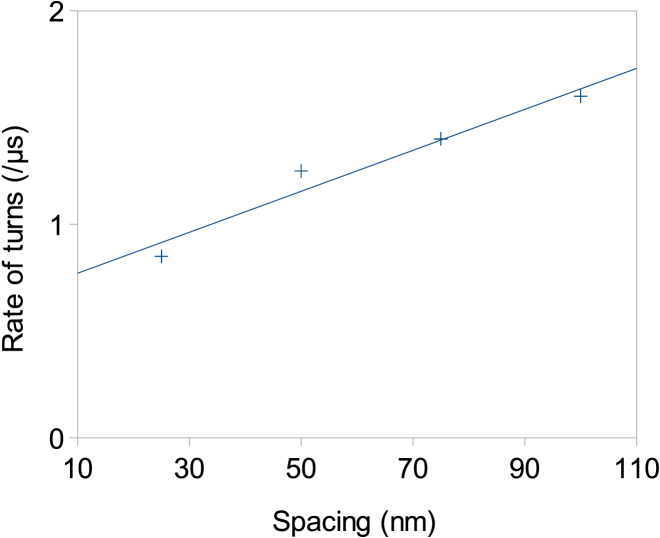
To characterize the influence of MAP tau protein spacing on mechanical behavior of a bundle under torsion, average crosslink spacings of 25, 50, 75, and 100 nm are investigated. Fig. 5 shows the rate of turns, i.e., the number of turns per μs, as a function of crosslink spacing. As the average spacing between MAP tau proteins increases, the rate of MT bundle turn increases in a linear fashion despite nonlinearities embedded in our model, e.g., uneven distribution of MAP tau and discontinuities. This is implying that MAP tau proteins are protecting the bundle from excessive deformation under torsional loading.

Figure 5.

Rate of turns (number of turns per microseconds) as a function of average crosslink spacing under a fixed torque magnitude of 10 nN.nm. Four different spacings are considered: 25, 50, 75, and 100 nm. A linear trend line is shown (f(x) = 0.0096x + 0.675 and R² = 0.952), suggesting a proportionality between rate of bundle turns and MAP tau spacing. To see this figure in color, go online.

Relaxation

To shed light on how axons relax after being subjected to torsional loading, the bundle is subjected to relaxation test after one turn of twisting. The MT bundle is subjected to a torsional loading until it is twisted approximately one turn and, then, the torsion is removed to let the bundle relax. Upon release of the torsion, all different types of energies show a substantial increase, i.e., 10- to 100-fold (see Section E in the Supporting Material), followed by a rapid relaxation toward a steady-state value within 0.5 μs (Fig. 6). Release of the torsional load leads to a rapid decrease in MT bending-energy proportion and a sharp increase in MAP tau tensile energy proportion. This implies that upon removal of the load, MAP tau proteins try to recover the original configuration of the bundle. However, our results show that MT bending energy reaches its preremoval value in a short time, i.e., less than half 1 μs, and the bundle eventually collapses. This is showing that MT bending energy and MAP tau crosslinks are not sufficient for an efficient recovery of the structure after removal of the external torsion. Therefore, further assessment of the relaxation behavior needs a more comprehensive model of the axonal cytoskeleton, i.e., a model that includes interconnection of a MT bundle to other cytoskeletal filaments.

Figure 6.

Energy distribution in a bundle relaxation experiment. The MT bundle is subjected to a torsional loading up to one turn and then the loading is removed at 1 μm. A steady state is reached at 2 μs. Release of the torsional load results in a sharp decrease in MT bending energy and a rapid increase in the proportion of MAP tau tensile energy. This suggests that MAP tau proteins try to recover the initial configuration of the bundle. Steric energy proportion remains roughly constant, suggesting that MT filaments spacing stays approximately constant during relaxation. To see this figure in color, go online.

The influence of torsion on failure under stretch

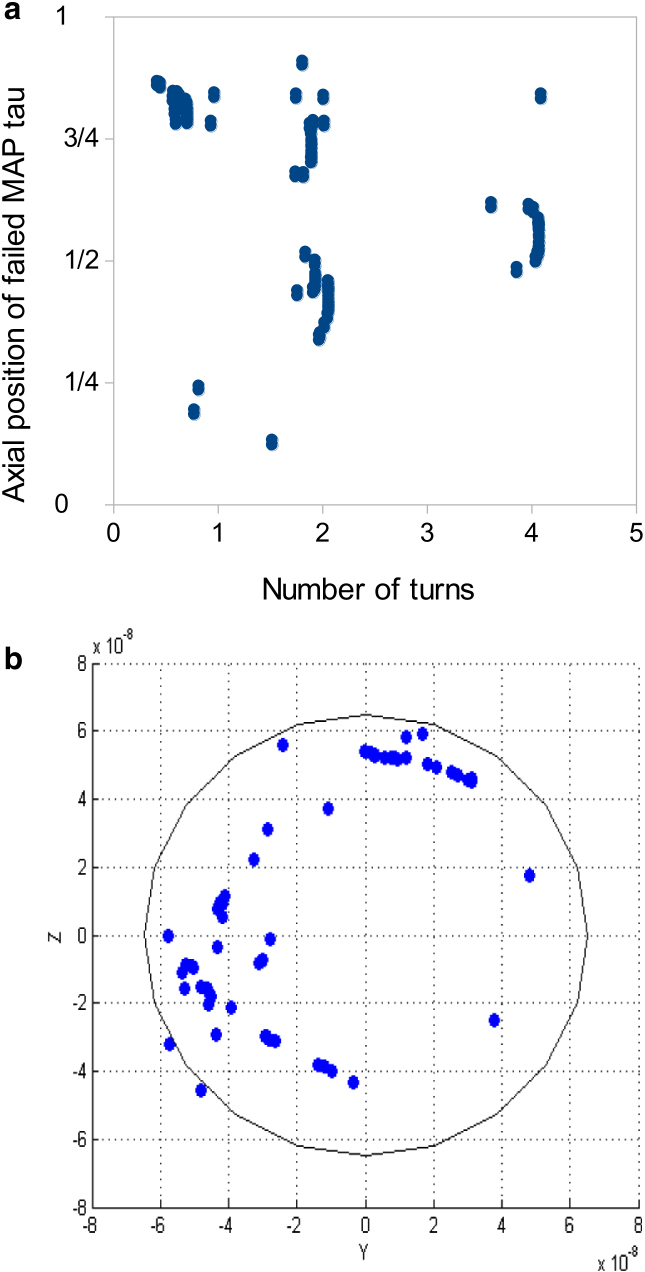
The influence of torsion on failure of the bundle under tension, characterized by rapid increase in number of failed elements, is studied by investigating the number of failed elements and rate of failure. The bundle is subjected to tension and is simultaneously twisted up to five turns. While the critical force for bundle failure is reported to be 10 nN in pure tension experiments (32), our results show that, in the presence of a simultaneous torsional load, failure occurs with a lower tensile force of 5 nN. Therefore, torsion decreases the critical tensional force and triggers the failure in lower forces. The number of failed MAP tau proteins increases in a stepwise manner in time (Fig. 7 g). One could speculate that the MAP tau crosslinks resist tension and build up tensile energy until they reach their critical strain, subsequently failing locally in groups of 10–100 elements (Fig. 8 a). These sets of tau proteins are located near discontinuities of the MT filaments. Furthermore, crosslink failure is initiated at the periphery of the bundle and after two turns, inner MAP tau proteins start breaking (Fig. 8 b), implying that outer filaments have been displaced more relative to each other.

Figure 7.

Mechanism of MT failure under the combination of a tensile force of F = 5 nN and the torsion of seven turns. (a–c) Detachment of the end of one of the filaments. (d–f) Detachment of the filament near a discontinuity. (g) Number of failed MAP tau proteins in time. (Curves) Different rates of turns, i.e., number of turns per microsecond. Higher twisting rate increases the number of failed MAP tau proteins and leads to earlier failure, compared to pure stretching. Number of failed MAP tau proteins increases in a stepwise fashion, implying that MAP tau proteins gradually store tensile energy until they reach their critical strain and fail in groups. To see this figure in color, go online.

Figure 8.

Effect of torsion on bundle failure under a F = 5 nN tensile force. (a) Axial coordinates of failed MAP tau proteins (in fraction of total length) as a function of number of bundle turns. Groups of crosslinks fail locally in certain regions of the bundle. A cluster of 30 MAP tau proteins fails just before one turn. After two turns, two groups of 20 and 15 MAP tau proteins break; after four turns, another set of 10 MAP tau proteins fails. Clusters of failed MAP tau proteins are located near discontinuities of MT filaments. (b) Radial position of failed tau proteins before two bundle turns. Most MAP tau failures are seen at the periphery of the bundle. (Open circle) The bundle. To see this figure in color, go online.

Torsion also seems to trigger failure of individual MT filaments, although it does not occur under pure stretching with the same tensile force (32). This behavior can be clearly seen in the progressive visualization of the bundle in Fig. 7, a–f. Due to failure of interconnecting MAP tau proteins, MT filaments are no longer tightly packed. This detachment of filaments usually starts at discontinuities or at the bundle ends, where the filaments have more freedom to move and MAP tau proteins are extremely stretched. Because filaments of the bundle are very close to each other due to torsion, steric energy between them is significantly increased. Upon failure of MAP tau proteins, steric repulsion pushes the filaments away from each other, which results in ejection of an entire filament out of the bundle. Therefore, a drastic increase in steric profile can be observed as an individual MT filament fails. As expected, the addition of a twisting movement to the stretching of MT bundle accelerates failure of the bundle. Torsion can not only increase the number of failed elements, but also advance the time at which the bundle fails.

Stretching of twisted MT bundles

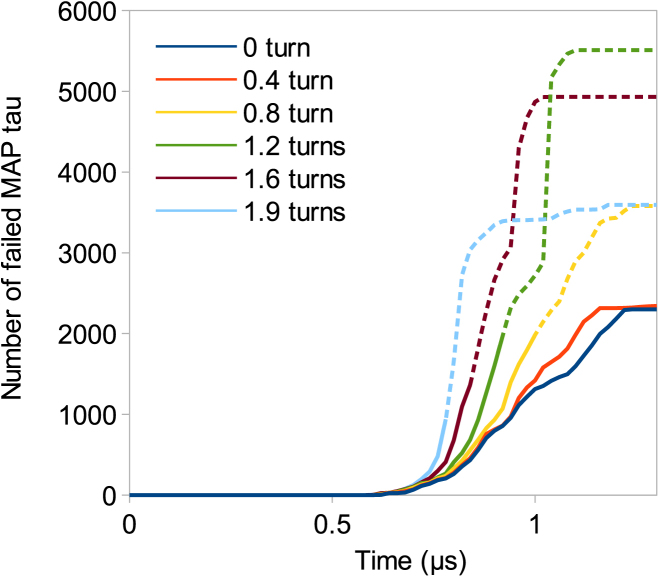
The stretching of a pretwisted MT bundle is also studied by applying a torsional loading from 0 to 0.5 μs and adding tension at 0.5 μs, while continuing the twisting. As expected, the more twisted the bundle before stretching, the more rapidly it will experience failure (Fig. 9). At the two ends of the bundle, stretching tends to unfold the filaments and straighten them, while they continue twisting in the middle. After 1.2 μs, the number of failed MAP tau proteins reaches a plateau. Final number of failed MAP tau is increased by the number of preturns of the bundle, which illustrates the harmful contribution of torsion on axon resistance to tension.

Figure 9.

Stretching of pretwisted MT bundles. Each of the six bundles is twisted by a certain number of turns before being stretched (represented by six colors in legend). (Dashed lines) Point at which an MT filament is ejected from the bundle (see Fig. 7, a–f). Final number of failed MAP tau increases with the number of turns of the bundle before stretching. To see this figure in color, go online.

The influence of torsion on energy distribution

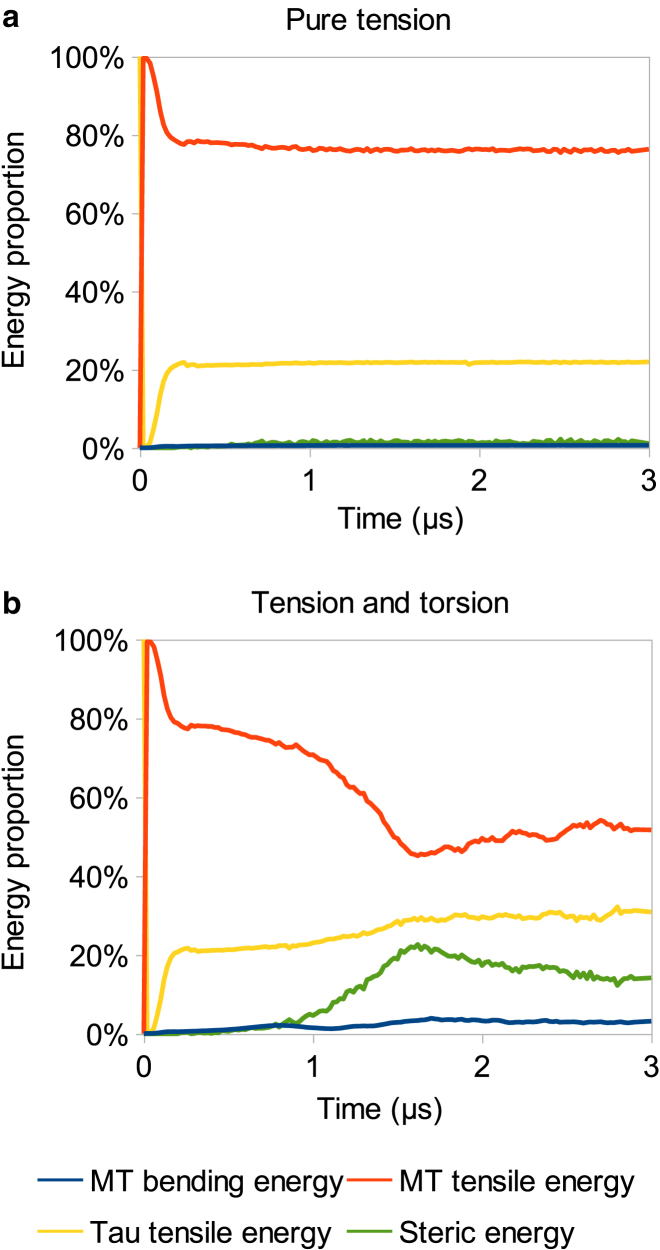
Our previous study showed that application of pure tension on MT bundles results in a steady-state behavior after 1–2 μs. However, MT bundles under simultaneous application of torsion and tension do not exhibit steady-state behavior (Fig. 10). While MT and MAP tau tensile energies are dominant in the case of pure tension (32), i.e., comprising ∼80 and 20% of the total energy, respectively, the addition of torsional loading results in a gradual increase of MAP tau tensile energy, MT bending energy, and steric energy, and the decrease of MT tensile energy. After two turns, MAP tau tensile energy and steric energy reaches 10 and 20% of the total energy, while MT tensile energy drops to 50%. Therefore, addition of torsion to the stretching of MT bundle fades out the role of MT tensile energy in favor of MAP tau tensile energy. Interestingly, at 1 μs, steric energy starts to rapidly increase until ∼1.5 μs. After this rapid increase, all types of energies are maintained at a steady-state value. This increase in steric energy followed by the steady-state behavior shows that the bundle is shrinking into a configuration of more tightly packed filaments. Upon this transition, MT bundle is capable of resisting the external load for longer time, while keeping its mechanical integrity.

Figure 10.

Effect of torsion on energy distribution under a F = 5 nN tensile force. (a) Energy distribution in the case of pure tension. A steady state is rapidly reached within the first microsecond. (b) Energy distribution in the case of combined torsional and tensile loading conditions. Addition of torsion influences the steady-state behavior, postponing the time at which energies stabilize, changing the steady-state values. The role of MT tensile energy is decreased, while steric energy role is becoming more significant due to torsion. To see this figure in color, go online.

Conclusions

It is very difficult to experimentally investigate the mechanical behavior of individual MT and MT bundles under torsion (14,34). In this study, we proposed a coarse-grained model to computationally study the mechanical behavior of MT bundles under external torsional loads. To the best of our knowledge, there is no pathological information available for characterizing how much axonal MT bundles can resist torsional loading. Obviously, a mere computational model, without validation by experimental or other computational studies, could not provide comprehensive and accurate results on this subject. However, the accuracy of our MT bundle model was previously assessed in two studies on tension and compression of individual and bundled MTs (32,33), where a large body of experimental results were used for validation. Based on the reported critical number of turns of 1.7 for single MTs subjected to torsion (35), which gives us a rough approximation of the expected range of critical number of turns, we chose to explore a wider range of up to seven bundle turns. We identified a critical number—three bundle turns—at which a change of regime was observed in steric energy. Rate of change in steric energy is remarkably increased at this point and MT filaments start to undergo chaotic deformations, specifically near discontinuities, leading to the shrinking of the bundle. MAP tau tensile energy and MT bending energy are the most important modes of energies, in the case of pure torsion. The influence of MAP tau spacing was shown to be essential in the mechanical behavior of the bundle, with the rate of turns of the bundle increasing linearly with the crosslink spacing. As in the case of pure stretching and compression of MT bundles (32,33), MAP tau proteins appear to be a protection mechanism against large twisting deformations that can occur in DAI.

Moreover, our results highlight the harmful contribution of torsion when combined with tensile loading, either under simultaneous loading or stretching of pretwisted bundles. Compared to our previous study on uniaxial tension of MT bundles (32), torsion is shown to weaken MT bundles by accelerating MAP tau failure. Interestingly, the number of failed MAP tau proteins increases in a stepwise manner, demonstrating how crosslinks gradually accumulate elastic tensile energy until breakage. MAP tau proteins were observed to fail in clusters localized at discontinuities and the radial periphery of MT filaments, implying that they are more stretched in these regions.

Finally, torsion also seems to trigger failure of individual MT filament near their discontinuities for a large number of bundle turns (typically seven turns). This type of failure is due to breaking of groups of interconnecting MAP tau proteins, leading to detachment of MT filaments from the bundle. This study, along with our previous studies on MT bundles (32,33), lays the foundation for future computational and experimental studies on axonal cytoskeleton to shed light on the underlying mechanisms of DAI.

Author Contributions

C.L., M.S., and M.R.K.M conceived and designed the experiments; C.L. performed the experiments; C.L., M.S., and M.R.K.M. analyzed the data; M.R.K.M. contributed reagents/materials/analysis tools; and C.L., M.S., and M.R.K.M. wrote the article.

Editor: Jennifer Ross.

Supporting Citations

Reference (45) appears in the Supporting Material.