Abstract
Cardiac Ca2+-induced Ca2+ release (CICR) occurs by a regenerative activation of ryanodine receptors (RyRs) within each Ca2+-releasing unit, triggered by the activation of L-type Ca2+ channels (LCCs). CICR is then terminated, most probably by depletion of Ca2+ in the junctional sarcoplasmic reticulum (SR). Hinch et al. previously developed a tightly coupled LCC-RyR mathematical model, known as the Hinch model, that enables simulations to deal with a variety of functional states of whole-cell populations of a Ca2+-releasing unit using a personal computer. In this study, we developed a membrane excitation-contraction model of the human ventricular myocyte, which we call the human ventricular cell (HuVEC) model. This model is a hybrid of the most recent HuVEC models and the Hinch model. We modified the Hinch model to reproduce the regenerative activation and termination of CICR. In particular, we removed the inactivated RyR state and separated the single step of RyR activation by LCCs into triggering and regenerative steps. More importantly, we included the experimental measurement of a transient rise in Ca2+ concentrations ([Ca2+], 10–15 μM) during CICR in the vicinity of Ca2+-releasing sites, and thereby calculated the effects of the local Ca2+ gradient on CICR as well as membrane excitation. This HuVEC model successfully reconstructed both membrane excitation and key properties of CICR. The time course of CICR evoked by an action potential was accounted for by autonomous changes in an instantaneous equilibrium open probability of couplons. This autonomous time course was driven by a core feedback loop including the pivotal local [Ca2+], influenced by a time-dependent decay in the SR Ca2+ content during CICR.
Introduction
Our understanding of human cardiac cell physiology has been greatly facilitated by combining limited human experimental data with mathematical myocyte models based on detailed and systematic knowledge gained by conducting animal experiments (1–3). Two of the most recent models of human ventricular cells (HuVECs), the GPB model (4) and the ORd model (5), were based on an extensive review of human data for membrane excitation, and demonstrated ionic mechanisms underlying the action potential (AP) as well as the Ca2+ transients at various stimulus frequencies. However, what is still required is a cell model that incorporates the updated mechanisms of Ca2+-induced Ca2+ release (CICR), since membrane excitation is largely modified by intracellular Ca2+ dynamics (6). Moreover, CICR is the key mechanism in coupling membrane excitation to muscle contraction.
The empirical equations used to describe CICR so far in most cardiac cell models are of limited use because they were largely simplified. For example, the functional coupling between L-type Ca2+ channels (LCCs) and ryanodine receptors (RyRs) was calculated by referring to a time-dependent increase of [Ca2+] in a single dyadic (or submembrane) space common to the whole population of RyRs within a cell. However, it is now well established that CICR is regulated by the tight coupling between LCCs and a cluster of RyRs individually for each Ca2+-releasing unit (CaRU) (7,8) (this is known as the local control theory). Here, we define the cluster of RyRs as a couplon separate from LCCs. Moreover, the activation and inactivation kinetics of RyR models have been elucidated in much more detail by recent experimental findings.
Greenstein and Winslow (9) formulated a computational model of the cardiac ventricular myocyte that included the stochastic calculation of 12,500 individual CaRUs gating according to the local control of CICR. Subsequently, Hinch (10) and Hinch et al. (11) succeeded in reducing the computational cost of that model by developing a new algorithm (a tightly coupled LCC-RyR model, known as the Hinch model) for calculating CICR processes explicitly for each combination of open or closed conformations of LCCs and a couplon, representing a hypothetical CaRU composed of a group of RyRs. In the Hinch model, the spread of activation to neighboring CaRUs is prevented by assuming that the released Ca2+ is largely diluted by the bulk cytosol separating individual CaRUs, and thus the activation of RyRs is roughly proportional to the LCC activation. However, it is well established that a large Ca2+ gradient occurs near the Ca2+-releasing site (12–17). Any Ca2+ accumulation around a CaRU in general might allow the spread of sequential activation of neighbors through an increase in local [Ca2+] outside the CaRU.
A localized Ca2+ depletion within the SR has been observed during Ca2+ sparks by confocal imaging (18–20). The effects of this Ca2+ depletion were examined by theoretical calculations of the stochastic activation of individual RyRs induced by the spatiotemporal evolution of [Ca2+] within the dyadic cleft. It was demonstrated that the depletion of local Ca2+ content in the terminal cisternae of the sarcoplasmic reticulum (SR) did indeed terminate the Ca2+ release of CaRUs in the absence of an inactivation state of RyRs (SJ model (21), LC model (22), and SM model (23)).
The inactivation of LCC is also a pivotal element in calculating the time evolution of the state transitions of CaRUs. However, most models of Ca2+-dependent inactivation (CDI) are not necessarily based on the cascade of molecular events of the CDI of LCCs (24–27). On the other hand, the Hinch model gives a Ca2+ concentration at the Ca2+-binding site for CDI, which is consistent with the widely accepted theoretical estimation of [Ca2+] near the ion channel exit (25,26,28–30). If the estimation of [Ca2+] at the ion channel exit is realistic, the shortening of AP evoked by increasing the [Ca2+]o (31,32) might be reproduced in a mathematical model through the CDI mechanism.
In our previous study (33), we used the Hinch model to examine the involvement of CICR in the development of early afterdepolarization (EAD) and delayed afterdepolarization (DAD) in a human ventricular myocyte model. Here, we decided that although the basic mechanisms of EAD and DAD would remain essentially the same, we had to improve the state transition of CaRU (11) by removing the rapid inactivation of RyR, since it has been reported that such inactivation is hardly observed in experiments (33–36). We revised the kinetics of the CICR model with respect to the Ca2+ dependency of the couplon closing rate, which was caused by the Ca2+-dependent activation of individual RyRs that constitute the couplon. We incorporated this revised CICR model into our HuVEC model. Using this HuVEC model, we demonstrated mechanisms underlying both graded Ca2+ release in the presence of local Ca2+ accumulation, and the controlled termination of regenerative CICR in the absence of RyR inactivation. Although detailed experiments of CICR have not yet been conducted in HuVECs, it may be timely to propose a comprehensive human ventricular myocyte model that includes membrane mechanisms, mechanistic CICR models, and the contraction of myofilaments.
Materials and Methods
Details regarding the parameters used in this work, the variables and their physical units, cell geometry, Ca2+ compartments, Ca2+ buffers, Ca2+ diffusion, dynamic equations for ion channels and transporters, the CaRU, and changes in ion concentrations and membrane potential, as well as supporting figures are provided in the Supporting Material. The source code of the model can be downloaded at http://www.eheartsim.com. In this section, the Ca2+ compartments, the distribution of ion channels and transporters within each compartment, the definition of nanodomain (nd), and modifications of the Hinch model are described.
Separation of Ca2+ compartments in the HuVEC model
Acsai et al. (12) found a higher [Ca2+] transient of 10–15 μM in a near releasing site (nrs). According to this finding, for our HuVEC model we divided the ion diffusion space (Vcyt) into three Ca2+ compartments (a junctional space (jnc), an intermediate zone (iz), and bulk space (blk), as indicated with different colors in Fig. 1):
| (1) |
The cytosolic Ca2+ gradients were represented in three discrete steps by [Ca2+]jnc, [Ca2+]iz, and [Ca2+]blk. Vjnc was model adjusted to 0.8% of the apparent cell volume (Vcell) to give an appropriate bias level for [Ca2+] around Ca2+-binding sites within a CaRU (denoted as [Ca2+]nd). The iz (= 3.5% of Vcell) defines an intermediate zone between jnc and blk, and may correspond to nrs in Acsai et al. (12).
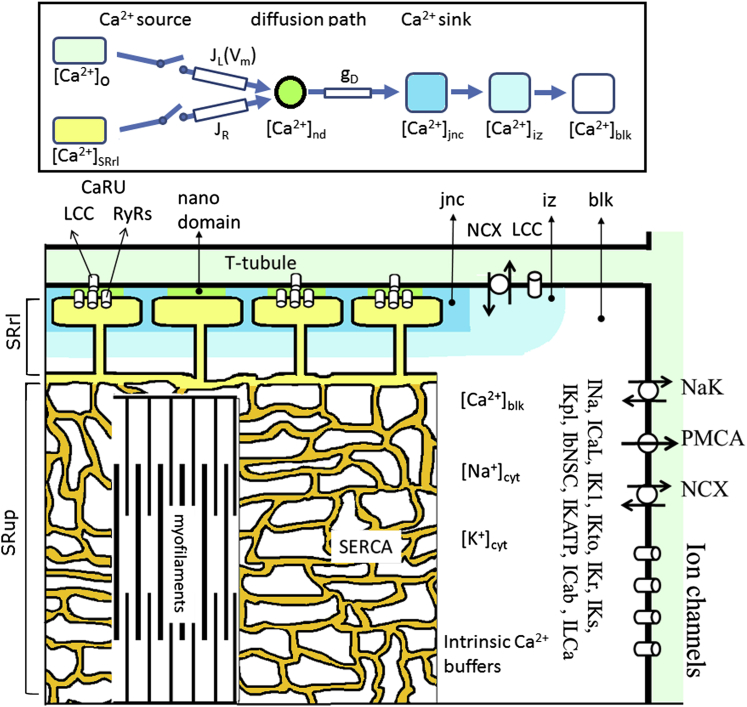
Figure 1.
Composition of the HuVEC model demonstrated by a half-sarcomere. The compartments of jnc, iz, and blk in the cytosol, SR, and T-tubule are filled with different colors. The ion channels and transporters are located on the sarcolemma, SERCA and RyRs are on the SR membrane, and the contractile fibers are in blk. A single CaRU consists of a hypothetical LCC and a couplon in the junctional cleft (filled with green color), and individual CaRUs are spatially separated from their neighbors by jnc. The inset at the top shows a schematic presentation of the diffusion pathway of Ca2+ from the Ca2+ sources to the sink. JL, JR, and gD represent the permeability of single LCCs and RyRs, and the Ca2+ flux rate from nd to jnc, respectively. The myofilaments were embedded in an SR network (SRup). ICaL: L-type Ca2+ current; INa: sum of Na+ currents in transient and late modes; INaT + INaL; IK1: inward rectifier K+ current; IKr: rapid component of delayed rectifier K+ current; IKs: slow component of delayed rectifier K+ current; IKto: transient outward K+ current; IKpl: plateau K+ current; Il(Ca): Ca2+-activated background cation current; ICab: background Ca2+ current; IKATP: ATP-sensitive K+ current; IbNSC: background nonselective cation current; NaK: Na+/K+ pump; NCX: Na+/Ca2+ exchanger; PMCA: plasma membrane Ca2+ ATPase; SERCA: sarco-/endoplasmic reticulum Ca2+ pump.
The ion channels and transporters were distributed on the sarcolemma. ICaL due to LCCs composing the CaRU at nd were assigned to jnc. To simulate CDI of whole-cell ICaL, we assigned 75% of the LCCs to the jnc, 10% to blk, and the rest to iz. Other [Ca2+]-related currents, such as IKs, ICab, IL(Ca), INCX (Na+/Ca2+ exchanger), and IPMCA, were distributed in iz (10%), and the rest of the currents were in blk (90%). All of the other channels and transporters were located in blk. The above assumption for NCX distribution seemed to be adequate for reconstructing the experimental recording of INCX evoked by the Ca2+ transient during 10- and 30-ms step pulses (12). Transferring half of the NCX from iz to jnc hardly affected the result because the [Ca2+]jnc transient diminished too rapidly to evoke NCX effectively (the absence of NCX in rat dyad was previously reported (37), although its exact location is still uncertain (38)). No compartments were assumed for Na+ and K+ because their diffusion was estimated to be rapid (39,40), and all ion channels or transporters independent of Ca2+ were assigned to cyt for the sake of simplicity.
Nanodomain Ca2+ in the CaRU
To derive an expression for the [Ca2+] sensed by the LCCs and RyRs, we used the rapid equilibrium approximation adopted by Hinch (10) and Hinch et al. (11). In this approach, the calcium in the nanodomain ([Ca2+]nd) is assumed to be in an instantaneous steady state, since the time constant for equilibrium in this region is considerably smaller than the open times of the LCCs or RyRs, so that the efflux of calcium into the adjoining sink (jnc in this study) is balanced by the currents through the LCCs and RyRs. Using the same approximation, we can define [Ca2+]nd as a function of [Ca2+] in two Ca2+ sources, SRrl ([Ca2+]SRrl) and extracellular space ([Ca2+]o), and in the Ca2+ sink compartment directly connected to nd ([Ca2+]jnc = [Ca2+]00) and Vm:
| (2) |
where fR (=JR/gD (11) or rRyR/rxfer (41)) and fL (=JL/gD (11) or PLCC/(Vds×rxfer) (41)) indicate the conductivity ratio between influx (flux from a couplon and a hypothetical unit of several LCCs) and efflux (diffusion from nd to the Ca2+ sink compartment next to nd) within nd. δV stands for zFVm/RT.
The first term of the numerator in Eq. 2, Ca00, is the [Ca2+] in a functional Ca2+ compartment, jnc in the HuVEC model, which provides a direct sink of Ca2+ efflux from nd and is calculated by time integration of Ca2+ fluxes. The second and third terms of the numerator indicate components that are directly dependent on Ca2+ fluxes through a couplon or LCC, respectively. The instantaneous equilibrium of [Ca2+]nd implies that nd is located on a diffusion pathway of Ca2+ fluxes from the source pools, i.e., the extracellular space for LCCs and the SRrl for couplons to a Ca2+ sink. Thus, [Ca2+]nd takes an intermediate level between the millimolar level of [Ca2+]o or [Ca2+]SR in the source pool and the micromolar range in the sink pool. In this study, the sink pool of Ca2+ is defined as junctional space (jnc). Thus, [Ca2+]jnc represents C00 in Eq. 2 and potentially is able to activate the CaRU in the absence of LCC activation, typically during a condition of Ca2+ overload of the SR. It should be noted that the [Ca2+]nd has not been defined in the conventional cardiac cell models published to date, including the GPB and ORd models, but is frequently used to calculate the inactivation of LCCs in biophysical studies (26,28,30,42), as well as in the single couplon model of CICR with (43) or without (22,23) LCCs. The NL contraction model of Negroni and Lascano (44) was used without modification.
Modification of the state-transition scheme in the Hinch model
We modified the original Hinch model in three ways. First, the rapid inactivation step of RyR was removed. This was because inactivation occurred too slowly (34,35,45), and CICR termination had been reproduced in the absence of this inactivation state in the SJ, LC, and SM models. The activation and deactivation rates of a RyR were determined based on single-channel recordings obtained experimentally. Second, the state transition to activate a couplon was separated into a triggering step and the subsequent regenerative activation step of RyRs, as was previously done for the full-stochastic SJ, LC, and SM models. In these models, the triggering step by LCCs was replaced simply by randomly opening one RyR (22,23). With regard to the gating properties of LCCs, we assumed that the Vm-dependent step and the Ca2+-dependent step are independent of each other, as described in Shirokov et al. (26). We determined the rate constants of LCC kinetics by using experimental data obtained from HuVECs (Fig. S2). Third, we approximated the closing kinetics of a couplon based on the coincidence of simultaneous closing of multiple RyR openings.
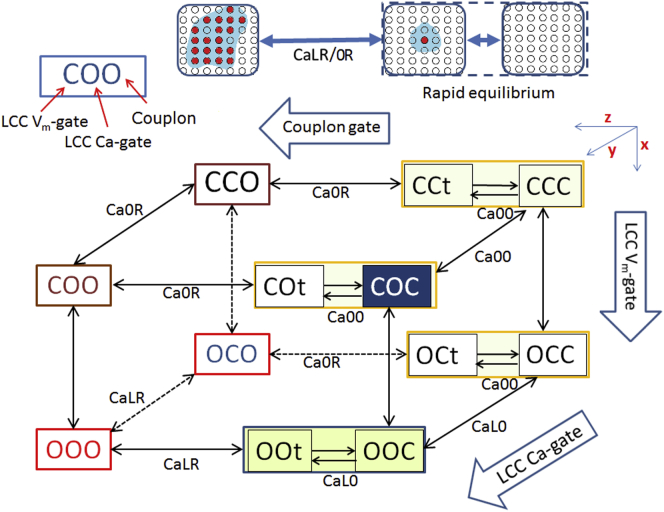
After the modifications described above, CaRU kinetics could be expressed by an eight-state transition scheme as shown in Fig. 2. The gating of Vm-dependent and Ca2+-dependent activations of LCCs and couplon activation are indicated along the x, y, and z axes, respectively. The probability of occupying a functional state of CaRU (Y) is denoted as Yxyz, where subscripts x, y, and z indicate open (O) or closed (C). The four kinds of [Ca2+]nd (Ca00, CaL0, Ca0R, and CaLR) calculated by Eq. 2 regulate the Ca2+-mediated state transition along the y and z axes. When L or R is closed, the subscript for [Ca2+]nd becomes 0 and the corresponding value of [Ca2+]nd is calculated by nullifying JL or JR, respectively, in Eq. 2. The YCCt, COt, OCt or OOt defined by the subscript t in the functional state of Y indicates the probability of a triggered state, driven by CaL0 or Ca00 as indicated in the scheme. Note that the regenerative step was determined by CaL0 and CaLR for Yooo and by Ca00 and Ca0R for the conformation states Ycoo, Ycco, and Yoco of CaRU.
Figure 2.
Scheme of the state transitions of the CaRU model (see text for further explanation). The inset shown at the top is a schematic illustration of a cluster of RyRs corresponding to the closed, triggered, and activated states of a couplon from right to left, respectively. Circles filled with red are open RyRs and open circles are closed ones. The blue stretch in the vicinity of open RyRs is an image of spreading Ca2+. The first activation of a single RyR within a couplon is achieved either by Ca2+ influx through an activated LCC or by a spontaneous increase in [Ca2+]nd during various Ca2+-overload conditions.
Determination of couplon kinetics
The opening (kco) and closing (koc) rate constants of RyR determined from the single RyR recordings under physiologically relevant conditions are variable in the literature (46) (Fig. S5). In this study, we adopted the rate constants used by Stern et al. (23), who referred to measurements by Guo et al. (47), to facilitate a comparison between the HuVEC model and the SM toy model. We adjusted the rates for temperature by introducing a temperature factor (Q10 = 3) after introducing a Hill equation for Ca2+ binding:
| (3) |
| (4) |
The original koc (0.118 ms−1) was multiplied by 4.8, referring to koc used in previous CICR models (see Fig. S5).
For the triggering step of opening a single RyR by an adjacent LCC or spontaneously, an instantaneous equilibrium was assumed, and the probability of the triggered state (ft) of a couplon was given by
| (5) |
In the regenerative step, an increasing number of RyRs are activated through nearest-neighbor activation by Ca2+ release within a couplon, as previously demonstrated in a full-stochastic simulation by Laver et al. (22) (see their Fig. 2). For practical purposes, this mechanism was approximated by a two-state transition model between full-open and closed states of a couplon. The forward rate krco and backward rate kroc of the regenerative step were determined from the single-channel RyR kinetics kco and koc by Eqs. 6 and 7:
| (6) |
| (7) |
The factor fn in Eq. 6 is a multiplying factor (= 7 in the HuVEC model) to express the spread of Ca2+ to activate nearest-neighbor RyRs within a couplon in the regenerative step. The last factor of Eq. 6 is adopted from the original SM model. Equation 7 is an empirical formula deduced by conducting a stochastic simulation of open-closed-state transitions of a number (NRyR = 10) of individual RyRs within a couplon, defining a closed event of couplon with simultaneous closure of all RyRs. The pC is a steady-state probability of the closed conformation of a RyR. The l (= 0.74) is a correcting factor for the probability of simultaneous closure of (NRyR − 1) RyRs. Thus, kroc decreases as kco increases with increasing [Ca2+]nd. The lifetime of open events measured in the stochastic simulation agreed well with the kroc determined by Eq. 7 at NRyR = 1–20 or at various [Ca2+]nd. For further explanation, see “Determination of the deactivation rate of a couplon” in Supporting Materials and Methods.
The rate of change in the open probability of a couplon (pO) in a two-state transition model is then expressed as follows:
| (8) |
We validated the overall activation and deactivation rates by performing a stochastic simulation of couplon activity (Fig. S6). Assuming the existence of 20,000 couplons in a whole cell, we observed 196 open events within 1000 ms, which is comparable to the 100 sparks/s reported for rat cardiac myocytes at a whole-cell level at rest (48).
Results
Excitation and contraction in our presented HuVEC model
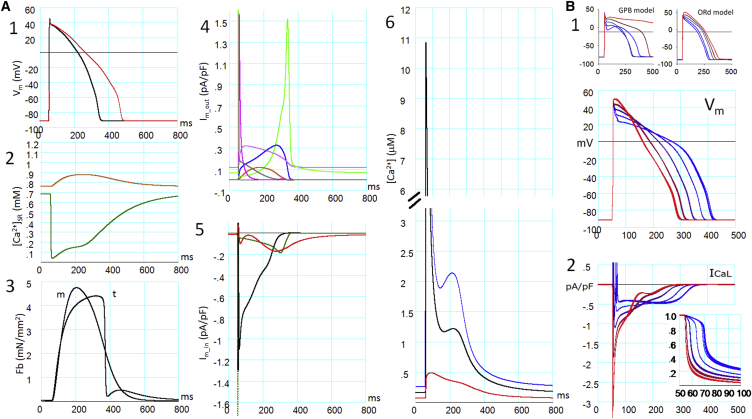
The new, to our knowledge, HuVEC model was able to restore a stable cycle of activity whenever the cycle length (CL) of stimulation was altered within the range examined (0.25–3 Hz; Fig. S9). A single cycle of activity is demonstrated in Fig. 3 A at a standard CL of 1000 ms. Fig. 3 A1 shows the control AP (black trace) and the AP after complete IKr block (red trace). The shape and the APD90 of these APs are quite comparable to those reported in Jost et al. (49) in both the control and during the IKr block: APD90 was prolonged from 291 to 424 ms (46% increase) as compared with 278–433 ms (56% increase) in Jost et al. (49). The standard AP parameters are comparable to those reported in ventricular myocytes (see the legend of Fig. 3 for references). The major plateau currents were ICaL, INaL, and INCX in the inward direction (Fig. 3 A5), and IK1, IKto, IKpl, IKr, IKs, and INaK in the outward direction (Fig. 3 A4). In Fig. 3 A2, [Ca2+]SRrl (green) rapidly decreased from ∼0.69 to a minimum level of ∼0.04 mM, and [Ca2+]SRup (chocolate) increased during the increase in [Ca2+]blk. The recovery of [Ca2+]SRrl (green in Fig. 3 A2) was relatively slow during the AP because of the remaining small open probability of couplons due to incomplete CDI of ICaL, as indicated by the plateau level of [Ca2+]iz (∼1.15 μM) at ∼200–300 ms in Fig. 3 A6 (black). After repolarization, the voltage gate of LCC was totally closed by ∼350 ms (black in Fig. 3 A5), and [Ca2+]SRrl (green in Fig. 3 A2) smoothly recovered during the diastolic period as a result of the Ca2+ supply from SRup. The peak magnitudes of the Ca2+ transient were 106.3, 11.1, and 0.49 μM in jnc (not shown), iz (black), and blk (red), respectively (Fig. 3 A6). The peak of developed tension (Fb) was quite delayed in the isotonic condition (t in Fig. 3 A3) compared with the isometric contraction (m in Fig. 3 A3), and relaxed quickly after the repolarization of AP in the NL contraction model (44).
Figure 3.
(A and B) A standard AP in the HuVEC model (A) and the effects of increased [Ca2+]o on the AP and ICaL (B). The AP was evoked by a 3-ms current injection at 50 ms. When stabilized at CL = 1000 ms, the AP parameters were measured. (A1, the resting potential) Approximately −91.4 mV (−84 mV (50), −81 mV (51), −87 mV (52)); maximum rate of rise of the AP: 244 Vs−1 (comparable to that in Péréon et al. (52)); duration at 90% repolarization (APD90): 287 ms (300 ms (51,53,54); and the plateau of Vm immediately after phase 1 repolarization: ∼+37.7 mV. The red AP was obtained when IKr was completely suppressed in a separate protocol. (A2) [Ca2+]SRup (chocolate) and [Ca2+]SRrl (green). (A3) Isotonic Fb at 6 mN/mm2 (trace showing the delayed peak, t) and isometric Fb at 0.91 μm half sarcomere length (m) in mN/mm2. (A4) Outward current components (IKto (magenta), IKr (blue), IKs (chocolate), IK1 (yellow-green), IKpl (gray), and INaK (pink)). (A5) Inward current components (INaL (dark green), ICaL (black), and INCX (red)). The negative peak of INaL at the onset of the AP is off the scale. INaT was not plotted. (A6) [Ca2+]jnc (blue), [Ca2+]iz (black), and [Ca2+]blk (red). The large transient peak of [Ca2+]jnc is off the scale and not shown. (B1) APs after a change in [Ca2+]o are superimposed in the GPB and ORd models (top). Gradient colors from blue to red are coded in reference to [Ca2+]o, which was increased from 0.45 to 7.2 mM by a factor of 2. The same values for [Ca2+]o were applied to the HuVEC model, and five AP traces were obtained after a change in [Ca2+]o are superimposed (bottom). (B2) Traces of the ICaL current and open probabilities of its Ca2+-dependent inactivation gate (inset, with an expanded timescale) are shown using the same color code as in (B1).
The responses of the model cell to varying stimulus frequencies over the range of 0.25–3 Hz were examined and the results agreed well with the experimental findings as well as simulation results in both GPB and ORd models (for details, see Fig. S9).
CDI of ICaL revealed by varying [Ca2+]o
The CDI of LCCs plays a pivotal role in regulating CICR. In our previous study (33), we confirmed that CDI was retarded by preventing SR Ca2+ release as demonstrated experimentally (12). Here, we further examined whether our CDI model, directly influenced by [Ca2+]nd in the Hinch formulation, could reproduce the other key experimental finding that an increase in [Ca2+]o shortens the duration of the AP (APD), accompanied by a positive shift of the AP plateau potential (as observed in rabbit atrial cells (32) and guinea-pig ventricular cells (55)). As a result, changes in AP obtained by varying [Ca2+]o to 0.45, 0.9, 1.8, 3.6 and 7.2 mM in Fig. 3 B1 (+37, +20, 0, −17, −35% change in APD measured at 50% repolarization, APD50) agreed well with the experimental findings (+30, 0, −27% change in APD50 by varying [Ca2+]o to 0.62, 2.5, and 10.0 mM (32), and +45, 0, −22% change in APD50 by varying [Ca2+]o to 0.01, 1.8, 5.4 mM (55)), although the results were obtained in different animals. It was evident that CDI was accelerated with increasing [Ca2+]o as shown by the open probability of the Ca2+-dependent inactivation gate in Fig. 3 B2 (inset). In contrast, APD was elongated with increasing [Ca2+]o in the GPB and ORd models, as shown in Fig. 3 B1. It should be noted that previous models mostly failed to reconstruct this APD shortening with increasing [Ca2+]o, except for those developed by Matsuoka et al. (56) and Grandi et al. (57), and the APD shortening effect was much smaller in those models compared with the HuVEC model. In the Hinch formulation of CaRU kinetics, the CDI of LCCs is determined by [Ca2+]nd, which is directly related to [Ca2+]o when the LCC is open (Eq. 2), and this in turn increases the CDI rate ε+ of LCCs (Eq. S5).
Initiation and termination of CICR during the AP
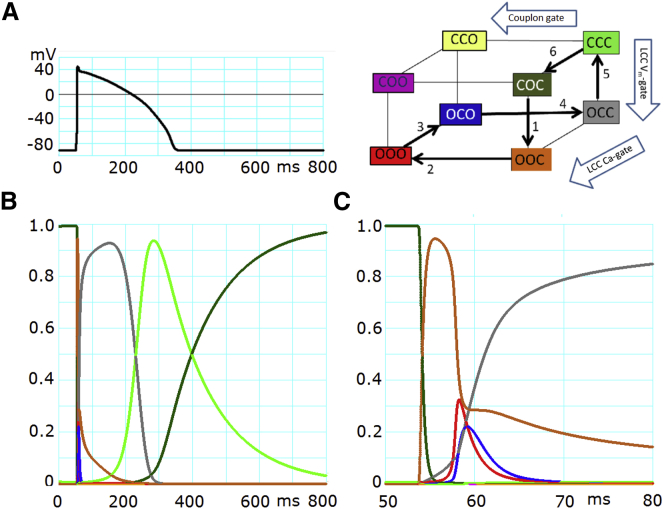
The state transitions of CaRU during the entire time course of an AP are shown together with Vm in Fig. 4, A and B. The transitions during the initial 15 ms of the AP are shown in Fig. 4 C on an expanded timescale. Just before the AP, ∼99.2% of CaRUs were in Ycoc (dark green) and the rest (0.8%) were in Yccc (lime), indicating that the Vm gate of LCC and the couplon gate were almost completely closed. At the onset of the AP, LCC was maximally activated to Yooc (chocolate, step 1 in Fig. 4, inset). The subsequent rapid opening of couplons (steps 2 and 3) is represented by transient peaks of Yooo (red) and Yoco (blue) in Fig. 4 C. The peak time in Yoco (blue, step 3) was only slightly delayed because CDI of LCCs is rapid (<∼1 ms). Since the Vm gate of LCC was continuously open, Ycoo (magenta) and Ycco (yellow) scarcely appeared during the AP. The couplons closed through these rapid state transitions, and the closed conformation of couplons, Yocc (gray), peaked at ∼100 ms after the AP onset. During the subsequent repolarizing phase shown in Fig. 4, A and B, Yocc (gray) was replaced by Yccc (lime) due to closure of the Vm gate of LCC (step 5). Finally, during diastole, the removal of CDI gradually proceeded to complete the recovery from Yccc (lime) to Ycoc (dark green) (arrow 6 in Fig. 4, inset).
Figure 4.
State transitions of CaRU during the AP. (A) The AP was triggered by a 3-ms current injection at 50 ms. (B) The probability of each state of CaRU is plotted on the same timescale as in (A) (ms). Each trace color indicates the state of CaRU of the corresponding color in the inset. Arrows 1–6 in the inset show the direction of major fluxes of the CaRU state transition after onset of the AP. (C) The time courses of the same state probabilities as in (A) are plotted on an expanded timescale for the initial period of 50–80 ms.
Role of the feedback loop in determining the time courses of initiation and termination of CICR
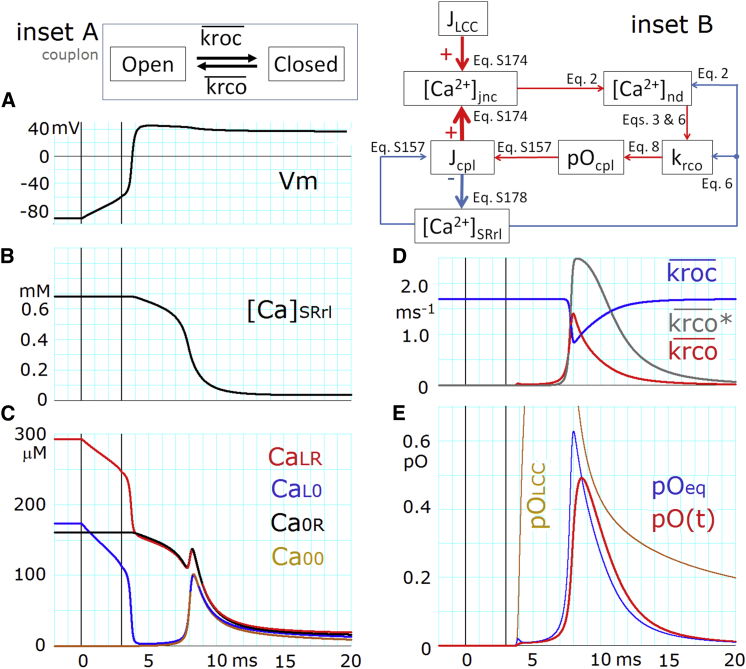
To identify key factors in determining the activation time course of a couplon in HuVEC model, the eight-state transition scheme in Fig. 4 (inset) was reduced to a two-state scheme of couplon kinetics (Fig. 5, inset A). The overall activation and deactivation rates, and , in this reduced scheme are given by a sum of the four activation rates (kxyc.xyo) and deactivation rates (kxyo.xyc) weighted by the probability (Yxyc and Yxyo) of staying in each state of the couplon:
| (9) |
The rate constants kxyc.xyo and kxyo.xyc are given by Eqs. 6 and 7. The deactivation rate transiently decreased due to decreases in pC when [Ca2+]nd was increased by activation of the couplon. An instantaneous equilibrium open probability of a couplon, pOeq, is then calculated by the following equation, using [Ca2+]jnc, [Ca2+]SRrl, and Vm at each time step of the time integration throughout the time course of pO(t):
| (10) |
Fig. 5 shows the time-dependent variables involved in determining and , such as Vm (Fig. 5 A), [Ca2+]SRrl (Fig. 5 B), and the four kinds of [Ca2+]nd (Fig. 5 C) on a common expanded timescale, in addition to the time course of and (Fig. 5 D). In Fig. 5 E, it is evident that pO(t) (red trace) always follows pOeq (blue) with a time constant τ:
| (11) |
| (12) |
In other words, whether CICR will develop (pOeq > pO(t)) or terminate (pOeq < pO(t)) is decided by the movement of pOeq. Fig. 5, inset B, shows the sequence of interactions among time-dependent variables involved in determining the time course of open probability of a couplon, pOcpl (pOeq or pO(t)), with corresponding equations.
Figure 5.
Activation and deactivation of couplons determined by the positive-feedback mechanism. (A) AP. (B) [Ca2+]SRrl. (C) [Ca2+]nd (CaLR, CaL0, Ca0R, and Ca00). The dotted curves of CaLR, CaL0, and Ca0R indicate that they are theoretical values and have virtually no influence on the kinetics, since both the couplon and LCC are mostly closed during this period. (D) The overall activation rate ( ) and deactivation rate ( ) of the couplon and were obtained after fixing [Ca2+]SRrl to a control value. (E) pO(t) (= Yooo + Ycoo + Yoco + Ycco, red), and pOeq and pOLCC (Yooo + Yooc; the peak is off the scale). The two vertical lines in all panels indicate the onset and offset of the stimulus current pulse. Inset A shows the reduced two-state transition of a couplon. Inset B shows the feedback loop formed by the five time-dependent variables, connected by five red arrows with equation numbers. The thick red and blue arrows indicate each Ca2+ release flux, which directly increases or decreases [Ca2+]jnc or [Ca2+]SRrl, respectively.
At the onset of an AP, LCC is immediately and almost fully activated (pOLCC in Fig. 5 E, chocolate trace). However, the rapid increasing phase in pOcpl (Fig. 5 E, red or blue) occurred with a significant delay of ∼4.5 ms after the onset of LCC activation. This delay is caused by the fact that the magnitude of ICaL largely decreases when Vm shifts from the resting potential toward more positive potentials. The magnitude of CaL0 rapidly decreases along the AP onset (blue trace in Fig. 5 C, and the minimum value is 3.35 μM at ∼4.5 ms), and thus CaL0 fails to trigger an immediate regenerative activation of the couplon. The low CaL0, however, activates a small but gradually increasing number of CaRUs, and thus the Ca2+ fluxes through couplons cause a delayed time-dependent increase in jnc ([Ca2+]jnc = Ca00, chocolate in Fig. 5 C). During a delay of ∼4.5 ms, this Ca2+ accumulation progressively increases to generate a rapidly rising foot in pOcpl. In Fig. 5, inset B, the variables connected by red arrows (pOcpl, Jcpl, [Ca2+]jnc, [Ca2+]nd and krco) compose a positive-feedback loop, which evokes the exponential activation of pOeq and thus pO(t).
On the other hand, [Ca2+]SRrl gradually decays during 4–8 ms because of increasing Ca2+ release from the SR (Fig. 5 B). This decay in [Ca2+]SRrl tends to interfere with the enhancements of in the positive-feedback loop, mainly by decreasing three parameters: 1) the factor (sloc0 + [Ca2+]SRrl) in Eq. 6; 2) [Ca]nd, as indicated in Fig. 5 C (Eq. 2); and 3) Jcpl (JCa_rel in Eq. S157 in Supporting Materials and Methods). The net balance between the competitive effects of increasing [Ca2+]jnc and decreasing [Ca2+]SRrl on the positive-feedback loop is positive during the rising phase (5–8 ms) and reverses its sign in the falling phase of CICR (>9 ms).
It should be noted that these findings are entirely consistent with the results of full-stochastic simulations of CICR in a single CaRU (22,23) showing that CICR termination is driven by the feedback loop between a decrease in [Ca2+] in the dyadic cleft and nopen (in analogy to the decreasing [Ca2+]jnc and pOcpl in the HuVEC model). Indeed, the [Ca2+]jnc (Ca00 in Eq. 2) is a major factor in determining [Ca2+]nd after the start of regenerative couplon activation (Fig. 5 C). The rising phase of activation of pO(t) (Fig. 5 E, red), lasting for only a few milliseconds, is also in good agreement with that observed in the full-stochastic simulation by Laver et al. (22).
To examine the influence of the last factor in Eq. 6, the (sloc0 + [Ca2+]SRrl) was fixed to a control value (= 0.7337 mM) before stimulus onset (Fig. 5 D). The appearance of the rising foot was slightly retarded, but the activation rate ( ∗) was enlarged significantly by this intervention (gray curve), and the deactivation time course was prolonged, indicating that the factor (sloc0 + [Ca2+]SRrl) indeed decelerates activation and enhances the termination of CICR.
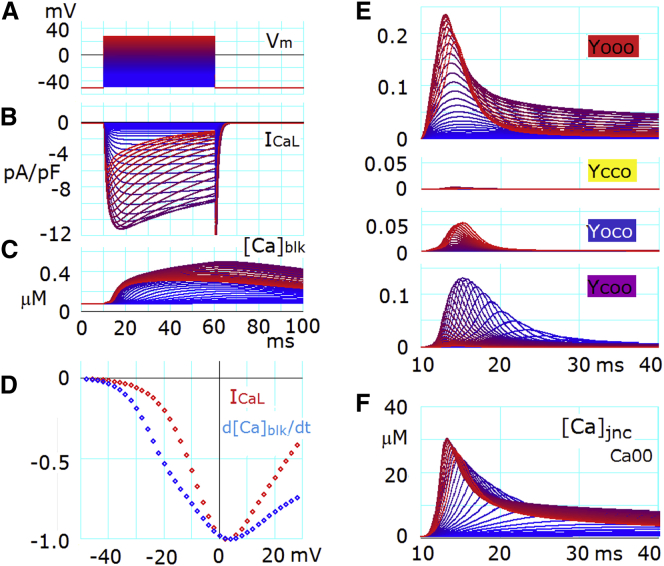
Graded Ca2+ release during voltage clamp in the ventricular cell model
In the feedback loop (Fig. 5, inset B), the component [Ca2+]jnc is common to all CaRUs in the HuVEC model. Thus, Ca2+ accumulation in jnc may compromise the graded Ca2+ release in voltage-clamp experiments. This possibility was examined as shown in Fig. 6. Test depolarizing pulses were applied at 2 mV increments from a holding potential of −50 mV. ICaL was activated in the usual voltage-dependent manner. In proportion to ICaL activation, the peak amplitudes of Yooo increased (Fig. 6, B and E, graph 1). At strong depolarizations, Yoco also appeared with increasing peak amplitude through CDI of LCC (Fig. 6, B and E, graph 3). In addition, Ycoo was activated with a markedly delayed time course of activation at negative potentials (Fig. 6 E, graph 4). The concomitant time evolution of Ycoo with Ca00 (= [Ca2+]jnc) (Fig. 6 F) indicated that this activation of Ycoo was largely due to the state transition from Ycoc to Ycoo evoked by the [Ca2+]jnc accumulation. At more positive test potentials, the peak of Ycoo decreased because an increasing number of CaRUs were activated by the Vm-dependent LCC activation pathway as observed during the AP, i.e., the same mechanism as indicated in Fig. 4 C and arrows 1–4 in the inset during the AP.
Figure 6.
Graded Ca2+ release evoked by voltage-clamp pulses. (A) Voltage-clamp pulses for 50 ms were applied from a holding potential of −50 mV to various depolarized levels, from −38 to +30 mV, in increments of 2 mV. All recordings in all panels except for (D) are plotted with gradient colors from blue to red, coded in reference to the test potentials shown in (A). (B) Whole-cell ICaL. (C) [Ca2+]blk. (D) The voltage relationship of peak ICaL (red) and peak d[Ca2+]blk/dt (blue) was recorded with test pulses in 2 mV increments, normalized by each peak value. (E) Time evolution of Yooo, Ycco, Yoco, and Ycoo. (F) Ca2+ accumulation in jnc is represented by Ca00.
To examine the influence of this CaRU activation through an increase in [Ca2+]jnc, we plotted the relationship between the test potential and the peak of d[Ca2+]blk/dt together with the peak ICaL-Vm relation after normalizing to their peaks as in a previous experimental study (7) (Fig. 6 D). It is evident that the HuVEC model captures key properties of the graded Ca2+ release even in the presence of local Ca2+ accumulation. The time courses of Ca2+ transients in blk evoked by each clamp pulse are superimposed in Fig. 6 C. One might be able to resolve the difference in the relationship between the dependencies of d[Ca2+]blk/dt and ICaL on Vm in the positive Vm range in the HuVEC model from experiment (7) by conducting voltage-clamp experiments under controlled levels of [Ca2+]SRrl.
Discussion
Mathematical analysis of couplon activation
CICR in the HuVEC model is based on biophysical mechanisms to a much larger extent than that in previous human or animal cell models, which mostly used the conventional common-pool model of CICR. Here, the CICR mechanisms are compared with the models specified for CICR rather than with other whole-cell models.
The two crucial and innovative assumptions in the tightly coupled LCC-RyR kinetic model (Hinch model) remain intact in our revised model. First, the compound kinetic states of the CaRU are defined by combinations of three different gates: the Vm-dependent and Ca2+-dependent gates of LCCs, and the activation gate of couplons. Second, the [Ca2+]nd around the Ca2+-binding sites for couplon activation and LCC inactivation is given by an instantaneous function of [Ca2+] in the two Ca2+ sources and the sink when the LCC and/or couplon are open (Eq. 2). To be consistent with the detailed stochastic models of CICR, however, the activation step of a couplon is separated into a triggering step and a regenerative step, which are driven by [Ca2+]nd, namely, Ca00 or CaL0, and Ca0R or CaLR, respectively (Fig. 2). The deactivation kinetics is approximated based on the simultaneous closure of multiple RyRs within a couplon.
To reveal the mechanistic principle of CICR, we compared empirical equations among the models (see Table S6 for a comparison of explicit mathematical descriptions of the regenerative step). In the toy version of the SM model, they analytically deduced a deterministic solution of the activation rate by assembling individual reaction steps. In the SJ model, the cooperative factors CFopen and CFclose were simply defined for the regenerative activation of RyRs and had a relatively small influence on the activation rate of a couplon (Fig. S5). In our modified Hinch model, we approximated the nearest-neighbor effect by using an activation rate (krco) that was sevenfold larger than the original single-channel rate (kco) (fn in Eq. 6), and kco was accelerated with increasing [Ca2+]nd (Eqs. 3 and 6). Thus, in all three models, the activation of a couplon was reduced to a two-state transition scheme. In both the SM and HuVEC models, the equilibrium open probability, pOeq, of a couplon was examined. Stern et al. (23) disclosed an unstable equilibrium pOeq (= number of open RyRs (nopen)/number of total RyRs (nry) at a given [Ca2+]SRrl) and successfully defined a threshold pOeq for both the activation and termination of couplon activity. The HuVEC model revealed that an instantaneous pOeq leads to time-dependent changes in pO(t), and that [Ca]jnc and [Ca]SRrl are time-dependent factors that are responsible for varying pOeq (or krco) via Eqs. 3, 6, and 10. Thus, the core feedback loop (Fig. 5, inset B) is fully consistent with the view that the initiation and termination of CICR is determined by mechanisms analogous to those suggested in recent stochastic models. In the future, investigators should analyze quantitative aspects of the threshold phenomenon systematically using mathematical approaches, such as bifurcation or phase-plane analyses, to gain deeper insights into the biophysical mechanisms that underlie excitation-contraction coupling in the HuVEC model.
Verification of assuming jnc and iz
In the HuVEC model, incorporation of jnc and iz into the CICR model was a prerequisite to represent the exponential Ca2+ gradient by discrete [Ca2+] steps around the Ca2+-releasing site during CICR. However, such a Ca2+ gradient near [Ca2+]nd or [Ca2+]ds was not included in the original Hinch model (Ca00 = [Ca2+]cyt in Eq. 2), and CaL0 was much lower than in the HuVEC model. Therefore, an activation rate constant larger than the experimental rate by more than two to three orders of magnitude was used (22,47) (see Fig. S5). This difficulty is overcome by the high [Ca2+]nd biased by the local Ca00 (= [Ca2+]jnc) in the HuVEC model. Furthermore, we found that the CaL0 was still too low to evoke an immediate activation of couplons by ICaL (Fig. 5 C), even when we used the sevenfold larger rate constant. This is because of the sharp Vm-dependent decrease of CaL0 at the AP plateau potential (Eq. 2). It turned out that the [Ca2+]jnc in the very limited volume of jnc was progressively increased even by the infrequent openings of couplons to generate the foot of rapid activation of couplons through the positive-feedback loop (Fig. 5, inset B).
The presence of jnc was a key factor in reproducing the experimental APD shortening with increasing [Ca2+]o. Fig. 3 B reveals enhanced CDI of LCC with increasing [Ca2+]o underlying the APD shortening. Indeed, ∼90% of CDI occurred within the initial 50 ms, during which time the peak [Ca2+]jnc was higher by ∼9-fold than the peak [Ca2+]iz, which may be comparable to [Ca2+] in the subsarcolemmal spaces of the GPB or ORd models. The presence of jnc was also essential in evoking DAD in the HuVEC model, as has been demonstrated elsewhere (33).
In a previous study, Wier et al. (7) made the interesting finding that although a brief ICaL tail current observed on repolarization from +80 mV to the holding potential (−40 mV) subsided within ∼2 ms, the decay of the Ca2+ transient due to Jcpl continued with a halftime of ∼9 ms at the holding potential. In our HuVEC model, this delayed closure of couplons after a brief ICaL tail (t1/2 = 0.9 ms, the time to reach half of the maximum amplitude from the off time of the test pulse) was well simulated by the rate of [Ca2+]jnc decay (t1/2 = 4.4 ms), which was attributed to the delayed diffusion of the accumulated Ca2+ from jnc to iz and blk. Since no space was assumed for Ca2+ accumulation in the original Hinch model, the Ca2+ transient evoked by RyR activation should closely follow the time course of the ICaL tail with a maximum delay of ∼1 ms, as determined by koc of RyR.
Taken together, the above findings justify the incorporation of jnc into the HuVEC model.
Ca2+ compartments: jnc, iz, SRrl, and SRup
The [Ca2+]nrs measured by Acsai et al. (12) was assigned to a functional space rather than a histologically defined one (58). When this large Ca2+ gradient was introduced into the HuVEC model, nrs was further divided into two hypothetical spaces, iz and jnc, and [Ca2+]jnc was used to represent Ca00 in the Hinch formalism of [Ca2+]nd (Eq. 2). Then, the volume of jnc was adjusted to reconstruct the key experimental and simulation results described above. Since the time course of CICR is largely determined by the size of jnc, Vjnc is compared with the volume of dyadic space (Vds), which is also critical for CICR kinetics in the stochastic simulations of a single CaRU. As shown in Table 1, the Vjnc in our model is apparently larger than the Vds assumed in other CICR models, but the difference is relatively small compared with the upper limit of Vds in the LC model. Considering the effects of fixed buffer sites on membrane phospholipids or the Debye layer, the Ca2+ distribution volume of ds may increase dramatically, as indicated in Stern et al. (23). The effective size of the compartment depends on various factors, such as the kinetics of the buffers (dissociation constants), the number of available binding sites, and the membrane surface area that encloses this compartment, but not on the myoplasmic volume that it encloses (58). Therefore, it is always important to evaluate the functional volume of each compartment comprehensively.
Table 1.
Comparison of the Volumes of Junctional Ca2+ Compartments and [CSQN]SRrl among the Models
| SJ Model | LC Model | SM Model | HuVEC Model | |
|---|---|---|---|---|
| Vds or Vjnc in the HuVEC model | 0.002–0.005a pL/cell | 0.0486–0.1215a pL/cell | 0.013–0.033a pL/cell | 0.303 pL/cell |
| 1.0 × 10−7 pL for each d.s. | 2.43 × 10−6 pL for each d.s. | cleft height 30 nm, (7 × 30)2 nm2 area for each d.s. | 0.8% Vcell | |
| VSRrl | 0.2–0.5a pL/cell | 0.08–0.21a pL/cell | 0.14 pL/cell | 0.46 pL/cell |
| 1.0 × 10−5 pL for each CaRU | 4.21 × 10−6 pL for each CaRU | 0.35% Vcell assumed in the HuVEC model | 1.2% Vcell | |
| [CSQN]SRrl | 10.0 mM | 30.0 mM | 30.0 mM | 3 mM |
| VSRup | infinite | 3.5% Vcell | 3.5% Vcell | 4.8% Vcell |
In the Hinch model, 50,000 CaRUs/cell and 2 × 10−7 pL/d.s. were assumed.
Calculated by assuming 20,000–50,000 CaRUs/cell.
Since [Ca2+]SRrl is one of central factors in driving the controlled termination of CICR (Fig. 5, inset B), we also compared VSRrl among different models together with [CSQN]SRrl (Table 1). Although VSRrl in the HuVEC model is ∼4-fold larger than the corresponding size of junctional SR in the SM model, it may be concluded that the Ca2+-releasing potency of the SR-releasing site is similar between the two, because 10-fold smaller Ca2+ buffering power is assumed in the HuVEC model compared with the SM model. Indeed, if the number of CaRUs within a cell is assumed to be 50,000 as in the Hinch model, VSRrl values in the SJ and LC models are within the same range as in the HuVEC model when a larger [CSQN]SRrl in each model is taken into account.
The extent of Ca2+ depletion in SRrl depends not only on VSRrl but also on the kinetics of VSRrl refilling and couplon gating. The time constant for the refilling of VSRrl in the HuVEC model is ∼200 ms, which is in agreement with that previously reported for rabbit (59). It should be noted, however, that the refilling time course and Ca2+ mobility in the SR varies between different studies (59,60). The recovery time course of local Ca2+ depletion, the so-called blink, is also variable between different studies (61,62). Furthermore, the separation of the SR volume into VSRrl and VSRup is still largely conventional and has not been explicitly determined based on experimental findings.
Limitations of the CICR model presented here
The HuVEC model successfully reproduced both electrical activity and Ca2+ dynamics, which were very similar to those observed in intact cells. However, the mathematical mechanisms developed in this model cell may not necessarily be a unique solution for intact cells. One limitation of the model is due to the large variety in the gating kinetics of RyRs (Fig. S5). Furthermore, if the functional size of SR Ca2+ compartments near the Ca2+-releasing site can be established experimentally, the model will be greatly improved and enhance our understanding of the effects of local SR Ca2+ depletion. To test the possibility that local SR Ca2+ depletion, which is responsible for terminating individual couplon open events, is engaged in terminating CICR at a whole-cell level, we formulated a dyadic model with a blink space (bs) in addition to the Hinch formalism (see Supporting Materials and Methods for a theoretical treatment of bs). Our preliminary simulation using this dyadic model with bs suggested that the general behavior of the model was essentially the same in electrically stimulated activity and voltage-clamp experiments.
Under pathophysiological conditions, Ca2+ waves spontaneously occur and propagate in myocytes. This Ca2+ wave cannot be reproduced in our HuVEC model because it has a single space of jnc and SRrl. Furthermore, in a previous study, Matsuda et al. (63) suggested that asynchronous CICR occurs spontaneously in multiple domains of the SR network within a single cell (for a simulation, see Chen et al. (64)). In that study, Matsuda et al. found that micro fluctuations remained in the recordings of the resting potential after several cyclic DAD events subsided, and suggested multiple origins of the spontaneous Ca2+ release with variable intrinsic rhythms under the condition of Ca2+ overload. Nonetheless, the assumption of common [Ca2+]jnc and [Ca2+]SRrl might be relevant in our simulations as long as the activation of all of the CaRUs within the cell are synchronized by an AP or a voltage-clamp pulse. To refine the CICR model, it may be necessary to conduct voltage-clamp experiments under controlled levels of [Ca2+]SRrl (58).
Author Contributions
A.N. designed the study. A.N., K.A., C.Y.C., H.M., and Y.H. performed research and developed the HuVEC model. A.N., Y.H., A.A., and K.A. analyzed the model and wrote the manuscript with T.P.
Acknowledgments
We thank Drs. T. Shimayoshi and Y. Takeda for fruitful discussions.
This work was supported by Grants-in-Aid from the Ministry of Education, Culture, Sports, Science and Technology of Japan (22590216 to C.C. and 22390039 to A.N.), a Grant-in-Aid for JSPS Fellows from the Japan Society for the Promotion of Science (to Y.H.), Program for Application of the Grants-in-Aid for Scientific Research (KAKENHI) (to Y.H.), and the Ritsumeikan-Global Innovation Research Organization at Ritsumeikan University.
Editor: Andrew McCulloch.
Footnotes
Supporting Materials and Methods, Supporting Results, nine figures, and six tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)00599-8.
Supporting Citations
References (65–90) appear in the Supporting Material.
Supporting Material
References
- 1.Priebe L., Beuckelmann D.J. Simulation study of cellular electric properties in heart failure. Circ. Res. 1998;82:1206–1223. doi: 10.1161/01.res.82.11.1206. [DOI] [PubMed] [Google Scholar]
- 2.Ten Tusscher K.H., Bernus O., Panfilov A.V. Comparison of electrophysiological models for human ventricular cells and tissues. Prog. Biophys. Mol. Biol. 2006;90:326–345. doi: 10.1016/j.pbiomolbio.2005.05.015. [DOI] [PubMed] [Google Scholar]
- 3.ten Tusscher K.H., Noble D., Panfilov A.V. A model for human ventricular tissue. Am. J. Physiol. Heart Circ. Physiol. 2004;286:H1573–H1589. doi: 10.1152/ajpheart.00794.2003. [DOI] [PubMed] [Google Scholar]
- 4.Grandi E., Pasqualini F.S., Bers D.M. A novel computational model of the human ventricular action potential and Ca transient. J. Mol. Cell. Cardiol. 2010;48:112–121. doi: 10.1016/j.yjmcc.2009.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.O’Hara T., Virág L., Rudy Y. Simulation of the undiseased human cardiac ventricular action potential: model formulation and experimental validation. PLOS Comput. Biol. 2011;7:e1002061. doi: 10.1371/journal.pcbi.1002061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Volders P.G., Kulcśar A., Szabo B. Similarities between early and delayed afterdepolarizations induced by isoproterenol in canine ventricular myocytes. Cardiovasc. Res. 1997;34:348–359. doi: 10.1016/s0008-6363(96)00270-2. [DOI] [PubMed] [Google Scholar]
- 7.Wier W.G., Egan T.M., Balke C.W. Local control of excitation-contraction coupling in rat heart cells. J. Physiol. 1994;474:463–471. doi: 10.1113/jphysiol.1994.sp020037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Stern M.D. Theory of excitation-contraction coupling in cardiac muscle. Biophys. J. 1992;63:497–517. doi: 10.1016/S0006-3495(92)81615-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Greenstein J.L., Winslow R.L. An integrative model of the cardiac ventricular myocyte incorporating local control of Ca2+ release. Biophys. J. 2002;83:2918–2945. doi: 10.1016/S0006-3495(02)75301-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hinch R. A mathematical analysis of the generation and termination of calcium sparks. Biophys. J. 2004;86:1293–1307. doi: 10.1016/S0006-3495(04)74203-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hinch R., Greenstein J.L., Winslow R.L. A simplified local control model of calcium-induced calcium release in cardiac ventricular myocytes. Biophys. J. 2004;87:3723–3736. doi: 10.1529/biophysj.104.049973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Acsai K., Antoons G., Sipido K.R. Microdomain [Ca2+] near ryanodine receptors as reported by L-type Ca2+ and Na+/Ca2+ exchange currents. J. Physiol. 2011;589:2569–2583. doi: 10.1113/jphysiol.2010.202663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Adachi-Akahane S., Cleemann L., Morad M. Cross-signaling between L-type Ca2+ channels and ryanodine receptors in rat ventricular myocytes. J. Gen. Physiol. 1996;108:435–454. doi: 10.1085/jgp.108.5.435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sipido K.R., Callewaert G., Carmeliet E. Inhibition and rapid recovery of Ca2+ current during Ca2+ release from sarcoplasmic reticulum in guinea pig ventricular myocytes. Circ. Res. 1995;76:102–109. doi: 10.1161/01.res.76.1.102. [DOI] [PubMed] [Google Scholar]
- 15.Trafford A.W., Díaz M.E., Eisner D.A. Comparison of subsarcolemmal and bulk calcium concentration during spontaneous calcium release in rat ventricular myocytes. J. Physiol. 1995;488:577–586. doi: 10.1113/jphysiol.1995.sp020991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Weber C.R., Ginsburg K.S., Bers D.M. Cardiac submembrane [Na+] transients sensed by Na+-Ca2+ exchange current. Circ. Res. 2003;92:950–952. doi: 10.1161/01.RES.0000071747.61468.7F. [DOI] [PubMed] [Google Scholar]
- 17.Weber C.R., Piacentino V., 3rd, Bers D.M. Na(+)-Ca(2+) exchange current and submembrane [Ca(2+)] during the cardiac action potential. Circ. Res. 2002;90:182–189. doi: 10.1161/hh0202.103940. [DOI] [PubMed] [Google Scholar]
- 18.Cannell M.B., Kong C.H. Local control in cardiac E-C coupling. J. Mol. Cell. Cardiol. 2012;52:298–303. doi: 10.1016/j.yjmcc.2011.04.014. [DOI] [PubMed] [Google Scholar]
- 19.Stern M.D., Cheng H. Putting out the fire: what terminates calcium-induced calcium release in cardiac muscle? Cell Calcium. 2004;35:591–601. doi: 10.1016/j.ceca.2004.01.013. [DOI] [PubMed] [Google Scholar]
- 20.Zalk R., Lehnart S.E., Marks A.R. Modulation of the ryanodine receptor and intracellular calcium. Annu. Rev. Biochem. 2007;76:367–385. doi: 10.1146/annurev.biochem.76.053105.094237. [DOI] [PubMed] [Google Scholar]
- 21.Sobie E.A., Dilly K.W., Jafri M.S. Termination of cardiac Ca(2+) sparks: an investigative mathematical model of calcium-induced calcium release. Biophys. J. 2002;83:59–78. doi: 10.1016/s0006-3495(02)75149-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Laver D.R., Kong C.H., Cannell M.B. Termination of calcium-induced calcium release by induction decay: an emergent property of stochastic channel gating and molecular scale architecture. J. Mol. Cell. Cardiol. 2013;54:98–100. doi: 10.1016/j.yjmcc.2012.10.009. [DOI] [PubMed] [Google Scholar]
- 23.Stern M.D., Ríos E., Maltsev V.A. Life and death of a cardiac calcium spark. J. Gen. Physiol. 2013;142:257–274. doi: 10.1085/jgp.201311034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Brunet S., Scheuer T., Catterall W.A. Cooperative regulation of Ca(v)1.2 channels by intracellular Mg(2+), the proximal C-terminal EF-hand, and the distal C-terminal domain. J. Gen. Physiol. 2009;134:81–94. doi: 10.1085/jgp.200910209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ferreira G., Yi J., Shirokov R. Ion-dependent inactivation of barium current through L-type calcium channels. J. Gen. Physiol. 1997;109:449–461. doi: 10.1085/jgp.109.4.449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shirokov R., Levis R., Ríos E. Ca(2+)-dependent inactivation of cardiac L-type Ca2+ channels does not affect their voltage sensor. J. Gen. Physiol. 1993;102:1005–1030. doi: 10.1085/jgp.102.6.1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yue D.T., Marban E. Permeation in the dihydropyridine-sensitive calcium channel. Multi-ion occupancy but no anomalous mole-fraction effect between Ba2+ and Ca2+ J. Gen. Physiol. 1990;95:911–939. doi: 10.1085/jgp.95.5.911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Neher E., Almers W. Fast calcium transients in rat peritoneal mast cells are not sufficient to trigger exocytosis. EMBO J. 1986;5:51–53. doi: 10.1002/j.1460-2075.1986.tb04176.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Stern M.D. Buffering of calcium in the vicinity of a channel pore. Cell Calcium. 1992;13:183–192. doi: 10.1016/0143-4160(92)90046-u. [DOI] [PubMed] [Google Scholar]
- 30.Tadross M.R., Tsien R.W., Yue D.T. Ca2+ channel nanodomains boost local Ca2+ amplitude. Proc. Natl. Acad. Sci. USA. 2013;110:15794–15799. doi: 10.1073/pnas.1313898110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kokubun S., Nishimura M., Noma A., Irisawa H. Membrane currents in the rabbit atrioventricular node cell. Pflugers Arch. 1982;393:15–22. doi: 10.1007/BF00582385. [DOI] [PubMed] [Google Scholar]
- 32.Seifen E., Schaer H., Marshall J.M. Effect of calcium on the membrane potentials of single pacemaker fibres and atrial fibres in isolated rabbits atria. Nature. 1964;202:1223–1224. doi: 10.1038/2021223a0. [DOI] [PubMed] [Google Scholar]
- 33.Asakura K., Cha C.Y., Noma A. EAD and DAD mechanisms analyzed by developing a new human ventricular cell model. Prog. Biophys. Mol. Biol. 2014;116:11–24. doi: 10.1016/j.pbiomolbio.2014.08.008. [DOI] [PubMed] [Google Scholar]
- 34.Valdivia H.H., Kaplan J.H., Lederer W.J. Rapid adaptation of cardiac ryanodine receptors: modulation by Mg2+ and phosphorylation. Science. 1995;267:1997–2000. doi: 10.1126/science.7701323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Fill M., Zahradníková A., Györke S. Ryanodine receptor adaptation. J. Gen. Physiol. 2000;116:873–882. doi: 10.1085/jgp.116.6.873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Näbauer M., Morad M. Ca2(+)-induced Ca2+ release as examined by photolysis of caged Ca2+ in single ventricular myocytes. Am. J. Physiol. 1990;258:C189–C193. doi: 10.1152/ajpcell.1990.258.1.C189. [DOI] [PubMed] [Google Scholar]
- 37.Scriven D.R., Dan P., Moore E.D. Distribution of proteins implicated in excitation-contraction coupling in rat ventricular myocytes. Biophys. J. 2000;79:2682–2691. doi: 10.1016/S0006-3495(00)76506-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Scriven D.R., Moore E.D. Ca2+ channel and Na+/Ca2+ exchange localization in cardiac myocytes. J. Mol. Cell. Cardiol. 2013;58:22–31. doi: 10.1016/j.yjmcc.2012.11.022. [DOI] [PubMed] [Google Scholar]
- 39.Hille B. Sinauer Associates; Sunderland, MA: 2001. Ion Channels of Excitable Membranes. [Google Scholar]
- 40.Swietach P., Spitzer K.W., Vaughan-Jones R.D. Na+ ions as spatial intracellular messengers for co-ordinating Ca2+ signals during pH heterogeneity in cardiomyocytes. Cardiovasc. Res. 2015;105:171–181. doi: 10.1093/cvr/cvu251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Greenstein J.L., Hinch R., Winslow R.L. Mechanisms of excitation-contraction coupling in an integrative model of the cardiac ventricular myocyte. Biophys. J. 2006;90:77–91. doi: 10.1529/biophysj.105.065169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Peterson B.Z., Lee J.S., Yue D.T. Critical determinants of Ca(2+)-dependent inactivation within an EF-hand motif of L-type Ca(2+) channels. Biophys. J. 2000;78:1906–1920. doi: 10.1016/S0006-3495(00)76739-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Williams G.S., Huertas M.A., Smith G.D. A probability density approach to modeling local control of calcium-induced calcium release in cardiac myocytes. Biophys. J. 2007;92:2311–2328. doi: 10.1529/biophysj.106.099861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Negroni J.A., Lascano E.C. Simulation of steady state and transient cardiac muscle response experiments with a Huxley-based contraction model. J. Mol. Cell. Cardiol. 2008;45:300–312. doi: 10.1016/j.yjmcc.2008.04.012. [DOI] [PubMed] [Google Scholar]
- 45.Györke S., Fill M. Ryanodine receptor adaptation: control mechanism of Ca(2+)-induced Ca2+ release in heart. Science. 1993;260:807–809. doi: 10.1126/science.8387229. [DOI] [PubMed] [Google Scholar]
- 46.Qin J., Valle G., Fill M. Ryanodine receptor luminal Ca2+ regulation: swapping calsequestrin and channel isoforms. Biophys. J. 2009;97:1961–1970. doi: 10.1016/j.bpj.2009.07.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Guo T., Gillespie D., Fill M. Ryanodine receptor current amplitude controls Ca2+ sparks in cardiac muscle. Circ. Res. 2012;111:28–36. doi: 10.1161/CIRCRESAHA.112.265652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Cheng H., Lederer W.J., Cannell M.B. Calcium sparks: elementary events underlying excitation-contraction coupling in heart muscle. Science. 1993;262:740–744. doi: 10.1126/science.8235594. [DOI] [PubMed] [Google Scholar]
- 49.Jost N., Virág L., Nattel S. Ionic mechanisms limiting cardiac repolarization reserve in humans compared to dogs. J. Physiol. 2013;591:4189–4206. doi: 10.1113/jphysiol.2013.261198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Peeters G.A., Sanguinetti M.C., Barry W.H. Method for isolation of human ventricular myocytes from single endocardial and epicardial biopsies. Am. J. Physiol. 1995;268:H1757–H1764. doi: 10.1152/ajpheart.1995.268.4.H1757. [DOI] [PubMed] [Google Scholar]
- 51.Li G.R., Feng J., Carrier M. Transmural heterogeneity of action potentials and Ito1 in myocytes isolated from the human right ventricle. Am. J. Physiol. 1998;275:H369–H377. doi: 10.1152/ajpheart.1998.275.2.H369. [DOI] [PubMed] [Google Scholar]
- 52.Péréon Y., Demolombe S., Escande D. Differential expression of KvLQT1 isoforms across the human ventricular wall. Am. J. Physiol. Heart Circ. Physiol. 2000;278:H1908–H1915. doi: 10.1152/ajpheart.2000.278.6.H1908. [DOI] [PubMed] [Google Scholar]
- 53.Li G.R., Feng J., Nattel S. Evidence for two components of delayed rectifier K+ current in human ventricular myocytes. Circ. Res. 1996;78:689–696. doi: 10.1161/01.res.78.4.689. [DOI] [PubMed] [Google Scholar]
- 54.Drouin E., Charpentier F., Le Marec H. Electrophysiologic characteristics of cells spanning the left ventricular wall of human heart: evidence for presence of M cells. J. Am. Coll. Cardiol. 1995;26:185–192. doi: 10.1016/0735-1097(95)00167-x. [DOI] [PubMed] [Google Scholar]
- 55.Kokubun S., Irisawa H. Effects of various intracellular Ca ion concentrations on the calcium current of guinea-pig single ventricular cells. Jpn. J. Physiol. 1984;34:599–611. doi: 10.2170/jjphysiol.34.599. [DOI] [PubMed] [Google Scholar]
- 56.Matsuoka S., Sarai N., Noma A. Role of individual ionic current systems in ventricular cells hypothesized by a model study. Jpn. J. Physiol. 2003;53:105–123. doi: 10.2170/jjphysiol.53.105. [DOI] [PubMed] [Google Scholar]
- 57.Grandi E., Pasqualini F.S., Severi S. Theoretical investigation of action potential duration dependence on extracellular Ca2+ in human cardiomyocytes. J. Mol. Cell. Cardiol. 2009;46:332–342. doi: 10.1016/j.yjmcc.2008.12.002. [DOI] [PubMed] [Google Scholar]
- 58.Livshitz L., Acsai K., Rudy Y. Data-based theoretical identification of subcellular calcium compartments and estimation of calcium dynamics in cardiac myocytes. J. Physiol. 2012;590:4423–4446. doi: 10.1113/jphysiol.2012.228791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Picht E., Zima A.V., Bers D.M. Dynamic calcium movement inside cardiac sarcoplasmic reticulum during release. Circ. Res. 2011;108:847–856. doi: 10.1161/CIRCRESAHA.111.240234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Swietach P., Spitzer K.W., Vaughan-Jones R.D. Ca2+-mobility in the sarcoplasmic reticulum of ventricular myocytes is low. Biophys. J. 2008;95:1412–1427. doi: 10.1529/biophysj.108.130385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Zima A.V., Picht E., Blatter L.A. Termination of cardiac Ca2+ sparks: role of intra-SR [Ca2+], release flux, and intra-SR Ca2+ diffusion. Circ. Res. 2008;103:e105–e115. doi: 10.1161/CIRCRESAHA.107.183236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Brochet D.X., Xie W., Lederer W.J. Quarky calcium release in the heart. Circ. Res. 2011;108:210–218. doi: 10.1161/CIRCRESAHA.110.231258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Matsuda H., Noma A., Irisawa H. Transient depolarization and spontaneous voltage fluctuations in isolated single cells from guinea pig ventricles. Calcium-mediated membrane potential fluctuations. Circ. Res. 1982;51:142–151. doi: 10.1161/01.res.51.2.142. [DOI] [PubMed] [Google Scholar]
- 64.Chen W., Aistrup G., Shiferaw Y. A mathematical model of spontaneous calcium release in cardiac myocytes. Am. J. Physiol. Heart Circ. Physiol. 2011;300:H1794–H1805. doi: 10.1152/ajpheart.01121.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Beuckelmann D.J., Näbauer M., Erdmann E. Intracellular calcium handling in isolated ventricular myocytes from patients with terminal heart failure. Circulation. 1992;85:1046–1055. doi: 10.1161/01.cir.85.3.1046. [DOI] [PubMed] [Google Scholar]
- 66.Powell T., Sturridge M.F., Twist V.W. Intact individual heart cells isolated from human ventricular tissue. Br. Med. J. (Clin. Res.) 1981;283:1013–1015. doi: 10.1136/bmj.283.6298.1013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Satoh H., Delbridge L.M., Bers D.M. Surface:volume relationship in cardiac myocytes studied with confocal microscopy and membrane capacitance measurements: species-dependence and developmental effects. Biophys. J. 1996;70:1494–1504. doi: 10.1016/S0006-3495(96)79711-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Jost N., Virág L., Varró A. Restricting excessive cardiac action potential and QT prolongation: a vital role for IKs in human ventricular muscle. Circulation. 2005;112:1392–1399. doi: 10.1161/CIRCULATIONAHA.105.550111. [DOI] [PubMed] [Google Scholar]
- 69.Sakakibara Y., Furukawa T., Wasserstrom J.A. Sodium current in isolated human ventricular myocytes. Am. J. Physiol. 1993;265:H1301–H1309. doi: 10.1152/ajpheart.1993.265.4.H1301. [DOI] [PubMed] [Google Scholar]
- 70.Mewes T., Ravens U. L-type calcium currents of human myocytes from ventricle of non-failing and failing hearts and from atrium. J. Mol. Cell. Cardiol. 1994;26:1307–1320. doi: 10.1006/jmcc.1994.1149. [DOI] [PubMed] [Google Scholar]
- 71.Iost N., Virág L., Papp J.G. Delayed rectifier potassium current in undiseased human ventricular myocytes. Cardiovasc. Res. 1998;40:508–515. doi: 10.1016/s0008-6363(98)00204-1. [DOI] [PubMed] [Google Scholar]
- 72.Gerdes A.M., Kellerman S.E., Schocken D.D. Structural remodeling of cardiac myocytes in patients with ischemic cardiomyopathy. Circulation. 1992;86:426–430. doi: 10.1161/01.cir.86.2.426. [DOI] [PubMed] [Google Scholar]
- 73.Shannon T.R., Wang F., Bers D.M. A mathematical treatment of integrated Ca dynamics within the ventricular myocyte. Biophys. J. 2004;87:3351–3371. doi: 10.1529/biophysj.104.047449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Pelzmann B., Schaffer P., Koidl B. L-type calcium current in human ventricular myocytes at a physiological temperature from children with tetralogy of Fallot. Cardiovasc. Res. 1998;38:424–432. doi: 10.1016/s0008-6363(98)00002-9. [DOI] [PubMed] [Google Scholar]
- 75.Magyar J., Iost N., Nanasi P.P. Effects of endothelin-1 on calcium and potassium currents in undiseased human ventricular myocytes. Pflugers Arch. 2000;441:144–149. doi: 10.1007/s004240000400. [DOI] [PubMed] [Google Scholar]
- 76.Fülöp L., Bányász T., Nánási P.P. Reopening of L-type calcium channels in human ventricular myocytes during applied epicardial action potentials. Acta Physiol. Scand. 2004;180:39–47. doi: 10.1046/j.0001-6772.2003.01223.x. [DOI] [PubMed] [Google Scholar]
- 77.Sun L., Fan J.S., Palade P.T. A model of the L-type Ca2+ channel in rat ventricular myocytes: ion selectivity and inactivation mechanisms. J. Physiol. 2000;529:139–158. doi: 10.1111/j.1469-7793.2000.00139.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Zhang J.F., Ellinor P.T., Tsien R.W. Molecular determinants of voltage-dependent inactivation in calcium channels. Nature. 1994;372:97–100. doi: 10.1038/372097a0. [DOI] [PubMed] [Google Scholar]
- 79.Matsuda H. Sodium conductance in calcium channels of guinea-pig ventricular cells induced by removal of external calcium ions. Pflugers Arch. 1986;407:465–475. doi: 10.1007/BF00657502. [DOI] [PubMed] [Google Scholar]
- 80.Yan D.H., Ishihara K. Two Kir2.1 channel populations with different sensitivities to Mg(2+) and polyamine block: a model for the cardiac strong inward rectifier K(+) channel. J. Physiol. 2005;563:725–744. doi: 10.1113/jphysiol.2004.079186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Ishihara K., Yan D.H. Low-affinity spermine block mediating outward currents through Kir2.1 and Kir2.2 inward rectifier potassium channels. J. Physiol. 2007;583:891–908. doi: 10.1113/jphysiol.2007.136028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Rajamani S., Eckhardt L.L., January C.T. Drug-induced long QT syndrome: hERG K+ channel block and disruption of protein trafficking by fluoxetine and norfluoxetine. Br. J. Pharmacol. 2006;149:481–489. doi: 10.1038/sj.bjp.0706892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Takeuchi A., Tatsumi S., Noma A. Ionic mechanisms of cardiac cell swelling induced by blocking Na+/K+ pump as revealed by experiments and simulation. J. Gen. Physiol. 2006;128:495–507. doi: 10.1085/jgp.200609646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Oka C., Cha C.Y., Noma A. Characterization of the cardiac Na+/K+ pump by development of a comprehensive and mechanistic model. J. Theor. Biol. 2010;265:68–77. doi: 10.1016/j.jtbi.2010.04.028. [DOI] [PubMed] [Google Scholar]
- 85.Smith N.P., Crampin E.J. Development of models of active ion transport for whole-cell modelling: cardiac sodium-potassium pump as a case study. Prog. Biophys. Mol. Biol. 2004;85:387–405. doi: 10.1016/j.pbiomolbio.2004.01.010. [DOI] [PubMed] [Google Scholar]
- 86.Tran K., Smith N.P., Crampin E.J. A thermodynamic model of the cardiac sarcoplasmic/endoplasmic Ca(2+) (SERCA) pump. Biophys. J. 2009;96:2029–2042. doi: 10.1016/j.bpj.2008.11.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Negroni J.A., Lascano E.C. A cardiac muscle model relating sarcomere dynamics to calcium kinetics. J. Mol. Cell. Cardiol. 1996;28:915–929. doi: 10.1006/jmcc.1996.0086. [DOI] [PubMed] [Google Scholar]
- 88.Brochet D.X., Yang D., Cheng H. Ca2+ blinks: rapid nanoscopic store calcium signaling. Proc. Natl. Acad. Sci. USA. 2005;102:3099–3104. doi: 10.1073/pnas.0500059102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Li G.R., Yang B., Nattel S. Transmembrane ICa contributes to rate-dependent changes of action potentials in human ventricular myocytes. Am. J. Physiol. 1999;276:H98–H106. doi: 10.1152/ajpheart.1999.276.1.H98. [DOI] [PubMed] [Google Scholar]
- 90.Pieske B., Kretschmann B., Hasenfuss G. Alterations in intracellular calcium handling associated with the inverse force-frequency relation in human dilated cardiomyopathy. Circulation. 1995;92:1169–1178. doi: 10.1161/01.cir.92.5.1169. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.