Spatial Correlations in Natural Scenes Modulate Response Reliability in Mouse Visual Cortex

Abstract

Intrinsic neuronal variability significantly limits information encoding in the primary visual cortex (V1). Certain stimuli can suppress this intertrial variability to increase the reliability of neuronal responses. In particular, responses to natural scenes, which have broadband spatiotemporal statistics, are more reliable than responses to stimuli such as gratings. However, very little is known about which stimulus statistics modulate reliable coding and how this occurs at the neural ensemble level. Here, we sought to elucidate the role that spatial correlations in natural scenes play in reliable coding. We developed a novel noise-masking method to systematically alter spatial correlations in natural movies, without altering their edge structure. Using high-speed two-photon calcium imaging in vivo, we found that responses in mouse V1 were much less reliable at both the single neuron and population level when spatial correlations were removed from the image. This change in reliability was due to a reorganization of between-neuron correlations. Strongly correlated neurons formed ensembles that reliably and accurately encoded visual stimuli, whereas reducing spatial correlations reduced the activation of these ensembles, leading to an unreliable code. Together with an ensemble-specific normalization model, these results suggest that the coordinated activation of specific subsets of neurons underlies the reliable coding of natural scenes.

SIGNIFICANCE STATEMENT The natural environment is rich with information. To process this information with high fidelity, V1 neurons have to be robust to noise and, consequentially, must generate responses that are reliable from trial to trial. While several studies have hinted that both stimulus attributes and population coding may reduce noise, the details remain unclear. Specifically, what features of natural scenes are important and how do they modulate reliability? This study is the first to investigate the role of spatial correlations, which are a fundamental attribute of natural scenes, in shaping stimulus coding by V1 neurons. Our results provide new insights into how stimulus spatial correlations reorganize the correlated activation of specific ensembles of neurons to ensure accurate information processing in V1.

Introduction

A challenge faced by the visual system is to rapidly and accurately extract salient features from rich natural scenes while discarding redundant information. The fidelity with which visual information is processed is limited by both the intrinsic variability of neurons and the correlation structure of the network (Shadlen and Newsome, 1998; Azouz and Gray, 1999; Averbeck et al., 2006; Moreno-Bote et al., 2014). Despite these sources of noise, evidence from several studies indicates that natural scenes are processed efficiently in V1 (Simoncelli and Olshausen, 2001; Olshausen and Field, 2004). This suggests that response variability is reduced for natural scenes, permitting information to be represented efficiently and with high fidelity (Borst and Theunissen, 1999). How this is achieved in V1 remains unclear.

The degree of trial-to-trial variability in a response is commonly measured in terms of reliability. A neuron is said to be reliable if it fires the same number of precisely timed spikes on every repetition of a stimulus (Tiesinga et al., 2008). Several physiological studies in cats have shown that both spike trains and subthreshold potentials are reliable and sparse when stimulated with full-field natural movies (Haider et al., 2010; Baudot et al., 2013). This coding strategy increases the amount of information conveyed per spike (Vinje and Gallant, 2002; Pecka et al., 2014). In contrast, vignetting these movies such that they only stimulate the classical receptive fields (RFs) of neurons degrades both reliability and sparseness. These results hint at a paradoxical population-coding regime, where response variability decreases when larger numbers of neurons are activated (Shadlen and Newsome, 1994; Renart and Machens, 2014). Supporting this idea, both attention (Cohen and Maunsell, 2009) and neuromodulatory mechanisms (Goard and Dan, 2009), which change correlations between neurons, also improve response reliability. However, the relationship between interneuronal correlations and reliable coding of natural scenes remains unexplored.

Apart from population coding, stimulus statistics are also known to influence reliability. A previous study showed that reliability was highest for natural scenes and weakest for simple stimuli, such as gratings and dense noise (Baudot et al., 2013). Statistically, sinusoidal gratings contain only one spatial frequency (SF), whereas dense noise contains a spectrum of different SFs with constant power spectral density. This is in contrast to natural scenes, which contain a power law distribution of SFs. Particularly, most natural scenes have higher power in the low SF bands (broad image features) and weaker power in high-SF bands (fine structural details; Ruderman and Bialek, 1994; Bar, 2004). It has been hypothesized that the visual system uses these unique statistical properties to efficiently encode information (Barlow, 2001; Simoncelli and Olshausen, 2001). This theory is bolstered by several psychophysical studies, which demonstrate that image statistics are critical for rapid and accurate discrimination (Torralba and Oliva, 2003; McCotter et al., 2005). However, how stimulus statistics modulate the reliability and, in turn, the efficiency of the neural code remains unknown. One hypothesis is that specific features of natural scenes improve response reliability by reducing correlated variability (Kohn and Smith, 2005; Snyder et al., 2014). To test this hypothesis, it is important to parametrically relate stimulus statistics to changes in population coding and neural reliability.

In this study, we sought to answer the following two questions. (1) What properties of natural scenes influence response reliability? (2) What population coding mechanisms improve reliability? To address these questions, we developed a novel stimulus set where we systematically perturbed spatial correlations in natural movies, while preserving their edge structure. By applying in vivo two-photon calcium imaging to layer 2/3 neurons in mouse V1, we found that spatial correlations in natural movies strongly influenced response reliability. Cluster analysis of neuronal responses showed that reliable coding was achieved via a stimulus-driven restructuring of interneuronal correlations. These findings, supported by a normalization model, demonstrate that a hallmark of reliable coding is the coordinated activation of specific neuronal ensembles.

Materials and Methods

Experiments

Animals and surgery.

Experiments were performed under protocols approved by the Massachusetts Institute of Technology's Animal Care and Use Committee and conformed to NIH guidelines. All data in this study were collected from adult (>8 weeks old) C57BL/6 (Charles River Laboratory) mice of either sex. Mice were anesthetized using isoflurane (3% induction, 1.5–2% during surgery). A custom-built metal head post was attached to the skull using dental cement (C&B-Metabond, Parkell), and a 3-mm-diameter craniotomy was performed over binocular V1 (∼2–3 mm lateral and 0.5 mm anterior to lambda). Care was taken not to rupture the dura mater. The core body temperature was maintained at 37.5°C using a heating blanket (Harvard Apparatus).

For anesthetized experiments, anesthesia was maintained with 0.5–0.8% isoflurane during imaging. A solution of Oregon Green BAPTA-1 AM (OGB1; 1 mm; Invitrogen) and Sulforhodamine 101 (SR-101; 100 μm; Invitrogen) was pressure injected (10 psi for 1 min; Picospritzer) into the brain 180–250 μm below the pial surface via a borosilicate glass pipette (5–7 MΩ tip resistance) under visual guidance. After confirming successful expression of OGB1 (∼20 min following injection), the craniotomy was covered with a 3 mm glass coverslip (Warner Instruments) and sealed with a silicone elastomer (Kwik-Sil; WPI).

For awake experiments, mice were first habituated for 5 d to head fixation on a custom-built stage. Once habituated, the mice received a microinjection of 100–200 nl of AAV1.Syn.GCaMP6f.WPRE.SV40 (University of Pennsylvania Vector Core, diluted to a titer of 10¹² genomes ml⁻¹), following which a cranial window was implanted over the craniotomy and sealed as described above. Mice were allowed to recover for 2–3 weeks to allow for adequate expression of the virus before imaging commenced. It has been shown previously that both OGB1 and GCaMP6f have similar response kinetics (Chen et al., 2013), permitting us to make direct comparisons of the influence of brain state on coding.

Two-photon calcium imaging and analysis.

Imaging was performed using a Prairie Ultima two-photon system (Bruker) driven by a Spectra Physics Mai-Tai laser passed through a Deep-See module (Spectra Physics) and a high-performance objective lens (25× Olympus XL Plan N objective, 1.05 numerical aperture). Cells were excited at 960 nm for OGB1 and 910 nm for GCaMP6f.

A custom-built MATLAB-based (MathWorks) software system was used to collect optimized raster scans at 50 frames/s and to perform offline data analysis, as described previously (Wilson et al., 2012, 2013). Briefly, image segmentation algorithms were first used to identify cell bodies from a scanned image (see Fig. 2A). Next, a genetic algorithm was used to determine the shortest scan path between cells, and this line scan was run at 50 Hz, ensuring a 90% dwell time inside the cells. This higher dwell time ensured calcium transients with slightly larger amplitudes (ΔF/F range, 20–50%). Frames with excessive brain movement were ignored.

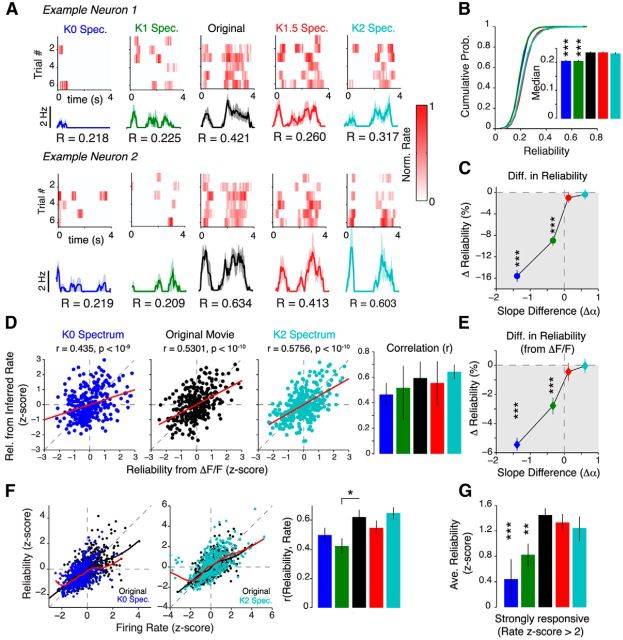
Figure 2.

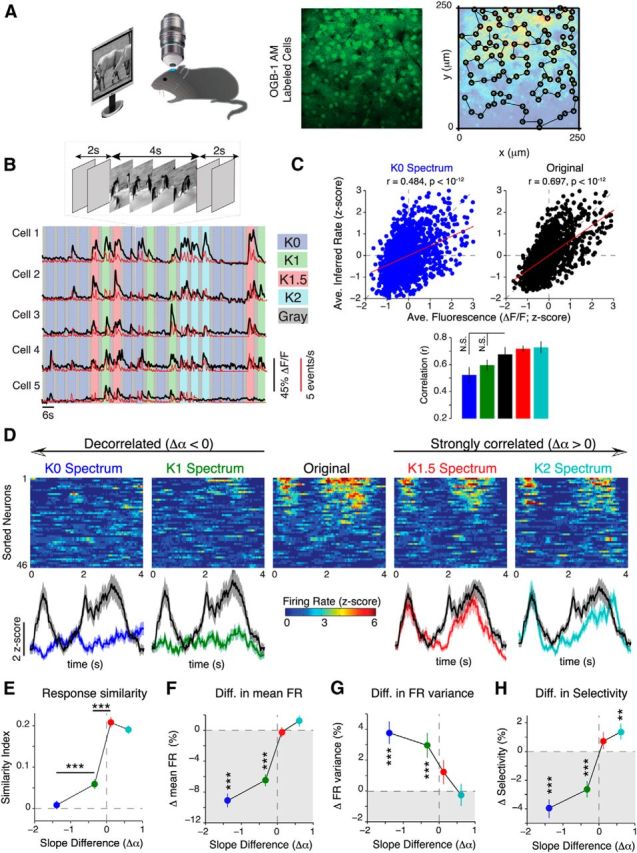
V1 neurons are sensitive to changes in spatial correlations. A, Left, Schematic of experimental setup. Middle, Representative neural population labeled with OGB1. Right, Neurons were detected with an automatic image segmentation algorithm and scanned with a custom line scan path (for details, see Materials and Methods). B, Top, Illustration of stimulus timing. Each movie was presented for 4 s and was flanked by 2 s gray screens. Bottom, Calcium transients (black) and deconvolved firing rates (red) from five representative neurons in response to a randomized sequence of stimuli. Each colored bar denotes the 4 s period over which a movie was presented. C, Top, Scatter plot showing the relationship between average fluorescence (ΔF/F) and inferred firing rate for both K0 spectrum (left) and original movies (right). The red lines show the linear least squares regression between ΔF/F and the inferred firing rate. Bottom, No significant difference in the Spearman's correlation between ΔF/F and the inferred firing rate between the different spectral conditions (p = 0.21, 1006 neurons from 16 mice). D, Top, Heat map showing trial-averaged firing rates (z-scored relative to spontaneous activity) from a population of 46 neurons. Neurons were sorted according to their mean response to the original movie. The same order was preserved in each heat map. Bottom, Population-averaged responses. The shaded area denotes SEM. E, Firing rate similarity index between neural responses to noise-masked movies and their original versions plotted as a function of the change in spectral slope. F–H, Percentage change in mean firing rate (FR; F), trial-to-trial FR variance (G), and selectivity (H) relative to the original movie. Data are presented as the median ± 95% confidence interval from 1006 neurons (16 mice). All p values in C and E–H were computed via Friedman's test followed by Bonferroni-corrected rank-sum tests. Colors are labeled in D. Error bars denote SEM. **p < 10⁻³; ***p < 10⁻⁴.

Significantly visually responsive cells were determined from the fluorescence time changes (ΔF/F) by performing a one-tailed Student's t test between visually evoked and spontaneous responses (gray screen collected for 2 min before start of experiment). Only cells with p < 10⁻³ were classified as visually responsive. Firing rates of these cells were then inferred using a fast nonnegative deconvolution algorithm (Vogelstein et al., 2010) using parameters that were verified previously in our lab (Wilson et al., 2012; El-Boustani and Sur, 2014). The Vogelstein algorithm infers the probability of spiking from calcium transients. To convert this probability into a firing rate (measured in events per second), we multiplied each probability by 50 Hz, the frequency at which the calcium transients were sampled. Unless stated otherwise, all data analysis was performed using inferred firing rates.

Visual stimuli

Creation of noise movies.

We developed an algorithm that allowed us to create noise images with a user-defined spectral slope. To do so, we took advantage of the inverse-square law: P ∼ k^−α, which translates to a circle with radius ∝ in two-dimensional Fourier space. Thus, we constructed all noise movies in the Fourier domain. We first defined a matrix of the same size as the original image (256 × 256 pixels) and then created a noise amplitude spectrum as a 2D circle of radius α, with α taking values from 0 (K0 movie) to $\sqrt{2}$ (K2 movie). This was due to the squared relationship between the amplitude spectrum and the power spectrum. To create the final noise image, we combined this noise amplitude spectrum with a random phase spectrum, where phase values were randomly sampled from the range 0–2π. The final noise images were visualized by computing its 2D inverse Fourier transform. Each frame of the noise movie was created using a new random seed, and as a result, the raw noise movies had no temporal correlations between frames.

Noise-masking procedure.

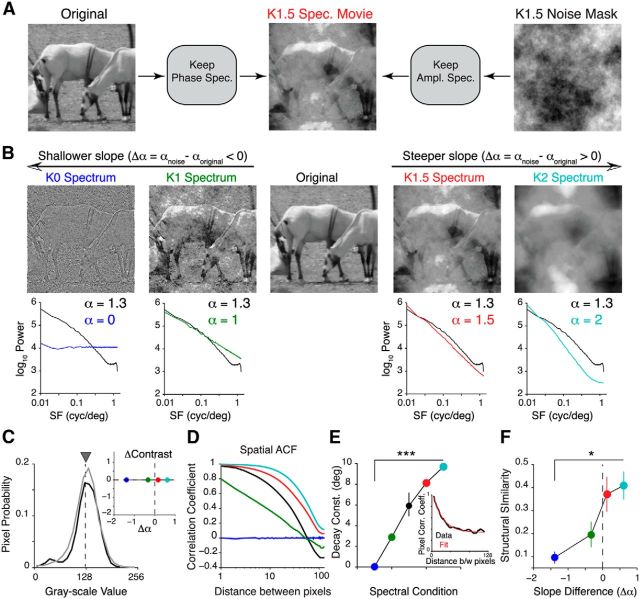
Figure 1A provides a schematic of the noise-masking procedure. First, each frame of a natural movie was decomposed into its Fourier components (phase and amplitude) via a 2D fast Fourier transform implemented in MATLAB. Next, a noise image was created as described above. The phase spectrum of the original movie was then combined with the amplitude spectrum of the noise movie. The resulting image was then inverse Fourier transformed to yield a noise-masked movie frame. This procedure was repeated for all frames. We used a total of five different natural movies, each 4 s in duration, from the van Hateren movie database (van Hateren and Ruderman, 1998).

Figure 1.

Perturbing spatial correlations in natural movies. A, Illustration of the noise-masking procedure. Briefly, we combined the Fourier phase spectrum of a natural movie frame with the amplitude spectrum of a synthetic noise mask to create a noise-masked movie frame. B, Top, Example frames from a set of noise-masked movies with four different levels of spatial correlations. Bottom, Comparison between the power spectra of these movies (colored lines) and the original movie (black line). Note that the slope of all original movies used in this study is 1.3. C, Pixel intensity distribution from one original movie (black) and its noise-masked variants (gray). All noise-masked movies were adjusted to have the same luminance (gray triangle), contrast (see inset), kurtosis, and skewness as the original movie. Inset, A plot of the change in contrast against the difference in spectral slope, computed relative to the original movie. D, Representative spatial ACFs of the noise-masked movies shown in B. E, Spatial decay constant obtained by fitting a single exponential function to the ACF (inset). The decay constant decreased as spatial correlations were removed from the stimulus (p < 10⁻⁵, 5 movies). The inset shows that the ACF can be well fit with a single exponential function. F, SSIM between noise-masked movies and their original versions. The SSIM was averaged over frames for each movie (1200 frames in total). The p values for F and E were computed using the Cochran–Armitage test for trend. Error bars indicate SEM. Colors indicate noise-masked movies labeled in B. *p < 0.05; ***p < 10⁻⁴.

Adjusting image statistics.

Gray scale values of each movie frame were discretized to 255 values, and each frame was normalized to have equal mean luminance (mean of luminance histogram, 128; mean luminance, 77 cd/m²; luminance range, 0.02–134 cd/m²) and contrast (SD of luminance histogram, 32). This normalization was performed using custom-written MATLAB code together with the lumMatch function in the SHINE toolbox (Willenbockel et al., 2010). To minimize differences between the different original movies, we used the sfMatch function to ensure that all original movies had the same SF distribution and amplitude spectra (α = 1.3, which was the average spectral slope of the selected movie database). We also used the histMatch function to match the histogram of an image with a target (set to the original movie) by remapping pixel values to how frequently they occur in the target histogram. This ensured that all pixel statistics, such as mean, contrast, kurtosis, and skewness, were the same for both the noise movies and the original movies. Additionally, we normalized each power spectrum to have the same integral; that is, all power spectra have the same total SF content. The noise-masking technique only reshuffles power into different bands, without changing the total SF content.

To slow down the movie from its original 60 Hz frame rate, we updated every three frames, creating an effective frame rate of 20 Hz. The monitor refresh rate was fixed at 60 Hz. All visual stimuli were displayed on a 23 inch gamma-corrected LCD monitor (Dell) covering a visual space of ∼96 × 54 deg². Stimuli were displayed using the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997).

Image quality metrics.

We assessed the impact of perturbing spatial correlations on the quality of image using the structural similarity index (SSIM). The SSIM uses image structural information, such as mean, variance, and covariance, to estimate dependencies between pixels (Wang et al., 2004). Specifically, we computed SSIM between images i and j using the following equation:

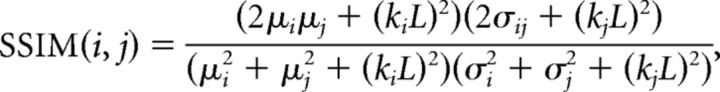where, μ_i,j and σ_i,j are the mean and SD of images i and j, respectively; σ_ij is the covariance; and L is the dynamic range of the image. Further details on the SSIM metric are provided by Wang et al. (2004).

Data analysis

Response similarity, sparseness, and reliability analysis.

Let the response of a neuron to trial i of movie A be f_i,A; then, the response similarity index (SI; Fig. 2) between natural movie A and a noise movie B was calculated using the following equation:

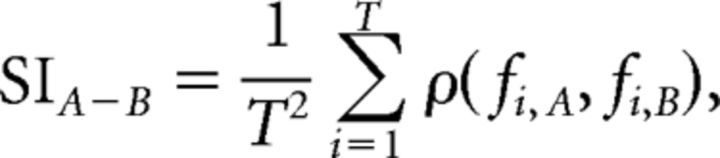where, ρ(f_i,A, f_i,B) is the Pearson correlation coefficient (CC), and T is the total number of trials. From this equation, SI is the average correlation of all possible pairwise combinations of single-trial response vectors of two movies. Lifetime sparseness (selectivity; Fig. 2) was computed using the following equation:

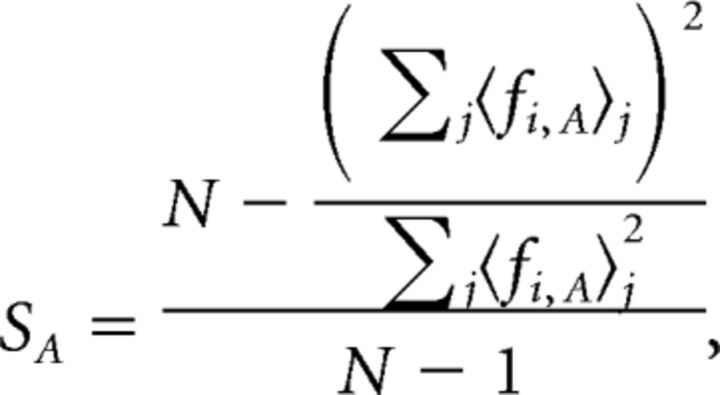where 〈 f_i,A〉_j is the trial-averaged response to frame j of movie A, and N is the total number of movie frames.

Similarly, response reliability to movie A (R_A) was calculated using the following equation:

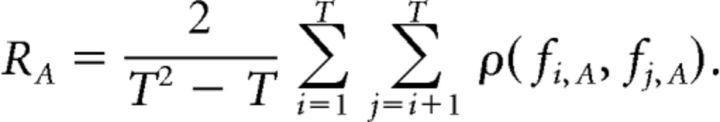Thus, the response reliability (Fig. 3) is the average correlation of all pairwise combinations of trials for a single movie. Only neurons with significant responses on more than five trials were selected for this analysis.

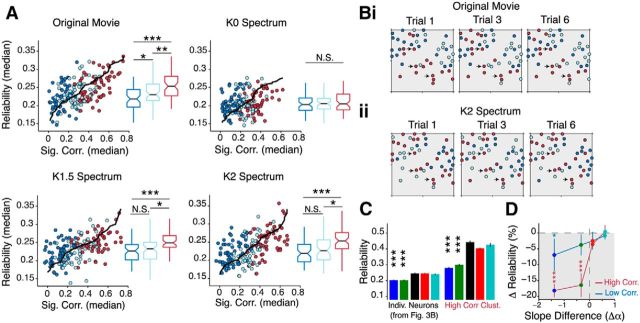
Figure 3.

Spatially decorrelating natural movies decreases trial-to-trial reliability. A, Example raster plots from two neurons, where each row is the normalized response to a single presentation of a movie. The trial-averaged response is shown below together with the reliability (R) values. The shaded area indicates the SEM. B, Cumulative distribution of reliability values. The inset shows the median reliability value. C, Percentage change in reliability relative to the original movie. D, Left, Scatter plots showing the relationship between reliability calculated from calcium signals (ΔF/F) and reliability calculated from inferred firing rates for K0 spectrum movies, original movies, and K2 spectrum movies. The red line shows the linear least-squares regression. All examples show a strong linear relationship between the two reliability measures (p values computed using Student's t test). Right, No significant difference in the Spearman's correlation between reliability calculated from ΔF/F and reliability calculated from inferred firing rates for all spectral conditions. E, Same plot as in C, but using reliability was computed from ΔF/F instead. Measured calcium signals also show a monotonic decrease in reliability as spatial correlations are removed from natural movies. Data in B, C, and E are presented as the median ± 95% CI. F, Scatter plot showing the relationship between reliability and mean firing rate, illustrated for K0 (left) and K2 movies (middle). The thick black and red lines are the local regression (LOESS) lines for the original movie and the noise movien respectively. Right, Quantification of the Spearman rank correlation coefficient between response reliability and mean firing rate for all noise movie conditions. Only K1 movies had a significantly smaller correlation (p = 0.035, two-tailed rank-sum test; 650 neurons). G, Quantification of the reliability of strongly responding neurons. Strongly responding neurons were defined as neurons, which had a firing rate >2 SDs above the original movie (z score > 2σ). Reliability was also z-scored to pool data from different experiments. Data in B–F were obtained from 650 neurons (16 mice). The p values were computed using Bonferroni-corrected two-tailed rank-sum tests relative to the original movie. Error bars denote SEM. *p < 0.05; **p < 10⁻³; ***p < 10⁻⁴.

To compute cluster activation reliability (see Fig. 10C), we used the same equation above, but instead let f_i,A be the population-averaged firing rate (i.e., averaged over all neurons in a population) of neurons on trial i of movie A.

Figure 10.

Highly correlated neural ensembles are reliably activated over multiple stimulus repetitions. A, Scatter plot of median reliability against median signal correlation for each population and movie. The solid black lines denote trends computed via LOESS regression. The box–whisker plots quantify reliability in each cluster. Colors are labeled in Figure 9. Bi, Bii, Cluster maps derived from interneuronal correlations on each trial. Representative examples are shown for three trials (1, 3, and 6) for both the original movie (Bi) and K2 movie (Bii). Neurons colored in red are strongly correlated with each other on each repetition of the stimulus. Almost the same clusters are reactivated on each trial for both stimuli (examples are indicated by black arrows). C, Quantification of median reliability within the high-correlation cluster. We computed trial-to-trial reliability using the averaged firing rate of all the neurons in the high-SC cluster (see Materials and Methods). This gives a measure of the reliability of activation of the entire cluster. For comparison, we plotted the individual neuron reliability on the left (same data as in Fig. 3B). For all stimulus conditions, pooling responses from neurons in a cluster improves reliability (p < 10⁻¹⁰, Kruskal–Wallis ANOVA between individual neuron and high-correlation cluster reliability). D, Percentage change in high- (dark red) and low-correlation (dark blue) cluster reliability plotted against spectral slope difference relative to the original movie. Data are presented as the median ± 95% CI from 16 mice. *p < 0.05; **p < 10⁻³; ***p < 10⁻⁴.

Mapping neuron spatial frequency preferences.

In experiments where we mapped the spatial frequency tuning of neurons (see Fig. 5), we presented alternating blocks of noise-masked movies and sinusoidal gratings at full contrast. Here, we used gratings with 2 Hz temporal frequency at eight different orientations (0–180°) and at nine different spatial frequencies [0.01 to 0.32 cycles/degree (cpd)]. Each grating was presented for 3 s and was flanked by 1 s gray screens. We quantified spatial frequency responses by fitting the following empirical difference-of-Gaussians function to the spatial frequency tuning curves (Sceniak et al., 2002):

Here R₀ is the spontaneous rate, measured from the 1 s blank screen epochs. The parameters (R_E,I, μ, and σ) were optimized to provide a least-square error fit of the data using the MATLAB function lsqcurvefit with the Levenberg–Marquardt algorithm. The quality of fit was assessed by calculating the adjusted R² (coefficient of determination) value as follows: R² = Σ_i(f − ŷ)/Σ_i(y − ŷ), where f is the fit and y is the raw data. Only neurons with fits better than 75% were selected for further analysis. The preferred spatial frequency and bandwidth (BWs) were determined empirically from the fitted curves. We defined the preferred spatial frequency as the spatial frequency that elicits the maximal response (i.e., preferred SF = μ). The bandwidth (measured in octaves) was computed as the log ratio of the SFs that elicited half the maximal response for the high-frequency cutoff to the low-frequency cutoff: BW = log₂(SF_high/SF_low).

Figure 5.

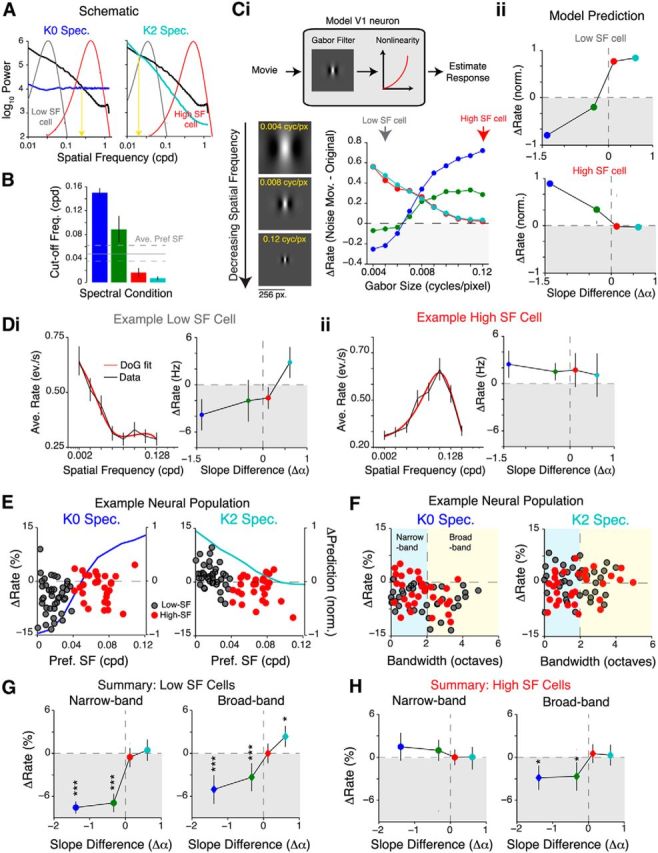
SF tuning of neurons cannot explain responses to noise-masked movies. A, Schematic illustrating the portion of the power spectrum sampled by a typical low-SF- (gray) or high-SF-preferring (red) cell. The yellow arrow indicates the cutoff frequency, which is defined as the SF at which the power in the noise-masked movie is the same as that in the original movie. B, Quantification of the cutoff frequency (cycles per degree) for the different spectral conditions. As expected, cutoff frequency is the highest for K0 and lowest for K2 movies. Data are pooled from five movies. The gray lines show the mean ± SEM preferred SF of 308 neurons (four mice). Ci, Top, Schematic of an LN model of a V1 neuron used to predict responses to the noise movies. Briefly, a Gabor filter was convolved with a noise-masked movie, and the resultant was rectified with a pointwise nonlinearity to obtain a predicted firing rate. Bottom, Plot showing the predicted firing rate difference (ΔRate = noise movie rate − original movie rate) for Gabor filters of different sizes. Decreasing the size of the Gabor filter is equivalent to increasing the preferred spatial frequency. Cii, Plots showing predicted firing rate difference of a typical low-SF-preferring cell (top, SF denoted by gray arrow in Ci) and high-SF-preferring cell (bottom, red arrow). Di, Left, Representative tuning curve of a low-SF-preferring cell, which responds more to the spatially correlated movies. The SF tuning curve of this cell is well fit with a difference of Gaussians model (red line). Right, Plot of firing rate difference of this neuron demonstrating that this cell responds more to K2 movies. Dii, Same plot as Di, but for a high-SF-preferring cell that responds more to spatially decorrelated movies instead. E, Plots of the difference in firing rate against the preferred SF. Data are from 78 simultaneously recorded neurons. Dark gray dots indicate low-SF-preferring neurons (SF, <0.04 cpd), and red dots indicate high-SF-preferring neurons. Also plotted on the same axes is the difference in firing rate predicted from the model in C to illustrate the expected trend. There was no statistically significant trend in the data for either spectral condition (K0, p = 0.65; K2, p = 0.071; Spearman's rank correlation coefficient). F, Plots of the difference in firing rate against SF tuning bandwidth. The same neurons as in E were sorted according to bandwidth (see Materials and Methods). Similar to E, dark gray dots indicate low-SF-preferring neurons, and red dots indicate high-SF-preferring neurons. The dashed vertical line separates narrowband neurons (bandwidth, <2 octaves) from broadband neurons. G, H, Difference in firing rates plotted against difference in slopes for low-SF-preferring cells (G) and high-SF-preferring cells (H). Cells were further partitioned into narrowband and broadband based on tuning bandwidth. *p < 0.05; ***p < 10⁻⁴.

Mapping receptive fields and measuring cortical magnification.

In experiments where we mapped the RF centers of neurons (see Fig. 8A), we presented sparse noise stimuli, which consisted of black and white squares (4 × 4° each, 1 pixel corresponded to 0.8°) on an isoluminant gray background (128 on a 256 gray scale). Each square was presented at a random location (7 × 12 grid) for 200 ms followed by a 300 ms blank period. The location of each black/white square was chosen from a pseudorandom distribution such that two consecutive squares were at least three nodes away from each other. Reponses to white squares were use to calculate the ON receptive field, and responses to black squares were used to calculate the OFF receptive field following methods described previously (Smith and Hausser, 2010). We computed the cortical magnification factor (CMF) in both the rostrocaudal (CMF_R–C) and mediolateral (CMF_M–L) axes by performing a linear regression between RF position (in degrees) and neuron position (in micrometers) and computing the slope of the best-fit regression line. The overall CMF was computed using the following equation: CMF = CMF_M–L × CMF_R–C. For neural populations in which we were not able to calculate the CMF (see Fig. 8B), we used a CMF of 1 × 10⁻³ mm²/deg² to scale between cortical space and visual space. This value is consistent with previously published reports (Garrett et al., 2014).

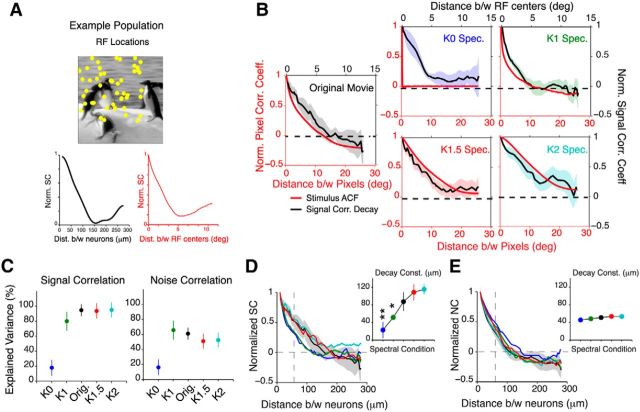
Figure 8.

Spatial organization of interneuronal correlations closely tracks stimulus correlations. A, Top, Example RF locations of a population of 50 neurons. Note, the RF centers are not drawn to scale. Bottom, SCs between neurons in this example population decay with increasing distance between neurons (left) and increasing separation between RFs (Euclidean distance between centers, right). B, Comparison between signal correlation decay (black lines) and stimulus ACF (red lines) for all spectral conditions. The shaded area denotes the 95% CI of the median computed from 16 mice. In most conditions, the decay of signal correlations (except K0 movies) between neurons closely tracks the stimulus ACF. C, Explained variance of the fit between the stimulus ACF and the signal correlation decay function. The ACF is able to explain up to 80% of the decay in signal correlations and 60% of the decay in noise correlations. Data are presented as median ± 95% CI. D, E, Signal correlation (D) and noise correlation (E) as a function of distance between neurons for all spectral conditions. The inset shows the average decay constants estimated from single exponential fit. Data in the inset are shown as mean ± SEM. The shaded area in D indicates the 95% CI of the median of the original movie. All data in B–E are from 16 mice. *p < 0.05; **p < 10⁻³.

Analysis of signal and noise correlation between neurons.

Signal correlations (SCs) between pairs of neurons were calculated as the Pearson correlation coefficient between trial-averaged responses binned at 200 ms. To compute noise correlations (NCs), we first subtracted the trial average from responses in each trial and then computed the Pearson CC between these mean-subtracted responses, again binned at 200 ms (Singh and Lesica, 2010).

To compute signal and noise correlation decay functions (see Fig. 8), we first binned neurons according to the pairwise Euclidean distance between their centroids, determined from the imaging software. On average, a majority of neurons were located within 20–180 μm of each other, and only <1% were separated by a distance of 300 μm. Next, we computed the median CC within each distance bin. We adjusted the bin width (range, 30–50 μm) to ensure at least five neurons per bin. Data were then pooled from different experiments by first normalizing the CC to the first distance bin and then by computing a bootstrapped estimate of the median CC and its 95% confidence interval (CI) for each subsequent bin. To estimate the decay constant, we fit single exponential functions to each correlation decay function using a least-squares algorithm, and assessed fit using an adjusted R² value. Only populations with R² > 80% were selected for further analysis.

Clustering analysis.

Clustering analysis (see Figs. 9, 10) was used to visually represent the correlation structure of the network. Clustering analysis was performed on all neurons in the imaged population and was repeated for each spectral condition. We first arranged either signal or noise correlation values in a matrix, where each element is the CC for a pair of neurons. Next, an agglomerative hierarchical clustering algorithm was used to cluster this matrix by maximizing between-cluster variance and minimizing within-cluster variance. Intercluster linkages were formed using the Ward metric, and within-cluster linkages were formed by minimizing the Euclidean distance between CCs. This was achieved via a custom-written code that used built-in MATLAB functions (linkage, pdist, and cluster). The optimal number of clusters (n̂, typically ranging between 2 and 4) were selected using the Calinski–Harabasz metric (Bayati et al., 2008), which minimizes within-cluster variance and maximized between-cluster variance according to the following formula:

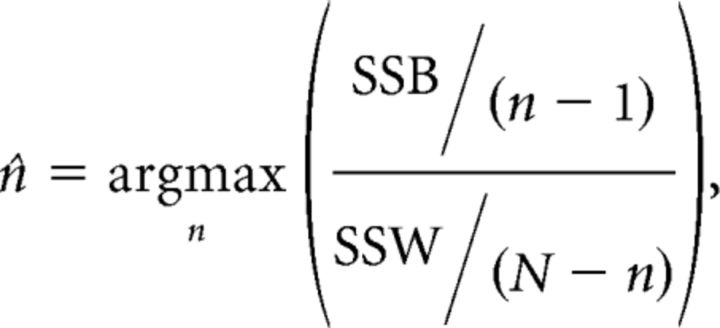where SSB = Σ_i (x_i − x̂)² and SSW = Σ_{j = 1}^N ∑_i (x_i − c(j))² are the between- and within-cluster sums of squares, respectively; x_i is the correlation coefficient of the ith element; and N is the maximum number of clusters, which was set to 4. The index i references all elements within a cluster, whereas the index j references the clusters. Neurons belonging to each cluster were color-coded as shown in Figure 9.

Figure 9.

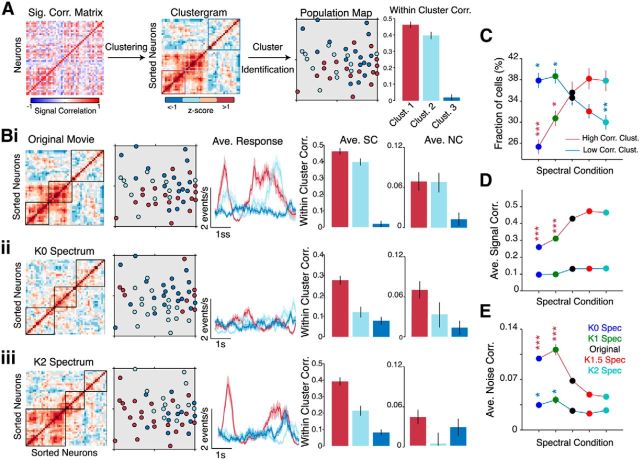
Clustering analysis reveals distinct ensembles of highly correlated neurons. A, Illustration of the clustering method used to group neurons based on their SC coefficients. The histogram shows average SC within each cluster. Error bars denote SEM. Bi–Biii, Clustering analysis applied to the same neural population in response to an original movie (Bi) and its K0 spectrum (Bii) and K2 spectrum versions (Biii). The color-coded population maps show a reorganization of the clusters to the different stimuli. The size of the population map is 250 × 250 μm. Subsequent panels show the average response of neurons in each cluster and a quantification of within-cluster signal and noise correlation coefficients. Error bars and shaded areas denote SEM across neurons in each cluster. C, Fraction of neurons in the high- (dark red) and low-correlation (dark blue) clusters for all stimulus conditions. D, E, Average signal correlation (D) and noise correlation (E) between neurons in each cluster. All data in D and E are presented as mean ± SEM from 16 mice. The p values were computed relative to the original movie using a post hoc Bonferroni-corrected rank-sum test. Colors of symbols indicate the correlation cluster. *p < 0.05; **p < 10⁻³; ***p < 10⁻⁴.

Discrimination analysis.

We used a template-matching algorithm to determine whether a single-trial response could be matched to one of five population templates (the five movies used in each spectral condition; see Fig. 11). This unsupervised classification was based on previous studies (Goard and Dan, 2009; Kampa et al., 2011). First, we created population templates for each movie by averaging (over trials) the responses of all neurons in a population. Next, individual trials for each neuron were assigned to a particular stimulus category by minimizing the Euclidean distance between the template and the single-trial response. The classified stimulus identities were then compared to the stimulus presentation to compute the percentage of correctly classified trials for each neuron. To test the dependence of the number of neurons on classification, we used a Monte Carlo sampling technique (repeated 500 times) to pick n neurons (range, 1 to population size) at random from the population with replacement. The single-trial responses from these n neurons were compared to the template as described above. The decoding accuracy was quantified by computing mutual information (MI) using the following equation:

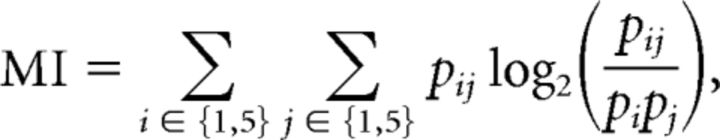where, p_ij is the probability of observing movie i given that the true label is j.

Figure 11.

Ensembles of correlated neurons efficiently encode natural scenes. A, Illustration of the decoding method. A single-trial response was classified into one of two movies (repeated for all possible pairs of movies) on the basis of its Euclidean distance to a population template (see Materials and Methods). B, Plot illustrating that decoding accuracy (percentage of correctly classified trials) increases as the number of neurons contributing to the single-trial response increases. Data in this plot are from a single population of neurons (46 neurons). C, Percentage changes in mutual information for both individual neurons (diamonds) and whole populations (circles). Data are presented as median ± 95% CI. The p values were computed using a post hoc Bonferroni-corrected rank-sum test relative to the original movie. Green asterisks, p values for individual neurons; red asterisks, p values for the population. D, Average discriminability for the individual neurons (left) and whole population (right) decomposed according to correlation cluster. The p values were computed using a one-tailed rank-sum test relative to the original movie. E, Comparison of mutual information for high- and low-correlation clusters relative to randomly sampled subpopulations of the same size. Data in C–E are from 16 mice. Error bars denote SEM. *p < 0.05; ***p < 10⁻⁴.

V1 linear–nonlinear normalization model.

We first determined a best-fit RF estimate from neural responses to two original movies using a bank of linear and nonlinear filters (Fig. 12). The spatial part of the linear filter bank was log-Gabor RFs, at 6 different orientations (0–180°) and ranged in size from 12 to 18° of visual angle (Bonin et al., 2011). Because we did not know the locations of the RFs a priori, we randomly picked 50 possible locations on the screen. The temporal part of the linear bank consisted of gamma functions with a range of temporal delays (140–200 ms). Responses from each branch of this filter bank were summed and then passed through a pointwise exponential nonlinearity to provide a response estimate. We used a least squares method to determine the best-fit model. Only neurons with adjusted R² values >80% were selected for further analysis.

Figure 12.

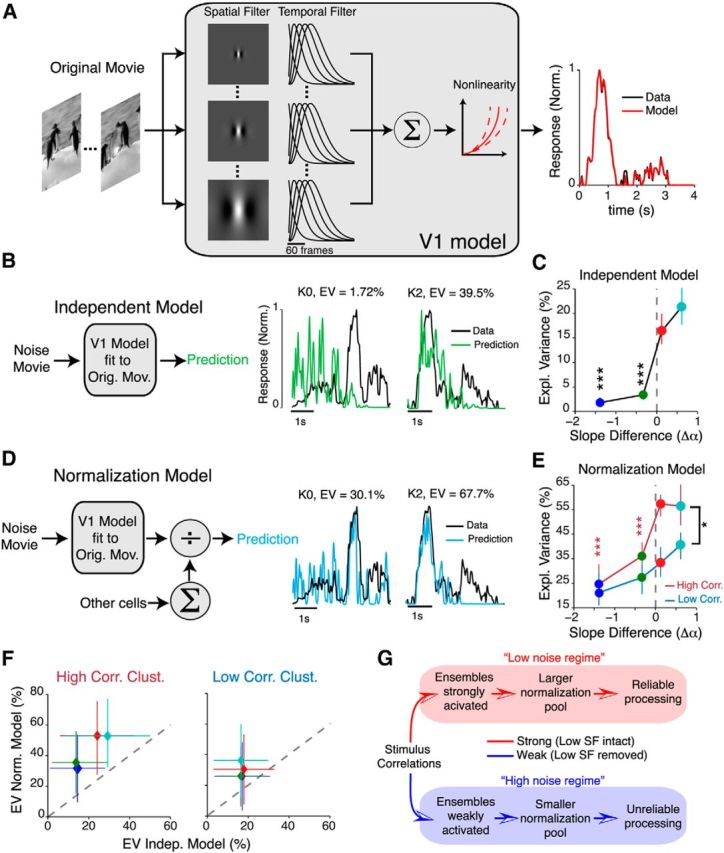
Linear–nonlinear cascade model with normalization explains responses to correlated stimuli. A, Schematic of the model used to determine the best receptive field estimate from responses to an original movie. B, Left, Schematic describing independent model. This model assumes no interactions between neurons. Right, Representative examples showing the predicted output of this model (green) relative to the real data (black) from two cells. EV, Explained variance. C, Percentage variance explained by the independent model. D, Left, Schematic describing normalization model. This model assumes interactions between neurons via the divisive normalization rule. Right, Responses of the same cells as B, but predicted with the normalization model instead. E, Percentage variance explained by the normalization model for all stimulus conditions. Here, the high- (dark red) or low-correlation (dark blue) clusters were separately considered as normalization pools. Red stars indicate comparisons performed for data in the high-correlation cluster (relative to the K2 movie). Black stars indicate comparisons between high- and low-correlation clusters. Data in C and E are presented as the median ± 95% CI from 239 neurons. F, Scatter plot comparing performance, in terms of explained variance of the normalization model relative to the independent model for both high-SC and low-SC clusters. The EV of the independent model was computed from neurons in each cluster, whereas the EV of the normalization model was computed by applying the divisive normalization rule to all neurons in each cluster. G, Schematic summarizing the main findings of this study. In the low noise regime, strong stimulus spatial correlations dynamically alter interneuronal correlations to change the normalization pool, ensuring reliable processing. In the high noise regime, weak stimulus correlations fail to activate ensembles, resulting in unreliable processing. *p < 0.05; ***p < 10⁻⁴.

In the independent model, we convolved each noise movie frame with the best-fit RF model for each neuron. In the normalization model, we modulated the output of each independent model (f) using the divisive normalization rule:

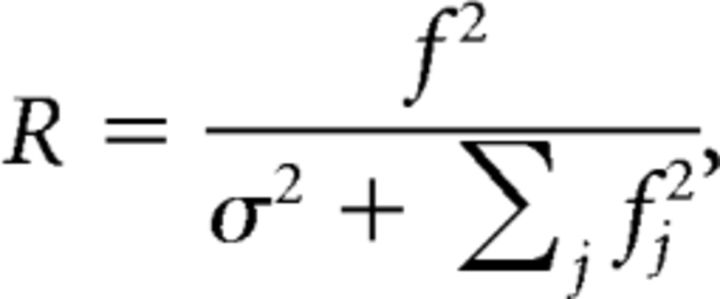where j indexes neurons in either the high- or low-correlation cluster. The adjusted R² was computed between the predicted and actual responses to assess the percentage of variance explained by each model.

Statistical analysis.

All statistical analysis was performed using custom-written scripts in MATLAB and R. No tests were conducted to determine sample size. Data from anesthetized experiments came from 16 mice, yielding a total of 1006 neurons. For reliability analysis, we picked neurons (650 neurons, 16 mice) that had significant visually evoked responses from six or more trials. These same 650 neurons were used for all correlation analysis. For SF tuning analysis, we collected data from 308 neurons for four mice. In awake experiments, we obtained data from 230 neurons in four mice.

Data were first tested for normality using the Shapiro–Wilk test. All data presented in this paper are nonnormally distributed; thus, all statistical tests were conducted using nonparametric statistics. Our experiments involved testing the influence of different movies on the same population of neurons; thus, all comparisons were performed using nonparametric repeated-measures ANOVA (Friedman test) with Bonferroni's correction for multiple comparisons. For Bonferroni corrections, the significance value was set to 0.05. Post hoc tests were performed using the two-tailed Wilcoxon rank-sum test. All other statistical tests that were performed are described in the text. The 95% CIs of the medians were computed by bootstrapping. In most figures, data are presented as the median ± 95% CI, unless stated otherwise. Visually nonoverlapping 95% CIs imply that the data are significant to at least p < 0.05.

Results

Perturbing spatial correlations in natural movies

With the aim of understanding the properties of natural scenes that influence reliability, we developed a novel noise-masking technique that allowed us to selectively increase or decrease second-order spatial correlations in time-varying natural scenes without altering their underlying edge structure (Fig. 1). To do so, we took advantage of the fact that power (P) in most natural images decreases with increasing SF (k) according to the power law P ∼ k^−α, where the parameter α is the spectral slope (van Hateren and van der Schaaf, 1998). White-noise images, for example, lack correlations between pixels, possess constant power in all SF bands, and have a zero spectral slope. Thus, the spectral slope can succinctly parameterize both spatial correlations and the distribution of SFs in natural images. Furthermore, because the phase spectrum contains information about edges, spatial correlations can be altered without significantly changing the saliency of an image (Wichmann et al., 2010). Thus, in our noise-masking technique, we preserved the phase spectrum and added noise masks with precisely defined spectral slopes to each frame of a set of natural movies (Fig. 1A; five movies; see Materials and Methods for details).

We used this method to generate movies with four different spectral slopes: 0, 1, 1.5, and 2, henceforth referred to as K0–K2 respectively. Example frames from these noise-masked movies together with their power spectra are shown in Figure 1B. Since changes in pixel statistics, especially mean luminance and contrast, are known to affect coding in the visual system (Bonin et al., 2006), we adjusted each noise-masked frame to have the same mean luminance, contrast, kurtosis, and skewness (Fig. 1C). As a result, our noise-masked movies differed only in their spectral slope and not in their relative distribution of light and dark pixels. For example, K0 movies possessed no spatial correlations between pixels and, consequentially, had a flat power spectrum (Fig. 1B) and a flat spatial autocorrelation function (ACF; Fig. 1D). Visually, edges in K0 movies appeared sharper than the original movie because of an increase in high SF power. K2 movies, on the other hand, were strongly spatially correlated and appeared blurry due to an increase in low SF power. Thus, our noise-masking technique is equivalent to applying a zero-phase SF filter to change the SF content of natural movies. Specifically, in K0 and K1 movies, low SF content is attenuated, whereas high SF content is attenuated in K1.5 and K2 movies.

Next, by fitting single exponential functions to each ACF, we parametrically measured the distance, in visual space, over which pixels remained strongly correlated (Fig. 1E, inset shows example fit). As expected, K2 movies had the largest decay constant, with pixels strongly correlated with each other up to a distance of ∼10°. In contrast, pixels in K1 movies became decorrelated beyond 3°. Thus, pixels in both K0 and K1 movies decorrelate within the span of a typical mouse V1 receptive field (5–7°; Niell and Stryker, 2008). Notably, the remarkably low variability in noise-masked movie data points reinforces the fact that these movies are spatially homogeneous: all noise-masked movies have the same power spectra regardless of differences in their phase spectrum.

In addition, we also assessed changes in image quality by computing a framewise SSIM between each noise movie and its original version. The SSIM uses image structural information, such as luminance and contrast, to assess the degree of similarity between two images. Images that are similar in appearance have a SSIM close to one, whereas statistically dissimilar images have a SSIM close to zero. We found that SSIM decreased as the difference in spectral slope became more negative (p = 0.036, Cochran–Armitage test for trend). This implies that K0 and K1 movies were the most dissimilar to their original version despite having edges that were visually sharper. Thus, our noise-masking technique revealed that perturbing the spectral slope alters the statistical structure of natural scenes by changing correlations between pixels.

Neurons respond to spatially decorrelated movies with weak responses

To assess how populations of neurons in layer 2/3 of V1 represented these noise-masked movies, we preformed high-speed two-photon calcium imaging in lightly anesthetized mice using the synthetic calcium indicator OGB1 (Fig. 2A). Our high-speed imaging method (Wilson et al., 2013) allowed us to scan a cortical area of 250 × 250 μm at a rate of 50 frames/s. Within each area, we were able to record up to 100 neurons simultaneously, out of which 46 ± 20 neurons (21 populations, 16 mice) were visually responsive. Firing rates were inferred from the calcium signals using a temporal deconvolution algorithm (Vogelstein et al., 2010; Fig. 2B). The parameters used for accurate deconvolution were determined in previous studies (Wilson et al., 2012; El-Boustani and Sur, 2014). Expectedly, we found a significant correlation between inferred firing rate and average fluorescence change for all spectral conditions (Fig. 2C), implying a strong correspondence between the measured calcium signal and inferred firing rate.

The majority of neurons responded strongly and synchronously to the original movie at distinct epochs (Fig. 2D, center panel). Surprisingly, the same neurons responded weakly, and at random times, to the decorrelated stimuli (K0 and K1 movies), which resulted in flat population-averaged responses (Fig. 2D, bottom row). In contrast, these neurons responded to K1.5 and K2 movies with similar amplitudes and during the same epochs as the original movie. We assessed how similar the noise movie firing dynamics were to the original movie by computing a similarity index (see Materials and Methods) for each neuron. On average, neural responses became more dissimilar as spatial correlations were removed from the movie, with responses to K0 movies being the most different (p < 10⁻⁶, Friedman test; 1006 neurons; 16 mice; Fig. 2E). The SI was also significantly lower for responses to K0 movies than responses to K1 movies (p = 8.12 × 10⁻⁵, Bonferroni-corrected rank-sum test). In contrast, both K1.5 and K2 movies evoked very similar responses to the original movie, even though they had stronger spatial correlations (p = 0.27, Bonferroni-corrected rank-sum test). When compared with image SSIM (Fig. 1D), these observations suggest that neurons in mouse V1 are highly sensitive to subtle changes in natural movie spatial correlations.

Flattening the power spectrum strongly decreased the mean firing rate of K0 and K1 movies relative to the original movie (p < 10⁻⁶, Friedman test with Bonferroni correction; 16 mice; Fig. 2F). Surprisingly, even though K1.5 and K2 movies had stronger spatial correlations than the original movie, they failed to evoke stronger firing rates (K1.5, p = 0.95; K2, p = 0.07, Bonferroni-corrected rank-sum tests). In addition, we found that the trial-to-trial variance for K0 and K1 movies also increased (p < 10⁻⁶, Friedman test with Bonferroni correction; 16 mice; Fig. 2G). Thus, V1 neurons have reduced and highly variable responses when spatial correlations are removed from natural movies.

Next, we computed lifetime sparseness from the inferred firing rates as a measure of selectivity to the different stimuli. By definition, a neuron with high lifetime sparseness responds selectively to only a few frames in the stimulus (Willmore et al., 2011). Not surprisingly, K0 and K1 movies evoked highly unselective responses, whereas increasing stimulus correlations increased lifetime sparseness (K1.5, p = 0.23; K2, p = 2.1 × 10⁻³, rank-sum test relative to original movie; 1006 neurons; Fig. 2H). Thus, the selectivity of V1 neurons is also strongly modulated by stimulus spatial correlations. Taken together, these observations support the conclusion that attenuating the low SF power of natural scenes has a detrimental effect on neural responses.

Decorrelating movies reduces response reliability

We next asked whether removing spatial correlations also affected response reliability. Reliability is traditionally measured in terms of the number of spikes produced by a neuron on every stimulus repetition (Tiesinga et al., 2008). However, because we did not have single spike resolution in our recordings, we reasoned that a highly reliable neuron would respond with stereotypical responses on every repetition and, as a result, would have a high, positive correlation coefficient between trials. Thus, we defined response reliability as the average Pearson's correlation coefficient between every pairwise combination of trials (see Materials and Methods). Since this metric quantifies the degree of response similarity between trials, it provides a measure of both reliability and temporal precision (Haider et al., 2010; Bathellier et al., 2012; Baudot et al., 2013).

Neurons responded reliably to the unperturbed movies, as well as their K1.5 and K2 spectrum versions (Fig. 3A). Relative to the original movie, we found no difference between K1.5 and K2 movie reliability (K1.5, p = 0.565; K2, p = 0.624, Bonferroni-corrected rank-sum test; Fig. 3B,C). In contrast, K0 and K1 movies evoked responses with significantly lower reliability (p < 10⁻⁶, Friedman test; 650 neurons; 16 mice; Fig. 3B,C), due to the high variability between trials. As expected, we also found a significant linear relationship between reliability measured using inferred firing rates and reliability measured using fluorescence signals for all spectral conditions (Fig. 3D). This implies that neurons, which had reliable inferred firing rates, also responded with reliable calcium transients. Therefore, removing spatial correlations and attenuating low SF power caused a strong monotonic decrease in response reliability (Fig. 3C,D). In contrast, attenuating high SF power did not change reliability.

Was the reduced reliability to decorrelated movies a consequence of reduced firing rates? We found a linear relationship between average firing rate and reliability, for all stimulus conditions (Spearman's ρ = 0.65 ± 0.22; p = 8.9 × 10⁻³; 650 neurons; Fig. 3F). Partitioning data according to firing rates, we found a small fraction of neurons that responded strongly to both K0 and K1 movies (132 of 650, z-score > 2σ above original movie response). Interestingly, despite having higher firing rates, these neurons still responded less reliably to both decorrelated movies (K0:, p < 10⁻⁴; K1, p = 0.035; 132 neurons; rank-sum test; Fig. 3G). Taken together, these results suggest that K0 and K1 movies evoke unreliable responses because they do not possess the appropriate spectral content. Thus, reliable coding of natural scenes requires intact low SF information.

Stimulus-induced changes in neuronal responses in awake mice

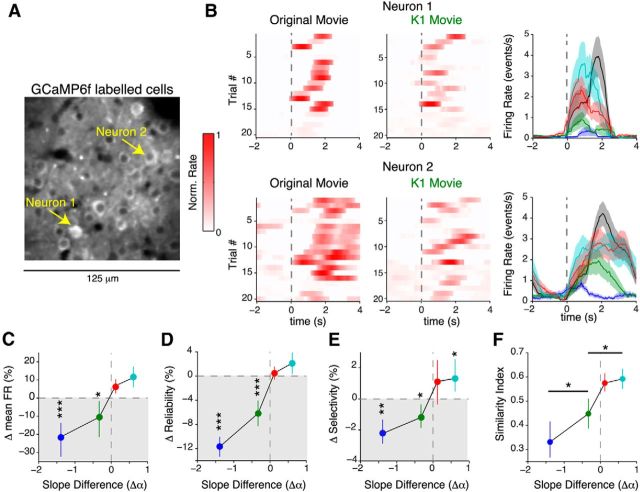
Our results so far show that the response properties of neurons in mouse V1 are sensitive to the spectral properties of the visual stimulus; specifically, removing spatial correlations decreases both response amplitudes and between-trial reliability. Since anesthesia is known to influence cortical computations (Haider et al., 2013), we next sought to extend the generality of these findings to awake mice by repeating the same experiments in passively viewing, head-fixed mice using the genetically encoded calcium indicator GCaMP6f instead of OGB-1 (Fig. 4A; see Materials and Methods).

Figure 4.

Decorrelated movies evoke weak and unreliable responses in awake mice. A, Two-photon image of a population of 29 neurons expressing GCaMP6f. See Materials and Methods for details. B, Example raster plots (left and middle) and trial-averaged response (right) of the two cells marked in A. Both cells responded strongly to the spatially correlated stimuli (original, K1.5, and K2 movies), but less so to K1 and very weakly to K0 movies. The shaded region indicates the SEM computed over 20 trials. C, Percentage change of mean firing rate relative to the original movie. Neurons in awake mice also responded with significantly lower firing rates to spatially decorrelated stimuli. The decrease in firing rate is commensurate with OGB1 data in anesthetized mice (Fig. 2E). D, Change in reliability relative to the original movie shows a strong decrease in reliability as spatial correlations are removed, similar to anesthetized animals (Fig. 3C). E, Significant reduction in selectivity (measured from lifetime sparseness) for K0 movies (p < 10⁻⁵), but less so for K1 movies (p = 0.012). F, Quantification of similarity index relative to the original movie. Similar to Figure 2D, response similarity monotonically decreased as spatial correlations were removed from the natural movie. The p values in F were computed using a post hoc rank-sum test relative to K2 movies. All other p values were computed via Bonferroni-corrected rank-sum test. Data for C–F are from 230 neurons (4 mice) and are represented as median ± 95% CI. *p < 0.05; **p < 10⁻³; ***p < 10⁻⁴.

Neurons in awake mice also responded to both K0 and K1 movies with significantly weaker responses than the original movie (p < 10⁻³, Friedman test with Bonferroni correction; 230 neurons; Fig. 4B). Surprisingly, firing rates to K1 movies were slightly higher than in anesthetized mice (p = 6.7 × 10⁻³, one-tailed rank-sum test relative to anesthetized data). However, despite this increase in firing rate, K1 movie responses were significantly less reliable (Fig. 4C) and unselective (Fig. 4D) than responses to original movies. Similar to data from anesthetized mice, we also found that removing spatial correlations led to a monotonic decrease in response similarity in awake mice (Fig. 4E).

Thus, our awake imaging experiments show that weak and unreliable responses to decorrelated stimuli are unlikely to be caused by a change in brain state imposed by anesthesia. Rather, decorrelated stimuli, which lack crucial low SF information, are not effective at eliciting reliable responses from V1 neurons.

Responses to noise-masked movies cannot be predicted from spatial frequency tuning

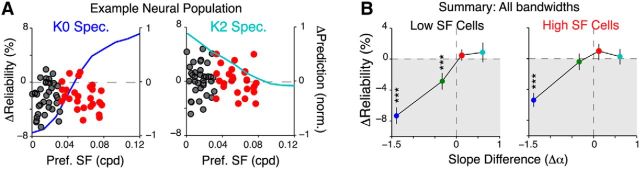
V1 neurons are known to be strongly selective for SF, in addition to orientation (Niell and Stryker, 2008; Gao et al., 2010). Since our noise-masking technique alters the SF content of natural movies by redistributing power in different bands, we next asked whether our observed results could be attributed to SF tuning properties alone (Fig. 5A). Specifically, because K2 movies have higher power in the low SF band (SF <0.012 cpd; Fig. 5B), we expected low SF-preferring neurons to respond more strongly to K2 movies than the original movie. Conversely, because K0 movies had more power than the original movie at SFs >0.14 cpd, we expected high-SF-preferring neurons to prefer K0 movies.

The spatial summation properties of V1 neurons have been traditionally modeled as a linear–nonlinear (LN) cascade (Movshon et al., 1978; Carandini et al., 1997). In this model, the linear component resembles the spatiotemporal RF, whereas the nonlinear component models the spike-generating mechanism. We used this simple model to predict the responses of neurons preferring different SFs (Fig. 5Ci, top). As expected, the model predicted that high-SF-preferring neurons would respond with higher firing rates to decorrelated movies, whereas low-SF-preferring neurons would prefer the more strongly correlated movies (Fig. 5Ci, bottom).

To test the veracity of this prediction, we determined SF tuning properties of neurons empirically from tuning curves that were well fit by a difference of Gaussians function (average R² = 82.4 ± 8.22%; 308 neurons; four mice). Surprisingly, only very few neurons obeyed the predicted trend. Representative responses of two neurons that obeyed the model's prediction are shown in Figure 5D. Rather, on average, both high-SF-preferring (neurons with preferred SF >0.04 cycles/degree) and low-SF-preferring cells responded weakly to K0 movies (Fig. 5E, left). Similarly, there was only a weak correlation between the actual and predicted firing rate difference for K2 movies (r = 0.153, Spearman's rank correlation coefficient; Fig. 5E, right).

V1 neurons also have different tuning bandwidths; that is, they respond to a range of SFs, in addition to their preferred SF. Thus, we next investigated the relationship between bandwidth and firing rate difference (Fig. 5F). This allowed us to further categorize neurons into narrowband (bandwidth of <2 octaves; 106 of 308 neurons) and broadband (202 of 308 neurons). On average, both narrowband and broadband low SF neurons responded marginally more to K2 movies than the original movie (broad, p = 0.042; narrow, p = 0.53; Bonferroni corrected rank sum test; Fig. 5G). In contrast, only narrowband neurons responded with marginally higher rates to K0 movies (Fig. 5H). Surprisingly, high-SF-preferring neurons responded equally to K2 movies (p = 0.871), even though high SF power was significantly attenuated in these movies. Thus, these results are notably different from the prediction of the simple model (Fig. 5Cii), suggesting that responses to the noise-masked movies cannot be predicted from SF tuning alone. Rather, neural activity is modulated by the entire power spectrum of natural scenes.

Additionally, we also found no correlation between reliability and preferred SF for either spectral condition (Fig. 6A). Both high- and low-SF-preferring neurons responded unreliably to K0 movies (both p < 10⁻⁵, Bonferroni corrected rank sum test; 308 neurons) and reliably to K2 movies (Fig. 6B). Interestingly, K1 movies evoked reliable responses from high- but not low-SF-preferring cells (high SF, p = 0.21, 130 neurons; low SF, p < 10⁻⁵, 178 neurons, Bonferroni corrected rank-sum test; Fig. 6B). These results support the hypothesis that reliability is a network-dependent phenomenon and may not be explained solely from the SF tuning properties of neurons.

Figure 6.

SF tuning properties cannot explain the decrease in reliability for decorrelated movies. A, Plot of difference in reliability (ΔReliability equals noise movie reliability minus original movie reliability) against preferred SF. The solid line denotes predicted difference in reliability from the model shown in Figure 5C. Reliability was calculated from predicted firing rate using the gradient of the regression between firing rate and reliability shown in Figure 3G. There was no statistically significant relationship between reliability and preferred SF for either spectral condition (K0, p = 0.85; K2, p = 0.89; Spearman's rank correlation coefficient). B, Reliability is low for K0 movies in both high- and low-SF-preferring cells. Data were not separated according to bandwidth. Compared to original movie, no significant difference was found for K1 movie reliability in high-SF-preferring cells. All data and error bars represent the median ± 95% CI from 308 neurons (4 mice). ***p < 10⁻⁴.

Perturbing spatial correlations bidirectionally modulates signal and noise correlations between neurons

Computations in L2/3 of visual cortex depend on an intricate balance between feedforward stimulus drive and recurrent network dynamics. As a result, the ability of V1 to encode information is influenced by both the structure and magnitude of correlations between neurons (Zohary et al., 1994; Ecker et al., 2011; Moreno-Bote et al., 2014). Thus, we sought to characterize how perturbing stimulus correlations altered interneuronal correlations. Specifically, we analyzed both signal correlation, which reflects similarities in evoked responses, and noise correlation, which captures the dependencies between neurons that are not locked to the external stimulus (Cohen and Kohn, 2011).

In response to unperturbed natural movies, neurons were on average positively signal correlated (mean ± SEM, 0.116 ± 0.003; 650 neurons; Fig. 7A), but only weakly noise correlated (0.031 ± 0.005; Fig. 7C), comparable to previous reports using similar preparations (Hofer et al., 2011; Cossell et al., 2015). Presenting decorrelated movies strongly decreased signal correlation and increased noise correlation (SC, p = 2.34 × 10⁻⁶; NC, p = 3.45 × 10⁻⁵, Bonferroni-corrected rank-sum test relative to original; Fig. 7A,C). In contrast, neurons maintained the same levels of signal and noise correlations in response to strongly correlated movies. Thus, removing spatial correlations from natural scenes not only increased trial-to-trial variability, but also increased correlated variability between neurons. These data also imply that perturbing spatial correlations in natural scenes is sufficient to drive the network into a weakly responsive and noisy coding regime (Churchland et al., 2010).

Figure 7.

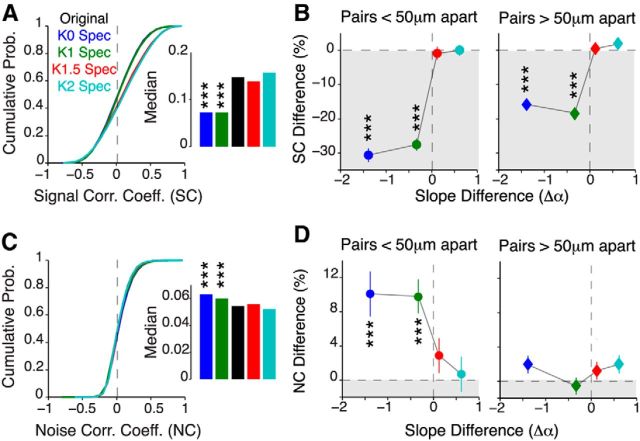
Bidirectional modulation of interneuronal correlations. A, Cumulative distribution of SCs for all spectral conditions. The inset shows the median SC. B, Pairwise difference in signal correlation as a function of spectral slope difference for neuron pairs <50 μm apart (left) and >50 μm apart (right). C, D, Same as A and B, but for NCs. All data are presented as the median ± 95% CI from 16 mice (650 neurons; 210,925 neuronal pairs). All p values were computed using a Friedman test followed by post hoc Bonferroni-corrected rank-sum test relative to the original movie. ***p < 10⁻⁴.

To better quantify how correlations changed between neurons, we computed, for each cell pair, a bootstrapped estimate of the percentage change in correlation relative to the original movie (Fig. 7B). We partitioned our data into pairs that were either located <50 μm (“neighboring pairs”) or >50 μm apart (“distant pairs”) to reflect the fact that neurons separated by <50 μm tend to have higher connectivity (Ko et al., 2011). Removing spatial correlations led to a significant reduction in signal correlations in both neighboring and distant pairs of neurons (p < 10⁻⁸, Friedman test with Dunn's test; 16 mice; Fig. 7D). In particular, K0 movies most strongly decorrelated neighboring neurons (30 vs 12% reduction). In contrast, noise correlation increased for only K0 and K1 movies in neighboring pairs, but remained stimulus invariant in distant pairs (Fig. 7C).

Next, we investigated how the spatial organization of interneuronal correlations changed for the different stimuli. In particular, we were interested in understanding the relationship between interneuronal correlations and stimulus correlations. To this end, we first used a sparse noise stimulus to map RF centers of neurons to compute a CMF (for details, see Materials and Methods). In the example population shown in Figure 8A, 1 deg² of visual space corresponded to 0.992 × 10⁻³ mm² of cortical space (CMF in the rostrocaudal axis, 32.3 × 10⁻³ mm/deg; CMF in the mediolateral axis, 30.7 × 10⁻³ mm/deg), which is consistent with previous studies of mouse visual cortex (Garrett et al., 2014). Importantly, within this example population, cells with neighboring RFs were more strongly signal correlated when stimulated with a natural movie than cells with distant RFs (Fig. 8A, bottom). This is primarily because neurons with neighboring RFs sample similar parts of the visual scene (Bonin et al., 2011; Cossell et al., 2015). As a consequence, signal correlations in all populations (Fig. 8B; 16 mice) decayed as the separation between neurons increased.

We then used the CMF to topographically map visual space into cortical distance. This permitted us to directly compare both signal correlations and the spatial ACF of the different movies on the same scale (Fig. 8B). For all imaged populations, the spatial decay of signal correlations closely matched the spatial ACF. In particular, the change in pixel correlations was able to explain >80% of the variance in the spatial organization of signal correlations for all spectral conditions, with the exception of K0 movies (Fig. 8C; 16 mice). Therefore, the spatial ACF provides a good model for signal correlations between V1 neurons, implying that correlations between neurons fall off as expected from the visual stimulus.

To further explore this notion, we quantified the spatial decay constant by fitting single exponentials to the signal correlation decay functions. Expectedly, this analysis revealed that signal correlations decayed the fastest between neurons in for both K0 and K1 movies (K0, p = 1.86 × 10⁻²; K1, p = 3.81 × 10⁻², rank-sum test relative to original; 16 mice; Fig. 8D), which was commensurate with the fact that pixel correlations also decayed quickly with distance in these stimuli (Fig. 1E). In stark contrast, these correlations persisted over a longer range when K2 movies (p = 6.27 × 10⁻²) were displayed. In particular, coupling between neurons remained strong even among neurons located >200 μm apart. Interestingly, comparing Figures 8D (inset) and 1E, we noticed that neurons were less correlated than expected when stimulated with K2 movies, as the signal correlation decay constant appeared to asymptote at ∼120 μm. This could be due to either decorrelation occurring earlier in the visual pathway or the limited spatial scale of our imaging method. Despite this, our results demonstrate that strongly correlated movies couple neurons located far apart in the cortex, without changing the coupling magnitude.

In contrast to signal correlations, noise correlations decayed exponentially between neurons (average R² of exponential fit, 87 ± 1.6%; 16 mice), with a decay constant of close to 50 μm, regardless of the stimulus condition (p = 0.67, Cochran–Armitage test for trend; Fig. 8E). As a consequence, the spatial ACF poorly predicted the decay in noise correlations (Fig. 8C). Thus, unlike the magnitude (Fig. 7C), the spatial structure of noise correlations is not significantly altered when stimulus correlations are removed. Taken together, these results indicate that perturbing spatial correlations bidirectionally alters both the spatial structure and magnitude of neuronal coactivation. Specifically, neighboring neurons that are located within 50 μm of each other become less signal correlated and more noise correlated when presented with weakly correlated stimuli.

Clustering analysis reveals ensembles of neurons that share similar functional properties

These findings raise an important question: how do changes in interneuronal correlations influence reliability? Previous studies have shown that neurons with similar orientation tuning or receptive fields are recurrently interconnected (Ko et al., 2011; Cossell et al., 2015). As a consequence, distinct neural ensembles are recruited by different visual stimuli (Harris and Mrsic-Flogel, 2013; Miller et al., 2014). However, it remains unclear how the activation of these ensembles improves coding reliability. Thus, we sought to elucidate the relationship between response reliability and interneuronal correlations. Specifically, we hypothesized that an increase in signal correlations should help to reduce response variability and increase reliability.

To test this hypothesis, we used an agglomerative hierarchical clustering technique to group neurons according to similarities in their correlation coefficients (Fig. 9A; for details, see Materials and Methods). This method allowed us to identify neurons that were either strongly or weakly correlated with their neighbors. We found that clusters within the same neural population reorganized depending on the level of spatial correlations in the stimulus (Fig. 9B). Neurons within each cluster responded with similar temporal dynamics, implying that all clustered neurons were simultaneously coactivated by the stimulus. Specifically, strongly correlated neurons in the original movie (Fig. 9Bi) became decorrelated when presented with a K0 movie (Fig. 9Bii). In response to K2 movies, however, highly correlated neurons were more dispersed throughout the imaged population (Fig. 9Biii), consistent with the result shown in Figure 8D. This example also demonstrates that even though K2 movies evoke the same absolute level of intraneuronal correlations as original movies, they recruit distinct ensembles of neurons.

The strongly correlated movies recruited a larger fraction of neurons in the high-correlation cluster (38% K2 vs 27% K0 movies; 16 mice; Fig. 9C). Surprisingly, the original movie recruited almost the same number of neurons in both high- and low-correlation clusters, suggesting that a sparse subset of neurons (36%) is active for natural movies. Additionally, K2 movies had fewer neurons in the low-correlation cluster compared to the original movie (p = 1.03 × 10⁻⁴, Kruskal–Wallis one-way ANOVA; 16 mice). This result confirmed that increasing spatial correlations in natural movies increased the proportion of active neurons. This also highlights the different coding strategy used by the visual cortex to process movies with different spectral properties.

Weakly correlated ensembles did not show a strong stimulus dependence in signal correlations (low-correlation cluster, p = 0.43, Kruskal–Wallis one-way ANOVA; 16 mice; Fig. 9D), as they were poorly driven by the different movies (Fig. 9Bi–Biii). We were surprised to find that decorrelated movies elicited stronger noise correlations than the original movie, even within the cluster of strongly responding cells (p = 1.24 × 10⁻⁵, Kruskal–Wallis one-way ANOVA with Bonferroni correction; 16 mice; Fig. 9E). Thus, movies that are unreliably processed are dominated by higher noise correlations.

Correlated ensembles of neurons reliably represent visual stimuli

Next, we analyzed how response reliability differed between the clusters of either strongly or weakly correlated neurons (Fig. 10A). In almost all recorded populations, the high-correlation cluster contained a larger fraction of reliable responders than the low-correlation cluster (mean ± SD, 29.8 ± 1.1% vs 14.6 ± 1.5%; p < 10⁻⁵, Wilcoxon two-tailed rank-sum test; 650 neurons). Consistent with this, strongly correlated neurons had more reliable responses than weakly correlated neurons for original, K1.5, and K2 movies, but not for the decorrelated movies (p < 10⁻⁵, Kruskal–Wallis one-way ANOVA with Bonferroni correction; 16 mice; Fig. 10A). Specifically, all clusters from the K0 movie condition were weakly reliable.

Are these clusters reliably activated from one trial to the next? To answer this question, we repeated this clustering analysis on responses obtained from individual trials. “Snapshots” of the same neural population taken during the first, third, and sixth stimulus repetitions (Fig. 10B) showed that for both the unperturbed and the K2 movie, neurons in the high-correlation cluster were reliably activated during each stimulus repetition. In particular, neurons that were strongly correlated on the first trial remained strongly correlated during even the sixth stimulus repetition. Examples of these neurons are indicated by black arrows in Figure 10B. Consistent with the idea that population coding decreases variability (Shadlen and Newsome, 1994), the high-correlation cluster was always more reliably activated than the individual neurons themselves (p < 10⁻¹⁰, Bonferroni-corrected rank-sum test between individual neurons and high-correlation cluster; Fig. 10C). However, this population coding strategy did not improve the reliability for either K0 or K1 movies. In stark contrast, the low-correlation cluster was unreliably activated by all spectral conditions (Fig. 10D). Taken together, our clustering analysis revealed the following: (1) neuronal ensembles dynamically reorganize depending on the spatial properties of the stimulus; (2) coding within these ensembles is highly reliable; (3) these ensembles are also reliably and stably activated over multiple stimulus repetitions.

Reliability enables accurate discrimination of strongly correlated stimuli

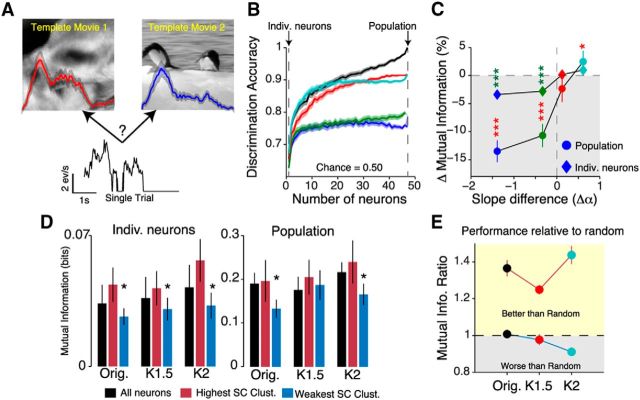
In principle, the highly reliable responses of correlated neurons should efficiently represent visual information by ensuring greater discriminability between the different movies. To further explore this idea, we performed linear decoding analysis on neural responses to assess the ability of neurons to discriminate different movies in each spectral condition. Specifically, we used a nearest means classifier (Fig. 11A; described in Materials and Methods) to predict from single-trial responses which movie had been presented (Goard and Dan, 2009; Kampa et al., 2011).

We measured discrimination accuracy by computing the fraction of correct classifications made by the classifier. Figure 11B exemplifies the decoding performance of a single population of neurons (46 neurons). In this population, discrimination accuracy improved as the number of neurons in the template increased. Interestingly, the classifier's performance saturated at ∼12 neurons, suggesting that all neuron groups larger than 12 provided the same information about the stimulus. We found a similar trend in all imaged populations (16 mice): increasing the number of neurons in the template, up to a limit, improved discrimination accuracy for correlated movies (original, 59.8 ± 0.05% vs 71.6 ± 0.11%; K2, 60.7 ± 0.06% vs 74.1 ± 0.11%; both p < 0.05, permutation test; data not shown). In contrast, pooling from a larger group of neurons failed to improve the decoding accuracy of decorrelated movies (individual vs population, K0, 56.4 ± 0.04% vs 58.1 ± 0.09%; p = 0.58).

To better characterize decoding accuracy, we computed MI, which is a measure of the reduction in uncertainty about the presented movie by knowledge of a single-trial response (see Materials and Methods). At the level of both individual neurons and the entire population, we found a significant reduction in MI as spatial correlations were removed from the stimulus (p < 10⁻⁶, Friedman test with Bonferroni correction; 16 mice; Fig. 11C). These results suggest that population coding does not improve the representation of decorrelated movies and is consistent with the result that these movies evoke decorrelated responses. Thus, regardless of their phase information, neurons are not able to discriminate between movies with either K0 or K1 spectra.

Does pooling over specific ensembles improve decoding accuracy? We restricted our analysis to correlated stimuli because decorrelated stimuli failed to reliably recruit neural ensembles (Fig. 10C). Strongly correlated neurons outperformed neurons that were either weakly correlated or randomly sampled from the population (original, p = 4.2 × 10⁻²; K1.5, p = 3.6 × 10⁻²; K2, p = 4.1 × 10⁻²; rank-sum test relative to all neurons; 16 mice; Fig. 11D, left). Additionally, pooling responses within the highly correlated ensembles resulted in a remarkably similar performance to the entire population. In contrast, decoding from just the weakly correlated clusters led to a significantly lower MI (p = 4.32 × 10⁻², rank-sum test relative to all neurons; Fig. 11D, right). Thus, despite containing fewer neurons, the high-correlation clusters were as good as the entire population at discriminating between the different stimuli.

Was this improved performance due to the fact that the ensembles for K1.5 and K2 movies contained a larger fraction of neurons? To answer this, we compared the MI obtained from randomly sampling subpopulations of the same size as either the high- or low-correlation cluster (Fig. 11E). For all stimuli, high-correlation clusters outperformed randomly sampled subpopulations. Thus, these results, together with our clustering analysis, indicate that visual information is encoded with high fidelity within ensembles of strongly correlated neurons.

An ensemble-specific normalization model explains responses to noise movies

Finally, we sought a simple model that could explain responses to noise movies by taking into account the unique pattern of ensemble activation. To this end, we further extended the model introduced in Figure 5Ci. First, we obtained best-fit RF estimates by fitting LN models to the original movie response of each neuron (Fig. 12A). Since we did not know the spatial locations or structures of RFs a priori, we had to estimate RFs by determining the least-squares best-fit model from a bank of linear filters, which were analogous to mouse V1 RFs (Ringach et al., 2002; Bonin et al., 2011; Fig. 12A). To prevent overfitting, we fit the model on 50% of the trials and used it to predict the remaining trials. On average, the best-fit RF model was able to explain up to 85.0 ± 13.9% of the variance in the response to original movies (for an example fit, see Fig. 12A). We restricted our subsequent analysis to only those neurons that could be well explained by this model (239 of 650 neurons).

Next, we used these RF models to predict responses to the various noise-masked movies. Specifically, we considered two alternative explanations. In the first, termed the independent model, we assumed that neurons acted independently, without interacting with other cells (Fig. 12B). In the second, termed the normalization model, we applied the divisive normalization rule (Carandini and Heeger, 2012) to pool activity from either the highly or weakly correlated clusters (Fig. 12D). Specifically, with the second model, we tested the hypothesis that the highly correlated cluster of neurons formed a normalization pool.

The independent model, which ignored population coding, poorly predicted noise movie responses (Fig. 12B): this model could explain only 1.3–3.4% of the variance of the K0 and 16.5–21.8% of the variance of K2 movie responses (p < 10⁻⁴, Friedman test with Bonferroni correction; 239 neurons; Fig. 12C). This result also affirmed our finding that SF tuning (or RF properties) alone are not able to predict responses to the noise movies (Fig. 5). In contrast, the normalization model outperformed the independent model in predicting noise movie responses (Fig. 12D). Considering only neurons in the high-correlation cluster as the normalization pool, the model allowed us to explain up to 55.7% of the variance of the K2 responses (Fig. 12E). In comparison, only 39.7% of the variance of the K2 responses could be explained by normalizing over neurons in the low-correlation cluster (p = 0.045, rank-sum test between high- and low-correlation clusters; 239 neurons). The normalization model demonstrated substantially higher prediction accuracy of K1.5 and K2 movies when responses were normalized over neurons in the high-correlation cluster (Fig. 12F), compared to the independent model. Hence, a parsimonious explanation for the decreased reliability for either K0 or K1 movies is a failure of these stimuli to activate a significant ensemble of correlated neurons. However, we cannot exclude the possibility that stimuli with different spatial correlations change the spatiotemporal structure of RFs (Fournier et al., 2011).

In summary, our results support the idea that pooling responses from correlated ensembles of neurons decreases intertrial variability. Notably, our work demonstrates that V1 has two distinct, stimulus-dependent coding regimes: a low noise regime, which is activated by movies that have strong spatial correlations and intact low SF information, and a high noise regime, which is activated by movies that lack these spatial correlations (Fig. 12G). In the low noise regime, interneuronal correlations reorganize to recruit more neurons, which in turn improves coding reliability and selectivity. In contrast, K0 and K1 movies, which lack the appropriate spectral content, fail to recruit these ensembles, resulting in a noisier code. Thus, the coding regime used by the visual cortex depends critically on the spectral statistics of the stimulus.

Discussion

The natural environment contains a vast amount of visual information, but not all of it is important to the behavior of an animal. As such, the visual system faces the challenging task of generating robust neural codes that parsimoniously convey this information. However, the mechanism by which this is achieved remains unknown. In this study, we used in vivo two-photon calcium imaging and a novel stimulus set to determine the statistical properties of natural scenes that ensure reliable coding. By perturbing the power spectrum in natural movies, we discovered that attenuating low SF information, which removed long-range correlations between pixels, resulted in an unreliable and unselective code. Surprisingly, the spatial structure of interneuronal correlations closely tracked stimulus correlations, leading to the activation of specific neural ensembles. Our study further revealed that only ensembles of correlated neurons reliably encoded the different movies. Taken together, we demonstrate that the unique spectral structure of natural scenes helps to improve coding fidelity by dynamically modulating interneuronal correlations in the visual cortex.

Power spectrum and image discrimination

Natural scenes are widely used to probe coding in V1. However, unlike simple stimuli such as sinusoidal gratings, natural scenes are statistically more complex and are harder to parameterize (Olshausen and Field, 2005). Without parameterization, it is difficult to relate neural response properties, such as reliability, to a single stimulus attribute. Phase randomization is commonly used to relate the statistics of natural images to coding. For example, two previous studies showed that randomizing the phase of natural scenes decreased selectivity and reliability of V1 neurons without altering the overall firing rate (Froudarakis et al., 2014; Pecka et al., 2014). Phase randomization destroys the edge structure of images but keeps spatial correlations intact. However, because these stimuli are nonparametric, these studies were not able to attribute changes in reliability to specific aspects of the phase spectrum.

Although the power spectrum contains relatively low-level features, such as spatial correlations, it is believed to play an important role in rapid image discrimination and classification (Bar, 2004; McCotter et al., 2005; Oliva and Torralba, 2007). Specifically, it provides diagnostic information about the spatial organization of objects within the scene, which is used to learn the gist of an image (Oliva and Torralba, 2006). To date, very little information exists on how the power spectrum influences coding in V1. In this study, we reasoned that an image that is easily discriminated should be coded more efficiently. Thus, we hypothesized that the power spectrum could modulate neural reliability, which in turn would increase the fidelity of information processing and facilitate image discrimination.

Our novel noise-masking technique allowed us to test this hypothesis and revealed that the mouse visual system is highly sensitive to perturbations in the power spectrum. Importantly, our parametric approach permitted us to relate changes in neural coding to changes in the spectral slope. Subtle changes in the spectral slope strongly modulated the firing rates of V1 neurons in both anesthetized (Fig. 2) and awake mice (Fig. 4). These results are consistent with previous studies, which found no difference in rates when only the structure of spatial correlations was left intact (Kayser et al., 2003; Froudarakis et al., 2014). Similar results were also found in the visual cortex of primates (Freeman et al., 2013). Importantly, we found that the trial-to-trial reliability of responses was also strongly modulated by the low SF content of the image (Figs. 3, 4). In particular, attenuating the low SF content (K0 or K1 movies) was more detrimental to neural coding than attenuating the high SF content (K1.5 or K2 movies).

We asked whether these results could be explained just from the SF tuning properties of V1 neurons. Surprisingly, a simple linear–nonlinear model based on SF tuning poorly explained our data (Figs. 5, 6). These results indicate that the observed changes in firing rate and reliability were not the result of simple spatial filtering properties of neurons alone. Rather, the nonlinear interaction between diversely tuned neurons, via divisive normalization, better explained the responses (Fig. 12). Thus, our work provides evidence that V1 processes broadband stimuli by integrating over multiple SF channels, presumably by altering correlations between channels.

Implications for natural scene processing

We show that neurons in mouse V1 respond more reliably to movies with strong low SF power. The low SF content in natural scenes is mainly large, coarse-grained objects, which can be used for basic scene recognition and motion discrimination (Bar, 2004). Our finding that mice respond similarly to movies that are much more strongly correlated than the original movie implies that mice primarily use their vision to extract coarse grained information from their visual environments, presumably to guide navigation in low-light conditions or to avoid aerial predators (Zoccolan, 2015 and references therein).

Interestingly, our results strongly support psychophysical studies that show that the human visual system also uses information in the low SF bands to rapidly and accurately discriminate natural scenes (McCotter et al., 2005; Gaspar and Rousselet, 2009). We show that attenuating these bands, even to a small degree (∼10 dB in the case of K1 movies), strongly degrades processing in V1. Additionally, neurons were not able to discriminate movies with decorrelated power spectra, despite large differences in their phase information (Fig. 11). Although we cannot draw easy parallels between the visual systems of mice and humans, our data, together with the results of Froudarakis et al. (2014), suggest that mouse V1 might also use spectral information in a similar manner. Specifically, stimuli that lack the appropriate spectral structure are processed less reliably, making them harder to discriminate. Further experiments, however, are required to determine how mice use spatial statistics to discriminate between different scenes (Vinken et al., 2014).

Effects of stimulus statistics on population coding

Why are movies with strong spatial correlations more reliably processed in V1? Our analysis revealed that neighboring neurons were more strongly noise correlated when stimulated with decorrelated movies. This suggests that shared variability between neurons is detrimental to the representation of weak stimuli, such as K0 movies (Zohary et al., 1994). One possible explanation to why correlated movies have lower noise correlations is that by coactivating distant neurons, these movies could increase inhibitory surround suppression (Adesnik et al., 2012; Snyder et al., 2014).

The high spatial resolution provided by two-photon microscopy permitted us to investigate the spatial organization of interneuronal correlations. Notably, neuronal coupling patterns changed with stimulus correlations suggesting that scenes with different spectral statistics recruit distinct neural ensembles. These findings add to the growing body of evidence that visual processing is performed by discrete clusters of functionally coupled neurons (Kampa et al., 2011; Miller et al., 2014; Okun et al., 2015). Remarkably, these strongly correlated ensembles were reliably and stably activated over multiple stimulus repetitions (Fig. 10). Additionally, although these ensembles comprised ∼30% of the population, they performed as well as the entire population in encoding various movies, supporting the notion of a sparse population code. Together, these results indicate that reading the activity of these clustered ensembles of neurons is sufficient to accurately discriminate different movies.

How these neural ensembles ensure reliable coding remains unknown. Our model proposes that these correlated ensembles could function as normalization pools. Divisive normalization is a canonical cortical computation (Carandini and Heeger, 2012) that is believed to be crucial for efficient coding (Schwartz and Simoncelli, 2001). One possibility is that normalization pools average responses from neurons and in doing so suppress cortical variability (Shadlen and Newsome, 1994). This has led to the notion that redundancy, through neuronal coupling, plays an important role in visual processing (Lin et al., 2015; Okun et al., 2015). Our work bolsters this idea by demonstrating that normalization pools can be dynamically recruited, in a stimulus-dependent manner, to ensure reliable and efficient coding.

Thus, our work establishes that stimulus correlations function in a manner similar to attention or neuromodulation to protect the neural code from intrinsic variability by increasing coupling between neurons (Moreno-Bote et al., 2014). In particular, by rapidly recruiting neural ensembles, scenes with naturalistic spatial correlations switch coding from a “high noise” to a “low noise” regime, where intrinsic variability is suppressed to permit reliable coding.

In conclusion, our study provides a novel insight into how the unique statistical features of the natural environment can modulate coding in V1. We provide strong evidence that spatial correlations are an important feature of natural scenes because of their role in shaping interneuronal correlations. Although we have focused on V1, we believe that similar coding strategies could also operate in other sensory modalities (Bandyopadhyay et al., 2010; Hires et al., 2015), consistent with this being a general principle of cortical computations.