Characterizing Cellular Biophysical Responses to Stress by Relating Density, Deformability, and Size

Abstract

Cellular physical properties are important indicators of specific cell states. Although changes in individual biophysical parameters, such as cell size, density, and deformability, during cellular processes have been investigated in great detail, relatively little is known about how they are related. Here, we use a suspended microchannel resonator (SMR) to measure single-cell density, volume, and passage time through a narrow constriction of populations of cells subjected to a variety of environmental stresses. Osmotic stress significantly affects density and volume, as previously shown. In contrast to density and volume, the effect of an osmotic challenge on passage time is relatively small. Deformability, as determined by comparing passage times for cells with similar volume, exhibits a strong dependence on osmolarity, indicating that passage time alone does not always provide a meaningful proxy for deformability. Finally, we find that protein synthesis inhibition, cell-cycle arrest, protein kinase inhibition, and cytoskeletal disruption result in unexpected relationships among deformability, density, and volume. Taken together, our results suggest that by measuring multiple biophysical parameters, one can detect unique characteristics that more specifically reflect cellular behaviors.

Introduction

Cellular biophysical properties reflect aggregate effects of particular cellular activities, such as malignant transformation, differentiation, cell-cycle progression, disease response, and apoptosis. Studying these properties can help provide insight into the underlying molecular mechanisms that govern cellular behavior. For example, an increase in the metastatic potential of cancer cells has been correlated with increased cell deformability (1, 2, 3, 4, 5, 6). Studies on differentiation have also reported that deformability decreases as stem cells become more differentiated (7, 8). The cell-cycle stage is known to be associated with changes in cell shape and deformability (9, 10). Red blood cells (RBCs) affected by malaria show decreased deformability and density (11, 12). Finally, previous studies have reported that apoptosis is related to volume shrinkage and changes in cell deformability (13, 14).

Another common physiological source of changes in cellular biophysical properties is shifts in extracellular osmolarity. Certain tissues, such as the kidney, are regularly exposed to dramatic osmolarity shifts and adjust their membrane surface area to allow for increases or decreases in cell volume to maintain a constant cortical tension (15). Articular cartilage in synovial joints, such as the knee and hip, is subjected to both static and dynamic mechanical compression during articulation, resulting in changes in the interstitial osmolarity of the cartilage tissue (16). This in turn can affect the biosynthesis rate, deformability, and volume of chondrocytes in the tissue (17, 18, 19). Moreover, the inability to respond to an osmotic challenge can result in impaired function, as is the case with T lymphocytes lacking the osmosensitive transcription factor NFAT5/TonEBP. Eliminating NFAT5/TonEBP expression prevents normal cell proliferation and development of adaptive immunity, likely due to an inability to adapt to the hyperosmolar conditions present in many lymphoid tissues (20).

Although most studies have focused on the measurement of individual biophysical parameters, increasing evidence shows that combining information from measurements of multiple parameters can improve prediction of cell state. RBCs from patients with thalassemia, a genetic disorder that leads to a measurable but not significant decrease in RBC volume, can be distinguished from healthy RBCs based on a simultaneous comparison of both mass and density, but not on either parameter individually (12). One can accurately predict the differentiation potential of stem cells by measuring the deformability of stem cells along with size, but not by measuring size alone (21, 22). By measuring deformability and diameter, one can also identify four types of malignant diseases from a pleural effusion, whereas such an identification based on a single parameter leads to an incomplete prediction of disease state (8). Measurements of the deformability and friction of cancer cells have revealed that reduced friction may play a role in further facilitating the passage of more deformable metastatic cancer cells through tight spaces (23).

Here, we used a murine pro-B cell line as a model system and measured multiple biophysical parameters of individual cells with a suspended microchannel resonator (SMR). First, to fully understand how cells respond to osmotic stress, we measured volume, density, and passage time through a narrow constriction. Increasing the media osmolarity led to increased density and decreased volume, as expected. In contrast to density and volume, passage time is nearly independent of osmolarity even though deformability changes considerably, indicating that passage time should be measured together with cell volume. Finally, we compared relationships between deformability and density for cells treated with various pharmacological perturbations, including latrunculin B, staurosporine, cycloheximide, rapamycin, and Torin 1.

Materials and Methods

Cell culture and preparation

FL5.12 cells, a murine pro-B lymphoid cell line, were cultured as previously described (24). Briefly, cells were cultured in RPMI media (Invitrogen, Grand Island, NY) supplemented with 10% (v/v) fetal bovine serum (Sigma-Aldrich, St. Louis, MO), 100 IU penicillin, 100 μg/mL streptomycin (Gemini, West Sacramento, CA), and 0.02 μg/mL IL-3 (R&D Systems, Minneapolis, MN) at 37°C. FL5.12 cells were exposed to an osmotic challenge or biochemical agent before each measurement. To maintain each condition during the experiment, the media used in the SMR were also supplemented with the same stimuli. For the osmotic challenge, cells were collected from the culture flask, centrifuged at 150 g for 5 min, resuspended in hypertonic or hypotonic media, and incubated for 30 min before each measurement. D-mannitol (182.17 g/mol; Sigma-Aldrich) and deionized H₂O (dH₂O) were added to the media for the hyperosmotic and hypoosmotic conditions, respectively. For the isoosmotic control group (300 mOsm/L), cells were resuspended in the untreated culture medium. For chemical perturbations, cells were resuspended and incubated in the media supplemented with 5 μg/mL latrunculin B for 30 min (Sigma-Aldrich), 2 μM staurosporine for 2 h (Enzo Life Sciences, Farmingdale, NY), 1 μg/mL or 10 μg/mL cycloheximide for 3 h (Sigma-Aldrich), 100 nM rapamycin (Santa Cruz Biotechnology, Dallas, TX) for 24 h, or 250 nM Torin 1 for 24 h (generously provided by Prof. David M. Sabatini, Massachusetts Institute of Technology). The control groups for these conditions were cells resuspended in the culture media supplemented with DMSO as the vehicle. The SMR data acquired at the start of the measurement were compared with those acquired at the end of the measurement to ensure that the data showed no time dependence.

Experimental systems

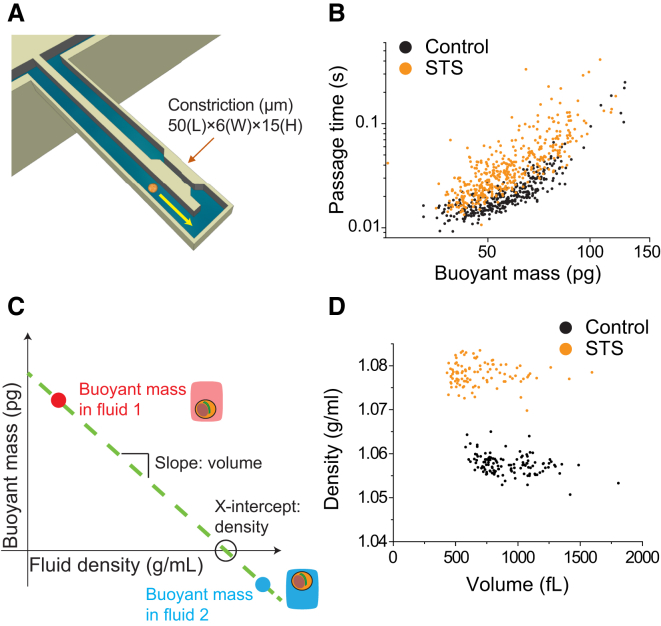
SMRs were fabricated at Innovative Micro Technology (Santa Barbara, CA). The overall instrumentation used for measurement and data acquisition was previously described in detail (25). Schematics of the experimental approaches are shown in Fig. 1. One SMR system was used to measure density and volume, and a separate SMR system was used to measure passage time. To measure density and volume, each cell was weighed in the SMR in two fluids as previously described (12). Briefly, a cell immersed in a fluid of low density (fluid 1, ∼1.01 g/mL) was flowed from a bypass channel through a channel embedded in a resonating cantilever, and trapped in an opposite bypass filled with a fluid of high density (∼1.1 g/mL). The direction of flow was reversed and the same cell was passed through the cantilever a second time, but now in fluid 2 (∼1.08 g/mL, a mixture of the high-density fluid and a residual amount of fluid 1). Each time the cell flowed through the cantilever, a buoyant mass measurement was recorded along with a corresponding fluid density value. The two buoyant masses were plotted versus their respective fluid densities to obtain a line with a slope corresponding to cell volume and an x-intercept corresponding to cell density (Fig. 1 C). As the value of cell density approached that of the fluid density, the cell buoyant mass became progressively smaller and thus more difficult to accurately determine. Therefore, using our current system, we were unable to quantify the density of cells that were exposed to very high osmotic stresses (>500 mOsm/L), since the value of the cell density approached that of the fluid 2 density. For all density measurements, a 7:3 mixture of cell media/iodixanol solution (OptiPrep Density Gradient Medium; Sigma-Aldrich) was used as the high-density fluid. In experiments involving osmotic stress, the osmolarity of this solution was adjusted with either mannitol or water to match that of fluid 1.

Figure 1.

Schematic diagrams of the approaches used to measure deformability, density, and volume, and examples of the data extracted from the measurements. (A) An SMR with a constriction measures the passage time and buoyant mass as a cell flows into an embedded microfluidic channel and transits through the constriction. (B) Passage time versus buoyant mass for the FL5.12 cell line shows the change in passage time induced by staurosporine (STS). (C) Measuring the buoyant mass of a single cell in two fluids of different densities allows the cell density and volume to be determined. (D) Cell density versus volume of FL5.12 cells treated with STS. Treatment with STS leads to an increase in density and a slight decrease in volume. To see this figure in color, go online.

To measure passage time, single cells were measured in an SMR with a constriction as previously described (23). Briefly, in this approach, a cell is flowed into the embedded microfluidic channel of the SMR and is deformed as it flows into the constriction. The constriction consists of a rectangular channel 6 μm wide, 15 μm deep, and 50 μm long. The cross-sectional area of the constriction is 90 μm² (6 μm wide × 15 μm deep) and the average diameter of FL5.12 cells is ∼12 μm (untreated control), indicating a maximum cross-sectional area of ∼113 μm². The narrow width of the constriction ensures that the cell will deform as it squeezes into the constriction’s entrance (entry) and then passes through the constriction channel (transit). The resonant frequency response of the SMR, which depends on the cell’s buoyant mass and position in the microfluidic channel, is tracked in real time as the cell passes through the channel. The passage time includes the total time required for the cell to slow down as it deforms to enter the constriction (entry time) and then to speed up as it travels through and exits the constriction (transit time). Here, we measured the passage time as a metric for cell deformability, which is defined as the total time required for the cell to deform to enter and then transit through the constriction. One can estimate the relative contribution of surface friction to the passage time by comparing the cell’s velocities during entry (entry velocity) and transit (transit velocity). Typically, the passage time is dominated by the entry time because the transit velocity is significantly faster than the entry velocity (23). We consistently observed dominance of the passage time by the entry time in a previous study (23) in which we measured seven adherent cell lines, including mouse embryonic fibroblasts, mouse lung cancer cell lines, and human lung cancer cell lines, as well as a mouse lymphoblastic leukemia cell line that was grown in suspension. We also measured cells in various conditions obtained, for example, by treating cells with latrunculin B or nocodazole, or coating the microchannel surface with positively charged poly-L-lysine. In all of these cell lines and treatments, the passage time was dominated by the entry time (23). Therefore, here we assume that friction can affect, but does not dominate, the differences in passage times. The fluidic channel was coated with poly(ethylene glycol) (1 mg/mL; PLL(20)-g[3.5]-PEG(2); Surface Technology) to reduce nonspecific adhesion of cells to the walls of the constriction. All measurements were acquired at room temperature under a constant applied pressure drop across the microchannel (0.15 psi) established by pressure regulators.

Data analysis

We converted the SMR frequency data to buoyant mass, passage time, volume, and density using previously described methods (12, 23). The data plotted in Figs. 2, C–E, and 3, A and C, represent volume, water content, passage time, and buoyant mass, respectively. These parameters are plotted with a logarithmic scale, which we consider to be the form that most accurately represents the data. Cell size follows a log-normal distribution, as previously reported (26). Passage time is expected to follow a log-normal distribution as well, since passage time has a strong power-law dependence on buoyant mass, as shown in Fig. 1 B (23, 27).

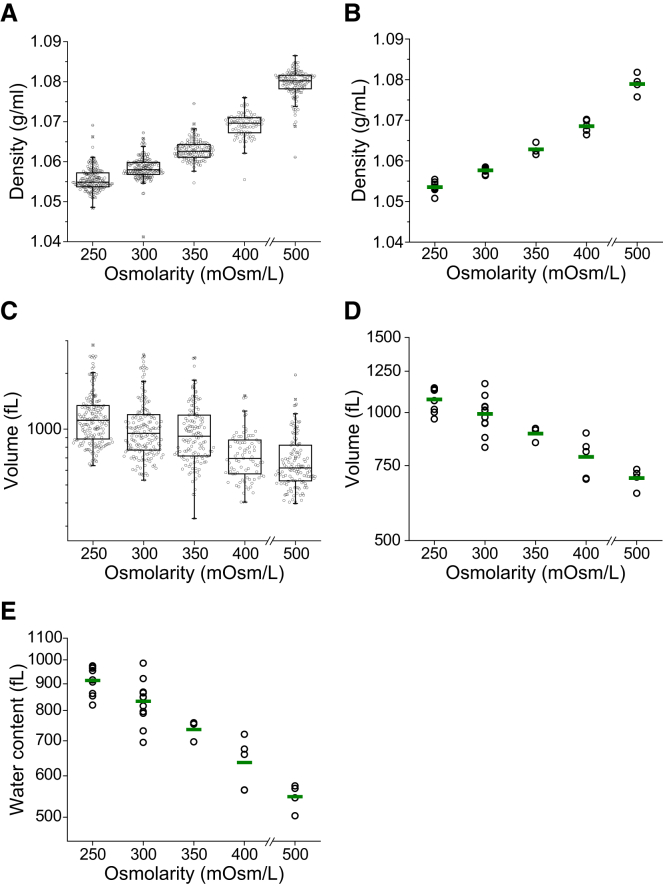
Figure 2.

Effect of osmotic stress on density and volume. FL5.12 cells are incubated in hypo- and hyperosmolar media for 30 min before and during the measurement. (A) Boxplots of density from a representative experiment. Each data point represents the density of an individual cell (n = 83–170). (B) Density changes resulting from osmotic stress across multiple replicates. A single point represents the geometric mean of one replicate and the green line indicates the mean from multiple replicates (n = 3–8 for each condition). (C) Boxplots of volume from a representative experiment. The data shown were measured simultaneously with density in (A). Each data point represents the volume of an individual cell. (D) Volume changes resulting from osmotic stress across multiple replicates. A single point represents the geometric mean of one replicate and the green line indicates the mean from all replicates (n = 3–8 for each condition). (E) Changes in cellular water content resulting from osmotic stress across multiple replicates. A single point represents the geometric mean of one replicate, and the green line indicates the mean from all replicates (n = 3–8 for each condition). To see this figure in color, go online.

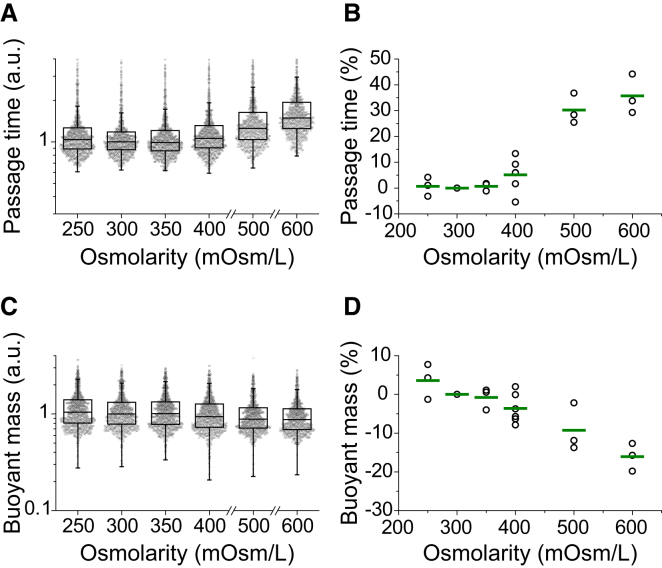
Figure 3.

Effect of osmotic stress on passage time and buoyant mass. FL5.12 cells were incubated in hypo- and hyperosmolar media for 30 min before and during the measurement. Passage time and buoyant mass were relatively unaffected by osmotic stress at 250, 350, and 400 mOsm/L. (A) Boxplots of passage time scaled by the median of the control (300 mOsm/L). Each data point represents the passage time of an individual cell (n = 972–1101). (B) Percentage change in the median passage time. The median passage time from each condition is normalized by the median of the control. A single point represents one replicate and the green line indicates the mean from multiple replicates (n = 3–6 for each condition). (C) Boxplots of buoyant mass scaled by the median of the control. The data shown were measured simultaneously with passage time in (A). Each data point represents the buoyant mass of an individual cell. (D) Percentage change in the median buoyant mass. The median buoyant mass from each condition is normalized by the median of the control. A single point represents one replicate and the green line indicates the mean from multiple replicates (n = 3–6 for each condition). To see this figure in color, go online.

As noted in previous studies (12, 23, 25), the SMR can be used to measure biophysical properties with high precision. The buoyant mass and the position of the center of mass of a particle passing through a constriction in the SMR can be measured with a precision near 1 pg and submicron, respectively (23). Additionally, the density and volume can be measured with a resolution of 0.001 g/mL and 3 fL, respectively (12). We can therefore attribute the variability observed in our measurements to inherent biological variations rather than experimental artifacts. For example, one source of a biological variation in size is related to the distribution of cells across the cell cycle. Interestingly, in our measurements, cells of similar buoyant mass showed a significant variation in passage time (Fig. 1 B), suggesting that in addition to a biological variation, such as in the cell cycle (10), the orientation of the cell upon entry into the constriction can cause a wide distribution (23, 28).

The buoyant mass obtained during passage-time measurements was converted to volume using the following equation:

$$V=\frac{b_m}{{\rho }_{cell}-{\rho }_{fluid}},$$

where V is the cell volume, b_m is the cell buoyant mass, ρ_cell is the average cell density obtained from a corresponding SMR density measurement, and ρ_fluid is the fluid density. The uncertainty that was contributed to the volume distribution by converting the buoyant mass using an average cell density was determined to be not significant based on a Monte Carlo estimate (Fig. S1 in the Supporting Material).

Statistically significant differences between density measurements were determined using a nonparametric rank-sum analysis (Wilcoxon rank sum) implemented in MATLAB (The MathWorks, Natick, MA). Changes in passage time were estimated and the statistical significance of those changes was tested by fitting data sets to a linear model in R. For all statistical tests, a p-value ≤ 0.05 was considered significant. In particular, since most statistical tests showed very small p-values (10⁻⁵⁰–10⁻⁵), we indicated those small p-values by p < 0.0001.

Results and Discussion

Characterizing the density and volume of cells exposed to osmotic stress

To characterize the biophysical effects of osmotic stress, we first measured changes in the density and volume of FL5.12 cells exposed to a range of osmolarities (Fig. 2). We varied the osmolarity of the cell medium from 250 to 600 mOsm/L by diluting the medium with dH₂O or concentrating it with D-mannitol. Due to limitations described in Materials and Methods, we were not able to measure the density and volume at 600 mOsm/L, although we did obtain passage time measurements. Cell density increased after exposure to hyperosmotic media and decreased after exposure to hypoosmotic media (Fig. 2 A), whereas the effect of osmotic stress on cell volume showed the opposite trend (Fig. 2 B). We expect that the primary source of this trend is the change in cellular water content (29, 30). Water has a lower density than most nonaqueous cellular components, particularly proteins, nucleic acids, and certain lipid conjugates (31, 32, 33). Thus, when an osmotic challenge leads to a change in volume, the ratio of water to nonaqueous components will change as well. If the cellular water fraction increases, the density will decrease. This is the case with hypoosmotic swelling, where the influx of water is associated with both a larger volume and a lower density. Similarly, the loss of water in the hyperosmotic case leads to both a decreased volume and an increased density. We estimated the change to water content using a previously described method (Supporting Material) and confirmed that hypoosmotic stress leads to an increase in water content, whereas hyperosmotic stress leads to a decrease in water content (Fig. 2 E).

Interestingly, cell density appears to have much less variability compared with volume. We found this to be true both when we examined a population of cells from a single measurement (Fig. 2, A and C) and when we compared the means of multiple measurements (Fig. 2, B and D). For the 300 mOsm/L measurement shown in the boxplot in Fig. 2, A and C, the interquartile range of density is ∼0.005 g/mL, or ∼0.5% of the mean, whereas the interquartile range of volume is ∼500 fL, or ∼25% of the mean. Similarly, the coefficient of variation (CV) of density is ∼0.3% and that of volume is ∼50%. We can attribute the wide volume range in part to differences in the cell-cycle stage in the population: the much narrower range of density could suggest that density remains relatively constant for a majority of the cell cycle. The variability over multiple experiments is shown in Fig. 2, B and D, where each point represents the geometric mean of a single measurement, and the green bar represents the mean across multiple measurements. In this case, the CV of volume is ∼10%, whereas that of density is 0.065%. This outcome further reinforces the notion that a biological mechanism maintains the narrow density distribution. As a possible explanation, we can consider density to be a reflection of the crowding of intracellular macromolecular components. Previous work has shown that the cytoplasm is extremely crowded, and that the level of crowding affects protein stability, adsorption to surfaces, and reaction rates (34, 35, 36). Thus, we can hypothesize that tight regulation of density results from a requirement to maintain a uniform level of crowding. An important consequence of the tight distribution of density relative to volume is that cells of similar densities will not always have the same volumes. Thus, simultaneous measurements of both density and volume are necessary to more accurately describe the cell state.

Characterizing the passage time and deformability of cells exposed to osmotic stress

Next, we determined how osmotic stress affects the passage of a cell through a narrow constriction by comparing the median passage times for osmotically stressed cells and an isoosmotic control. In contrast to cell density and volume, the effect of an osmotic challenge on passage time was relatively small (Fig. 3). The changes in passage time after osmotic challenges of 250, 350, and 400 mOsm/L were 0.68%, 0.66%, and 5.1%, respectively (Fig. 3 B). However, increasing the media osmolarity to 500 and 600 mOsm/L resulted in an ∼30% increase in passage time. Similarly, after exposure to osmotic stress, cellular buoyant mass did not deviate significantly from the control (3.6, −0.79, and −3.6% changes for 250, 350, and 400 mOsm/L, respectively; Fig. 3 D). Exposure to 500 and 600 mOsm/L media resulted in a further decrease in buoyant mass (−9.2% and −16%, respectively), suggesting that buoyant mass decreases as osmolarity increases.

The relatively small changes in passage time and buoyant mass resulting from osmotic stress between 250 and 400 mOsm/L can be attributed to simultaneous, compensatory changes in density and volume. For example, as a cell is compressed due to an osmotic challenge, its density increases while its volume decreases. As a cell becomes denser due to water loss, cell deformability decreases by molecular crowding within cytoplasm (30), which in turn increases the passage time (23). Therefore, although a denser cell should exhibit a longer passage time due to its decreased deformability (Fig. 4), its smaller volume concurrently decreases the passage time (23, 27). As a result, the overall change in passage time caused by osmotic stress is relatively small. These results demonstrate that passage time reported independently of size may not always predict cell deformability, and that one must compare passage times for cells of similar size to decouple the effects of varying size and deformability (23).

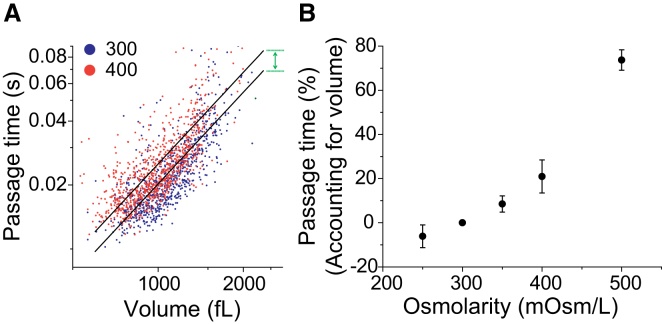
Figure 4.

Determining deformability from passage time by accounting for cell volume. Volume is obtained by converting single-cell buoyant mass data using the population average density. (A) Passage time versus volume from the two data sets (from Fig. 3, isoosmotic and hyperosmotic conditions) in a log-log scale is fitted to the linear models (black lines) with a fixed slope and variable intercepts corresponding to the two conditions. The deformability is determined by the ratio of passage times given the same cell volume, which is acquired from the difference between the two intercepts (green arrow). (B) Dependence of deformability (percentage change in passage time based on cell volume) on the osmolarity of the media. The data used are the same as shown in Fig. 3. To see this figure in color, go online.

Buoyant mass is a convenient size metric because it is measured simultaneously with passage time for individual cells (see Fig. 1 and “Data analysis” above). However, buoyant mass depends on cell volume and density, and, like passage time, is susceptible to compensatory changes in these parameters. Buoyant mass is defined as the product of the volume and the difference between the cell density and the density of the surrounding fluid; thus, the increase in density after osmotic compression would lead to an increase in buoyant mass, and the decrease in volume would lead to a decrease in buoyant mass. Indeed, we find that the buoyant mass remains relatively unaffected by osmotic compression (350 and 400 mOsm/L; Fig. 3, C and D). Thus, we define deformability as the passage time of a cell accounting for its volume, thereby eliminating the dependence of passage time on size (Fig. 4) (23). By using an average value for population density, which has a variance 100-fold smaller than that of both buoyant mass and volume, we can convert buoyant mass to volume with only minimal error contributions (Fig. 2, A and C; Fig. S1) (12, 37). This is an improvement over the methods used in previous studies, in which we performed the same conversion but started instead with a volume distribution from a commercial Coulter counter (23, 38). A plot of each data set on a log-log scale is subsequently fit to lines with a fixed slope and variable intercepts (Fig. 4 A). The deformability is determined by the ratio of passage times given the same cell volume, which is acquired from the difference between the two intercepts (green arrow) and is then converted to a percentage (Fig. 4 B).

After accounting for volume, we can identify a significant difference between two cells of the same volume exposed to different values of media osmolarity (−6.1%, 8.5%, and 21% changes for 250, 350, and 400 mOsm/L, respectively), which demonstrates that cells become stiffer by hyperosmotic compression and more deformable by hypoosmotic swelling. In other words, although the population of cells as a whole still exhibits a passage time similar to that observed for the isoosmotic control (Fig. 3 B), the viscoelasticity of an individual cell is changed by osmotic stress (Fig. 4 B). The observed decrease in deformability caused by hyperosmotic compression and determined by a longer passage time is consistent with previous studies, one of which linked the change to cytoplasmic crowding resulting from water loss (30, 39, 40). An increase in deformability due to a hypoosmotic challenge has also been reported (19, 39, 41), but is not consistent among all studies (40), likely due to discrepancies in the measurement techniques and cell lines used. Our results indicate that one should take the volume into consideration when relating passage time through a constriction to cellular deformability.

Characterizing cell states by deformability, density, and volume

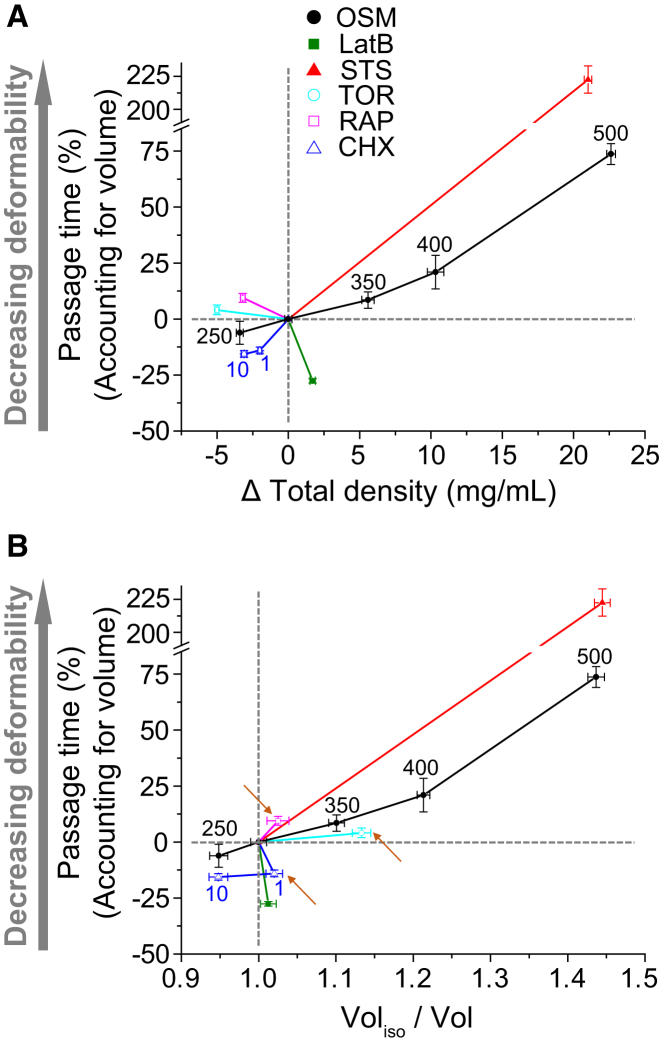
When cells are exposed to an osmotic challenge, changes in density or volume correlate with changes in deformability due to the dependence of all three parameters on the osmolarity of the surrounding fluid (Fig. 2 A). However, a general relationship among density, volume, and deformability cannot be established a priori, since cellular activity or external stimuli can affect cellular composition and cytoskeletal proteins, which can affect density, volume, and deformability independently of each other (1, 12). Similarly, a change in volume alone cannot predict density or deformability, except when cells change their volume only by water exchange. Thus, we next sought to investigate representative relationships of deformability versus density and volume (Fig. 5), which would allow us to demonstrate how cell states can be characterized by multiple biophysical properties. In addition to an osmotic challenge, FL5.12 cells were exposed to the following conditions: latrunculin B, staurosporine, cycloheximide (1 μg/mL or 10 μg/mL), rapamycin, and Torin 1. A summary of the effects of these drugs is provided in Table S1. Density, volume, and deformability were measured using the same methods as previously described. Passage time accounting for volume was then plotted versus density (Fig. 5 A) and volume (Fig. 5 B).

Figure 5.

Deformability versus density and volume for various conditions: osmotic challenge (250, 350, 400, and 500 mOsm/L), latrunculin B (LatB), staurosporine (STS), 1 μg/mL and 10 μg/mL of cycloheximide (CHX), rapamycin (Rap), and Torin 1 (Tor). Changes in deformability, density, and volume after treatments are quantified based on the isoosmotic control (untreated, 300 mOsm/L) in each experiment. Plots are divided into four quadrants, defined by two gray dotted lines. (A) The percentage change in passage time accounting for volume is plotted versus the change in density. The correlation between changes in deformability and density depends on the mechanism associated with each treatment. (B) The percentage change in passage time accounting for volume is plotted versus the change in volume. Rap, Tor, and CHX (1 μg/mL) are located in different quadrants compared with (A) (arrows). Vertical error bars represent the standard deviation of the mean. Horizontal error bars (density and volume) represent the standard error of the mean. All treatments induce a significant change in density (p < 0.0001, Wilcoxon rank sum). All treatments, except Torin 1 (p = 0.0501), induce a significant change in passage time (p < 0.0001, linear model). The data for the osmotic challenge are the same as those shown in Fig. 4. For the other conditions, we measured ∼200 cells and ∼1000 cells for density and deformability, respectively. To see this figure in color, go online.

Increases in osmolarity led to increases in density and decreases in volume and deformability, represented by the black solid lines in Fig. 5, A and B. Latrunculin B, however, led to an increase in deformability accompanied by a slight increase in density and an insignificant change in volume (Fig. 5, A and B, green line). A small increase in volume by latrunculin B was previously reported (42). This outcome likely results from the relatively specific behavior of latrunculin B, which complexes with actin monomers to inhibit actin polymerization (43). These changes may result in a slight change in cellular water content due to shifting hydration layers in the proteins, which may be sufficient to change density, but not volume (44).

Treatment with staurosporine (Fig. 5, A and B, red line) maintained the same relationship between density and deformability as we observed with osmotic stress, but with a greater change in deformability. A cell undergoing apoptosis by staurosporine typically shows an apoptotic volume decrease and denser cytoplasm, which is consistent with our measurements of volume and density (45). Staurosporine can also lead to cell-cycle arrest (46), inhibit protein synthesis independently of caspase activation (47), and delocalize myosin II (48). Therefore, a decrease in deformability after staurosporine treatment may be related to impaired myosin activity, which may explain why staurosporine leads to a much greater change in deformability than does hyperosmotic compression.

Treatment with 10 μg/mL of cycloheximide decreased density similarly to what we observed under a hypoosmotic condition (250 mOsm/L), but resulted in a greater increase in deformability. The increase in deformability caused by cycloheximide treatment, which inhibits protein synthesis, is consistent with a previous study (49). Interestingly, the biological effects of cycloheximide depend on the concentration and cell type used. For example, although cycloheximide is cytotoxic at low concentrations to Jurkat cells, it has no effect on CEM C7 cells at low or high concentrations, even though both are human leukemic cell lines (50). Moreover, studies of different cell types exposed to low levels of cycloheximide have shown that it may have cytoprotective effects (51). This concentration dependence may explain the slight discrepancy between the changes in density and volume observed with 1 μg/mL and 10 μg/mL of cycloheximide (Fig. 5, A and B, arrows). Since cycloheximide can also induce elongation or arrest of the cell cycle, which may affect the protein content and cell volume (52, 53), the relationship between volume and density is difficult to predict. Thus, although density and volume are inversely correlated at the higher concentration, they are directly correlated at the lower concentration.

Similarly to the case with cycloheximide, we also noticed that Torin 1 and rapamycin induced decreases in both density and volume, providing another example of how volume is not always inversely related to density (arrows in Fig. 5 B). This outcome may be attributed to the biological effect of Torin 1 and rapamycin, which block mTOR, leading to cell-cycle arrest at the G₁/S transition and inhibiting protein synthesis (54, 55). Previous studies have shown that cell volume and deformability depend on cell cycle stage (10). The slight decrease in population volume may thus be attributed to arrest in S phase. A decrease in density could be due to lower levels of both protein and DNA. In addition, Torin 1 and rapamycin are also known to affect actin polymerization and protein synthesis (56, 57, 58, 59). Previous studies have demonstrated that Torin 1 and rapamycin can inhibit actin polymerization (57); however, rapamycin can also increase actin polymerization in RBL-2H3 cells (56), suggesting that the slight decrease in cell deformability by these mTOR inhibitors may be induced by the change in actin structure.

We would also like to note that the drugs used in our study typically cause a more significant change in deformability than does osmotic stress. For example, staurosporine induces a >200% change in passage time, and the deformability of FL5.12 cells is increased by cycloheximide regardless of changes in density or volume. This suggests that the integrity of the cytoskeletal structure can play a more important role in deciding deformability than the changes driven by water exchange. However, Zhou et al. (30) previously showed that a latrunculin A-induced weakening of cytoskeletal rigidity was overwhelmed by a stiffening of the cytoplasm induced by very high osmotic stress (∼1000 mOsm/L), suggesting that a change in the cytoskeletal structure does not always dominate cell deformability.

Conclusions

We have shown the value of measuring multiple biophysical parameters concurrently. Although volume is the most commonly identifiable cell-size metric, density can reveal additional information for understanding the mechanical properties of cells. Density may represent changes in structure or composition, as well as the crowdedness in the cytoplasm, which may not be directly related to volume but may still affect deformability. Grover et al. (12) previously found that measurements of density enable the identification of cell states that are not detectable by other cell-size metrics, such as volume and mass. However, changes in deformability may not necessarily lead to changes in any size metric, particularly if the deformability change is associated with changes in structural proteins. Thus, by combining measurements of deformability and density, we can detect more specific biophysical characteristics that refine our representation of the cell state.

Author Contributions

S.B., V.C.H., and S.R.M. designed research. S.B. and V.C.H. performed research. S.B. and V.C.H. analyzed data. S.B., V.C.H., and S.R.M. wrote the manuscript.

Editor: Jochen Guck.

Supporting Citations

Reference (60) appears in the Supporting Material.