Power and Sample Size for Randomized Phase III Survival Trials under the Weibull Model

Abstract

Two parametric tests are proposed for designing randomized two-arm phase III survival trials under the Weibull model. The properties of the two parametric tests are compared with the non-parametric log-rank test through simulation studies. Power and sample size formulas of the two parametric tests are derived. The impact on sample size under mis-specification of the Weibull shape parameter is also investigated. The study can be designed by planning the study duration and handling nonuniform entry and loss to follow-up under the Weibull model using either the proposed parametric tests or the well known non-parametric log-rank test.

1 Introduction

In randomized clinical trials, the primary interest is often to compare the survival distributions between treatment groups. To have adequate power to detect a pre-specified treatment difference, sample size calculation is of particular importance. Various researchers have proposed methods for sample size calculations for randomized clinical trials with a time-to-event endpoint. Some of these methods were discussed under the proportional hazards model (Freedman, 1982; Schoenfeld, 1983; Lakatos, 1988; Collett, 2003; and others). Most of these methods were derived under the assumption of an exponential distribution because of the simplicity of a constant hazard function (George and Desu, 1977; Bernstein and Lagakos, 1978; Lachin, 1981; Rubenstein et al., 1981; Schoenfeld and Richter, 1982; Lachin and Foulkes, 1986; and many others). Commercially available software packages, including PASS, nQuery and EAST, also implement methods for calculating sample size based on an exponential model and proportional hazards model. The same is true in the standard text books (Chow et al., 2003; Julious, 2010), where sample size calculation under the Weibull model is not usually considered. Only a few of the existing methods for power and sample size calculations consider the Weibull distribution. For example, Heo et al. (1998) derived a sample size formula under a proportional Weibull model, but test statistics were not discussed in their paper. Recently, Jiang et al. (2012) proposed a simulation method to calculate sample size for group sequential trials under a proportional Weibull model, but it is a computationally intensive method with restrictive assumptions. Lu et al. (2012) derived sample size formulas for a non-proportional Weibull model for designing a two-stage seamless adaptive trial. For survival data, the exponential and Weibull distribution are the two most frequently used parametric models. Of the two distribution forms, the Weibull distribution is more appropriate to describe time-to-event data than the exponential distribution in most cases because it includes the shape parameter in addition to the scale parameter, with a decreasing or increasing hazard (Jiang et al., 2012). In advanced stage cancer studies, the survival rate usually dramatically drops towards the end of the study. Such characteristics of the survival time distribution can be better approximated by a Weibull distribution. In general, a survival trial under the Weibull model with a common shape parameter can be designed under the proportional hazards model using the well known log-rank test. However, a parametric test derived under the Weibull model could be expected to have better properties than the non-parametric log-rank test. No comparison has been made between the parametric test and the non-parametric log-rank test under the Weibull model in the literature.

The rest of this paper is organized as follows. In Section 2, two parametric tests are proposed under a proportional Weibull model. Sample size formulas are derived. Nonuniform entry and loss to follow-up are also discussed. In Section 3, empirical type I error and power of the proposed two parametric tests are compared with the non-parametric log-rank test by simulation studies. An example is given in Section 4 to illustrate a randomized two-arm cancer survival trial design by using the proposed methods. The final conclusion is presented in Section 5.

2 Test Statistics and Sample Size Calculation

Two parametric test statistics are discussed in this section to provide power and sample size calculations for designing randomized two-arm survival trials. Assume that time-to-event variable T_j of a subject from the j^th group follows the Weibull distribution with a common shape parameter κ and scale parameter ρ_j, j = 1, 2. That is, T_j has survival distribution function

$$S_j(t)=e^{-{({\rho }_{j}t)}^{\kappa }},$$

and hazard function

$$h_j(t)=\kappa {\rho }_j^{\kappa }{t}^{\kappa -1}.$$

The shape parameter κ indicates the degree of acceleration (κ > 1) or deceleration (κ < 1) of the hazard over time. In a cancer trial, the median survival time is an intuitive endpoint for clinicians. The median survival time of the j^th group for the Weibull distribution can be calculated as $m_j={\rho }_j^{-1}{\{\mathit{log}(2)\}}^{1/\kappa }$. Therefore, the Weibull survival distribution can be expressed as

$$S_j(t)=e^{-\mathit{log}(2){(\frac{t}{m_j})}^{\kappa }},j=1,2.$$

The hypotheses of a randomized two-arm trial defined by median survival times can be expressed as

$$H_0:m_1=m_2\mathit{\text{vs}}.H_1:m_1\ne m_2.$$

2.1 Test Statistics and Sample Size Formulas

To derive the test statistics, we assume that the common shape parameter κ is known or can be estimated from historical data. Good quality historical data from standard treatment group can provide estimates of the Weibull parameters that are reliable for the planned study design. For notation convenience, we convert the scale parameter ρ_j to a hazard parameter ${\lambda }_j={\rho }_j^{\kappa }=\mathit{log}(2)/m_j^{\kappa }$. Then the above hypotheses on median survival times are equivalent to the following hypotheses:

$$H_0^{\ast }:{\lambda }_1={\lambda }_2\mathit{\text{vs}}.H_1^{\ast }:{\lambda }_1\ne {\lambda }_2,$$

where the hazards ratio is Δ = λ₁/λ₂ = R^κ, with R = m₂/m₁.

Now, suppose during the accrual phase of the trial, n_j subjects of the j^th group are enrolled in the study. Let

$$X_{ij}=min(T_{ij},C_{ij})\text{and}{\delta }_{ij}=I(T_{ij}\le C_{ij}),i=1,\dots ,n_j,j=1,2$$

be the observed times from entry to an event and event indicator, respectively, where T_ij is the true event time from a Weibull distribution with shape parameter κ and scale parameter ρ_j, and C_ij is a non-informative censoring time, which is assumed to be independent of T_ij. The likelihood function is given by

$$L({\lambda }_1,{\lambda }_2)={\lambda }_1^{d_1}{\lambda }_2^{d_2}{e}^{-{\lambda }_1{U}_1-{\lambda }_2{U}_2},$$

where $d_j={\sum }_{i=1}^{n_j}{\delta }_{ij}$ is the total number of events observed in j^th group and $U_j={\sum }_{i=1}^{n_j}{X}_{ij}^{\kappa }$ is the cumulative follow-up time penalized by the Weibull shape parameter κ. The maximum likelihood estimate of λ_j can be derived as

$${\widehat{\lambda }}_j=d_j/U_j,$$

and its variance is approximately ${\widehat{\lambda }}_j^2/d_j$ which can be obtained from the Fisher information matrix.

The distribution of λ̂_j is often skewed. This is partly because λ̂_j is restricted to be nonnegative value. A logarithmic transformation logλ̂_j takes the value over the entire real line, so the asymptotic normality is expected to be more accurate. Using the delta method, the variance of logλ̂_j is approximately 1/d_j. Thus a standardized statistic of logλ̂₁ – logλ̂₂

$$Z_1=\mathit{log}(U_2{d}_1/U_1{d}_2){(d_1^{-1}+d_2^{-1})}^{-1/2},$$

is an asymptotically standard normal distribution under the null hypothesis which was derived under the exponential model by Schoenfeld and Richter (1982). We call it the Schoenfeld test statistic. To calculate the power, let p_j be the probability of a subject from the j^th group having an event during the study, and assume that the randomization treatment allocation ratio is π as n₂ = πn₁. Then under the alternative hypothesis Δ = λ₁/λ₂(> 1), Z₁ is an approximately normal distribution with mean $n_1^{1/2}\kappa \mathit{log}(R){(p_1^{-1}+{\pi }^{-1}{p}_2^{-1})}^{-1/2}$ and unit variance. Therefore, given a significance level α, the power (1 – β) of the Z₁ test under the alternative is given by

$$\mathit{\text{power}}\simeq \mathrm{\Phi }\{n_1^{1/2}\kappa \mathit{log}(R){(p_1^{-1}+{\pi }^{-1}{p}_2^{-1})}^{-1/2}-z_{1-\alpha /2}\},$$

where Φ(·) is the standard normal distribution function and z_1–α/2 = Φ⁻¹(1 – α/2). Thus, sample size of the first group based on the Z₁ test can be calculated as

$$n_1=\frac{{(z_{1-\alpha /2}+z_{1-\beta })}^2(p_1^{-1}+{\pi }^{-1}{p}_2^{-1})}{{[\kappa \mathit{log}(R)]}^2}.$$ (1)

Sprott (1973) showed that the distribution of ${\widehat{\varphi }}_j={\widehat{\lambda }}_j^{1/3}$ in small samples is much more closely approximated by a normal distribution than is λ̂_j. Then ${\widehat{\varphi }}_j={\widehat{\lambda }}_j^{1/3}$ is approximately normal with mean ${\varphi }_j={\lambda }_j^{1/3}$ and variance estimate ${\widehat{\varphi }}_j^2/(9d_j)$ (Lawless, 1992). Therefore, the test statistic

$$Z_2=\frac{{\widehat{\varphi }}_1-{\widehat{\varphi }}_2}{{\{{\widehat{\varphi }}_1^2/(9d_1)+{\widehat{\varphi }}_2^2/(9d_2)\}}^{1/2}},$$

is an approximately standard normal distribution under the null hypothesis. We call it the Sprott test statistic. It rejects the null hypothesis if |Z₂| > z_1–α/2. Thus, the power of the Sprott test under the alternative is determined by

$$\mathit{\text{power}}\simeq \mathrm{\Phi }\{3n_1^{1/2}{(R^{2\kappa /3}{p}_1^{-1}+{\pi }^{-1}{p}_2^{-1})}^{-1/2}(R^{\kappa /3}-1)-z_{1-\alpha /2})\},$$

and sample size of the first group based on the Sprott test can be calculated as

$$n_1=\frac{{(z_{1-\alpha /2}+z_{1-\beta })}^2(R^{2\kappa /3}{p}_1^{-1}+{\pi }^{-1}{p}_2^{-1})}{9{(R^{\kappa /3}-1)}^2}.$$ (2)

To compare the proposed parametric test statistics with the non-parametric method, we introduce the log-rank test (Cox and Oakes, 1984) as follows: Let t₍₁₎ < t₍₂₎ < … < t_(k) denote the k distinct event times by pooling the two samples. In the j^th group there are d_sj events at the time t_(s) for j = 1, 2 and s = 1, 2, …, k. Also suppose that the number at risk at t_(s) in the j^th group is n_sj, and n_s = n_s1 + n_s2 for the total number at risk at t_(s), and d_s = d_s1 + d_s2 for the number of events at t_(s). The log-rank statistic is defined as

$$L=\sum _{s=1}^k(d_{s1}-e_{s1}),$$

where e_s1 = n_s1d_s/n_s is the expected number of events in the first group, and the variance of the log-rank statistic is

$$V=\sum _{s=1}^k\frac{n_{s1}{n}_{s2}{d}_s(n_s-d_s)}{n_s^2(n_s-1)}.$$

Under a proportional hazards model S₂(t) = [S₁(t)]^γ, for small values of the log hazards ratio log(Δ) = log(1/γ), and the standardized log-rank statistic Z₃ = L/V^1/2 is an approximately normal distribution with mean log(Δ)V^1/2 and unit variance (Tsiatis, 1982; Sellke and Siegmund, 1983). Thus, the sample size of the log-rank test can be derived at the alternative γ = γ₁(< 1) as (Collett, 2003; Schoenfeld, 1983)

$$n_1=\frac{{(\pi +1)}^2}{\pi }\frac{{(z_{1-\alpha /2}+z_{1-\beta })}^2}{{[\mathit{log}(\mathrm{\Delta })]}^2(p_1+\pi p_2)},$$ (3)

where Δ = 1/γ₁ = R^κ under the Weibull model. The total sample size is n = n₁ + n₂ = (π + 1)n₁.

2.2 Sample Size under Uniform Entry

To calculate the number of subjects required for the study, we need to calculate p_j, the probability of a subject in the j^th group having an event during study. Typically, assume that subjects are accrued over an accrual period of length t_a with an additional follow-up period of length t_f. A subject enters the study at time u, the entry time is uniformly distributed on [0, t_a], and no subject drops out or is lost to follow-up during the study. Then the probability of a subject having an event during the study under the Weibull model can be calculated by

$$p_j=1-\frac{1}{t_a}{\int }_{t_f}^{t_a+t_f}{e}^{-\mathit{log}(2){(\frac{t}{m_j})}^{\kappa }}dt,j=1,2.$$ (4)

This integration can be obtained numerically. Therefore, given the design parameters: κ, m₁, m₂, α, β, π, t_f and t_a, the number of subjects n required for the study can be calculated using formulas (1)-(3).

In an actual trial design, if there are historical data for the standard treatment group showing that the Weibull distribution provides a satisfactory model and gives reliable estimates for median survival time (m₁) and shape parameter κ, and if the investigators can also provide an estimate of the median survival time (m₂) of the new treatment based on a literature review or data from a pilot study on the new treatment, then the trial can be designed as discussed above. However, if there are no such historical data to provide full information on the Weibull parameters, then an alternative way to estimate the shape parameter is by using the following relationship:

$$\kappa =\frac{\mathit{log}(\mathrm{\Delta })}{\mathit{log}(m_2/m_1)},$$

where, m₁ and m₂ can be obtained as discussed above and the hazard ratio Δ can be obtained by the expectation for the new treatment that can increase the survival rate S₁(x) from the standard treatment to S₂(x) of the new treatment, where x is a landmark point. That is Δ = logS₁(x)/logS₂(x). Of course, one question is whether a rough estimate of the shape parameter can still provide a reliable study design. To answer this question, it is necessary to investigate the sensitivity of the sample size or power under mis-specification of the shape parameter. Simulation studies were conducted (see Section 4) and the results showed that the impact on the sample size and power is small under mis-specification of the shape parameter κ when it lays within a reasonable range (κ ± 30%κ).

Another issue in designing an actual trial is that, given the accrual time t_a, calculating the sample size is often impractical because we may not be able to enroll the total number of patients as planned in the given accrual duration. It is more practical to design the study starting with given the accrual rate r and then calculating the required accrual time t_a. This can be accomplished under the Weibull model assumption. First the integration in the probability formula (4) is approximated using Simpson's rule,

$$p_j=1-\frac{1}{6}\{S_j(t_f)+4S_j(0.5t_a+t_f)+S_j(t_a+t_f)\}.$$ (5)

Then, using the total sample size formula based on (1)-(3), for example (1), we can define a root function of the accrual time t_a

$$\text{root}(t_a)=r{t}_a-\frac{(\pi +1){(z_{1-\alpha /2}+z_{1-\beta })}^2(p_1^{-1}+{\pi }^{-1}{p}_2^{-1})}{{[\kappa \mathit{log}(R)]}^2}.$$

Now the accrual time t_a can be obtained by solving the root equation root(t_a) = 0 numerically in Splus/R using the uniroot function. The total sample size required for the study is approximately n = [rt_a]⁺, where [x]⁺ denote the smallest integer greater than x.

2.3 Sample Size under Nonuniform Entry and Loss to Follow-up

In section 2.2, we discussed sample size calculation under the usual assumptions of uniform entry and censoring only administratively at the end of the trial. Here, we will briefly discuss how to handle nonuniform entry and loss to follow-up.

Consider a general entry time distribution G(u) with density function g(u), for example, a truncated exponential entry distribution over the interval [0, t_a], with density (Lachin and Foulkes, 1986; Grisp and Curtis, 2007)

$$g(u)=\frac{v{e}^{-vu}}{1-e^{-v{t}_a}},$$

where v is the parameter reflecting the subject accrual pattern. For v > 0, the entry distribution is convex, whereas for v < 0, the entry distribution is concave, and v = 0 corresponds to a uniform entry on interval [0, t_a]. Then, the probability of a subject having an event during the study can be calculated by

$$p=1-{\int }_0^{t_a}S(t_a+t_f-u)dG(u)=1-{\int }_{t_f}^{t_a+t_f}S(t)g(t_a+t_f-t)dt,$$

where $S(t)=e^{-\mathit{log}(2){(\frac{t}{m})}^{\kappa }}$. This integration can be obtained numerically.

To consider loss to follow-up, let u be the entry time of a subject, with distribution G(u), which implies an exposure period F = t_a + t_f − u, and let T be the event time. In addition, let s denote the time of loss to follow-up, which follows a loss distribution H(s) over the complete follow-up interval [0, t_a + t_f]. Then, the probability of a subject having an event during the study can be calculated by (Lachin and Foulkes, 1986)

$$p={\int }_0^{t_a}P[T<\mathit{min}(F,s)]g(u)du={\int }_0^{t_a}{\int }_0^{t_a+t_f-u}g(u)f(t)[1-H(t)]dtdu,$$

where f(t) = κρ^κt^κ−1e^−(ρt)κ is the Weibull density function. Assuming that the accrual time is a piece-wise constant function, this integral can be calculated numerically too (see Appendix).

3 Comparisons of Power and Sample Size

In this section we conducted simulation studies to compare the power and type I error of the three test statistics under various scenarios. In the simulations, the survival distribution of the j^th group was taken as S_j(t) = e^{−log(2)(t/m_j)κ}, which is the Weibull distribution with shape parameter κ and median survival time m_j, j = 1, 2. The parameter settings for the simulation studies were κ = 0.5, 1, and 2 to reflect cases of decreasing, constant, and increasing hazard functions. The ratio R = m₂/m₁ under the null and alternative hypothesis was set to be between 1.0 and 2.0, with other parameters fixed as follows: m₁ = 1, accrual period t_a = 5 and follow-up time t_f = 2. For the proportional hazards model, under the Weibull distribution, the hazard ratio Δ = R^κ.

The simulations were performed for a variety of sample sizes, n = 30, 50, and 100 per group for equal allocation. We assumed subjects were recruited with a uniform distribution over the accrual period t_a and followed for t_f. A subject was censored if his/her event time was longer than t_a + t_f − u, where u was the time when the subject entered the study. We further assumed that no subject was lost to follow-up during the study period t_a + t_f. In each parameter configuration, 100,000 observed samples of censored event times were generated from the Weibull distribution to calculate the test statistics under the null or alternative hypothesis. The nominal significance level was set to be 0.05, and the standard error of the simulated empirical type I error based on 100,000 random samples was $\sqrt{0.05\ast 0.95/100,000}=0.00069$. The proportions rejecting the null under the true null hypothesis (R = 1) represent the estimated empirical type I error. The proportions rejecting the null under the alternative hypothesis (R > 1) represent the estimated empirical power. The simulated empirical type I errors and powers in various scenarios are summarized in Table 1. Highlighted values are those that exceed the nominal level plus three standard errors of the simulation.

Table 1.

Comparison of simulated empirical type I error (R = 1) and power (R > 1) of three test statistics based on 100,000 simulation runs for the Weibull distribution with nominal type I error level 0.05 (two-sided test).

			R = m2/m1
κ	Test	n1 = n2	1.0	1.1	1.2	1.3	1.5	1.8	2.0
0.5	Schoenfeld	30	0.050	0.053	0.061	0.072	0.102	0.158	0.198
	Sprott		0.052	0.055	0.063	0.073	0.107	0.164	0.205
	Log-rank		0.052	0.055	0.063	0.074	0.106	0.162	0.202
	Schoenfeld	50	0.051	0.055	0.066	0.087	0.137	0.234	0.302
	Sprott		0.051	0.056	0.070	0.089	0.142	0.240	0.305
	Log-rank		0.052	0.056	0.071	0.089	0.140	0.238	0.302
	Schoenfeld	100	0.049	0.060	0.086	0.125	0.229	0.414	0.534
	Sprott		0.050	0.060	0.088	0.126	0.229	0.413	0.532
	Log-rank		0.050	0.060	0.088	0.127	0.228	0.412	0.529
1	Schoenfeld	30	0.052	0.066	0.106	0.165	0.319	0.564	0.699
	Sprott		0.051	0.066	0.106	0.165	0.320	0.566	0.699
	Log-rank		0.054	0.069	0.108	0.163	0.313	0.550	0.683
	Schoenfeld	50	0.051	0.075	0.143	0.242	0.483	0.784	0.893
	Sprott		0.050	0.075	0.143	0.240	0.484	0.785	0.894
	Log-rank		0.053	0.076	0.142	0.237	0.476	0.774	0.885
	SR	100	0051	0098	0.233	0.422	0.772	0.972	0.995
	Sprott		0.051	0.098	0.236	0.425	0.771	0.972	0.995
	Log-rank		0.052	0.098	0.234	0.421	0.765	0.970	0.994
2	Schoenfeld	30	0.052	0.117	0.292	0.525	0.874	0.994	0.999
	Sprott		0.051	0.114	0.288	0.524	0.873	0.994	0.999
	Log-rank		0.056	0.117	0.283	0.506	0.852	0.991	0.999
	Schoenfeld	50	0.050	0.161	0.445	0.741	0.981	1.000	1.000
	Sprott		0.049	0.159	0.441	0.740	0.980	1.000	1.000
	Log-rank		0.053	0.159	0.433	0.726	0.975	1.000	1.000
	Schoenfeld	100	0.049	0.267	0.727	0.958	1.000	1.000	1.000
	Sprott		0.050	0.266	0.728	0.957	1.000	1.000	1.000
	Log-rank		0.050	0.264	0.720	0.953	1.000	1.000	1.000

The highlighted values are those that exceed the nominal level plus three standard errors of the simulation.

The simulation results showed that the log-rank test was slightly liberal when the sample size was small. The type I error of the Schoenfeld test and Sprott test were satisfactorily close to the nominal level of 0.05 in all scenarios. The powers of the Schoenfeld test, Sprott test, and log-rank test were very close, even though the power of the log-rank test dropped slightly when R was getting large.

The sample sizes calculated using formulas (1)-(3) for various hazards ratios are given in Table 2. The Schoenfeld test, Sprott test, and log-rank test gave almost identical sample sizes, which is consistent with the power simulation results. The empirical powers for the corresponding sample sizes given in Table 2 were based on 20,000 simulation runs. The simulated empirical powers of the Schoenfeld test, Sprott test, and log-rank test were all close to the nominal power of 90%, with a few exceptions in which the powers of the log-rank test dropped to 86%-87% when sample sizes were small.

Table 2.

Comparison of the required sample size (power) per group (n₁ = n₂) for the three tests with 90% nominal power and 5% type I error under the Weibull model (two-sided test).

		R = m2/m1
κ	Test	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	2.0
0.5	Schoenfeld	12335 (90)	3406 (90)	1662 (91)	1020 (90)	709 (90)	533 (90)	422 (90)	347 (90)	293 (90)	253 (90)
	Sprott	12334 (90)	3405 (90)	1661 (90)	1019 (90)	708 (90)	532 (90)	421 (90)	346 (91)	292 (90)	252 (90)
	Log-rank	12333 (90)	3405 (90)	1660 (90)	1019 (90)	708 (90)	531 (90)	420 (90)	345 (90)	291 (90)	251 (90)
1	Schoenfeld	2510 (90)	693 (90)	338 (90)	208 (90)	145 (90)	109 (90)	87 (91)	71 (90)	61 (91)	53 (91)
	Sprott	2510 (90)	693 (90)	338 (90)	208 (90)	145 (90)	109 (90)	87 (91)	72 (91)	61 (91)	53 (91)
	Log-rank	2510 (90)	693 (90)	338 (90)	208 (89)	144 (90)	109 (89)	86 (89)	71 (90)	60 (90)	52 (90)
2	Schoenfeld	582 (90)	160 (90)	78 (90)	48 (90)	33 (90)	25 (90)	20 (91)	16 (90)	14 (91)	12 (91)
	Sprott	583 (90)	161 (91)	79 (91)	49 (91)	34 (91)	26 (91)	21 (92)	17 (92)	15 (93)	13 (93)
	Log-rank	582 (90)	160 (89)	78 (89)	48 (90)	33 (88)	25 (88)	20 (88)	16 (86)	14 (87)	12 (87)

Empirical powers (in brackets) for the corresponding sample sizes were calculated based on 20,000 simulated runs under the same parameter setting.

To study the sensitivity of three tests against the shape parameter, sample size and empirical power are also calculated under mis-specification of the shape parameter within a range of κ ± 30%κ. The empirical powers were obtained through simulation based 20,000 runs. The results (Table 3) showed that the mis-specification of the shape parameter has only small impact on the study study power for all three test statistics.

Table 3.

Sample size (power) under mis-specification of the Weibull shape parameter κ for the three tests with 90% nominal power and 5% type I error (two-sided test).

			Mis-specification rate of κ
Δ	κ	Test	1	0.7	0.8	1.2	1.3
1.5	0.5	Schoenfeld	189 (90)	213 (93)	204 (92)	176 (88)	170 (87)
		Sprott	188 (90)	211 (93)	203 (93)	175 (88)	170 (88)
		Log-rank	187 (90)	210 (93)	202 (92)	174 (87)	169 (87)
	1	Schoenfeld	145 (90)	165 (94)	157 (92)	138 (89)	136 (88)
		Sprott	145 (90)	165 (94)	156 (92)	138 (89)	136 (88)
		Log-rank	144 (89)	164 (93)	156 (92)	138 (89)	135 (88)
	2	Schoenfeld	130 (90)	134 (91)	132 (91)	129 (90)	129 (90)
		Sprott	130 (90)	135 (91)	132 (91)	130 (90)	129 (90)
		Log-rank	129 (89)	134 (91)	132 (90)	129 (89)	129 (89)
2.0	0.5	Schoenfeld	72 (91)	82 (94)	79 (93)	67 (89)	64 (88)
		Sprott	70 (91)	80 (94)	77 (93)	65 (88)	63 (87)
		Log-rank	69 (90)	79 (93)	75 (92)	64 (87)	62 (86)
	1	Schoenfeld	53 (91)	62 (94)	58 (93)	49 (89)	48 (88)
		Sprott	53 (91)	61 (95)	58 (93)	50 (89)	49 (89)
		Log-rank	52 (90)	60 (94)	57 (92)	49 (88)	48 (87)
	2	Schoenfeld	45 (90)	47 (92)	46 (91)	45 (90)	44 (90)
		Sprott	46 (91)	48 (92)	47 (92)	45 (90)	45 (90)
		Log-rank	45 (89)	47 (91)	46 (90)	45 (89)	44 (88)
2.5	0.5	Schoenfeld	46 (92)	53 (95)	50 (94)	42 (90)	40 (88)
		Sprott	44 (91)	50 (94)	48 (93)	40 (88)	39 (88)
		Log-rank	42 (90)	48 (93)	46 (92)	39 (88)	38 (87)
	1	Schoenfeld	32 (91)	39 (96)	36 (94)	30 (90)	29 (89)
		Sprott	32 (91)	38 (95)	35 (94)	30 (90)	29 (90)
		Log-rank	31 (89)	37 (94)	35 (93)	29 (88)	29 (88)
	2	Schoenfeld	26 (90)	28 (92)	27 (92)	26 (90)	26 (90)
		Sprott	27 (91)	29 (93)	28 (92)	27 (91)	27 (91)
		Log-rank	26 (88)	28 (90)	27 (89)	26 (88)	26 (88)

Sample sizes are calculated under mis-specified value of κ. Empirical powers (in brackets) are calculated for the corresponding sample sizes under the true value of κ based on 20,000 simulated runs.

4 An Example

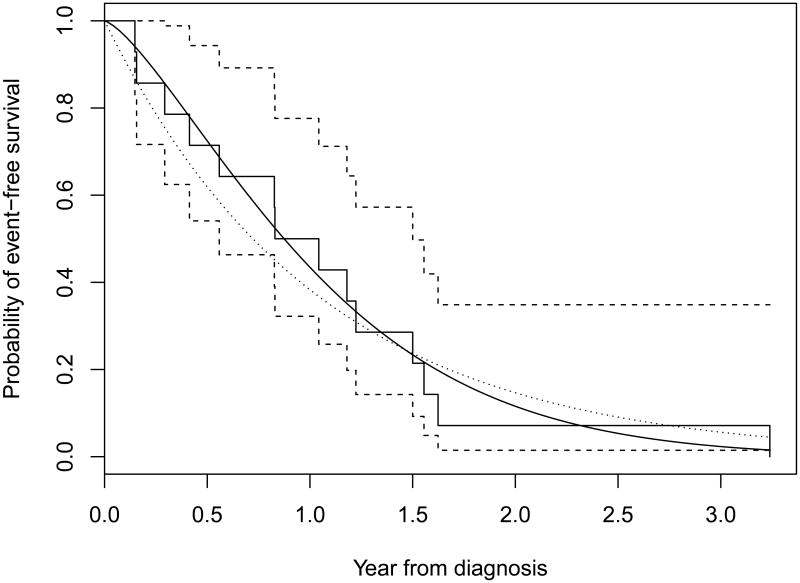
Rhabdoid tumors are aggressive pediatric malignancies with a poor prognosis. Over the past 5 years, St. Jude Children's Research Hospital accrued 14 pediatric patients with recurrent or refractory non-CNS rhabdoid tumors treated with conventional chemotherapy. The median event-free survival is only about 1 year, where the event is defined as disease relapse or death. All 14 patients had events within about 3 years. The Weibull model was fitted in R to the data, resulting an estimate (standard error) of the shape parameter κ = 1.37(0.28) and median event-free survival time of m₁ = 0.936 years. For comparison, the exponential model was also fitted to the data and the Kaplan-Meier curve and fitted exponential and Weibull survival curves were plotted on the same Figure. The log likelihood for the Weibull model was -13.60 whereas, for the exponential model, it was -14.60. The likelihood ratio test statistic was 2[-13.60-(-14.60)]=2.0, which was not significant compared with a chi-square percentile with one degree of freedom. However the log likelihood value and curve fitting suggest that the Weibull model provides a more satisfactory model than the exponential model. Now, suppose that we would like to design a multi-center randomized two-arm trial to assess the effectiveness of the small molecule inhibitor alisertib versus conventional chemotherapy for this group of patients. Patients will be randomized with equal allocation to each treatment group. The hypotheses of the planned study are H₀ : m₁ = m₂ vs. H₁ : m₁ ≠ m₂. The investigators would like to detect a half year difference of median event-free survival times between the alisertib treatment group to the conventional chemotherapy group, or equivalently to detect a hazard ratio Δ = 1.80, with 90% power and 5% type I error, and 2 years of follow-up after last patient enrolled on study. Assume this multi-center trial has the capacity to enroll and treat 20 patients per year. Then under the assumption of the Weibull model, with uniform entry and no loss to follow-up, the required total study durations are 6.26 and 6.36 years, or total sample sizes are 126 and 128 patients for the Schoenfeld test/log-rank test and Sprott test, respectively.

Figure. Kaplan-Meier Curve and Fitted Survival Distributions.

Step functions are Kaplan-Meier survival curve and its 90% confidence boundaries. Solid and dotted curves are the fitted Weibull and exponential survival distributions, respectively.

5 Conclusion

Two parametric test statistics and corresponding sample size formulas are proposed under the Weibull model. Within the parameter setting of the simulation, the results showed that both the Schoenfeld test and Sprott test preserve the type I error very well. The non-parametric log-rank test also preserves the type I error well for moderate and large samples, but it is slightly liberal in the case of small sample sizes. The empirical powers of the three tests are very close. Therefore the non-parametric log-rank test is still competitive against the proposed parametric tests. This is not surprising, because the log-rank test is fully efficient under the proportional hazards model (Schoenfeld and Ritcher, 1982). Even through the asymptotic normality of the two parametric tests is more accurate than that of the log-rank test for small samples, the log-rank test is well-known and is available in most commercial software packages. Therefore all three tests can be used to design a randomized two-arm trial under the Weibull model by planning the study accrual duration and handling nonuniform entry and loss to follow-up.

Appendix

By changing the order of integration, we have

$$p={\int }_0^{t_a}P[T<\mathit{min}(F,s)]g(u)du={\int }_0^{t_a}{\int }_0^{t_a+t_f-u}g(u)f(t)[1-H(t)]dtdu={\int }_0^{t_f}{\int }_0^{t_a}g(u)f(t)[1-H(t)]dudt+{\int }_{t_f}^{t_a+t_f}{\int }_0^{t_a+t_f-t}g(u)f(t)[1-H(t)]dudt.$$

Suppose the accrual rate is a piece-wise constant function, without loss of generality, and assume it is uniformly distributed on [0, t_a]. Then the above integral is simplified as

$$p={\int }_0^{t_f}f(t)[1-H(t)]dt+\frac{1}{t_a}{\int }_{t_f}^{t_a+t_f}(t_a+t_f-t)f(t)[1-H(t)]dt.$$

Inserting the Weibull density f(t) = κρ^κt^κ−1e^−(ρt)κ and exponential losses to follow-up distribution H(t) = 1 − e^ηt into above integrals, we obtain

$$p={\int }_0^{t_f}\kappa {\rho }^{\kappa }{t}^{\kappa -1}{e}^{-{(\rho t)}^{\kappa }-\eta t}dt+\frac{1}{t_a}{\int }_{t_f}^{t_a+t_f}(t_a+t_f-t)\kappa {\rho }^{\kappa }{t}^{\kappa -1}{e}^{-{(\rho t)}^{\kappa }-\eta t}dt,$$

which can be integrated numerically. If we assume that both survival and loss to follow-up distributions are exponential, that is f(t) = λe^−λt and H(t) = 1 − e^ηt, then the above two integrations can be integrated as

$$p=\frac{\lambda }{\lambda +\eta }\{1-\frac{e^{-(\lambda +\eta )t_f}-e^{-(\lambda +\eta )(t_a+t_f)}}{t_a(\lambda +\eta )}\}$$

which is given by Lachin and Foulkes (1986).