Probing DNA Stiffness through Optical Fluctuation Analysis of Plasmon Rulers

Abstract

The distance dependent plasmon coupling between biopolymer tethered gold or silver nanoparticles forms the foundation for the so-called Plasmon Rulers. While conventional Plasmon Ruler applications focus on the detection of singular events in the far-field spectrum, we perform in this Letter a ratiometric analysis of the continuous spectral fluctuations arising from thermal interparticle separation variations in Plasmon Rulers confined to fluid lipid membranes. We characterized Plasmon Rulers with different DNA tethers and demonstrate the ability to detect and quantify differences in the Plasmon Ruler potential and tether stiffness. The influence of the nature of the tether (single-stranded versus double-stranded DNA) and the length of the tether is analyzed. The characterization of the continuous variation of the interparticle separation in individual Plasmon Rulers through optical fluctuation analysis provides additional information about the conformational flexibility of the tether molecule(s) located in the confinement of the deeply subdiffraction limit interparticle gap and enhances the versatility of Plasmon Rulers as tool in Biophysics and Nanotechnology.

Plasmon rulers (PRs) are self-assembled dimers of noble metal nanoparticles (NPs) linked by a biopolymer, in most cases DNA, which have been demonstrated to act as dynamic molecular rulers.^1–4 The far-field scattering spectra of a pair of gold or silver NPs is dominated by coupled charge density oscillations (plasmons) along the long dimer axis. The resonance wavelength, λ_res, of the superradiant longitudinal plasmon mode continuously red-shifts with decreasing interparticle separation, S, once the NPs have approached each other to within approximately one NP diameter.^5–8 This spectral shift is phenomenologically understood in a semiclassical charge oscillator model. The restoring force acting on the displacement charge in the individual NPs decreases due to the increased charge screening that results from the accumulation of opposite charge densities around the gap.⁶ The far-field spectral properties of gold and silver PRs as function of interparticle separation have been characterized in detail,^9–13 and it was demonstrated that PRs offer unique opportunities for monitoring distances on longer length and time scales than is possible with conventional molecular rulers based on Fluorescence Resonance Energy Transfer (FRET)¹⁴ between organic dyes.

So far, research in the area of PRs has primarily focused on the characterization of the electromagnetic coupling and quantification of the λ_res(S) relationship^{1,2,6–9,11,13,15–20} as well as on their application as biosensors that use singular changes in the spectral position and/or intensity of the scattering spectra as signal transducer. These changes were associated with variations in the average interparticle separation as a result of analyte binding,^4,21 hybridization,^1,22–24 or other effects that act upon the tether molecule(s)^25,26. A related application is the use of plasmon coupling to monitor spectral shifts that occur during endocytosis and trafficking of NPs targeted at cell surface receptors.^27–31 In most cases the monitored spectral changes were irreversible, but a few selected studies have also demonstrated the detection of reversible events, such as modulation of the salt-concentration dependent persistence length¹ of the PR tether or the binding and subsequent unbinding of an analyte to a PR tether³². One aspect common to all of these PR applications is that they were based on the detection of discrete conformational changes that result in distinct spectral shifts in the time domain. Continuous PR signal fluctuations due to thermal variations in S encode, however, additional important information about the stiffness of the DNA tether in the PRs as the effective tether constant k_eff is according to the equipartition theorem inversely proportional to the variance σ²(S) of the interparticle separation S:³³

$$k_{\mathit{\text{eff}}}=k_{\mathrm{B}}\mathrm{T}/{\mathrm{\sigma }}^2(S)$$ (Eq.1)

A systematic analysis of these continuous signals requires new PR imaging and analysis strategies that go beyond the detection of singular events. Recently, optical fluctuation analysis of long range propagating surface plasmon resonances has been introduced as a means to quantify cellular motions on a gold film.³⁴ In this Letter we expand this concept and apply it to monitor the separation between two gold NPs with coupled localized surface plasmon resonances (LSPRs). In particular, we demonstrate that optical fluctuation analysis of PRs in ratiometric darkfield microscopy^4,35,36 facilitates an optical quantification of S fluctuations, which provide insight into the interparticle potential φ and the PR tether constant k_eff.

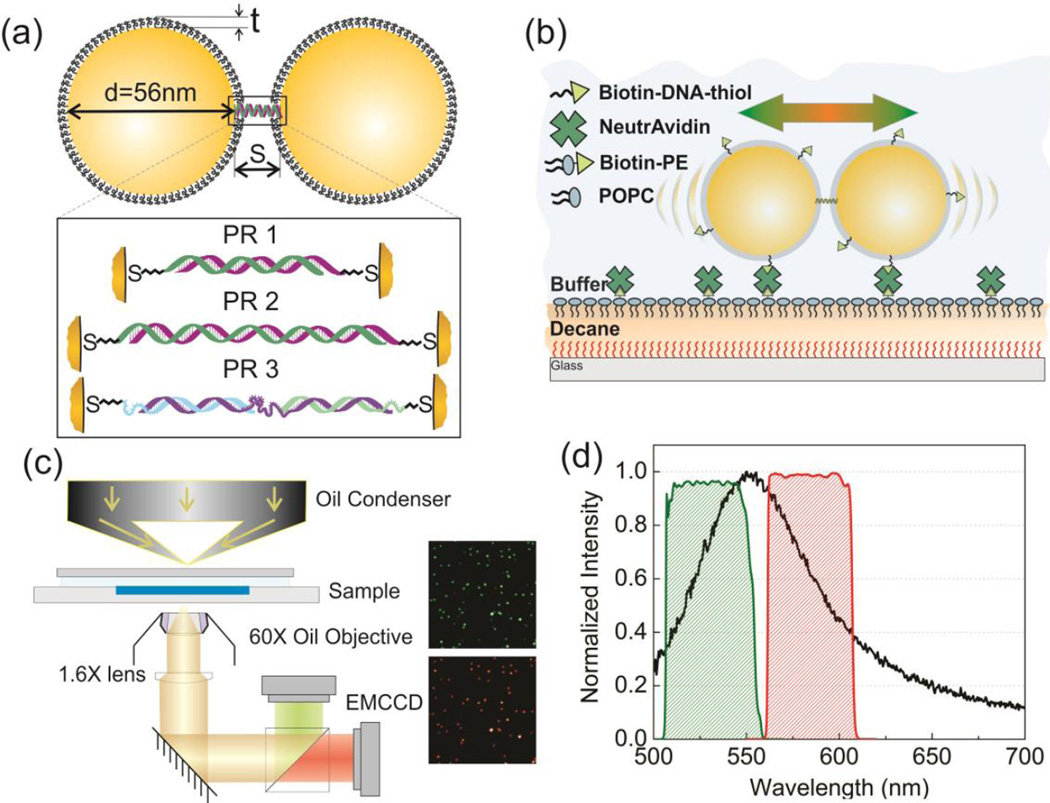
Figure 1a provides a schematic overview of the PRs used in this work. In a first approximation the PRs can be described as two particles with diameter d, covered by a polymer brush of thickness t and with zeta potential ζ that are linked by one (or multiple) DNA strand(s) generating an effective tether with stiffness k_eff. The tethered NPs explore the interparticle potential φ through thermal motion, and they experience a friction described by the coefficient ξ. At any given time, the potential energy for an individual PR is proportional to the extension x = S – S₀, where S₀ is the equilibrium interparticle separation. Depending on the available thermal energy, a PR tether can access a range of interparticle separations and the probability of a specific extension x is assumed to be proportional to its Boltzmann weight:^{37, 38}

$$P(x)~e^{-\frac{\phi (x)}{kT}}$$ (Eq.2)

The goal of this manuscript is to characterize φ(x) through analysis of the continuous spectral fluctuations in S at the single PR level for different DNA tethers between the NPs and determine the respective k_eff and S₀ values.

Figure 1.

(a) Model of Plasmon Rulers PR1-3. The inset shows details of the PR tethers. PR1: 30 bps dsDNA; PR2: 52 bps dsDNA; PR3: ssDNA/dsDNA hybrid (see text). (b) Schematic of the experimental approach. PRs are confined to a two-dimensional lipid monolayer assembled on a decane cushion. Fluctuations in the interparticle separation of individual PRs result in spectral shifts that are monitored by ratiometric imaging. (c) Microscope set-up and representative images of PR2 on the 530nm (green) and 585nm (red) channel. (d) PR scattering spectrum (average of 20 PR3s, black line) and transmission spectra of the 40 nm bandpass filters centered at 530nm (green) and 585nm (red).

RESULTS AND DISCUSSION

PR Assembly

All PRs were assembled from colloidal citrate stabilized gold NPs using a DNA programmed self-assembly strategy. We chose NPs with a diameter of 56 ± 2.4 nm for these experiments to obtain a high signal-to-noise ratio in optical imaging. Two flavors of NPs were tethered by annealing thiol-bound single stranded DNA (ssDNA) handles either directly to each other or to a third ssDNA linker. For details regarding the NP functionalization and assembly procedures, please refer to the Supporting Information. Figure S1 contains SEM images of purified PRs. The DNA handles were embedded in a brush of 30 nucleotides long ssDNAs to passivate the NP surface and stabilize the NPs. A fraction of the brush ssDNAs was biotinylated. Rational assembly strategies of PRs containing a single DNA molecule connecting the NPs have been developed,³⁹ but they require a lengthening of the DNA handle and subsequent purification of NP-DNA conjugates in an additional intermediate step. We applied in this work a simpler conventional PR assembly strategy²¹ and minimized the probability of multiple tether formation by using different DNA handle concentrations on the two NP flavors. One flavor contained a high concentration of DNA handles grafted to the NP surface while the DNA handle density on the second flavor was very low. We do not rule out the possibility that a small fraction of PRs had more than one tether. This heterogeneity may broaden the determined k_eff value distribution but does not question the generality of the spectral fluctuation based analysis strategy developed in the following. In fact, our quantitative S analysis in PRs will improve the conceptual understanding of the “tether” in PRs. The physical behavior of the DNA molecule(s) located in the nanoconfinement between two highly charged NP surfaces containing a brush of other ssDNAs can be complex⁴⁰ and is difficult to probe with conventional experimental tools.

The zeta potential of the NPs used for the PR assembly was ζ = −19.2 mV under the chosen buffer conditions (10mM Tris PH8.0, 50mM NaCl). The thickness of the DNA brush around the NPs was determined by dynamic light scattering (DLS) as t = 3.4 nm. We investigated three different PR systems in this work, which we refer to as PR1–3 throughout the manuscript (Figure 1a). In PR1 the NPs were tethered by 30 base pairs (bps) long double-stranded DNAs (dsDNAs), and in PR2 the NPs were tethered by 52 bps long dsDNAs. Different from PR1 and PR2, the PR3 tether contained - by design - both ssDNA and dsDNA segments. In the PR3 tether geometry 10 nucleotide long ssDNA tails on each side are followed by 20 bps long double stranded segments that are connected by a 40 nucleotide long central ssDNA segment. The worm-like chain (WLC) model⁴¹ predicted end-to-end distances for the DNA tethers used in this work are 9.4 nm (PR1), 16.0 nm (PR2) and 15.9 nm (PR3).

Membrane-confined PR Assay

Our experimental strategy to construct the PR potential φ requires a continuous monitoring of the PR spectrum as function of time. After these spectral traces are converted into S trajectories using an appropriate calibration relationship, φ(x) is determined by the probability distribution of the interparticle separations (see Supporting Information for more details). One caveat of this general approach is that a characterization of the spectral response of freely diffusing PRs is met by a series of fundamental experimental challenges. For once, the random tumbling of a PR performing Brownian motion in solution results in rapid changes of the relative orientation of the dimer with regard to the optical axis of the microscope. Since the optical response of a PR is dominated by the longitudinal plasmon mode along the long dimer axis,^2,4,6 changes in the projection of the incident E-field onto this axis are accompanied by changes in the shape and intensity of the recorded scattering spectra.⁴ Furthermore, the spatial emission pattern of the individual PRs also depends on the orientation of the dipole emitters in space.⁴² Consequently, PR orientation changes cause signal modulations that are independent of actual separation fluctuations. To eliminate the complications associated with a three-dimensional PR diffusion, we confined the long PR axis to a two-dimensional fluid plane where rotational motions and lateral displacements of the PRs do not cause intensity or spectral changes under unpolarized whitelight illumination. We experimentally implemented this confinement by binding the PRs to a fluid lipid membrane. We assembled a 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) monolayer at the water/alkane interface between the aqueous buffer and a thin decane film deposited on a hydrophobic glass substrate (see Figure 1b and Supporting Information). Biotin-phosphatidylethanolamin (biotin-PE) was integrated into the lipid monolayerspec at a concentration of 0.5 mol% to allow for an uncomplicated binding of the biotin-functionalized PRs using established biotin-Neutravidin binding chemistries.

The higher viscosity and the additional friction⁴³ associated with the membrane reduces the thermal interparticle fluctuations and the lateral NP diffusion, we measured typical diffusion constants of D ≈ 0.7 µm²/s for individual 56 nm diameter NPs. The slope of the PR potential itself and therefore k_eff is in a first approximation, however, independent of the ambient medium and we will, consequently, include an analysis of the interparticle potential in our quantitative analysis (vide infra).

Ratiometric Tracking of Membrane Confined PRs

The need to acquire spectral information from laterally diffusing PRs, ideally with high temporal resolution, excludes the use of a conventional imaging spectrometer as this technique provides spectral information only from a small fixed area in the focal plane. Instead, we used a ratiometric widefield imaging approach in which the entire field of view is imaged simultaneously on two wavelength channels, λ₁ and λ₂.^35,44,45 The monitored wavelengths are located on the blue (λ₁) and red (λ₂) flank of the longitudinal PR resonance.^35,36 The spectral information of an individual PR is then contained in the intensity distribution on the two monitored channels, here quantified as:

$$R=(I_{\lambda 1}-I_{\lambda 2})/(I_{\lambda 1}+I_{\lambda 2})$$ (Eq.3)

In our experimental set-up (Figure 1c) the PRs were illuminated with whitelight through a darkfield condenser. We validated that the light incident in the imaging plane was unpolarized (Figure S2). The light scattered from the individual PRs was collected through an oil immersion objective (NA = 0.65) and split into two beams using a 560 nm dichroic. The separated beams passed bandpass filters centered at λ₁ = 530 nm and λ₂ = 585 nm, respectively, with a spectral width of approximately 40 nm (Figure 1d) before they were collected on two separate electron enhanced charge coupled device (EMCCD) detectors (see Movie1 in Supporting Information). The intensities of a PR on the two images, I _λ1 and I_λ2, were obtained by integrating their fitted point spread functions (PSFs) on the two color channels.

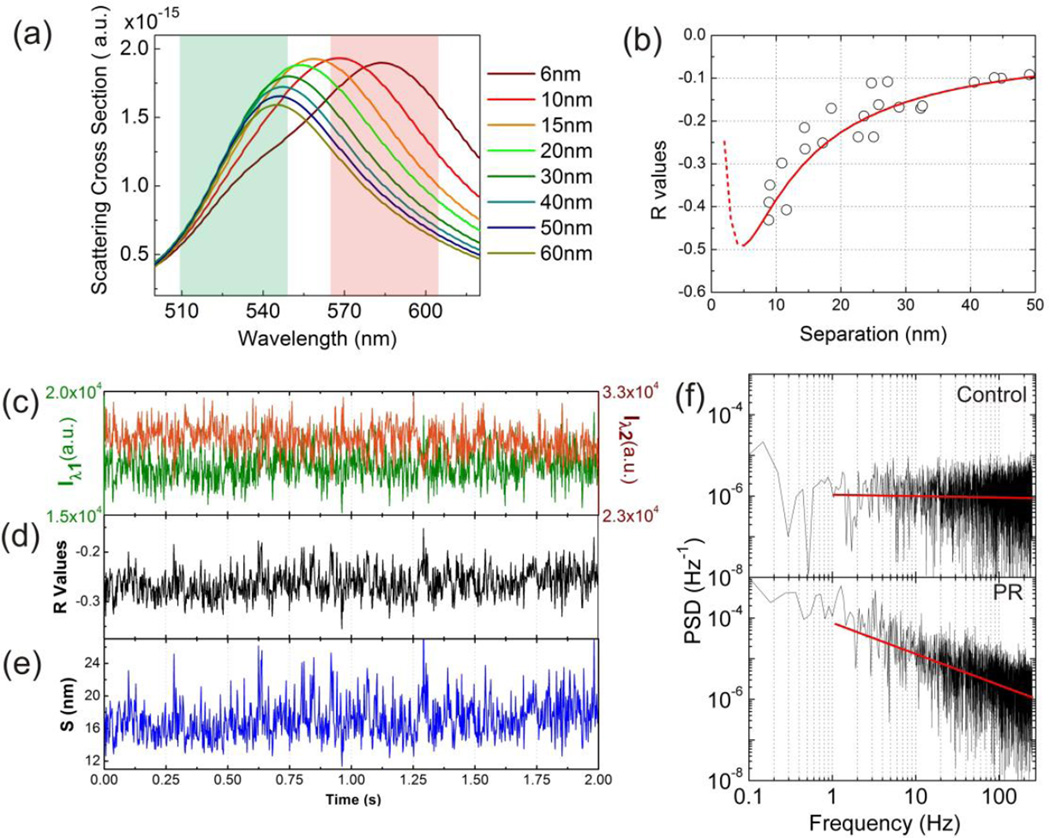
We simulated the scattering spectra of NP dimers with various interparticle separations using finite-difference time domain (FDTD) simulations (Figure 2a) and derived I_λ1 and I_λ2 values by integrating the simulated scattering intensities. The latter were obtained by multiplying the FDTD simulated scattering cross-sections with the excitation profile of the Tungsten whitelight lamp over the widths of the chosen filters (see Supporting Information). The R(S) relationship obtained from the FDTD simulations is plotted as red line in Figure 2b. By inversion of this relationship we obtained the S(R) relationship required to convert R trajectories into S trajectories. We note in passing that the sharp turn at S < 5nm in the R(S) relationship in Figure 2b is the result of the strong electromagnetic coupling between the NPs at short interparticle separations, which shifts the coupled longitudinal plasmon resonance out of the range of the two monitored wavelength channels. Consequently, the transverse mode with a peak wavelength of about 540 nm dominates the detected light for S < 5 nm, and the R values show a steep increase in this range. As the NPs used in this work were covered by polymer brushes with a thickness t ≈ 3.4 nm, separations with S < 5nm are non-physical for PR1–3. Trajectories with average R values (R̄) < −0.5 indicate agglomerates or touching PRs and were excluded in Figure 3d and all subsequent data analysis. Less than 5% of the non-compacted PRs fell in this spectral range.

Figure 2.

(a) FDTD simulated scattering cross-sections of dimers with various interparticle separations. The green and red colored areas represent the spectral ranges of the bandpass filters of the two monitored color channels. (b) R(S) calibration generated from FDTD simulations (red line) and experimental validation data (black circle). (c) Scattering intensity trajectory of a representative PR2 recorded with a frame rate of 490 fps simultaneously on the I_λ1 (green) and I_λ2 (red) channel. (d) and (e) show the corresponding R and S trajectories. (f) Power spectral density (PSD) of the R-trajectory shown in (d) (bottom) and an individual 80 nm diameter gold NP (top) for comparison. The linear decay of the PSD for the PR in the log-log plot confirms a power law dependence. The constant PSD for the individual gold NP is characteristic of a random (white) noise process.

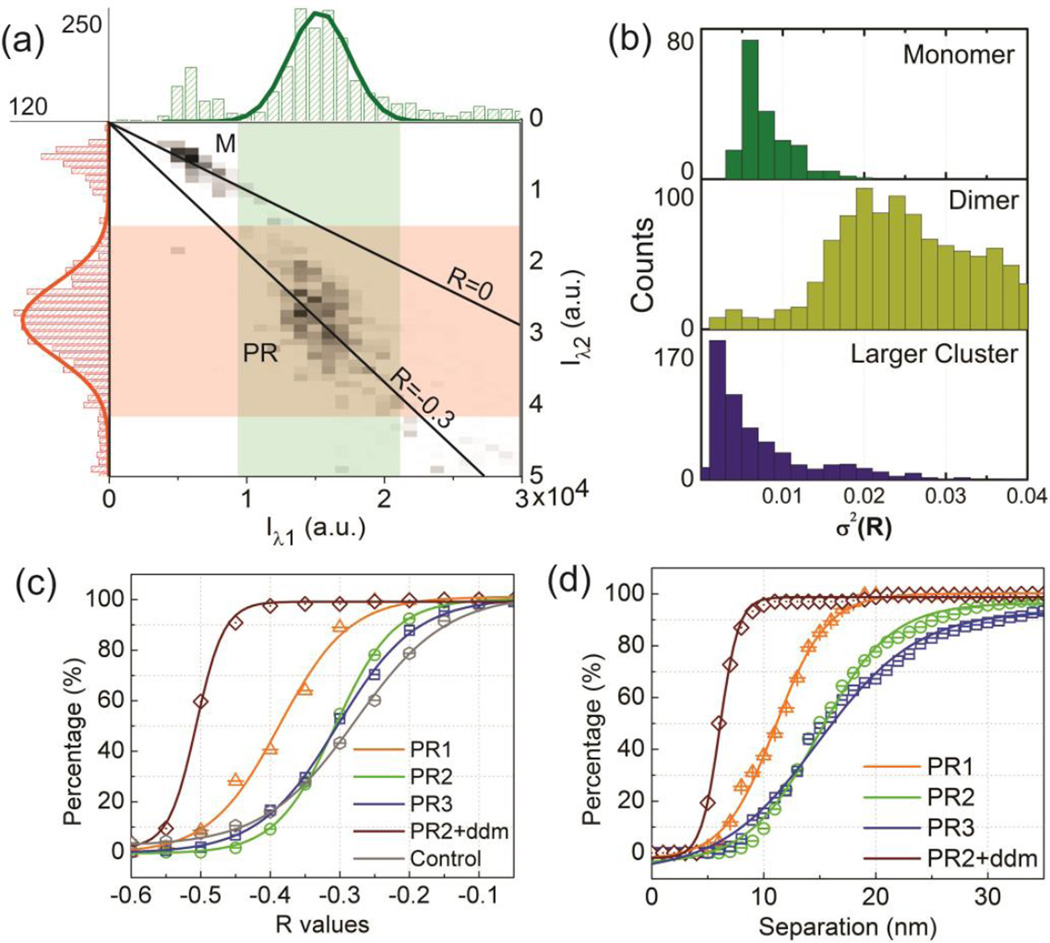
Figure 3.

(a) Average intensity distribution in the 530 channel (green) and 585 channel (red) for individual scatterers diffusing on the lipid membrane after PR binding. The intensities cluster in two distinct groups, which are assigned to NP monomers (M) and PRs. Signals in the high intensity tail of the distribution are assigned to larger clusters. (b) Distribution of spectral variance, measured as σ²(R), for monomers, dimers and larger clusters diffusing on the membrane with a linear polarizer in the detection beam path. The significant higher variance for dimers is consistent with the anisotropic shape of the PRs. If the long axes aligns with the analyzer axis, the intensity is much higher than for the orthogonal orientation. (c) and (d) Cumulative distribution plots of R̄ (c) and S̄ (d) for PR1-3, the dendrimer compacted PR2 and 80nm gold NPs.

We validated the derived R(S) calibration curve experimentally by measuring the R values and interparticle separations of 22 NP dimers (Figure S3b). The dimers were assembled through template guided self-assembly^12,46,47 on a transparent ITO coated glass substrate. The R values were obtained using the ratiometric darkfield imaging approach outlined above; the S values of the imaged dimers were subsequently determined by inspection in the SEM. Although the experimental data (open circles in Figure 2b) show some spread due to the limited spatial resolution of the SEM and the heterogeneity of the NP shapes, overall the experimental R(S) data accurately follow the FDTD predicted trend.

The performed simulations also indicate that the chosen filters with a bandwidth of 40 nm achieve a similar sensitivity (as defined by the slope) in R(S) as much narrower bandpass filters (Figure S3a). At the same time, the broader filters cover almost the entire spectral range of the PRs, which maximizes the detected signal. A high temporal resolution is desirable for monitoring thermal fluctuations in PRs with continuously variable interparticle separation, but in practice one has to compromise between temporal resolution and signal-to-noise. In this manuscript, we tracked PRs with a frame rate of 490 frames per seconds (fps) (acquisition time: 2 ms) in a total view of 40 × 40 µm² . Exemplary I_λ1 and I_λ2 and 2e contain the corresponding R and S trajectories. In the following, we will use S trajectories like this one to analyze the continuous fluctuations in the interparticle separation of individual PRs. The power spectral density (PSD) of the R trajectory in the log-log plot in Figure 2f falls off with a slope of −0.77, indicating a stationary process with some positive long-range autocorrelation (Hurst factor⁴⁸, H = 0.89). Figure 2f also contains a plot of the PSD for an individual 80 nm gold NP with comparable scattering intensity as the PR. The PSD for the 80 nm NP is systematically shifted to lower values and remains nearly constant across the investigated frequency range. The observed slope of ≈ 0 is characteristic of white noise and indicates a signal with rapidly decaying autocorrelation (H = 0.5). The observed differences in the PSDs are a first indication of a contribution from interparticle fluctuations in the PR signal.

Our PR samples always contained some contaminations; a typical PR sample contained ~70% dimers and the remaining ~30% were individual nanoparticles and larger agglomerates based on SEM analysis (Figure S1c). Furthermore, some of the dimers were not tethered by a DNA but consisted of touching or fused NPs and were, therefore, also not applicable to an optical fluctuation analysis. We identified the PR sub-population (DNA tethered NP dimers) based on their characteristic intensity and polarization properties. Figure 3a shows the distribution of the trajectory-averaged intensities on the two monitored wavelength channels and their cross-correlation for approximately 1100 different PR2 dimers. The clustering of the data around specific intensity values indicates the presence of three discrete sub-populations. The lowest intensity peak (M) is assigned to the monomer, the next highest intensity peak (PR) to the polymer tethered NP dimer. Larger agglomerates and fused NPs form the high intensity tails of the distributions. These assignments are consistent with the measured polarization properties of the scattered light. After placing an analyzer with a fixed polarization in the beampath of the collected light, the anisotropic PRs show a much larger variance in R than the more symmetric monomers and larger agglomerates (Figure 3b).

A comparison of the relative intensities on the two monitored wavelength channels (λ₁ = 530 nm, λ₂ = 585 nm) in Figure 3a confirms that the relative contribution from the red channel is increased in PRs when compared to individual NPs due to plasmon coupling. The red-shift is revealed by lower average R values for the PRs as indicated in the figure. This electromagnetic coupling and the resulting spectral shift form the basis for the PR as molecular ruler in general and for the optical quantification of S fluctuations in particular. We recorded > 1000 R trajectories each for PR1 −3. For PR2 we also monitored the spectral fluctuations after compaction of the PRs by highly positively charged fourth generation polyamidoamine (PAMAM) dendrimers. We included 80 nm gold nanoparticles as controls in this study as these NPs have similar scattering intensities as the investigated PRs but lack signal fluctuations due to variations in S. Figure 3c contains cumulative distributions of the trajectory-averaged R values (R̄) for the different PRs and the 80 nm NP controls; a red-shift results in more negative R values. The cumulative probability distributions of R̄ for PR2 and PR3 superimpose, indicating – in good agreement with the WLC model predictions – almost identical average interparticle separations. The distribution of the 80 nm NP controls is only slightly blue-shifted from those of PR2 and PR3, confirming that the 80 nm diameter NP LSPR lies in the same spectral range as the PR2–3 resonances. Consistent with a shorter interparticle separation in PR1, the cumulative distribution of PR1 is red-shifted relative to those of PR2 and PR3. The largest red-shift (= shortest interparticle separation) is obtained for PR2 after compaction of the DNA tether by dendrimers. Overall, the obtained R̄] distributions confirm that the chosen ratiometric imaging approach can successfully distinguish PRs with different DNA tether lengths.

In the next step, we applied the derived R(S) conversion to this data set to generate the corresponding cumulative probability distributions for the traj ectory-averaged S (5) values (Figure 3d). The average interparticle separations (:=S̄₀) for the PRs are obtained from these plots as the separations where the cumulative probability reaches 50%. This analysis yields S̄₀≈ 15.5 nm for PR2 and PR3, and S̄₀≈ 10.7 nm for PR1. For the dendrimer compacted PR2 we obtain S̄₀≈ 6.0 nm, indicative of a complete collapse of the DNA tether. For PR2–3 the derived interparticle separations lie within 0.5 nm of the WLC model predictions, but for PR1 the obtained S̄₀ is 1.3 nm longer than the WLC prediction. Considering that the dsDNA tethers also contain very floppy terminal carbon linkers (C6 chain lengths) that orient at very low forces, the tentative effect of stretching on the DNA is still moderate even in case of the 30 bps dsDNA tether.

Based on the correspondence between the experimental S̄₀ and the zero-force WLC predictions we conclude i) that the PRs are mainly linked by individual tethers and ii) that the effect of NP associated forces, typically described in the context of a DLVO model⁴⁹, on the PR tether length is weak and that the PR potential around the equilibrium separation is primarily determined by the intrinsic properties of the DNA. We emphasize that our results were obtained at NaCl concentrations of approximately 50 mM. Previous correlated cryo-EM / dark-field microscopic studies performed with much lower (1 mM NaCl) salt concentration have shown that dsDNA tethered PRs can be stretched by electrostatic repulsion between NPs.³⁹ It will be instructive to investigate the influence of the salt concentration on the PR mechanical response in future studies as the ionic strength impacts both the persistence length of the DNA tethers^50,51 as well as the charge screening of the negatively charged NPs^52,53.

Quantification of Spectral Fluctuations

In the next step, we will validate whether our ratiometric tracking approach is sufficiently sensitive to detect continuous thermal fluctuations in the interparticle separation. We quantify in this manuscript the fluctuations in the signal of individual PRs as the variance of R:

$${\sigma }^2(R)=\frac{1}{n}{\sum }_{i=1}^n{(R_i-\overline{R})}^2$$ (Eq.4)

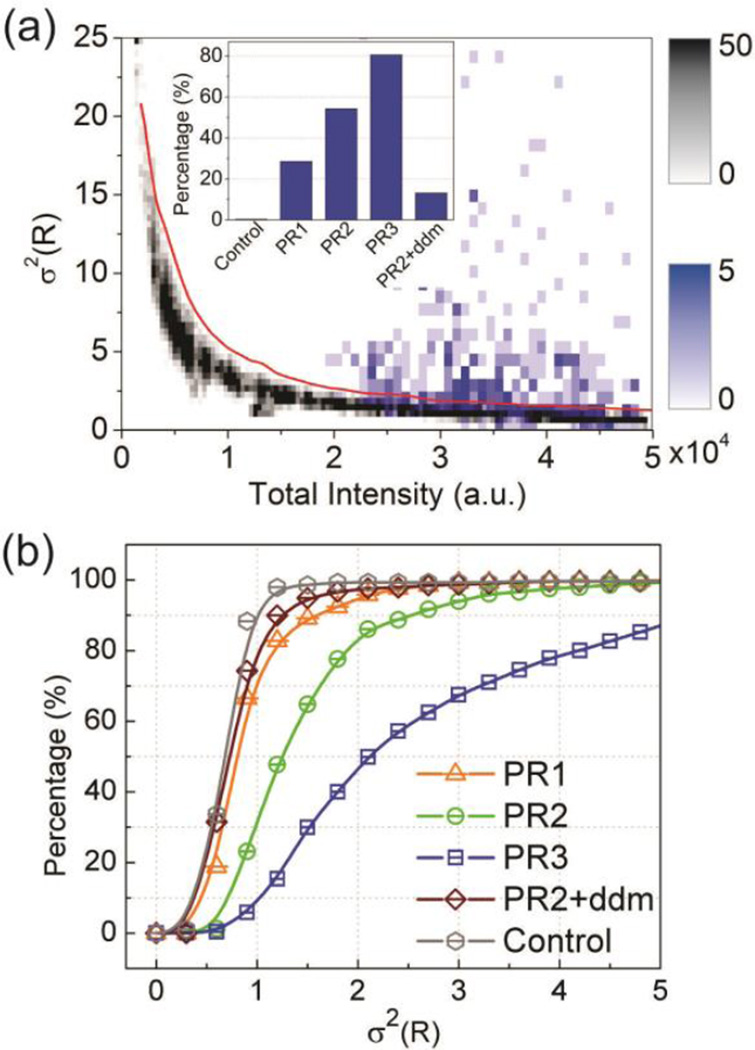
where n is the length of the trajectory. The experimentally measured PR intensities, I_λ1 and I_λ2, have systematic intensity-dependent contributions from different noise sources (dark, read-out and photon noise) as well as from fluctuations in S. The variance of any individual Poisson distributed signal increases linearly with intensity, but the behavior of an intensity ratio, such as R is more complex. To evaluate the dependence of the variance of R on the total intensity in the absence of S fluctuations, we first analyzed σ²(R) from 80 nm diameter gold NP controls recorded at different incident light intensities (gray colormap, Figure 4a). The histogram plot of the experimental σ²(R) data as function of intensity shows a high variance at low intensities that drops off with increasing intensity as the signal-to-noise ratio improves. For the analysis of the PR variance due to potential S fluctuations, it is important to operate in the intensity regime where the σ²(R) vs. intensity relationship of the 80 nm NPs is almost flat. The σ²(R) data for PR3 included as blue colormap in Figure 4a confirm that the assembled PRs indeed lie in this regime with low instrumental noise. Strikingly, although 80 nm diameter NPs and PR3 have comparable spectral and intensity properties, the σ²(R) distributions for PR3 and NP control trajectories differ significantly. The PRs show on average a much higher variance than NPs with identical intensity. This increase in σ²(R) confirms an additional source of R fluctuations for the DNA tethered NPs that is absent in the NP controls. We attribute the increase in σ²(R) to spectral changes associated with fluctuations in S. In the subsequent analysis, we only included PRs that showed significant S fluctuations as indicated by a σ²(R) that was ≥ 3 standard deviations (stdevs) higher than the average of the 80 nm diameter gold NP controls in the same intensity range. The inset in Figure 4a summarizes the fraction of the recorded trajectories that fulfilled this selection criterion for 80 nm NP controls, PR1–3 and PR2 after DNA compaction through dendrimers (+ ddm).

Figure 4.

(a) Variance σ²(R) as function of the trajectory-averaged total intensity (I_λ1 + I_λ2) for 80nm gold NPs (gray) and PRs (PR3, blue). The histogrammed data are plotted as colormaps as indicated. The inset shows the fraction of trajectories of PR1-3, PR2 + dendrimer (ddm) and 80 nm gold NPs controls (no S fluctuations) with σ²(R) values that were ≥ 3 stdevs larger than for 80 nm NP controls of comparable intensity. (b) Cumulative probability distributions of σ²(R) for PR1-3, PR2 + ddm, and 80 nm NP control.

Probing the PR Tether Stiffness

Given the functional relationship between S and R and considering the equipartition theorem from Eq. 1, we can conclude that the observed spectral fluctuations encode information about the PR tether. For an interpretation of the measured R fluctuations in the context of an effective PR tether stiffness, it is important to consider how the finite temporal resolution of the data acquisition affects any derived mechanical properties. All data in this work were recorded with an acquisition time of 2 ms, and the observed R and derived S values represent averages over this time window. One important consequence of the averaging is that the derived σ² values underestimate the real variances of R and S. It follows from Eq. 1 that an underestimation of σ² results in an overestimation of k_eff . As this is a systematic effect that applies equally to all investigated systems, the comparison of the recorded σ²(S) values can still provide information about the relative stiffness of different PRs. For the recorded data, the shift of the σ²(R) distribution to larger values in Figure 4b implies that k_eff increases in the order PR3 (ssDNA/dsDNA hybrid) > PR2 (52 bps dsDNA) > PR1 (30 bps dsDNA) > dendrimer compacted PRs.

In the next step, we determined the extension probability distribution P(x) for the individual PRs from the S(t) trajectories and constructed the potentials φ(x) for PR1 −3 using the logarithmic expression of Eq. 2:

$$\phi (x)/kT=-\text{ln}(P(x))+C$$ (Eq.5)

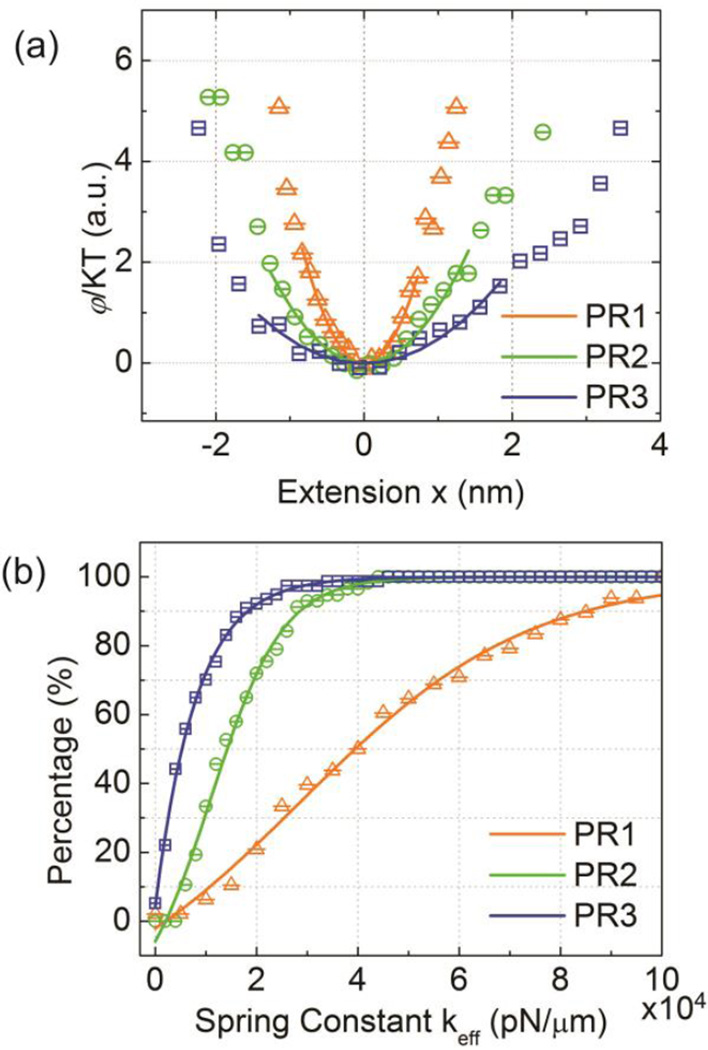
The potential φ and the extension x are averages over the acquisition time, and C is an unknown constant. Since our primary goal is a comparative analysis of the PR tether stiffness, which depends on the derivative of the potential, C was adjusted to yield φ(x=0) = 0. Figure 5a plots the resulting φ(x) for representative examples of PR1–3.

Figure 5.

(a) Representative PR potentials (φ/kT) for PR1-3. (b) Cumulative distribution function of the fitted k_eff values obtained close to the respective equilibrium separation S̄₀.

For |x| < 2 nm the potentials of PR1–3 are all well described by parabolic fits, indicating that the three membrane-confined PRs behave as entropic springs for small displacements from the equilibrium position with elasticities characterized by Hookean spring constants. Consistent with the trends observed for the σ²(R) values, the width of the potential increases in the sequence PR3 > PR2 > PR1. Especially the difference between PR2 and PR3 is important for the validation of our approach. As PR2 and PR3 have similar S̄₀ values, we can exclude in this case a systematic error in the shape of the constructed potentials due to differences in the slope of the R(S) calibration curve (Figure 2b). The detection of significant differences in the potentials of these two PRs further confirms that the performed optical fluctuation analysis probes the mechanical properties of the PR tether. Interestingly, many of the investigated PR3, including the one shown in Figure 5a, show some asymmetric broadening in φ(x) for large extensions. This behavior can be rationalized in terms of the different forces that determine the PR potential in the limit of large positive and negative x. At very short interparticle separations (i.e. large negative x values) the potential in PR3 is dominated by the repulsive interactions between the NPs. These interactions are primarily determined by the polymer brushes grafted on the NPs, which are essentially identical for all investigated PRs, and that constrain the minimum interparticle separation. In contrast, for large positive extensions φ(x) is determined by the PR tethers. Since the S̄₀ values for PR1 and PR2 are close to the contour length of the respective dsDNA molecules a further extension is associated with a significant energetic cost. The central ssDNA segment in PR3 has a shorter persistence length (1.5 vs. 53 nm)^54,55 than dsDNA and provides the tether with some additional “slack” that allows PR3 to explore longer interparticle separations. Even in the case of PR3 the asymmetric behavior becomes prominent only at relatively high energies, underlining that overall the PR behavior will be dominated by the Hookean response.

For a systematic comparison of the relative stiffness of all investigated PRs we performed parabolic fits around the potential minima. From the fitted spring constants k_fit we determined the effective tether constants k_eff by correcting for the residual signal fluctuations from instrumental and detection noise obtained from 80 nm NP controls of equal intensity as k_control:

$$\frac{1}{k_{\mathit{\text{eff}}}}=\frac{1}{k_{\mathit{\text{fit}}}}-\frac{1}{k_{\mathit{\text{control}}}}$$ (Eq.6)

The average $k_{\mathit{\text{eff}}}(\overline{k_{\mathit{\text{eff}}}})$ values are 39500 pN/µm (PR1), 14300 pN/µm (PR2), and 5400 pN/µm (PR3) and the corresponding stretch moduli $\gamma (=\overline{k_{\mathit{\text{eff}}}}\times L)$ are 423 pN, 222 pN, 84 pN, respectively. The determined γ values are much smaller than the stretch modulus of dsDNA of γ_long = 1000–1500 pN^55–59 determined in tweezer pulling experiments with long (thousands of bps) dsDNA molecules. We do point out that several experimental^60–62 and theoretical studies^63,64 have reported that short (sub-persistence length) dsDNAs can be significantly softer (≈ one order of magnitude) in the absence of applied forces. While this effect might be of relevance in our measurements as well, more importantly, our optical fluctuation analysis of the PRs does not distinguish between different sources of conformational fluctuations, including tether stretching and bending as well as rolling of the alkyl-chain tethered NPs,⁶⁵ to σ²(S). We attribute the lower γ values to the presence of multiple sources of S fluctuations in our experiment. The resulting gain in S fluctuations decreases the experimentally observed apparent force constant k_eff.

Despite these limitations in the current implementation of the plasmonic force sensor, the ability to probe the structural dynamics of individual PRs remains valuable for detecting relative differences in the mechanical PR tether response. Our measurements confirm that PRs with dsDNAs (PR1–2) have higher tether stiffnesses than PR3 with a dsDNA-ssDNA hybrid tether. Furthermore, optical fluctuation analysis makes it possible to assess the effect of increasing nanoconfinement (i.e. decreasing S) on the structural dynamics of PRs containing tethers with similar stiffnesses. The measured increase in γ by a factor of approximately 2 when the 52 bps dsDNA in PR2 is replaced with a 30 bps dsDNA in PR1 indicates decreased interparticle fluctuations due to a reduction in DNA bending (and possibly NP rolling) as consequence of the increased steric hindrance of these motions in PRs that contain the NPs in closer vicinity. The gradual increase in γ between PR2 and PR1, both of which are significantly smaller than γ_long, is consistent with the S̄₀ value for PR1 that is slightly longer than expected based on the zero force WLC prediction.

In conclusion, due to the unique photophysical stability and the relative small size of the NP probes, the outlined PR approach complements existing force measurement techniques, such as optical⁶⁶/magnetic tweezers⁶⁷, FRET based sensors⁶⁸ or evanescent field scattering³⁷ approaches. In particular, the NPs of the PR assay are considerably smaller than the micron-sized polystyrene or magnetic beads used in conventional optical/magnetic tweezers and evanescent field scattering methods and, unlike conventional fluorescence based approaches, PRs are not negatively affected by blinking or bleaching. In this proof-of-principle study we have demonstrated that ratiometric imaging of membrane confined PRs can provide detailed insight into the average interparticle separation as well as the continuous interparticle fluctuations of PRs at the single dimer level. Using an experimentally validated R(S) relationship, we obtained average interparticle separations of 10.7 nm (30 bps dsDNA; PR1), 15.5 nm (52 bps dsDNA; PR2), and 15.5 nm (two 20 bps dsDNA segments connected by a 40 nucleotide ssDNA; PR3). All PRs were found to exhibit significant higher variances in their spectral fluctuations than individual NPs of identical intensity, confirming that thermal conformational fluctuations in the PRs are detectable and quantifiable by optical means. PRs with different tether stiffness (ssDNA vs. dsDNA) were successfully distinguished. For PRs containing dsDNA tethers of different lengths (PR1 and PR2), optical fluctuation analysis was demonstrated to provide further insight into the impact of increasing confinement on the conformational flexibility of the dsDNA in the PR gap. Nanoconfinement is ubiquitous in biology⁶⁹ and nanotechnology⁴⁰ and the PR assay developed in this manuscript provides a very useful tool to improve our understanding of how the confinement of a polymer into a nanoscale volume impacts its chemical and mechanical properties.