Significance
It is well understood that parasitism may help to explain the evolution of mating strategies, but host behavior is, in turn, critical to the transmission and therefore the evolution of parasites. Despite this clear reciprocity, we lack a coevolutionary theory of mate choice and parasite virulence. We show how coevolution leads to a wide range of dynamics, including cycling and stable strategies, and that this resolves a key criticism of the role of parasites in mate choice: that parasites will evolve to be avirulent, thus reducing their impact on mating strategies. Coevolution also leads to new predictions for the role of several host and parasite traits on selection for mate choice that will guide future experimental and comparative work.
Keywords: host–parasite coevolution, mate choice, virulence, transmission avoidance, sexually transmitted infection
Abstract
Parasites are thought to play an important role in sexual selection and the evolution of mating strategies, which in turn are likely to be critical to the transmission and therefore the evolution of parasites. Despite this clear interdependence we have little understanding of parasite-mediated sexual selection in the context of reciprocal parasite evolution. Here we develop a general coevolutionary model between host mate preference and the virulence of a sexually transmitted parasite. We show when the characteristics of both the host and parasite lead to coevolutionarily stable strategies or runaway selection, and when coevolutionary cycling between high and low levels of host mate choosiness and virulence is possible. A prominent argument against parasites being involved in sexual selection is that they should evolve to become less virulent when transmission depends on host mating success. The present study, however, demonstrates that coevolution can maintain stable host mate choosiness and parasite virulence or indeed coevolutionary cycling of both traits. We predict that choosiness should vary inversely with parasite virulence and that both relatively long and short life spans select against choosy behavior in the host. The model also reveals that hosts can evolve different behavioral responses from the same initial conditions, which highlights difficulties in using comparative analysis to detect parasite-mediated sexual selection. Taken as a whole, our results emphasize the importance of viewing parasite-mediated sexual selection in the context of coevolution.
Since Hamilton and Zuk (1) first proposed that parasitism may explain the existence of secondary sex traits such as the peacock’s tail, there has been considerable interest in the role that parasites play in sexual selection and the evolution of mating strategies (2–19). A prominent theory, known as the transmission-avoidance hypothesis, posits that secondary sex traits, and more generally, mating strategies, have evolved to limit the risk of contracting an infection (10). Although this theory emphasizes the importance of parasites in determining mating strategies, it is clear that different mating strategies will have an impact on infectious disease transmission and therefore influence parasite evolution. However, despite this clear interdependence we lack a coevolutionary theory of mating strategies that captures reciprocal adaptations by both species.
Sex can leave individuals at risk of infection due to sustained close contact with sexual partners or through the transfer of genetic material (20). Hence, sexually transmitted infections, which are common in both plants (21) and animals (22), are likely to be a key factor in the evolution of mating strategies. Furthermore, sexually transmitted infections typically exhibit different epidemiological dynamics (17, 23) and disease outcomes (e.g., sterility rather than mortality; ref. 22) to other infectious diseases. In an important paper, Knell (11) suggested that sexually transmitted infections will evolve to become less harmful to hosts that experience selection for disease-avoidance traits, which in turn will reduce sexual selection in the host. Because this has been overlooked in studies that only consider host evolution (1, 10, 14, 15, 24), it would appear that the potential importance of parasite-mediated sexual selection may have been overstated. Although Knell recognized the importance of feedback for selection in the host, it is hard to intuit the consequences of the full coevolutionary interaction (i.e., feedback in both directions). If, for example, disease-avoidance behavior leads to the evolution of less harmful parasites that subsequently weaken the need for choosiness, will the system remain in a stable state, or will selection favor more harmful parasites? Here, we theoretically explore the full dynamical coevolution of mate choice and parasite virulence. We show that coevolution can lead to fluctuating selection (cycling) and stable strategies at intermediate levels of mate choice and virulence, and therefore prevent the loss of parasite-mediated sexual selection. Furthermore, we show how optimal virulence and choosiness is critically dependent on a range of other host and parasite traits.
Modeling
We model the spread of a sexually transmitted parasite in a serially monogamous population, where disease causes a reduction in host reproductive success but does not increase mortality (we refer to the reduction in host reproductive success as “virulence”) (Methods). We assume that hosts are able to detect the health of prospective partners and preferentially choose mates that show fewer signs of disease. This is reasonable given that parasites can reduce mating success and can be detected directly (e.g., ectoparasites) or indirectly (e.g., visible lesions) (1, 2, 9, 25), and that precopulatory displays sometimes involve exposure of cloaca or genitalia, which may reveal signs of disease (7). There is also a precedent for individuals to prefer healthy social contacts, relying on visual, behavioral, or olfactory cues to determine the condition of other individuals (26–28). We explore a variety of functional forms that are involved in mate choice (Supporting Information), but here we focus on a power law relationship (Eq. 1). We assume that there is a positive relationship between the transmission rate of the parasite and the extent of damage caused to the host, resulting in a loss of fecundity for infected individuals. Such relationships are typically used to study the evolution of virulence in lethal infections (29–31), and are supported by strong evidence from a number of systems (32, 33). Few studies have directly looked for transmission-virulence relationships among parasites that reduce host fecundity rather than increase mortality, although Ebert et al. (34) found a negative relationship between reproduction by a bacterial parasite (Pasteuria ramosa) and the fecundity of its host (Daphnia magna).
Disease-associated reductions in fecundity may be interpreted as direct harm to reproductive tissues, as in the case of Chlamydia or gonorrhea infections that cause pelvic inflammatory disease, or a general reduction in parental health that lowers the number of surviving offspring (e.g., smaller clutch size or reduced investment per offspring). The fecundity of infected individuals is given by , where mediates the strength of the relationship with parasite transmissibility () (the fecundity of uninfected hosts is 1). We use a decelerating trade-off between the transmission rate and virulence because fecundity cannot decrease below zero. However, the results are consistent for an accelerating trade-off (Supporting Information). For the sake of simplicity, we assume that mate choice is based on the perceived fecundity of prospective partners and is not dependent on the condition of the focal individual. The rate at which sexual partnerships form (Eq. 1) decreases with a stronger preference for healthy mates (), higher disease incidence (if hosts exhibit mate choice), virulence (smaller ), and costs of being choosy (). The parameter represents a general reduction in pair formation due to choosy behavior. Hence, a preference for healthy mates reduces the probability of pairing with individuals carrying virulent disease, but will also reduce the overall rate at which pairs are formed. We assume that mutual mate choice occurs, which allows us to model hosts as nonselfing simultaneous hermaphrodites, but this assumption is relaxed in the Supporting Information.
Results
Epidemiology.
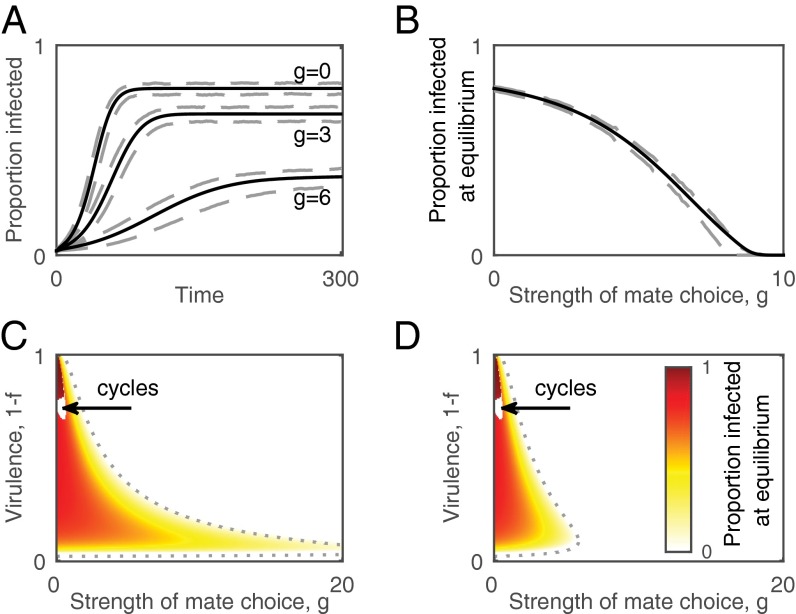
Hosts that express a preference for healthy mates can have a large impact on the basic reproductive number, (i.e., the expected number of secondary infections caused by a single infectious individual in an otherwise susceptible population), of a sexually transmitted parasite, reducing both the rate at which new infectious cases occur and the equilibrium prevalence of disease (Fig. 1; Supporting Information). A nonlinear relationship exists between the preference for healthy mates, the transmission rate, and (Eq. S7), which means that relatively small changes in host behavior or parasite life-history traits can lead to drastic changes in disease incidence. Costs of being choosy also constrain , as they reduce the average pairing rate. The parasite usually remains endemic at a unique (locally asymptotically) stable equilibrium or goes extinct, but the system can exhibit persistent epidemiological cycling (stable limit cycles) when virulence is moderately high and the strength of mate choice is low (Fig. 1 and Fig. S1).
Fig. 1.
Epidemiological dynamics and equilibrium prevalence of infection in the deterministic and stochastic models. (A and B) Mate choice reduces both the rate at which disease spreads and the equilibrium prevalence of infection. (A) Time series showing the proportion of the host population infected during the course of an epidemic for different levels of mate choice, g. (B) The proportion of the population infected at the unique (locally asymptotically) stable endemic equilibrium as a function of choosiness. Solid lines show the output from the deterministic model and dashed lines show 1 SD either side of the mean from 500 simulations of the individual-based model. (C and D) Intermediate levels of virulence and low levels of mate choice maximize disease prevalence. (C) No costs of mate choice (c = 0). (D) Low costs of mate choice (c = 0.1). Dotted curves show the epidemic threshold, R0 = 1. Arrows point to regions with epidemiological cycles (Fig. S1). Fixed parameters: β = 1, εH = εP = 0, η = 0.25, d = 0.2, h = 0.002, m = 0.05, P = 1, r = 1.
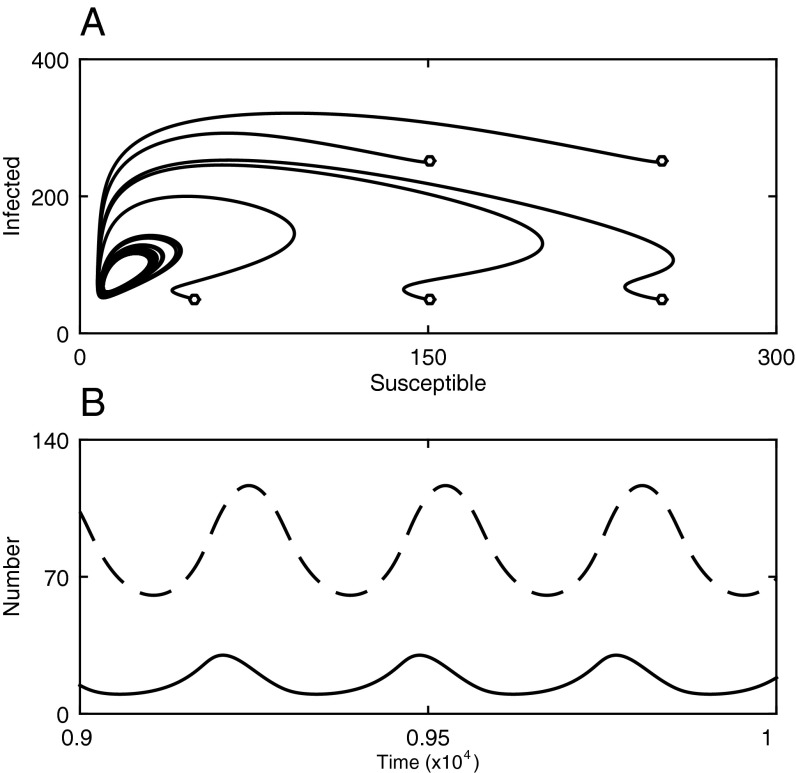
Fig. S1.
Epidemiological cycling is possible when virulence (1 − f) is moderately high and the strength of host mate choosiness (g) is low. (A) Epidemiological cycling is characterized by stable limit cycles (markers show trajectories from different initial conditions). (B) A typical limit cycle showing fluctuations in the number of individuals that are susceptible (solid) and infected (dashed). Fixed parameters as in Fig. 1, with: c = 0.1, g = 0.25, β = 5.
Evolution of Virulence.
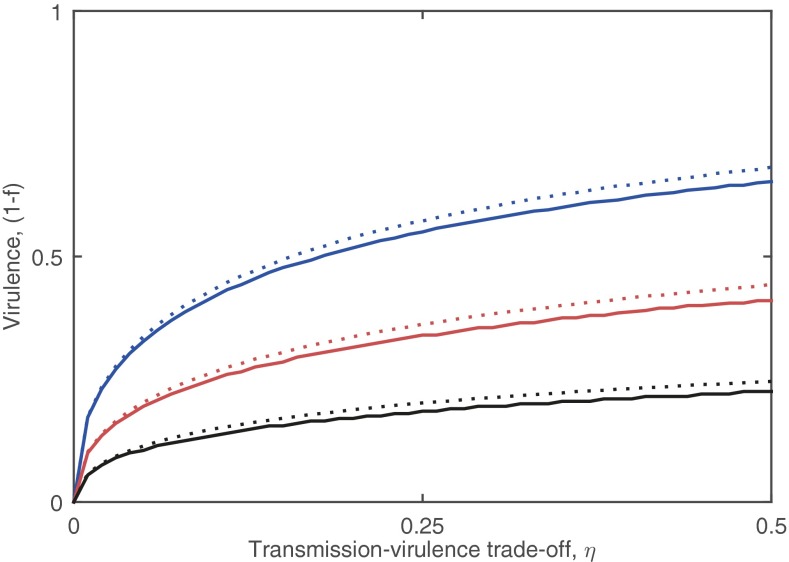
The full evolutionary simulations show that provides a qualitative prediction for the evolution of virulence (Fig. S2). is constrained by mate choice such that high and low levels of virulence both cause parasite extinction (; Fig. 2A). Hence, an intermediate level of virulence must be optimal in the presence of mate choice , as extreme virulence is unsustainable. This pattern holds for more general relationships between transmission, virulence, and mate choice, provided: (i) the parasite tends toward full castration as ; and (ii) the rate of pair formation decreases with stronger mate choice and virulence. We tested this prediction using adaptive dynamics (ecoevolutionary game theory) (35) and stochastic simulations of an individual-based model (IBM) (Methods). We found that the evolution of virulence is indeed constrained by mate choice so that parasites evolve to be neither too harmful nor benign (Fig. 2B) and that the expression for provides a reasonably good approximation for the evolutionarily stable level of virulence (Fig. S2).
Fig. S2.
The evolutionary stable level of virulence obtained using adaptive dynamics (solid curves) and R0 maximization (dotted). R0 slightly overestimates the evolutionarily stable level of virulence (as it lacks population structuring), but provides a good approximation for the adaptive dynamics result. Colors correspond to different values of the mate choice parameter, g: g = 1/3 (blue); g = 1 (red); and g = 3 (black). Fixed parameters as in Fig. 2.
Fig. 2.
Evolution of virulence when hosts are choosy. (A) Mate choice constrains R0, such that both high and low levels of virulence lead to parasite extinction (R0 < 1; horizontal gray line). Curves show R0 for different values of the mate choice parameter, g: g = 1/3 (solid); g = 1 (dashed); and g = 3 (dotted). (B) Optimal level of virulence (1 − f) from the adaptive dynamics approach (dotted curves) compared with simulation data from the individual-based model [mean ±1 SD; g = 1/3 (black), g = 1 (gray), and g = 3 (white)]. The evolved level of virulence increases at a decelerating rate as the trade-off with transmission increases (greater η), but stricter mate choice (greater g) reduces optimal virulence. Fixed parameters as in Fig. 1, with εP = 0.1 and c = 0.
Coevolution.
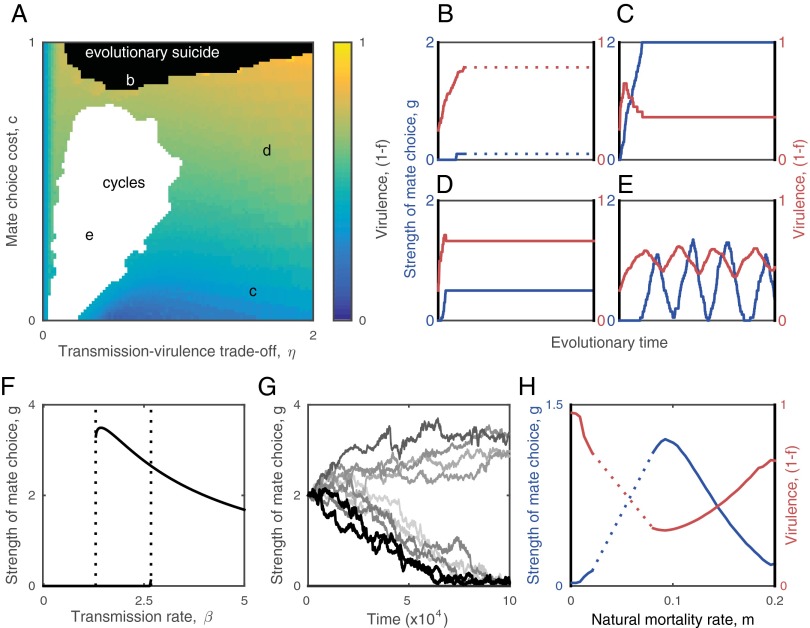
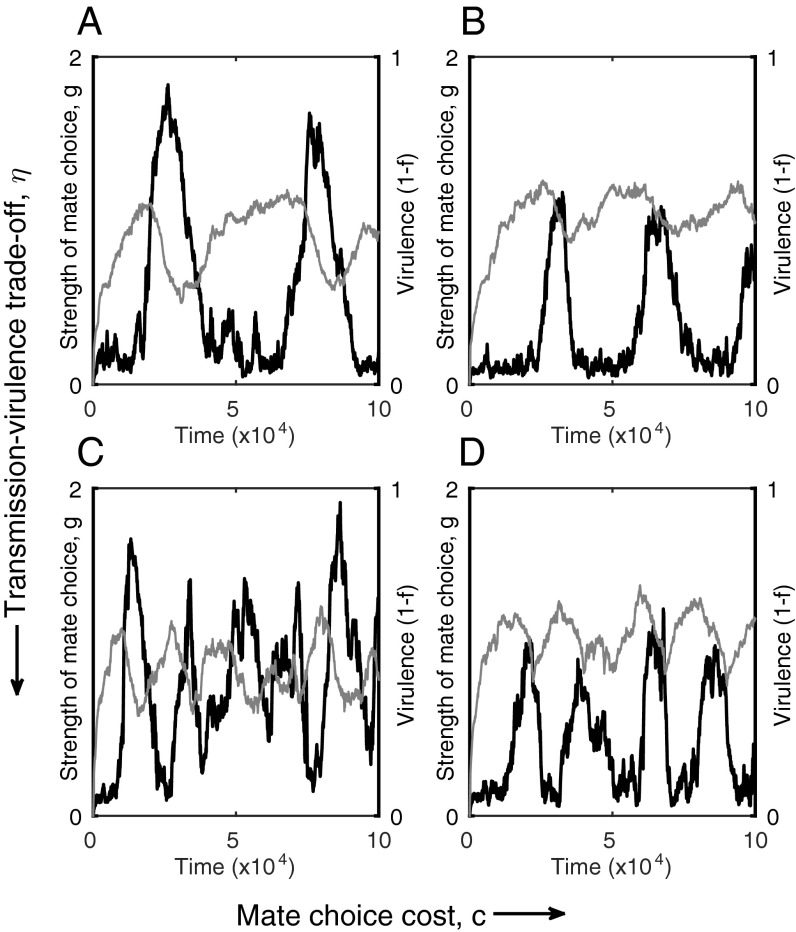
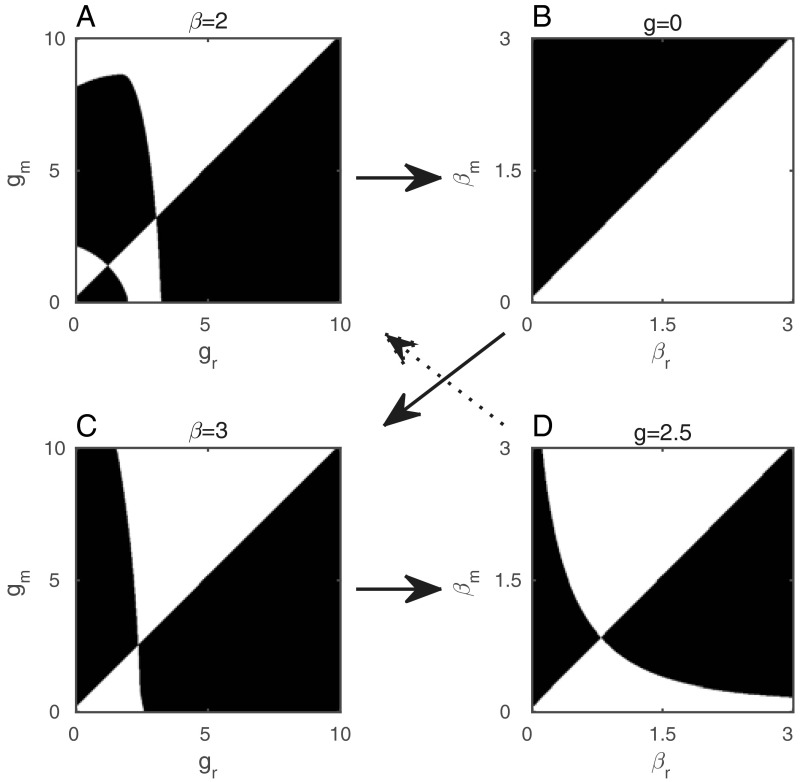
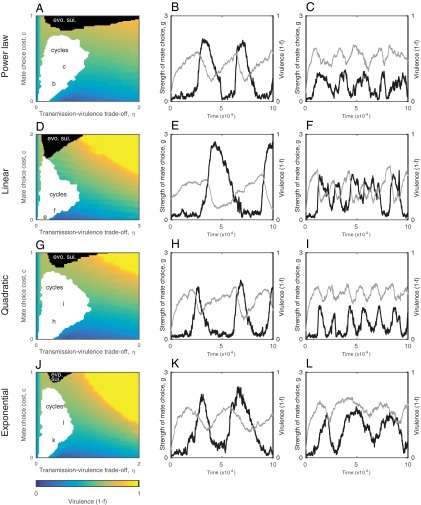
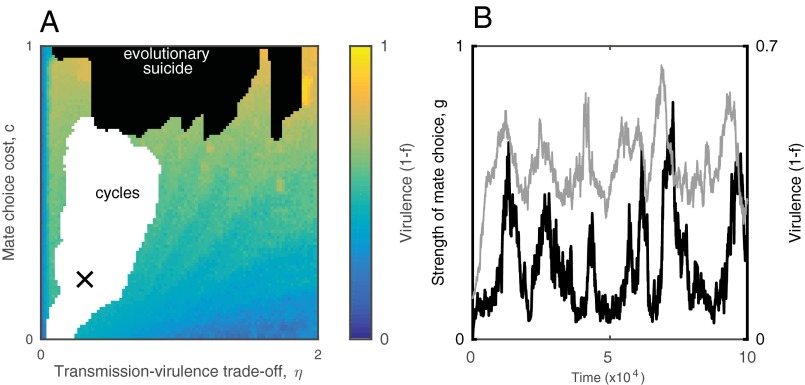
Thus far, the analysis has focused on how fixed levels of mate choice affect the epidemiological and evolutionary dynamics of the parasite. However, mating behavior should evolve in response to changes in disease prevalence and virulence. Hereafter, the strength of mate choice is assumed to be a heritable trait that coevolves with the transmission rate and hence virulence . Overall, coevolution leads to an inverse relationship between choosy behavior and virulence (Figs. 3 and 4). This is because high levels of choosiness select against virulence, whereas more transmissible and more virulent parasites perform best when hosts are less choosy. Three qualitatively different coevolutionary outcomes are possible: (i) runaway selection for virulence when being choosy is too costly to be a viable option for hosts (high ), which can drive the host (and hence the parasite) population to low levels and cause stochastic extinctions (evolutionary suicide; Fig. 3B); (ii) coevolutionarily stable strategies at intermediate levels of virulence and mate choice, when the trade-off between transmission and virulence is relatively strong compared with the cost of mate choice or vice versa (i.e., high and low , Fig. 3C; or low and moderate to high , Fig. 3D); and (iii) coevolutionary cycling for low to moderate costs of mate choice and intermediate relationships between transmission and virulence (Figs. 3E and 4). The system can also exhibit bistability, where hosts evolve either choosy or nonchoosy behavior from the same initial conditions, with the outcome determined by genetic drift during the early stages of coevolution that is reinforced by positive frequency-dependent selection (Fig. 3 F and G).
Fig. 3.
Coevolutionary dynamics of host mate choosiness and parasite virulence. (A) The evolved level of virulence increases as mate choice becomes more costly (as c increases), but it may cycle with host mate choosiness (white region). Coevolutionary trajectories for the strength of mate choice (g; blue) and virulence (1 − f; red) at points b–e are shown in the corresponding subplots. (B) Runaway selection for virulence leading to evolutionary suicide (as indicated by the dotted line). (C and D) Mate choice evolves to restrict virulence. (E) Coevolutionary cycling. (F) Bifurcation diagram showing the optimal strength of mate choice for fixed values of the transmission rate, β. Intermediate transmission rates can lead to bistablility. (G) Different coevolutionary outcomes arising from the bistability shown in F. Each trajectory corresponds to a single simulation of the IBM, seeded with the same initial conditions. The effects of the bistability are clearest when the transmission rate is allowed to coevolve with mate choice, but is constrained to a finite range (here: 1.5 ≤ β ≤ 2.5). Such constraints are likely to exist in real populations due to restrictions in both hosts (e.g., limits on sexual contact rates) and parasites (e.g., infectious dose). (H) Mate choice is maximized (and virulence minimized) for intermediate natural mortality rates, m. The dotted region indicates cycling and solid lines correspond to coevolutionarily stable strategies. All panels except G were generated by adaptive dynamics. Fixed parameters as in Fig. 1, with c = 0.1 and εH = εP = 0.01.
Fig. 4.
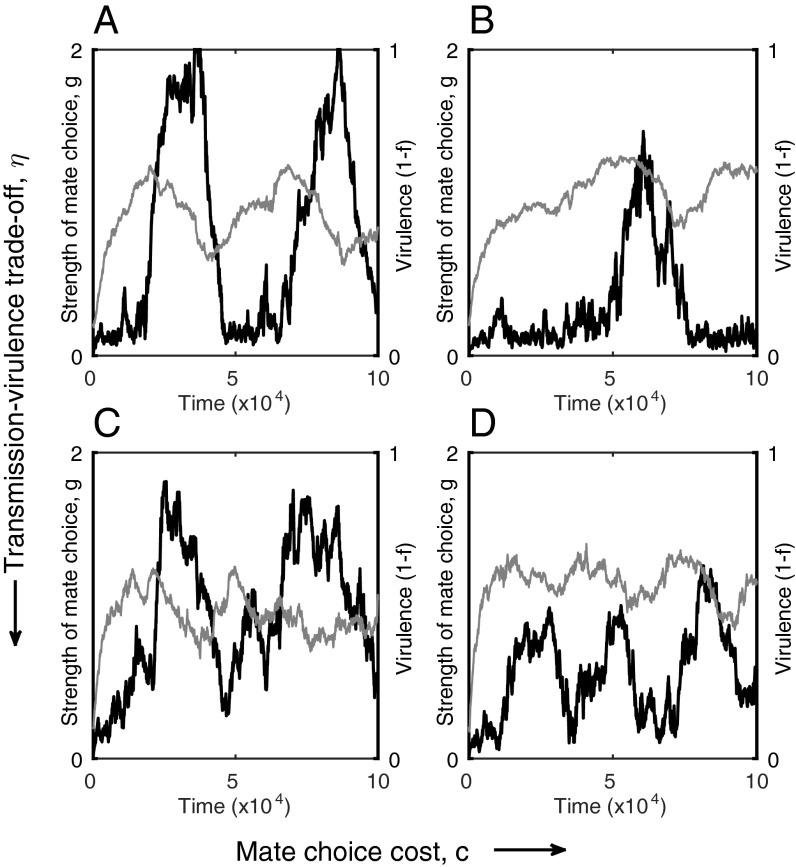
Coevolutionary cycling in the individual-based model. (A and B) Small values of η produce lower frequency oscillations, which are characterized by short intervals of strong mate choice (black) and low virulence (gray), interspersed with long intervals of weak mate choice and higher virulence (virulence increases slowly due to a weak relationship with transmission. (C and D) Larger values of η produce higher frequency oscillations (virulence changes rapidly due to the strong relationship with transmission). Oscillations tend to have large amplitude when mate choice is not too costly (low c; A and C), but their magnitude decreases with higher costs (high c; B and D). Fixed parameters as in Fig. 1, with εH = εP = 0.02, (A) η = 0.3, c = 0.2; (B) η = 0.3, c = 0.4; (C) η = 0.5, c = 0.2; (D) η = 0.5, c = 0.4.
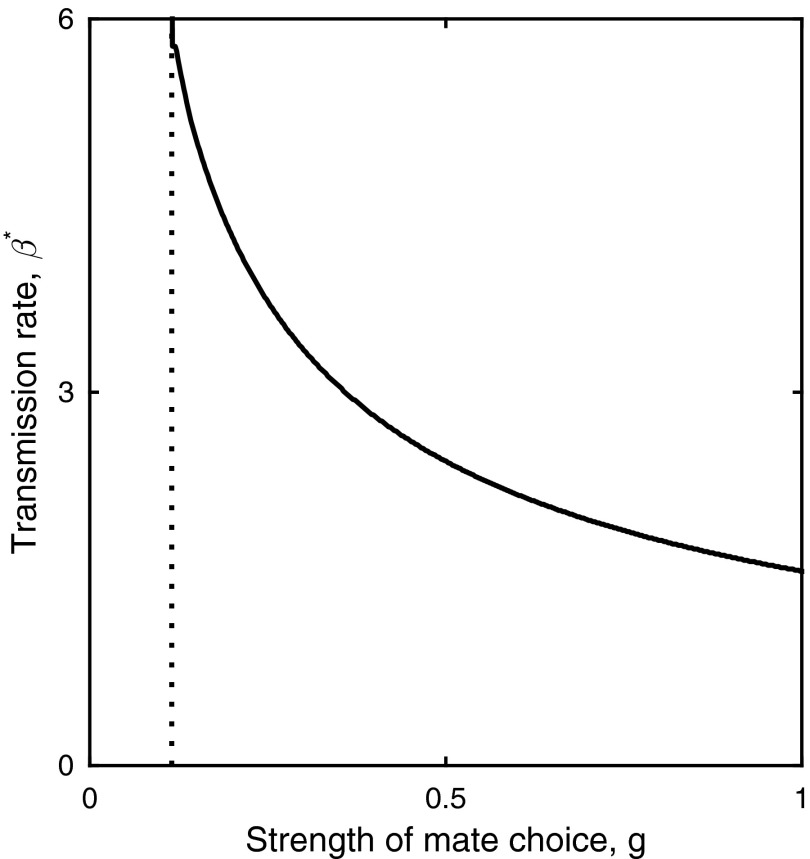
Coevolutionary cycling occurs due to a delay in selection for greater choosiness following an increase in virulence (Fig. 3E). Changes in transmissibility (hence virulence) produce two bifurcations (Fig. 3F) that cause the host population to switch back and forth between more and less choosy behavior as the parasite coevolves. A lack of mate choice selects for a higher transmission rate (and hence virulence) in the parasite (Figs. S3 and S4), which eventually crosses a threshold where choosy behavior becomes optimal. The subsequent increase in choosy behavior selects against virulence, which crosses another threshold and leads to selection against choosy behavior, allowing the cycle to repeat (Fig. S3). Simulations of the stochastic IBM reveal that coevolutionary cycling is a common outcome and is not caused by assumptions inherent to the analytical method (e.g., separation of time scales and weak selection; Fig. 4). Further, simulations suggest that the frequency of coevolutionary cycles tends to increase with the strength of the transmission–virulence trade-off and that the amplitude of the oscillations tends to decrease with greater costs of mate choice (Fig. 4).
Fig. S3.
Pairwise invasion plots (PIPs) for (A and C) hosts and (B and D) parasites, showing how the coevolutionary dynamics in Fig. 3 B–E arise. Shaded regions indicate where mutants can invade. Arrows show how coevolutionary dynamics can unfold. For example, an initial lack of mate choice (A) selects for a higher transmission rate (and hence virulence) in the parasite (B). Eventually this may cross a threshold so that choosy behavior becomes optimal (C) (if not, then virulence continues to increase, potentially leading to evolutionary suicide, as in Fig. 3B). The subsequent increase in choosy behavior selects against virulence, lowering the transmission rate (D). The system may then tend toward a stable pair of strategies in each population (similar to C and D here, corresponding to the dynamics in Fig. 3 C and D), or the reduction in virulence can select against choosiness (A), leading to coevolutionary cycling (dotted arrow, as in Fig. 3E). Fixed parameters as in Fig. 1, with c = 0.1.
Fig. S4.
Optimal values for the transmission rate, β, decrease as the strength of mate choice, g, increases. Runaway selection for β (and hence virulence) occurs to the left of the dotted line. Fixed parameters as in Fig. 3F.
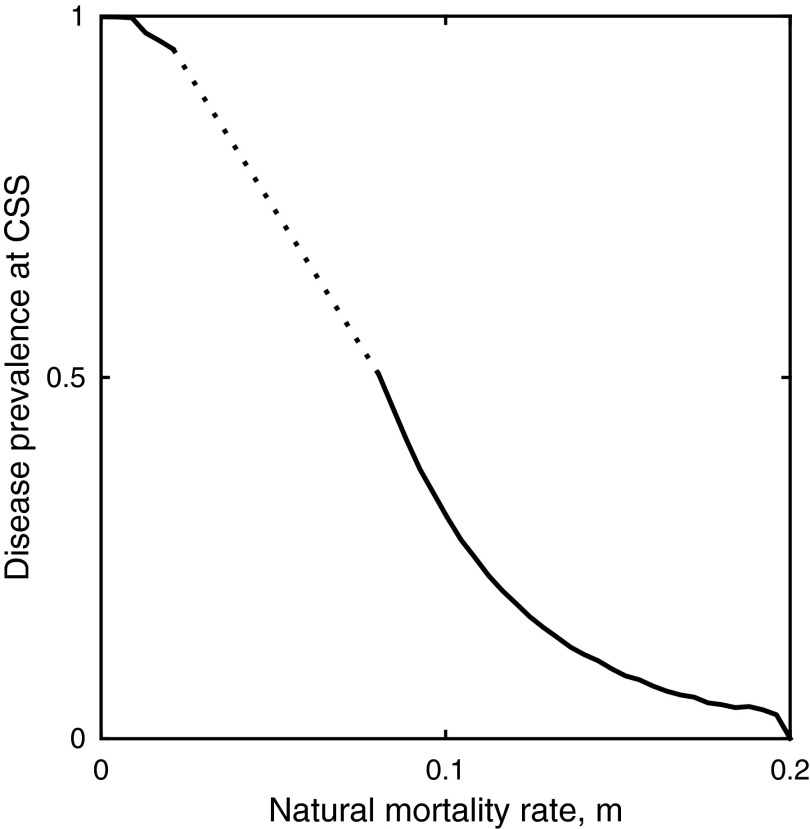
The coevolutionary outcome is dependent on the life span of the host; cycling occurs for a fairly broad range of parameters, but not when hosts are short lived or have very low natural mortality rates (i.e., large or very small ; Fig. 3H). Hosts with intermediate life spans evolve the highest levels of mate choice and the parasite evolves to be avirulent; whereas short- and long-lived hosts evolve low levels of mate choice and have a more virulent parasite. The peak at intermediate life expectancies is attributable to changes in the prevalence of disease, which increases with host longevity (Fig. S5). Disease is relatively rare when hosts are short lived, so the costs of mate choice are likely to outweigh the benefits of avoiding disease because most prospective mates are uninfected. Disease is common when hosts are long lived, so choosy individuals have difficulty finding suitable mates and therefore produce very few offspring; hence, choosiness is too costly when disease prevalence is high. For hosts with intermediate life spans, the risk of infection is sufficiently high as to make choosiness advantageous for avoiding disease, but is not so high as to drastically reduce the availability of suitable mates.
Fig. S5.
Disease prevalence at the continuously stable strategies (CSS) in Fig. 3H decreases with the natural mortality rate, m (i.e., as the host life span decreases). The dotted region indicates coevolutionary cycling. Fixed parameters as in Fig. 3.
Discussion
Although a large number of studies have explored the effects of sexual contact patterns on epidemiology or parasite evolution, or the consequences of parasite-mediated sexual selection for the evolution of mate choice (2–19), to our knowledge this is the first examination of both host mating behavior and parasite virulence in a coevolutionary context. Ecological feedbacks are crucial in shaping selection in both hosts and parasites (36–41). Host defenses often reduce disease incidence at the population level, which decreases selection for defense mechanisms and increases selection for counter adaptations in the parasite. Knell (11) argued that ecological feedbacks would therefore select against disease-avoidance traits and that previous models may have overstated the importance of parasitism in sexual selection. However, our full coevolutionary model shows that this lack of disease-avoidance behavior can select for more harmful parasites, which modulate host evolution, leading to continual feedback in both directions. Thus, viewing host–parasite relationships in a coevolutionary context can prevent the predicted loss of disease-avoidance traits, providing support for parasite-mediated sexual selection.
We have shown that coevolution can lead to stable levels of mate choice and virulence, cycling, runaway selection for virulence and evolutionary suicide. Sustained cycling has not previously been observed in the context of mate choice and parasites, although Graves and Duvall (42) conjectured that ecological feedbacks could produce these dynamics. Our key insight is that coevolution and ecological dynamics can generate sustained cycles in host choosiness and parasite virulence. Coevolutionary cycling is more likely to occur when hosts have intermediate life spans, choosiness carries a small to moderate cost and transmissibility has moderate effects on virulence (i.e., low ; Fig. 3 A and H). Stable strategies are common for short- or very long-lived hosts and for either very weak or strong relationships between transmissibility and virulence. High costs of choosiness can produce stable strategies, but excessive costs can cause runaway selection for virulence, and even evolutionary suicide when high virulence drastically reduces the number of hosts (called “demographically stochastic evolutionary suicide” in ref. 43). Alternatively, hosts may evolve to be either nonchoosy or very choosy from the same starting conditions (bistability), which generally occurs for intermediate transmission rates and moderate levels of virulence (Fig. 3F). Drift initially causes the population to move toward one of two locally stable attractors, which is then reinforced by positive frequency-dependent selection. Bistability has important consequences for identifying the role of parasitism in mating behavior, as separate populations could evolve markedly different levels of mate choice even though they are both challenged by similar parasites.
Our model makes two important predictions at the interspecific level, which could be tested by comparative studies and meta-analyses. First, transmission-avoidance traits should vary inversely with virulence. This may seem counterintuitive, as from an individual perspective disease-avoidance traits are most beneficial when prospective partners harbor virulent parasites. However, if the costs of choosiness are relatively high, then hosts may evolve to be less prudent, which benefits more virulent parasites. Conversely, if choosiness is not very costly, then hosts may evolve to have a strong preference for healthy mates, selecting against virulence. This relationship can clearly lead to cycling, but the model demonstrates that different costs and trade-offs can also produce stable strategies that are inversely related. Second, hosts with intermediate life spans are more likely to exhibit transmission-avoidance behavior than short- and long-lived hosts. Intuitively we can understand this result from the ecological feedbacks in the full coevolutionary system. The disease is chronic, so prevalence increases with host life span (Fig. S5). For short-lived hosts, disease prevalence is relatively low and the costs of choosiness are effectively high, so transmission-avoidance behavior is not advantageous. For long-lived hosts, there is little chance of avoiding disease, as prevalence is relatively high; thus, choosiness is not beneficial. Hosts with intermediate life spans, however, have moderate levels of disease, so the ability to discriminate between infected and noninfected individuals is advantageous. This pattern is reminiscent of other biological phenomena that are predicted to peak at intermediate levels of disease, including investment in immune responses (44), sociality (45), sexual reproduction (41), and serial monogamy (19). Life span has previously been shown to be important in the evolution of defenses against parasitism, but existing theory has tended to focus on immune responses rather than behavioral defenses (46).
Hamilton and Zuk’s (1) suggestion that secondary sex traits have evolved to signal genetic quality in the form of resistance to parasitism differs from the transmission-avoidance hypothesis, which states that secondary sex traits, and more generally, mating strategies, have evolved to limit exposure to disease. However, because resistant individuals are more likely to be free from infection, they will tend to experience greater mating success in both scenarios, so the theories are not mutually exclusive. Crucially, Hamilton and Zuk (1) recognized that coevolutionary cycling would prevent the loss of heritable variation in fitness that plagues other good genes theories (the “lek paradox”), as hosts would need to continually adapt to an ever-changing parasite. However, despite the importance of coevolution being highlighted in their seminal paper, it has received little attention in theoretical studies on parasite-mediated sexual selection, especially in the context of the transmission-avoidance hypothesis. The transmission-avoidance hypothesis does not require secondary sex traits for parasites to influence the evolution of mating strategies. Hence, for the sake of simplicity, the model presented herein assumes that host health is detectable in the absence of these showy traits (e.g., by genital inspection) and does not make any explicit predictions about their evolution. More generally, however, if host health is difficult to judge then it is possible that showy traits would increase the effectiveness of transmission-avoidance behavior, which may be a means of detecting less obvious infections.
Our model makes several simplifying assumptions, the implications of which warrant testing in future work. For example, the use of continuous mate choice functions means that individuals can distinguish infinitesimal differences between parasite phenotypes and respond accordingly (mistake-free). We have also assumed that sexual contacts do not occur outside of partnerships, an individual’s choosiness is independent of their current condition and all pairs end at the same rate (divorce does not depend on condition, and disease affects fecundity, rather than mortality). A simple extension to the model would be to allow pairs with lower fecundity to divorce at a higher rate, or for choosiness to vary depending on an individual’s infection status. We have focused on sterilizing sexually transmitted parasites as they are inherently linked to host mating success, but other parasites and disease outcomes are also likely to influence mating strategies. Disease-associated mortality would, however, alter the nature of ecological feedbacks on disease prevalence by reducing the longevity of infection (and hence increasing the rate at which partnerships end), and alternative modes of transmission would reduce the overall benefits of mate choice. These factors may therefore select for lower choosiness, which could limit the potential for coevolutionary cycling.
Although parasite-mediated sexual selection has been the primary focus of the present study, our results have general implications for understanding the evolution of sterilizing infections, which are predicted to fully castrate their hosts in the absence of vertical transmission, host tolerance, or limited dispersal (37, 47, 48). We have shown that host behavioral adaptations to avoid transmission are also a viable means of constraining virulence in sterilizing infections.
Our work supports a growing body of theory that parasites play a key role in shaping the evolution of mating strategies (12, 14, 15, 17, 19, 24), but empirical evidence for parasite-mediated sexual selection is mixed. Host behavior consistent with the transmission-avoidance hypothesis has been identified among birds (2–4), rodents (49, 50), fish (51), fruit flies (52), and humans (53), yet no evidence has been found in studies of beetles (13, 16) and nonhuman primates (54). It has been suggested that inspection (and pecking) of the female cloaca by male birds could be an attempt to detect parasites (7, 10), although this may simply be a means of stimulating the female to eject sperm from previous males (55). Identifying the means by which hosts detect infected individuals is especially difficult in the absence of visual cues (e.g., in asymptomatic infections). Behavioral cues are likely to be important indicators of host condition, and some evidence points toward olfactory mechanisms as a means of detecting disease (50, 53). Many parasites are capable of remaining asymptomatic for long periods of time, but are still highly transmissible (e.g., Chlamydia, HIV). Our results suggest that sexually transmitted parasites have evolved to become asymptomatic due to the fact that even a very weak preference for healthy mates can greatly reduce transmission. Parasites that are primarily transmitted during mating are therefore likely to experience stronger selection to be cryptic, which may explain why asymptomatic outcomes are generally more common among sexually transmitted infections (22). For example, syphilis rapidly evolved to become milder and less conspicuous following its introduction to Europe during the fifteenth century, most likely due to transmission-avoidance behavior in the human population (56).
To conclude, our key insight is that coevolution is critical to understanding the role of parasites in sexual selection. Crucially, ecological feedbacks that are intrinsic to the host–parasite interaction prevent the loss of mate choice due to reductions in virulence, in contrast to previous predictions (11). We therefore emphasize the importance of understanding the evolution of host and parasite traits in a coevolutionary context, and suggest that parasites are fundamental to the evolution of mating strategies.
Methods
Model Description.
We model the dynamics of a chronic sexually transmitted parasite in a serially monogamous population, where hosts are hermaphroditic and exhibit mutual mate choice (parasite-avoidance behavior). Disease transmission occurs at a rate when a sexual partnership consists of an infectious and a susceptible individual (for simplicity, we assume there is no nonsexual transmission, transmission outside of partnerships or superinfection). Infection causes a permanent reduction in host fertility, , from (uninfected) to , but has no effect on mortality. The parameter modifies the strength of the relationship between the transmission rate and virulence (reduction in host reproductive success, , such that more transmissible infections are associated with greater virulence (e.g., due to the production of more transmission stages). We assume that the transmission–virulence trade-off is decelerating because fecundity cannot decrease below zero (but see Supporting Information for an accelerating trade-off). Unpaired members of the population encounter each other at random and perform a precopulatory assessment of the health (fertility) of their prospective mate (self-assessment does not occur). Encounters between unpaired members of the population occur randomly at a per-capita rate of , where is the base pair formation rate and is the number of unpaired individuals (encounters are frequency dependent, so the overall rate of pair formation is independent of ). Given that two unpaired individuals, and , encounter each other, the probability that will accept as a mate is given by , which is the product of: (i) the probability that does not reject by being overly cautious; and (ii) the probability that does not reject based on signs of disease. We set these two probabilities to be and , respectively, so that , where and are the strength of mate choice of (i.e., preference for healthy mates) and fertility of , respectively, and represents a general reduction in pair formation (a potential cost of being choosy). The functional form of is chosen so that it decreases as: (i) the fertility of prospective mates decreases (individuals become less attractive due to disease); (ii) as the strength of mate choice increases (individuals are more choosy); and (iii) as the cost of choosiness increases (choosy individuals are more cautious). However, the exact form of is not important, as our results are robust to other functional forms that satisfy these general criteria (see Supporting Information for an exploration of linear, quadratic, and exponential forms of , which produce qualitatively similar results, Figs. S6 and S7). Because mate choice is mutual, the probability that both individuals accept each other as mates is equal to the product of and . The rate at which and form a sexual partnership is therefore:
| [1] |
Fig. S6.
Coevolutionary dynamics of host mate choosiness and parasite virulence for different pairing probability functions, Pij: (A–C) power law (Eq. S13); (D–F) linear (Eq. S14); (G–I) quadratic (Eq. S15); and (J–L) exponential (Eq. S16). The dynamics are broadly similar for the different functions, as described in Fig. 3. The evolved level of virulence increases as mate choice becomes more costly (as c increases), but it may exhibit coevolutionary cycling with host mate choosiness (white region). The black region indicates evolutionary suicide, where selection for high virulence leads to host and parasite extinction when choosy behavior is too costly. Evolutionary suicide does not occur in the yellow region as the trade-off with the transmission rate is sufficiently strong to prevent host extinction. Letters in the cycling region correspond to simulations of the individual-based model in the second and third columns. Fixed parameters as in Fig. 3.
Fig. S7.
Coevolutionary dynamics of host mate choosiness and parasite virulence when there is an accelerating trade-off between the transmission rate and virulence (Eq. S17). The dynamics are qualitatively similar to those described for a decelerating trade-off (Fig. 3). (A) The evolved level of virulence increases as mate choice becomes more costly (as c increases), but it may exhibit coevolutionary cycling with host mate choosiness (white region). The black region indicates evolutionary suicide, where selection for high virulence leads to host and parasite extinction. (B) Coevolutionary cycling in the individual-based model, corresponding to the cross in A. Fixed parameters as in Fig. 3.
The rate at which individual forms a partnership with any unpaired individual is equal to . Sexual partnerships end if either individual dies (all hosts have a mortality rate of ) or decides to terminate the partnership (divorce, which occurs at a rate per pair). All partnerships therefore last an average of time units, irrespective of their composition. Individuals leaving a pair are immediately able to form new sexual partnerships. A partnership between individuals with fertilities and produces offspring at a rate of , where is the maximum birth rate, is the current population size, and is the strength of density-dependence on reproduction. Only paired individuals are able to produce offspring. We analyze the epidemiological dynamics and evolutionary stability of the system using a deterministic pair formation model (PFM), which for monomorphic populations is given by Eq. 2, where indicates the number of susceptible infectious pairs (similarly for and ) and classes without brackets represent unpaired members of the population. The total population size is therefore , where and the birth rate is .
| [2A] |
| [2B] |
| [2C] |
| [2D] |
| [2E] |
The first terms in Eq. 2A and 2B represent individuals that have just become unpaired (due to divorce or partner death; second terms in Eq. 2C–E) and the second terms (first terms in Eq. 2C–E) give the rate at which new partnerships are formed.
Model Analysis.
We use adaptive dynamics to establish the invasion success of “mutant” hosts or parasites into a resident population, which amounts to a separation of ecological and evolutionary timescales (35). We use numerical methods to determine (co)evolutionary dynamics (Supporting Information). The local selection gradient (i.e., the direction in which the populations will evolve) is represented graphically in pairwise invasion plots (PIPs) and through a bifurcation analysis. We verify the deterministic predictions using an asynchronous stochastic IBM, which relaxes many simplifying assumptions of the adaptive dynamics approach (e.g., separation of ecological and evolutionary timescales, weak selection, hermaphroditic hosts; Fig. S8). In the IBM, the transmission rate and strength of mate choice are quantitative traits that vary within the populations. Hosts inherit the strength of mate choice from a randomly chosen parent. Similarly, parasites inherit the transmission rate of the previous generation. In both cases, the trait for the new generation is given by , where is the trait value of the previous generation, scales the mutation rate ( for hosts and for parasites) and is a normally distributed random number with mean 0 and SD 1. Simulations are run for 105 time units and are initiated with monomorphic host and parasite populations (Datasets S1 and S2).
Fig. S8.
Coevolutionary cycling in the individual-based model with dioecious hosts and female-only mate choice. The coevolutionary dynamics are broadly similar to those for the hermaphroditic model in Fig. 4. (A and B) Small values of η produce lower frequency oscillations, which are characterized by short intervals of strong mate choice (black) and low virulence (gray), interspersed with long intervals of weak mate choice and higher virulence (virulence increases slowly due to a weak relationship with transmission). (C and D) Larger values of η produce higher frequency oscillations (virulence changes rapidly due to the strong relationship with transmission). Oscillations tend to have large amplitude when mate choice is not too costly (low c) (A and C), but their magnitude decreases with higher costs (high c) (B and D). Fixed parameters as in Fig. 4, with (A) η = 0.3, c = 0.2; (B) η = 0.3, c = 0.4; (C) η = 0.5, c = 0.2; (D) η = 0.5, c = 0.4.
SI Methods: Polymorphic Model
The pair formation model (PFM) presented in the main text can be generalized for polymorphic populations, where hosts differ in their strength of mate choice and parasites differ in their transmission rates and effects on fertility . Susceptible individuals are grouped by host phenotype and infectious individuals are classed by both host and parasite phenotype . The number of unpaired individuals is given by and the total population size is:
| [S1] |
where sums are taken over all possible combinations of subscripts. The polymorphic PFM is given by:
| [S2A] |
| [S2B] |
| [S2C] |
| [S2D] |
| [S2E] |
where is the probability that an individual with mate choice parameter accepts an infected individual with fertility as a mate, is the equivalent probability when the nonfocal individual is not infected, is the sum of all pairs containing individuals in class , if and is 0 otherwise, and is the birth rate for new offspring with phenotype , given by:
| [S3] |
with sums taken over all possible combinations of pairs.
Derivation and Analysis of
The basic reproductive number, , is the expected number of secondary infections caused by a single infectious individual in an otherwise susceptible population. We derive for the monomorphic model (Eq. 2) by first linearizing the system about the disease-free equilibrium:
| [S4] |
| [S5] |
can be calculated from this linearization by applying a next generation method. We set to be the zero matrix except with (thus corresponding to new infections), and , so that corresponds to movement between classes and loss from the system. is then equal to the dominant eigenvalue () of the matrix
| [S6] |
which is lower triangular, so the starred entries are of no concern as the eigenvalues lie along the leading diagonal. Hence, has two zero eigenvalues and one nonzero eigenvalue, , which means that
| [S7] |
It is not immediately obvious from this equation how the strength of mate choice affects , but note that can be rewritten in the following form:
| [S8] |
where are positive coefficients and . Differentiating with respect to gives:
| [S9] |
which is always negative when (when virulence is positive or mate choice is costly) and tends toward 0 as . Thus, both the initial growth rate of an epidemic and the equilibrium prevalence of infection are constrained by stricter mate choice (Fig. 1).
In the absence of mate choice , is an increasing function of , so the parasite should evolve to fully castrate the host. If hosts experience mate choice , however, can be rewritten in the following form:
| [S10] |
where are positive coefficients. Recall that , so as and as . Hence for extreme values of , which means that both high and low levels of virulence are unsustainable (Fig. 2A).
This argument holds for other relationships between transmission, virulence, and mate choice, provided the rate of pair formation, , is a decreasing function of , and tends to 0 as the parasite tends to its maximum virulence. More generally, we can write:
| [S11] |
| [S12] |
where are positive constants. Dividing by and taking the limit gives as . Hence, a decelerating relationship is not required to constrain virulence.
Adaptive Dynamics Routine
We use a numerical adaptive dynamics routine to determine (co)evolutionary trajectories (C++ code available in Datasets S1 and S2). The routine is stochastic, so we run 10 simulations for each parameter value and record the most common behavior (cycling, evolutionary suicide or coevolutionarily stable strategies). The coevolutionary routine is as follows:
-
i)
Set initial host and parasite trait values and find the ecological equilibrium using an ordinary differential equation (ODE) solver.
-
ii)
Choose a focal population (host or parasite) at random and select a resident phenotype. Set the mutant trait value to be above or below the chosen resident trait value, where is the mutation size. If the mutant trait value is below a minimum threshold (0 for hosts, for parasites), or is already present in the population, then repeat this process until the mutant is both unique and above the minimum threshold.
-
iii)
Call the ODE solver, using the ecological output from the previous run with the mutant initially present at a low frequency. After time units, check to see if the distribution of phenotypes has reached equilibrium, has yet to reach equilibrium, or is cycling.
-
a)
If the population has reached equilibrium, remove any phenotypes that are below an extinction threshold.
-
b)
If the population has yet to reach equilibrium (and is not cycling), remove the mutant with probability , where governs the strength of demographic stochasticity and is the frequency of the mutant phenotype. Demographic stochasticity accounts for the fact that the selection gradient may be much greater in one population than the other. Call the ODE solver again, and repeat this process until either the population reaches equilibrium (step 3a) or the mutant is removed due to demographic stochasticity.
-
c)
If the phenotypes have reached a stable limit cycle, then do not incorporate demographic stochasticity.
-
a)
-
iv)
Repeat steps (ii) and (iii) for a given number of iterations.
Ecological Dynamics
The ecological dynamics of the monomorphic system (Eq. 2) lead to one of four outcomes: (i) parasite extinction; (ii) host and parasite extinction; (iii) a unique, stable endemic equilibrium; or (iv) stable limit cycles. Parasite extinction occurs when or when the host birth rate falls below the natural mortality rate (e.g., due to high virulence and low mate choice). If and the host birth rate remains higher than the mortality rate, then the population either tends toward a unique (locally asymptotically) stable endemic equilibrium, or toward a stable limit cycle (Fig. S1). Stable limit cycles occur over a relatively narrow range of parameters, when virulence is moderately high and mate choice is weak (Fig. 1 C and D). The uniqueness and stability of the endemic equilibrium, and the stability of limit cycles were verified using extensive numerical simulations.
Evolution of Virulence: Comparison Between Adaptive Dynamics and Maximization
In the main text, we test the qualitative prediction that mate choice constrains the evolution of virulence using a combination of adaptive dynamics and simulations of a stochastic IBM. We explore the evolution of virulence numerically, as we are unable to obtain a mathematical expression for the parasite invasion condition due to the high level of population structuring that arises from pair formation. Fig. S2 compares the adaptive dynamics result with a prediction based only on the maximization of Overall, maximization provides a good approximation for the optimal level of virulence.
Alternative Pair Formation Functions
In our model, we define to be the probability that individual will accept individual as a mate, given that the two individuals meet. In the main text, we use a power law relationship to link the choosiness of individual , , the fertility of individual , , and a cost of being choosy, , such that:
| [S13] |
Here, we show that the results are consistent for other functional forms of , all of which have the following in common: the fertility of prospective mates decreases (individuals become less attractive due to disease) as: (i) the strength of mate choice increases (individuals are more choosy); and (ii) the cost of choosiness increases (choosy individuals are more cautious). We generalize our results by using the following linear (Eq. S14), quadratic (Eq. S15), and exponential (Eq. S16) functions:
| [S14] |
| [S15] |
| [S16] |
In the case of the power law, quadratic, and exponential relationships, is the product of: (i) the probability that does not reject by being overly cautious; and (ii) the probability that does not reject based on signs of disease. For the power law relationship, these probabilities are and , respectively; for the quadratic relationship, they are and (, otherwise ); and for the exponential relationship they are and . The linear model makes a slightly different mechanistic assumption: is 1 minus the probability of rejecting a mate due to caution or due to disease , given that these probabilities are statistically independent. In other words, if the probability of rejecting a mate due to extra caution is and due to signs of disease is , then the probability of accepting a mate in the linear model is , and in the nonlinear models is . Fig. S6 shows that the linear, quadratic, and exponential forms of produce qualitatively similar dynamics to the power law form of that is presented in the main text.
Accelerating Virulence
In the main text we assume that there is a decelerating relationship between the transmission rate , and virulence , such that . This ensures that the trade-off is strictly monotonic, as virulence cannot increase above 1 (full castration). Most theory on the evolution of lethal parasites requires an accelerating trade-off to constrain virulence, but Eqs. S11 and S12 show that this is not the case for a sexually transmitted infection that reduces host fecundity. Fig. S7 shows that our results are consistent when there is an accelerating trade-off, with:
| [S17] |
Dioecious Individual-Based Model
The stochastic IBM presented in the main text is a direct analog of the deterministic model, consisting of nonselfing hermaphroditic hosts. Here, we relax the assumptions of hermaphroditism and mutual mate choice by adapting the IBM to consist of dioecious hosts and restricting mate choice to a single sex (females). The dioecious model is identical to the hermaphroditic model, with the following exceptions: (i) males can only pair with females, and vice versa; (ii) offspring are male or female with equal probability; and (iii) all individuals inherit their mate choice parameter from a random parent, but only females express this trait (i.e., males behave phenotypically as if ). Fig. S8 demonstrates that coevolutionary cycling is not unique to the hermaphroditic model and that the effects of costs of mate choice and the virulence-transmission trade-off parameter are qualitatively similar in the two models.
Supplementary Material
Acknowledgments
We thank M. Brockhurst, M. Cant, M. Keeling, K. King, T. Pizzari, and three anonymous reviewers for extremely helpful comments on the manuscript. Funding for this work was provided by the Natural Environment Research Council (Grant NE/K014617/1) and a Biotechnology and Biological Sciences Research Council studentship.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
See Commentary on page 13139.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1508397112/-/DCSupplemental.
References
- 1.Hamilton WD, Zuk M. Heritable true fitness and bright birds: A role for parasites? Science. 1982;218(4570):384–387. doi: 10.1126/science.7123238. [DOI] [PubMed] [Google Scholar]
- 2.Borgia G, Collis K. Female choice for parasite-free male satin bowerbirds and the evolution of bright male plumage. Behav Ecol Sociobiol. 1989;25(6):445–454. [Google Scholar]
- 3.Borgia G, Collis K. Parasites and bright male plumage in the satin bowerbird (Ptilonorhynchus violaceus) Am Zool. 1990;30(2):279–285. [Google Scholar]
- 4.Clayton DH. Mate choice in experimentally parasitized rock doves: Lousy males lose. Am Zool. 1990;30(2):251–262. [Google Scholar]
- 5.Clayton DH. The influence of parasites on host sexual selection. Parasitol Today. 1991;7(12):329–334. doi: 10.1016/0169-4758(91)90211-6. [DOI] [PubMed] [Google Scholar]
- 6.Kirkpatrick M, Ryan MJ. The evolution of mating preferences and the paradox of the lek. Nature. 1991;350:33–38. [Google Scholar]
- 7.Sheldon BC. Sexually transmitted disease in birds: Occurrence and evolutionary significance. Philos Trans R Soc Lond B Biol Sci. 1993;339(1290):491–497. doi: 10.1098/rstb.1993.0044. [DOI] [PubMed] [Google Scholar]
- 8.Able DJ. The contagion indicator hypothesis for parasite-mediated sexual selection. Proc Natl Acad Sci USA. 1996;93(5):2229–2233. doi: 10.1073/pnas.93.5.2229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hamilton WJ, Poulin R. The Hamilton and Zuk hypothesis revisited: A meta-analytical approach. Behaviour. 1997;134(3):299–320. [Google Scholar]
- 10.Loehle C. The pathogen transmission avoidance theory of sexual selection. Ecol Modell. 1997;103(2-3):231–250. [Google Scholar]
- 11.Knell RJ. Sexually transmitted disease and parasite-mediated sexual selection. Evolution. 1999;53(3):957–961. doi: 10.1111/j.1558-5646.1999.tb05389.x. [DOI] [PubMed] [Google Scholar]
- 12.Thrall PH, Antonovics J, Dobson AP. Sexually transmitted diseases in polygynous mating systems: Prevalence and impact on reproductive success. Proc Biol Sci. 2000;267(1452):1555–1563. doi: 10.1098/rspb.2000.1178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Abbot P, Dill LM. Sexually transmitted parasites and sexual selection in the milkweed leaf beetle, Labidomera clivicollis. Oikos. 2001;92(1):91–100. [Google Scholar]
- 14.Boots M, Knell RJ. The evolution of risky behaviour in the presence of a sexually transmitted disease. Proc Biol Sci. 2002;269(1491):585–589. doi: 10.1098/rspb.2001.1932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kokko H, Ranta E, Ruxton G, Lundberg P. Sexually transmitted disease and the evolution of mating systems. Evolution. 2002;56(6):1091–1100. doi: 10.1111/j.0014-3820.2002.tb01423.x. [DOI] [PubMed] [Google Scholar]
- 16.Webberley KM, Hurst GDD, Buszko J, Majerus MEN. Lack of parasite-mediated sexual selection in a ladybird/sexually transmitted disease system. Anim Behav. 2002;63(1):131–141. [Google Scholar]
- 17.Ashby B, Gupta S. Sexually transmitted infections in polygamous mating systems. Philos Trans R Soc Lond B Biol Sci. 2013;368(1613):20120048. doi: 10.1098/rstb.2012.0048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Balenger SL, Zuk M. Testing the Hamilton-Zuk hypothesis: Past, present, and future. Integr Comp Biol. 2014;54(4):601–613. doi: 10.1093/icb/icu059. [DOI] [PubMed] [Google Scholar]
- 19.McLeod DV, Day T. Sexually transmitted infection and the evolution of serial monogamy. Proc R Soc B. 2014;281(1796):20141726. doi: 10.1098/rspb.2014.1726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Knell RJ, Webberley KM. Sexually transmitted diseases of insects: Distribution, evolution, ecology and host behaviour. Biol Rev Camb Philos Soc. 2004;79(3):557–581. doi: 10.1017/s1464793103006365. [DOI] [PubMed] [Google Scholar]
- 21.Mink GI. Pollen and seed-transmitted viruses and viroids. Annu Rev Phytopathol. 1993;31:375–402. doi: 10.1146/annurev.py.31.090193.002111. [DOI] [PubMed] [Google Scholar]
- 22.Lockhart AB, Thrall PH, Antonovics J. Sexually transmitted diseases in animals: Ecological and evolutionary implications. Biol Rev Camb Philos Soc. 1996;71(3):415–471. doi: 10.1111/j.1469-185x.1996.tb01281.x. [DOI] [PubMed] [Google Scholar]
- 23.Anderson RM, May RM. Infectious Diseases of Humans: Dynamics and Control. Oxford Univ Press; Oxford, UK: 1991. [Google Scholar]
- 24.Thrall PH, Antonovics J, Bever JD. Sexual transmission of disease and host mating systems: Within-season reproductive success. Am Nat. 1997;149(3):485–506. [Google Scholar]
- 25.Metz AL, Hatcher L, Newman JA, Halvorson DA. Venereal pox in breeder turkeys in Minnesota. Avian Dis. 1985;29(3):850–853. [PubMed] [Google Scholar]
- 26.Kavaliers M, Colwell DD, Choleris E. Parasites and behavior: An ethopharmacological analysis and biomedical implications. Neurosci Biobehav Rev. 1999;23(7):1037–1045. doi: 10.1016/s0149-7634(99)00035-4. [DOI] [PubMed] [Google Scholar]
- 27.Loehle C. Social barriers to pathogen transmission in wild animal populations. Ecology. 1995;76(2):326–335. [Google Scholar]
- 28.Hart BL. Behavioral adaptations to pathogens and parasites: Five strategies. Neurosci Biobehav Rev. 1990;14(3):273–294. doi: 10.1016/s0149-7634(05)80038-7. [DOI] [PubMed] [Google Scholar]
- 29.Levin SA, Pimentel D. Selection of intermediate rates of increase in parasite-host systems. Am Nat. 1981;117(3):308–315. [Google Scholar]
- 30.Anderson RM, May RM. Coevolution of hosts and parasites. Parasitology. 1982;85(Pt 2):411–426. doi: 10.1017/s0031182000055360. [DOI] [PubMed] [Google Scholar]
- 31.Bremermann HJ, Pickering J. A game-theoretical model of parasite virulence. J Theor Biol. 1983;100(3):411–426. doi: 10.1016/0022-5193(83)90438-1. [DOI] [PubMed] [Google Scholar]
- 32.de Roode JC, Yates AJ, Altizer S. Virulence-transmission trade-offs and population divergence in virulence in a naturally occurring butterfly parasite. Proc Natl Acad Sci USA. 2008;105(21):7489–7494. doi: 10.1073/pnas.0710909105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Atkins KE, et al. Modelling Marek’s disease virus (MDV) infection: Parameter estimates for mortality rate and infectiousness. BMC Vet Res. 2011;7(1):70. doi: 10.1186/1746-6148-7-70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ebert D, Carius HJ, Little T, Decaestecker E. The evolution of virulence when parasites cause host castration and gigantism. Am Nat. 2004;164(Suppl 5):S19–S32. doi: 10.1086/424606. [DOI] [PubMed] [Google Scholar]
- 35.Geritz SAH, Kisdi E, Meszena G, Metz JAJ. Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evol Ecol. 1998;12:35–37. [Google Scholar]
- 36.Gandon S, Day T. Evolutionary epidemiology and the dynamics of adaptation. Evolution. 2009;63(4):826–838. doi: 10.1111/j.1558-5646.2009.00609.x. [DOI] [PubMed] [Google Scholar]
- 37.Best A, White A, Boots M. Resistance is futile but tolerance can explain why parasites do not always castrate their hosts. Evolution. 2010;64(2):348–357. doi: 10.1111/j.1558-5646.2009.00819.x. [DOI] [PubMed] [Google Scholar]
- 38.Ashby B, Gupta S. Parasitic castration promotes coevolutionary cycling but also imposes a cost on sex. Evolution. 2014;68(8):2234–2244. doi: 10.1111/evo.12425. [DOI] [PubMed] [Google Scholar]
- 39.Ashby B, Gupta S, Buckling A. Effects of epistasis on infectivity range during host-parasite coevolution. Evolution. 2014;68(10):2972–2982. doi: 10.1111/evo.12479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Boots M, White A, Best A, Bowers R. How specificity and epidemiology drive the coevolution of static trait diversity in hosts and parasites. Evolution. 2014;68(6):1594–1606. doi: 10.1111/evo.12393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ashby B, King KC. Diversity and the maintenance of sex by parasites. J Evol Biol. 2015;28(3):511–520. doi: 10.1111/jeb.12590. [DOI] [PubMed] [Google Scholar]
- 42.Graves BM, Duvall D. Effects of sexually transmitted diseases on heritable variation in sexually selected systems. Anim Behav. 1995;50:1129–1131. [Google Scholar]
- 43.Parvinen K. Evolutionary suicide. Acta Biotheor. 2005;53(3):241–264. doi: 10.1007/s10441-005-2531-5. [DOI] [PubMed] [Google Scholar]
- 44.van Baalen M. Coevolution of recovery ability and virulence. Proc Biol Sci. 1998;265(1393):317–325. doi: 10.1098/rspb.1998.0298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bonds MH, Keenan DC, Leidner AJ, Rohani P. Higher disease prevalence can induce greater sociality: A game theoretic coevolutionary model. Evolution. 2005;59(9):1859–1866. [PubMed] [Google Scholar]
- 46.Boots M, Donnelly R, White A. Optimal immune defence in the light of variation in lifespan. Parasite Immunol. 2013;35(11):331–338. doi: 10.1111/pim.12055. [DOI] [PubMed] [Google Scholar]
- 47.O’Keefe KJ, Antonovics J. Playing by different rules: The evolution of virulence in sterilizing pathogens. Am Nat. 2002;159(6):597–605. doi: 10.1086/339990. [DOI] [PubMed] [Google Scholar]
- 48.Lipsitch M, Siller S, Nowak MA. The evolution of virulence in pathogens with vertical and horizontal transmission. Evolution. 1996;50(5):1729–1741. doi: 10.1111/j.1558-5646.1996.tb03560.x. [DOI] [PubMed] [Google Scholar]
- 49.Edwards JC, Barnard CJ. The effects of Trichinella infection on intersexual interactions between mice. Anim Behav. 1987;35(2):533–540. [Google Scholar]
- 50.Kavaliers M, Colwell DD, Choleris E. Parasites and behaviour: An ethopharmacological perspective. Parasitol Today. 2000;16(11):464–468. doi: 10.1016/s0169-4758(00)01786-5. [DOI] [PubMed] [Google Scholar]
- 51.Kennedy CEJ, Endler JA, Poynton SL, McMinn H. Parasite load predicts mate choice in guppies. Behav Ecol Sociobiol. 1987;21:291–295. [Google Scholar]
- 52.Jaenike J. Parasitism and male mating success in Drosophila testacea. Am Nat. 1988;131(5):774–780. [Google Scholar]
- 53.Moshkin M, et al. Scent recognition of infected status in humans. J Sex Med. 2012;9(12):3211–3218. doi: 10.1111/j.1743-6109.2011.02562.x. [DOI] [PubMed] [Google Scholar]
- 54.Nunn CL. Behavioural defences against sexually transmitted diseases in primates. Anim Behav. 2003;66(1):37–48. [Google Scholar]
- 55.Davies NB. Polyandry, cloaca-pecking and sperm competition in dunnocks. Nature. 1983;302:334–336. [Google Scholar]
- 56.Knell RJ. Syphilis in renaissance Europe: Rapid evolution of an introduced sexually transmitted disease? Proc Biol Sci. 2004;271(Suppl 4):S174–S176. doi: 10.1098/rsbl.2003.0131. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.