Abstract
A parametric working memory network stores the information of an analog stimulus in the form of persistent neural activity that is monotonically tuned to the stimulus. The family of persistent firing patterns with a continuous range of firing rates must all be realizable under exactly the same external conditions (during the delay when the transient stimulus is withdrawn). How this can be accomplished by neural mechanisms remains an unresolved question. Here we present a recurrent cortical network model of irregularly spiking neurons that was designed to simulate a somatosensory working memory experiment with behaving monkeys. Our model reproduces the observed positively and negatively monotonic persistent activity, and heterogeneous tuning curves of memory activity. We show that fine-tuning mathematically corresponds to a precise alignment of cusps in the bifurcation diagram of the network. Moreover, we show that the fine-tuned network can integrate stimulus inputs over several seconds. Assuming that such time integration occurs in neural populations downstream from a tonically persistent neural population, our model is able to account for the slow ramping-up and ramping-down behaviors of neurons observed in prefrontal cortex.
Introduction
The physical world is described in terms of continuous (analog) quantities, such as space, direction, time, velocity and frequency. Through evolution, animals and humans must have developed the mental ability not only to encode analog physical quantities as sensory stimuli, but also to remember such quantities by virtue of an active internalized representation in working memory. A basic question in neuroscience is how analog physical stimuli are represented and stored in memory in the brain. Starting in the 1980s, neurophysiologists have investigated this question, with a focus on spatial information. In a delayed response task, an animal is required to remember the spatial location of a sensory cue across a delay period of a few seconds. Neurons in the parietal cortex (Gnadt and Anderson, 1989; Chafee and Goldman-Rakic, 1998) and prefrontal cortex (Funahashi et al., 1989; Rainer et al., 1998) show persistent activity that is correlated with memory maintenance during the delay period. Mnemonic neural activity is selective to spatial locations, quantified by a bell-shaped tuning. That is to say, a given neuron shows an elevated delay in activity only for a relatively narrow range of positional cues, and the spatial information is encoded by ‘what’ neurons fire significantly during the memory period. A similar coding strategy is also used by the neural system that encodes and predicts an animal’s head direction (see Sharp et al., 2001; Taube and Bassett, 2003).
More recently, another form of working memory for analog quantities was discovered in a somatosensory delayed response experiment (Romo et al., 1999; Brody et al., 2003). In this task, the monkey is trained to compare the frequencies of two vibrotactile stimuli separated in time by a delay of 3–6 s; therefore the behavioral response requires the animal to hold in working memory the frequency of the first stimulus across the delay period. It was found that neurons in the inferior convexity of the prefrontal cortex show persistent activity during the delay, with the firing rate of memory activity varying monotonically with the stimulus frequency. Therefore, the stimulus is encoded by the firing rates at which all neurons discharge spikes. Similarly, in the oculomotor system that maintains a fixed eye position between quick saccades, persistent neuronal activity is proportional to the eye position (Robinson, 1989; Aksay et al., 2000). We emphasize that the meaning of tuning curve for delay period activity is profoundly different from that of responses to sensory inputs. Conventionally, the stimulus selectivity of neuronal firing during stimulus presentation is quantified by a tuning curve. For example, the higher the input intensity, the larger the neural response. By contrast, in a working memory task, the mnemonic neural activity is measured after the transient stimulus is withdrawn, during the delay period. If a working memory network exhibits a family of delay period activity that is monotonically tuned to a feature of the transient stimulus, this entire family of mnemonic activities with different firing rates must be all realizable under exactly the same external conditions (during the delay when external inputs are absent). How a cortical network, for example in the prefrontal cortex, can be capable of such a feat presents an intriguing open question in neuroscience.
Persistent neural activity during working memory is generated internally in the brain, either by recurrent circuit mechanisms (Lorente de Nó, 1933; Goldman-Rakic, 1995) or by intrinsic cellular mechanisms (Camperi and Wang, 1998; Egorov et al., 2002). According to the attractor model of persistent activity (Amit, 1995; Wang, 2001), a neural assembly has a resting state at a low firing rate, as well as a stable active (‘attractor’) state at an elevated firing rate that is self-sustained by reverberative excitation. Recently, this idea has been extended to the realm of working memory of an analog physical quantity, and tested rigorously using biophysically based recurrent network models. In models of spatial working memory, the spatial locations are encoded by a continuum of ‘bell-shaped’ localized persistent states (‘bump attractors’) (Camperi and Wang, 1998; Compte et al., 2000; Gutkin et al., 2001; Tegnér et al., 2002; Ermentrout, 2003; Renart et al., 2003a). In neural integrators in the oculomotor circuit, persistent firing rate of each neuron varies linearly with the gaze position (Cannon et al., 1983; Robinson, 1989). As a result, if rates of different neurons are plotted against each other, they fall on a straight line in the ‘firing-rate space’. This observation led to the theoretical concept of ‘line attractors’ (Seung, 1996).
It was recognized (Cannon et al., 1983; Seung et al., 2000a,b) that very fine tuning of synaptic feedback is necessary to create such monotonically tuned neural integrators in models. The feedback must be finely tuned, so that if the firing rate of a neuron is altered by a transient input, then the resulting change in synaptic feedback to the neuron is exactly the amount required to maintain the new firing rate. Any mis-tuning of the feedback results in an exponential decay or growth of firing rates away from the desired memory state to one of a few stable levels. The drift occurs with a persistence time proportional to the synaptic time constant divided by the fractional error in the tuning (Seung et al., 2000b), such that synaptic weights must be tuned to one part in a hundred if the desired network time constant (10 s) is 100-fold longer than the synaptic time constant (100 ms).
Koulakov et al. (2002) recently proposed a mechanism without the fine-tuning requirement. The idea is to combine many robust, bistable groups to form a system with multiple stable states. If there are enough bistable units, which switch to persistent active states following transient stimuli of different strengths, the summation of neural units’ outputs will become indistinguishable from a continuous quantity that encodes the stimulus feature. Such an integrator or memory device is similar to the stable digital memory of a computer (which can simulate analog quantities). One salient feature of the Koulakov model is that each individual neuron’s tuning curve of delay period activity displays a significant jump in the firing rate between the resting state and active memory states. Whether this prediction is consistent with experimental data from neural integrators (Aksay et al., 2000; Nakamagoe et al., 2000) remains unclear.
In this paper, we present a new model of persistent activity monotonically tuned to an analog stimulus feature. Our model was designed to reproduce the prefrontal neural activity in the vibrotactile delayed matching-to-sample experiment (Romo et al., 1999; Brody et al., 2003). Conceptually, this model is similar to that of Seung et al. (2000a), and we present a mathematically precise description of what is meant by the requirement of network fine-tuning for this class of working memory models. Furthermore, in order to apply our model to the prefrontal cortex during parametric working memory, we elaborated on existing models in several important ways. First, we used large neural networks (12 000 neurons), appropriate for cortical circuits, in contrast to the oculomotor neural models with only tens of neurons. Secondly, our model has a locally structured circuit architecture, whereas in Seung et al.’s model (Seung et al., 2000a) synaptic connections are globally determined by a gradient-descent optimization algorithm. Thirdly, noise is absent in the models of Seung et al. (2000a) and Koulakov et al. (2002), and the robustness of network behavior against noise was not assessed. Cortical neurons receive a large amount of background noise inputs, which are taken into account in our model. Fourthly, in both integrator models (Seung et al., 2000a; Koulakov et al., 2002), neurons are silent in the resting state. By contrast, prefrontal neurons show spontaneous activity at low rates prior to stimulus presentation, and our model reproduces such spontaneous neural activity in the resting state. Fifthly, our model includes both excitatory and inhibitory neural populations. Finally, we propose a two-network model that reproduces both positively and negatively monotonic neurons which have been observed experimentally in prefrontal neurons.
Materials and Methods
Network Architecture
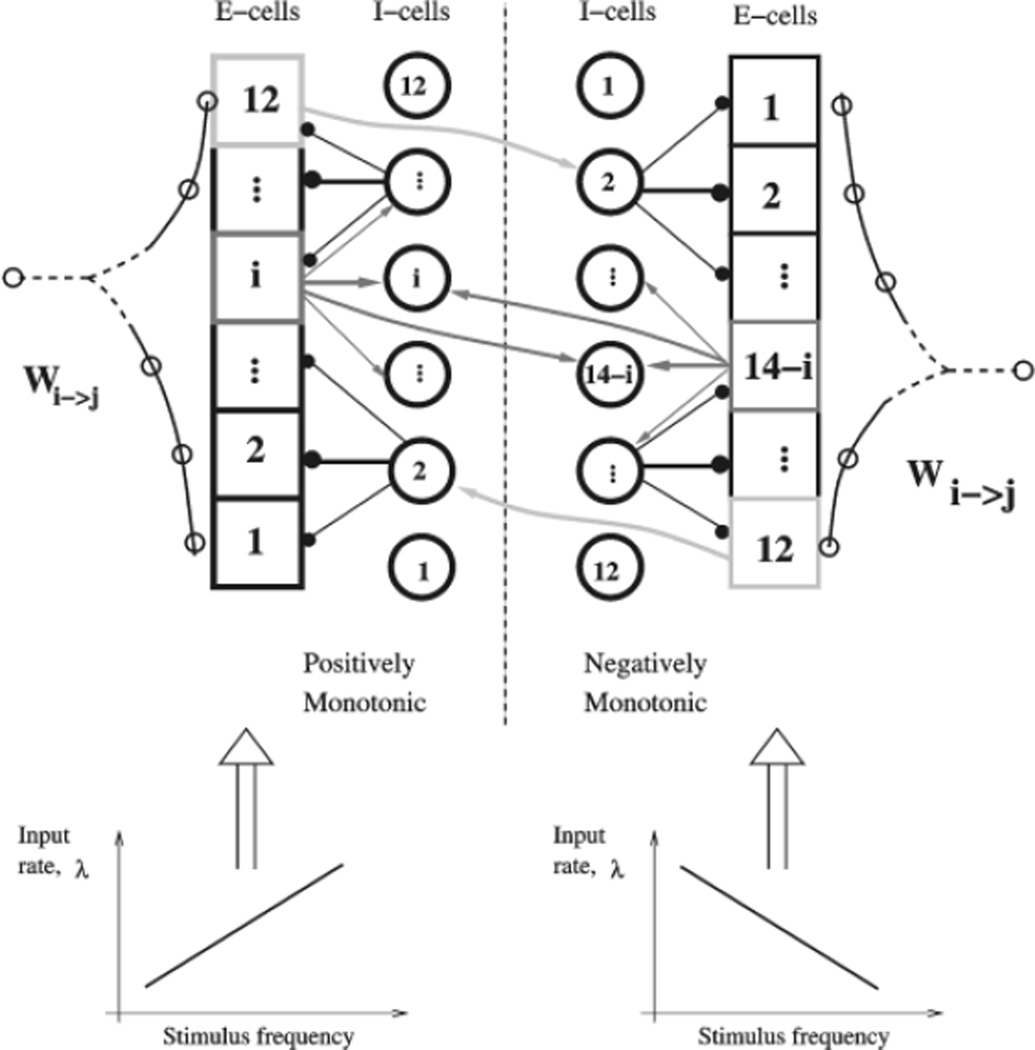
Our network model represents a cortical local circuit composed of a number (typically two sets of 12) of neural groups or ‘columns’ (Fig. 1). The two halves of the network represent the two sets of cells that receive either positively monotonic or negatively monotonic transient input from neurons in S2 (Salinas et al., 2000). Each neural group (labeled by i = 1, 2,…, 12; 1*,2*,…, 12*) contains 400 excitatory cells and 100 inhibitory cells, so we simulate 12 × 2 × 500 = 12 000 cells in total. With such a large number of neurons per column, the instantaneous firing rate of the group is a meaningful quantity that encodes the information in the network. Individual spike times are noisy, and any data for a single neuron are only uncovered by averaging over many trials.
Figure 1.
Schematic model architecture with asymmetric connectivity. Two mirror networks of positively and negatively monotonic neurons receive transient input respectively from positively and negatively tuned neurons in S2. Each network has an excitatory pyramidal cell population (squares) and an inhibitory interneuron population (circles). Neurons are divided into 12 groups per network. Synaptic connections are stronger within the same group than between two groups. The connectivity is asymmetrical, so that the activation threshold by stimulus is the lowest for neural group 1 and highest for neural group 12. Populations of inhibitory interneurons are shown as circles. The two networks interact through pyramid-to-interneuron connections, resulting in cross-inhibition. See text for more details.
The connectivity from group j to group i, Wj→i, is structured such that synaptic connections are stronger between cells within a column than between two columns. The strong recurrent excitation within a column means that each column is close to being bistable — that is, the self-excitation within a column is not enough to raise the firing rate when all cells are in the spontaneous state, but is almost enough to maintain a high firing rate if the cells are given transient excitation. The strengths of connections with other groups is key to the maintenance of higher firing rates, and to obtaining a large number of different stable states. The neurons within a column are all connected identically (all-to-all), so receive identical recurrent input. They are only differentiated by the background noise they receive.
The connection strength between two neural groups decays exponentially with the difference in their labels, as shown in Figure 1 for the E-to-E connections between excitatory cells. All connections with inhibitory cells (E-to-I, I-to-E and I-to-I) are strongest within a column and decay symmetrically between columns. The E-to-E network architecture has a ‘high-to-low’ asymmetry, in the sense that if j > i, then Wi→j < Wj→i. This results in a gradient of effective excitability across the network, with the groups with the lowest labels being most excitable. Such a distribution of excitability is important for the network to show a graded response to a range of stimuli.
A fixed gradient of intrinsic thresholds (produced by a range of leak conductances for example) can be used to generate a range of excitabilities to external stimuli. Both Koulakov et al. (2002) and Seung et al. (2000a) used such a network. Koulakov et al. included symmetric connectivities between neurons of differing thresholds, but with very low strength, such that the feedback to a neuron within a group was significantly greater than the feedback to a neuron from its effect on other neurons with different thresholds. Hence, the concept of Koulakov et al.’s network is one of a discrete set of bistable groups, each of which switch to an excited state following a different magnitude of input.
In Seung et al.’s network, far more feedback comes to a cell through its connections to other cells (apart from the most excitable cell, which is bistable while all others are silent). In Seung et al.’s line attractor network, asymmetrical connections are necessary, with stronger synaptic weights from low- to high-threshold neurons. This is because the whole network is designed to have a linear input–output relation. When just one cell (the lowest threshold) is firing, the change in output comes solely from that cell, so connections from that cell are strong. When all neurons are firing, the same change in input causes all cells to increase in output. For the total change in output to be the same, the output from higher threshold cells must be progressively smaller. Hence high-to-low connections are weaker than low-to-high.
In all three cases, a range of excitabilities is used to ensure that a wide range of inputs leads to different responses in the network. A single bistable group of neurons can only distinguish whether a stimulus is greater or lower than its single threshold. A range of thresholds allows for more stimuli to be distinguished. In the prefrontal cortex, it is unlikely that there are columns or neural groups with large systematic differences in their intrinsic excitability. Hence we use systematic differences in the synaptic strengths between populations (which are readily altered through learning mechanisms) to create groups of neurons that require different strengths of stimulus for their firing rate to deviate strongly from their spontaneous rate. Such a network results in stronger connections from higher threshold to lower threshold neurons. This is evident, as it is the extra excitation arising from the stronger synaptic weights from higher-threshold populations that causes low-threshold populations to be more readily excited by external input. Since silent cells cannot influence the activity of other cells, however strong the connections, this effect is absent without spontaneous activity. Such is the case in the other models (Seung et al., 2000a; Koulakov et al., 2002).
Our complete model contains two such networks connected by reciprocal inhibition (Fig. 1). The model receives input from two types of cells, which mimic the outputs of two neuronal types in cortical area S2 that show responses to vibrotactile stimuli (but not persistent delay activity). The positively monotonic cells increase their firing rate with larger stimulus frequency, while negatively monotonic cells act oppositely (Salinas et al., 2000). We assume that the two types of transient inputs from S2 project to the two different networks in our model. This assumption automatically leads to both positively and negatively monotonic tuning of the PFC cells in our model.
Single Neurons and Synapses
In the spiking network model, we simulate the individual cells as leaky integrate-and-fire neurons (Tuckwell, 1988). All inputs to a cell are given in terms of excitatory or inhibitory conductances, which give rise to currents that are integrated over time in the membrane potential. Once the membrane potential reaches a threshold, the cell fires an action potential and the membrane potential is reset to a fixed value for a refractory time, before temporal integration continues. The full dynamical equations are presented in the Supplementary Material.
Our network makes the simplification that afferent input reaches cells through AMPA receptor-mediated (AMPAR) synapses of 2 ms time constant, while recurrent activity is transmitted purely through the slower NMDA receptors (NMDARs), with 100 ms time constant. The importance for working memory of the relative abundances and strengths of AMPARs and NMDARs has been investigated elsewhere (Wang, 1999; Compte et al., 2000), showing the deleterious effect of a large ratio of AMPARs to NMDARs in recurrent synapses. Here, we utilize the slow time-constant of NMDARs in recurrent connections to enhance the time-constant of the entire network (Seung et al., 2000b).
All excitatory, recurrent synapses exhibit short-term presynaptic facilitation and depression (Varela et al., 1997; Hempel et al., 2000). We implement the scheme described by Matveev and Wang (2000), which assumes a docked pool of vesicles containing neurotransmitter, where each released vesicle is replaced with a time constant, τd. The finite pool of vesicles leads to synaptic depression, as when the presynaptic neuron fires more rapidly than vesicles are replaced, no extra excitatory transmission is possible. Such synaptic depression contributes to stabilizing persistent activity at relatively low rates, strongly enhancing the postsynaptic effect of NMDAR saturation. For example, a synapse with 16 docking sites and a docking time constant of 0.5 s has a maximum rate of vesicle release of 32 per second. Such saturation in the recurrent excitation reduces the excitatory feedback significantly, even for firing rates of <20 Hz. This allows the network to have stable states of persistent activity with relatively low firing rates (e.g. 15 Hz), where the incremental increase in feedback excitation is already diminishing as the firing rate rises.
Synaptic facilitation helps to stabilize the network to noise, because brief fluctuations in activity do not get transmitted through recurrent excitatory synapses — in particular, the resting, spontaneous state of each group is more stable. Whereas the cues of 0.5 or 1 s duration, which cause a response in the network, elicit many action potentials and facilitate the synapses in a group that is driven into the active persistent state. Note that our network is not designed to use the longer time constants of the facilitating synapses as the basis of temporal integration (Shen, 1989).
Stimulus
The stimulus to the network is modeled by fast synaptic excitation mediated by AMPA receptors, with a maximum conductance of 3 nS. The sensory stimulus frequency, s, is expressed in terms of the rate, λ, of the presynaptic Poisson spike train. Here specifically, we used λ = 5s, with s ranging from 10 to 40 Hz (the flutter range). When the positively monotonic cells receive the lowest stimulus input, the negatively monotonic cells receive the highest, and vice versa. Hence the negatively monotonic cells receive a stimulus of approximately (50 – s) Hz, where s is the vibrational stimulus frequency. Note that for a given cue, the stimulus is of the same strength to all neurons with the same sign of tuning.
In the last section, where we analyze the ability of the network to integrate a stimulus over longer periods of time, we apply the Poisson input to the positively monotonic neurons only.
Experimental Data
The experimental data we compared with our model were taken from extracellular recordings from microelectrodes in the inferior convexity of the prefrontal cortex in macaque monkeys, as described elsewhere (Romo et al., 1999; Brody et al., 2003). The task was a delayed comparison of vibrational frequency, which required the monkey to remember the ‘flutter’ frequency of an initial vibrotactile stimulus on its finger, during the 3 or 6 s delay period. In this paper, we present some examples of spike trains from single neurons that exhibited persistent stimulusdependent activity throughout the delay.
Data Analysis
Unless otherwise stated, all firing-rate histograms and tuning curves for the simulations were calculated from single neurons separately, averaged over ten simulations with different seeds in the random number generator for external noise. We used a Gaussian smoothing of time window 150 ms before binning spikes to generate the histograms. For model simulations, tuning curves were obtained with an average firing rate of between 3 and 6 s after the offset of the stimulus. The tuning curves for the experimental data contain an average firing rate of between 0.5 and 2.5 s after the offset of the stimulus for a 3 s delay protocol, and between 0.5 and 5.5 s after the end of the stimulus for a 6 s delay protocol. We did not use the initial and final 0.5 s of the delay, because different activity during the stimulus or response could affect the data in these time intervals after smoothing.
Results
Monotonically Tuned Persistent Activity
The neural spiking in our model is compared with that seen during the delay period of the somatosensory delayed-frequency comparison experiment of Romo (Romo et al., 1999; Brody et al., 2003). The experiment consists of an initial somatosensory vibrational stimulus of fixed (0.5 or 1 s) duration followed by a delay period (of 3–6 s), then a second stimulus of identical duration but different frequency to the first. The monkey must indicate which stimulus frequency is the greater, a task which requires memory of the initial stimulus frequency during the delay. The monkey is able to perform the task, and indeed, Romo’s group observed neurons whose firing rates vary monotonically with stimulus frequency, persistently during the delay. Such neurons could subserve the mnemonic function necessary for the task. By careful adjustment of the connectivity strengths between neural groups, our model network reproduces such persistent neural activity. The issue of fine-tuning of parameters will be discussed later.
The tuned model was simulated with a stimulation protocol similar to that used in the experiment. The network is initially in a resting state, where most excitatory neurons fire in the range of 1–8 Hz. A transient (1 s) stimulus is introduced to all the neurons in the network, with an intensity assumed to be proportional to the vibrational frequency in the experiment (see Materials and Methods). Neurons increase their spike discharges in response to the stimulus, which leads to reverberative excitation through recurrent connections. This intrinsic synaptic excitation is able to sustain persistent activity after the stimulus offset. Our network is in two halves, each half corresponding to neurons that receive either positively monotonic or negatively monotonic input from S2. S2 contains such oppositely tuned cells, which do not show persistent activity (Salinas et al., 2000).
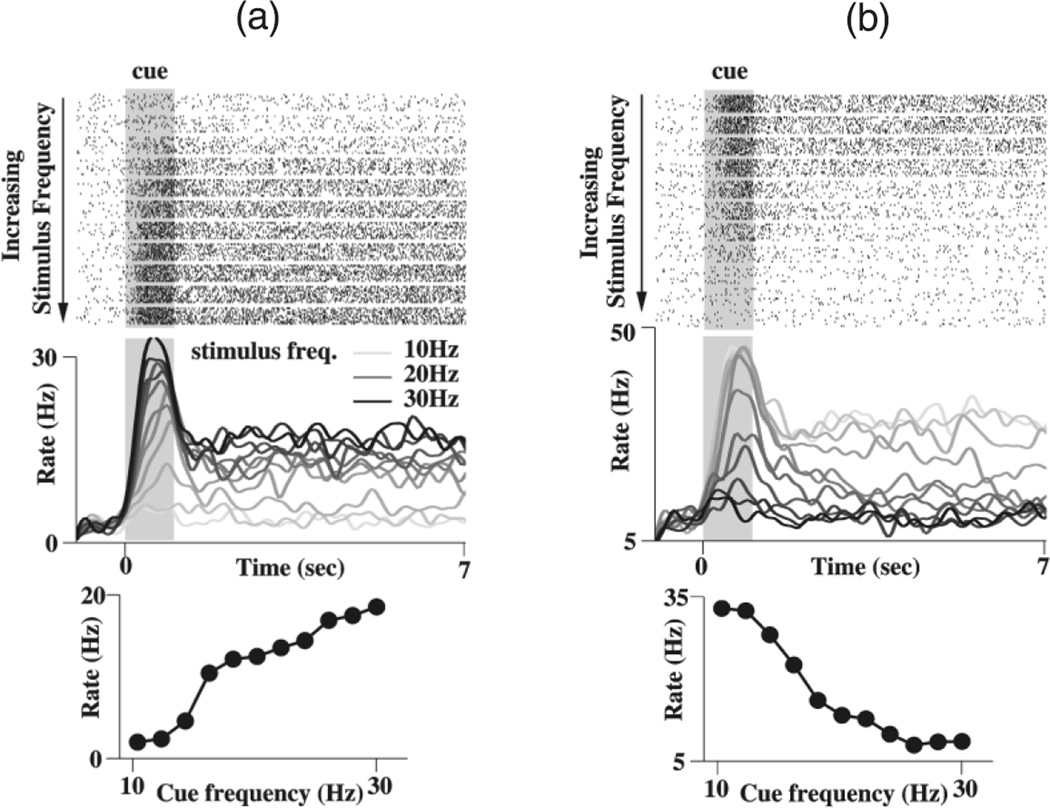
Figure 2 shows the activities of two representative neurons. In Figure 2a, a single neuron shows delay period activity that monotonically increases with the stimulus frequency. This neuron belongs to the first half of our network model which receives a stronger input with a higher stimulus frequency. The larger transient neural responses recruit more recurrent excitation which can sustain persistent activity at a higher rate. In contrast, the neuron in Figure 2b shows a monotonically decreasing tuning of its mnemonic activity. This neuron belongs to the second half of our network model, which receives less inputs with a higher stimulus frequency, hence the recruited recurrent excitation as well as the resulting persistent activity is lower.
Figure 2.
Persistent neural activity of the parametric working memory model. (a) A positively monotonic, excitatory cell. Top panel: rastergrams, showing spikes in blocks of 10 trials, each block corresponding to a fixed stimulus frequency. The cell initially fires spikes at a few Hertz spontaneously. A transient stimulus (shaded) produces a large response, followed by persistent activity after the stimulus offset. The firing rate of both the transient response and persistent activity increases with the stimulus frequency. Middle panel: trial-averaged neural firing rate, where darker shades of gray represent increasing stimulus frequency. Bottom panel: the tuning curve shows the average rate in the last 5s of the delay period following each stimulus. (b) A negatively monotonic inhibitory interneuron, same plots as (a).
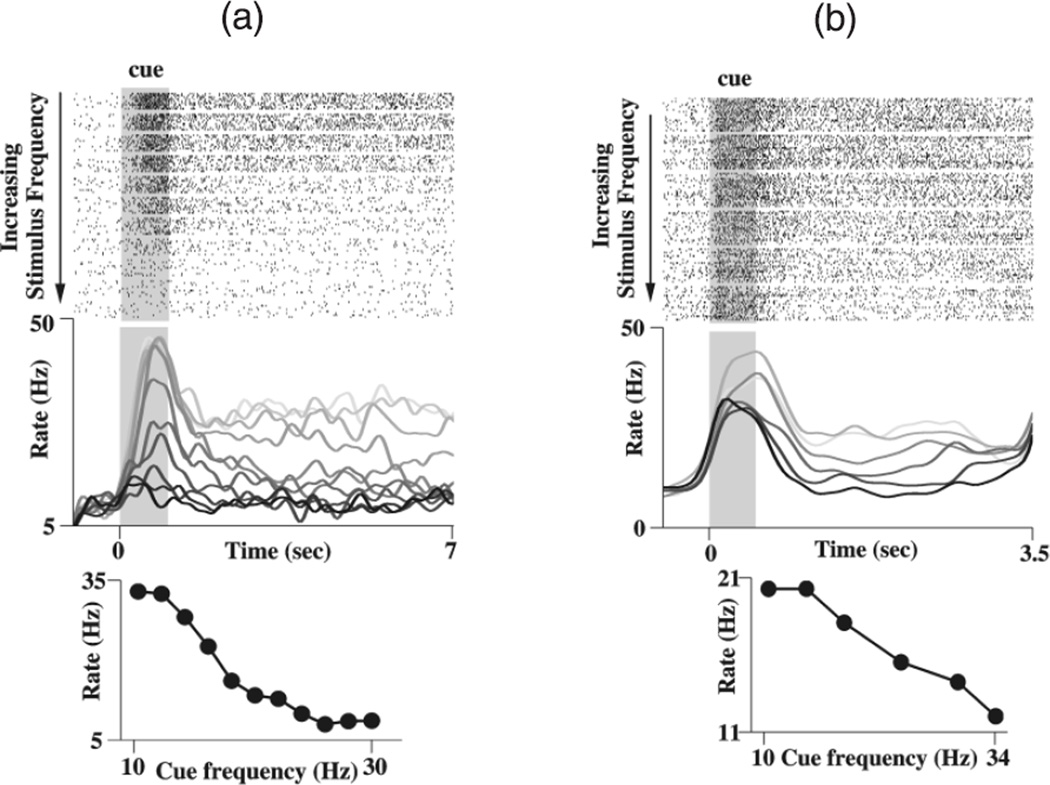
Our model simulations (Fig. 2) can be compared with the experimentally observed neural activity in the prefrontal cortex during the vibrotactile experiment (Fig. 3). The model neurons fire most strongly during the transient response to stimulus, then settle to a persistent rate which is monotonically dependent on the stimulus frequency (middle panels). The tuning curves (lower panels) are clearly monotonic and demonstrate parametric working memory. The average firing rates of neurons in the interval between 2 and 5 s after the end of the stimulus exhibit a quasi-linear or sigmoidal dependence on stimulus frequency.
Figure 3.
Sustained delay activity of prefrontal cortical neurons recorded from macaque monkeys during parametric working memory. (a) A positively monotonic neuron. (b) A negatively monotonic neuron. Same format as Figure 2
Different neural groups have different activation thresholds, and show persistent activity at different rates for a given stimulus. This is similar to the models of Seung et al. (2000a) and Koulakov et al. (2002). In these cases, neurons have different intrinsic input thresholds for spike discharges. In the present model, the synaptic connections are asymmetrical (Fig. 1; see Materials and Methods). As a result, neural groups receive progressively more overall recurrent excitation from left to right across the network. This way, neural group 1 has the lowest threshold and group 12 has the highest threshold, when driven by external inputs. This range of excitability allows the network to have a range of responses to varying stimuli. Because the tuning is monotonic, the stimulus frequency is encoded and stored in memory not by what neurons fire significantly, but at what rates all neurons fire. Because of background noise, and because the network is sensitive to parameter tuning (see below), even the averaged population firing rate of an individual neural column shows significant temporal fluctuations. The memory of the stimulus is better maintained by persistent activity pooled across the entire network of all neural groups.
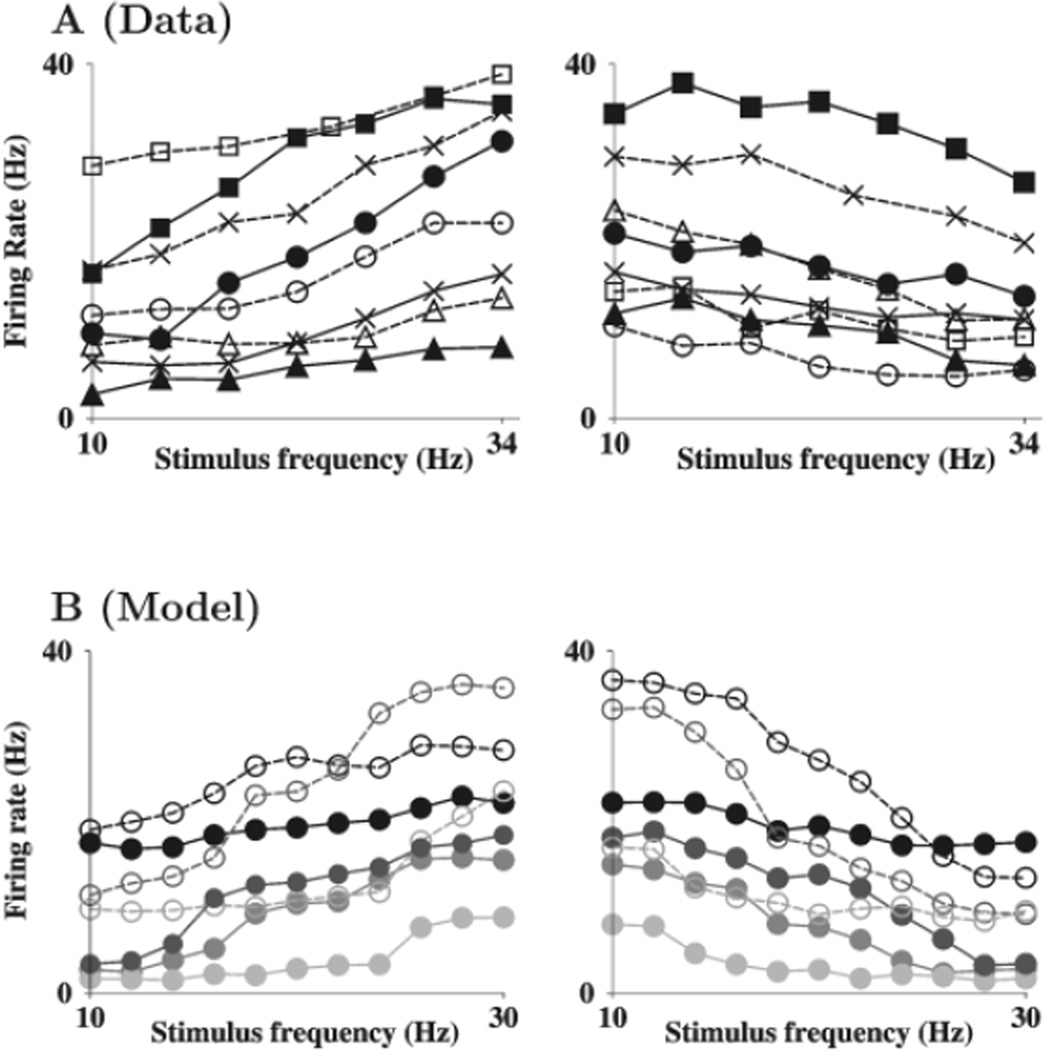
The experimentally observed tuning curves of prefrontal neurons are very diverse; some are linearly tuned with the vibration frequency, others show sigmoid-shaped tuning (Fig. 4A). Our model reproduces to a large degree this diversity of tuning curves of single neurons (Fig. 4B). Our model has four types of neurons, both positively and negatively monotonic types of pyramidal cells and interneurons. The interneurons have different intrinsic properties (see Supplementary Material), as they are designed to be fast-spiking and generally have a higher firing rate than pyramidal cells. We found that the tuning curves of interneurons are more linear than those of pyramidal cells. This can be explained by the fact that interneurons receive broad excitation from the pyramidal cells; averaging over a few hard sigmoid functions yields a more linear function.
Figure 4.
Diversity of tuning curves of persistent neural activity in prefrontal neurons and our model. (A) Examples of positively monotonic (left) and negatively monotonic (right) tuning curves from the experimental database. (B) Examples chosen to indicate the full variety of tuning curves from model simulations. Note the quasi-continuous nature of the curves, with small rate jumps. Filled circles: excitatory cells; open circles: interneurons.
Robustness to Heterogeneity
A key issue in evaluating the biological feasibility of our network is a determination of its robustness to variations of the parameters. The key parameters that we tuned were the connection strengths. To assess the effects of mis-tuning, we multiplied the synaptic strengths Wi→j by (1 + ηgi→j)(1 + ηni→j) where ηgi→j is sampled for each group of neurons, drawn from a Gaussian distribution with standard deviation σg, while ηni→j is sampled separately for each neuron, drawn from a Gaussian of standard deviation σn. The leak conductances also varied, with a standard deviation of 1.2 nS (i.e. ±3%).
We found that the more deleterious way to mis-tune is to scale up or down all the connection strengths for a particular neural group (σg > 0). We find that 5% population heterogeneity causes a clear drift in firing rates to a few stable persistent states. The network loses its ability to discriminate many different inputs, and a large gap in firing rates (typically up to 15–20 Hz) opens up for some neurons when the stimulus is strong enough to propel the network from one discrete stable state to another. The time constant for drift is still long (2–3 s), but that is diminished enough to limit the network’s ability to distinguish >3 or 4 stimulus strengths after 6 s. A less damaging variation is to scale up or down all connections to individual neurons separately and randomly (σg = 0 and σn > 0). Indeed, the mnemonic ability of the network is maintained with a 10% variation in synaptic strengths for each individual neuron, while the heterogeneity in the inter-group connection strength is ±1%. The firing rates after different stimuli remain separate throughout the delay period of 6 s and neuronal responses are qualitatively indistinguishable from those presented in Figures 2 and 4. Such heterogeneity within a population does lead to a greater variety of tuning curves, as, unlike the homogeneous case, heterogeneity allows tuning curves to be different for each of the 100 inhibitory or 400 excitatory cells within a population.
Such stability to heterogeneity within a population may not be a surprise. Assuming that neurons are uncorrelated or weakly correlated, heterogeneities of single neurons can be averaged out across a large neural population. Indeed, a 10% variation of individual neuronal properties results in only an ~0.5% variation in the average properties of 400 neurons. However, our results do indicate that with the large numbers of neurons available in the cortex, tuning of single neuronal parameters no longer needs to be extremely precise.
Mean-field Analysis of Model Networks
To elucidate the precise requirements for parametric working memory behavior, we carried out mathematical analysis of the mean-field approximation of our biophysically based spiking model. The mean-field approach (Amit and Brunel, 1997; Hansel and Sompolinsky, 1998; Brunel, 2001; Brunel and Wang, 2001; Renart et al., 2003b) is to replace quantities such as synaptic conductances by their averages, ignoring their fluctuations due to individual spikes. The mean-field approximation is useful, as it allows us to describe a whole population of spiking neurons with their average activity. Hence, we can rapidly solve for the stable states of the system, and observe how those states change as a function of parameters like the connection strengths, or intrinsic excitability. A detailed account of the mean field equations can be found in the Supplementary Material. We found that the mean-field calculations are confirmed qualitatively by simulations of the original spiking model, but an adjustment of parameters is necessary to match precisely the behaviors of the two models quantitatively.
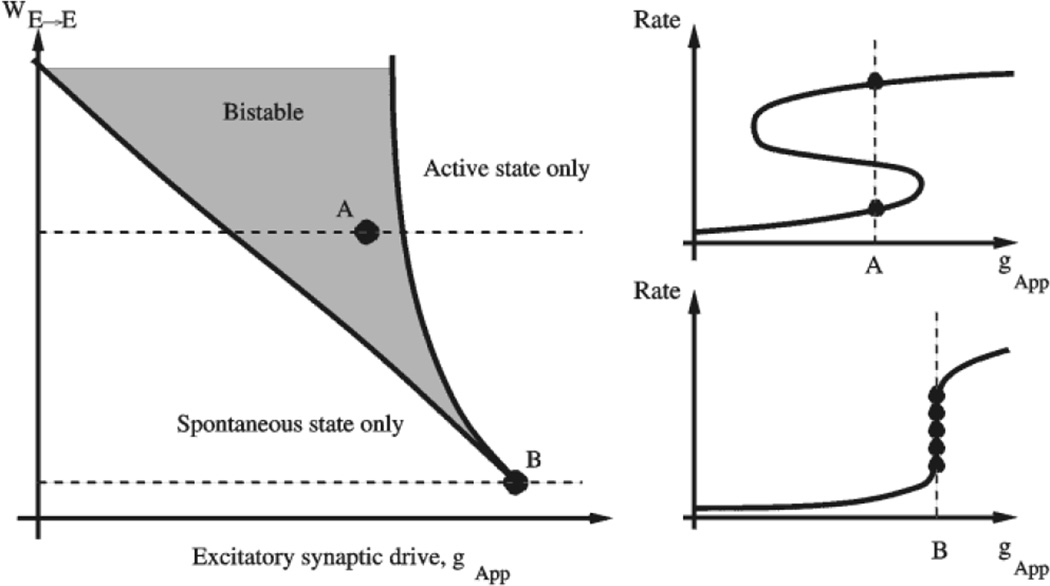
To help understand the results of our mean-field analysis, let us first consider schematically one neural group with recurrent excitation. When the recurrent strength WE→E is above a critical value, a bistability between the resting spontaneous state and an active persistent state is produced by strong recurrent excitation. The bistability persists over a range of applied excitation, determined by the excitatory synaptic drive conductance, gApp, to the neurons. This is illustrated schematically in Figure 5, where the network behavior is shown on the plane of the two parameters WE→E and gApp. While WE→E is a measure of the recurrent excitation, multiplying feedback from within the neural group, gApp is a constant excitatory drive, which would arise, for example, from other neural groups. A change in intrinsic parameters which alters the firing thresholds of neurons, will shift the whole diagram along the axis of gApp. In particular, the larger the leak conductance, gL, the larger the required drive, gApp, to achieve firing threshold and bistability.
Figure 5.
Fine-tuning of parametric working memory model. Schematic illustration of a neural group with recurrent excitation. Left panel: network behavior as a function of the recurrent strength WE→E and applied excitatory input, gApp. When WE→E is above a critical value (e.g. point A), a bistability between a resting state and an active persistent state occurs in a range of gApp. This range shrinks to zero at the critical value of WE→E, point B, which is called a ‘cusp’. Right panel: there is a trade-off between robust bistability but with a large gap in the firing rates of the two stable states (upper figure) and fine-tuning to the cusp where there can be a continuous range of firing rates (lower figure).
With WE→E far above the critical value (point A on the left panel of Fig. 5), the bistability range of gApp is wide and the behavior is robust. However, there is a large gap in the firing rates between the active and resting states (right panel of Fig. 5). In order to realize a quasi-continuum of firing rates, WE→E should be as close to the critical value as possible (the point B, which is called a ‘cusp’ in the theory of dynamical systems). However, in this case the value of gApp must be precisely tuned (Seung et al., 2000b). Moreover, for a single neural group, the quasicontinuous range of firing rates is actually quite small (a few Hertz), largely determined by the properties of a single neuron’s input–output relation (Brunel, 2001). The range of response should be increased for two reasons. First, a wider range allows a wider range of stimulus strengths to be encoded by the network. Secondly, if neurons encode the stimulus over a large range of firing rates, the sensitivity of the network is increased, as different stimuli cause larger changes in firing rates that are more easily decoded. The limited range can be increased by utilizing a large number of interconnected neural groups with different thresholds. The recruitment of each new neural group increases the excitatory drive to, hence activity of, those already active neural groups, leading to a much larger quasi-continuous range of persistent firing rates.
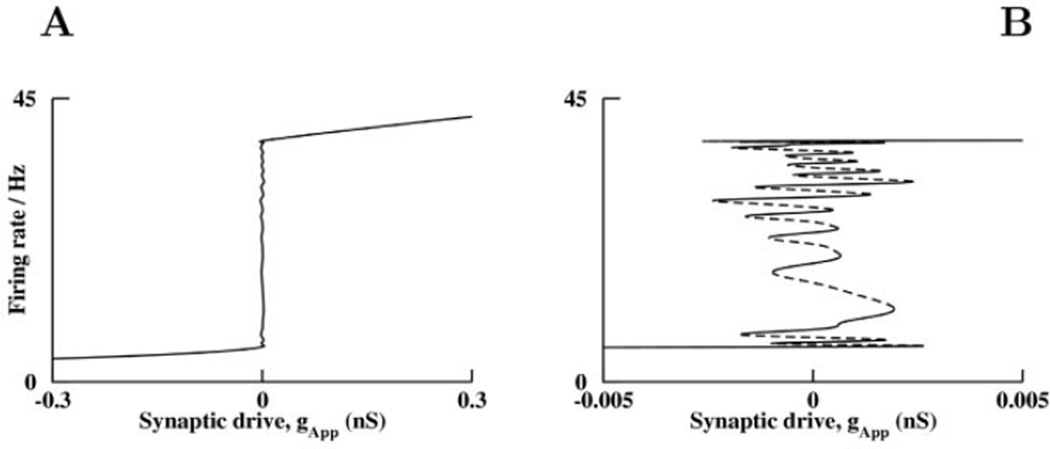
The mean-field analysis of our complete two-network model demonstrates a large number of stable states over a very narrow range of synaptic drive (Fig. 6). Our model network has as many cusps as the number of excitatory neural groups, and tuning the whole network to a continuous attractor requires an alignment of cusps so that the system can be tuned to all of them at once. The ideal vertical line of Figure 5 becomes wavy on a fine scale when many neural groups are combined to make a continuum. It is the nearness of the system to many cusps that allows the stable states to be close together, and results in a long time constant for drift following any stimulus. If connections within the system are varied randomly, the cusps are no longer aligned, but as there are a large number of cusps, the system will still be near a few of them and typically have more than one stable state. Hence, random mis-tuning does not cause a severe detriment to the network properties. However, a global mis-tuning (such as a global scaling of all synapses) will result in drifts of firing rates as described in previous work (Seung et al., 2000a,b).
Figure 6.
Bifurcation diagram of the finely tuned parametric working memory model, as a function of applied synaptic drive conductance, gApp. Synaptic drive is an offest conductance for demonstration purposes, that we add to the positively montonic neurons and subtract from the excitatory input to negatively monotonic neurons. A negative drive means the positively monotonic neurons have reduced synaptic excitation. A shift in any intrinsic neuronal parameter has a similar effect on the system. All the stable states are computed using the mean field theory for the entire network of twelve positively monotonic and twelve negatively monotonic, excitatory and inhibitory, neural groups. These persistent states are plotted as the firing rates of cells in neural group 3. (A) A quasi-continuum of stable firing rates is possible with correct tuning of applied synaptic drive. (B) An enlargement of the region near the quasi-continuous attractor indicates a discrete number of stable persistent states close to the number of neural groups, with small changes in firing rate between states. Portions of the curve with negative slopes are the branches of unstable states (dashed lines).
Time Integration
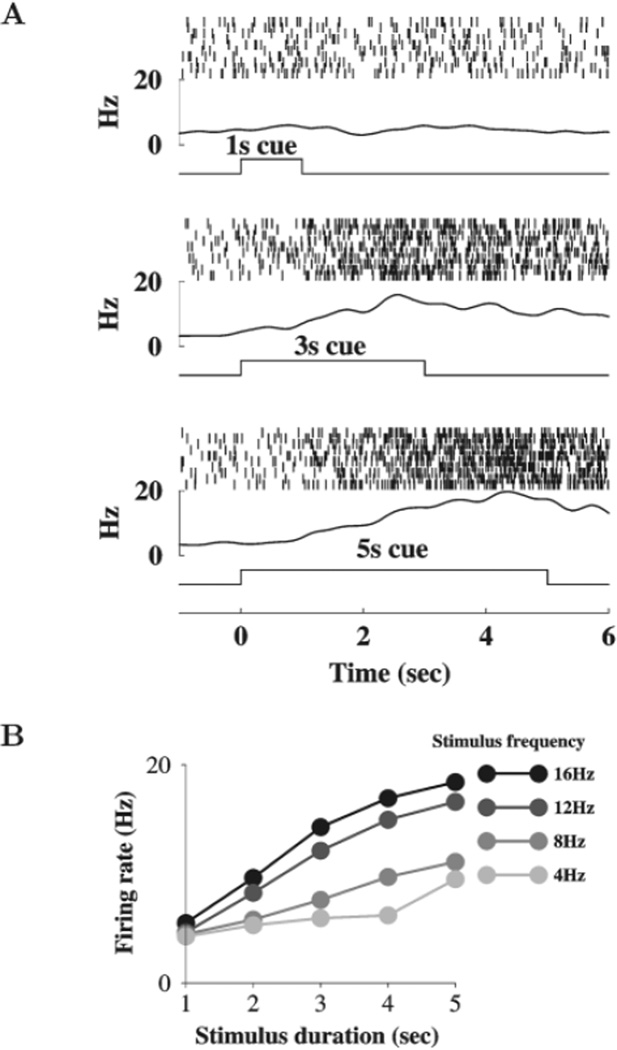
A line attractor network converts a transient input into a persistent output which is proportional to the input amplitude, so in that sense it performs an integration of the input. However, if the computation is truly mathematical integration, neurons should also be able to integrate over time, i.e. the firing rate of persistent activity should reflect the time duration of an input stimulus. To assess the temporal properties of integration by our network, we carried out a series of trials where the strength and frequency of the stimulus were fixed but the duration of the stimulus changed.
The results presented in Figure 7 show that the network can integrate an input slowly in time, over many s (Fig. 7A). Equivalent slow integration is observed in the mean-field network described in the previous section. Such a slow time course of integration is remarkable given that the longest biophysical time constant of the model is 100 ms. Once the stimulus ends, the network maintains a level of activity that is monotonically dependent on the stimulus duration (Fig. 7B). Optimal time integration occurs provided that the input strength is not too small (below a critical threshold) or too large (beyond which saturation occurs).
Figure 7.
Time integration of a stimulus with different duration and amplitude. (A) The network can integrate a stimulus over a long time (1, 3 and 5 s), as shown by the rastergrams and population firing rates. (B) The firing rate of persistent activity (averaged between 3 and 6 s after the stimulus offset) is plotted as a function of stimulus duration, different curves correspond to different stimulus frequencies (4, 8, 12 and 16 Hz, with increasingly darker shades of gray). Note that linear dependence on the time duration of the stimulus occurs for moderate input strengths.
The threshold and saturation effects imply that the integration is not ‘pure’ in the sense that if average firing rates are plotted as a function of the product of stimulus frequency and duration, they do not fall on a universal curve. A doubling of the stimulus duration with a halving of the frequency, in general produces a smaller response. Experimental tests of the temporal scaling properties of integration in both the oculomotor system and working memory system would be illuminating.
Ramping Neurons
Finally, we investigated the issue of diversity of neural responses observed in the somatosensory discrimination experiment. During the delay period, persistent activity of many prefrontal-cortical neurons is not tonic, but evolves slowly over time. Some neurons tune to the stimulus early in the delay, others late in the delay. Moreover, average rates of some neurons ramp down or ramp up. The two types of temporal dependence are correlated with each other, but are not identical. Here, we investigate the two subtypes of neurons, which do not necessarily show any stimulus dependence, but whose average rates ramp up or ramp down during the delay. These are only two kinds of time dependence, out of a greater variety reported by Brody et al. (2003).
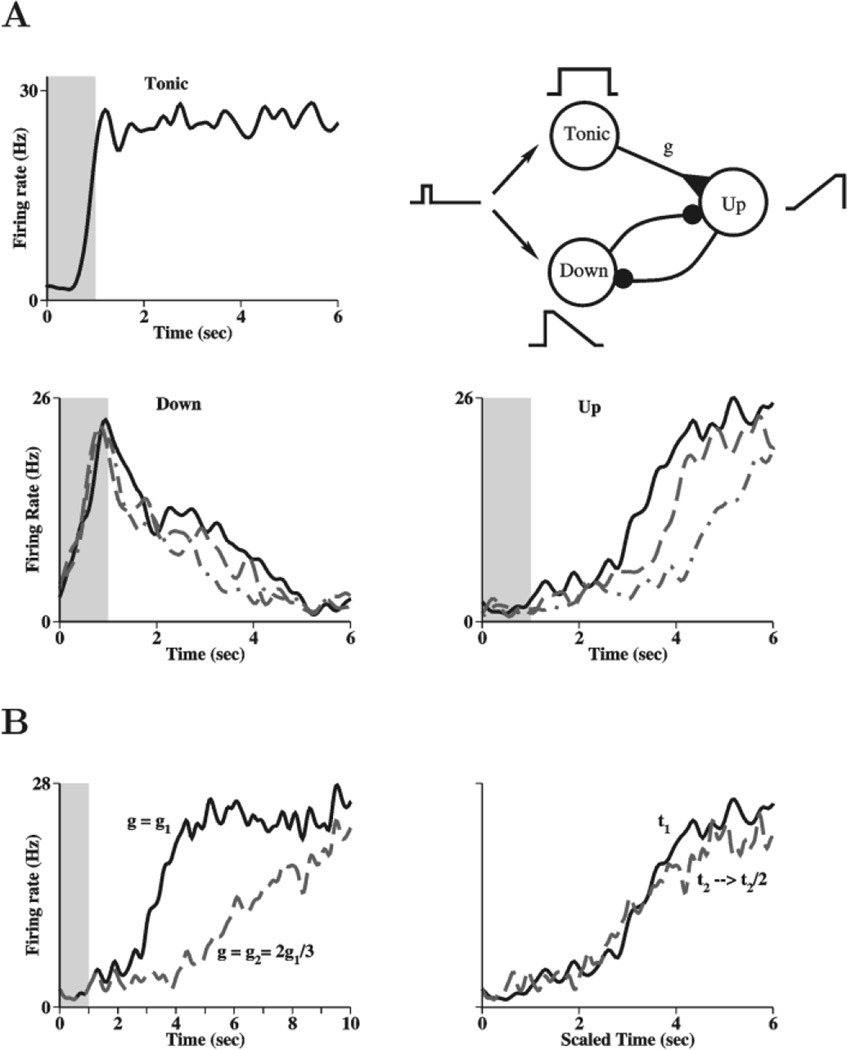
To generate such neurons, we extended our model to include three sets of neurons (each having 12 neural groups), each structured like the positively monotonic half of our previous network (Fig. 8A, upper right). The first neural population shows tonic persistent activity during the delay, as in our original model, but at a saturated rate that is independent of stimulus strength (Fig. 8A, upper left). It is assumed that the first neural population sends excitatory projections to the second population which integrates the inputs slowly in time, as in the previous subsection. Consequently, the second neural population shows slow ramp-up spike discharges during the delay period (Fig. 8A, lower right). Furthermore, the second and third neural populations are reciprocally connected by inhibition (Constantinidis et al., 2002). The transient stimulus activates the third neural population and, as the second neural population ramps up over a few s, the third population is progressively inhibited; therefore its activity ramps down during the delay (Fig. 8A, lower left). Similarly, the initial activity of the third population delays the ramping up of the second population in a closely matched tug-of-war that is resolved by the extra tonic input from the first to the second population. Note that these ramping behaviors occur during the delay, while there is no applied stimulus.
Figure 8.
Diversity of delay period activity: tonic, early and late neurons. (A) Schematic diagram of an extended model with three neural populations (all are positively monotonic with the stimulus frequency). The first network (Tonic) shows tonic persistent activity and projects with strength g to a second network (Up), which integrates the inputs slowly to generate ramping-up activity during the delay. The third network (Down) displays a transient activation by the stimulus, and ramping-down time course of delay period activity due to the progressive inhibition from population 2. The trial-averaged firing rates for three different cells from each type of network are shown for 5 s following the stimulus frequency. (B) Neurons in population 2 ramp-up with a slope and a delay that depend on the input synaptic strength. Left panel: control (black, solid), and when the synaptic strength, g, from the tonic population 1 is reduced by one-third (gray, dashed). Right panel: when the time is scaled by half for the gray, dashed curve, the two time courses closely resemble each other.
Experimentally it was found that the rate of evolution of time-dependent neurons is plastic. For example, when the delay duration is doubled from one block of trials to another (say, from 3 s to 6 s), the ramping slope of delay activity is roughly reduced by a factor of 2, so that a ramping neuron reaches the same final activity level at the end of the delay (Brody et al., 2003). Our model (Fig. 8A, upper right) suggests a synaptic mechanism for such plasticity. Since ramping neurons integrate inputs from the tonic neural population, the ramp slope depends on the strength of synapses between the two neural populations. Indeed, when this synaptic conductance is reduced by one-third (from g1 to 2g1/3) the time course of a ramping neuron is delayed and slowed (Fig. 8B, left panel). However, if the timescale is compressed by a factor of two, the ramping time course becomes superposable with that in the control case (Fig. 8B, right panel), similar to the experimental observations (Brody et al., 2003).
Discussion
In this paper we presented a large-scale cortical network model (with 12 000 neurons) for parametric working memory. The main results are threefold. First, our model reproduces the salient neural activity data from monkey prefrontal cortex in a somatosensory delayed discrimination experiment (Romo et al., 1999; Brody et al., 2003). A model with two inhibitorily coupled networks reproduces positively and negatively monotonic neurons, and a diversity of tuning curves of memory activity. Secondly, we show that there is a trade-off between robust network behavior with large jumps in the tuning curves, and fine-tuned network behavior with a quasi-continuum of attractor states. The fine-tuning of our model is mathematically identified to be a precise alignment of cusps in the bifurcation diagram of the network. This is also true for the model of Seung et al. (2000a) (data not shown). Thirdly, we show that the finely tuned network can integrate stimulus inputs over many s, even though single neurons and synapses operate at timescales of 10–100 ms. Assuming that such time integration occurs in downstream neural populations that receive inputs from a tonically persistent neural population, our model is able to reproduce the ramping-up and and ramping-down behaviors of some time-dependent neurons observed in the prefrontal cortex (Romo et al., 1999; Brody et al., 2003).
The key to the ability of a neural network to encode monotonically and remember a continuous quantity, and integrate inputs in the mathematical sense, is to achieve an effective time constant of many seconds. At least three biological implementations of such integration are conceivable.
First, single neurons and synapses may possess mechanisms with very long intrinsic time constants, such as synaptic facilitation (Shen, 1989) or intracellular calcium release from stores (Loewenstein and Sompolinsky, 2002). Alternatively, a single neuron could tune positive internal feedback (from calcium channels) to generate a longer cellular time constant from its faster intrinsic mechanisms (Durstewitz, 2003). Recently, Egorov et al. (2002) reported experimental evidence for a slow (seconds) integration process in single neurons of the rat layer V entorhinal cortex. The underlying mechanisms remain to be elucidated.
Secondly, a network may contain a number of bistable and independently switchable neural groups (Koulakov et al., 2002). The continuous variable can then be encoded by the number of neural groups that are switched on; and such a digital code can be close to a continuous representation if the number of neural groups is large. However, this scenario predicts significant gaps in the tuning curves of memory neurons, due to the jumps between the resting state and active persistent states, that are not seen in neural data from working memory experiments. It remains to be seen whether gaps in the firing rate could be rendered insignificant with biophysically realistic mechanisms.
Thirdly, a network can be tuned judiciously toward a continuum of attractor states (Seung, 1996; Seung et al., 2000a). Our simulations show that a finely tuned model compares favorably with the experimental data, without large gaps in the tuning curves of mnemonic neural activity. The inherent problem of a trade-off between robustness to noise and heterogeneity versus a continuum of stable states is ameliorated by the cross-inhibition between positively and negatively monotonic groups, as well as the large number of neurons in the system. In our network there are a total of 24 excitatory neural groups, each with strong recurrent feedback adjusted to be at the ‘cusp’ to produce a continuous attractor over a small range of inputs (Figs 5 and 6). With 24 continuous attractors available, the whole network is able to be in the vicinity of several of them robustly. Near the attractor states the effective time constant of the network is much longer than the intrinsic cellular or synaptic time constants (Seung et al., 2000b).
In the brain, fine-tuning of a recurrent network is likely to be accomplished by some activity-dependent homeostatic mechanisms (Marder, 1998; Turrigiano et al., 1998; Turrigiano, 1999; Turrigiano and Nelson, 2000; Renart et al., 2003a). For example, consider a neural group with excitatory feedback (shown in Fig. 5). Assuming that regulatory processes (operating at timescale of days) stabilize the long-term firing rate of neurons at ~8–15 Hz (the ‘goal’ or ‘target’ rate), then the network will be naturally tuned to the narrow parameter region near the cusp (with continuous attractor states). Figure 6 emphasizes that for the tuned system shown, the average firing rate can only be in the range of 8–15 Hz if the conductance offset, gApp (in this case zero) exactly matches the position of the vertical line. Hence a coarse monitoring of average firing rate (Turrigiano, 1999; Turrigiano and Nelson, 2000) could lead to a very fine tuning of neuronal parameters.
Such a homeostatic mechanism would combat and compensate any mis-tuning of cellular or synaptic parameters, so that the network would be stabilized near the cusp in spite of parameter mis-tuning. Theoretical work suggests that such a homeostatic mechanism works effectively in a continuous attractor model for spatial working memory (Renart et al., 2003a). It would be interesting to see whether the same kind of ideas can be applied to parametric working memory models.
It can be noted from Figure 5 that tuning a system to a cusp requires adjustment of two parameters. Durstewitz (2003) has suggested that as well as mean firing rate, a cell could monitor its variance in activity as a second parameter to tune. Noting that the variance is typically maximal at a line attractor, where fluctuations are not damped, Durstewitz suggests that a neuron can utilize such information. Further experimental work will be very useful to demonstrate the feasibility of such cellular tuning processes.
With appropriate network connectivity (Fig. 8) our model can reproduce cells which have a delay from the end of the stimulus until they begin to ramp up. Moreover, the length of delay and rate of ramping-up can be scaled in time by modification of synaptic strengths. Other mechanisms could produce delays, such as utilizing slow currents within neurons, but there are no known mechanisms whereby such intrinsic currents could change their time constants. Durstewitz (2003) has suggested a similar synaptic learning mechanism, but where the strength of input from other cells affects a neuron’s intrinsic ramping rate. Experimentally, whether a change in the duration of the delay does give rise to the kind of synaptic modification suggested by our model is not known and remains to be studied in the future.
As well as a time variation of average firing rates, neurons in the prefrontal cortex can also exhibit a time variation in their tuning to the stimulus. The two behaviors are correlated, because when the average firing rate is very low, there is typically little stimulus dependence, as a strong stimulus dependence would cause a range of firing rates across stimuli, resulting in an average firing rate that differs significantly from the spontaneous rate. However, during the delay some neurons can maintain a near constant, typically high average firing rate, while the spread of firing rates is large only early or late in the delay. We speculate that a strategy similar to the one we outlined above could generate many of these other types of time-dependent behavior observed experimentally.
To conclude, we would like to emphasize that, at present, it remains unproven that the continuous attractor paradigm is a necessary and accurate description of spatial or parametric working memory circuits. Because of experimental constraints, typically only a relatively small number (<10) of stimuli are used in working memory experiments, such as the oculomotor response task (Funahashi et al., 1989) or the somatosensory discrimination task (Romo et al., 1999). Moreover, even if a large number of discrete stimuli are sampled, animals tend to categorize these values when possible, and avoid the difficult task of memorizing a continuous quantity (Hernandez et al., 1997). Hence, further experiments are desirable to rigorously test whether the internal representation of an analog stimulus in working memory is truly continuous.
Supplementary Material
Acknowledgments
P.M. was supported by IGERT and an NIH Career Award, 1K25 MH064497–01. X.J.W. and P.M. received support from the NIMH (MH62349), the Alfred Sloan Foundation and the Swartz Foundation. R.R.’s research was partially supported by an International Research Scholars Award from the Howard Hughes Medical Institute and the Millennium Science Initiative-CONACYT.
Footnotes
Supplementary Material
Supplementary material can be found at: http://www.cercor.oupjournals.org
References
- Aksay E, Baker R, Seung HS, Tank DW. Anatomy and discharge properties of pre-motor neurons in the goldfish medulla that have eye-position signals during fixations. J Neurophysiol. 2000;84:1035–1049. doi: 10.1152/jn.2000.84.2.1035. [DOI] [PubMed] [Google Scholar]
- Amit DJ. The hebbian paradigm reintegrated: local reverberations as internal representation. Behav Brain Sci. 1995;18:617–626. [Google Scholar]
- Amit DJ, Brunel N. Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb Cortex. 1997;7:237–252. doi: 10.1093/cercor/7.3.237. [DOI] [PubMed] [Google Scholar]
- Brody CD, Hernandez A, Zainos A, Lemus L, Romo R. Timing and neural encoding of somatosensory parametric working memory in macaque prefrontal cortex. Cereb Cortex. 2003;13:000–111. doi: 10.1093/cercor/bhg100. [DOI] [PubMed] [Google Scholar]
- Brunel N. Persistent activity and the single-cell frequency–current curve in a cortical network model. Network. 2001;11:261–280. [PubMed] [Google Scholar]
- Camperi M, Wang X-J. A model of visuospatial working memory in prefrontal cortex: recurrent network and cellular bistability. J Comput Neurosci. 1998;5:383–405. doi: 10.1023/a:1008837311948. [DOI] [PubMed] [Google Scholar]
- Cannon SC, Robinson DA, Shamma S. A proposed neural network for the integrator of the oculomotor system. Biol Cybern. 1983;49:127–136. doi: 10.1007/BF00320393. [DOI] [PubMed] [Google Scholar]
- Chafee MV, Goldman-Rakic PS. Matching patterns of activity in primate prefrontal area 8a and parietal area 7ip neurons during a spatial working memory task. J Neurophysiol. 1998;79:2919–2940. doi: 10.1152/jn.1998.79.6.2919. [DOI] [PubMed] [Google Scholar]
- Compte A, Brunei N, Goldman-Rakic PS, Wang X-J. Synaptic mechanisms and network dynamics underlying spatial working memory in a cortical network model. Cereb Cortex. 2000;10:910–923. doi: 10.1093/cercor/10.9.910. [DOI] [PubMed] [Google Scholar]
- Constantinidis C, Williams GV, Goldman-Rakic PS. A role for inhibition in shaping the temporal flow of information in prefrontal cortex. Nat Neurosci. 2002;5:175–180. doi: 10.1038/nn799. [DOI] [PubMed] [Google Scholar]
- Durstewitz D. Self-organizing neural integrator predicts interval times through climbing activity. J Neurosci. 2003;23:5342–5353. doi: 10.1523/JNEUROSCI.23-12-05342.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egorov AV, Hamam BN, Fransen E, Hasseimo ME, Alonso A. Graded persistent activity in entorhinal cortex neurons. Nature. 2002;420:173–178. doi: 10.1038/nature01171. [DOI] [PubMed] [Google Scholar]
- Ermentrout B. Dynamical consequences of fast-rising, slowdecaying synapes in neuronal networks. Neural Comput. 2003 doi: 10.1162/089976603322385054. (in press). [DOI] [PubMed] [Google Scholar]
- Funahashi S, Bruce CJ, Goldman-Rakic PS. Mnemonic coding of visual space in the monkey’s dorsolateral prefrontal cortex. J Neurophysiol. 1989;61:331–349. doi: 10.1152/jn.1989.61.2.331. [DOI] [PubMed] [Google Scholar]
- Gnadt JW, Anderson RA. Memory related planning activity in posterior parietal cortex of macaque. Exp Brain Res. 1989;70:216–220. doi: 10.1007/BF00271862. [DOI] [PubMed] [Google Scholar]
- Goldman-Rakic PS. Cellular basis of working memory. Neuron. 1995;14:477–485. doi: 10.1016/0896-6273(95)90304-6. [DOI] [PubMed] [Google Scholar]
- Gutkin BS, Laing CR, Colby CL, Chow CC, Ermentrout GB. Turning on and off with excitation: the role of spike-timing asynchrony and synchrony in sustained neural activity. J Comput Neurosci. 2001;11:121–134. doi: 10.1023/a:1012837415096. [DOI] [PubMed] [Google Scholar]
- Hansel D, Sompolinsky H. Modeling feature selectivity in local cortical circuits. In: Koch C, Segev I, editors. Methods in neuronal modeling. 2nd edn. Cambridge, MA: MIT Press; 1998. pp. 499–567. [Google Scholar]
- Hempel CM, Hartman KH, Wang X-J, Turrigiano GG, Nelson SB. Multiple forms of short-term plasticity at excitatory synapses in rat medial prefrontal cortex. J Neurophysiol. 2000;83:3031–3041. doi: 10.1152/jn.2000.83.5.3031. [DOI] [PubMed] [Google Scholar]
- Hernandez A, Salinas E, Garcia R, Romo R. Discrimination in the sense of flutter: new psychophysical measurements in monkeys. J Neurosci. 1997;17:6391–6400. doi: 10.1523/JNEUROSCI.17-16-06391.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koulakov AA, Raghavachari S, Kepecs A, Lisman JE. Model for a robust neural integrator. Nat Neurosci. 2002;5:775–782. doi: 10.1038/nn893. [DOI] [PubMed] [Google Scholar]
- Loewenstein Y, Sompolinsky H. Program no. 266.13, abstract viewer/itinerary planner. Washington, DC: Society for Neuroscience; 2002. [Google Scholar]
- Lorente de Nó R. Vestibular–ocular reflex arc. Arch Neurol Psychiatry. 1933;30:245–291. [Google Scholar]
- Marder E. From biophysics to models of network function. Annu Rev Neurosci. 1998;21:25–45. doi: 10.1146/annurev.neuro.21.1.25. [DOI] [PubMed] [Google Scholar]
- Matveev V, Wang X-J. Implications of all-or-none synaptic transmission and short-term depression beyond vesicle depletion: a computational study. J Neurosci. 2000;20:1575–1588. doi: 10.1523/JNEUROSCI.20-04-01575.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakamagoe K, Iwamoto Y, Yoshida K. Evidence for brainstem structures participating in oculomotor integration. Science. 2000;288:857–859. doi: 10.1126/science.288.5467.857. [DOI] [PubMed] [Google Scholar]
- Rainer G, Asaad WF, Miller EK. Memory fields of neurons in the primate prefrontal cortex. Proc Natl Acad Sci USA. 1998;95:15008–15013. doi: 10.1073/pnas.95.25.15008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renart A, Song P, Wang X-J. Homeostatic synaptic plasticity leads to robust spatial working memory function without fine-tuning of cellular properties. Neuron. 2003a;38:473–485. doi: 10.1016/s0896-6273(03)00255-1. [DOI] [PubMed] [Google Scholar]
- Renart A, Brunei N, Wang X-J. Mean-field theory of recurrent cortical networks: working memory circuits with irregularly spiking neurons. In: Feng J, editor. Computational neuroscience: a comprehensive approach. Boca Raton, FL: CRC Press; 2003b. [Google Scholar]
- Robinson DA. Integrating with neurons. Annu Rev Neurosci. 1989;12:33–45. doi: 10.1146/annurev.ne.12.030189.000341. [DOI] [PubMed] [Google Scholar]
- Romo R, Brody CD, Hernandez A, Lemus L. Neuronal correlates of parametric working memory in the prefrontal cortex. Nature. 1999;339:470–473. doi: 10.1038/20939. [DOI] [PubMed] [Google Scholar]
- Salinas E, Hernandez A, Zainos A, Romo R. Periodicity and firing rate as candidate neural codes for the frequency of vibrotactile stimuli. J Neurosci. 2000;20:5503–5515. doi: 10.1523/JNEUROSCI.20-14-05503.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seung H. How the brain keeps the eyes still. Proc Natl Acad Sci USA. 1996;93:13339–13344. doi: 10.1073/pnas.93.23.13339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seung HS, Lee DD, Reis BY, Tank DW. Stability of the memory of eye position in a recurrent network of conductance-based model neurons. Neuron. 2000a;26:259–271. doi: 10.1016/s0896-6273(00)81155-1. [DOI] [PubMed] [Google Scholar]
- Seung HS, Lee DD, Reis BY, Tank DW. The autapse: a simple illustration of short-term analog memory storage by tuned synaptic feedback. J Comput Neurosci. 2000b;9:171–185. doi: 10.1023/a:1008971908649. [DOI] [PubMed] [Google Scholar]
- Sharp PE, Blair HT, Cho J. The anatomical and computational basis of the rat head-direction cell signal. Trends Neurosci. 2001;24:289–294. doi: 10.1016/s0166-2236(00)01797-5. [DOI] [PubMed] [Google Scholar]
- Shen L. Neural integration by short term potentiation. Biol Cybern. 1989;61:319–325. doi: 10.1007/BF00203180. [DOI] [PubMed] [Google Scholar]
- Taube JS, Bassett JP. Persistent neural activity in head direction cells. Cereb Cortex. 2003;13:000–111. doi: 10.1093/cercor/bhg102. [DOI] [PubMed] [Google Scholar]
- Tegnér J, Compte A, Wang X-J. The dynamical stability of reverberatory neural circuits. Biol Cybern. 2002;87:471–481. doi: 10.1007/s00422-002-0363-9. [DOI] [PubMed] [Google Scholar]
- Tuckwell HC. Introduction to theoretical neurobiology. Cambridge: Cambridge University Press; 1988. [Google Scholar]
- Turrigiano GG. Homeostatic plasticity in neuronal networks: the more things change the more they stay the same. Trends Neurosci. 1999;22:221–227. doi: 10.1016/s0166-2236(98)01341-1. [DOI] [PubMed] [Google Scholar]
- Turrigiano GG, Nelson SB. Hebb and homeostasis in neuronal plasticity. Curr Opin Neurobiol. 2000;10:358–364. doi: 10.1016/s0959-4388(00)00091-x. [DOI] [PubMed] [Google Scholar]
- Turrigiano GG, Leslie KR, Desai NS, Rutherford LC, Nelson SB. Activity-dependent scaling ofquantal amplitude in neocortical neurons. Nature. 1998;391:892–896. doi: 10.1038/36103. [DOI] [PubMed] [Google Scholar]
- Varela JA, Sen K, Gibson J, Post J, Abbott LF, Nelson SB. A quantitative description of short-term plasticity at excitatory synapses in layer 2/3 of rat primary visual cortex. J Neurosci. 1997;17:7926–7940. doi: 10.1523/JNEUROSCI.17-20-07926.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X-J. Synaptic basis of cortical persistent activity: the importance of NMDA receptors to working memory. J Neurosci. 1999;19:9587–9603. doi: 10.1523/JNEUROSCI.19-21-09587.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X-J. Synaptic reverberation underlying mnemonic persistent activity. Trends Neurosci. 2001;24:455–463. doi: 10.1016/s0166-2236(00)01868-3. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.