Comparing INLA and OpenBUGS for hierarchical Poisson modeling in disease mapping

Abstract

The recently developed R package INLA (Integrated Nested Laplace Approximation) is becoming a more widely used package for Bayesian inference. The INLA software has been promoted as a fast alternative to MCMC for disease mapping applications. Here, we compare the INLA package to the MCMC approach by way of the BRugs package in R, which calls OpenBUGS. We focus on the Poisson data model commonly used for disease mapping. Ultimately, INLA is a computationally efficient way of implementing Bayesian methods and returns nearly identical estimates for fixed parameters in comparison to OpenBUGS, but falls short in recovering the true estimates for the random effects, their precisions, and model goodness of fit measures under the default settings. We assumed default settings for ground truth parameters, and through altering these default settings in our simulation study, we were able to recover estimates comparable to those produced in OpenBUGS under the same assumptions.

1. Introduction

In Bayesian modeling there are many challenges in conventional use of posterior sampling via MCMC for inference (1). One challenge is the need to evaluate convergence of posterior samples, which often requires extensive simulation and can be very time consuming. Software for implementing MCMC is now widely used and the packages WinBUGS, OpenBUGS, as well as certain SAS procedures and selected R packages such as MCMCpack (2), can provide access to these methods.

An Integrated Nested Laplace Approximation (3–7) has been implemented as an R package (INLA) targeted at performing Bayesian analyses without having to use posterior sampling methods. Unlike MCMC algorithms, which rely on Monte Carlo integration, the INLA package performs Bayesian analyses via numerical integration, and so does not require extensive iterative computation. In most cases, Bayesian estimation using the INLA methodology takes much less time as compared to estimation using MCMC. However, there have been few, if any, attempts at comparison of these packages’ performance capabilities with respect to spatial models in a disease mapping context. In this study, we compare how INLA performs in different modeling situations to OpenBUGS (8) via the BRugs package in R (9).

Here, we are particularly interested in comparing these packages for conventional Poisson data models when spatial structures are present in the covariates as well as through uncorrelated and correlated spatial random effects. We have designed models that express these attributes in different ways and apply them to mimic their use for disease mapping. These models are all commonly implemented for Bayesian analysis. We are also interested in exploring the different options available in INLA to optimize estimation as well as goodness of fit for these particular models to determine if INLA can perform in an equivalent fashion to OpenBUGS. For the analyses, we used the following versions of software and packages: R version 3.0.3, OpenBUGS version 3.2.3 rev 1012 (using default sampler settings), INLA version 0.0.1403203700, and BRugs version 0.8.3. We are aware that there are now more recent versions of these programs, but, as of August 2014, we were able to reproduce these results in the latest versions as well.

This paper is developed as follows. First, we discuss the development of our simulated dataset and the different models used for comparison. Next, we describe the methods used for comparing the performance of R-INLA and OpenBUGS. Following that, we display results, and finally, we discuss the benefits of one package versus the other under different scenarios.

2. Methods

2.1. Simulated Data and Models

In this paper, focus is on the use of INLA versus MCMC in a disease mapping context. Performance of the two methods is compared for the commonly used convolution model with spatially-varying and non-spatially-varying predictor variables. To evaluate the performance of these alternative approaches, we simulate data to establish realistic ground truth for disease risk variation. A common model for small area counts of disease is the Poisson data model. Specifically, define a count outcome as y in the i^th small area. We assume a map of m small areas. In addition, we assume an expected count (e_i) is available in each small area. Thus, our outcome has the distribution

$$y_i~\mathit{\text{Pois}}({\mu }_i)$$

$${\mu }_i=e_i{\theta }_i$$

In our simulations, we fix the expected rate for the area, and hence focus on the estimation of relative risk. To complete the parameterization, we assume a relative risk (θ_i) which is parameterized with a range of different risk models.

To satisfy this we chose the county map of the state of Georgia USA, which has 159 areas (counties). Hence, i = (1,…159) for this county set. We fix e_i at one for all models; while this is a simplifying assumption, it allows us to reduce the amount of variability present in the simulations. Furthermore, the assumption represents data associated with a fairly sparse disease presence.

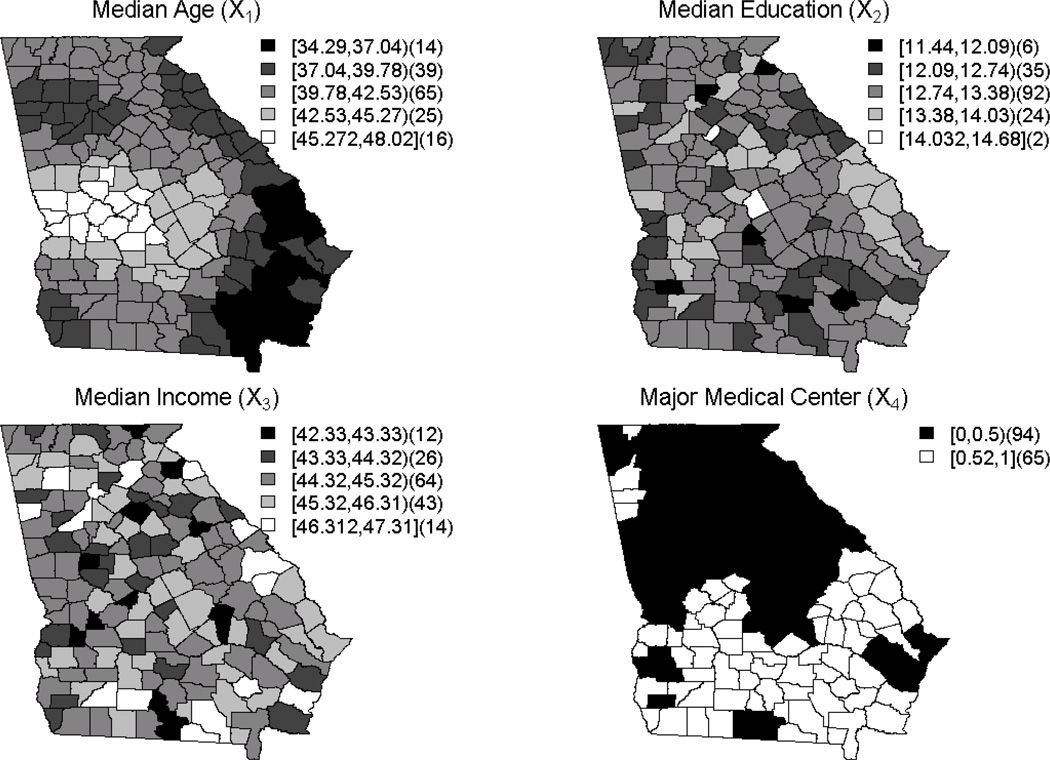
We examined six basic models for risk (M1 up to M6) which have different combinations of covariates and random effects as might be found in common applications. First, we generated four spatially varying predictors with different spatial patterns. The four chosen were median age (x₁ ), median education (x₂), median income (x₃), and a binary predictor representing presence/absence of a major medical center in a county ( x₄). These variables are county-level measures for the 159 counties in the state of Georgia. We chose these variables because it is important to represent a range of different spatial structures and types of predictors. Furthermore, observed predictors/covariates could have spatial correlation and so we included this in the definition of two of the predictors (median age and major medical center). Table 1 displays the predictors generated via simulation and their parameterization where the Gaussian parameters are the mean and variance. Also, note that the spatial predictors have a covariance structure applied, and this is explained in detail later.

Table 1.

Description of predictor variables and their simulation.

Variable	Spatial	Distribution (marginal)
Median Age (years)	Yes	x1 ~ Norm(40,4)
Median Education (years)	No	x2 ~ Norm(13,4)
Median Income (thousands)	No	x3 ~ Norm(45,1)
Major Medical Center (Yes/No)	Yes	π ~ Norm(0,25) logit (p) = π x4 ~ Bern (p)

These distributions lead to measures that reflect typical values for these variables. For example, the median age for a county in the U.S. is roughly 40, and the values do not vary much from one county to the next. Similar explanations can be applied to both the median education and median income variables. For the major medical center variable, this indicated marginal distribution leads to roughly half of the counties answering ‘yes’ to having a major medical center. These variables have been selected as placeholders, and should be thought of as representing any of the typical variables one might utilize in building disease mapping models.

The spatially-structured covariates were generated using the RandomFields package in R (10). The simulation uses the county centroid as a location to create a Gaussian Random Field (GRF), which is defined via a covariance structure. We assume a Gaussian covariance structure, and this assumption leads to a stationary and isotropic process (11). We specify this structure by using the RMgauss() command. We assume a power exponential covariance model of the form:

$$C(r)=e^{-\alpha r^2}$$

where r is the Euclidean distance between two centroids and the covariance parameter (α) is set as α = 1. Following the selection of the covariance structure, we must also set the mean of the GRF to create the same marginal distributions as described in Table 1 using the RMtrend() command. Finally, to simulate the GRF, we use the RFsimulate() command to create a GRF and assign a value to the spatial covariate. There is only a slight extension that must be applied when the spatial covariate is binary such as x₄. To create this variable, we use a GRF to simulate π mentioned in Table 1, rather than the covariate itself. From there, we simulate from a Bernoulli distribution to give the binary indicators for each county using expit (π) for the probabilities. The heat maps for these random fields can be seen in Supplemental Figure 1 Appendix A.2; while there is truly only one value simulated for each county, we interpolated these maps to better illustrate the distribution.

The distribution of all covariates, x₁,…, x₄, on the Georgia county base map is illustrated in Figure 1. Notice that the median age and major medical center reflect the heat maps shown in Supplemental Figure 1 Appendix A.2 and appear to have spatially dependent distributions. Though we have defined the mean and covariance structure of these GRF’s, the distribution can still take on many forms, and these variables reflect only one realization of the distribution.

Figure 1.

Display of the spatial distribution of simulated covariates per county.

Furthermore, picking these two variables (x₁ and x₄) to have the spatial structure also leads to at least one variable with spatial structure included in all of the first 5 models that we simulated which are shown in Table 2. Note that v_i follows an intrinsic CAR model with precision τ_v. M6 is simply a convolution model that allows us to explore how the spatial covariates may be affecting the spatial random effects, u and v. For these simulations, we fix the covariates as one realization from the distributions described in Table 1 and generate the outcomes using a fixed set of parameters ( e_i = 1, α₀ = 0.1, α₁ = 0.1, α₂ = −0.05, α₃ = −0.05, α₄ = 0.5, τ_u = 1 and τ_v = 1). While the magnitude of the α’s are quite small, this guarantees that the outcome variable has sparse disease patterning. We also use only one realization of the uncorrelated and correlated random effects described in Table 2. Then, log (θ_i) is calculated based on the fixed parameters and realizations. Finally, we generate the outcome as a Poisson variate with mean θ_i since e_i is fixed at one. The simulated datasets consist of sets of counts: $\left\{y_{\mathit{\text{ij}}}^{*}\right\},j=(1,\dots ,200)$ where j denotes the j^th simulated dataset.

Table 2.

Description of simulated model contents.

Model	Log relative risk
M1	log (θi) = 1 + 0. 1 x1i − 0.05x2i
M2	log (θi) = 1 + 0.1 x1i − 0.05x2i + ui ui ~ Norm(0,1)
M3	log (θi) = 1 + 0.1 x1i − 0.05x2i + ui + vi ui ~ Norm(0,1), vi ~ CAR (τv), τv = 1
M4	log (θi) = 1 + 0.1 x1i − 0.05x2i − 0.05x3i + 0.5x4i
M5	log (θi) = 1 + 0.1x1i − 0.05x2i − 0.05x3i + 0.5x4i + ui + vi ui ~ Norm(0,1), vi ~ CAR (τv), τv = 1
M6	log (θi) = 1 + ui + vi ui ~ Norm(0,1), vi ~ CAR (τv), τv = 1

For the uncorrelated and correlated spatial effects, u and v, mentioned in Table 2, we fix both precisions, τ_u and τ_v , to be one during the simulation process. Their equality guarantees that one of the spatial effects will not dominate the model and lead to identifiability issues (12). The uncorrelated spatial effect is distributed N (0,1); this is specified as such for simplicity as well as easy identification in the model fitting process. The correlated spatial random effect in these models is generated using the R package BRugs (9) such that they have an Improper conditional autoregressive (ICAR) (13) structure as follows:

$$v_i~N(\frac{1}{n_i}\sum _{i-l}{v}_l,\frac{1}{n_i{\tau }_v})$$

where i ≠ l, n_i is the number of neighbors for county i, and i ~ l indicates that the two counties i and l are neighbors (13). This set of neighbors simply includes the immediate neighborhood. Including these types of effects in spatial disease mapping models is very common as there is typically an uncorrelated random noise that varies from county to county as well as a correlated random structure that induces correlation based on neighborhoods.

Additional Simulation Variants

In the analysis described above, we mean centered the predictors to help in model goodness of fit. Another standardization technique for these types of analysis involves mean centering then dividing by the standard deviation per predictor. We created such a dataset using the M5 model (full predictor set with convolution random effects) to assess the effect of this standardization.

In addition, we also examined the effect of varying the precision of random effects to assess performance of model fit. Now, the true correlated spatial effect has a precision of 0.5. The uncorrelated spatial effect still has a precision of one, but we simulate a new realization of the variable. Because the precisions are no longer equal, this could lead to the masking, or domination effect eluded to earlier (12). Following the simulations of the new spatial effects, we created new Poisson outcomes with the same six models, aside from the spatial random effects, indicated in Table 2. These datasets are considered the validation datasets.

2.2. Fitted Models

The fitted models F1–F6 are described in Table 3. Note that v_i is an intrinsic CAR model with precision τ_v These models are based on the default prior distributions for INLA and vary by the number of covariates considered as well as the spatial random effects included to give a wide range of models as reflected in the simulation data section above. As part of examining the ability of INLA and OpenBUGS to recover true risk, we considered a variety of prior specifications. We changed the Gamma prior distributions on the precisions, τ_u and τ_v, to the following: Gam(2,1), Gam(1,1), and Gam(1,0.5). Of these options, Gam(1,0.5) offers the best alternative to the default prior distribution, Gam(1,5e– 05), as it is the most non-informative of the prior distributions explored. Since Gam (1,5e – 05) is the default non-informative prior distribution for precisions in INLA, we assumed this as default for our comparable OpenBUGS models. We would also like to note that when the outcome is Gaussian distributed, the default settings for INLA is a reasonable choice, and this is likely why it is set as such.

Table 3.

Fitted model description.

Model	Description
F1	log (θi) = a0 + a1x1i + a2x2i aj ~ Norm(0, τα) where τα is fixed
F2	log (θi) = a0 + a1x1i + a2x2i + ui aj ~ Norm(0, τα), where τα is fixed ui ~ Norm(0, τu), τu ~ Gam(1,5e – 05)
F3	log (θi) = a0 + a1x1i + a2x2i + ui + vi aj ~ Norm(0, τα), where τα is fixed ui ~ Norm(0, τu), τu ~ Gam(1,5e – 05) vi ~ CAR (τv), τv ~ Gam(1,5e – 05)
F4	log (θi) = a0 + a1x1i + a2x2i + a3x3i + a4x41 aj ~ Norm(0, τα), where τα is fixed
F5	log (θi) = a0 + a1x1i + a2x2i + a3x3i + a4x41 + ui + vi aj ~ Norm(0,τα), where τα is fixed ui ~ Norm(0,τu), τu ~ Gam(1,5e – 05) vi ~ CAR(τv), τv ~ Gam(1,5e – 05)
F6	log (θi) = a0 + ui + vi aj ~ Norm(0,τα), where τα is fixed ui ~ Norm(0,τu), τu ~ Gam(1,5e – 05) vi ~ CAR (τv), τv ~ Gam (1,5e –05)

To attempt recovering the ground truth indicated in the simulation data section, we build these models in both INLA and WinBUGS to assess the two packages’ recovery abilities. These abilities are assessed as described in the comparison techniques section below. Also, note that we mean center the fitted continuous predictors to aid in model fit.

In this paper, we do not consider model misspecification; we simply use the appropriate fitted model applied to the corresponding simulated data. From here on, we will refer to these results with respect to the fitted model and simulated data that are being used. For example, M1 simulated data with F1 fitted model will be referred to as M1F1.

Fitting Models to Simulation Variants

We also fit the models to these variants using the Gam(1,0.5) prior distribution in a similar fashion to that described previously in this section to determine how this dataset characteristic affect the model fits. These models will be referred to as, for example, M5F5S and M5F5V respectfully. S denotes standardization and V denotes spatial precision variant.

2.3. Comparison Techniques

For this study, we build equivalent models in INLA and OpenBUGS based on the prior distributions indicated in Table 2 and fit them to the 200 datasets all simulated in the same manner. For the OpenBUGS model, this is accomplished using the BRugs package in R.

Comparisons of the models on the two different packages is accomplished by calculating the mean squared error (MSE) of the parameter estimates, fitted y values, and the relative risk (θ) as well as mean squared predictive error (MSPE), the number of effective parameters (pD), mean deviance $(\overline{D(\theta )})$ and deviance information criterion (DIC) for each model.(14)

We compute MSE for the parameter estimates, outcome measures, and relative risk as well as MSPE as follows:

$$\mathit{\text{MSE}}(\alpha )=\sum _{j=1}^J\frac{{({\alpha }_j-{\widehat{\alpha }}_j)}^2}{J},$$

$$\mathit{\text{MSE}}(M)=\sum _{i=1}^n\frac{{(y_i^{*}-{\widehat{y}}_i)}^2}{n},$$

$$\mathit{\text{MSE}}(\theta )=\sum _{i=1}^n\frac{{({\theta }_i^{*}-{\theta }_i)}^2}{n},\text{and}$$

$$\mathit{\text{MSPE}}=\sum _{i=1}^n\frac{{(y_i^{*}-y_{i,\mathit{\text{pred}}})}^2}{n}$$

where α_j, ${\theta }_i^{*}$, and $y_i^{*}$ are the true fixed and simulated values respectively such that the * indicates simulated values. Furthermore, J is the number of covariates considered in each specific model, and n is the number of counties. MSE(α) uses the posterior values of the parameter estimates since sampling is not available in INLA. These measurements are all averaged over the 200 simulated datasets. To access ŷ in OpenBUGS, we must collect the posterior values of µ_i from the samples; we use this same value for θ_i since they are equivalent because the expected rate, e_i, is set at one. To access y_{i, pred} we simply set up code such that it is distributed Poisson with mean µ_i. Note that y_pred is initialized rather than data-read to generate predictive values. An example of our OpenBUGS model code is located in the Appendix section A.1. To calculate the MSPE in INLA, we must create copies of all of the model components, append these copies to the original vectors, add in an additional “iid” random effect, and create an empty vector, rather than a copy, to append to the outcome variable. Now, the vector that typically only contains ŷ_i will have length 2n where the second half is the predicted y values to use as y_{i, pred} in the MSPE calculation. An example using M3F3 can be found in Appendix section A.1.

Computations for the D(θ), pD, and DIC are built into and easily attainable in both packages. They are calculated as follows:

$$D(\theta )=-2\sum _i\text{log}(p(y_i|\theta )),$$

$${\mathit{\text{pD}}}_{\mathit{\text{OpenBUGS}}}=\overline{D(\theta )}-D(\theta ),$$

$${\mathit{\text{pD}}}_{\mathit{\text{INLA}}}=n-\mathit{\text{tr}}\{Q(\theta )Q^{*}{(\theta )}^{-1}\},\text{and}$$

$$\mathit{\text{DIC}}=\overline{D(\theta )}+\mathit{\text{pD}}$$

respectively. The first two formulas show the definitions of deviance in OpenBUGS and INLA respectively. To calculate $\overline{D(\theta )}$ from D(θ) produced in OpenBUGS, we simply average this value over a sample from the converged Markov chain (15). Using D(θ) from INLA to calculate $\overline{D(\theta )}$ requires a two-step process that initially computes the conditional mean using univariate numerical integration for each i = (1,…159) (5). Next, θ is integrated out of the expression with respect to p(θ |y). Furthermore, the deviance for INLA is calculated at the posterior mean (or mode in the case of hyperparmeters) of the latent field rather than the posterior mean of all parameters as seen in OpenBUGS. pD_OpenBUGS is the classical definition of pD, and D(θ) is calculated as the deviance computed at the posterior mean estimates. For pD_INLA, n is the number of observations, Q(θ) is the prior precision matrix, and Q*(θ) is posterior covariance matrix of the Gaussian approximation (5). We average these estimates over the 200 simulated datasets to gain an overall assessment of performance

For all of these measures of goodness of fit, lower values indicate a superior model. However, valid comparisons can only be made within models as the likelihoods change when the outcome being modeled changes. Furthermore, a lower value in one software package does not necessarily mean that it fits better than the other package as the DIC calculations do differ from one to the other. In this situation, MSE and MSPE are the best outlets for comparing across platforms.

3. Results

In order to have comparable results, we must run the OpenBUGS models to convergence. While we are not able to confirm convergence for all 200 datasets easily, we do check a representative percentage of the datasets by way of the Brooks-Gelman-Rubin (BGR) diagnostic plots available in OpenBUGS. All plots indicate that we achieve convergence for these 6 models, and we always extend the model runs for 2500 iterations per chain beyond the convergence point in these test datasets.

Table 4 shows the parameter estimates and their significances associated with each model as well as the truth. Compared to the truth, most models do well with recovery for the fixed effects, with default precision prior distribution. The estimates associated with the spatial variables, x₁ and x₄, are well estimated much of the time while this is not true for the non-spatial ones. This could be due to the fact that the true values of these parameters have larger magnitudes. These issues are common across both OpenBUGS and R-INLA. As far as τ_u and τ_v are concerned, the estimates show that INLA is far overestimating the true values of the precision parameters; OpenBUGS is also overestimating τ_v but not nearly as much as INLA. The INLA Laplace models (INLA(FL)) indicate that we specified for INLA to use the full Laplace strategy rather than the default simplified Laplace strategy (INLA(SL)) (16). With this specification, we see that there are not many differences with respect to the fixed effect estimates. It is interesting that the standard deviations associated with INLA(SL) and INLA(FL) are the same in nearly all situations when rounded to the hundredth decimal place. We also note that the estimates for α₁ change by a fair margin when comparing M1F1 to M3F3 or M4F4 to M5F5. Similarly, the estimates for α₄ change when comparing M4F4 to M5F5. As both α₁ and α₄ are spatial covariates, this may indicate influence from the spatial random effect estimates.

Table 4.

Parameter estimates associated with both statistical software packages, based on the default precision prior distribution.

Model	α0	α1	α2	α3	α4	τu	τv
M1F1 OpenBUGS	0.081 (0.08)	0.097 (0.03)*	−0.055 (0.15)	---	---	---	---
M1F1 INLA(SL)	0.085 (0.08)	0.097 (0.03)*	−0.056 (0.16)	---	---	---	---
M1F1 INLA(FL)	0.082 (0.08)	0.097 (0.03)*	−0.055 (0.16)	---	---	---	---
M2F2 OpenBUGS	0.128 (0.12)	0.163 (0.03)*	−0.052 (0.23)	---	---	0.955 (0.20)	---
M2F2 INLA(SL)	0.152 (0.12)	0.164 (0.04)*	−0.054 (0.22)	---	---	18654 (18573)	---
M2F2 INLA(FL)	0.148 (0.12)	0.164 (0.04)*	−0.054 (0.22)	---	---	18654 (18573)	---
M3F3 OpenBUGS	0.122 (0.12)	0.166 (0.04)*	−0.018 (0.23)	---	---	0.938 (0.19)	209.47 (177)
M3F3 INLA(SL)	0.145 (0.12)	0.165 (0.04)*	−0.018 (0.23)	---	---	12490 (12472)	18768 (18541)
M3F3 INLA(FL)	0.141 (0.12)	0.166 (0.04)*	−0.018 (0.23)	---	---	12490 (12472)	18768 (18541)
M4F4 OpenBUGS	−0.123 (0.10)	0.101 (0.02)*	−0.040 (0.15)	−0.054 (0.07)	0.481 (0.14)*	---	---
M4F4 INLA(SL)	−0.122 (0.11)	0.101 (0.02)*	−0.041 (0.16)	−0.054 (0.07)	0.486 (0.14)*	---	---
M4F4 INLA(FL)	−0.127 (0.11)	0.101 (0.02)*	−0.040 (0.16)	−0.054 (0.07)	0.487 (0.14)*	---	---
M5F5 OpenBUGS	0.016 (0.14)	0.160 (0.04)*	−0.05 (0.21)	−0.100 (0.10)	0.237 (0.21)	0.940 (0.20)	189.57 (165)
M5F5 INLA(SL)	0.020 (0.15)	0.161 (0.04)*	−0.061 (0.23)	−0.105 (0.11)	0.279 (0.21)	18345 (18245)	18446 (18385)
M5F5 INLA(FL)	0.014 (0.12)	0.161 (0.04)*	−0.061 (0.23)	−0.105 (0.11)	0.279 (0.21)	18345 (18245)	18446 (18385)
M6F6 OpenBUGS	0.149 (0.12)	---	---	---	---	0.955 (0.20)	202.77 (172)
M6F6 INLA(SL)	0.172 (0.12)	---	---	---	---	17989 (17800)	18712 (18558)
M6F6 INLA(FL)	0.169 (0.12)	---	---	---	---	17989 (17800)	18712 (18558)
Truth	0.1	0.1	−0.05	−0.05	0.5	1	1

The notation is as follows: average of means, (average of standard deviations), and * indicates a well estimated variable.

Supplemental Table 1 in Appendix section A.2 shows the goodness of fit measures associated with each model and software package. Some of these estimates appear to be exactly the same after rounding, but in actuality they are different numbers. Here, we see some differences among the models both within and across platforms. For the models without random effects (M1F1 and M4F4), the pD values are very close, and INLA (FL) produces significantly lower values than INLA(SL). This relationship carries over for the DIC in most cases as that measure is directly related to the pD. The MSPE and MSE(M) estimates produced by both packages are nearly identical, but when the Laplace strategy is applied in INLA, it produces higher estimates for the spatial models (M2F2, M3F3, M5F5, and M6F6). This table also includes results for the models using the alternative precision prior distributions. When we adjust the precision prior distributions for OpenBUGS, we begin to see significant differences in the pD and thus the DIC produced for the convolution models (M3F3, M5F5, and M6F6). Note that when running OpenBUGS for the altered prior distributions, there are a few (no more than 3 per model) datasets that lead to negative pD values in M3F3, M5F5, and M6F6. We remove these results from the mean calculations.

Table 5 illustrates how the precision parameters change after alterations to the default settings. In addition to changing the default prior distributions, the inla.hyperpar() command is also explored to try and attain better estimates of the hyperparameters involved with estimating the random components of the models. While this function only affects the hyperparameter estimates, all others remain the same. It is obvious that these estimates are different from the original estimates located in the first row, but they still do not reflect the true values. In fact, they are further away from the truth by making the effects more precise (17).

Table 5.

Altered INLA precision estimates compared to the original estimates as well as the truth.

Model	parameter	M2F2	M3F3	M5F5	M6F6	True value
INLA Gam(1,5e-05)	τu	18656 (18577)	12491 (12475)	18485 (18381)	17990 (17804)	1
	τv	---	18770 (18546)	18570 (18440)	18714 (18563)	1
INLA Ga(1,5e-05) inla.hyperpar()	τu	22376 (15350)	15037 (10514)	21962 (15924)	21886 (15046)	1
	τv	---	21938 (16641)	21920 (15989)	22525 (15636)	1
INLA Gam(1,0.5)	τu	0.98 (0.20)	1.03 (0.23)	1.07 (0.25)	1.06 (0.24)	1
	τv	---	3.92 (2.44)	3.42 (2.22)	3.94 (2.43)	1
OpenBUGS Gam(1,0.5)	τu	0.94 (0.19)	1.00 (0.23)	1.03 (0.25)	3.34 (2.08)	1
	τv	---	1.04 (0.26)	3.79 (2.24)	3.76 (2.25)	1
OpenBUGS Gam(1,5e-05)	τu	0.96 (0.20)	0.94 (0.19)	0.94 (0.20)	0.96 (0.20)	1
	τv	---	209.47 (177)	189.57 (165)	202.77 (172)	1

The next set of precision estimates relate to the models where we specified Gam(1,0.5) as the prior distribution. Results for the Gam(2,1)and Gam(1,1) priors are located in Supplemental Table 2 Appendix section A.2. Changing these prior distributions greatly alters the results with respect to the precision estimates while the fixed and goodness of fit estimates for these models remain nearly identical. In fact, the standard deviations of the estimates remain very close to the originals. It is obvious that R-INLA improves drastically with respect to the precision estimates related to both effects, correlated and uncorrelated. While OpenBUGS produces more precise estimates under the default settings, changing the prior distributions continues to improve the accuracy of those estimates in this package as well. We see now that the estimates produced in INLA reflect those produced in OpenBUGS very closely. This is true for all of the alternative prior options explored. Again, the Gam(1,1) prior seems to perform the best as it produces estimates that are the closest to the truth in all cases and for both packages. Unlike the goodness of fit measures, though, the differences seen here are not significant within the alternative prior distributions.

The last alteration we attempt involves scaling the models based on the Scaling IMGRF models tutorial on the INLA website, and these results can also be found in Supplemental Table 2 Appendix section A.2 (18). We make this alteration using the Gam(1,5e – 05) and Gam(1,0.5) prior distributions only. This tutorial suggests implementing the following global command: inla. setOption (scale.model.default = TRUE) to scale the global variance of the model such that ${\sigma }_{\mathit{\text{GV}}}^2(x)=1$, then the reference variance, ${\sigma }_{\mathit{\text{ref}}}^2(x)$, is used to scale the hyperprior as follows: $\frac{\tau }{{\sigma }_{\mathit{\text{ref}}}^2(x)}$ Based on the results below, we can see that this modification does not always ensure that the precisions are closer to the truth (19).

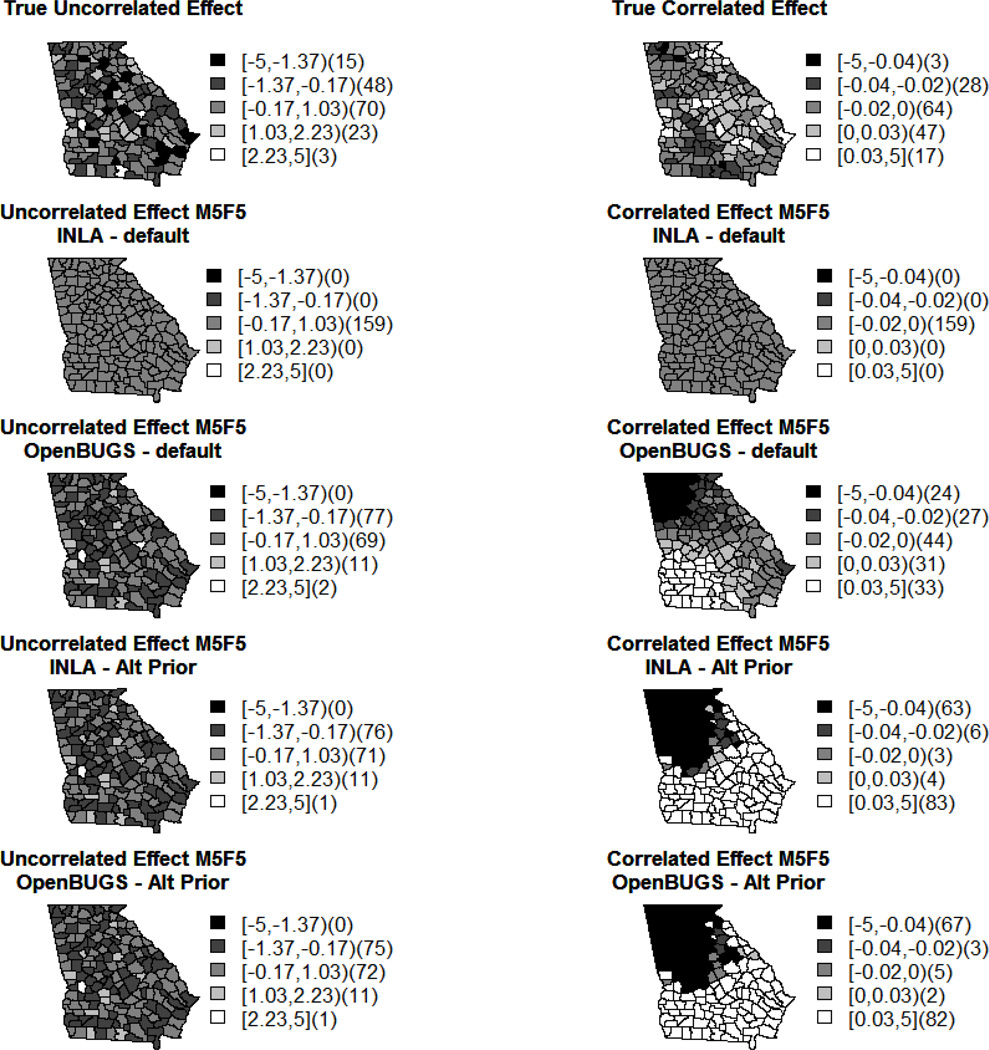
Figure 2 shows how the models in OpenBUGS and INLA recover the uncorrelated and correlated spatial effects respectively using M5F5. The other model estimate maps can be found in Supplemental Figures 2–5 Appendix A.2. The values dislpayed are averaged over the 200 datasets; furthermore, the ‘truth’ is only one realization of the random effect, but this is what we used to simulate the outcomes. Note that all of these maps have been scaled in the same way as the plot displaying the true effect to gain a better comparison and understanding of the relationship being displayed, and this is why the INLA plots appear to have no variation. OpenBUGS seems to be recovering both effects better than INLA under the default settings, but neither set of models are performing as well as we would like with respect to the correlated random effect, v. The INLA estimates seem to be much closer to zero than they should be, and this is supported by the larger precision estimates shown in Tables 3 and 5 above. Also, the discrepancies among the correlated effects may be reflecting the spatial nature of some of the covariates. Furthermore, others have noted correlated spatial effects behaving too smoothly in certain cases.

Figure 2.

The true and average estimated spatial effects as calculated in INLA and OpenBUGS under default and alternative priors using M5F5.

The maps notated as M5F5p display the uncorrelated and correlated effects produced in INLA and OpenBUGS when the prior distributions for τ_u and τ_v are changed from Gam(1,5e – 05), the default, to Gam(1,0.5). This prior alteration results in a much better reproduction of the spatial random effects, as reflected in the precision estimates displayed in Table 5. The uncorrelated effects are very similar for both INLA and OpenBUGS, and they also reflect the truth much better than before with the default prior distributions. As far as the correlated effects are concerned, we see that the estimations for these effects are almost identical when looking at the results produced in OpenBUGS and INLA, but they still do not reflect the truth as well as we may like. As mentioned before, though, these effects do reflect the smoothness expected among correlated effects as well as the spatial structures present in some of the covariates. These figures also reflect the results produced for the other alternative precision prior distributions, as they are alike. Finally, Supplemental Figure 6 Appendix A.2 is the sum of the correlated and uncorrelated random effects seen in Supplemental Figures 4 and 5. This figure looks much alike Supplemental Figure 4 as the magnitude of the uncorrelated effect is larger than that of the correlated one. This may be one of the factors inhibiting our ability to appropriately recover the correlated random effect.

Simulation Variants

The results in Supplemental Table 3 Appendix A.2 show the fit of M5F5S when the covariates are standardized rather than only mean centered for the simulation process. These results show that standardization leads to a well estimated α₄, but also some larger standard deviations with respect to OpenBUGS for α₂ and α₃. Note that α₁ for INLA(FL) is very close to being well estimated. The precision estimates for OpenBUGS continue to be slightly closer to the truth though this is not statistically significant.

Supplemental Table 4 Appendix A.2 shows the goodness of fit measures for the standardized models, and these results show similar patterns. We cannot truly compare the deviance and DIC measures presented here to the previous results since the outcomes are different, but we can look at the patterns among the other measures. We continue to see a separation with respect to the MSPE while the different MSE estimates are nearly identical. Supplemental Figure 7 Appendix A.2 illustrates the maps of the uncorrelated and correlated effects produced for the standardized model, M5F5S. These maps look comparable to what we saw previously for M5F5, and we still see much likeness when comparing the INLA results to the OpenBUGS results.

The results in Supplemental Table 5 Appendix A.2 show the re-fit of the models with a Gam(1,0.5) prior on the precisions of the spatial random effects with the validation dataset, which offers a different distribution for the correlated random effect, and a different realization of the uncorrelated random effect. For the INLA models, we continued to use the Laplace strategy for a better fit. Based on these results, we are still seeing changes in the estimates for α₁ when comparing models M1F1V and M3F3V; this time we actually see this estimate fail to be well estimated in M3F3V while it is well estimated in M1F1V. We also see this occur for α₁ when comparing M4F4V to M5F5V. For α₄ in M4F4V and M5F5V, the estimates are different, but they are not well estimated in either model. Also, the standard deviations are larger. With respect to the precision estimates, we still see an overestimation of the correlated effect, τ_v , while the uncorrelated effect, τ_u, is recovered fairly well. Even though the truth for τ_v is smaller in this validation study compared to the first simulated dataset, some of the estimates seen in the table are actually higher in this situation.

Supplemental Table 6 Appendix A.2 shows the goodness of fit estimates for the models using the validation dataset. We see OpenBUGS producing at least slightly lower MSE(M) and MSPE values than INLA(FL). For MSE(0), the relationship is alike the models with the original data in that OpenBUGS consistently produces slightly lower estimates when spatial random effect are considered. The mean deviance is very similar for all models and packages. Note that there were also some negative pD values for M5F5V and M6F6V in OpenBUGS; these were removed in the same way as before.

Supplemental Figures 8 and 9 Appendix A.2 demonstrate how well the models recover the true uncorrelated and correlated spatial random effects when applied to the validation dataset. Here we see an analogous situation to the first set of simulated data in that the uncorrelated effect is recovered very well while the correlated is not recovered quite as well as we would like it to be. We also notice, again, that the correlated effect is smoother than the true correlated effect. Furthermore, the INLA(FL) results are very similar to the OpenBUGS results just as we noted. One difference is that there is not as much of a change in the estimation when it comes to comparing M6F6V with the others that include covariates. This may be because the true correlated spatial effect is distributed more similarly to the spatial covariates. Following that, Supplemental Figure 10 Appendix A.2 shows the sum of the correlated and uncorrelated random effects, and as seen before, this looks well estimated because the correlated effect is of a much smaller magnitude compared to the uncorrelated effect. Because of this, it also looks analogous to Supplemental Figure 8.

4. Discussion

The results above show some substantial differences in the performances of INLA and OpenBUGS. For the default settings, we see that many of the fixed effect parameter estimates are alike for the two software packages, but the differences become more evident when looking at the goodness of fit measures and spatial random effect estimates. OpenBUGS seems to outperform INLA when spatial random effects are included in the model. This is shown in the MSE(M) and MSPE when spatial random effects are added to the models as well as the individual plots of the produced estimated spatial effects which is to be expected based on the precision estimates. Furthermore, we note improvements to the INLA(SL) models when we specify the full Laplace strategy and even more still after altering the default precision prior settings.

INLA does have an advantage over OpenBUGS in computation time. The computing time for these 200 simulations is no more than a couple of hours for INLA while it takes OpenBUGS several days. Obviously, these times fluctuate depending on the computer specifications, what other processes are actively running on the system in use, and, in the case of OpenBUGS, the number of parameters that are being collected. If we did not need to recover u, v, y_pred or µ, the computation time could be much shorter, but even taking that into account, OpenBUGS will never be as fast as INLA. Note that we run all simulations on the same server, so these arguments are appropriate. This indicates that, especially for simpler models, if computation time is an issue, then INLA may be the better option. Additionally, R-INLA is noted for being able to apply non-discrete spatial effects (20).

A shortcoming for INLA involves the ability to use hyperparameters as flexibly as in OpenBUGS. For example, we were unable to implement prior distributions for the standard deviations in INLA, while this can be done easily in OpenBUGS. Placing prior distributions on the standard deviations rather than fixing them or placing them on the precisions can lead to better model fits in some situations. Furthermore, there is not an easy way to place hyperprior distributions on the precisions of the fixed effects.

There are many options in INLA for improving the models. Initially, we explore specifying the use of a full Laplace approximation strategy in INLA, but this does not lead to different parameter estimates and takes a longer time to complete for the 200 datasets and 6 models. Specifying the full Laplace strategy did, however, lead to different goodness of fit measures that were closer to those produced with OpenBUGS. Furthermore, the simplified Laplace strategy is not sufficient for computing predictive measures (17). There is one other strategy that can be implemented, the Gaussian, and it is the most efficient but least accurate (16). Following that, we explore using the inla.hyperpar() option with no avail. This option is supposed to improve the hyperparameter estimates, but, as displayed in Table 5, these results actually brought the estimates further from the truth. This function is defined as a way to retrieve more precise estimates of the hyperparameters (17), and this is how it behaves in this simulation study. We also consider changing the default prior distributions with respect to the precision parameters for both the INLA(FL) and OpenBUGS models, and the results are much improved. Both the uncorrelated and correlated random effect estimates are much closer to the truth. There also appears to be less separation between the estimates produced in OpenBUGS versus those produced in INLA(FL). Of the options attempted for these altered prior distributions, the Gam(1,1) prior preformed the best, but it is also the most informative. The Gam(1,0.5) option is a good choice as it is still fairly non-informative. Furthermore, it still shows substantial improvements over the default settings. Finally, implementing the model scaling feature did not aid in the models gaining estimates closer to the truth, which is what we are aiming for. It seems as though this feature is mostly for assisting in model interpretability and comparability.

When we apply the models to the validation datasets we see very similar patterns to those present in the first simulation datasets, but there were also some differences.

Fewer of the covariates were well estimated in the validation dataset. Also, the correlated random effect estimates did not vary as much from model to model as in the first datasets, but they were still not as close to the truth as we would like for them to be. This could be due to the fact that the true correlated spatial effect is slightly closer in its distribution to the spatially structured covariates. Furthermore, the uncorrelated effect estimates do not seem to be recovered quite as well. These differences may be due to the masking effects from either the spatially structured covariates or the unequal true precision values. We see similarities with the patterns present in the goodness of fit measures though these values cannot be compared directly because the model ingredients are not the same.

During this study, we uncovered many interesting properties associated with both packages for these types of spatial disease mapping models. One relates to having a mixture of spatially structured covariates as well as spatial random effects. There appears to be a type of masking that occurs when both are present in the model. This is seen in two ways. First, by looking at the parameter estimates presented in Table 3; here, we notice that the estimates for α₁ change from M1F1 to M3F3. A comparable change occurs for α₄ when considering M4F4 verses M5F5. In the second case, α₄ changes from being well estimated to no longer being well estimated. Second, the masking effect is seen by comparing the correlated spatial effect estimates associated with M6F6 to all other models. Since M6F6 does not have any covariates, spatial or otherwise, we can see that the covariates may be playing a role in changing the estimates produced. Note that this was not as evident in the validation study, especially with respect to the plots of the correlated spatial random effect estimates.

Another interesting property of these models is that, in general, the correlated spatial effect tends to be overestimated and well as overly smooth which is evident in the figures produced above. We also do not see the non-spatial covariates being well estimated in any of the models. This could be due to the fact that the magnitudes of the true estimates are smaller than the others. Furthermore, when considering the validation dataset, we see that the models have a more difficult time recovering the true effects, and this may be due to the occurrence of a masking effect from the unequal true precisions (12).

5. Conclusion

Ultimately, INLA, in its default state, does not perform as well as OpenBUGS with respect to the precision parameter estimates for the spatial random effects, but it is much more computationally efficient. Through this simulation study, we learned that by specifying the full Laplace strategy, we result in better fitting models that are equivalent to OpenBUGS. Furthermore, altering the precision prior distributions for correlated and uncorrelated random effects brings these estimates much closer to the truth as well as to the values produced by OpenBUGS when the same prior distributions are used. Thus, for Poisson modeling in disease mapping, it is of utmost importance to adjust the default settings when using INLA as an alternative for Bayesian Analysis, especially when spatial random effects are included in the models.

• The default priors in INLA are not suitable in the disease mapping framework.

• We explore many options for improving INLA results.

• INLA’s main advantage over OpenBUGS is computation time.

• INLA is unable to use hyperparameters as flexibly as in OpenBUGS.

• INLA and OpenBUGS can produce comparable results with appropriate alterations.