Dynamical analysis of periodic bursting in piece-wise linear planar neuron model

Abstract

A piece-wise linear planar neuron model, namely, two-dimensional McKean model with periodic drive is investigated in this paper. Periodical bursting phenomenon can be observed in the numerical simulations. By assuming the formal solutions associated with different intervals of this non-autonomous system and introducing the generalized Jacobian matrix at the non-smooth boundaries, the bifurcation mechanism for the bursting solution induced by the slowly varying periodic drive is presented. It is shown that, the discontinuous Hopf bifurcation occurring at the non-smooth boundaries, i.e., the bifurcation taking place at the thresholds of the stimulation, leads the alternation between the rest state and spiking state. That is, different oscillation modes of this non-autonomous system convert periodically due to the non-smoothness of the vector field and the slow variation of the periodic drive as well.

Introduction

The biological nervous system is a very complex information network composed of innumerable coupling neurons, and it can encode, transfer and integrate information by firing activities. The firing activities of nervous system are mainly embodied in generation and processing of action potential pulses by neurons, and thus neural information coding is reflected by time rhythms and oscillating patterns of impulse firing sequences (Yang and Lu 2008; Du et al. 2010). Neurons often exhibit bursting phenomenon, which distinctly characterized by alternating phases of spiking and rest state. Sometimes the bursting behavior is referred to as “mixed-mode oscillations” in some literatures (Marszalek and Trzaska 2010). Its dynamical behavior and classification have been investigated in many neural firing experiments (Harris-Warrick and Flamm 1987; Johnson et al. 1992) and theoretical studies (Zhang et al. 2014; Xu and Wang 2014).

A series of neuron models has been built which can accurately reflect corresponding action potential shapes for different neuronal cell types (Hodgkin and Huxley 1952; Rinzel and Lee 1987; Chay et al. 1995; Izhikevich 2003; Dong et al. 2014). Typically such models, being based around that of Hodgkin and Huxley (1952), are high dimensional and usually need to be analyzed using singular perturbation theory. Besides, a class of one dimensional integrate-and-fire (IF) type model is often advocated since it is easy to analyze (Tiesinga 2002). However, disadvantages of both cases are existed. For example, the high dimensional models do not necessarily pave the way for tractable network studies, while the IF models do not quite capture the dynamics of a truly excitable system with gating variables (Coombes 2008). Thus a search for planar models possessing one voltage and one gating variable that can mimic the behavior of high dimensional conductance based models is naturally operated. Perhaps the most famous example of such a model is the FitzHugh–Nagumo model (Fitzhugh 1961; Nagumo et al. 1962), which has many of the same characteristics as the Hodgkin–Huxley model. Inspired by this, piece-wise linear (PWL) nullclines is introduced to build a broader class of PWL models that can describe the rich dynamical behavior of many common cell types (Yamashita and Torikai 2014).

As far as theoretical analysis is concerned, analysis of bursting has been studied by many authors, for example Rinzel (1985), Sherman and Rinzel (1992) and Smolen et al. (1993). They revealed the inherent dynamical nature of bursting by some crucial bifurcations. On the basis of these works, Izhikevich (2000) considered more comprehensive bifurcations associated with bursting and provided a more complete theoretical classification, that is top–down fast–slow dynamical bifurcation analysis, which has been extended to be used in non-autonomous system recently.

However, up to now, most of the work is confined to the smooth systems. Because of the non-smoothness of the vector field of non-smooth systems, there’s an obvious difference between the bifurcation mechanism of non-smooth systems and that of smooth system (Qin and Lu 2009). Besides, the analysis method applied to smooth systems could not be appropriate for non-smooth systems (Simpsona and Meiss 2012). The bursting phenomena of non-smooth systems especially under non-autonomous condition are still the open problems. In recent years, a class of planar models possessing one voltage and one gating variable that can mimic the behavior of high dimensional neuron models is extensive studied (Jaume et al. 2013). In this case the PWL element has been introduced to mathematical models. This gives rise to the so-called McKean model (McKean 1970; Tonnelier 2003). How to understand the behavior of these PWL systems is very important to study the effect of bursting in fundamental functions of the brain such as information transmission, encoding and processing.

In this paper, the two-dimensional McKean model of a single neuron activity, which is a piecewise linear model is explored. The non-smooth model with a periodic drive is focused on. Specifically, we analyze this non-smooth model with a slowly varying periodic drive and study the interaction of the fast-slow dynamics with the non-smooth bifurcation.

The model and numerical simulations

The McKean model is a planar PWL models that can mimic the firing response of several different cell types. It can be written as system (1) (Coombes 2008),

$$\begin{array}{cc}\hfill C\dot{v}& =f(v)-w+I,\hfill \\ \hfill \dot{w}& =g(v,w)=v-\mathit{\gamma }w,\hfill \\ \hfill \end{array}$$ 1

where f(v) is given by

$$f(v)=\left\{\begin{array}{cc}-v,\hfill & v<a/2\\ v-a,\hfill & a/2\le v\le (1+a)/2\\ 1-v,\hfill & v>(1+a)/2\end{array}\right.$$

Here, v is membrane potential, C > 0, γ > 0 and f(v) is a piecewise linear caricature of the cubic FitzHugh–Nagumo nonlinearity $f(v)=v(1-v)(v-a)$, whilst g(v, w) describes the linear dynamics of the gating variable and I is an external drive (Coombes 2008). For the neuronal systems, the stimulation may be constant or not, for example, a periodic stimulation. Thus, the external drive is let in the form as $I=cos({\mathit{\omega }}_{0}t)$ here.

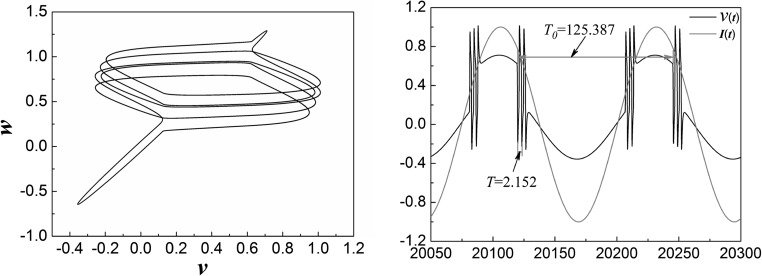
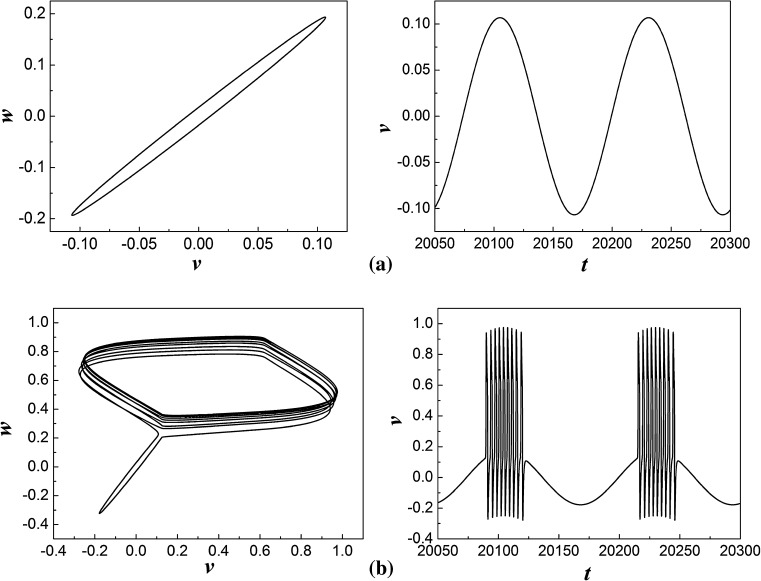
In order to reveal the dynamical behavior of this system, these parameters are fixed at C = 0.1, a = 0.25, γ = 0.55 as Ref. Coombes (2008) shows, meanwhile ω₀ is set as ω₀ = 0.05. The periodic bursting can be observed by numerical simulation (seen in Fig. 1).

Fig. 1.

Phase portraits and time series of system (1)

In order to explore the interior relation between the behavior of bursting and the periodic stimulation, time-dependence of stimulation is overlaid on the time series of the system. During each longest period demonstrated in the time series, which is the same as the period of the external drive, another frequency can be observed from the time series, which is much higher than the frequency of stimulation (see Fig. 1). The co-existence of these two frequencies leads the dynamics of the system exhibit fast–slow effect. In the following, we will investigate the mechanism of this periodic bursting based on non-smooth bifurcation in details.

Non-smooth bifurcation mechanism

Firstly, for the autonomous case, that is, the value of I is fixed, system (1) can be described as follows,

$$\begin{array}{cc}\hfill C\dot{v}& =f(v)-w+I_0\hfill \\ \hfill \dot{w}& =v-\mathit{\gamma }w,\hfill \\ \hfill \end{array}$$ 2

where $f(v)=\left\{\begin{array}{cc}-v,\hfill & v<a/2\\ v-a,\hfill & a/2\le v\le (1+a)/2\\ 1-v,\hfill & v>(1+a)/2\end{array}\right.$.

Two switching boundaries exist, denoted by Σ₁: v = a/2 and Σ₂: v = (1 + a)/2. Thus, three equilibria can be observed for different certain values of current, which expressed as

$$\begin{array}{cc}\hfill E_0:& \left\{v=\mathit{\gamma }{I}_0/(\mathit{\gamma }+1),w=I_0/(\mathit{\gamma }+1)\right\}\text{for}v<a/2,\hfill \\ \hfill E_1:& \left\{v=\mathit{\gamma }(a-I_0)/(\mathit{\gamma }-1),w=(a-I_0)/(\mathit{\gamma }-1)\right\}\hfill \\ \hfill & \text{for}a/2\le v\le (1+a)/2,\hfill \\ \hfill E_2:& \left\{v=\mathit{\gamma }(1+I_0)/(\mathit{\gamma }+1),w=(1+I_0)/(\mathit{\gamma }+1)\right\}\hfill \\ \hfill & \text{for}v>(1+a)/2.\hfill \\ \hfill \end{array}$$

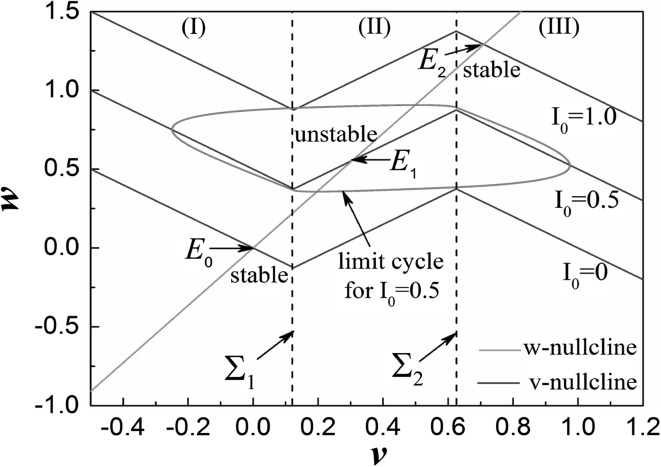
It is worth pointing out that, only one equilibrium point could be obtained for one certain fixed drive under the above parameters due to the piecewise linearity of f(v). For example, Fig. 2a shows the distribution of the equilibria with different values of I₀. It could be found that, the w-nullcline intersects different branches of the v-nullcline only once. The stabilities of these crossing points, i.e., the equilibria of the associated autonomous systems, are determined by the eigenvalues of the related linearization matrix. Specifically, the stability of E₀ {v = 0, w = 0} for I₀ = 0 is determined by the eigenvalues of J₀, while the stabilities of E₁ {v = 0.3055, w = 0.5556} for I₀ = 0.5 and E₂ {v = 0.7097, w = 1.2903} for I₀ = 1.0 are determined by the eigenvalues of J₁ and J₂ respectively. J₀ and J₁, J₂ are expressed as follows with the above parameters,

$$\begin{array}{cc}\hfill J_1& =\left|\begin{array}{cc}1/C& -1/C\\ 1& -\mathit{\gamma }\end{array}\right|=\left|\begin{array}{cc}10.0& -10.0\\ 1& -0.55\end{array}\right|\hfill \\ \hfill & \text{with eigenvalues}{\mathit{\lambda }}_1=8.9470,{\mathit{\lambda }}_2=0.5029,\hfill \\ \hfill J_0& =J_2=\left|\begin{array}{cc}-1/C& -1/C\\ 1& -\mathit{\gamma }\end{array}\right|=\left|\begin{array}{cc}-10.0& -10.0\\ 1& -0.55\end{array}\right|\hfill \\ \hfill & \text{with eigenvalues}{\mathit{\lambda }}_1^{{}^{\prime }}=-1.7642,{\mathit{\lambda }}_2^{{}^{\prime }}=-8.7858.\hfill \\ \hfill \end{array}$$

Fig. 2.

Distribution of the equilibria of system (2) with different values of I ₀

Obviously, the equilibria E₀ and E₂ are stable nodes, while E₁ is an unstable node. And because the equilibrium for I₀ = 0.5 is unstable, it can be observed from numerical simulation that the behavior of the autonomous system exhibits periodic oscillation for I₀ = 0.5 (see Fig. 2).

Now we turn to the non-autonomous case with the input varies periodically, i.e., $I=cos({\mathit{\omega }}_{0}t)$. Though system (1) is a non-autonomous system, it can be looked as an autonomous system at any certain moment and we can regard the time-dependent external drive as a bifurcation parameter that moves the system through three distinct states.

To investigate the bifurcation mechanism, we introduce the transformation ${\mathit{\omega }}_{0}t=\mathit{\theta }$, which leads the vector field to a “generalized autonomous” form, described as system (3), and f(v) here has the same form as it in system (1).

$$\begin{array}{cc}\hfill C\dot{v}& =f(v)-w+cos(\mathit{\theta }),\hfill \\ \hfill \dot{w}& =v-\mathit{\gamma }w,\hfill \\ \hfill \end{array}$$ 3

Because of the linear structure of the system, though non-smooth, we now assume the “solution” of system (3) can be written as

$$\begin{array}{cc}& \left\{(v,w)\left|v=k_{11}sin\mathit{\theta }+k_{12}cos\mathit{\theta }+k_{10},\right.\right.\hfill \\ \hfill & \left.w=k_{21}sin\mathit{\theta }+k_{22}cos\mathit{\theta }+k_{20}\right\}\hfill \\ \hfill \end{array}$$ 4

By substituting this “solution” (4) into the system (3), one may obtain three types of coefficients in the “solution” corresponding to different conditions. The details can be described as:

1. for a/2 ≤ v≤(1 + a)/2,

   $$\begin{array}{cc}\hfill k_{11}& ={\mathit{\omega }}_0\left(C{\mathit{\omega }}_0^2+C{\mathit{\gamma }}^2-1\right)/\left(C^2{\mathit{\omega }}_0^4+C^2{\mathit{\omega }}_0^2{\mathit{\gamma }}^2\right.\hfill \\ \hfill & \left.-2C{\mathit{\omega }}_0^2+{\mathit{\omega }}_0^2+{\mathit{\gamma }}^2-2\mathit{\gamma }+1\right),\hfill \\ \hfill k_{12}& =-\left({\mathit{\omega }}_0^2+{\mathit{\gamma }}^2-\mathit{\gamma }\right)/\left(C^2{\mathit{\omega }}_0^4+C^2{\mathit{\omega }}_0^2{\mathit{\gamma }}^2\right.\hfill \\ \hfill & \left.-2C{\mathit{\omega }}_0^2+{\mathit{\omega }}_0^2+{\mathit{\gamma }}^2-2\mathit{\gamma }+1\right),\hfill \\ \hfill k_{21}& ={\mathit{\omega }}_0(C\mathit{\gamma }-1)/\left(C^2{\mathit{\omega }}_0^4+C^2{\mathit{\omega }}_0^2{\mathit{\gamma }}^2\right.\hfill \\ \hfill & \left.-2C{\mathit{\omega }}_0^2+{\mathit{\omega }}_0^2+{\mathit{\gamma }}^2-2\mathit{\gamma }+1\right),\hfill \\ \hfill k_{22}& =-\left(C{\mathit{\omega }}_0^2+\mathit{\gamma }-1\right)/\left(C^2{\mathit{\omega }}_0^4+C^2{\mathit{\omega }}_0^2{\mathit{\lambda }}^2\right.\hfill \\ \hfill & \left.-2C{\mathit{\omega }}_0^2+{\mathit{\omega }}_0^2+{\mathit{\gamma }}^2-2\mathit{\gamma }+1\right),\hfill \\ \hfill k_{10}& =a\mathit{\gamma }/(\mathit{\gamma }-1),k_{20}=a/(\mathit{\gamma }-1);\hfill \\ \hfill \end{array}$$

2. for v > (1 + a)/2,

   $$\begin{array}{cc}\hfill k_{11}& ={\mathit{\omega }}_0\left(C{\mathit{\omega }}_0^2+C{\mathit{\gamma }}^2-1\right)/\left(C^2{\mathit{\omega }}_0^4+C^2{\mathit{\omega }}_0^2{\mathit{\gamma }}^2\right.\hfill \\ \hfill & \left.-2C{\mathit{\omega }}_0^2+{\mathit{\omega }}_0^2+{\mathit{\gamma }}^2+2\mathit{\gamma }+1\right),\hfill \\ \hfill k_{12}& =\left({\mathit{\omega }}_0^2+{\mathit{\gamma }}^2+\mathit{\gamma }\right)/\left(C^2{\mathit{\omega }}_0^4+C^2{\mathit{\omega }}_0^2{\mathit{\gamma }}^2\right.\hfill \\ \hfill & \left.-2C{\mathit{\omega }}_0^2+{\mathit{\omega }}_0^2+{\mathit{\gamma }}^2+2\mathit{\gamma }+1\right),\hfill \\ \hfill k_{21}& ={\mathit{\omega }}_0(C\mathit{\gamma }+1)/\left(C^2{\mathit{\omega }}_0^4+C^2{\mathit{\omega }}_0^2{\mathit{\gamma }}^2\right.\hfill \\ \hfill & \left.-2C{\mathit{\omega }}_0^2+{\mathit{\omega }}_0^2+{\mathit{\gamma }}^2+2\mathit{\gamma }+1\right),\hfill \\ \hfill k_{22}& =-\left(C{\mathit{\omega }}_0^2-\mathit{\gamma }-1)\right)/\left(C^2{\mathit{\omega }}_0^4+C^2{\mathit{\omega }}_0^2{\mathit{\gamma }}^2\right.\hfill \\ \hfill & \left.-2C{\mathit{\omega }}_0^2+{\mathit{\omega }}_0^2+{\mathit{\gamma }}^2+2\mathit{\gamma }+1\right),\hfill \\ \hfill k_{10}& =\mathit{\gamma }/(\mathit{\gamma }+1),k_{20}=1/(\mathit{\gamma }+1);\hfill \\ \hfill \end{array}$$

3. for v < a/2,

   $$\begin{array}{cc}\hfill k_{11}& ={\mathit{\omega }}_0\left(C{\mathit{\omega }}_0^2+C{\mathit{\gamma }}^2-1\right)/\left(C^2{\mathit{\omega }}_0^4+C^2{\mathit{\omega }}_0^2{\mathit{\gamma }}^2\right.\hfill \\ \hfill & \left.-2C{\mathit{\omega }}_0^2+{\mathit{\omega }}_0^2+{\mathit{\gamma }}^2-2\mathit{\gamma }+1\right),\hfill \\ \hfill k_{12}& =-\left({\mathit{\omega }}_0^2+{\mathit{\gamma }}^2-\mathit{\gamma }\right)/\left(C^2{\mathit{\omega }}_0^4+C^2{\mathit{\omega }}_0^2{\mathit{\gamma }}^2\right.\hfill \\ \hfill & \left.-2C{\mathit{\omega }}_0^2+{\mathit{\omega }}_0^2+{\mathit{\gamma }}^2-2\mathit{\gamma }+1\right),\hfill \\ \hfill k_{21}& ={\mathit{\omega }}_0(C\mathit{\gamma }-1)/\left(C^2{\mathit{\omega }}_0^4+C^2{\mathit{\omega }}_0^2{\mathit{\gamma }}^2\right.,\hfill \\ \hfill & \left.-2C{\mathit{\omega }}_0^2+{\mathit{\omega }}_0^2+{\mathit{\gamma }}^2-2\mathit{\gamma }+1\right),\hfill \\ \hfill k_{22}& =-\left(C{\mathit{\omega }}_0^2+\mathit{\gamma }-1\right)/\left(C^2{\mathit{\omega }}_0^4+C^2{\mathit{\omega }}_0^2{\mathit{\lambda }}^2\right.\hfill \\ \hfill & \left.-2C{\mathit{\omega }}_0^2+{\mathit{\omega }}_0^2+{\mathit{\gamma }}^2-2\mathit{\gamma }+1\right),\hfill \\ \hfill k_{10}& =0,k_{20}=0.\hfill \\ \hfill \end{array}$$

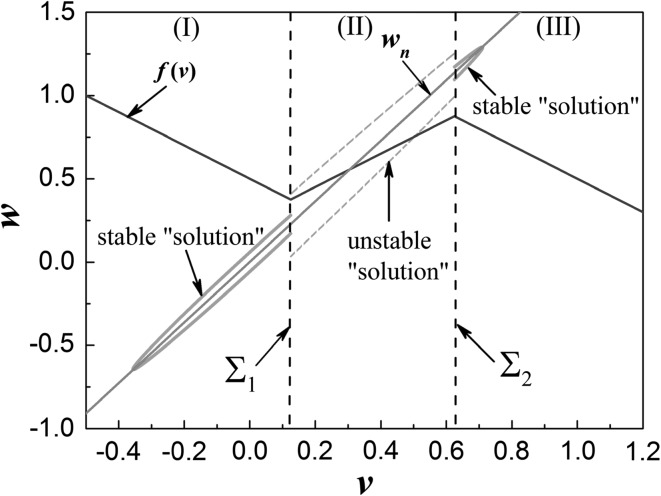
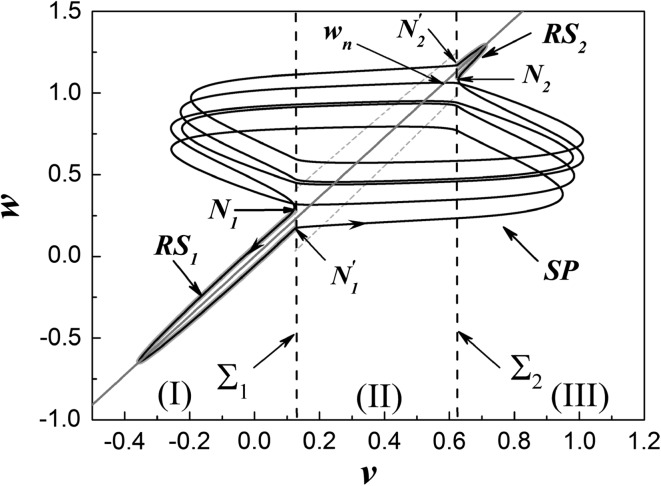
The “solution” expressed by Eq. (4) can be regarded as “generalized equilibrium point” of system (3), which is described as a “generalized autonomous system” above. And the stability of these solutions can be determined by the eigenvalues associated with the linearized matrix of the vector field. Further computation reveals that these Jacobian matrixes and the eigenvalues related to the “solution” can be expressed in the same forms expressed above for the autonomous case because of the piecewise linear structure of the equation. That is, while the parameters are still fixed at those values in above, the “solution” is a stable node for v > (1 + a)/2 or v < a/2, i.e., for $I>[a(\mathit{\gamma }+1)-\mathit{\gamma }+1]/2\mathit{\gamma }$ or $I<a(\mathit{\gamma }+1)/2\mathit{\gamma }$. While $a/2\le v\le (1+a)/2$, the “solution” is an unstable node for $a(\mathit{\gamma }+1)/2\mathit{\gamma }\le I\le [a(\mathit{\gamma }+1)-\mathit{\gamma }+1]/2\mathit{\gamma }$. The distribution of the “solutions” of system (3) is presented in Fig. 3, where the pink solid lines (the solid curves in region I and region III) denote the stable “solutions” while the pink dash lines (the diagonal dash lines) represent the unstable “solutions”. The green line (the diagonal straight line) w_n is the nullcline of w. Above (below) w_n, we have $\dot{w}<0$ ($\dot{w}>0$).

Fig. 3.

The “generation solution” of system (3)

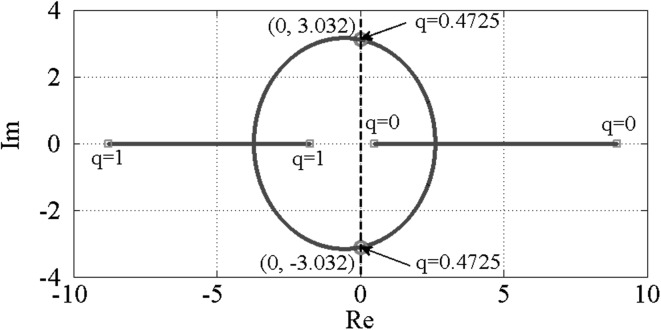
However, the classical continuous Jacobian matrix cannot be obtained because the vector field of this system is non-smooth. According to differential inclusions, we can use the generalized differential of Clarke to set up a generalized Jacobian matrix to explore the bifurcation of the equilibrium at the switch boundary (Leine and van Campen 2006; Leine 2006). The generalized Jacobian of system (3), expressed by $J_G(q)=\{q{J}_1+(1-q)J_0,\forall q\in [0,1]\}$, at the bifurcation point is the closed convex hull of the Jacobians on each side of the switching boundary (Leine 2006). The eigenvalues of J_G(q), denoted by ${\mathit{\lambda }}_{G1,2}$, are set-valued and form a path in the complex plane with q as path parameter (see Fig. 4).

Fig. 4.

Set of eigenvalues of the generalized Jacobian of system (3)

The path in Fig. 4, from which it may be found that, the eigenvalues of J_G(q) are purely imaginary for q = 0.4725. The path of the eigenvalues of J_G(q) shows that discontinuous Hopf bifurcation occurring at the switch boundaries (Leine and van Campen 2006; Leine 2006). According to bifurcation theory, the absolute value of this purely imaginary implies the oscillating frequency generated from this bifurcation, which is calculated at ω_t = 3.032 (shown in Fig. 4).

Now we explain the mechanism of the periodic bursting based on non-smooth bifurcation theory. Real solution of system (1), that is, the phase portraits shown in Fig. 1 is projected onto the distribution diagram of the “generalized equilibrium” of the non-autonomous system which is demonstrated in Fig. 3 (shown in Fig. 5).

Fig. 5.

Overlap of the “solution” and the real solution

In Fig. 5, we see that the “generalized solution” located in regions (I) and (III) is quite close to the actual solution. However, there is less similarity between the generalized and real solutions in region (II), which is due to the slowly varying input current.

The “generalized equilibrium points” are stable nodes in region (I) as well as region (III), and they lose their stability at the switch boundaries Σ₁ and Σ₂ respectively via discontinuous Hopf bifurcation. Thus, the trajectory will be disengaged from these stable attractors and tend to move along the limit cycles generating from the bifurcation. Because the value of the drive is variable, this kind of periodic oscillation has been maintained within the corresponding value range of the drive until the trajectory is drawn to the stable “solution” again. Meanwhile, the periodicity of the variation of the drive may lead the behavior of the system transfer between these two different states periodically and slowly. The slow-fast effect appears due to the order gap between the two frequencies, i.e., the frequency of the periodic drive and the frequency generated from discontinuous Hopf bifurcation. To be specific, the frequency of the periodic drive is related to the slow-rest state and the frequency generated from discontinuous Hopf bifurcation is related to the fast-spiking state. Based on the analysis above, the motion of system (1) in one period is described in detail as follows.

Point N₁ is set as the starting point, which is located at the switching boundary Σ₁. Notice that point N₁ is above the nullcline w_n, the value of w will decrease since $\dot{w}<0$. That is to say, the orbit runs downward at point N₁ as the arrow on the phase path shows. The anticlockwise direction of the trajectory can be demonstrated by the time series plotted in Fig. 1. The trajectory may move exactly along the stable “solution” with the angular frequency of stimulation (ω₀ = 0.05) until it reaches to the switching boundary Σ₁ at the point $N_1^{{}^{\prime }}$ when the amplitude of the current I reaches the threshold, which is given by $I=a(\mathit{\gamma }+1)/2\mathit{\gamma }\approx 0.3523$. The value of angular frequency of the oscillations obtained from simulation, i.e., ${\mathit{\omega }}_{0S}=2\mathit{\pi }/T_0\approx 0.050$ matches the frequency found in the analysis. Note that the passage remaining on the “solution” is relatively slow, which can be called as rest state (RS₁).

Once the slowly-varying current passes through the bifurcation value, namely, discontinuous Hopf bifurcation, the trajectory crosses the switching boundary Σ₁ at the point $N_1^{{}^{\prime }}$ and circles with the angular frequency ω_t = 3.032 determined by this bifurcation. The value of ω_t is much higher than ω₀, so the passage related to ω_t is relatively fast, called as spiking (SP₁). The frequency of SP₁ also can be verified by the numerical simulation above. Based on time series shown in Fig. 1, the associated angular frequency can be computed as ${\mathit{\omega }}_S=2\mathit{\pi }/T\approx 2.920$, which is very asymptotic to the frequency ω_t generated from discontinuous Hopf bifurcation. Then the trajectory evolves close to this frequency until the amplitude of I reaches a second critical value of 0.7614 obtained from the above analysis. The orbits converge to the stable nodes quickly at N₂ and move along these stable attractors again until it meet the switching boundary Σ₂. Like the pervious status, this passage also can be called as rest state (RS₂). After that the “solution” loses its stability via discontinuous Hopf bifurcation at $N_2^{{}^{\prime }}$, which is similar to that of $N_1^{{}^{\prime }}$, and then the spiking state (SP₂) appears again until the trajectory reaches the point N₁ to begin another period.

It is worth pointing out that, as the analysis presented above, there exists two threshold values of the external drive, i.e., $I_1=a(\mathit{\gamma }+1)/2\mathit{\gamma }$ and $I_2=[a(\mathit{\gamma }+1)-\mathit{\gamma }+1]/2\mathit{\gamma }$. It means that, when and only when the value of the drive could reach these two threshold values periodically and relatively slowly, the type of periodic bursting demonstrated above will be observed. That is, if the amplitude of the drive $A_I<\text{min}\{\left|I_1\right|,\left|I_2\right|\}$, bursting phenomenon will not be observed. If $\text{min}\{\left|I_1\right|,\left|I_2\right|\}<A_I<\text{max}\{\left|I_1\right|,\left|I_2\right|\}$, bursting can be obtained when one of the rest state branch of the phase portrait disappeared. For instance, we consider the two input currents of different amplitude expressed as $I=0.3cos({\mathit{\omega }}_{0}t)$ and $I=0.5cos({\mathit{\omega }}_{0}t)$. The associated dynamical behaviors, i.e., the limit cycle and the periodic bursting with one rest state can be seen in Fig. 6.

Fig. 6.

Phase portraits and time series of system (1) for a $I=0.3cos({\mathit{\omega }}_{0}t)$ and b $I=0.5cos({\mathit{\omega }}_{0}t)$

Conclusions

Bursting phenomenon can be observed for the PWL planar McKean model with periodic stimulation. The stimulation acts as a control parameter varying periodically and relatively slowly, which induces the dynamical behavior of the system exhibits a transition between the rest state and the spiking state. Since the vector field is non-smooth, it is discontinuous Hopf bifurcation occurring at the non-smooth boundaries that connect the two states. The frequency generated by discontinuous Hopf bifurcation is related to the fast-spiking passage while the frequency of stimulation is associated with the slow-rest passage. The nature of the external drive, i.e., amplitude and frequency is important to the fire pattern of the neuron model. It might be interesting to explore the relationship between the periodic input and the neuron’s spiking output.