Abstract
Oscillation is an important cellular process that regulates timing of different vital life cycles. However, in the noisy cellular environment, oscillations can be highly inaccurate due to phase fluctuations. It remains poorly understood how biochemical circuits suppress phase fluctuations and what is the incurred thermodynamic cost. Here, we study three different types of biochemical oscillations representing three basic oscillation motifs shared by all known oscillatory systems. In all the systems studied, we find that the phase diffusion constant depends on the free energy dissipation per period following the same inverse relation parameterized by system specific constants. This relationship and its range of validity are shown analytically in a model of noisy oscillation. Microscopically, we find that the oscillation is driven by multiple irreversible cycles that hydrolyze the fuel molecules such as ATP; the number of phase coherent periods is proportional to the free energy consumed per period. Experimental evidence in support of this general relationship and testable predictions are also presented.
Keywords: Biochemical oscillations, energy dissipation, noise, phase diffusion, network motif
I. INTRODUCTION
Living systems are dissipative, consuming energy to perform key functions for their survival and growth. While it is clear that free energy [1–3] is needed for physical functions, such as cell motility [4] and macromolecule synthesis [5], it remains poorly understood whether and how regulatory functions are enhanced by free energy consumption. The relationship between biological regulatory functions and nonequilibrium thermodynamics has been an active area in biophysics [6–11]. For example, recent studies in different cellular adaptation processes demonstrated that the cost-performance trade-off follows a universal relationship, independent of the detailed biochemical circuits [8, 9].
Oscillatory behaviors exist in many biological systems, e.g., glycolysis [12], cyclic AMP signaling [13], cell cycle [14–16], circadian rhythms [12, 17], and synthetic oscillators [18, 19]. These biochemical oscillations are crucial in controlling the timing of life processes. Much is known now about the structure of biochemical circuits responsible for these oscillatory behaviors. There are a few basic network motifs, illustrated in Figure 1a, which are responsible for all known biochemical and genetic oscillations [12, 13, 16–18]. These network motifs share a few essential features, such as nonlinearity, negative feedback, and a time delay, as summarized by Novak and Tyson in [20]. However, in small systems such as a single cell, the dynamics of oscillations are subject to large fluctuations from the environment, due to their small sizes. Thus, one may ask how biological systems maintain coherence of oscillations amidst these fluctuations [21]. Here, we study the thermodynamic cost of controlling oscillation coherence in different representative oscillatory systems and investigate whether there is a general relationship between the accuracy of the oscillation and its minimum free energy cost that may apply to all biochemical oscillations.
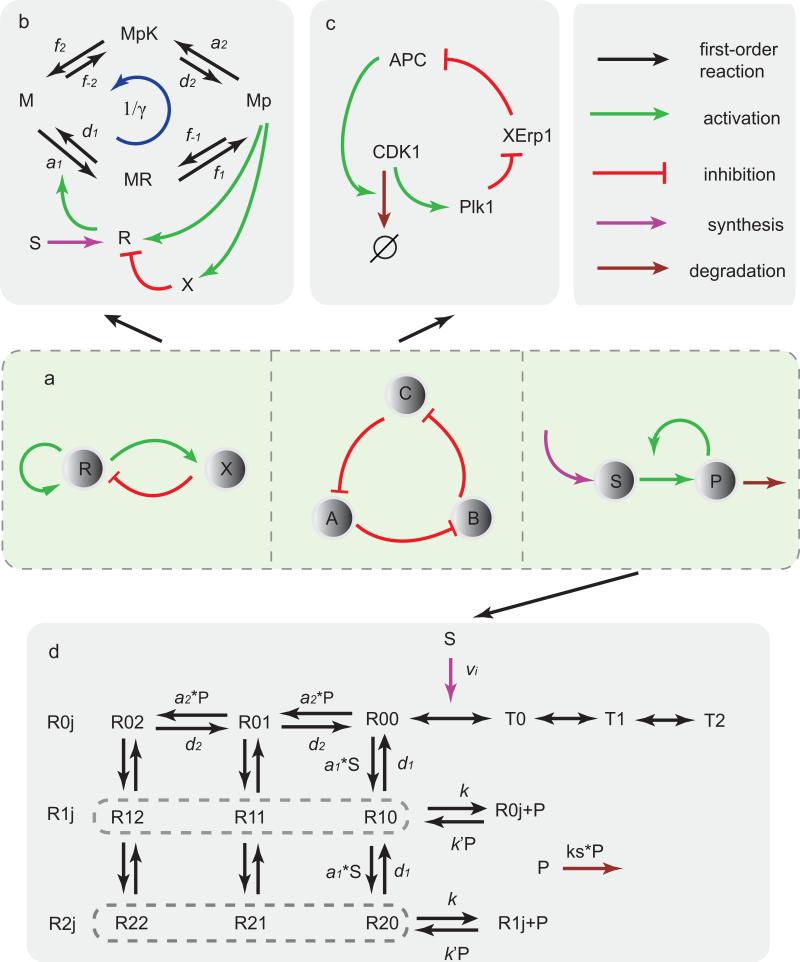
Figure 1.
Different network motifs and the corresponding biochemical oscillatory systems. (a) Illustrations of three network motifs for oscillation: activator-inhibitor, repressilator, and substrate-depletion. Lines with different colors stand for different reactions. (b) The activator-inhibitor model with a phosphorylation-dephosphorylation (PdP) cycle. R and K catalyse two opposing reactions M ↔ Mp (phosphorylation and dephosphorylation) through different intermediate complexes MR and MpK. Mp activates both R (activator) and X (inhibitor). X inhibits R by enhancing its degradation. Parameter γ = d1f–1d2f–2/(a1f1a2f2) is introduced to characterize the reversibility of the system. S is the basic synthesis rate. (c) The “repressilator” model of cell cycle in eukaryotic cells. In the simplified network, CDK1 activates Plk1, Plk1 activates APC by suppressing the inhibitor of APC, XErp1, and APC degrades CDK1, forming the mutually activing/inhibiting loop. (d) The glycolysis network. The allosteric enzyme's protomer has two states, R (binding with P) and T (unbinding with P), and only R has the catalysis activity. Each Ri,j, with i = 1,2, ···, ni and j = 1,2, ···, nj represent the number of P and S bound to R, here we used ni = nj = 2. Each Ri,j can undergo reactions of Ri,j + S ↔ Ri,j+1 ↔ Ri,j + P. Detailed descriptions and rate values are given in SI.
We study three specific models, the activator-inhibitor (AI) model, the repressilator model, and the allosteric glycolysis model, chosen to exemplify the three different basic oscillation motifs, as shown in Fig. 1. For all the systems studied, a finite (critical) amount of free energy is needed to drive them to oscillate. Beyond the onset of oscillation, extra free energy dissipation must be applied to reduce the phase diffusion constant and thus enhance the coherence time and phase accuracy of the oscillations. A general inverse relationship between the phase diffusion constant and the free energy dissipation is found in all three models studied. The parameters in this inverse relationship and the range of its validity depend on the details of the system. This general energy-accuracy relation for noisy oscillations is also verified analytically in the noisy complex Stuart-Landau equation. In the following, we report these results followed by a in-depth discussion of a plausible general microscopic mechanism/strategy for energy-assisted noise suppression.
II. MODELS AND RESULTS
A. Three biochemical oscillators representing the basic network motifs
All known biochemical and genetic oscillators contain at least one of the basic motifs (or their variance) in network topology [20, 22]. To search for general principles in these noisy oscillatory systems, we study three biochemical systems (Fig. 1), each representing one of the three basic network motifs responsible for oscillatory behaviors. The rst one is the activator-inhibitor (AI) system, where a negative feedback is interlinked with a positive feedback (Left panel, Fig. 1a). This regulatory motif is common in biological oscillators, like the circadian clock in cyanobacteria [23, 24], cell cycle in frog egg [25, 26], cAMP signaling in Dictyostelium, and genetic oscillators in synthetic biology [19, 27, 28]. We implement this motif in a simplified biological network with a phosphorylation-dephosphorylation cycle (Fig. 1b). The second model is a repressilator, which consists of three components connected in a negative feedback loop, such that each component represses the next one in the loop, and is itself repressed by the previous one (Middle panel, Fig. 1a). The rst synthetic genetic oscillator was built with this motif [18]. Many important transcriptional-translational oscillators also use this motif as their backbone, such as circadian clock in mammalian cells [17], NF-κB signaling [29], and the p53-mdm2 oscillations in cancer cells [30]. Here, we take the repressilator composed of CDK1, Plk1, and APC in a cell cycle as our case study (Fig. 1c). The third oscillatory network motif we studied is the substrate-depletion model [31] (the last panel in Fig. 1a), where substrate S is converted by a process that is ampli ed autocatalytically by the product P . Examples of substrate-depletion motif are oscillations in glycolysis [12, 32] and Calcium signaling [33]. Here, we examine the noise effect in glycolysis oscillations, where the allosteric enzyme PFK catalyzes substrate to product in a network shown in Fig. 1d. To show the generality of our results, we have also studied the brusselator model, which represents one of the simplest chemical systems that can generate sustained oscillations. The brusselator is a special kind of substrate-depletion model.
In our study, we introduced a parameter γ to characterize the reversibility of the biochemical networks. In a reaction loop, γ corresponds to the ratio of the product of the reaction rates in one direction (e.g., counter-clock-wise) and that in the other direction (e.g., clock-wise). When γ = 1, the system is in equilibrium without any free energy dissipation. For γ ≠= 1, free energy is dissipated. Here, we study the relationship between the dynamics and the energetics of the biochemical networks by varying γ. The mathematical details of the four models are described in the Supplemental Information (SI); all parameters (e.g., reaction rates, concentrations, time, and volumes) are shown here as dimensionless numbers with their units explained in SI.
B. Phase diffusion reduces the coherence time
In all four models that we studied, there is an onset of oscillation as γ decreases below a critical value γc (< 1). This means that a finite critical free energy dissipation (Wc > 0) is needed to generate an oscillatory behavior (see Fig. S1 in SI). In Fig. 2a, two trajectories of the concentration of the inhibitor X are shown for γ = 10–5 < γc in the activator-inhibitor model, where γc = 2 × 10–3. As evident in Fig. 2a, biochemical oscillations are noisy. To characterize the coherence of the oscillation in time, we computed the auto-correlation function C(t) for a given concentration variable x in the network. As shown in Fig. 2b, C(t) follows a damped oscillation:
| (1) |
where T is the period and τc defines a coherence time for the oscillation.
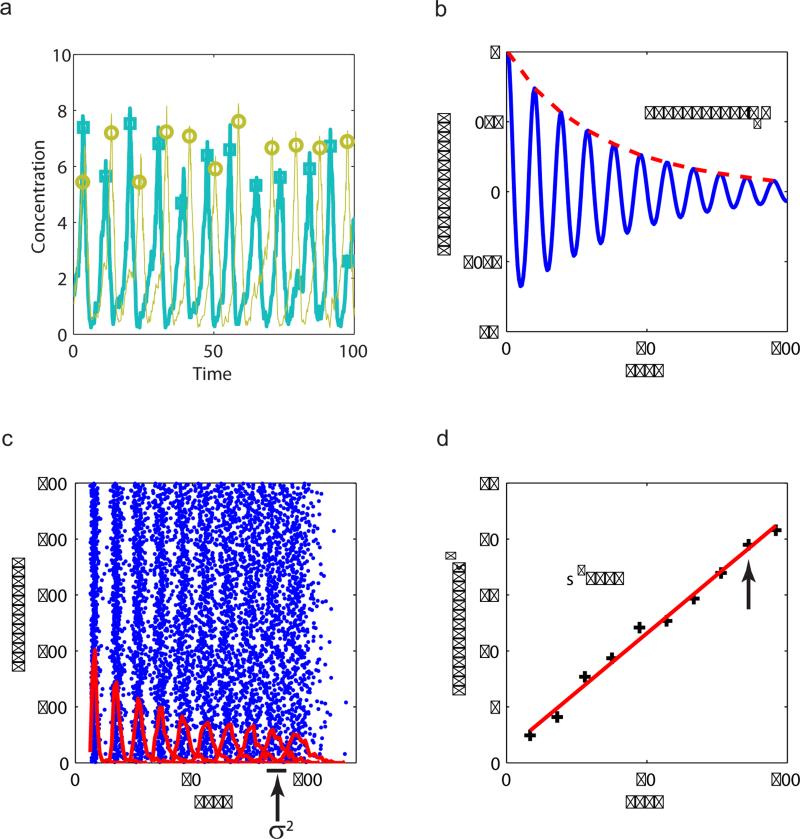
Figure 2.
Correlation and phase diffusion of the noisy oscillations in the activator-inhibitor model. (a) Two noisy oscillation time series (trajectories) of the inhibitor (X) concentration, with the peaks labeled by circles and squares. (b) The auto-correlation function C(t) (defined in Eq. 1) decays exponentially with a correlation time τc = 37.7. (c) Raster plot of the peak times for 500 different trajectories starting with the same initial condition. The distributions of the peak times for each consecutive peaks are shown by red lines. The peak time variance δ2 is shown. (d) Peak time variance δ2 goes linearly with the average peak time, with the linear coefficient defined as the peak time diffusion constant. Here, parameters are V = 50, γ = 10–5. We nd D = 0.2 and α ≡ D/T2 ≈ 0.07.
The oscillatory state breaks time translation invariance (symmetry) of the underlying biochemical system. As a result, the phase of the oscillation is a soft mode and follows diffusive dynamics in the presence of noise. To quantify the phase diffusion, we simulated many trajectories in the model(s) with the same parameters and the same initial conditions. In Fig. 2c, the peak times for 500 trajectories in the AI model are shown in a raster plot together with the peak time distributions (red lines). The variance (σ2) of the distribution versus the average peak time is shown in Fig. 2d. It is clear that the variance goes linearly with time, confirming the diffusive nature of the phase, and the linear slope deffines a peak time diffusion constant D. It is easy to show that the coherence time τc is inversely proportional to D:
| (2) |
where α is a constant dependent on the waveform (α = (2π2)–1 for a sine wave).
C. Free energy dissipation suppresses phase diffusion
As γ decreases below γc, more free energy is dissipated. What is the effect of the additional free energy dissipation beyond the onset of oscillation? From the chemical reaction rates, we can compute the free energy dissipation rate [34]:
| (3) |
where and are the forward and backward fluxes of the ith reaction, and free energy is in units of thermal energy. For the activator-inhibitor and glycolysis models, we calculated the energy dissipation rate using Eq. 3. For systems with continuum stochastic dynamics described by Langevin equations (e.g., the brusselator and the repressilator models), we can obtain the steady-state distribution by solving the corresponding Fokker-Planck equation or by direct stochastic simulations (see Fig. S2 in SI for an example). From , we computed the phase space uxes and the free energy dissipation rate following [9] (see the Methods section and SI for details). For oscillatory systems, the dissipation rate Ẇ varies in a period T. We define to characterize the free energy dissipation per period per volume.
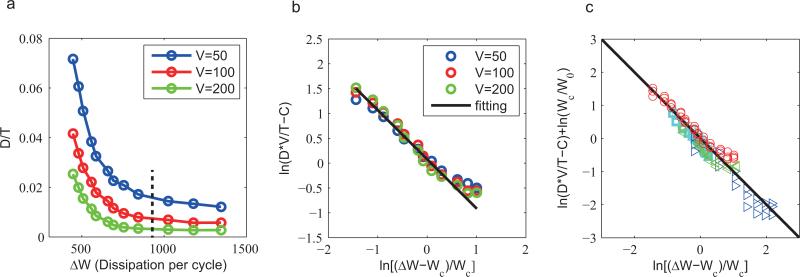
For each of the four models, ΔW and the dimensionless peak time diffusion constant D/T were computed for different parameter values (reaction rates, protein concentrations) in the oscillatory regime γ < γc and for different volume V. As shown in Fig. 3a for the activator-inhibitor model, D/T decreases as the energy dissipation ΔW increases and eventually saturates to a fixed value when ΔW → ∞ (i.e., γ = 0). The phase diffusion constants scale inversely with the volume V. As shown in Fig. 3b, V × D/T for different volumes collapsed onto a simple curve, which can be approximated by:
| (4) |
where Wc is the critical free energy, and W0 and C are intensive constants (independent of volume), whose values are given in the legend of Fig. 3. Eq.4 also holds true for the other models (repressilator, brusselator and glycolysis) we studied, see Fig. 3c and Fig. S3 in SI for details.
Figure 3.
Relation between the dimensionless diffusion constant (D/T) and free energy dissipation per period per volume (ΔW, in units of thermal energy kBTr with Tr the room temperature). Detailed descriptions of the models and parameters can be found in SI. (a) D/T versus ΔW for the activator-inhibitor model with different volume V. The black dashed line indicates the hydrolysis free energy of one ATP molecule ΔG(0) ≈ 12kBTr, which corresponds to γ ≈ 10–5.2 in our model. (b) Results from (a) for different volumes collapseonto the same curve when D/T is scaled by V. The data, plotted in log-log scale, is fitted well by the scaling form V × D/T–C = W0 × (W – Wc)α (black line). The fitting parameters are: Wc = 360.4,W0 = 379.7 ± 89.6, α = –0.988 ± 0.114, C = 0.6 ± 0.2. (c) The scaling plot, ln(V D/T – C) versus ln(ΔW – Wc), for all oscillatory models studied in this paper (see Fig. 1 and SI for details). different symbols represent different models, red circle: activator-inhibitor; cyan squares: repressilator; blue triangles: brusselator; green triangles: glycolysis. For each model, the data is shifted by ln(Wc/W0) to align. All data points lie close to the black line with a slope of –1, showing the generality of the inverse dependence of phase diffusion on free energy dissipation (Eq. 4). The fitting parameters are given in (b) for the activator-inhibitor model and in Fig. S3 for the other models.
D. The free energy sources and experimental evidence
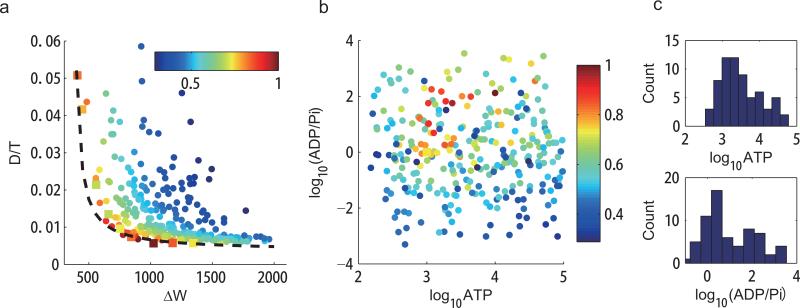
What is the free energy source driving the biochemical oscillations? For the activator-inhibitor model, the free energy is provided by ATP hydrolysis in the phosphorylation-dephosphorylation (PdP) cycle (see Fig. 1a). Besides the standard free energy ΔG0 of ATP hydrolysis, the total free energy dissipation per period ΔW also depends on (and thus can be controlled by) the concentrations of ATP, ADP and the inorganic phosphate Pi. In the activator-inhibitor model, we can include ATP, ADP, and Pi explicitly in the reactions (see Method). Here, we study how these concentrations ([ATP], [ADP], and [Pi]) affect the phase diffusion of the oscillation. In Fig. 4a, we show the phase diffusion constant (D/T) versus the dissipation per period (ΔW) for 300 sets of randomly chosen concentrations [ATP], [ADP], and [Pi]. Remarkably, all the points lie above an envelope curve (the dotted line), which follows Eq.4. This envelope curve de nes the best performance of the biochemical network, i.e., the minimum free energy ΔWm needed to achieve a given level of phase coherence. For each choice of the concentrations ([ATP], [ADP], [Pi]), a functional efficiency E can be defined as the ratio of ΔWm and the actual cost ΔW for the same performance (D/T). The efficiency is represented by color in Fig. 4a&b. We investigated how efficiency depends on the three concentrations. As shown in Fig. 4b&c, the efficiency E does not simply increase with the ATP concentration; instead it peaks near a particular level of [ATP], at which the forward (counter-clock-wise in Fig. 1b) rates along different steps of the PdP cycle are matched. Similarly, E does not have any clear dependence on [ADP] or [Pi] level, it is high near a fixed ratio of [ADP]/[Pi], when the backward (clock-wise in Fig. 1b) rates along the different steps of the PdP cycle are matched. In SI we show in a simple model of chemical reaction cycles that with a constant energy dissipation, i.e., a fixed γ, phase diffusion approaches its minimum when the forward and the backward rates along different steps of the cycle, e.g., the PdP cycle, are matched.
Figure 4.
The dependence of phase diffusion on the ATP, ADP, and Pi concentrations. We studied the activator-inhibitor model with 300 randomly chosen parameters of dimensionless [ATP], [ADP] and [Pi] (see Methods). We chose V = 100. (a) D/T versus ΔW for the 300 different parameter choices. All the points lie above an envelope curve, which follows Eq. 4 with D/T = 1.94/(ΔW–400)+0.0036. Points in square indicate the points shown in Fig. 3. For a given value of D/T , the corresponding minimal energy dissipation ΔWmin is computed according to the fitted envelope curve. The efficiency is defined as E ≡ ΔWmin/ΔW. Colors of the points indicate the efficiency. (b) Distribution of the 300 randomly sampled points in the parameter space ([ATP], [ADP]/[Pi]). Colors of the points indicate the efficiency as in (a). Points with high efficiency are clustered. (c) Distribution of [ATP], and [ADP]/[Pi] for parameter choices with high efficiency E ≥ 0.75. The most probable parameter values for high efficiency are [ATP] ≈ 103, [ADP] ≈ [Pi], which corresponds to a1 = a2, f–1 = f–2 in the kinetic equations. This result indicates that high efficiency is achieved when the kinetic rates in the two halves of the PdP cycle (phosphorylation and dephosphorylation) are matched.
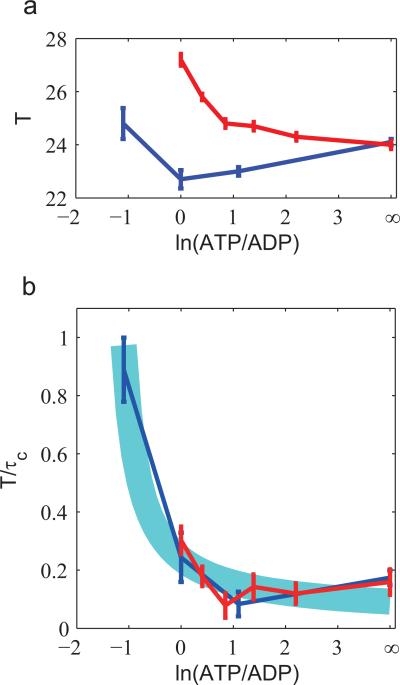
These predicted dependence of oscillatory behaviors on [ATP], [ADP], and [Pi] concentrations, as shown in Fig. 4, may be tested experimentally by measuring peak-to-peak time variations or equivalently the correlation time for different nucleotide concentrations. As reported in two recent studies [35, 36], the oscillatory dynamics of the phosophorylated KaiC protein in a reconstituted circadian clock from cyanobacteria (the Kai system) have been measured in media with different ATP/ADP ratios. We analysed the data according to Eq. 1 and obtained the correlation time (τc) and the period (T) for different ATP/ADT ratios (see SI and Fig. S4 in SI for details). In Fig. 5, we plotted the period and the phase diffusion versus ln([ATP]/[ADP]), which is the entropic contribution to the free energy dissipation. As the ATP/ADP ratio increases, the period changes little. In contrast, the phase diffusion T/τc ≡ α–1D/T decreases significantly and eventually saturates at high ATP/ADP ratios, consistent with the relationship between energy dissipation and phase diffusion discovered here.
Figure 5.
Experimental evidence from Ref.[36] (blue curve) and Ref.[35] (Red curve). The two experiments measured the oscillation of KaiC phosphorylation in vitro in media with different ATP/ADP ratios. The autocorrelation functions were calculated from the original data and fitted by a exponential decay cosine function A cos (2πt/T)e–t/τc, where T is the period, and τc is the correlation time. ln(ATP/ADP) represents the entropic contribution to the free energy. (a) The period T is robust against changes in the ATP/ADP ratio. Error bars represent standard deviations. (b) T/τc ≡ α–1D/T decreases with ln(ATP/ADP) and eventually saturates at large ATP/ADP ratio, consistent with our theoretical prediction. The data can be fitted by Eq. (4): T/τc = C + 0.28/(ln(ATP/ADP) ln(ATP/ADP)c), as represented by the thick blue line (line width comparable to the average standard deviation in the experimental data), with ln(ATP/ADP)c = –1.4 and C = 0.04. Taking the standard hydrolysis free energy of ATP, ΔG(0), to be 12kBTr (Tr is the room temperature), we have Wc/(kBTr) = ΔG(0)/(kBTr) + ln(ATP=ADP)c = 10.6.
E. Analytical results from the noisy Stuart-Landau equation
To understand the relationship between phase accuracy and energy dissipation, we consider the noisy Stuart-Landau equation for x,y:
| (5) |
where a, b, c, d, (b, c, d > 0) are real variables, and 〈ηi(t)ηj(t′)〈 = 2Δδijδ(t – t′). The corresponding equation in polar coordinates are:
| (6) |
where ηr = η1(t) cos θ + η2(t) sin θ, and ηθ = –η1(t) sin θ/r + η2(t) cos θ/r. For a > 0, the system starts to oscillate with a mean amplitude .
Phase can be de ned without ambiguity when the amplitude fluctuation is smaller than . This leads to . When Δ is small, the phase diffusion constant is determined by expanding the phase velocity around r = rs. This leads to , with . Approximately we have . The phase fluctuation δθ ≡ θ – Ω(rs)t follows a diffusive behavior with the diffusion constant given by:
| (7) |
where .
It is clear from Eq. 5 that detailed balance is broken and the system is dissipative. To compute the free energy dissipation, we rst determine the phase-space probability distribution function P (x, y, t). Solving the Fokker-Planck equation in polar coordinate, we obtain the steady state probability Ps(r,θ):
| (8) |
where is the normalization constant.
We compute the system's entropy production rate Ṡ [37, 38], from which we obtain the minimum free energy dissipation (see SI for details): , where Te is an (effective) temperature of the environment and kB the Boltzmann constant, we set kBTe = 1 here. The period of the oscillation is T = 2π/〈Ω(r)〉. The energy dissipated in one cycle is:
| (9) |
Under the conditions of and small Δ, we have (see SI for details):
| (10) |
When , higher order terms can be neglected, and ΔW is linearly dependent on a:
| (11) |
where ξ = 2πb/(cΔ) + 2πd2/(bc2), and Wc = 8πd/c > 0.
Eliminating a from Eq. 7&11, the relation between phase diffusion and energy dissipation emerges:
| (12) |
where C = 0, W0 = ξκΔ. The region where Eq.12 holds is given by , where the lower bound is limited by phase ambiguity, and the upper bound is given by the linear regime of ΔW. The noise strength affects the lower bound. The phase-amplitude correlation parameter d controls the upper bound (see SI and Fig. S5 for details).
In general, C > 0 when the noise strength of the two variables (x and y) vary independently, see SI for an analytical derivation (based on small noise expansion) and Fig. S6 for a direct simulation demonstration. In a system with multiple variables, large energy dissipation may completely suppress fluctuations in some of the variables. However, other variables, which are not subject to the energy-assisted noise control mechanism, can introduce a finite contribution to the phase diffusion resulting in a finite C.
Eq.12 has the same form as Eq. 4 obtained empirically from studying different biochemical networks. Analysis of the noisy Stuart-Landau equation clearly shows that free energy dissipation is used to suppress phase diffusion. The parameters in this relationship and the range of its validity depend on the details of the system. However, the inverse dependence of phase diffusion on energy dissipation appears to be general.
III. DISCUSSION
Oscillations are critical for many biological functions that require accurate time control, such as circadian clock, cell cycle, and development. However, biological systems are inherently noisy. The phase of a noisy oscillator uctuates (diffuses) without bound and eventually destroys the coherence (accuracy) of the oscillation. Specifically, the number of periods Nc in which the oscillation maintains its phase coherence is given by Nc = τc/T = αT/D, which decreases with the phase diffusion constant. Here, our study shows that free energy dissipation can be used to reduce phase diffusion and thus prolong the coherence of the oscillation. A general relationship between the phase diffusion constant and the minimum free energy cost, as given in Eq. 4, holds true for all the oscillatory systems we studied here. The amplitude fluctuations also decrease with free energy dissipation (see Fig. S7 in SI for details), as fluctuations in phase and amplitude are coupled in realistic systems. Our study thus establishes a cost-performance tradeoff for noisy biochemical oscillations.
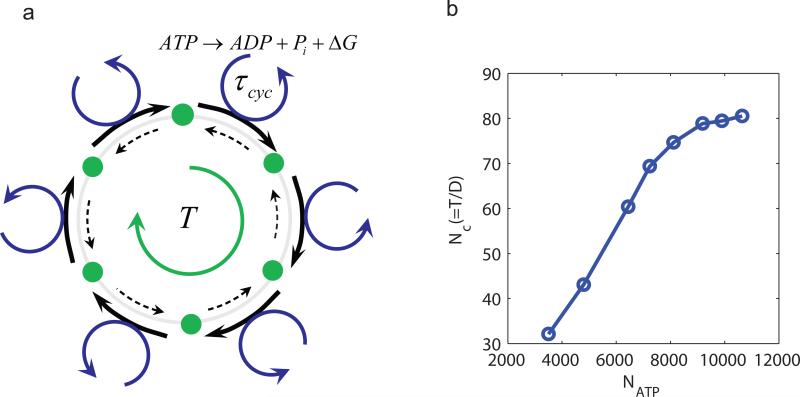
How do biological systems use their free energy sources (e.g., ATP) to enhance the accuracy of the biochemical oscillations? As illustrated in Fig. 6a, a biochemical oscillation can be considered as a clock, which goes through a series of time-ordered chemical states (green dots) during each period. These chemical states are characterized by the conformational and chemical modification (e.g., phosphorylation) states of the key proteins or protein complexes in the system. The forward transition from one state to the next is coupled to a PdP cycle (blue arrowed circle) driven by hydrolysis of one ATP molecule. For each forward step, the reverse transition introduces a large error in the clock. The system suppresses these backward transitions by utilizing the ATP hydrolysis free energy. However, this is just one half of the story. Even in the absence of the reverse transition, the time duration between two consecutive states is highly variable due to the stochastic nature (Poisson process) of the chemical transitions. A general strategy of increasing accuracy is averaging [39]. In the case of biochemical oscillations, each period may consist of multiple steps, each powered by at least one ATP molecule. As a result of averaging, the error in the period should go down as the number of steps increases. Specifically, we expect that the variance of the period should be inversely proportional to the total number of ATP hydrolyzed NATP ∝ T/τcyc in each period T, where τcyc is the average PdP cycle time, which is essentially the ATP turnover time. Consequently, the number of coherent period Nc = αT/D should be proportional to the number of ATP hydrolyzed in each period. We checked this prediction by varying the kinetic rates in the PdP cycle to change τcyc (see Methods section for details). In Fig. 6b, it is shown that the accuracy of the oscillation (clock), as measured by Nc, is enhanced by the number of ATP molecules hydrolyzed in each period. This result reveals a general strategy for oscillatory biochemical networks to enhance their phase coherence by coupling to multiple energy consuming cycles in each period. For the cyanobacteria circadian clock, each KaiC molecule has two phosphorylation sites. In principle a full circadian cycle should consume 2 ATP molecules per KaiC monomer. Interestingly, approximately 15 ATP molecules are consumed per KaiC molecule per period [40]. Our study suggests that the extra ATP molecules may be used to increase the phase coherence of the circadian clock.
Figure 6.
Oscillation coherence increases with the number of ATP hydrolyzed per period. (a) Illustration of a biochemical oscillation as a clock in phase space. The intermediate states (green dots) are represented as the “hour ticks” of the clock. The transition from one tick to the next is coupled with a ATP hydrolysis cycle. The free energy release ΔG from the hydrolysis cycle powers the forward transition (thick solid arrow) and/or suppresses the backward transition (thin dotted arrow). The number of ATP consumed per enzyme molecule in each period T is given by T/τcyc, where τcyc is the average cycle time. (b) The accuracy of the oscillation, characterized by the number of correlated (coherent) periods Nc, increases linearly with the total number of ATP consumed per period NATP before saturating at very high NATP. We varied NATP by changing the cycle time (see Methods for details), we used V = 100 here.
Biological systems need to function robustly against variations in its underlying biochemical parameters (rates, concentrations) [41, 42]. For oscillatory networks, the free energy dissipation needs to reach a critical value (Wc) to drive the system to oscillate. We showed here that additional free energy cost in excess of Wc is needed to make the oscillation more accurate, as demonstrated explicitly in Eq. 4. In addition to this accuracy-energy tradeoff, we found that larger energy dissipation can also enhance the system's robustness against its parameter variations. Take the activator-inhibitor model, for example: the concentrations of enzyme M (MT) and phosphatase K (KT) may vary from cell to cell. We search for the existence of oscillation in the (MT, KT) space for different values of γ. Robustness is de ned as the area of the parameter space where oscillation exists. As shown in Fig. S8 in the SI, the robustness increases as the system becomes more irreversible, i.e., when more free energy is dissipated. This suggests a possible general tradeoff between the functional robustness and energy dissipation in biological networks.
IV. METHODS
Simulation Methods
The Gillespie algorithm [43] is used for the stochastic simulations of the reaction kinetics. The parameters in Fig. 2 and Fig. 3 for the activator-inhibitor model is k0 = k1 = k3 = 1(t–1), k2 = 1(c–1t–1), k4 = 0.5(t–1), S = 0.4(c), KT = 1(c), MT = 10(c), a1 = a2 = 100(c–1t–1), f1 = f2 = d1 = d2 = 15(t–1), , with c the arbitrary concentration and t the time. Parameters for the other three models are given in SI. For given kinetic rates and the volume V , we simulated 1000 trajectories starting with the same initial condition. For the jth trajectory, we obtained its ith peak time tij from the trajectory xj(t) after smoothing (smooth function in MATLAB was used). The peak positions for two trajectories are shown in Fig. 2a. For all the trajectories, we computed the mean of their ith peak time , and variance , where N is the total number of trajectories. The average period T is given by T = mi/i. Asymptotically, depends linearly on mi (Fig. 2d), and the slope of this linear dependence is the peak time diffusion constant D, which has the dimension of time. The phase diffusion constant Dϕ is linearly proportional to D: Dϕ = (2π)2D/T. For the repressilator and the brusselator models, we simulated the stochastic kinetic equations to a sufficiently long time (10000 periods) to obtain the time-averaged distribution , where represents the phase space. We used to compute free energy dissipation.
Random Sampling
We can include ATP, ADP, and Pi explicitly in the reactions: M + R + ATP ⇀ M · R · ATP ⇀ Mp + R + ADP and MpK ⇀ M + K + Pi. The affected kinetic rates are a1 = a1,0[ATP], f–1 = f–1,0[ADP], f–2 = f–2,0[Pi], where a1,0 = 0.1, f–1,0 = f–2,0 = 1 are constants. The energy parameter γ for the PdP cycle can now be expressed as: γ = (d1d2f–1,0f–2,0[ADP][Pi])/(a1,0a2f1f2[ATP]). Random sampling in the ([ATP], [ADP], [Pi]) space is performed (in log scale) in the region by using Latin hypercube sampling (the lhs-design function in MATLAB). The reference concentrations [ATP]0, [ADP]0, and [Pi]0 are set to unity and their actual values are absorbed into the baseline reaction rates a1,0, f–1,0 and f–2,0, which are given in the legend of Fig. 4.
ATP consumption
In the activator-inhibitor model, the ATP consumption rate is , where and are the uxes for the M → Mp and Mp → M reactions, respectively. We varied the overall reaction kinetics, e.g., τcyc and the ATP consumption rate, by introducing a timescale factor B for all four rates d1 = d2 = Bd, f1 = f2 = Bf, where d = 15, f = 15 are the original values used in this paper (see SI). By changing the rates this way, the free energy release of ATP hydrolysis ΔG = –ln γ = ln(a1f1a2f2/(d1f–1d2f–2)) is unchanged. We varied B ∈ [0.2.2], and computed the total number of ATP consumed per period and Nc for Fig. 6b.
Supplementary Material
ACKNOWLEDGEMENT
We thank Dr. Michael Rust for sharing the experimental data in [35]&[36]. This work is partly supported by a NIH grant (R01GM081747 to Y.T.), a NSFC grant (11434001 to Q.O.), and a MSTC grant (2012AA02A702 to Q.O.).
Footnotes
VI. AUTHOR CONTRIBUTIONS
Y.T. and Q.O. initiated the work; Y.C., H.W., Q.O. and Y.T. designed the research; Y.C. performed simulation; Y.C. and Y.T. contributed the analytical results; Y.C., Q.O., and Y.T. wrote the paper.
References
- 1.Eisenberg E, Hill TL. Muscle contraction and free energy transduction in biological systems. Science. 1985;227:999–1006. doi: 10.1126/science.3156404. [DOI] [PubMed] [Google Scholar]
- 2.Hill TL. Free energy transduction and biochemical cycle kinetics. Academic Press; New York: 1977. [Google Scholar]
- 3.Qian H, Beard DA. Cambridge texts in biomedical engineering. Cambridge University Press; Cambridge: 2008. Chemical biophysics :quantitative analysis of cellular systems. [Google Scholar]
- 4.Jülicher F, Ajdari A, Prost J. Modeling molecular motors. Rev Mod Phys. 1997;69:1269. [Google Scholar]
- 5.Nelson DL, Lehninger AL, Cox MM. Lehninger principles of biochemistry. Macmillan Publisher; New York: 2008. [Google Scholar]
- 6.Bialek W, Setayeshgar S. Physical limits to biochemical signaling. Proc Natl Acad Sci U S A. 2005;102:10040–5. doi: 10.1073/pnas.0504321102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hu B, Chen W, Rappel WJ, Levine H. Physical limits on cellular sensing of spatial gradients. Phys Rev Lett. 2010;105:048104. doi: 10.1103/PhysRevLett.105.048104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lan G, Sartori P, Neumann S, Sourjik V, Tu Y. The energy-speed-accuracy tradeoff in sensory adaptation. Nat Phys. 2012;8:422–428. doi: 10.1038/nphys2276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lan G, Tu Y. The cost of sensitive response and accurate adaptation in networks with an incoherent type-1 feed-forward loop. J R Soc Interface. 2013;10:20130489. doi: 10.1098/rsif.2013.0489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Skoge M, Naqvi S, Meir Y, Wingreen NS. Chemical sensing by nonequilibrium cooperative receptors. Phys Rev Lett. 2013;110:248102. doi: 10.1103/PhysRevLett.110.248102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lang AH, Fisher CK, Mora T, Mehta P. Thermodynamics of statistical inference by cells. Phys Rev Lett. 2014;113:148103. doi: 10.1103/PhysRevLett.113.148103. [DOI] [PubMed] [Google Scholar]
- 12.Goldbeter A. Biochemical oscillations and cellular rhythms: the molecular bases of periodic and chaotic behaviour. Cambridge University Press; Cambridge: 1996. [Google Scholar]
- 13.Martiel JL, Goldbeter A. A model based on receptor desensitization for cyclic amp signaling in dictyostelium cells. Biophys J. 1987;52:807–28. doi: 10.1016/S0006-3495(87)83275-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pomerening JR, Sontag ED, Ferrell JE. Building a cell cycle oscillator: hysteresis and bistability in the activation of cdc2. Nature Cell Biology. 2003;5:346–351. doi: 10.1038/ncb954. [DOI] [PubMed] [Google Scholar]
- 15.Tsai TY-C, et al. Robust, tunable biological oscillations from interlinked positive and negative feedback loops. Science. 2008;321:126–129. doi: 10.1126/science.1156951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ferrell JJ, Tsai TY, Yang Q. Modeling the cell cycle: why do certain circuits oscillate? Cell. 2011;144:874–85. doi: 10.1016/j.cell.2011.03.006. [DOI] [PubMed] [Google Scholar]
- 17.Hogenesch JB, Ueda HR. Understanding systems-level properties: timely stories from the study of clocks. Nat Rev Genet. 2011;12:407–16. doi: 10.1038/nrg2972. [DOI] [PubMed] [Google Scholar]
- 18.Elowitz MB, Leibler S. A synthetic oscillatory network of transcriptional regulators. Nature. 2000;403:335–8. doi: 10.1038/35002125. [DOI] [PubMed] [Google Scholar]
- 19.Stricker J, et al. A fast, robust and tunable synthetic gene oscillator. Nature. 2008;456:516–519. doi: 10.1038/nature07389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Novak B, Tyson JJ. Design principles of biochemical oscillators. Nat Rev Mol Cell Biol. 2008;9:981–91. doi: 10.1038/nrm2530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Barkai N, Leibler S. Circadian clocks limited by noise. Nature. 2000;403:267–8. doi: 10.1038/35002258. [DOI] [PubMed] [Google Scholar]
- 22.van Dorp M, Lannoo B, Carlon E. Generation of oscillating gene regulatory network motifs. Phys Rev E. 2013;88:012722. doi: 10.1103/PhysRevE.88.012722. [DOI] [PubMed] [Google Scholar]
- 23.Nakajima M, et al. Reconstitution of circadian oscillation of cyanobacterial kaic phosphorylation in vitro. Science. 2005;308:414–415. doi: 10.1126/science.1108451. [DOI] [PubMed] [Google Scholar]
- 24.Rust MJ, Markson JS, Lane WS, Fisher DS, O'Shea EK. Ordered phosphorylation governs oscillation of a three-protein circadian clock. Science. 2007;318:809–12. doi: 10.1126/science.1148596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Goldbeter A. A minimal cascade model for the mitotic oscillator involving cyclin and cdc2 kinase. Proc Natl Acad Sci U S A. 1991;88:9107–11. doi: 10.1073/pnas.88.20.9107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pomerening JR, Kim SY, Ferrell JE., Jr Systems-level dissection of the cell-cycle oscillator: bypassing positive feedback produces damped oscillations. Cell. 2005;122:565–578. doi: 10.1016/j.cell.2005.06.016. [DOI] [PubMed] [Google Scholar]
- 27.Danino T, Mondragon-Palomino O, Tsimring L, Hasty J. A synchronized quorum of genetic clocks. Nature. 2010;463:326–30. doi: 10.1038/nature08753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Prindle A, et al. A sensing array of radically coupled genetic biopixels. Nature. 2012;481:39–44. doi: 10.1038/nature10722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Krishna S, Jensen MH, Sneppen K. Minimal model of spiky oscillations in nf-kappab signaling. Proc Natl Acad Sci U S A. 2006;103:10840–5. doi: 10.1073/pnas.0604085103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Geva-Zatorsky N, et al. Oscillations and variability in the p53 system. Mol Syst Biol. 2006;2:0033. doi: 10.1038/msb4100068. 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Szallasi Z, Stelling J, Periwal V. System modeling in cell biology: from concepts to nuts and bolts. MIT Press; Cambridge, Mass.: 2006. [Google Scholar]
- 32.Goldbeter A, Lefever R. Dissipative structures for an allosteric model. application to glycolytic oscillations. Biophys J. 1972;12:1302–15. doi: 10.1016/S0006-3495(72)86164-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Dupont G, Berridge M, Goldbeter A. Signal-induced Ca2+ oscillations: Properties of a model based on Ca2+-induced Ca2+ release. Cell calcium. 1991;12:73–85. doi: 10.1016/0143-4160(91)90010-c. [DOI] [PubMed] [Google Scholar]
- 34.Qian H. Phosphorylation energy hypothesis: open chemical systems and their biological functions. Annu Rev Phys Chem. 2007;58:113–42. doi: 10.1146/annurev.physchem.58.032806.104550. [DOI] [PubMed] [Google Scholar]
- 35.Rust MJ, Golden SS, O'Shea EK. Light-driven changes in energy metabolism directly entrain the cyanobacterial circadian oscillator. Science. 2011;331:220–3. doi: 10.1126/science.1197243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Phong C, Markson JS, Wilhoite CM, Rust MJ. Robust and tunable circadian rhythms from differentially sensitive catalytic domains. Proc Natl Acad Sci U S A. 2013;110:1124–1129. doi: 10.1073/pnas.1212113110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Tome T, de Oliveira MJ. Entropy production in irreversible systems described by a fokker-planck equation. Phys Rev E. 2010;82:021120. doi: 10.1103/PhysRevE.82.021120. [DOI] [PubMed] [Google Scholar]
- 38.Seifert U. Entropy production along a stochastic trajectory and an integral uctuation theorem. Phys Rev Lett. 2005;95:040602. doi: 10.1103/PhysRevLett.95.040602. [DOI] [PubMed] [Google Scholar]
- 39.Berg HC, Purcell EM. Physics of chemoreception. Biophys. J. 1977;20:193–219. doi: 10.1016/S0006-3495(77)85544-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Terauchi K, et al. Atpase activity of kaic determines the basic timing for circadian clock of cyanobacteria. Proc Natl Acad Sci U S A. 2007;104:16377–16381. doi: 10.1073/pnas.0706292104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Barkai N, Leibler S. Robustness in simple biochemical networks. Nature. 1997;387:913–7. doi: 10.1038/43199. [DOI] [PubMed] [Google Scholar]
- 42.Ma W, Trusina A, El-Samad H, Lim WA, Tang C. De ning network topologies that can achieve biochemical adaptation. Cell. 2009;138:760–73. doi: 10.1016/j.cell.2009.06.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J Chem Phys. 1977;81:2340–2361. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.