Robust Scoring Functions for Protein-Ligand Interactions with Quantum Chemical Charge Models

Abstract

Ordinary least square (OLS) regression has been used widely for constructing the free scoring functions for protein-ligand interaction. However, OLS is very sensitive to the existence of outliers, and models constructed using it are easily affected by the outliers or even the choice of the dataset. On the other hand, determination of atomic charges is regarded as of central importance, because the electrostatic interaction is known to be a key contributing factor for biomolecular association. In the development of the AutoDock4 scoring function, only OLS was conducted, and the simple Gasteiger method was adopted. It is therefore of considerable interest to see whether more rigorous charge models could improve the statistical performance of the AutoDock4 scoring function. In this study, we have employed two well-established quantum chemical approaches, namely the restrained electrostatic potential (RESP) and the Austin-Model 1-Bond Charge Correction (AM1-BCC) methods, to obtain atomic partial charges, and we have compared how different charge models affect the performance of AutoDock4 scoring functions. In combination with robust regression analysis and outlier exclusion, our new protein-ligand free energy regression model with AM1-BCC charges for ligands and Amber99SB charges for proteins achieve lowest root-mean squared error of 1.637 kcal/mol for the training set of 147 complexes and 2.176 kcal/mol for the external test set of 1427 complexes. The assessment for binding pose prediction with the 100 external decoy sets indicates very high success rate of 87% with the criteria of predicted RMSD less than 2 Å. The success rates and statistical performance of our robust scoring functions are only weakly class-dependent (hydrophobic, hydrophilic, or mixed).

INTRODUCTION

Evaluation of the binding affinities of drug-like molecules with the target proteins is crucial for discriminating drug candidates from weak-binding or even non-binding small molecules. Most, if not all, computational docking methods rely greatly on empirical or semi-empirical scoring functions to evaluate protein-ligand interactions. Rigorous statistical mechanical approaches for evaluation of binding free energies are theoretically most satisfactory,^{1, 2} but such approaches are computationally too demanding for virtual screening. The simplest forms of evaluating protein-ligand binding affinity are empirical scoring functions^3–6 based on the quantitative structure-activity relationships (QSAR) approach pioneered by Hansch,⁷ or semi-empirical models with molecular mechanics-based energetics.^8–11 Common in these approaches is multivariate regression. Semi-empirical models based on molecular mechanics have the advantages of easier rational interpretation of binding modes, and they are more sensitive to protein conformational changes. This is particularly important when protein dynamics and flexibility are to be accommodated.^12–14 Frequently used energetic terms include dispersion/repulsion (i.e. van der Waals energy), electrostatic energy, hydrogen bond energy, desolvation energy, hydrophobic interaction, torsional entropy, etc.^{8, 9} Among these terms, the atomic partial charges of biomolecules is considered of central importance, because they are crucial for evaluation of the long-ranged electrostatic interaction, which is known to be a key contributing factor for biomolecular association. Due to the extremely low computational cost, especially when facilitated with pre-calculated grid maps, current molecular docking programs often use regression models with distance-dependent molecular descriptors or energy terms to predict the possible binding poses of a small molecule, to evaluate its binding affinity, or to use for large scale virtual chemical library screening for rapidly limiting the chemical space and for subsequent identification of potential drugs.

Intuitively, inclusion of more energetic terms or molecular descriptors in a scoring function may provide a more complete description of protein-ligand interactions and a more accurate binding free energy model. However, the introduction of many variables in a regression model can often lead to the over-fitting problem,¹⁵ which is caused by the vast emptiness of high dimensional multivariate space. On the other hand, the selection of molecular descriptors or energetic terms will also dictate the performance and applicability of such free energy models.¹⁶

The AutoDock4 scoring function⁹ is a semi-empirical scoring function that is embedded in the automated molecular docking software package, AutoDock, and has been widely adopted in virtual screening of drug candidates and prediction of ligand binding poses in protein pockets. The energetic terms in the AutoDock4 scoring function include van der Waals interaction, electrostatic interactions, hydrogen bonding interactions, desolvation free energy, and loss of ligand torsional entropy upon binding. The atomic charges used to evaluate the electrostatics energy term of the AutoDock4 were prepared using the Gasteiger charge model,¹⁷ whose primary advantages lie in its simplicity and speed. However, such charge calculations can generate atomic charges that are less accurate than those determined by quantum chemical methods. For example, the dipole moment of the well-known polar molecule dimethyl sulfoxide (DMSO) calculated by the Gasteiger model is only 2.96 Debye (D), which is quite different from the results of RESP (4.61 D) and AM1-BCC (4.57 D). (The dipole moment of DMSO in solution can be estimated¹⁸ from its measured dipole moment in vacuum (3.96 D¹⁹) to be about 4.7 D) Due to the increase of computing power, ab initio quantum mechanical calculations can now be performed routinely, and some recent studies have indicated that docking calculations using more accurate atomic charges can indeed predict binding poses more accurately.^20–22 However, in these studies the more advanced charge models were not employed to construct new scoring functions, which may weaken the assertion that the more advanced charge models have superior predictive power. If a charge model is qualitatively and quantitatively different from the charge model used to develop a scoring function, one can expect large prediction errors. In other words, simply employing more accurate atomic charge models should not generally lead to better predictions of binding poses and binding affinities. Weighting coefficients of scoring functions in the empirical QSAR models need to be recalibrated.

In this study, we report our investigation of the influence of different charge models on the AutoDock4 scoring function, in order to see how different charge models affect the performance of the same functional form of the AutoDock4 scoring function. Our ordinary least square regression analyses indicated that AM1-BCC or RESP charges for ligands in combination with Amber99SB charges for proteins yielded lower root-mean-squared errors (RMSE). Because proper outlier exclusion is also important for calibration of empirical scoring functions, we have performed robust regressions and analyzed outliers. The performances of robust regression in several QSAR modeling tasks have been reported, ²³ and it was concluded that robust regression is always better than ordinary least square regression. Recently, we performed robust regression to delineate the influence of the data set on the calibration of empirical scoring functions for protein-ligand interactions.²⁴ Here we compare the statistical performance of the new robust regression models with different charge combinations on both the training set and a large external test set. We have also tested the performance of binding pose prediction of the new robust models on the 100 external decoy sets²⁵ that have been widely used in the assessment of protein-ligand scoring functions,^{26, 27} as well as on a new decoy set of 195 complexes.²⁸

METHODS

Functional form of AutoDock4 Scoring function

Improvements of the AutoDock4 (AD4) scoring function⁹ over its predecessor, AutoDock3,⁸ include a refined functional form of the desolvation energy, more atom types, and a significantly larger training dataset. The AD4 scoring function comprises five energetic terms: the van der Waals interaction, hydrogen bonding, electrostatic interaction, desolvation energy, and torsional entropy. The AD4 scoring function predicts the binding free energy with the following formula:

$$\Delta G_{bind}=W_{vdw}\times \sum _{i,j}(\frac{A_{ij}}{r_{ij}^{12}}-\frac{B_{ij}}{r_{ij}^6})$$

$$+W_{H-bond}\times \sum _{i,j}E(t)(\frac{C_{ij}}{r_{ij}^{12}}-\frac{D_{ij}}{r_{ij}^{10}})$$

$$+W_{estat}\times \sum _{i,j}\frac{q_i{q}_j}{\epsilon (r_{ij})r_{ij}},$$

$$+W_{desol}\times \sum _{i,j}(S_i{V}_j+S_j{V}_i)e^{(-r_{ij}^2/2{\sigma }^2)}$$

$$+W_{tor}\times N_{tors}$$

The weighting coefficients W_i were obtained by regression analysis of the experimental binding affinity information collected in Ligand Protein Database (LPDB).²⁹ The van der Waals potential energy is a typical 12-6 form, where parameter A_ij and B_ij were adopted from the ’84 Amber force field.³⁰ The hydrogen bonding term is based on a 12-10 potential, weighted by a directional term, E(t). The electrostatic interaction is calculated with a screened Coulomb potential.³¹ The desolvation term is included by calculating the surrounding volume of an atom (V_i), weighted by the atomic solvation parameter (S_i) and an exponential term with a distance weighting factor σ (0.35 Å in AutoDock4). The final term represents the torsional entropy term, which is calculated simply by counting the number of rotatable bonds of a ligand.³²

Charge models

In this work, we focus on the two charge models, RESP³³ and AM1-BCC,³⁴ that have been used widely in molecular dynamics simulations with the AMBER force field. RESP (Restrained ElectroStatic Potential)³³ is a two-stage restrained electrostatic fit charge model. While the geometry of the molecule was taken from experimental structures, the quantum mechanical electrostatic potentials (ESP) based on the 6-31G* basis set were evaluated at the shells of points with the density of one point/Ų at each of 1.4, 1.6, 1.8 and 2.0 times the van der Waals radii of the molecule. Then, atom-centered model charges were derived by minimizing the differences between the reproduced ESP and the original QM ESP plus the deviation from the minimum of a hyperbolic restraint function. In the first stage of the fitting process, no forced symmetry is applied, and a weak restraint is used. In the second stage, the charges on equivalent atoms are forced to be the same, and a strong restraint is used. Quantum mechanical calculations were performed by GAUSSIAN 09³⁵ at the Hartree-Fock (HF) level with the 6-31G* basis set.³⁶ The RESP atomic charges were computed by using Antechamber of the AMBER 11 suite based on the GAUSSIAN output file and were saved as the Tripos Mol2 format. Subsequently, the ADT program (prepare_ligand4.py) enables the conversion from the mol2 file to the pdbqt file format with the RESP atomic charges obtained.

As a semi-empirical approach, AM1-BCC is a quick and efficient atomic charge model that aims to achieve the accuracy of RESP.^{34, 37} The AM1 charges were first calculated from the MOPAC 6 program for the individual molecule. The “am1bcc” program of the Antechamber package assigned bond type and atom type, and then performed bond charge corrections (BCCs) that were parameterized against the HF/6-31G* electrostatic potentials of a set of training compounds. The Tripos mol2 file with AM1-BCC atomic charges was saved by the Antechamber program and then converted to the ligand pdbqt file by the ADT program (prepare_ligand4.py).

The atomic charges of proteins were retrieved from the AMBER parm99SB force field parameters, which were mainly derived by the RESP methodology.^{18, 38, 39} The residue name was assigned to comply with the Amber naming scheme, e.g. histidine with hydrogens on both nitrogens (HIP), histidine with hydrogen on the epsilon nitrogen (HIE), histidine with hydrogen on the delta nitrogen (HID), disulfide bonded cysteine (CYX) and so on. Subsequently, the LEaP program of AMBER 11 was employed to produce the coordinates and parameter/topology files, which were used to generate the “pqr” files with atomic charges and radii with the “ambpdb” program. These atomic charges then substituted the charges in the original “pdbqt” files that were generated by the ADT program (prepare_receptor4.py) with default settings.

Preparation of protein and ligand structural files

Before the calculations of atomic charges for the ligands, first, hydrogen atoms need to be added and the net charges of the molecules should be determined. The ligand structural information was extracted from a complex with the form of biological assembly in Protein Data Bank, and then hydrogen atoms were added by OpenBabel,⁴⁰ net charges calculated by the “estimateFormalCharge” function in Chimera.⁴¹ Because OpenBabel does not always assign correct protonation states, we further checked the protonation assignment of each ligand carefully and correct its mistakes by our in-house scripts

The protonated states of receptors and ligands were obtained from a previous preparation of Huey et al.⁹ Similarly, ligands were optimized by using local search capability of AutoDock⁸ to avoid too close contact in the crystallographic atomic structural model.

It should be noted that many cofactors exist in several complexes of LPDB. These cofactors are neither amino acids nor parts of ligands, but they are often required for biological activity. Occasionally, these cofactors are located near ligands and are also inside the grid box of pre-calculated protein-ligand interactions. In the original version of AutoDock4 scoring function, the atomic charges of cofactors were also determined by the Gasteiger method.⁹ To be consistent in the charge models of ligands in this work, the RESP and AM1-BCC models were also utilized on these cofactors. Some of the RESP charges of the cofactors can be retrieved from the literature: the charges of heme group were obtained from Autenrieth et al.⁴² (for cytochrome c) and Oda et al.⁴³ (for cytochrome P450).

Because the AutoDock4 scoring function was calibrated for united atom models, the nonpolar hydrogen atoms were merged and united atom charges calculated by the ADT program (prepare_ligand4.py or prepare_receptor4.py). In the next sections of this article, the abbreviations “AP” for AM1-BCC (Ligand)/Amber PARM99SB (Protein); “RP” for RESP (Ligand)/Amber PARM99SB (Protein) have been adopted.

Calculation of energetic terms

To evaluate the various energetic terms, the grid maps of different atom types of ligand were constructed by the “autogrid4” programs, with a grid spacing of 0.375Å. The grid center was positioned at the geometrical center of a ligand, and the grid box was adjusted according to the size of a ligand, plus 22.5 Å. Subsequently, the “autodock4” program was used to calculate the energetic terms of protein-ligand interactions by setting the parameter as “epdb” in the AutoDock parameter file (dpf).

Adjustment of atomic solvation parameters

The atomic charges are related to both the electrostatics term and the desolvation term, and the latter term in AutoDock4 was developed along the lines of Wesson et al.⁴⁴ and Stouten et al.⁴⁵ The atomic solvation parameter and the amount of desolvation are required for evaluating the energetic term of desolvation. The atomic solvation parameter (S_i) in AD4 was determined by a simple linear model:

$$S_i=(AS{P}_k+QASP\times |q_i|),k=\mathrm{C},\mathrm{A},\mathrm{N},\mathrm{O},\mathrm{S},\mathrm{H}$$

where ASP_k and QSAP are the intercept and the regression coefficient, respectively; q_i is the atomic charge. In this work, we adopt the approach of Bikadi et al.⁴⁶ to tune the QASP values for different atomic charge models and retain other calibrated parameters in the original desolvation function of AutoDock4. The new QASP parameters were adopted as 0.006393 and 0.006383 for RP and AP, respectively.

Robust regression with the FAST-LTS algorithm

We performed robust regression analyses with the least trimmed squares (LTS) estimator,⁴⁷ which has high breakdown point, and the influence of the outliers can be mitigated. The computational cost of LTS regression for systems in this study (dataset size < 200; the number of variables < 6) is a few minutes using a single core Xeon X5690 core.

Instead of minimizing the sum square of all residuals of a data set with size n, as in OLS regression, the LTS regression minimizes the sum of squared residuals over a subset of h samples:

$$\sum _{i=1}^h{(r^2)}_{i:n}$$

In calculating the LTS estimator, first all the squared residuals r_i‘s are sorted, and the h smallest squared residuals are selected to calculate the estimator. The absolute residual |r_i| of a sample point i can be considered as its distance to the constructed hyperplane, i.e., the multivariate linear regression model. The detailed analysis of LTS has been described by Rousseeuw et al.^{48, 49} The FAST-LTS algorithm⁴⁹ implemented as “ltsReg” in the “robustbase” package⁵⁰ of R (http://www.r-project.org/) was used in this work. The FAST-LTS algorithm starts with randomly selecting p samples, where p is the number of variables in the regression model. Then, a hyperplane (dimension p-1) through these p samples is constructed. The residuals of all n samples are evaluated with respect to the constructed p-subset hyperplane and then sorted. According to the calculated residuals of all the samples, a new subset of h samples with smallest absolute residuals was selected. Subsequently, two C-steps (where C stands for “concentration”) are carried out. In a C-step, the ordinary least squares regression is performed on the h-subset selected in the previous procedure, all the n residuals are evaluated with respect to this regression model and sorted. Only two C-steps are needed because the data size in our system is smaller than 600.⁴⁹ This procedure will be repeated 10⁸ times, and the 10 models with lowest sum of squares of the h smallest residuals will be conducted with more C-steps until convergence. The convergence in FAST-LTS algorithm means that the sum of squared residuals over a subset of h samples of m-1^th C-step is the same as the m^th C-step. According to the practice of Rousseeuw et al.⁴⁹, m is often below 10. Finally, the model with lowest sum of squares is reported. The entire procedure was repeated twice to confirm that the results are identical.

RESULTS and DISCUSSION

Ordinary least square regression models with three charge combinations

To understand the inadequacy of using different charge models with the original AutoDock4 scoring function, we first calculated the root-mean squared error (RMSE) between the experimental binding free energy and the binding free energy estimated by the original AD4 scoring function, but with the charges calculated with the RESP model. A very large RMSE value, 7.3 kcal/mol, was found, indicating that recalibrating coefficients is indispensable when different charge models are used. If the Gasteiger charge model was used, as in the original AD4 scoring function, a much smaller RMSE of 2.542 kcal/mol was obtained. Because the PDB entries 1sre and 1stp have been identified as outliers in the previous study,⁸ the OLS calibration was done with the remaining 187 complexes. However, these two entries were included in the robust regression, where we showed that these two outliers can indeed be identified. With OLS regression, the AD4 scoring functions with RESP and AM1-CC charges for ligands and AMBER Parm99SB charges for proteins yield slightly lower RMSEs, as shown in Table 1.

Table 1.

OLS regression results of AutoDock4 scoring function with different charge models

Combinations		Coefficients of energetic terms
Ligand	Protein	Size	Wdesolv	Westat	Whbond	Wtors	Wvdw	RMSE
Gasteiger	Gasteiger	187	0.120	0.142	0.121	0.283	0.172	2.542
AM1-BCC	Amber99SB	187	0.093	0.125	0.077	0.279	0.167	2.523
RESP	Amber99SB	187	0.107	0.132	0.090	0.301	0.167	2.471

All RMSE values are in kcal/mol.

F-statistics: all p-values < 2.2×10⁻¹⁶

Progressively removing the outliers in OLS regression analysis

In the previous section, we performed the OLS regression for the AutoDock4 scoring function to calibrate new coefficients with various charge models. To our knowledge, most, if not all, empirical or semi-empirical scoring functions for protein-ligand interaction are constructed by OLS regression. Selection of training dataset is always crucial for the OLS regression approach because the influence of outliers is usually very significant. The resistance of OLS to outliers is almost zero, and the fitted model will probably be affected by any arbitrary outlier. In contrast, the robust regression is usually less influenced by outliers.⁴⁸

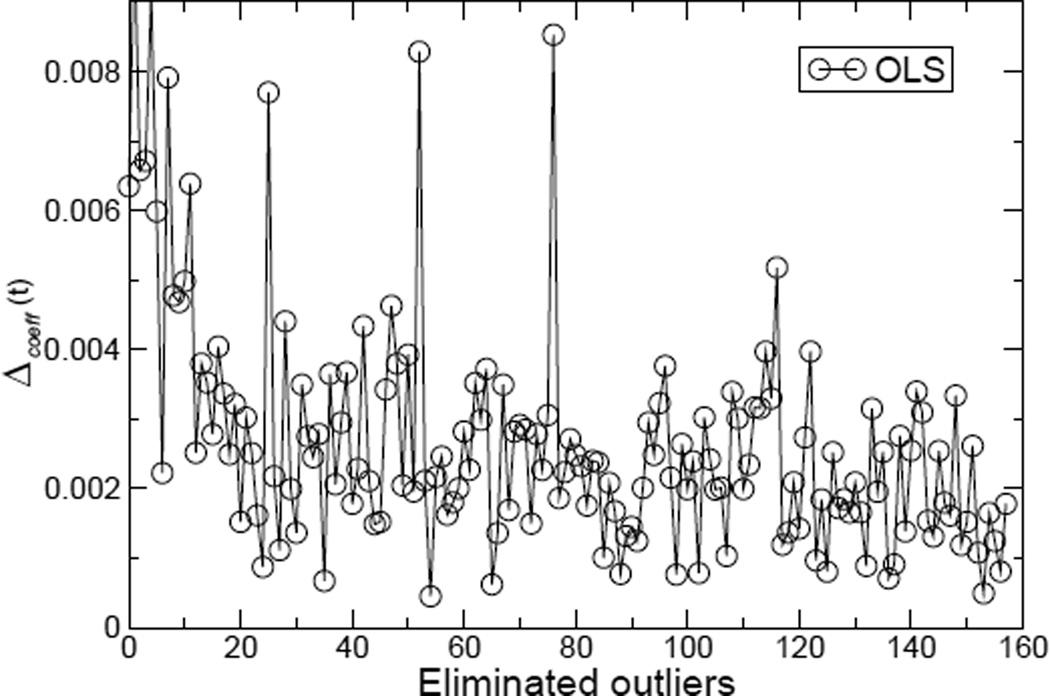
On the other hand, it may be anticipated that OLS regression could be improved if the samples with large residuals (probable outliers) are removed, which may (wrongly) suggest that OLS with progressive outlier removal can finally generate the same model as the one generated by robust regression. To assess how OLS models evolve by removing the most apparent outliers, we perform an initial OLS regression with the entire dataset with N samples; we then remove the sample with largest residual (i.e., the most apparent outlier), and the OLS regression is performed on the dataset with N-1 samples. This so-called evolutionary regression procedure⁵¹ is repeated until the dataset size is 30. The coefficients of the N-sample regression model will be compared with the coefficients of the N-1 sample regression model to assess the stability of the models, and the average of mean coefficient difference, Δ_coeff(t) is calculated as follows:

$${\Delta }_{coeff}(t)=\sqrt{\frac{1}{5}\sum _{i=1}^5{(W_{i,t}-W_{i,t-1})}^2}$$

W_i,t represents the coefficient of the i^th energetic term in the t^th regression after t samples with the largest residuals are removed. From the curve of Δ_coeff(t) shown in Figure 1, it can clearly be seen that progressively removing the outliers does not lead to stable models with the OLS regression analysis. Note that with LTS robust regression we simply obtain a straight line Δ_coeff(t) = 0 for the number of eliminated outliers less than N-h (i.e., 0-97).

Figure 1.

The average of mean coefficient difference Δ_coeff(t) versus the number of eliminated outliers. Note that the models are still very unstable even after one third or more of large residual data points are regarded as outliers and eliminated. The charge combination is RP.

Difference between OLS and LTS regression analysis

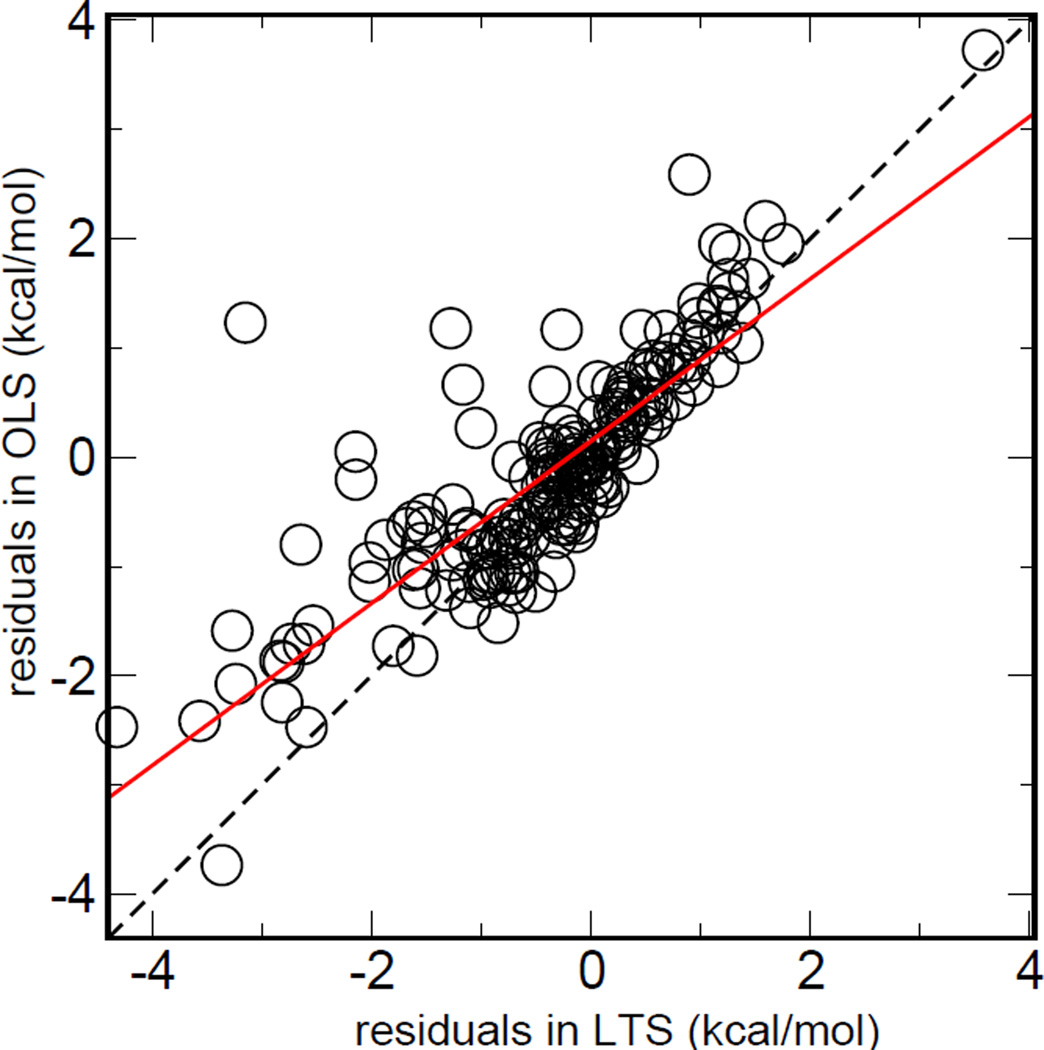
To illustrate the difference between OLS and LTS regression analysis, the residual-residual plot (RR-plot)^{52, 53} was made, as shown in Figure 2, which is the scatter plot of the residuals from two regression analyses. The RR plot can be used to characterize the disparity of residuals defined by different methods. Figure 2 indicates that there are indeed significant disparities between the residuals defined by the OLS and LTS methods. It can also be observed that the LTS residuals of most data points with strong disparity are larger. As a result, the outliers possess larger residuals from robust regression but smaller residual from OLS, which make the solid line tilted. This phenomenon also reflects the capacity of resistance to the outliers of different regression models.

Figure 2.

The Residual-Residual plots between OLS and LTS. The charge combination is RP. The solid red line was obtained by linear fitting between residuals from two regression methods. If no outlier blends with the training set, the residuals of OLS regression and robust regression will be similar to the identity line (dashed). The sloped red solid line shows the capacity of resistance to the outliers of different regression models.

Distribution of residuals of three charge models

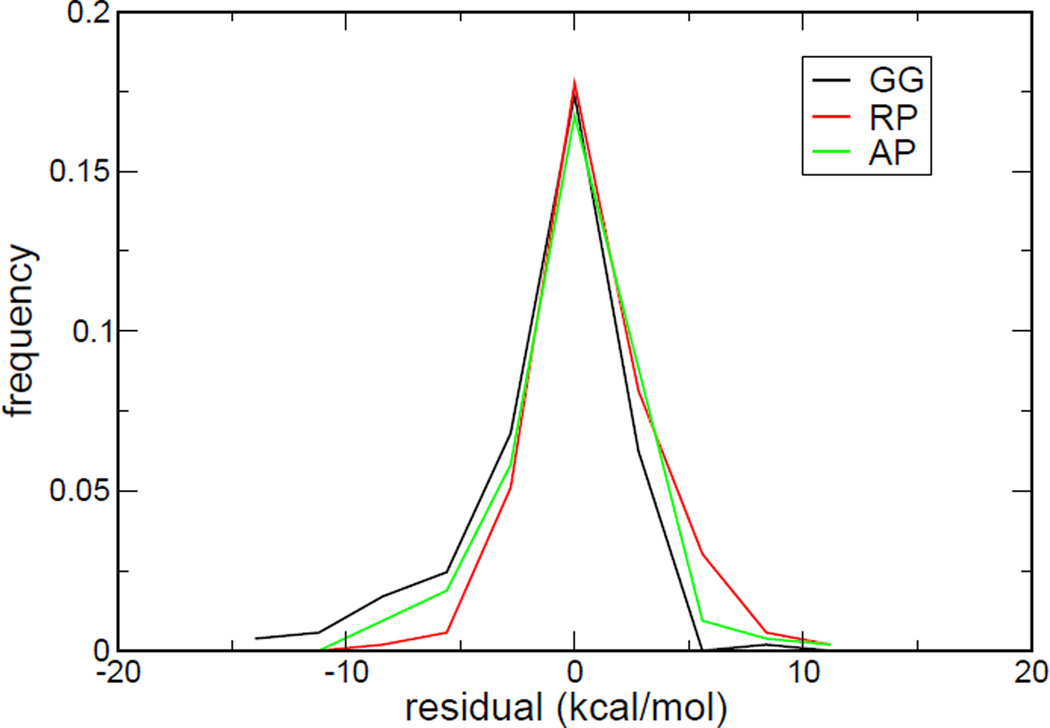
Although robust regression will fit to the majority of data and the models constructed by robust regression are insensitive to outliers, the outliers in the data set still contribute to the RMSE of a model. To reiterate, if there are only a few outliers in a dataset, the models (i.e., their coefficients) constructed by robust regression will not be affected, but these outliers will still deteriorate the statistical performance of the models. To fairly assess the statistical performance of a model, it is still important to identify the outliers of a dataset. Figure 3 gives the distributions of residuals for robust regression models with three charge combinations. It is interesting to note that the residuals of the model with the AP charge combination give the most symmetric distribution, and therefore most “Gaussian-like.” The distributions of residuals of the models with the GG and RP charge combinations are rather skewed. It can also be observed that the distribution of residuals of the GG model has a long tail on the left-hand side of the distribution.

Figure 3.

The histograms of residuals based on the model constructed by robust regression analyses. The black, red and green lines represent residuals distributions of GG, RP and AP models, respectively.

Identification of common outliers to three charge models

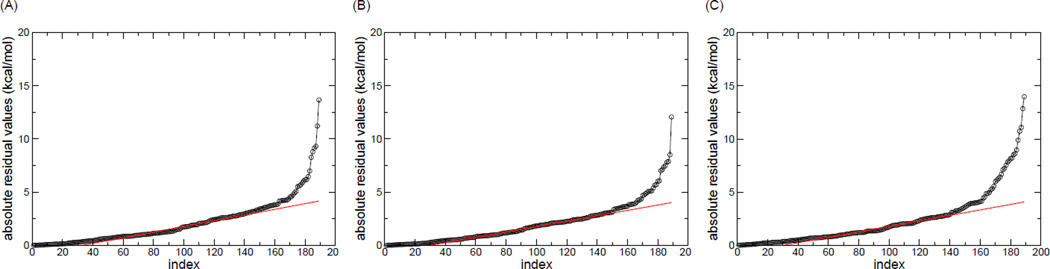
A natural strategy to determine the data set for model construction is to remove the common outliers to three charge models. To determine the common outliers, the residuals obtained from the LTS regression were first sorted as shown in Figure 4. To facilitate easy recognition of outliers, a red line that fit the residuals between top 25% and 75% was drawn. A data point that is too far away (larger than the criterion shown below) from the red line in Figure 4 is considered as an outlier. The criterion for the outlier detection here is defined as the absolute value of the y-intercept of the red line. It is seen that the GG model possess the largest number of outliers, compared to the AP and RP models. We removed the union of identified outliers from three charge model combinations and finally obtained a common dataset of 147 complexes. In the following sections, these 147 complexes will be designated as the “clean” set. The outliers of three robust models are listed in Tables S1, S2 and S3 of Supporting Information.

Figure 4.

Sorted absolute residuals based on robust regression analysis for the (A) RP and (B) AP and (C) GG charge combinations. The index represents the rank of residuals. Red lines are fitted to the residuals between top 25% and 75%.

To obtain the final regression models with three charge combinations, another OLS regression on the clean set was performed, following the previous robust regression procedure.⁴⁸ In the following sections, the models constructed by first outlier detection with LTS regression analysis and then OLS regression are called “robust models.” Table 2 gives the robust models for the three charge combinations and their RMSE’s on the training set (i.e., the clean set). It can be seen that the RAP model (robust model with the charge combination AP) has the lowest RMSE value of 1.637 kcal/mol. It should be noted that the performance of the RGG or RRP model is almost as good as that of the RAP model, which may be due to the fact that the bad data points has been removed. More detailed comparisons of different charge combinations are discussed in the last subsection of this section.

Table 2.

Coefficients of the robust AutoDock4 scoring functions. The size of the clean set is 147.

Models	Coefficients of different energetic terms
	Wdesolv	Westat	Whbond	Wtors	Wvdw	RMSE
AutoDock4RGG	0.0996	0.0241	0.1806	0.3594	0.1734	1.664
AutoDock4RAP	0.0993	0.0491	0.1565	0.3422	0.1736	1.637
AutoDock4RRP	0.0954	0.0661	0.1521	0.3618	0.1698	1.641

All RMSE values are in kcal/mol.

F-statistics: all p-values < 2.2×10⁻¹⁶

We further performed two types of cross-validation, the leave-one-out cross-validation (LOO-CV) and leave-group-out cross validation (LGO-CV), shown in Table 3. LOO-CV is a popular approach, but it has recently been discussed for its possible fallacies.⁵⁴ Shao demonstrated LOO-CV is asymptotically inconsistent⁵⁵ and Golbraikh showed the high value q² of LOO-CV is the necessary but not the sufficient condition for a good QSAR model with high predictive power.⁵⁶ Therefore, we also performed the leave-group-out cross-validation (LGO-CV), which is also known as the Monte-Carlo cross-validation (MCCV). LGO-CV is conducted by randomly sampling a test set from a group of data points with as many iterations as possible. Based on the suggestions of Konovalov et al.²³, we divided the clean set into one half for training and one half for testing. With 1000 iterations, the average values of S_PRESS and q² were summarized in Table 3. The S_PRESS and q² are given by following equations:

$$S_{PRESS}=\sqrt{\frac{\sum _i{(E_{i,\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}.}-E_{i,\text{exp}.})}^2}{N-k}};q^2=1-\frac{\sum _i{(E_{i,\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}.}-E_{i,\text{exp}.})}^2}{\sum _i{(E_{i,\text{exp}.}-E_{i,\text{mean}})}^2}.$$

Table 3.

Cross-validation of three robust regression models in this work

Combination	LOO-CV		MCCV
	SPRESSS	q2	SPRESS	q2
AutoDock4RGG	1.732	0.675	1.782	0.657
AutoDock4RAP	1.707	0.684	1.749	0.670
AutoDock4RRP	1.711	0.683	1.755	0.668

All RMSE values and S_PRESS are in kcal/mol.

E_pred. and E_exp. are the predicted and experimental binding free energy, respectively. E_mean. is the mean value of experimental binding free energy of all observed cases. N is the size of the training set. The degree of freedom, k, is 5 for all the regression models in this study. The results shown in Table 3 indicate that all assessments of cross-validation are comparable for the performance on the training set. It was shown that the RAP and RRP models gave slightly smaller prediction errors and higher correlations, compared to the RGG model, but the differences in the numerical values of this statistical assessment may not be significant.

Assessment with external complexes

To assess whether the performances of our new robust models are sensitive to the dataset, a benchmark on an external dataset of protein-ligand complexes from PDBbind^{57, 58} was conducted. PDBbind is currently the largest public database that contains the structural information and binding affinities of receptors and ligands. We started with the dataset with 1741 protein-ligand complexes from the 2009 version of PDBbind, which is the so-called “refined set.” In the PDBbind refined set, ligands with added hydrogens and Gasteiger charges have been prepared, and receptors structural files are arranged as biological assemblies. We first filtered out 211 complexes whose net charges of ligands are not consistent with the calculation with the “estimateFormalCharge” function of Chimera. In addition to these ligands with problematic net charges and protonated states, some complexes have problems in atomic charges or energy calculations. For example, MOPAC or GAUSSIAN could not be used to calculate too large molecules within an acceptable time, autogrid4 cannot generate maps for the molecule with more than 32769 atoms, and autodock4 cannot calculate the energies of a ligand with more than 32 torsions. These complexes were further removed. Finally, 1427 complexes from the PDBbind refined set was used as the test set in this study.

Table 4 shows the statistical performances of the three robust AutoDock4 scoring functions and two other recent protein-ligand scoring models, SFCscore⁴ and PDSE-SVM,⁵ on PDBbind data sets. The three robust AutoDock4 scoring functions have significantly higher correlations (R_P, Pearson’s correlation coefficient; R_S, Spearman’s correlation coefficient), as well as smaller standard deviations (SD) and mean errors (ME). For the comparison with SFCscore, we only showed the results of their models that were constructed by multivariate linear regression. Because the test set we used (PDBbind v2009) and the test set of PDSE-SVM (PDBbind v2005) have an overlap of only 634 complexes, we also made an assessment by using the refined set of PDBbind version 2005. Our robust AutoDock4 scoring functions gave comparable results (R_p = 0.540–0.578, R_s = 0.553–0.601) to the performance of PDSE-SVM. Our assessment indicated that AutoDock4^RGG gave slightly better statistics than AutoDock4^RRP. However, the small difference in the numerical values of statistics may not be significant.

Table 4.

Performance of the robust AutoDock4 scoring functions and two other recent scoring functions tested with the PDBbind data sets

scoring function	Ntrain	Ntest	Rp	Rs	SD	ME
AutoDock4RGG	147	1427	0.604	0.615	1.61	1.26
AutoDock4RAP	147	1427	0.606	0.617	1.60	1.25
AutoDock4RRP	147	1427	0.595	0.610	1.62	1.26
original AutoDock4GG	187	1427	0.562	0.594	1.66	1.31
sfc_290m	290	919	0.492	0.555
sfc_229m	229	919	0.501	0.558
sfc_frag	130	919	0.525	0.576
PDSE-SVM	278	977	0.517	0.535	1.84	1.42

SD and ME are presented in the pK_d unit. The binding free energy in kcal/mol at 298 K was converted to the pK_d unit by dividing with the factor of −1.36.

F-statistics: all p-values < 2.2×10⁻¹⁶

Assessment of binding pose prediction with external decoys

The performance of binding pose prediction of the three robust AutoDock4 scoring functions and the original AutoDock4 GG model were assessed by the decoy sets of 100 protein-ligand complexes from Wang et al..²⁵ In this test, 100 ligand conformations near the binding site in each complex were generated by using AutoDock3, and the native ligand conformation of each complex was also included. All structural information with hydrogens added for ligands and receptors are available.⁵⁹ After the atomic charges were calculated, we performed local minimizations to optimize too close contacts of original structures (only for native ligand conformations) in the same procedure as the preparation of the LPDB training dataset. The mean values of RMSD’s between the original and minimized conformation are 0.57Å, 0.66Å and 0.74Å for RGG, RAP and RRP, respectively.

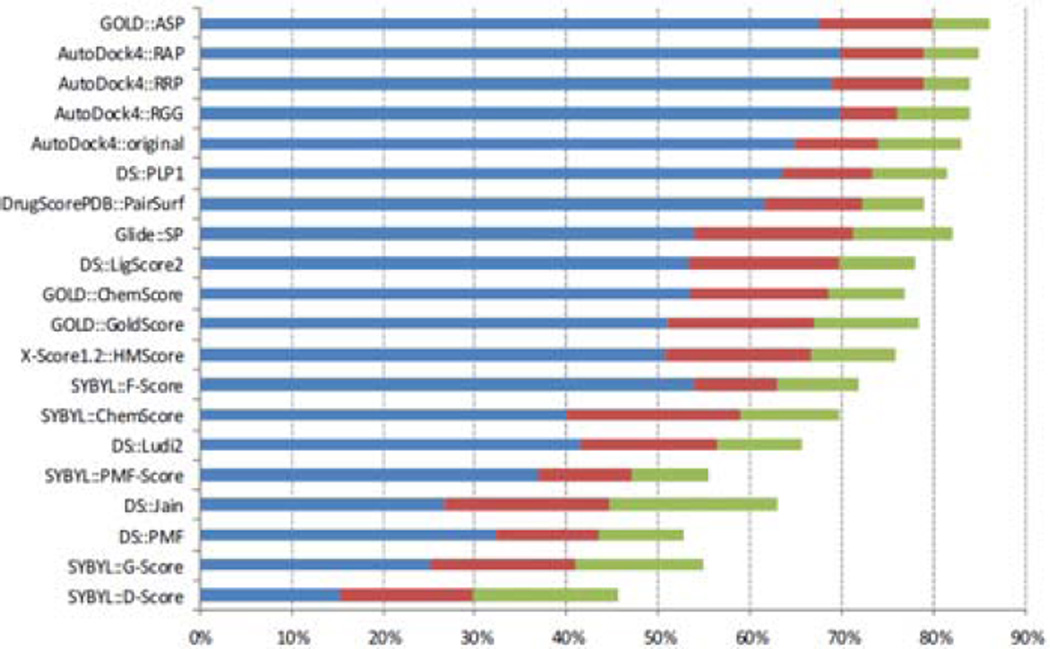
Ideally, if a scoring function could recognize near-native structures among a set of decoys, at least some of the near native conformations (i.e., with small RMSD’s with respect to the native ligand conformation) should have the best scores or the lowest predicted binding free energies. Thus, each conformation with lowest predicted energy and corresponding RMSD with respect to the native conformation was recorded. The success rate can be defined according to different criteria, as shown in Table 5, which gives success rates of AutoDock4 scoring functions and other scoring functions. We found that AutoDock4 made a remarkably improvement compared to AutoDock3 on the same decoy set. The RAP model can even achieve the same success rates of DrugScore^CSD. The RAP and RRP models are not identical, although AM1-BCC is a semi-empirical quantum mechanical model that aimed to reproduce the RESP results as much as possible. On the other hand, we should stress that the performance also strongly depends on the test set. In 2009, Cheng et al.²⁸ published a comparative assessment of scoring functions on a new decoy set, which consists of 195 complexes with reassessed quality of structures, binding data, and components of protein complexes. The ligand conformations were obtained from four docking software packages, with the aim to reduce the bias in binding pose selection. Figure 5 gives the comparison of the success rates of AutoDock4 scoring functions and 16 scoring functions. The robust AutoDock4 functions achieve excellent success rates compared to most of other scoring functions, as shown in Figure 5. To assess whether our robust functions exhibit strong class-dependence, we delineate the success rate results into three classes (hydrophilic, hydrophobic, and mixed). Table 6 summarizes the success rates in these three classes of 100 complexes.²⁵ The robust AutoDock4 functions achieve outstanding success rates in all three classes. It is noted that there is no difference in the accuracy of binding pose prediction between using the RAP charge model and the original AutoDock 4 scoring function for the hydrophobic class of complexes, but there is a significant difference for the hydrophilic class. To further investigate the potential reasons for such observed differences, we inspected at the cases that were predicted differently by these two scoring functions, and found that the four d-xylose isomerase complexes (8xia, 4xia, 2xia and 2xis) in hydrophilic class could be successfully predicted by RAP, but not by the original AutoDock4 scoring function. These cases have some common features: two metals (magnesium or manganese) and a d-xylose in the active site. The difference between the estimated energies of the native poses of d-xylose from RAP and the original AutoDock4 scoring function is mainly due to the electrostatic energetic term (~0.7 kcal/mol) between an oxygen atom of ligand and an metal on the protein site. The different charges of the oxygen atom result in different electrostatic interaction.

Table 5.

Success rates of binding site prediction by different scoring functions^a

	success rate (%) for different rmsd criteria
scoring function	≦1Å	≦1.5Å	≦2Å	≦2.5Å	≦3Å
DrugScoreCSD	83	85	87
AutoDock4RAP	83	85	87	87	87
AutoDock4RGG	80	82	86	86	86
AutoDock4RRP	79	81	84	85	85
original AutoDock4GG	74	76	79	79	79
Cerius2/PLP	63	69	76	79	80
SYBYL/F-Score	56	66	74	77	77
Cerius2/LigScore	64	68	74	75	76
DrugScore	63	68	72	74	74
Cerius2/LUDI	43	55	67	67	67
X-Score	37	54	66	72	74
AutoDock3	34	52	62	68	72
Cerius2/PMF	40	46	52	54	57
SYBYL/G-Score	24	32	42	49	56
SYBYL/ChemScore	12	26	35	37	40
SYBYL/D-Score	8	16	26	30	41

^aExcept for the results of the AutoDock4 scoring functions, the results of DrugScore^CSD and other scoring functions were taken from Velec et al.²⁶ and Wang et al.,²⁵ respectively.

^bScoring functions are sorted by the number of cases under 2Å.

Figure 5.

Comparison of the success rates of AutoDock4 scoring functions and 16 scoring functions provided by Cheng et al.²⁸ The cutoffs are rmsd < 1.0 Å (blue bars), < 2.0 Å (red bars), and < 3.0 Å (green bars), respectively. The native binding poses of ligands were included in the decoy sets. Scoring functions are sorted by the number of cases under 2Å.

Table 6.

Success rates of binding pose prediction of various scoring functions^a on three classes of complexes

	success rate (%; rmsd ≦2Å)
	Overall	hydrophilic	mixed	hydrophobic
scoring function	(100)	(44)	(32)	(24)
AutoDock4RAP	87	89	91	79
AutoDock4RGG	86	86	91	79
AutoDock4RRP	84	84	91	75
original AutoDock4GG	79	77	81	79
Cerius2/PLP	76	77	78	71
SYBYL/F-Score	74	75	75	71
Cerius2/LigScore	74	77	75	67
DrugScorePDB	72	73	81	58
Cerius2/LUDI	67	75	66	54
X-Score	66	82	59	46
AutoDock3	62	73	53	54
Cerius2/PMF	52	68	44	33
SYBYL/G-Score	42	55	34	29
SYBYL/ChemScore	35	32	34	42
SYBYL/D-Score	26	23	28	29

^aData were adopted from Wang et al.²⁵ except for AutoDock4 scoring functions.

^bScoring functions are sorted according to the overall success rates.

Performance of three models for large dipole moment cases

So far, our assessments indicate that the robust model with the GG charge combination (Gasteiger models for both ligand and protein) can achieve similar statistical performances of the robust models with the other two charge combinations, in which quantum chemical calculations need to be carried out. One possible explanation for such close performances could be attributed to the heterogeneity of the data set. Regression analysis, when properly performed, provides the suitable (and subtle) balances among different energetic terms, and the shortcoming or the inaccuracy of some energetic terms can be mitigated by reducing their weighting coefficients. It is therefore worthwhile to assess the three robust models with different charge combinations in the subset of the test set, where the differences of the charges models could be most pronounced. Because different charge models (Gasteiger, RESP, AM1-BCC) mainly affect the distributions of the partial charges of the molecules, not the total charge of the molecules, we should be able to see the differences of the charge models on the subset in which ligands are neutral. On such subset of complexes with neutral ligands, it is especially of interest to see the dependence of statistical performance on the dipole moments of ligands, because the dipole moments give the largest contribution to the electrostatic energies for the neutral ligands.

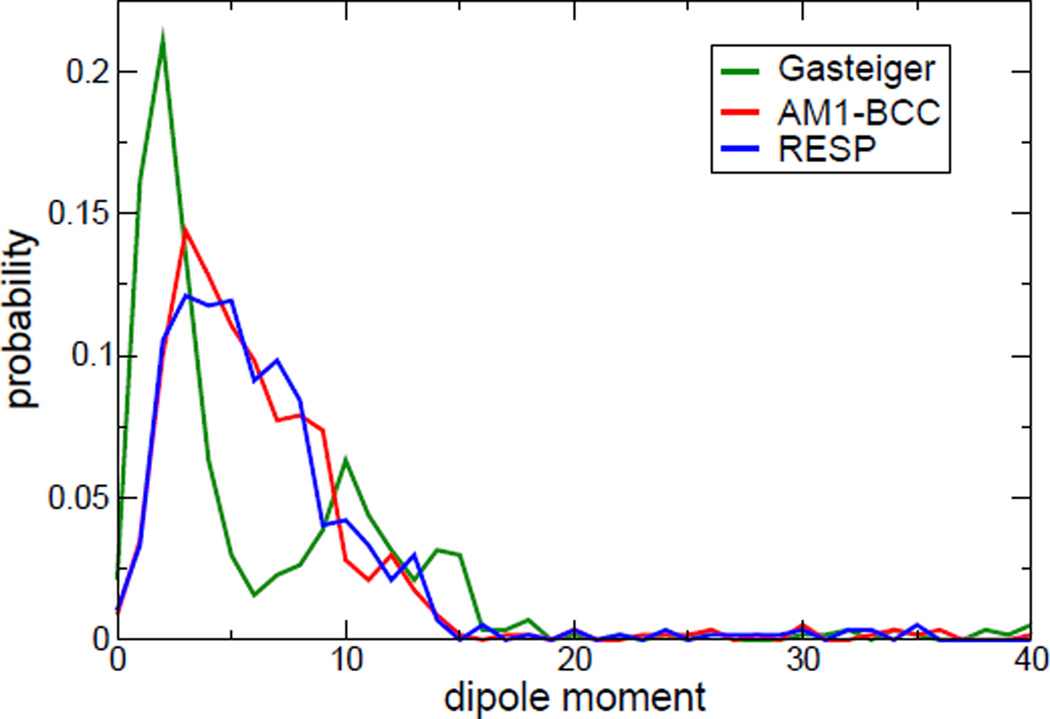
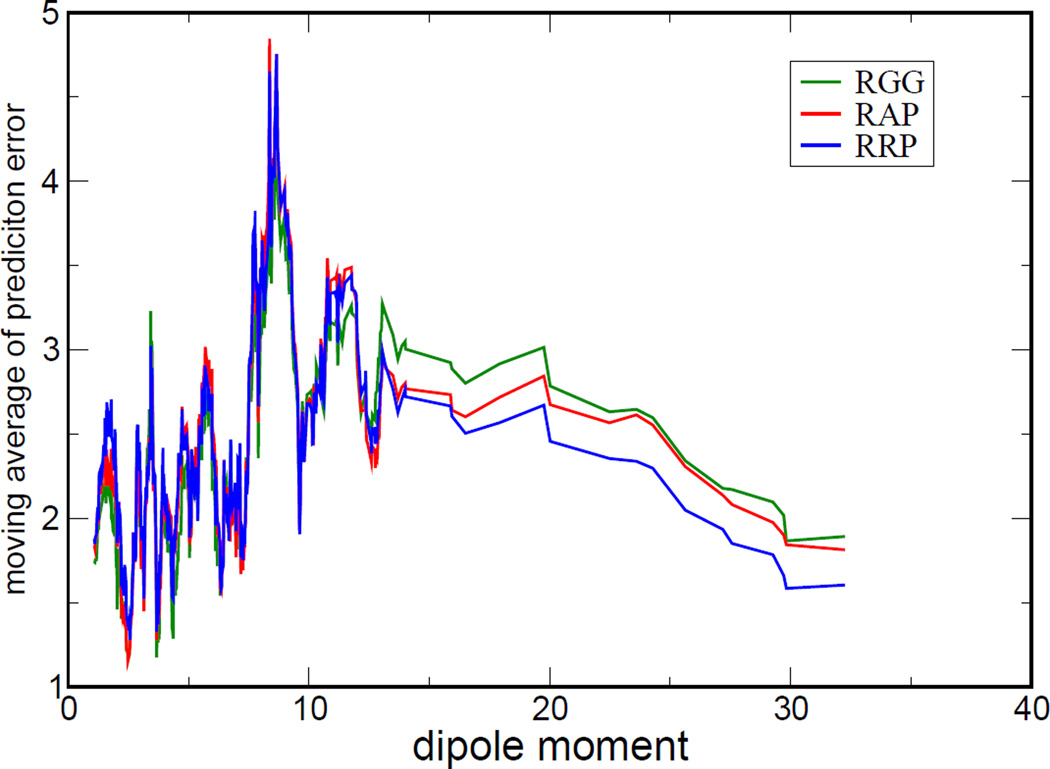
For the 569 neutral ligands of the PDBbind test set, the dipole moment distributions according to three kinds of charge models are shown in Figure 6. One can easily recognize the differences in the distributions of the dipole moments calculated with three different charge models. We further sorted the prediction errors according to the dipole moments and took moving average to smooth out the large fluctuation for clearer visualization of their tendencies, shown in Figure 7. We can see pronounce differences of prediction errors for the cases with large dipole moments (larger than 12.5 Debye, from Figure 6). In Table 7, according to the RMS prediction errors it was clearly indicated that RRP has the best statistical performance for the subset of complexes with neutral ligands having large dipole moments. We also analyzed the dipole moment distributions and prediction errors in our training set, whose size may in turn be too small to provide significant statistical differences. The results are given in Supporting Information (Figure S1, S2 and Table S4).

Figure 6.

The distributions of dipole moments (Debye) of 569 neutral ligands. The values of dipole moment were calculated by three charge models.

Figure 7.

Moving average of prediction errors (in kcal/mol) versus dipole moments (in Debye). The prediction error was the deviation between estimated and experimental binding free energy. The values of dipole moment were sorted according to the dipoles calculated with the RESP charge model.

Table 7.

RMS prediction errors of AutoDock4 scoring functions for neutral ligands in the testing set

scoring function	569 cases	43 casesa
AutoDock4RGG	3.004	3.022
AutoDock4RAP	3.087	2.755
AutoDock4RRP	3.088	2.702
original AutoDock4GG	3.253	2.938

^aThese 43 cases are large dipole moment ligands. (Debye > 12.5)

All values of RMS prediction errors are in kcal/mol.

CONCLUSION

We have constructed three robust protein-ligand free energy models for three popular charge combinations. The combination of AM1-BCC or RESP charges for ligands and Amber99SB charges for proteins perform statistically better than the combination of Gasteiger charges for ligands and proteins does. Our results also indicate that the use of more advanced charge models may lead to more accurate estimates of protein-ligand binding free energy, especially for the protein-ligand complexes with large dipole moment neutral ligands.

Nevertheless, construction of free energy models (or scoring functions) for protein-ligand interactions based on regression analysis remains a challenging task. There are many uncertainties in the experimental information and in the preparation of protein and ligand files, e.g., determination of protonation states, number of rotatable bonds, etc. In this work, the flexibility of the protein-ligand complex was not yet explicitly taken into account for constructing the scoring functions. The contribution of stable water molecules in the protein binding pocket was also not yet included. The metals were only treated in the classical manner, and the consideration of the entropy contribution is certainly incomplete. Yet, with robust regression, we were able to show the five energy terms in the AutoDock4 scoring functions can capture the essential picture of the protein-ligand interactions. It should be stressed that the same scoring function was applied in AutoDock4 to both binding pose prediction and binding free energy evaluation, and its molecular-mechanics based semi-empirical nature allows sensitive recognition of protein conformational changes. This is not the case for many protein-ligand scoring functions that adopt relatively coarse-grained potential or crude distance criteria, e.g. XSCORE, ChemScore, PLP, etc.

Our analyses for the performances of different scoring functions on the subset of neutral ligand may indicate that the accuracy of such regression models may be improved still further when the protein-ligand complexes are suitably classified. However, this also implies that a larger training set is needed if multivariate regression is to be applied for different protein-ligand interaction classes. Construction of larger databases with structural and binding affinity information of protein-ligand complexes, similar to the endeavor of PDBbind, is indispensable for establishing such two-staged (first class identification and model selection, and then free energy prediction) free energy models.