Abstract
Conventional superconductors were long thought to be spin inert; however, there is now increasing interest in both (the manipulation of) the internal spin structure of the ground-state condensate, as well as recently observed long-lived, spin-polarized excitations (quasiparticles). We demonstrate spin resonance in the quasiparticle population of a mesoscopic superconductor (aluminium) using novel on-chip microwave detection techniques. The spin decoherence time obtained (∼100 ps), and its dependence on the sample thickness are consistent with Elliott–Yafet spin–orbit scattering as the main decoherence mechanism. The striking divergence between the spin coherence time and the previously measured spin imbalance relaxation time (∼10 ns) suggests that the latter is limited instead by inelastic processes. This work stakes out new ground for the nascent field of spin-based electronics with superconductors or superconducting spintronics.
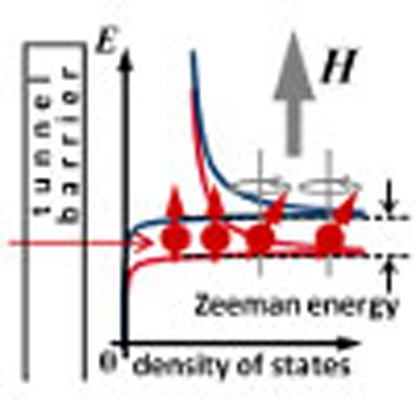 Conventional superconductors were thought to be spin inert, but long-lived, spin-polarized excitations, or quasiparticles, have recently been observed. Here, the authors demonstrate quasiparticle spin resonance in the mesoscopic superconductor aluminium and estimate the spin coherence time.
Conventional superconductors were thought to be spin inert, but long-lived, spin-polarized excitations, or quasiparticles, have recently been observed. Here, the authors demonstrate quasiparticle spin resonance in the mesoscopic superconductor aluminium and estimate the spin coherence time.
Spin/magnetization relaxation and coherence times, respectively, T1 and T2, initially defined in the context of NMR, are general concepts applicable to a wide range of systems, including quantum bits1,2,3,4. If one thinks of spins as classical magnetic moments, T1 is the time over which they align with an external magnetic field, while T2 is the time over which Larmor-like precessions of the spins around the external field remain phase coherent2. (T1 is sometimes also called the longitudinal or spin-lattice relaxation time and T2 the transverse relaxation time.) T1∼T2 for conduction electrons in most normal metals3,5,6,7.
In a typical electron spin resonance (ESR) experiment, electrons are immersed in an external homogenous static magnetic field, H. Microwave radiation creates a perturbative transverse magnetic field (perpendicular to the static field) of frequency fRF. The power P(H, fRF) absorbed by the spins from the microwave field is determined, usually by measuring the fraction of the incident microwaves that is not absorbed, that is, either transmitted or reflected. When H is tuned to its resonance value, 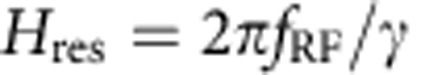 —with γ the gyromagnetic ratio—the electron spins precess around H and P(H, fRF) is maximal. P(H, fRF) is proportional to the imaginary part of the transverse magnetic susceptibility, i.e. to
—with γ the gyromagnetic ratio—the electron spins precess around H and P(H, fRF) is maximal. P(H, fRF) is proportional to the imaginary part of the transverse magnetic susceptibility, i.e. to 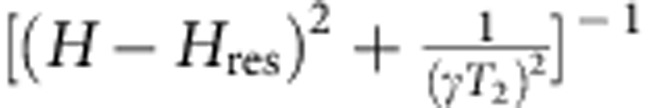 in the case of a linearly polarized field8. Thus, T2=2/(γΔH), where ΔH is the full width at half maximum of the power resonance as a function of H.
in the case of a linearly polarized field8. Thus, T2=2/(γΔH), where ΔH is the full width at half maximum of the power resonance as a function of H.
At first glance, these ideas might seem to be irrelevant to conventional Bardeen–Cooper–Schrieffer (BCS) superconductors, as the BCS superconducting ground state is a condensate of Cooper pairs of electrons with opposite spins (in a singlet state)9. It has recently been demonstrated, however, that a non-equilibrium magnetization can appear in the quasiparticle (that is, excitation) population of a conventional superconductor, with T1 on the order of several nanoseconds10,11,12,13,14.
This raises the question of T2 for these non-equilibrium quasiparticles; however, the short penetration depth of magnetic fields in type-I superconductors (∼16 nm for bulk aluminium) creates difficulties for the observation of quasiparticle spin resonance (QSR): firstly, the signal is small—for normal metals, conduction ESR measurements are typically carried out on macroscopic foils tens of microns thick3,15, and, second, the magnetic field in the superconductor is highly inhomogeneous16. (In type-II and unconventional superconductors, the entry of vortices into the sample can solve the first problem but not the second.)
In the following, we overcome these obstacles using thin-film samples and two novel on-chip microwave detection techniques to perform QSR experiments on superconducting aluminium. We find T2∼100 ps<<T1∼10 ns (ref. 12), in contrast to normal metals where T1∼T2, and identify spin–orbit scattering as the main decoherence mechanism.
Results
Devices and measurement set-up
Our devices are thin-film superconducting (S) bars, with a native insulating (I) oxide layer, across which lie normal metal (N) and either superconducting (S′) or ferromagnetic (F) electrodes (in the cases of devices B and A, respectively). Here S and S′ are both aluminium, I is Al2O3, F is cobalt with an aluminium capping layer and N is thick aluminium with a critical magnetic field of ∼50 mT (ref. 17). In all the data shown here, the N electrodes are in the normal state. The F electrodes are not used here, but rather in frequency-domain measurements of T1 reported elsewhere10. Device A, lying atop a Si/SiO2 substrate, is shown in Fig. 1. As in previous experiments, the NIS junctions have ‘area resistances' of ∼6 × 10−6 Ω cm2 (corresponding to barrier transparencies of ∼1 × 10−5) and tunnelling is the main transport mechanism across the insulator. (See Supplementary Information of ref. 12.) Measurements were performed at temperatures down to 60 mK, in a dilution refrigerator. On the basis of conductance measurements across the NIS juctions, S has a superconducting gap of 205±10 μV (265±10 μV) in device A (device B), corresponding to critical temperatures of 1.34±0.07 K (1.75±0.07 K) in the BCS theory.
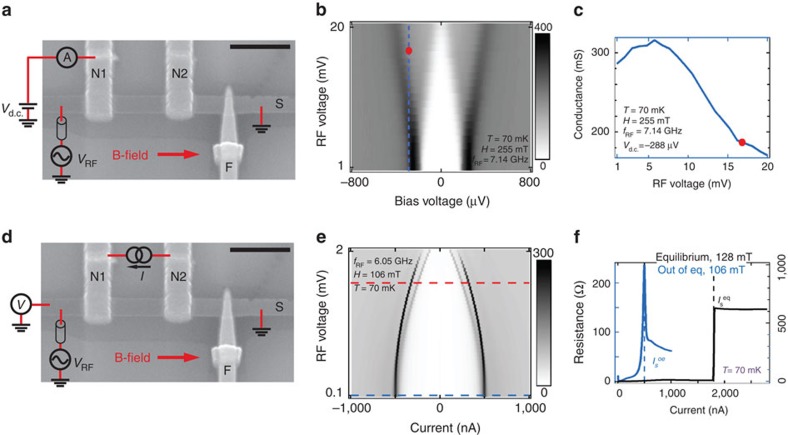
Figure 1. Two on-chip microwave power detection schemes for superconducting (hybrid) devices.
(a,c) Scanning electron micrograph of a device nominally identical to Device A (scale bar, 1 μm) and schematic drawings of the two measurement set-ups. (Data shown are from Device A unless otherwise stated.) In both cases, a static magnetic field, H is applied parallel to a superconducting bar (S, Al) and a sinusoidal signal of root mean squared amplitude VRF and frequency fRF in the microwave range applied across the length of S (with a lossy coaxial cable in series), resulting in a high-frequency field perpendicular to H. To detect the spin precession of the quasiparticles in S, two on-chip detection methods are used. (a) Detection scheme 1: a voltage Vd.c. is applied between S and a normal electrode (N1, thick Al) with which it is in contact via an insulating tunnel barrier (I, Al2O3). The differential conductance G=dI/dVd.c. is measured, where I is the current between N1 and S. (b) G as a function of Vd.c. and nominal VRF (at the output of the generator and not accounting for attenuation in the lines). The red dot indicates the operation point of the detector for the data in Fig. 2:  , Vd.c.=−288 μV. For any given frequency, we define
, Vd.c.=−288 μV. For any given frequency, we define 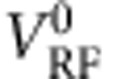 as the VRF (at the output of the generator) at which the effective voltage at the device is the same as that for fRF=7.14 GHz and VRF=16.81 mV. (See Supplementary Note 2 and Supplementary Fig. 2). (c) A slice of b at Vd.c.=−288 μV (blue dashed line in b) with the operation point indicated. (d) Detection scheme 2: a current Id.c. is injected along the length of S. We measure either the voltage V between the ends of the S bar or the differential resistance R=dV/dId.c.. We record in particular the switching current IS at which S first becomes resistive. (e) R as a function of Id.c. and nominal VRF (not accounting for attenuation in the lines). The switching current IS at which S become resistive appears here as a peak in R. IS can be seen to decrease monotonically with VRF. The red dashed line indicates the operation point of the detector for the data in Fig. 3: VRF=0.8
as the VRF (at the output of the generator) at which the effective voltage at the device is the same as that for fRF=7.14 GHz and VRF=16.81 mV. (See Supplementary Note 2 and Supplementary Fig. 2). (c) A slice of b at Vd.c.=−288 μV (blue dashed line in b) with the operation point indicated. (d) Detection scheme 2: a current Id.c. is injected along the length of S. We measure either the voltage V between the ends of the S bar or the differential resistance R=dV/dId.c.. We record in particular the switching current IS at which S first becomes resistive. (e) R as a function of Id.c. and nominal VRF (not accounting for attenuation in the lines). The switching current IS at which S become resistive appears here as a peak in R. IS can be seen to decrease monotonically with VRF. The red dashed line indicates the operation point of the detector for the data in Fig. 3: VRF=0.8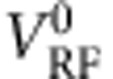 . (f) The blue trace is the first slice of e (blue dashed line in e) at VRF=0.1 mV. The black trace is a two terminal measurement of the S bar, in the absence of microwaves, with a constant corresponding to the resistance of the lines subtracted. The difference in IS between the two indicates that the S bar is strongly out of equilibrium in our second (switching current) detection scheme. (See Supplementary Note 4).
. (f) The blue trace is the first slice of e (blue dashed line in e) at VRF=0.1 mV. The black trace is a two terminal measurement of the S bar, in the absence of microwaves, with a constant corresponding to the resistance of the lines subtracted. The difference in IS between the two indicates that the S bar is strongly out of equilibrium in our second (switching current) detection scheme. (See Supplementary Note 4).
A static magnetic field H is applied in the plane of the device and parallel to the S bar (Fig. 1a). S has a thickness of d∼8.5 nm (6 nm) for device A (device B), well within the magnetic field penetration depth λ, which we expect to be 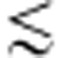 315 nm (375 nm) in our samples at 70 mK. (See Supplementary Note 1 and ref. 18 for details on this estimate.) The ratio of the orbital energy
315 nm (375 nm) in our samples at 70 mK. (See Supplementary Note 1 and ref. 18 for details on this estimate.) The ratio of the orbital energy 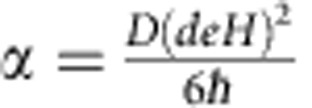 to the Zeeman energy
to the Zeeman energy 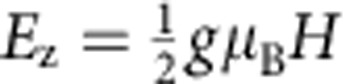 is ∼0.32 (0.22) for the quasiparticles in S in device A (device B) at 0.5 T
is ∼0.32 (0.22) for the quasiparticles in S in device A (device B) at 0.5 T  the highest measured resonant magnetic field Hres. It is lower at lower fields. Therefore, the Zeeman energy is always dominant and we are in the ‘paramagnetic limit'16,19,20. Here D is the diffusion constant, e the electron charge, g the Landé g-factor, μB the Bohr magneton and ℏ Planck's constant. (See Supplementary Note 1 for details.) The data shown below are from device A unless otherwise stated.
the highest measured resonant magnetic field Hres. It is lower at lower fields. Therefore, the Zeeman energy is always dominant and we are in the ‘paramagnetic limit'16,19,20. Here D is the diffusion constant, e the electron charge, g the Landé g-factor, μB the Bohr magneton and ℏ Planck's constant. (See Supplementary Note 1 for details.) The data shown below are from device A unless otherwise stated.
A sinusoidal radio frequency signal of frequency 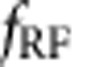 and root mean squared amplitude VRF is applied across the length of the S bar (via a lossy, that is, resistive coaxial cable). The resulting supercurrent flowing along the length of S serves primarily to produce the desired high-frequency magnetic field perpendicular to H; secondarily, it also breaks some Cooper pairs and thus increases the quasiparticle population. Microwave radiation due to the supercurrent thus impinges on the quasiparticle spins in S. Some of this radiation is absorbed by the quasiparticle spins, and the rest transmitted to and absorbed by the surrounding environment. The ‘transmitted radiation' can appear as a voltage across a tunnel junction between S and N; this is the basis of our first detection scheme (DS1; Fig. 1a). It can also be absorbed by the superconducting condensate, thus reducing the density of Cooper pairs and the current IS at which S becomes resistive, known as the switching current; this is the basis of our second detection scheme (DS2; Fig. 1c). Both of our detection schemes for P(H, fRF) are therefore entirely ‘on-chip'.
and root mean squared amplitude VRF is applied across the length of the S bar (via a lossy, that is, resistive coaxial cable). The resulting supercurrent flowing along the length of S serves primarily to produce the desired high-frequency magnetic field perpendicular to H; secondarily, it also breaks some Cooper pairs and thus increases the quasiparticle population. Microwave radiation due to the supercurrent thus impinges on the quasiparticle spins in S. Some of this radiation is absorbed by the quasiparticle spins, and the rest transmitted to and absorbed by the surrounding environment. The ‘transmitted radiation' can appear as a voltage across a tunnel junction between S and N; this is the basis of our first detection scheme (DS1; Fig. 1a). It can also be absorbed by the superconducting condensate, thus reducing the density of Cooper pairs and the current IS at which S becomes resistive, known as the switching current; this is the basis of our second detection scheme (DS2; Fig. 1c). Both of our detection schemes for P(H, fRF) are therefore entirely ‘on-chip'.
In DS1 (Fig. 1a), we apply a bias voltage Vd.c. across an NIS junction and measure its differential conductance G=dI/dVd.c. using standard lock-in techniques. (I is the current across the junction.) Figure 1b shows such traces as a function of VRF, in which we see a flattening of the coherence peaks in a monotonic manner. (This is similar to the effect of classical rectification10.) Figure 1c shows a slice of Fig. 1b at Vd.c.=−288 μV. G across the junction can be seen to be an effective microwave power meter at the chosen operating point (red dot). We define 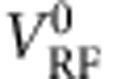 (for any given frequency) as the reference VRF (at the output of the generator) at which the effective voltage at the device is the same as that for fRF=7.14 GHz and VRF=16.81 mV. (See Supplementary Note 2 and Supplementary Fig. 2).
(for any given frequency) as the reference VRF (at the output of the generator) at which the effective voltage at the device is the same as that for fRF=7.14 GHz and VRF=16.81 mV. (See Supplementary Note 2 and Supplementary Fig. 2).
In DS2 (Fig. 1d), we measure the voltage–current characteristic of the S bar and record the switching current IS. A current Id.c. is injected from one N electrode to another and the resulting voltage V across the length of the bar is measured. Figure 1e shows the differential resistance R=dV/dId.c. of the S bar as a function of Id.c. and of VRF. The peaks in these traces correspond to IS. IS can be seen to depend monotonically on VRF and is thus also a good measure of the latter.
Our on-chip detection provides improved sensitivity compared with earlier work on the spin resonance of conduction electrons in normal metals (CESR)3,21. Indeed, based on calculations for CESR measurements on macroscopic samples, it was previously thought that CESR signals in type-I superconductors would be unmeasurably small22. This is no doubt why, while a considerable amount of work has been done on the CESR in normal metals since the 1950s, to our knowledge only one such measurement has been performed on a bulk BCS superconductor (Nb) in the vortex state, close to the critical field23,24,25.
Quasiparticle spin resonance
Having characterized our two microwave power meters, we now perform QSR measurements using each of them in turn, and compare the results of both.
In the first set of measurements, using DS1, we operate the NIS junction detector—which is to say measure the differential conductance G=dI/dVd.c. across it—at a fixed Vd.c. of −288 μV and 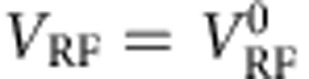 . (G(Vd.c., H) traces in the absence of microwaves are shown in Supplementary Fig. 1). As can be seen in Fig. 1c, at this operation point, small decreases in the absorbed power will result in a proportional increase in G. (It can also be seen that we remain in the linear regime in the measurements in Fig. 2).
. (G(Vd.c., H) traces in the absence of microwaves are shown in Supplementary Fig. 1). As can be seen in Fig. 1c, at this operation point, small decreases in the absorbed power will result in a proportional increase in G. (It can also be seen that we remain in the linear regime in the measurements in Fig. 2).
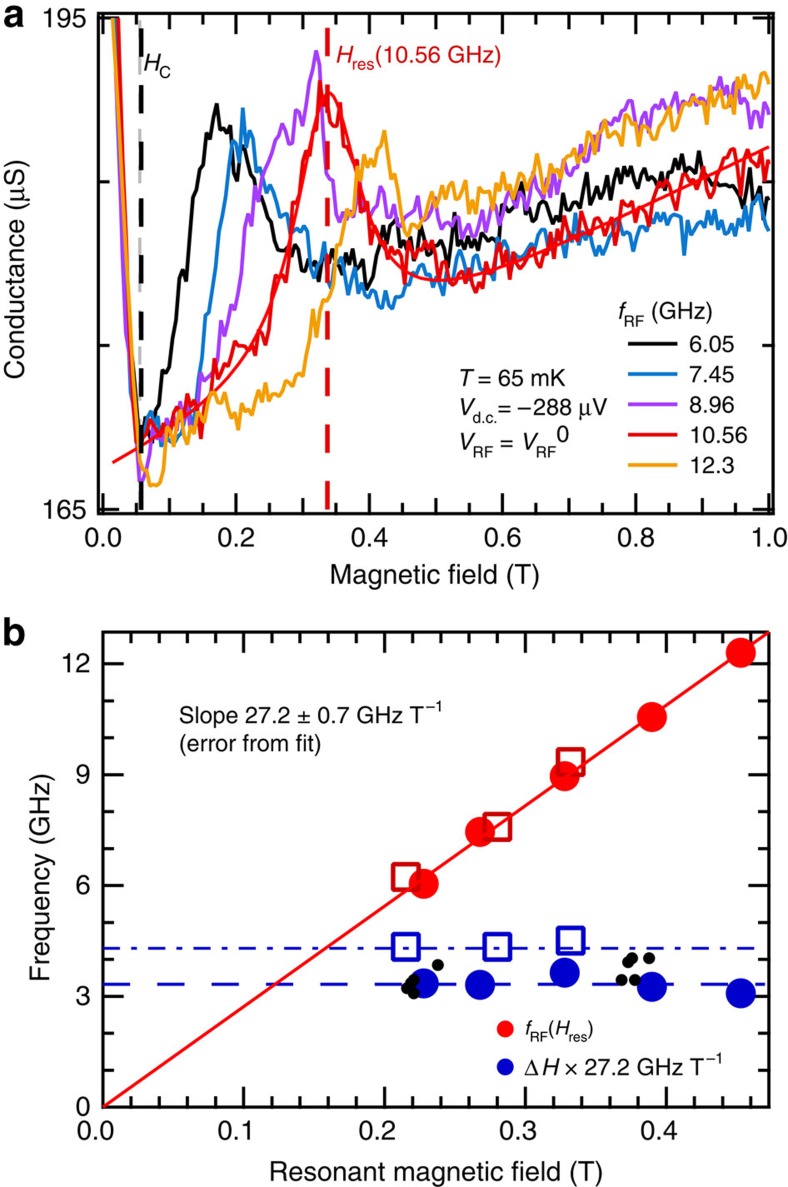
Figure 2. Spin resonance in conductance across tunnel junction.
(a) NIS junction conductance G as a function of H at Vd.c.=−288 μV and 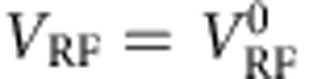 for different fRF. The black vertical line indicates the critical field of N. Hres and ΔH are obtained for each fRF by fitting a Lorentzian with a linear background. The fit for fRF=10.56 GHz is shown (thin red line) and Hres indicated with a red vertical line. (b) Hres and ΔH the resonance linewidth (full width at half maximum) as a function of fRF (red and blue circles, respectively). A linear fit to Hres(fRF) data gives a Landé g-factor of 1.95±0.2. The black dots indicate values obtained at different powers or with the second detection scheme. (See Supplementary Note 3 and Supplementary Fig. 3). All dots and circles have been offset by 53 mT to account for a systematic shift in the applied magnetic field during the associated cooldown. The squares indicate values obtained from Device B, in which S is 6-nm thick.
for different fRF. The black vertical line indicates the critical field of N. Hres and ΔH are obtained for each fRF by fitting a Lorentzian with a linear background. The fit for fRF=10.56 GHz is shown (thin red line) and Hres indicated with a red vertical line. (b) Hres and ΔH the resonance linewidth (full width at half maximum) as a function of fRF (red and blue circles, respectively). A linear fit to Hres(fRF) data gives a Landé g-factor of 1.95±0.2. The black dots indicate values obtained at different powers or with the second detection scheme. (See Supplementary Note 3 and Supplementary Fig. 3). All dots and circles have been offset by 53 mT to account for a systematic shift in the applied magnetic field during the associated cooldown. The squares indicate values obtained from Device B, in which S is 6-nm thick.
Figure 2a shows G(H) at several different fRF. As expected, each trace shows a resonance, that is, an increase in G(H) due to the fact that more power is being absorbed by precessing quasiparticle spins and therefore less appearing across the NIS junction. We determine Hres and ΔH by a Lorentzian with a linear-in-H background signal to these data. The background comes from magnetic-field-induced orbital depairing in the quasiparticle density of states. This measurement was repeated at different fRF; Hres as a function of fRF is shown in Fig. 2b. A linear fit to the data gives a g-factor of 1.95±0.2, consistent with previous measurements of electrons in Al in the normal state26,27.
Note that ΔH may be larger than its intrinsic value if, for instance, the static field is inhomogeneous in the region of interest2. This would then lead to an underestimate of T2. In our samples, however, d/2<<λ, as mentioned above. Thus, the magnetic field seen by the quasiparticles is homogeneous to 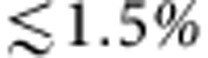 in the superconductor, much smaller than the ΔH we measure, and our estimate of T2 is unaffected by magnetic field inhomogeneity. This is confirmed by the fact that ΔH does not depend on Hres, as can be seen in Fig. 2b. Field homogeneity has been a challenge for both ESR and NMR measurements performed on macroscopic type-II superconductors. In these, specimen dimensions greater than λ mean that the field decays significantly within the specimen, and additional complications often arise from the presence of vortices.
in the superconductor, much smaller than the ΔH we measure, and our estimate of T2 is unaffected by magnetic field inhomogeneity. This is confirmed by the fact that ΔH does not depend on Hres, as can be seen in Fig. 2b. Field homogeneity has been a challenge for both ESR and NMR measurements performed on macroscopic type-II superconductors. In these, specimen dimensions greater than λ mean that the field decays significantly within the specimen, and additional complications often arise from the presence of vortices.
In the second set of measurements, we use DS2. As can be seen in Fig. 1e, small decreases in the absorbed microwave power will result in a proportional increase in the switching current IS. We first measure the differential resistance R=dV/dId.c. of the S bar as a function of Id.c. and of H at fRF=6.05 GHz, VRF=0.8 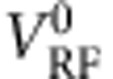 (Fig. 3a). We observe an increase in IS at H=0.17 T, which we identify as Hres—at this field, the quasiparticle spins enter into resonant precession, thus absorbing more microwave power. Less power is then transferred to the superconducting condensate and IS increases.
(Fig. 3a). We observe an increase in IS at H=0.17 T, which we identify as Hres—at this field, the quasiparticle spins enter into resonant precession, thus absorbing more microwave power. Less power is then transferred to the superconducting condensate and IS increases.
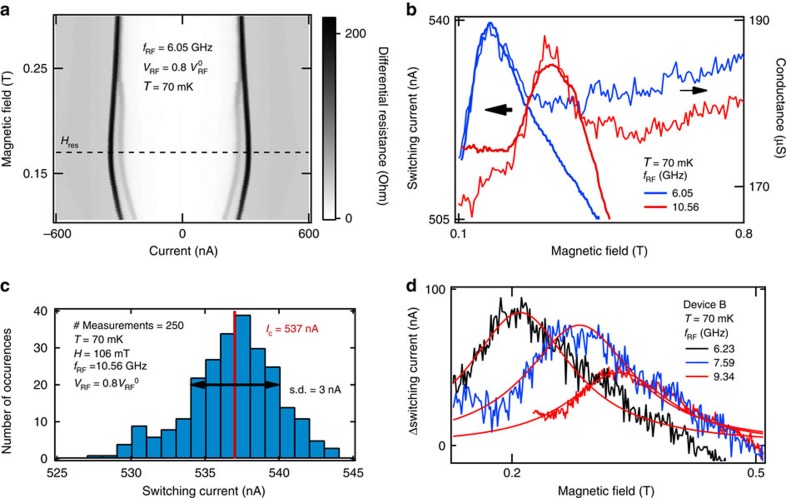
Figure 3. Spin resonance in supercurrent, comparison of detection schemes.
(a) Differential resistance R of the S bar as a function of H and Id.c. with fRF=6.05 GHz, VRF=0.8 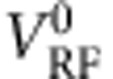 . At Hres∼0.17 T, the resonant field, the switching current IS can be seen to increase, indicating that less microwave power is being transmitted to the superconducting condensate as more power is absorbed by the quasiparticles in S. (b) Switching current IS as a function of static magnetic field H for two different fRF. (Here a slight change was made to the measurement circuit: With reference to Fig. 1d, the current is applied between N2 and F instead of between N1 and N2, hence the slightly higher IS: the current injection electrodes are closer together.) Superimposed on these traces are the conductance traces from Fig. 2a at the same fields. Hres and ΔH can be seen to be similar for both measurement methods. The bold red trace has been offset downwards by 19 nA. (c) The switching currents in b are averages of ∼200 measurements, with a s.d. of ∼3 nA. Here we show a histogram of 250 switching currents corresponding to the first point in the bold red trace in b. Current was driven long the length of the S bar and the voltage measured between N1 and N2. (Voltage and current leads are thus switched with respect to b). (d) Device B: switching current IS as a function of static magnetic field H for three different fRF, with a linear background subtracted (thick lines). Hres and ΔH obtained from the fits (thin red lines) are shown in Fig. 2b. These IS values are averages of ∼500 measurements.
. At Hres∼0.17 T, the resonant field, the switching current IS can be seen to increase, indicating that less microwave power is being transmitted to the superconducting condensate as more power is absorbed by the quasiparticles in S. (b) Switching current IS as a function of static magnetic field H for two different fRF. (Here a slight change was made to the measurement circuit: With reference to Fig. 1d, the current is applied between N2 and F instead of between N1 and N2, hence the slightly higher IS: the current injection electrodes are closer together.) Superimposed on these traces are the conductance traces from Fig. 2a at the same fields. Hres and ΔH can be seen to be similar for both measurement methods. The bold red trace has been offset downwards by 19 nA. (c) The switching currents in b are averages of ∼200 measurements, with a s.d. of ∼3 nA. Here we show a histogram of 250 switching currents corresponding to the first point in the bold red trace in b. Current was driven long the length of the S bar and the voltage measured between N1 and N2. (Voltage and current leads are thus switched with respect to b). (d) Device B: switching current IS as a function of static magnetic field H for three different fRF, with a linear background subtracted (thick lines). Hres and ΔH obtained from the fits (thin red lines) are shown in Fig. 2b. These IS values are averages of ∼500 measurements.
In Fig. 3b, we show IS as a function of H at two different frequencies. (IS is the average of 200 switching current values obtained from V(Id.c.) measurements.) The expected resonance appears at both frequencies. To compare results from the two different detection schemes, we superimpose on these traces data from Fig. 2a at the same fRF. We see that both Hres and ΔH are the same for both detection schemes. We also verified that Hres and ΔH are independent of VRF (see Supplementary Note 3, Supplementary Fig. 3 and black dots in Fig. 2b).
As DS2 is sensitive to a longer portion of the S bar compared with DS1, the agreement between the two detection schemes is further confirmation that the magnetic field is quite homogenous along the entire length of the S bar between the two N electrodes. Thus, our results for T2 reported below should be reasonably close to the intrinsic value.
The spin coherence time 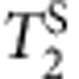 for 8.5-nm-thick superconducting aluminium (device A) is 95±20 ps as determined from ΔH (the full width at half maximum of the resonance) in Figs 2a and 3b; this is fairly constant within the range of accessible fields (Fig. 2b). Measurements on device B, in which S is 6-nm thick yielded
for 8.5-nm-thick superconducting aluminium (device A) is 95±20 ps as determined from ΔH (the full width at half maximum of the resonance) in Figs 2a and 3b; this is fairly constant within the range of accessible fields (Fig. 2b). Measurements on device B, in which S is 6-nm thick yielded 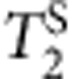 =70±15 ps (Figs 2b and 3d). Both the order of magnitude of
=70±15 ps (Figs 2b and 3d). Both the order of magnitude of 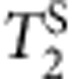 , as well as the fact that it is inversely proportional to the film thickness, are consistent with spin coherence limited primarily by
, as well as the fact that it is inversely proportional to the film thickness, are consistent with spin coherence limited primarily by 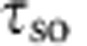 , the Elliott–Yafet spin–orbit scattering time5,12,26,27,28,29,30,31,32,33,34,35,36.
, the Elliott–Yafet spin–orbit scattering time5,12,26,27,28,29,30,31,32,33,34,35,36.
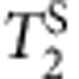 is, however, relatively unaffected by the quasiparticle density: In device A, the linewidths measured by DS1 and DS2 are identical (Fig. 3b), whereas the quasiparticle density is estimated to be about two orders of magnitude higher in the supercurrent measurements (with injection across the tunnel junctions) than in the conductance measurements. (See Fig. 1f, Supplementary Note 4 and ref. 37.) In device B, the linewidth remained unchanged at temperatures of up to 600 mK and at injection currents (across an NIS junction) of up to 42 nA.
is, however, relatively unaffected by the quasiparticle density: In device A, the linewidths measured by DS1 and DS2 are identical (Fig. 3b), whereas the quasiparticle density is estimated to be about two orders of magnitude higher in the supercurrent measurements (with injection across the tunnel junctions) than in the conductance measurements. (See Fig. 1f, Supplementary Note 4 and ref. 37.) In device B, the linewidth remained unchanged at temperatures of up to 600 mK and at injection currents (across an NIS junction) of up to 42 nA.
Equilibrium measurement of the spin-flip time
It is thus reasonable to compare 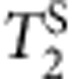 with an independent estimate of
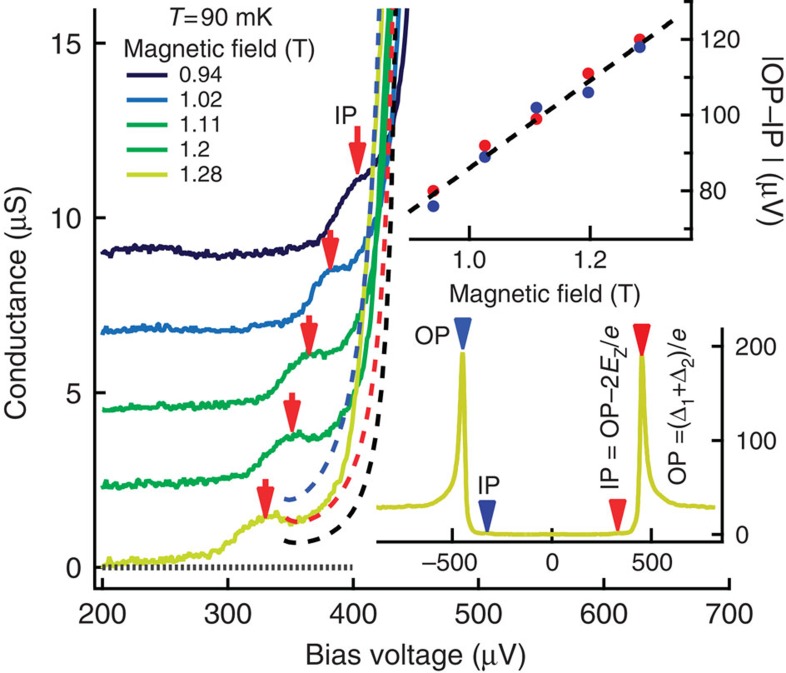
with an independent estimate of 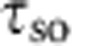 from G(Vd.c.) measurements across an SIS′ junction in device B, following work by Tedrow and Meservey on Al thin films20,31,38. (Here S′ is a 8.5-nm-thick superconducting Al counter electrode.) In the absence of spin–orbit coupling, as spin is conserved in tunnelling between S and S′, G(Vd.c.) shows a peak at Vd.c.=(Δ+Δ′)/e at all fields (with Δ (Δ′) the superconducting energy gap of S (S′)) and the Zeeman effect is effectively invisible. In the presence of small but finite spin–orbit coupling, spin mixing modifies the density states for each spin and leads to a small conductance peak at a lower voltage Vd.c.=(Δ+Δ′−2Ez)/e, whose height ∼
from G(Vd.c.) measurements across an SIS′ junction in device B, following work by Tedrow and Meservey on Al thin films20,31,38. (Here S′ is a 8.5-nm-thick superconducting Al counter electrode.) In the absence of spin–orbit coupling, as spin is conserved in tunnelling between S and S′, G(Vd.c.) shows a peak at Vd.c.=(Δ+Δ′)/e at all fields (with Δ (Δ′) the superconducting energy gap of S (S′)) and the Zeeman effect is effectively invisible. In the presence of small but finite spin–orbit coupling, spin mixing modifies the density states for each spin and leads to a small conductance peak at a lower voltage Vd.c.=(Δ+Δ′−2Ez)/e, whose height ∼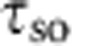 (Fig. 4). (At very strong spin–orbit coupling, the two peaks merge; spin orbit then has the same effect on the conductance trace as a depairing magnetic field20.) A fit using the BCS density of states and the theory outlined in refs 20, 38 yields a spin-mixing parameter b of 0.018±0.002 and
(Fig. 4). (At very strong spin–orbit coupling, the two peaks merge; spin orbit then has the same effect on the conductance trace as a depairing magnetic field20.) A fit using the BCS density of states and the theory outlined in refs 20, 38 yields a spin-mixing parameter b of 0.018±0.002 and 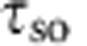 =45±5 ps, which agrees well with
=45±5 ps, which agrees well with 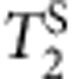 above, as well as previous measurements31 (Fig. 4).
above, as well as previous measurements31 (Fig. 4).
Figure 4. Independent measurement of spin mixing due to the spin–orbit interaction.
Device B: conductance G as a function of voltage Vd.c. across an SIS′ junction, at different magnetic fields H (offset by 2.2 μS). Apart from the principal, outer peak (OP) at Vd.c.=(Δ+Δ′)/e, with Δ (Δ′) the superconducting energy gap of S (S′), a smaller, inner peak (IP) can be seen at ∼Vd.c.=(Δ+Δ′−2EZ)/e, with EZ the Zeeman energy. Fitting the data at H=1.28 T to numerical calculations based on refs 20, 38 (red dotted line) yields a spin–orbit time 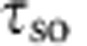 of 45±5 ps. Numerical results for
of 45±5 ps. Numerical results for 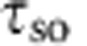 =23 and 69 ps are also shown (blue and black dotted lines, respectively). Lower inset: full-conductance trace at H=1.28 T, showing all peaks. Upper inset: distance in Vd.c. between outer and inner peaks at positive (red dots) and negative (blue dots) energies. The black dotted line, which has a slope of 2EZ/e, is a guide to the eye.
=23 and 69 ps are also shown (blue and black dotted lines, respectively). Lower inset: full-conductance trace at H=1.28 T, showing all peaks. Upper inset: distance in Vd.c. between outer and inner peaks at positive (red dots) and negative (blue dots) energies. The black dotted line, which has a slope of 2EZ/e, is a guide to the eye.
Discussion
We now address the conspicuous divergence between 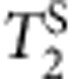 and
and 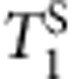 , the latter previously determined to be on the order of ∼10 ns in films of similar thickness12. In comparison, in normal Al,
, the latter previously determined to be on the order of ∼10 ns in films of similar thickness12. In comparison, in normal Al, 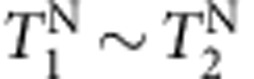 ∼50 ps in such films at 4 K (ref. 12). (Note that
∼50 ps in such films at 4 K (ref. 12). (Note that 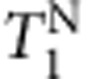 depends on the film thickness12,26,27,33,34,35,36).
depends on the film thickness12,26,27,33,34,35,36).
The striking effect can be understood by considering that spin imbalance (that is to say non-equilibrium magnetization) in superconductors can be thought of, in a simple picture, as having contributions from both a spin-dependent shift in the quasiparticle chemical potentials as well as spin-independent heating of the quasiparticle population11,39,40. The former can be characterized by 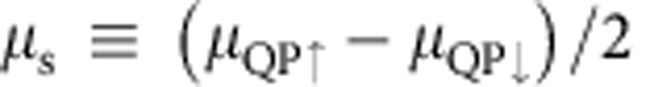 —with μQPα the chemical potential of the spin-α quasiparticles—and the latter by an effective temperature T*. (A more general description could be based on, for example, the quasiparticle distribution function for each spin).
—with μQPα the chemical potential of the spin-α quasiparticles—and the latter by an effective temperature T*. (A more general description could be based on, for example, the quasiparticle distribution function for each spin).
T* and μs should relax on different timescales, respectively, the inelastic scattering time 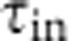 and the spin-mixing time
and the spin-mixing time 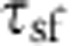 (dominated in thin-film Al by
(dominated in thin-film Al by 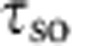 ).
). 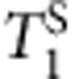 is then the longer of
is then the longer of 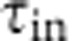 and
and 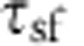 , whereas
, whereas 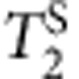 should be affected only by
should be affected only by 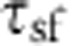 but not
but not 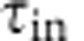 –
–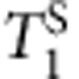 and
and 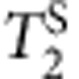 in superconductors can thus be quite different. That the previously determined value for
in superconductors can thus be quite different. That the previously determined value for 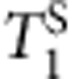 is close to the inelastic relaxation time in Al, estimated to be ∼5 ns from ref. 41 is consistent with spin relaxation being limited by
is close to the inelastic relaxation time in Al, estimated to be ∼5 ns from ref. 41 is consistent with spin relaxation being limited by 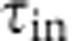 and in particular quasiparticle–quasiparticle interactions41,42. We note that the quasiparticle–phonon interaction time
and in particular quasiparticle–quasiparticle interactions41,42. We note that the quasiparticle–phonon interaction time 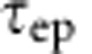 —over which the whole system relaxes to equilibrium—has recently been determined in frequency-domain measurements in 20-nm-thick Al films at 100 mK to be ∼1.6 μs (ref. 43), much longer than both
—over which the whole system relaxes to equilibrium—has recently been determined in frequency-domain measurements in 20-nm-thick Al films at 100 mK to be ∼1.6 μs (ref. 43), much longer than both 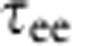 and
and  . Thus,
. Thus, 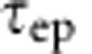 should not be a limiting timescale for either
should not be a limiting timescale for either 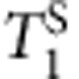 or
or  .
.
In contrast, spin accumulation in normal metals is impervious to T* and is due only to μs. Spin relaxation in normal Al then occurs over 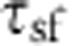 , which also governs spin coherence. Thus,
, which also governs spin coherence. Thus, 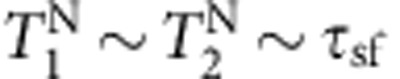 and indeed these terms are sometimes used interchangeably in the literature.
and indeed these terms are sometimes used interchangeably in the literature.
Our results are, in sum, consistent with spin–orbit scattering as the main spin decoherence mechanism in thin-film superconducting Al, and also with a picture in which T1 and T2 diverge in superconductors due to the plural sources of spin accumulation in these systems. This has implications for (coherent) computing possibilities using superconducting spintronic devices44, and also raises new questions about the interactions between the two sources of spin imbalance in the simple picture presented above, as well as of both with the superconducting condensate39,40.
Our methods for measuring the coherence time can in principle be extended to other superconducting materials—both conventional and unconventional—as long as they can be nanostructured. A little more speculatively, our work also calls to mind the NMR experiments performed on superfluid 3He, which were critical for identifying its different phases and in particular their spin (triplet) structure; it opens up analogous perspectives in (unconventional) superconductivity, where (the manipulation of) the internal structure of Cooper pairs is now an active field of enquiry.
Methods
Sample fabrication and transport measurements
We fabricate our samples with standard electron-beam lithography and angle evaporation techniques in an electron-beam evaporator with a base pressure of 5 × 10−9 mbar. We first evaporated ∼6 nm (∼8.5 nm) of Al for device B (A), which is then oxidized at 8 × 10−2 mbar for 10′ to produce a tunnel barrier, then 100 nm of Al at an angle. For device B, we then evaporated 8.5 nm at another angle. (In device A, 40 nm of Co and 4.5 nm of Al are evaporated at the second angle, but these electrodes were not used in this work.) All transport measurements were carried out in a 3He–4He dilution refrigerator with a base temperature of 60 mK. Differential resistances were measured with standard lock-in techniques. The switching currents IS reported here are the mean values of 200–500 measurements.
Additional information
How to cite this article: Quay, C. H. L. et al. Quasiparticle spin resonance and coherence in superconducting Aluminium. Nat. Commun. 6:8660 doi: 10.1038/ncomms9660 (2015).
Supplementary Material
Supplementary Figures 1-4, Supplementary Notes 1-4 and Supplementary References
Acknowledgments
We thank H. Hurdequint and J. Fabian for helpful discussions on conduction ESR in normal metals and semiconductors, and R.W. Ogburn for helpful comments on the manuscript. This work was funded by an ANR Blanc grant (MASH) from the French Agence Nationale de Recherche. C.S. thanks the CNRS and the Université Paris-Sud for funding his sabbatical at the Laboratoire de Physique des Solides.
Footnotes
Author contributions C.Q.H.L., M.W., Y.C. and M.A. fabricated the samples and performed the measurements. All the authors contributed to the data analysis and the writing of the manuscript.
References
- Abragam A. Principles of Nuclear Magnetism Oxford Univ. Press (1983). [Google Scholar]
- Kittel C. Introduction to Solid State Physics. 8th edn Wiley (2004). [Google Scholar]
- Yafet Y. in Solid State Physics Vol. 14, eds Seitz F., Turnbull D. 1–98Academic Press (1963). [Google Scholar]
- Koppens F. H. L. et al. Driven coherent oscillations of a single electron spin in a quantum dot. Nature 442, 766–771 (2006). [DOI] [PubMed] [Google Scholar]
- Žutic I., Fabian J. & Das Sarma S. Spintronics: fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004). [Google Scholar]
- Schumacher R. T. & Slichter C. P. Electron spin paramagnetism of lithium and sodium. Phys. Rev. 101, 58–65 (1956). [Google Scholar]
- Pines D. & Slichter C. P. Relaxation times in magnetic resonance. Phys. Rev. 100, 1014–1020 (1955). [Google Scholar]
- Pottier N. Physique Statistique Hors d'équilibre : Processus Irréversibles Linéaires EDP Sciences (2007). [Google Scholar]
- Schrieffer J. R. Theory Of Superconductivity Perseus Books, Reading (1999). [Google Scholar]
- Quay C. H. L., Dutreix C., Chevallier D., Bena C. & Aprili M. Frequency-domain measurement of the spin imbalance lifetime in superconductors. Preprint at <http://arXiv:1408.1832> (2014).
- Chevallier D. et al. Frequency-dependent spin accumulation in out-of-equilibrium mesoscopic superconductors. Preprint at <http://arXiv:1408.1833> (2014).
- Quay C. H. L., Chevallier D., Bena C. & Aprili M. Spin imbalance and spin-charge separation in a mesoscopic superconductor. Nat. Phys. 9, 84–88 (2013). [Google Scholar]
- Hübler F., Wolf M. J., Beckmann D. & v. Loehneysen H. Long-range spin-polarized quasiparticle transport in mesoscopic al superconductors with a zeeman splitting. Phys. Rev. Lett. 109, 207001 (2012). [DOI] [PubMed] [Google Scholar]
- Wolf M. J., Hübler F., Kolenda S., v. Loehneysen H. & Beckmann D. Spin injection from a normal metal into a mesoscopic superconductor. Phys. Rev. B 87, 024517 (2013). [Google Scholar]
- Beuneu F. & Monod P. The Elliott relation in pure metals. Phys. Rev. B 18, 2422–2425 (1978). [Google Scholar]
- Tinkham M. Introduction to Superconductivity. 2 edn Dover (1996). [Google Scholar]
- Meservey R. & Tedrow P. M. Properties of very thin aluminum films. J. Appl. Phys. 42, 51–53 (1971). [Google Scholar]
- Anthore A., Pothier H. & Esteve D. Density of states in a superconductor carrying a supercurrent. Phys. Rev. Lett. 90, 127001 (2003). [DOI] [PubMed] [Google Scholar]
- Meservey R., Tedrow P. M. & Fulde P. Magnetic field splitting of the quasiparticle states in superconducting aluminum films. Phys. Rev. Lett. 25, 1270–1272 (1970). [Google Scholar]
- Fulde P. High field superconductivity in thin films. Adv. Phy. 22, 667–719 (1973). [Google Scholar]
- Griswold T. W., Kip A. F. & Kittel C. Microwave spin resonance absorption by conduction electrons in metallic sodium. Phys. Rev. 88, 951–952 (1952). [Google Scholar]
- Aoi K. & Swihart J. C. Theory of electron spin resonance in type-I superconductors. Phys. Rev. B 2, 2555–2560 (1970). [Google Scholar]
- Vier D. C. & Schultz S. Observation of conduction electron spin resonance in both the normal and superconducting states of niobium. Phys. Lett. A 98, 283–286 (1983). [Google Scholar]
- Yafet Y., Vier D. C. & Schultz S. Conduction electron spin resonance and relaxation in the superconducting state. J. Appl. Phys. 55, 2022–2024 (1984). [Google Scholar]
- Yafet Y. Conduction electron spin relaxation in the superconducting state. Phys. Lett. A 98, 287–290 (1983). [Google Scholar]
- Beuneu F. The g factor of conduction electrons in aluminium: calculation and application to spin resonance. J. Phys. F 10, 2875 (1980). [Google Scholar]
- Nishida A. & Horai K. Investigation of the temperature dependence of the conduction-electron-spin-resonance transmission in aluminum. J. Phys. Soc. Japn 57, 4384–4390 (1988). [Google Scholar]
- Elliott R. J. Theory of the effect of spin-orbit coupling on magnetic resonance in some semiconductors. Phys. Rev. 96, 266–279 (1954). [Google Scholar]
- Fabian J. & Sarma S. D. Band-structure effects in the spin relaxation of conduction electrons (invited). J. Appl. Phys. 85, 5075–5079 (1999). [Google Scholar]
- Fabian J. & Das Sarma S. Phonon-induced spin relaxation of conduction electrons in aluminum. Phys. Rev. Lett. 83, 1211–1214 (1999). [Google Scholar]
- Tedrow P. M. & Meservey R. Direct observation of spin-state mixing in superconductors. Phys. Rev. Lett. 27, 919–921 (1971). [Google Scholar]
- Poli N. et al. Spin injection and relaxation in a mesoscopic superconductor. Phys. Rev. Lett. 100, 136601 (2008). [DOI] [PubMed] [Google Scholar]
- Jedema F. J., Heersche H. B., Filip A. T., Baselmans J. J. A. & Wees B. J. v. Electrical detection of spin precession in a metallic mesoscopic spin valve. Nature 416, 713–716 (2002). [DOI] [PubMed] [Google Scholar]
- Zaffalon M. & van Wees B. J. Spin injection, accumulation, and precession in a mesoscopic nonmagnetic metal island. Phys. Rev. B 71, 125401 (2005). [Google Scholar]
- van Staa A., Wulfhorst J., Vogel A., Merkt U. & Meier G. Spin precession in lateral all-metal spin valves: Experimental observation and theoretical description. Phys. Rev. B 77, 214416 (2008). [Google Scholar]
- Valenzuela S. O. & Tinkham M. Spin-polarized tunneling in room-temperature mesoscopic spin valves. Appl. Phys. Lett. 85, 5914–5916 (2004). [Google Scholar]
- de Visser P. J. et al. Number fluctuations of sparse quasiparticles in a superconductor. Phys. Rev. Lett. 106, 167004 (2011). [DOI] [PubMed] [Google Scholar]
- Maki K. & Tsuneto T. Pauli paramagnetism and superconducting state. Prog. Theor. Phys. 31, 945–956 (1964). [Google Scholar]
- Krishtop T., Houzet M. & Meyer J. S. Nonequilibrium spin transport in Zeeman-split superconductors. Phys. Rev. B 91, 121407 (2015). [Google Scholar]
- Silaev M., Virtanen P., Bergeret F. S. & Heikkilä T. T. Long-range spin accumulation from heat injection in mesoscopic superconductors with zeeman splitting. Phys. Rev. Lett. 114, 167002 (2015). [DOI] [PubMed] [Google Scholar]
- van Son P. C., Romijn J., Klapwijk T. M. & Mooij J. E. Inelastic scattering rate for electrons in thin aluminum films determined from the minimum frequency for microwave stimulation of superconductivity. Phys. Rev. B 29, 1503–1505 (1984). [Google Scholar]
- Santhanam P. & Prober D. E. Inelastic electron scattering mechanisms in clean aluminum films. Phys. Rev. B 29, 3733–3736 (1984). [Google Scholar]
- Pinsolle E. & Reulet B. Private communication .
- Linder J. & Robinson J. W. A. Superconducting spintronics. Nat. Phys. 11, 307–315 (2015). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figures 1-4, Supplementary Notes 1-4 and Supplementary References